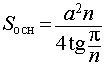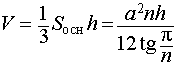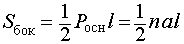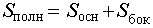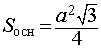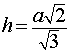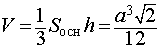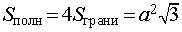Примеры решений по аналитической геометрии в пространстве
В этом разделе вы найдете бесплатные примеры решений задач по аналитической геометрии в пространстве, которые относятся к исследованию пирамиды. Обычно в такой задаче нужно найти длины ребер, углы между ребрами, уравнения граней пирамиды и их площади, объем пирамиды, угол между ребром и гранью, уравнение высоты, длину высоты пирамиды и т.д.
Решения задачи о пирамиде онлайн
Задача 1. Для пирамиды с вершинами в точках $A_1, A_2, A_3, A_4$ найти:
А) длину ребра $A_1A_2$;
Б) угол между ребрами $A_1A_2$ и $A_1A_4$;
В) уравнение плоскости $A_1A_2A_3$;
Г) площадь грани $A_1A_2A_3$;
Д) угол между ребрами $A_1A_4$ и плоскостью $A_1A_2A_3$;
Е) уравнение высоты, опущенной из точки $A_4$ на грань $A_1A_2A_3$;
Ж) объем пирамиды $A_1A_2A_3A_4$.
Задача 2. Даны координаты вершин пирамиды $$A(12;11;17), B(14;12;14), C(13;14;15), D(12;21;12).$$ Найти:
– объем пирамиды;
– площадь грани $ABC$;
– уравнение плоскости, проходящей через точки $B,C,D$;
– длину высоты пирамиды, опущенной на грань $ABC$.
Задача 3. Пирамида $АВСD$ задана координатами своих вершин: $$А(4, -1,0), B(2, 3, 4), C(-1, 4, 1), D(4, -3, 5).$$ Найдите:
1. угол между ребрами $АВ$ и $АС$,
2. уравнение ребра $АВ$,
3. уравнение грани $АВС$,
4. уравнение высоты, опущенной из вершины $D$, на грань $АВС$,
5. выясните, образуют ли векторы $АВ, АС, АD$ линейно независимую систему,
6. координаты вектора $MN$, если $М$ – середина ребра $AD$, $N$ – середина ребра $ВC$,
7. разложите вектор $MN$ по базису $AB, AC, AD$, если он таковым является.
Онлайн решение Пирамиды по координатам вершин
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
| A ( ; ; ), B ( ; ; ), C ( ; ; ), D ( ; ; ) |
Примечание: дробные числа записывайте Округлять до -го знака после запятой. Пирамиды. Правильные пирамиды. Теорема Эйлера. Формулы для объема, площади боковой поверхности и площади полной поверхности пирамиды
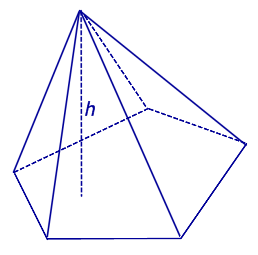
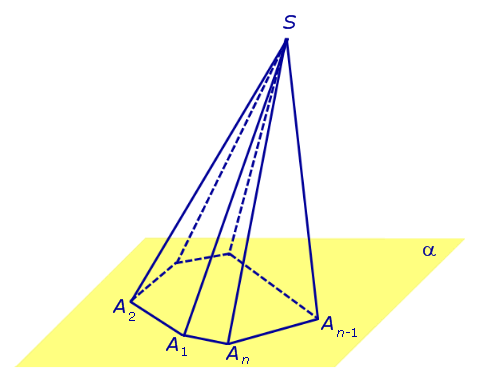
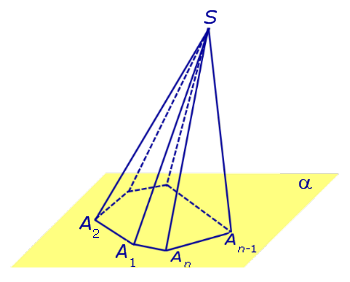
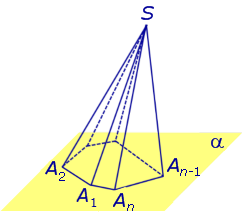
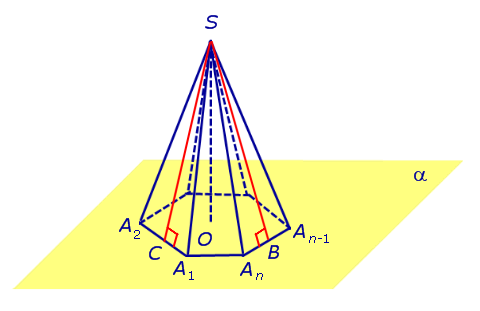
ПирамидыРассмотрим произвольную плоскость α , произвольный выпуклый n – угольник A1A2 . An , расположенный в этой плоскости, и точку S , не лежащую в плоскости α . Определение 1. Пирамидой ( n – угольной пирамидой) называют фигуру, образованную отрезками, соединяющими точку S со всеми точками многоугольника A1A2 . An (рис. 1) .
Точку S называют вершиной пирамиды. Точки A1 , A2 , . , An , S часто называют просто вершинами пирамиды. Боковые ребра и ребра основания пирамиды часто называют просто ребрами пирамиды. Множество всех боковых граней пирамиды составляет боковую поверхность пирамиды. Боковые грани и основание пирамиды часто называют просто гранями пирамиды. Полная поверхность пирамиды состоит из основания пирамиды и ее боковой поверхности. Теорема Эйлера. Для любой пирамиды справедливо равенство:
Доказательство. Заметим, что у n – угольной пирамиды (n + 1) вершина, n боковых граней, 1 основание, n ребер основания и n боковых ребер. Следовательно, у n – угольной пирамиды (n + 1) грань и 2n ребер. то теорема Эйлера доказана. Правильные пирамиды. Свойства правильной пирамиды
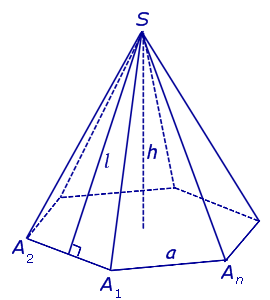
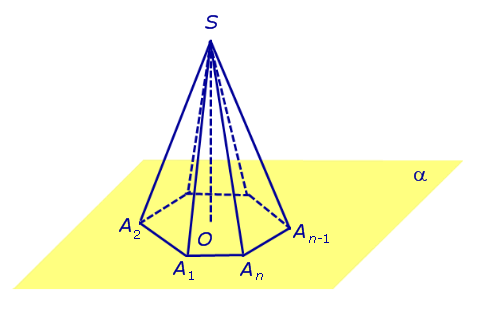
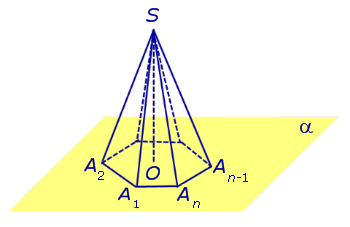
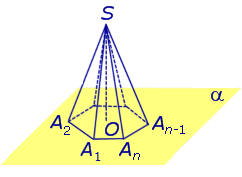
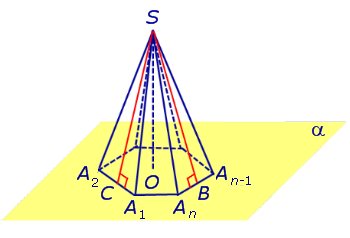
Замечание 2. Если центр основания A1A2 . An правильной пирамиды SA1A2 . An обозначить буквой O , то длина отрезка SO будет равняться высоте пирамиды. Часто и сам отрезок SO называют высотой пирамиды, опущенной из вершины S . Определение 4. Высоту боковой грани правильной пирамиды, опущенную из вершины S , называют апофемой .
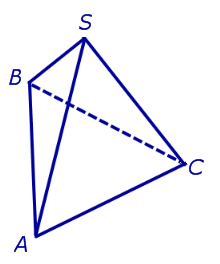
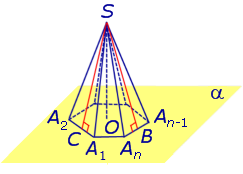
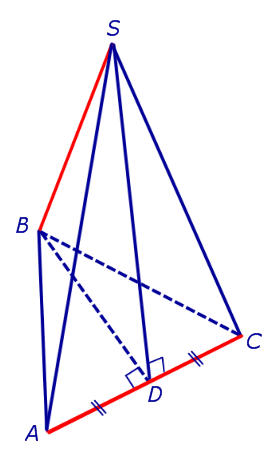
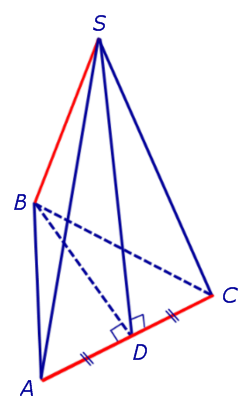
На рисунке 3 отрезок SB – апофема грани SAnAn-1 и отрезок SC – апофема грани SA2A1 . Замечание 3 . У любой правильной n – угольной пирамиды можно провести n апофем. Свойства правильной пирамиды: Все боковые ребра правильной пирамиды равны. Все боковые грани правильной пирамиды являются равными равнобедренными треугольниками. У любой правильной пирамиды все апофемы равны. Все боковые ребра правильной пирамиды образуют с плоскостью основания пирамиды равные углы. Все боковые грани правильной пирамиды образуют с плоскостью основания пирамиды равные двугранные углы. Тетраэдры. Правильные тетраэдрыОпределение 5. Произвольную треугольную пирамиду называют тетраэдром. Утверждение. У любой правильной треугольной пирамиды противоположные ребра попарно перпендикулярны. Доказательство. Рассмотрим правильную треугольную пирамиду SABC и пару ее противоположных ребер, например, AC и BS . Обозначим буквой D середину ребра AC . Поскольку отрезки BD и SD являются медианами в равнобедренных треугольниках ABC и ASC , то BD и SD перпендикулярны ребру AC (рис. 4).
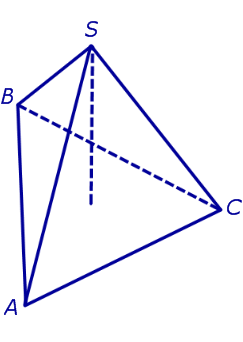
По признаку перпендикулярности прямой и плоскости заключаем, что прямая AC перпендикулярна плоскости BSD. Следовательно, прямая AC перпендикулярна прямой BS , что и требовалось доказать. Определение 6. Правильную треугольную пирамиду, у которой все ребра равны, называют правильным тетраэдром (рис. 5).
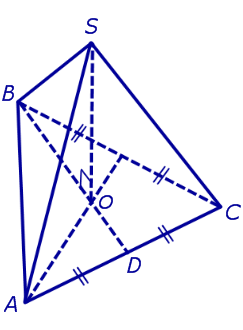
Задача. Найти высоту правильного тетраэдра с ребром a . Решение. Рассмотрим правильный тетраэдр SABC . Пусть точка O – основание перпендикуляра, опущенного из вершины S на плоскость ABC. Поскольку SABC – правильная пирамида, то точка O является точкой пересечения медиан равностороннего треугольника ABC. Следовательно,
где буквой D обозначена середина ребра AC (рис. 6).
По теореме Пифагора из треугольника BSO находим
Ответ. Формулы для объема, площади боковой и полной поверхности пирамидыВведем следующие обозначения
Тогда справедливы следующие формулы для вычисления объема, площади боковой и полной поверхности пирамиды :
Формулы для объема, площади боковой и полной поверхности:
Формулы для объема, площади боковой и полной поверхности:
Формулы для объема, площади боковой и полной поверхности: [spoiler title=”источники:”] http://mathhelpplanet.com/static.php?p=onlayn-resheniye-piramidy http://www.resolventa.ru/uslugi/uslugischoollos.htm [/spoiler] |
Онлайн решение Пирамиды по координатам вершин
Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольной пирамиды (тетраэдра):
1) чертёж пирамиды по координатам её вершин;
2) длины и уравнения рёбер, медиан, апофем, высот;
3) площади и уравнения граней;
4) система линейных неравенств, определяющих пирамиду;
5) основания и точка пересечения медиан (центроид);
6) уравнения плоскостей, проходящих через вершины параллельно противолежащим граням;
7) объём пирамиды;
8) основания, площади и уравнения биссекторов;
9) углы между рёбрами, между рёбрами и гранями, двугранные (внутренние между гранями), телесные;
10) параметры и уравнения вписанной и описанной сфер;
Внимание! Этот сервис может не работать в браузере Internet Explorer.
Запишите координаты вершин пирамиды и нажмите кнопку.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Примечание: дробные числа записывайте
через точку, а не запятую.
Округлять до -го знака после запятой.
Как найти уравнение ребра пирамиды
Внимание! Если вы делали заказ после 19.08.2021, вход в новый Личный кабинет — тут
Неправильный логин или пароль.
Укажите электронный адрес и пароль.
Пожалуйста, укажите электронный адрес или номер телефона, который вы использовали при регистрации. Вам будет отправлено письмо со ссылкой на форму изменения пароля или SMS сообщение с новым паролем.
Инструкция по изменению пароля отправлена на почту.
Чтобы зарегистрироваться, укажите ваш email и пароль
Нажимая кнопку «Зарегистрироваться» вы даете согласие на обработку персональных данных в соответствии с политикой конфеденциальности.
Пирамида в геометрии — элементы, формулы, свойства с примерами
Вы уже знакомы с пирамидой, т. е. многогранником, одна грань которого является многоугольником, а остальные грани-треугольники имеют общую вершину.
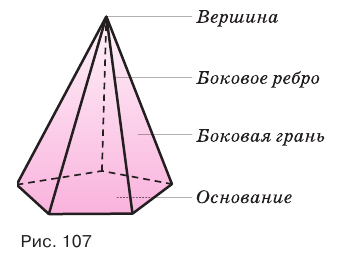
Треугольные грани пирамиды, имеющие общую вершину, называют боковыми гранями, а эту общую вершину — вершиной пирамиды. Ребра боковых граней, сходящиеся в вершине пирамиды, называют боковыми ребрами пирамиды. Многоугольник, которому не принадлежит вершина пирамиды, называют основанием пирамиды (рис. 107).
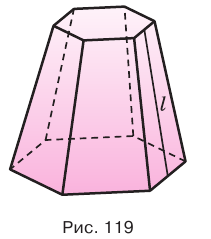
Пирамиды разделяют на треугольные, четырехугольные, пятиугольные и т. д. в зависимости от количества сторон их оснований. Пирамида, изображенная на рисунке 107, — пятиугольная, а на рисунке 108, — восьмиугольная. Треугольную пирамиду называют еще тетраэдром. У тетраэдра все грани являются треугольниками (рис. 109).
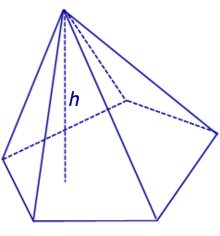
Перпендикуляр, проведенный из вершины пирамиды к плоскости ее основания, называется высотой пирамиды. На рисунке 108 показана высота 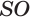
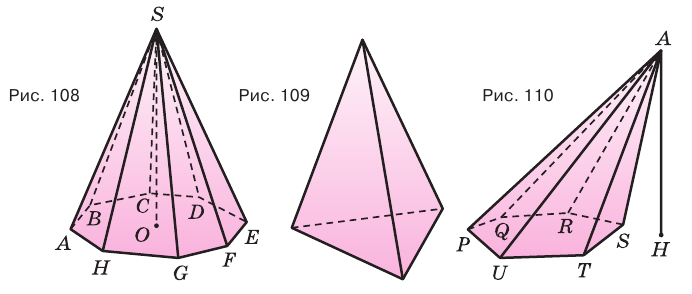
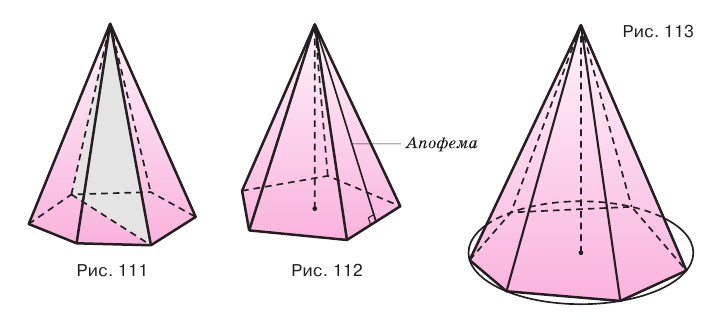
Плоскость, проходящая через два боковых ребра пирамиды, не принадлежащие одной грани, называется диагональной плоскостью, а сечение пирамиды диагональной плоскостью — диагональным сечением. На рисунке 111 показано диагональное сечение шестиугольной пирамиды.
Пирамида, основанием которой является правильный многоугольник, а основание ее высоты совпадает с центром этого многоугольника, называется правильной пирамидой (рис. 112).
Высота боковой грани правильной пирамиды, проведенная из ее вершины, называется апофемой пирамиды.
Отметим, что в правильной пирамиде:
- боковые ребра равны;
- боковые грани равны;
- апофемы, равны;
- двугранные углы при основании равны;
- двугранные углы при боковых ребрах равны;
- каждая точка высоты равноудалена от вершин основания;
- каждая точка высоты равноудалена от ребер основания;
- каждая точка высоты равноудалена от боковых граней.
Отметим, что если в пирамиде равны все:
- боковые ребра, то около ее основания можно описать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 113);
- двугранные углы при основании, то в это основание можно вписать окружность, и центр этой окружности совпадает с основанием высоты пирамиды (рис. 114).
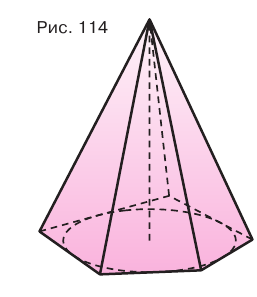
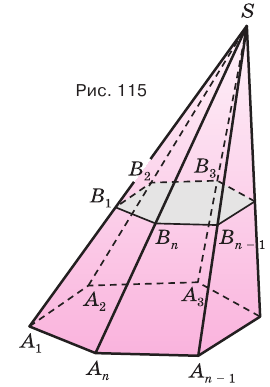
Боковые грани составляют боковую поверхность пирамиды, а боковые грани вместе с основанием — полную поверхность пирамиды.
Вы знаете, что боковая поверхность правильной пирамиды равна произведению полупериметра ее основания и апофемы.
Теорема 1.
Если пирамиду пересечь плоскостью, параллельной основанию, то:
- а) боковые ребра и высота разделяются на пропорциональные части;
- б) в сечении получается многоугольник, подобный основанию;
- в) площади сечения и основания относятся как квадраты их расстояний от вершины пирамиды.
Используя рисунок 115, докажите эту теорему самостоятельно.
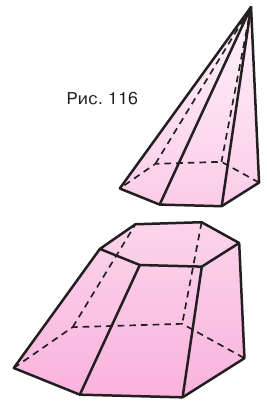
Секущая плоскость, параллельная основанию пирамиды, разделяет ее на две части (рис. 116). Одна из этих частей также является пирамидой, а другая — многогранником, который называется усеченной пирамидой.
Параллельные грани усеченной пирамиды называются ее основаниями (рис. 117). Основания усеченной пирамиды — подобные многоугольники, стороны которых попарно параллельны, поэтому ее боковые грани являются трапециями.
Высотой усеченной пирамиды называется перпендикуляр, проведенный из какой-либо точки одного основания пирамиды к плоскости другого основания.
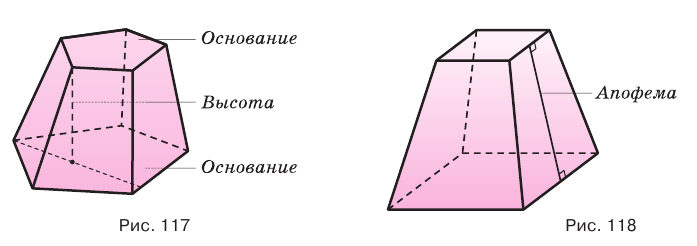
Усеченная пирамида называется правильной, если она является частью правильной пирамиды. Высота боковой грани правильной усеченной пирамиды называется апофемой усеченной пирамиды. На рисунке 118 показана четырехугольная правильная усеченная пирамида и одна из ее апофем.
Теорема 2.
Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров ее оснований и апофемы:
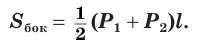
Доказательство:
Пусть есть правильная 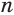 -угольная усеченная пирамида (рис. 119). Пусть
-угольная усеченная пирамида (рис. 119). Пусть 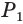 и
и 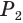 — соответственно периметры нижнего и верхнего оснований и
— соответственно периметры нижнего и верхнего оснований и 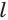 — апофема пирамиды.
— апофема пирамиды.
Боковая поверхность данной пирамиды состоит из 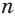 равных трапеций. Пусть
равных трапеций. Пусть 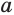 и
и 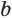 — основания одной из этих трапеций, тогда ее площадь равна
— основания одной из этих трапеций, тогда ее площадь равна 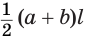 . Учитывая, что боковая поверхность пирамиды состоит из
. Учитывая, что боковая поверхность пирамиды состоит из 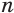 таких трапеций, получим, что
таких трапеций, получим, что
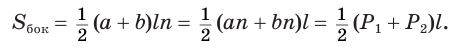
Теперь установим формулу для вычисления объема пирамиды.
Тела, имеющие равные объемы, называются равновеликими.
Теорема 3.
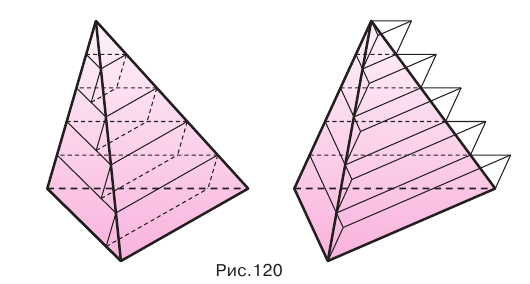
Треугольные пирамиды с равновеликими основаниями и равными высотами равновелики.
Доказательство:
Пусть есть две треугольные пирамиды с равновеликими основаниями и равными высотами (рис. 120). Разделим высоты одной и другой пирамид на 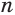 долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на
долей и через точки деления проведем плоскости, параллельные основаниям. Этим самым пирамиды разделяются на 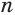 частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
частей. Для каждой части первой пирамиды построим наибольшие по объему призмы, целиком содержащиеся в пирамиде, а для каждой части другой пирамиды — наименьшие по объему призмы, целиком содержащие эту часть.
Пусть 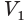 и
и 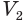 — объемы первой и второй пирамид, a
— объемы первой и второй пирамид, a  и
и  — суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в
— суммарные объемы призм, построенных для этих пирамид. При счете от оснований пирамид призма в 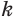 -й части первой пирамиды равновелика призме для
-й части первой пирамиды равновелика призме для 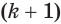 -й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем
-й части второй пирамиды, так как у этих призм равновелики основания и равные высоты. Поэтому объем  больше объема
больше объема  на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна
на объем первой призмы, у которой основанием является основание второй пирамиды, а высота равна 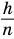 , где
, где 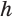 — высота пирамиды (см. рис. 120), т.е.
— высота пирамиды (см. рис. 120), т.е. 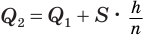 , или
, или 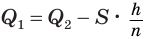 , где
, где 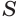 — площадь основания пирамиды. Теперь учтем, что
— площадь основания пирамиды. Теперь учтем, что 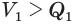 , a
, a 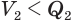 . Поэтому
. Поэтому 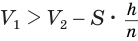 , или
, или 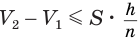 . При увеличении значения переменной
. При увеличении значения переменной 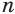 значение выражения
значение выражения 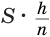 стремится к нулю, а это означает, что
стремится к нулю, а это означает, что 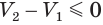 , или
, или

Такие же рассуждения можно провести, если первую и вторую пирамиды поменять ролями. В результате получим неравенство

Из неравенств (1) и (2) следует, что 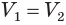 .
.
Теорема 4.
Объем пирамиды равен третьей доле произведения площади ее основания и высоты:
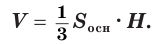
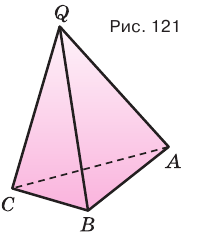
Доказательство:
Пусть есть треугольная пирамида  (рис. 121). Достроим ее до призмы
(рис. 121). Достроим ее до призмы  с основанием
с основанием 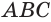 (рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида
(рис. 122). Отделим от призмы данную пирамиду, получится четырехугольная пирамида 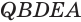 (рис. 122 и 123). Диагональная плоскость
(рис. 122 и 123). Диагональная плоскость 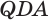 разделяет ее на две пирамиды
разделяет ее на две пирамиды  и
и  , у которых одна и та же высота, проведенная из вершины
, у которых одна и та же высота, проведенная из вершины 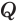 , и равные основания
, и равные основания 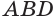 и
и 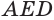 . Поэтому, в соответствии с теоремой 3, пирамиды
. Поэтому, в соответствии с теоремой 3, пирамиды  и
и  равновелики. Сравним пирамиду
равновелики. Сравним пирамиду  с данной пирамидой
с данной пирамидой  . У них равные основания
. У них равные основания 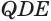 и
и  и высоты, проведенные из вершин
и высоты, проведенные из вершин 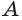 и
и 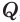 , поэтому эти пирамиды также равновелики. Получается, что все три пирамиды
, поэтому эти пирамиды также равновелики. Получается, что все три пирамиды  ,
,  и
и  равновелики. Поскольку объем призмы
равновелики. Поскольку объем призмы  равен произведению
равен произведению  площади
площади 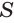 основания
основания  и высоты призмы
и высоты призмы 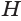 , которая равна высоте пирамиды
, которая равна высоте пирамиды  , то объем пирамиды
, то объем пирамиды  , т. е. третьей части призмы
, т. е. третьей части призмы  , равен третьей доле этого объема, т. е.
, равен третьей доле этого объема, т. е. 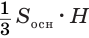 .
.
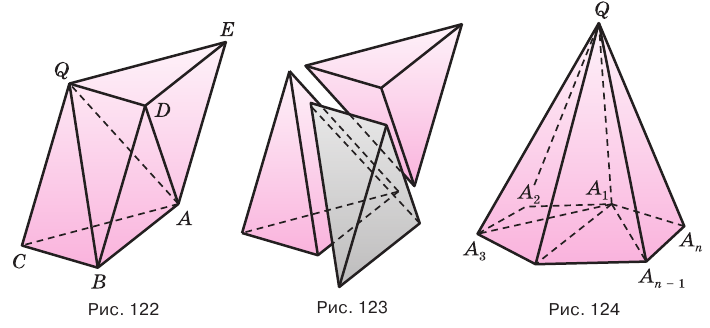
Пусть теперь есть произвольная пирамида 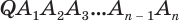 (рис. 124). Через диагонали
(рис. 124). Через диагонали 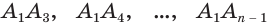 основания
основания 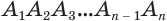 , выходящие из одной вершины
, выходящие из одной вершины 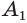 , проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды
, проведем диагональные сечения, они разделят данную пирамиду на треугольные пирамиды 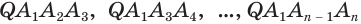 . Поскольку все они имеют общую высоту
. Поскольку все они имеют общую высоту  , то
, то
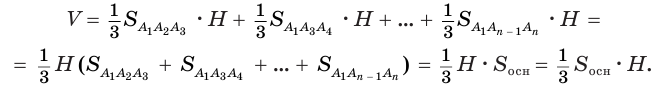
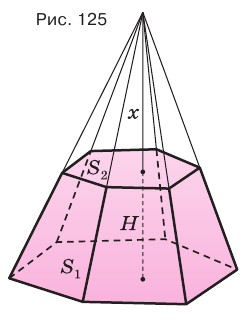
Пример:
Найдем объем усеченной пирамиды, нижнее и верхнее основания которой имеют площади 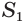 и
и 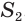 , а высота равна
, а высота равна  (рис. 125).
(рис. 125).
Для этого достроим данную усеченную пирамиду до полной. Пусть высота дополнительной пирамиды равна 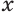 . Искомый объем
. Искомый объем 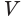 можно найти как разность объемов полной и дополнительной пирамид:
можно найти как разность объемов полной и дополнительной пирамид:
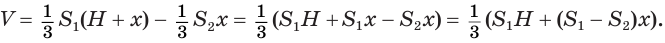
Чтобы найти высоту 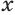 , используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
, используем установленное в теореме 1 утверждение о том, что площади сечений пирамиды относятся как квадраты их расстояний от вершины:
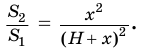
Решим это уравнение, учитывая, что  и
и  — положительные числа:
— положительные числа:
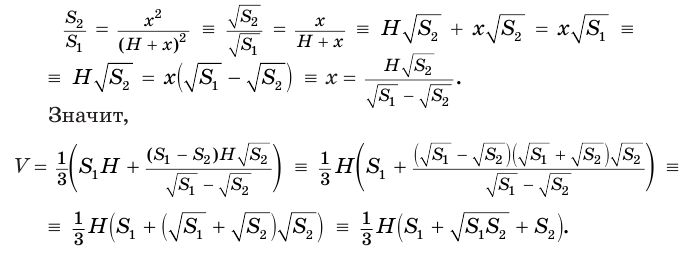
Таким образом, объем 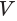 усеченной пирамиды равен третьей доле произведения высоты
усеченной пирамиды равен третьей доле произведения высоты 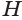 пирамиды и суммы площадей
пирамиды и суммы площадей  и
и  оснований пирамиды и их среднего геометрического
оснований пирамиды и их среднего геометрического 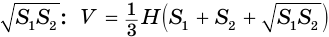 .
.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Конус в геометрии
- Сфера в геометрии
- Шар в геометрии
- Правильные многогранники в геометрии
- Возникновение геометрии
- Призма в геометрии
- Цилиндр в геометрии
- Стереометрия — формулы, определение и вычисление
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
источники:
http://reshka.feniks.help/vysshaya-matematika/analiticheskaja-geometrija/dany-koordinaty-vershin-piramidy
http://www.evkova.org/piramida
Пример 1:
Даны координаты вершин пирамиды А1А2А3А4.
Найти:
1) координаты и модули векторов А1 А2и А1 А4;
2) угол между ребрами А1 А2и А1 А4;
3) площадь грани А1 А2 А3;
4) объем пирамиды;
5) уравнение прямой А1 А2;
6) уравнение плоскости А1 А2 А3;
7) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3.
Сделать чертеж.
А1 (0; 4; -4), А2 (5; 1; -1), А3 (-1; -1; 3), А4 (0; -3; 7).
Решение от преподавателя:



Пример 2:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
1. А1 (7; 7; 3), А2 (6; 5; 8), А3 (3; 5; 8), А4 (8; 4; 1).
Решение от преподавателя:






Пример 3:

Решение от преподавателя:
Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-3)(1*2-0*3) – (y-2)((-2)*2-3*3) + (z+2)((-2)*0-3*1) = 2x + 13y – 3z-38 = 0
Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
Уравнение прямой A1A4: ![]()
γ = arcsin(0.267) = 15.486o
Уравнение высоты пирамиды через вершину A4(0,2,2)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0 ![]()
![]()
Уравнение плоскости через вершину A4(0,2,2)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: 2x + 13y – 3z-38 = 0
2(x-0)+13(y-2)-3(z-2) = 0
или
2x+13y-3z-20 = 0
Пример 4:

Решение от преподавателя:
Даны координаты пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
- Уравнение плоскости.
Если точки A1(x1; y1; z1), A2(x2; y2; z2), A3(x3; y3; z3) не лежат на одной прямой, то проходящая через них плоскость представляется уравнением:
|
= 0 |
Уравнение плоскости A1A2A3
(x-0)(3*2-8*3) – (y-1)(3*2-(-3)*3) + (z-1)(3*8-(-3)*3) = -18x – 15y + 33z-18 = 0
Упростим выражение: -6x – 5y + 11z-6 = 0
2) Угол между прямой A1A4 и плоскостью A1A2A3.
Синус угла между прямой с направляющими коэффициентами (l; m; n) и плоскостью с нормальным вектором N(A; B; C) можно найти по формуле: 
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
Уравнение прямой A1A4: 


γ = arcsin(0.193) = 11.128o
3) Уравнение высоты пирамиды через вершину A4(0,5,4)
Прямая, проходящая через точку M0(x0;y0;z0) и перпендикулярная плоскости Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется симметричными уравнениями:
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0


4) Уравнение плоскости через вершину A4(0,5,4)
Плоскость, проходящая через точку M0(x0;y0;z0) и параллельная плоскости
Ax + By + Cz + D = 0 имеет направляющий вектор (A;B;C) и, значит, представляется уравнением:
A(x-x0) + B(y-y0) + C(z-z0) = 0
Уравнение плоскости A1A2A3: -6x – 5y + 11z-6 = 0
-6(x-0)-5(y-5)+11(z-4) = 0
или
-6x-5y+11z-19 = 0
5) Координаты вектора A1A4(0;4;3)
Уравнение прямой, проходящей через точку А1(0,1,1) параллельно вектору А1А2(0,4,3) имеет вид:

Пример 5:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:




Пример 6:

Решение от преподавателя:
1) Даны координаты вершин пирамиды: A1(0,1,1), A2(3,4,4), A3(-3,9,3), A4(0,5,4)
Координаты векторов.
Координаты векторов: A1A2(3;3;3) A1A4(0;4;3)
Модули векторов (длина ребер пирамиды)
Длина вектора a(X;Y;Z) выражается через его координаты формулой: 


Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:  , где a1a2 = X1X2 + Y1Y2 + Z1Z2
, где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(3;3;3) и A1A3(0;4;3):

А1 = arccos(0,808)
Найдем площадь грани с учётом геометрического смысла векторного произведения:
S =![]()
Найдем векторное произведение
=i(3*2-8*3) – j(3*2-(-3)*3) + k(3*8-(-3)*3) = -18i – 15j + 33k

3) Объем пирамиды.
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
Координатывекторов:A1A2(3;3;3) A1A3(-3;8;2) A1A4(0;4;3) :
|
|
|
где определитель матрицы равен:
∆ = 3*(8*3-4*2)-(-3)*(3*3-4*3)+0*(3*2-8*3) = 39
Пример 7:

Решение от преподавателя:
- Угол между ребрами.
Угол между векторами a1(X1;Y1;Z1), a2(X2;Y2;Z2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2 + Z1Z2
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):
γ = arccos(0) = 90.0030 - Площадь грани
Площадь грани можно найти по формуле:
где
Найдем площадь грани A1A2A3
Найдем угол между ребрами A1A2(-2;1;3) и A1A3(3;0;2):

Площадь грани A1A2A3 - Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
|
|
|
|
|
где определитель матрицы равен:
∆ = (-2)*(0*4-0*2)-3*(1*4-0*3)+(-3)*(1*2-0*3) = -18
Пример 8:
Даны координаты вершин пирамиды А1А2А3А4 . Найти:
1) длину ребра А1А2;
2) угол между рёбрами А1А2 и А1А4 ;
3) угол между ребром А1А4 и гранью А1А2А3;
4) площадь грани А1А2А3;
5) объём пирамиды;
6) уравнение прямой А1А2;
7) уравнение плоскости А1А2А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3;
Сделать чертёж.
А1(3; 5; 4), А2(8; 7; 4), А3(5; 10; 4), А4(4; 7; 8).
Решение от преподавателя:
1) Длина ребра A1A2;

2) угол между ребрами А1А2 и А1А4;

3) угол между ребрами А1А4 и гранью А1А2А3;

Найдем уравнение стороны А1А4:

Вектор нормали: ![]() к плоскости А1А2А3.
к плоскости А1А2А3. ![]()

4) площадь грани А1А2А3;
![]()
5) объем пирамиды;

6) уравнение прямой А1А2;

7) уравнение плоскости А1А2А3;

Итак: z=4 – уравнение плоскости А1А2А3.
8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3.
A4O – высота:
Уравнение A4O:
![]()
Т.к. ![]() , то
, то
![]()
В результате получаем уравнение высоты:
![]()


Пример 9:
Даны координаты вершин пирамиды А1А2А3А4.
Найти: 1) длину ребра А1 А2;
2) угол между ребрами А1 А2и А1 А4;
3) угол между ребром А1 А4 и гранью А1 А2 А3;
4) площадь грани А1 А2 А3;
5) объем пирамиды;
6) уравнение прямой А1 А2;
7) уравнение плоскости А1 А2 А3;
8) уравнение высоты, опущенной из вершины А4 на грань А1 А2 А3. Сделать чертеж.
А1 (4; 4; 10), А2 (4; 10; 2), А3 (2; 8; 4), А4 (9; 6; 9).
Решение от преподавателя:


Гуру
(2594),
закрыт
10 лет назад
Андрей Степанов
Просветленный
(22749)
10 лет назад
1)Если известны координаты начальной и конечной точек ребра пирамиды: вычисляете координаты вектора, совпадающего с этим ребром по координатам его начальной и конечной точет, затем состаляете каноническое уравнение прямой (уравнение с направляющим вектором) . В качестве направляющего вектора возьмите найденный Вами вектор, совпадающий с ребром.
Каноническое уравнение прямой:
(x – x0)/a = (y – y0)/b =(z – z0)/c
Здесь (a, b, c) – направляющий вектор прямой.
(х0, y0, z0) – точка, лежащая на данной прямой. Можно взять любую из точек ребра (любую из вершин, между которыми проходит ребро) .
2)Объем пирамиды вычисляется по формуле:
V = (1/2)*S*h
где S – площадь основания пирамиды,
h – высота пирамиды
как найти площадь основания (грани пирамиды) см. п. 3)
Высоту найдете как перпендикуляр, опущенный на плоскость АВС и проходящий через точку D (посмотрите же наконец в учебнике – тут надо целую главу из учебника переписать и десяток формул вместе с объяснениями к ним! Учиться надо было! )
3) АDC – это треугольник. Площадь треугольника ADC равна модулю векторного произведения векторов АD и AC:
S = |[ADxAC]|
Вычисляете координаты векторов AD и AC по координатам точек А, С, D. Составляете матрицу векторного произведения, раскладываете ее по первой строке, находите вектор. Вычисляете его модуль – находите площадь.
Читайте учебники!
Успехов!


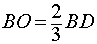
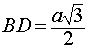 ,
,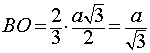 .
.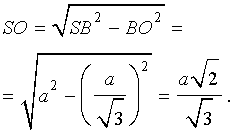
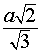
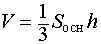 ,
,