Как найти уравнение второй диагонали ромба

даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин

даны уравнения двух сторон ромба 2x+y-2=0 и 2x+y-8=0 и ур-е его диагонали x+y-4=0. найти координаты вершин

ПОМОГИТЕ ПОЖАЛУЙСТА РЕШИТЬ. ))
нужно само решение)

я получила 2 точки с координатами, вершины из которых идет диагональ, как найти остальные точки? так то их видно и найти можно, но как это записать правильно? нужно точное решение (

Избыточное количество уравнений
х=4-у
Первые вершины:
8-2у+у-2=0 6-у=0 у=6
и. т. д
Далее рисуешь по координатам и находишь остальные точки

Даны уравнения двух сторон ромба x – 4y + 7 = 0 ; 3x + y – 5 = 0 и одна из его вершин M(5, 1)?

Математика | 10 – 11 классы

Даны уравнения двух сторон ромба x – 4y + 7 = 0 ; 3x + y – 5 = 0 и одна из его вершин M(5, 1).

Составить уравнение диагоналей ромба.

С подробным решением.

Находим вершину как точку пересечения заданных прямых :

х – 4у + 7 = 0| х – 4у + 7 = 0

3х + у – 5 = 0|x4 = 12x + 4у – 20 = 0.

– – – – – – – – – – – – – – – – – – – 13x – 13 = 0, x = 13 / 13 = 1.

Y = – 3x + 5 = – 3 * 1 + 5 = 2.

Пусть это точка А(1 ; 2).

Выясним, принадлежит ли точка М(5 ; 1) заданным прямым :

x – 4y + 7 = 0 5 – 4 * 1 + 7 = 8≠0,

3x + y – 5 = 0 3 * 5 + 1 – 5 = 11≠0.

Значит, точка М на одной диагонали с точкой А.

Находим координаты точки О – точки пересечения диагоналей как середину АМ :

О((1 + 5) / 2 = 3 ; (2 + 1) / 2 = 1, 5) = (3 ; 1, 5).

Находим уравнение прямой через точку М(5 ; 1), параллельную прямой 3х + у – 5 = 0.

Пересечение этой прямой с прямой х – 4у + 7 = 0 даст точку В.

ВМ : 3(х – 5) + 1(у – 1) = 0, 3х – 15 + у – 1 = 0 3х + у – 16 = 0.

По схеме, по которой найдена точка А, находим координаты точки В :

х – 4у + 7 = 0, х – 4у + 7 = 0,

3х + у – 16 = 0|x4 = 12х + 4у – 64 = 0.

13x – 57 = 0 x = 57 / 13, y = – 3x + 16 = – 3 * 57 / 13 + 16 = ( – 171 + 208) / 13 = 37 / 13.

По координатам точек В и О находим уравнение диагонали ВС :

Уравнение в виде y = k · x + b .

В этом уравнении :

k – угловой коэффициент прямой (k = tg(φ), φ – угол, который образует данная прямая с положительным направлением оси OX) ;

b – y – координата точки (0 ; b), в которой искомая прямая пересекает ось OY.

K = (yB – yA) / (xB – xA) = (1, 5 – (2, 846154)) / (3 – (4, 384615)) = 0, 972 ;

b = yB – k · xB = 1.

5 – (0, 972) · (3) = yA – k · xA = 2, 846154 – (0, 972) · (4, 384615) = – 1, 417 .

Искомое уравнение : y = 0, 972x – 1, 417.

Аналогично находим уравнение диагонали АМ :

k = (yB – yA) / (xB – xA) = (1 – (2)) / (5 – (1)) = – 0, 25 ;

b = yB – k · xB = 1 – ( – 0, 25) · (5) = yA – k · xA = 2 – ( – 0.

Искомое уравнение : y = – 0, 25x + 2, 25.

Сторона ромба равна 17 см, а одна из диагоналей – 12см?

Сторона ромба равна 17 см, а одна из диагоналей – 12см.

Найди вторую диагональ ромба.

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76?

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 19, а одна из диагоналей ромба равна 76.

Найдите углы ромба.

Найти координаты вершин ромба, если известны уравнения двух его сторон 2х – у + 4 = 0 и 2х – у + 10 = 0, и уравнение одной из его диагоналей х + у + 2 = 0?

Найти координаты вершин ромба, если известны уравнения двух его сторон 2х – у + 4 = 0 и 2х – у + 10 = 0, и уравнение одной из его диагоналей х + у + 2 = 0.

Одна из диагоналей ромба равна 10, а его площадь 120?

Одна из диагоналей ромба равна 10, а его площадь 120.

Найдите сторону ромба.

Сторона ромба равна 50см, а одна из диагоналей равна 96см?

Сторона ромба равна 50см, а одна из диагоналей равна 96см.

Найдите площадь ромба.

Если одна из диагоналей ромба равна стороне ромба тогда тупой угол ромба равен : 1) 135° 2)150° 3)120° 4)165° с решением?

Если одна из диагоналей ромба равна стороне ромба тогда тупой угол ромба равен : 1) 135° 2)150° 3)120° 4)165° с решением.

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68?

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68.

Найдите углы ромба.

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68?

Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно 17, а одна из диагоналей ромба равна 68.

Найдите углы ромба.

Дан ромб с диагоналями 8 см и 12 см известно что диагонали ромба лежат на координатных осях ?

Дан ромб с диагоналями 8 см и 12 см известно что диагонали ромба лежат на координатных осях .

Найдите координаты вершин ромба и длину стороны ромба .

Одна из диагоналей ромба равна его стороне?

Одна из диагоналей ромба равна его стороне.

Найти углы ромба.

На этой странице сайта, в категории Математика размещен ответ на вопрос Даны уравнения двух сторон ромба x – 4y + 7 = 0 ; 3x + y – 5 = 0 и одна из его вершин M(5, 1)?. По уровню сложности вопрос рассчитан на учащихся 10 – 11 классов. Чтобы получить дополнительную информацию по интересующей теме, воспользуйтесь автоматическим поиском в этой же категории, чтобы ознакомиться с ответами на похожие вопросы. В верхней части страницы расположена кнопка, с помощью которой можно сформулировать новый вопрос, который наиболее полно отвечает критериям поиска. Удобный интерфейс позволяет обсудить интересующую тему с посетителями в комментариях.

1)48×(1 / 6) = 8(машин) автобусов 2)48 – 8 = 40(машин) осталось 3)40×(3 / 4) = 30(машин) легковых Ответ : 30 легковых машин на автостоянке.

А)49б)37в) – 14, 1г)32, 05.

2 задача k : 100 так как 3 делим на 3 получается 1 100 : 100 = 1 итог k = 1.

Вот решение а, б и г. В решать не стала. Там слишком большие числа) Удачи)).

– x – 65 = 106 – 11 – × – 65 = 95 – × = 95 + 65 – × = 160 × = – 160.

106 – (x + 65) = 11 106 – x – 65 = 11 41 – x = 11 – x = 11 – 41 – x = – 30 x = 30.

1. = x ^ ( – 12) / x ^ ( – 15) = 1 / (x ^ ( – 3)) = x ^ 3 ; Якщо, х = 4, то 4 ^ 3 = 64. Відповідь : 64. 2. = – 5 * √16 = – 5 * 4 = – 20. Відповідь : – 20. 3. = 3125 ^ ( – 1 / 5) = 1 / (√3125 ^ (1 / 5)) = 1 / 5 = 0, 2. Відповідь : 0, 2. 4. = 2 ^..

Пусть X шаров во второй связке, тогда получим уравнение. 5x = x + 56 5x – x = 56 4x = 56 x = 56 / 4 x = 14 Во второй связке 14 шаров = > 14 + 56 = 70 шаров в первой связке. Ответ : 70 шаров ; 14 шаров.

1) 80 – 10 = 70 Ответ 70 ударив за хвалыну робыть серце дорослои людыны.

80 – 10 = 70 ударов в минуту делает сердце взрослого человека 80 > 70.

Решение математических задач

Дана система линейных уравнений:

Доказать её совместность и решить двумя способами:

• 1) Методом Гаусса;
• 2) средствами матричного исчисления.

Докажем совместность системы. Составим расширенную матрицу системы и с помощью элементарных преобразований приведем ее к ступенчатому виду.

rang(A)= rang()=3по теореме Кронекера-Капелли система совместна.

1) Решим систему по формулам Крамера:

2) Решим систему средствами матричного исчисления.

Решение системы АХ=В находится по формуле:

где А -1 – матрица, обратная к матрице А.

А -1 находится по формуле:

Даны векторы а(4; 7; 8),b (9; 1; 3),c(2; -4; 1) и d(1; -13; -13) в некотором базисе. Показать, что векторы а, в, с образуют базис, и найти координаты вектора d в этом базисе.

Векторы образуют базис, если они линейно независимы. Условием линейной независимости векторов служит следующее условие: смешанное произведение векторов отлично от нуля.

Вычислим смешанное произведение векторов .

векторы линейно независимы, а значит образуют базис.

Пусть координаты вектора в базисе следующие: . Разложение вектора по базису имеет вид: . Подставим координаты векторов:

Решим систему методом Крамера:

Ответ: координаты вектора в базисе следующие: (-2;1;0).

Даны координаты вершины пирамиды А₁А₂А₃А₄:

• 1)длину ребра А₁А₂;
• 2)угол между ребрами А₁А_{2 И}А₁А₄;
• 3)угол между ребром А₁А₄ и гранью А₁А₂А₃;
• 4)площадь грани А₁А₂А₃;
• 5)объем пирамиды;
• 6)уравнение прямой А₁А₂;
• 7)уравнение плоскости А₁А₂А₃;
• 8)уравнение высоты, опущенной из вершины А₄ на грань А₁А₂А₃. Сделать чертеж.

1) Длина ребра А₁А₂ совпадает с длиной вектора

2) Угол между ребрами А₁А_{2 И} А₁А₄ найдем используя формулу скалярного произведения:

3) Угол между прямой (L) и плоскостью () Ax+By+Cz+D=0 находится по формуле:

(m;n;p)-это координаты направляющего вектора прямой А₁А₄.

Вектор является направляющим вектором прямой А₁А₄.

Для нахождения уравнения плоскости, содержащей грань А₁А₂А₃ используем уравнение плоскости, проходящей через три точки:

4) Площадь треугольника, построенного на векторах и находится по формуле:

– векторное произведение векторов

5) Площадь пирамиды, построенной на векторах , и находится по формуле:

где – смешанное произведение векторов.

6)Для нахождения уравнение прямой А₁А₂ воспользуемся каноническим уравнением прямой:

где (m;n;p) – координаты направляющего вектора прямой А₁А₂.

Вектор является направляющим вектором прямой А₁А₂.

• 7) Уравнение плоскости А₁А₂А₃:
• 8) Высота (Н), опущенная из вершины А₄ на грань А₁А₂А₃ перпендикулярна плоскости А₁А₂А₃, а значит направляющий вектор прямой Н параллелен вектору-нормали плоскости А₁А₂А₃, поэтому в качестве направляющего вектора прямой Н можно взять вектор-нормаль плоскости . Высота Н проходит через вершину А₄, поэтому можно записать каноническое уравнение высоты:

• 1)
• 2)
• 3)
• 4)
• 5)
• 6)
• 7)
• 8)

Даны уравнения одной из сторон ромба x – 3y + 10 = 0 и одной его диагоналей x + 4y – 4 = 0; диагонали ромба пересекаются в точке P(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.

Найдем точку М – точку пересечения стороны и диагонали:

Диагонали ромба точкой пересечения делятся пополам, поэтому Р(0;1) – середина отрезка MN, где M и N противоположные вершины ромба.

Запишем уравнение стороны NK, проходящей параллельно стороне (МТ):

Если прямые параллельны, то их угловые коэффициенты равны.

– уравнение прямой NK

Найдем уравнение второй диагонали ромба (ТК). Диагонали ромба перпендикулярны, поэтому их угловые коэффициенты связаны соотношением: .

• (ТК)
• (ТК)

Найдем точку Т – точку пересечения диагонали ТК и прямой МТ:

Запишем уравнение прямой ТN, используя формулу прямой, проходящей через две точки:

– уравнение стороны ТN

Сторона КМ параллельна стороне TN, поэтому угловые коэффициенты этих прямых равны.

– уравнение стороны МК

Составить уравнение и построить линию, расстояние каждой точки которой от точки А (-1; 0) вдвое меньше расстояния ее от прямой x = -4.

Пусть М(x;y) – точка, лежащая на искомой прямой.

Расстояние от точки (х₀;у₀) до прямой Ах+Ву+С=0 определяется формулой:

Расстояние от М до прямой равно:

По условию задачи , т.е.

Возведем обе части равенства в квадрат:

– уравнение искомой линии.

График полученной линии – парабола, ветви направлены вправо, вершина параболы в точке (-2,5;0), пересечение с осью ординат в точках (0;) и (0;).

Линия задана уравнением в полярной системе координат

• 1) построить линию по точкам, начиная от до и придавая значения через промежуток ;
• 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс – с полярной осью;
• 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия.

1) Построим линию по точкам, начиная от до и придавая значения через промежуток

[spoiler title=”источники:”]

http://matematika.my-dict.ru/q/6604092_dany-uravnenia-dvuh-storon-romba-x/

http://vuzlit.com/887071/reshenie_matematicheskih_zadach

[/spoiler]

Светило науки – 9801 ответ – 46531 помощь

Все формулы длины диагоналей ромба

1. Ромб — частный случай параллелограмма

2. Противоположные стороны — параллельны

3. Все четыре стороны — равны

4. Диагонали пересекаются под прямым углом (90°)

5. Диагонали являются биссектрисами

a — сторона ромба

D — большая диагональ

d — меньшая диагональ

α — острый угол

β — тупой угол

Формулы диагоналей через сторону и угол, ( D d ):

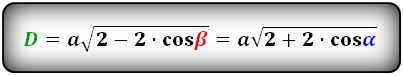
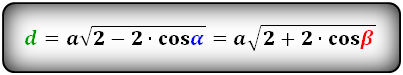
Формулы диагоналей через сторону и половинный угол, ( D d ):

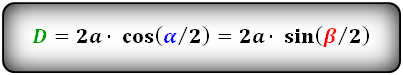
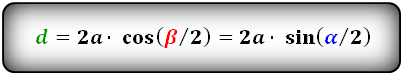
Формулы диагоналей через сторону и другую диагональ, ( D d ):

Формулы диагоналей через угол и другую диагональ, ( D d ):

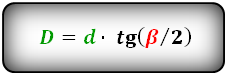
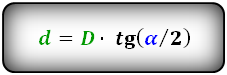
Формулы диагоналей через площадь ( D d ):

Ромб. Формулы, признаки и свойства ромба

Признаки ромба

∠BAC = ∠CAD или ∠BDA = ∠BDC

Δ ABO = Δ BCO = Δ CDO = Δ ADO

Основные свойства ромба

∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC

AC 2 + BD 2 = 4AB 2

Сторона ромба

Формулы определения длины стороны ромба:

1. Формула стороны ромба через площадь и высоту:

2. Формула стороны ромба через площадь и синус угла:

3. Формула стороны ромба через площадь и радиус вписанной окружности:

4. Формула стороны ромба через две диагонали:

5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):

6. Формула стороны ромба через большую диагональ и половинный угол:

7. Формула стороны ромба через малую диагональ и половинный угол:

8. Формула стороны ромба через периметр:

Диагонали ромба

Формулы определения длины диагонали ромба:

d ₁ = a √ 2 + 2 · cosα

d ₁ = a √ 2 — 2 · cosβ

d ₂ = a √ 2 + 2 · cosβ

d ₂ = a √ 2 — 2 · cosα

d ₁ = 2 a · cos ( α /2)

d ₁ = 2 a · sin ( β /2)

d ₂ = 2 a · sin ( α /2)

d ₂ = 2 a · cos ( β /2)

7. Формулы диагоналей через площадь и другую диагональ:

8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:

Периметр ромба

Периметром ромба называется сумма длин всех сторон ромба.

Длину стороны ромба можно найти за формулами указанными выше.

Формула определения длины периметра ромба:

Площадь ромба

Формулы определения площади ромба:

4. Формула площади ромба через две диагонали:

5. Формула площади ромба через синус угла и радиус вписанной окружности:

6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):

Окружность вписанная в ромб

Формулы определения радиуса круга вписанного в ромб:

1. Формула радиуса круга вписанного в ромб через высоту ромба:

2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:

3. Формула радиуса круга вписанного в ромб через площадь и синус угла:

4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:

5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:

6. Формула радиуса круга вписанного в ромб через две диагонали:

r =	d 1 · d 2
2√ d 1 2 + d 2 2

7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Диагонали ромба

Онлайн калькулятор для расчёта длины диагоналей ромба

Ромб — это параллелограмм у которого все стороны равны.

Свойства ромба:

• Диагонали ромба делят его углы пополам.
• Cумма углов прилежащих к одной стороне равна 180°.
• Диагонали ромба пересекаются под прямым углом (90°).
• Диагонали ромба в точке пересечения делятся попалам.
• Диагонали ромба являются биссектрисами его углов.

Диагональ — это отрезок, соединяющий несмежные вершины многоугольника или многогранника.

Формулы расчёта диагонали ромба

Длину диагоналей ромба можно посчитать несколькими способами. В зависимости от известных данных, для расчёта применяют следующие формулы:

0 Пользователей и 1 Гость просматривают эту тему.

---

---

---

---

---

---

---

---

---

---

Автор	Сообщение
	Заголовок сообщения: Найти уравнение второй диагонали ромба и сторон Добавлено: 01 янв 2015, 19:31
Начинающий Зарегистрирован: 01 янв 2015, 19:20 Сообщений: 5 Cпасибо сказано: 0 Спасибо получено: 0 раз в 0 сообщении Очков репутации: 1	Даны уравнения двух сторон ромба x+2y-13=0 и x+2y-7=0 и уравнение его диагонали x-y+2=0 . Найти уравнение второй диагонали и сторон.
Вернуться к началу

butoxors	Заголовок сообщения: Re: Найти уравнение второй диагонали ромба и сторон Добавлено: 02 янв 2015, 00:33
	для меня это тёмный лес…
Вернуться к началу

mad_math	Заголовок сообщения: Re: Найти уравнение второй диагонали ромба и сторон Добавлено: 02 янв 2015, 01:17
	butoxors писал(а): для меня это тёмный лес… А для меня скукота.
Вернуться к началу