Как найти уравнения директрис парабол – Сайт, где вы сможете решить свои вопросы

Уравнение директрисы параболы

Содержание:

Что такое директриса параболы
Каноническое уравнение параболы
Уравнение директрисы параболы, если вершина не в пересечении осей координат
- Алгоритм расчета
Фокус параболы
Примеры решения задач

Что такое директриса параболы

Определение

Директриса параболы — такая прямая, кратчайшее расстояние от которой до любой точки, принадлежащей параболе, точно такое же, как расстояние от этой точки до фокуса.

Вершина параболы — точка пересечения параболы с ее осью. Она считается началом системы координат, канонической для данной кривой.

Вершина — середина перпендикуляра, опущенного из фокуса на директрису. Таким образом, директриса перпендикулярна оси симметрии и проходит на расстоянии р/2 от вершины параболы. Число р — фокальный параметр, расстояние от фокуса до директрисы. Поскольку все параболы подобны, именно эта характеристика определяет масштаб конкретной параболы.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Каноническое уравнение параболы

Каноническое уравнение параболы:

(y^2;=;2px)

Парабола

Если расположить параболу слева от оси ординат, уравнение примет вид:

(y^2;=;-;2px)

Парабола отрицательное уравнение

Уравнение директрисы параболы, если вершина не в пересечении осей координат

Формула директрисы параболы имеет вид:

(х;=;-frac р2)

Если вершину перенести в точку ((x_0;;y_0)), отличную от начала осей координат, каноническое уравнение примет вид:

({(y;-;y_0)}^2;=;2p;times;(x;-;x_0))

Алгоритм расчета

Если уравнение параболы приведено в виде квадратного многочлена, перенесем все слагаемые с y в левую часть уравнения, а с х — в правую.
Упростим выражение, выделив полный квадрат относительно одной из переменных.
Введем новые переменные ((x_1;;y_1)), чтобы привести уравнение к каноническому виду, ведя при этом отсчет с новой точки начала координат.
Вычислим параметр р и фокус, запишем уравнение директрисы.
Вернемся к старым координатам, заменив ((x_1;;y_1)) на х и y.

Фокус параболы

Определение

Расстояние от точки фокуса (F) до любой точки параболы равняется расстоянию от этой точки к директрисе.

Фокус параболы

Чтобы составить уравнение директрисы, нужно знать фокальный параметр.

Определение

Фокальный параметр — половина длины хорды, проходящей через её фокус перпендикулярно фокальной оси.

Примеры решения задач

Задача №1

Составить уравнение директрисы параболы (y^2;=;6x).

Решение

Сравнив каноническое уравнение с данным, получим:

(2р = 6 )

(р = 3)

(frac р2;=;frac32)

Уравнение директрисы — (х;=;-frac р2.)

В данном случае оно будет выглядеть так:

(х;=;-;frac32)

Задача №2

Найти директрису параболы, заданной уравнением (4х^2;-;12х;+;y;+;6;=;0.)

Решение

Преображаем многочлен, находим полный квадрат относительно переменной х:

(4х^2;-;12х;+;y;+;6;=;0;Rightarrow;4(х^2;-;3х);+;y;+;6;=;0;Rightarrow;;4((х^2;-;2;timesfrac32х;+;frac94);-;frac94);+;y;+;6;=;0;Rightarrow;)

(;Rightarrow;(4;{(х;-;frac32)}^2;-;9;+;y;+;6;=;0;Rightarrow;y;-;3;=-;4;{(х;-;frac32)}^2;Rightarrow;{(х;-;frac32)}^2;=;-;frac14;(y;-;3))

Пусть ((y — 3)) будет (y_1), а ((х;-;frac32)) — (х_1).

Тогда, перенеся начало координат в точку ((x_1;;y_1)), получим каноническое уравнение (х_1^2;=;-{textstylefrac14}y_1).

(2р;=;frac14;Rightarrow;р;=;frac18;Rightarrow;frac р2;=;frac1{16})

Тогда уравнение директрисы — (y_1=;frac1{16}).

Заменив (y_1) на ((y — 3)), получим уравнение: (y;–;3;=;frac1{16})

Следовательно, (y;–;frac{49}{16};=;0).

В старой системе координат уравнение директрисы:

(16у — 49 = 0, у;=;frac{49}{16}).

Насколько полезной была для вас статья?

Рейтинг: 3.17 (Голосов: 18)

Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»

Текст с ошибкой:

Расскажите, что не так

Поиск по содержимому

Источник

Директриса параболы

оксана николаевна кузнецова

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

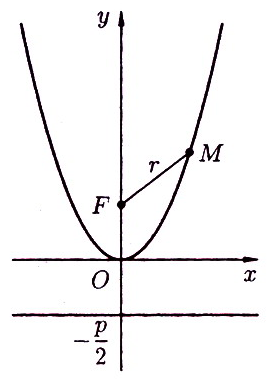
Директрисой параболы называют такую прямую, кратчайшее расстояние от которой до любой точки $M$, принадлежащей параболе точно такое же, как и расстояние от этой же точки до фокуса параболы $F$.

Фокус и директриса параболы

Рисунок 1. Фокус и директриса параболы

Основные понятия параболы

Отношение расстояний от точки $M$, лежащей на параболе, до этой прямой и от этой же точки до фокуса $F$ параболы называют эксцентриситетом параболы $ε$.

Сделаем домашку
с вашим ребенком за 380 ₽

Уделите время себе, а мы сделаем всю домашку с вашим ребенком в режиме online

Бесплатное пробное занятие

*количество мест ограничено

Чтобы найти эксцентриситет параболы, достаточно воспользоваться следующей формулой из определения эксцентриситета:
$ε =frac{MF}{MM_d}$, где точка $M_d$ – точка пересечения перпендикуляра, опущенного из точки $M$ c прямой $d$.

Определение 2

Каноническая парабола задается уравнением вида $y^2 = px$, где $p$ обязательно должно быть больше нуля.

Более часто приходится иметь дело с параболой, вершина которой не находится в точке начала координатных осей, и тогда уравнение параболы приобретает следующий вид:

$y = ax^2 + bx + c$, при этом коэффициент $a$ не равен нулю.

Чтобы найти директрису такой параболы, необходимо от такой формы перейти к канонической, ниже в примерах показано, как это сделать.

Расстояние от фокуса до директрисы параболы называется её фокальным параметром $p$.
Уравнение директрисы канонической параболы имеет следующий вид: $x=-p/2$

Алгоритм составления уравнения директрисы параболы, заданной не каноническим уравнением

«Директриса параболы» 👇

Чтобы составить уравнение директрисы параболы, вершина которой не находится на пересечении осей координат, достаточно воспользоваться следующим алгоритмом:

Перенесите все слагаемые с $y$ в левую часть уравнения, а с $x$ – в правую.
Упростите полученное выражение.
Введите дополнительные переменные чтобы прийти к каноническому виду уравнения.

Пример 1

Составьте уравнение директрисы параболы, описанной уравнением $4x^2 + 24 x – 4y + 36 = 0$

Переносим все слагаемые с $y$ в левую часть и избавляемся от множителя, получаем:

$y^2 = x^2 + 6x – y + 9$
Приводим в форму квадрата:

$(x + 3)^2 = y$
Вводим дополнительные переменные $t = x + 3$ и $y = z$
Получаем следующее уравнение: $t^2 = z$
Выражаем $p$ из канонического уравнения параболы, получаем $p = frac{y^2}{2x}$, следовательно, в нашем случае $p = frac{1}{2}$.
Уравнение директрисы приобретает следующий вид: $t = -frac{1}{4} cdot t$. Подставляем $t$ и получаем следующее уравнение директрисы $x = -3frac{1}{4}$.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Дата последнего обновления статьи: 09.12.2022

Источник

Парабола, её форма, фокус и директриса.

Начать изучение
Свойства параболы.

Начать изучение
Уравнение касательной к параболе.

Начать изучение

Парабола, её форма, фокус и директриса.

Определение.

Параболой называется линия, которая в некоторой декартовой прямоугольной системе координат определяется каноническим уравнением
$$
y^{2}=2pxlabel{ref15}
$$
при условии (p > 0).

Из уравнения eqref{ref15} вытекает, что для всех точек параболы (x geq 0). Парабола проходит через начало канонической системы координат. Эта точка называется вершиной параболы.

Форма параболы известна из курса средней школы, где она встречается в качестве графика функции (y=ax^{2}). Отличие уравнений объясняется тем, что в канонической системе координат по сравнению с прежней оси координат поменялись местами, а коэффициенты связаны равенством (2p=a^{-1}).

Фокусом параболы называется точка (F) с координатами ((p/2, 0)) в канонической системе координат.

Директрисой параболы называется прямая с уравнением (x=-p/2) в канонической системе координат ((PQ) на рис. 8.11).

парабола

Рис. 8.11. Парабола.

Свойства параболы.

Утверждение.

Расстояние от точки (M(x, y)), лежащей на параболе, до фокуса равно
$$
r=x+frac{p}{2}.label{ref16}
$$

Доказательство.

Вычислим квадрат расстояния от точки (M(x, y)) до фокуса по координатам этих точек: (r^{2}=(x-p/2)^{2}+y^{2}) и подставим сюда (y^{2}) из канонического уравнения параболы. Мы получаем
$$
r^{2}=left(x-frac{p}{2}right)^{2}+2px=left(x+frac{p}{2}right)^{2}.nonumber
$$
Отсюда в силу (x geq 0) следует равенство eqref{ref16}.

Заметим, что расстояние от точки (M) до директрисы также равно
$$
d=x+frac{p}{2}.nonumber
$$

Следовательно, мы можем сделать следующий вывод.

Утверждение.

Для того чтобы точка (M) лежала на параболе, необходимо и достаточно, чтобы она была одинаково удалена от фокуса и от директрисы этой параболы.

Доказательство.

Докажем достаточность. Пусть точка (M(x, y)) одинаково удалена от фокуса и от директрисы параболы:
$$
sqrt{left(x-frac{p}{2}right)^{2}+y^{2}}=x+frac{p}{2}.nonumber
$$

Возводя это уравнение в квадрат и приводя в нем подобные члены, мы получаем из него уравнение параболы eqref{ref15}. Это заканчивает доказательство.

Параболе приписывается эксцентриситет (varepsilon=1). В силу этого соглашения формула
$$
frac{r}{d}=varepsilonnonumber
$$
верна и для эллипса, и для гиперболы, и для параболы.

Уравнение касательной к параболе.

Выведем уравнение касательной к параболе в точке (M_{0}(x_{0}, y_{0})), лежащей на ней. Пусть (y_{0} neq 0). Через точку (M_{0}) проходит график функции (y=f(x)), целиком лежащий на параболе. (Это (y=sqrt{2px}) или же (y=-sqrt{2px}), смотря по знаку (y_{0}).) Для функции (f(x)) выполнено тождество ((f(x))^{2}=2px), дифференцируя которое имеем (2f(x)f'(x)=2p). Подставляя (x=x_{0}) и (f(x_{0})=y_{0}), находим (f'(x_{0})=p/y_{0}) Теперь мы можем написать уравнение касательной к параболе
$$
y-y_{0}=frac{p}{y_{0}}(x-x_{0}).nonumber
$$
Упростим его. Для этого раскроем скобки и вспомним, что (y_{0}^{2}=2px_{0}). Теперь уравнение касательной принимает окончательный вид
$$
yy_{0}=p(x+x_{0}).label{ref17}
$$

Заметим, что для вершины параболы, которую мы исключили, положив (y_{0} neq 0), уравнение eqref{ref17} превращается в уравнение (x=0), то есть в уравнение касательной в вершине. Поэтому уравнение eqref{ref17} справедливо для любой точки на параболе.

Утверждение.

Касательная к параболе в точке (M_{0}) есть биссектриса угла, смежного с углом между отрезком, который соединяет (M_{0}) с фокусом, и лучом., выходящим из этой точки в направлении оси параболы (рис. 8.12).

Доказательство.

Рис. 8.12. Касательная к параболе.

Рассмотрим касательную в точке (M_{0}(x_{0}, y_{0})). Из уравнения eqref{ref17} получаем ее направляющий вектор (boldsymbol{v}(y_{0}, p)). Значит, ((boldsymbol{v}, boldsymbol{e}_{1})=y_{0}) и (cos varphi_{1}=y_{0}/boldsymbol{v}). Вектор (overrightarrow{FM_{0}}) имеет компоненты (x_{0}=p/2) и (y_{0}), а потому
$$
(overrightarrow{FM_{0}}, boldsymbol{v})=x_{0}y_{0}-frac{p}{2}y_{0}+py_{0}=y_{0}(x_{0}+frac{p}{2}).nonumber
$$
Но (|overrightarrow{FM_{0}}|=x_{0}+p/2). Следовательно, (cos varphi_{2}=y_{0}/|boldsymbol{v}|). Утверждение доказано.

Заметим, что (|FN|=|FM_{0}|) (см. рис. 8.12).

Источник

Параболой
называется множество всех точек
плоскости, каждая из которых равноудалена
от заданной точки, называемой фокусом
и заданной прямой, называемой директрисой.

Каноническое
уравнение параболы имеет вид

,
(51)

где число

,
равное расстоянию от фокуса

до директрисы

,
называется параметром
параболы. Координаты фокуса

.
Точка

называется вершиной параболы, длина
отрезка

– фокальный
радиус точки

,
ось

– ось симметрии
параболы.

Рисунок
69 Рисунок 70

Уравнение директрисы

параболы имеет вид

;

фокальный радиус
вычисляется по формуле

.

В прямоугольной
системе координат парабола, заданная
каноническим уравнением

,
расположена так, как указано на рисунке
69.

Замечания.

1) Парабола,
симметричная относительно оси

и проходящая через точку

(рисунок 70), имеет уравнение

(52)

Уравнение директрисы:

,
фокальный радиус точки

параболы

.

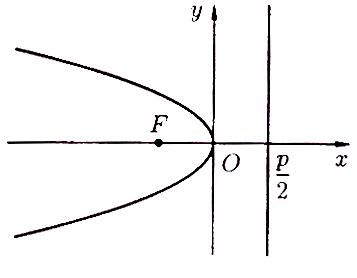
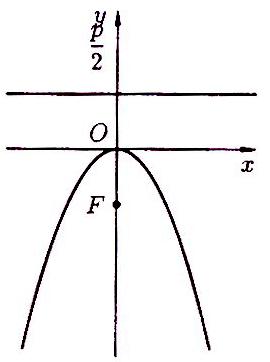
Рисунок 71 Рисунок
72

(53)

(54)

3) На рисунках 73 –
76 приведены графики парабол с осями
симметрии, параллельными координатным
осям.

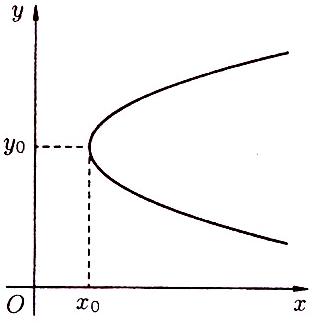
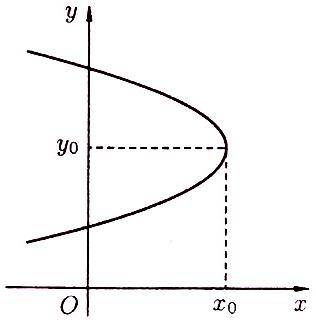
Рисунок 73 Рисунок
74

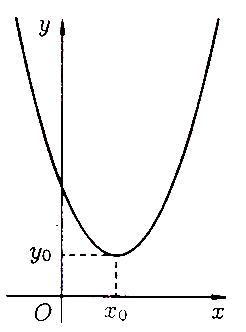
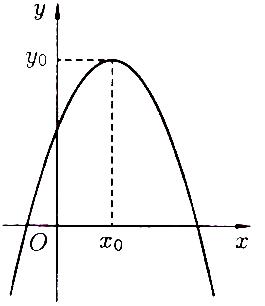
Рисунок 75 Рисунок
76

Практическое занятие № 5 Кривые второго порядка

Задача 1

Составить уравнение
окружности, проходящей через три точки

,

,

.

Решение:

Подставим координаты
точек

в данное уравнение:

.

От второго уравнения
отняли первое уравнения и результат
поставили на первое место. От третьего
уравнения отняли первое уравнения и
результат поставили на второе место.
Третье уравнение оставили без изменения.

Ответ.

Задача 2

Привести уравнение
кривой к каноническому виду и изобразить
кривую, которая определяется уравнением:

.

Решение:

,
сгруппируем переменные.

,
вынесем за скобки.

,
в скобках дополним до полного квадрата.

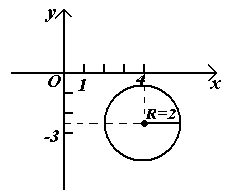
сгруппируем по
формуле полного квадрата.

Уравнение окружность
с центром в точке

и

.
Рисунок 77

Задача 3.

Установить вид
кривой по следующим уравнениям:

а)

; б)

;
в)

и сделать чертеж.

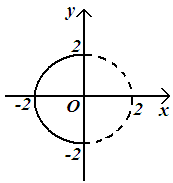
Решение.

а)

:

.
Возведем в квадрат правую и левую часть
уравнения.

.
Мы получили уравнения окружности с
центром в точке

и радиусом

Рисунок
78

б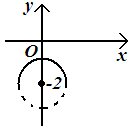
)

,

.
Возведем в квадрат правую и левую часть
уравнения.

Уравнения окружности
с центром в точке

и радиусом

.

Рисунок
79

в)

,

.
Возведем в квадрат правую и левую часть
уравнения.

.
Дополним до полного квадрата правую
часть.

.

.
Получили уравнения окружности с центром
в точке

и радиусом

.

Рисунок 80

Задача 4

Дано уравнение
эллипса

.
Найти:

а) длины его
полуосей;

б) координаты
фокусов;

в) эксцентриситет
эллипса;

г) уравнения
директрис и расстояние между ними;

д) точки эллипса,
расстояние от которых до левого фокуса

равно 12.

Р
ешение.
Разделив обе части уравнения на 1176 мы
получим уравнение эллипса в каноническом
виде

.

а) длины полуосей
эллипса

,

,
т.е.

,

.

б) координаты
фокусов. Так как

,
то

,

.
Следовательно,

и

.
Рисунок
81

в) эксцентриситет
эллипса. Так как

,
то

.

г) уравнения
директрис имеют вид

.
Тогда
,
т.е.

и

;
расстояние между ними

.

д) точки эллипса,
расстояние от которых до левого фокуса

равно 12. По формуле

находим абсциссу точки, расстояние от
которой до точки

равно 12:

,
т.е.

.
Подставляя значение

в уравнение эллипса, найдем ординату
этой точки:

,

,

.

Условию задачи
удовлетворяет точка

.

Задача 5

Показать, что
уравнение

определяет эллипс, найти его оси,
координаты центра и эксцентриситет
(изобразить эллипс).

Р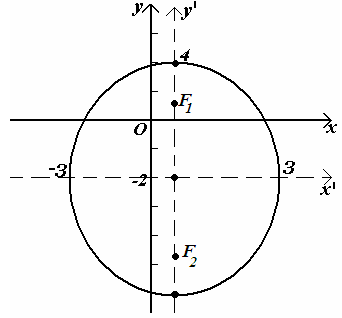
ешение.
Преобразуем данное уравнение кривой.

Сгруппировали
переменные и вынесли за скобки

коэффициенты при
наивысших степенях. В каждой скобке
выделим полный квадрат.

.Раскроем
скобки.

.
Получили уравнение эллипса,

центр находится
в точке

.
Из уравнения находим:

,

и

,

.
Рисунок 82

Поэтому

.
Эксцентриситет эллипса

.

Задача 6

Составить уравнение
эллипса с центром в начале координат и
фокусами, лежащими на оси

.
Эллипс проходит через точки

и

.

Решение.

Уравнение эллипса
имеет вид:

.
Так как эллипс проходит через точки

и

,
то их координаты удовлетворяют уравнению
эллипса:

и

.
Умножая второе равенство на

и складывая с первым, находим

,
т.е.

.
Подставляя найденное значение

в первое уравнение, получаем

,
откуда

.
Таким образом, искомое уравнение эллипса
есть

.

Ответ.

Задача 7

Составить уравнение
эллипса, если известны его эксцентриситет

,
фокус

и уравнение соответствующей директрисы

.

Решение.

По теореме:
Отношение
расстояний от любой точки эллипса до
фокуса и соответствующей директрисы
равно эксцентриситету, рассмотрим любую
точку

принадлежащую эллипсу, значит

.

;

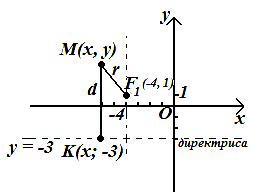
Рисунок 82

Ответ.

Задача 8
Установить вид линии, которая определяется
следующим уравнением

и
изобразить ее.

Решение.

.
Возведем в квадрат правую и левую часть
уравнения.

.
Перенесем переменную в левую часть и
выделим полный квадрат.

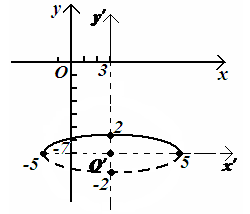
Получили уравнения
эллипса.

Центр эллипса
находится в точке

.

Рисунок 83

Задача 9

Составить уравнение
эллипса, если известны его эксцентриситет

,
фокус

и уравнение соответствующей директрисы

.

Решение.

Точка

принадлежит эллипсу, если отношение
расстояний до фокуса и соответствующей
директрисы равно

,
т.е.

.

Рисунок 84

Ответ.

.

Задача 10

Дано уравнение
гиперболы

.
Найти:

а) длины его
полуосей;

б) координаты
фокусов;

в) эксцентриситет
гиперболы;

г) уравнения
асимптот и директрис; и нарисовать
кривую.

Решение.

Разделив обе части
уравнения на 16, приведем уравнение
гиперболы к каноническому виду

:

а) длины его полуосей

,

,
т.е.

,

;

б) координаты
фокусов. Используя соотношение

,
находим

,
т.е.

.
Координаты фокусов:

и

;

в) эксцентриситет
гиперболы. По формуле

находим

;

г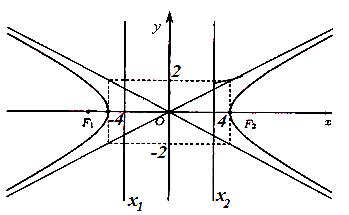
)
уравнения асимптот и

директрис найдем
по формулам

и

:

и

.

Рисунок 85

Задача 11

Составить уравнение
гиперболы, если ее фокусы лежат на оси

и расстояние между ними равно 10, а длина
действительной оси равна 8.

Решение.

Искомое уравнение
гиперболы имеет вид

.
Согласно условию

,

;

,

.
Из соотношения

найдем мнимую полуось

:

,

.
Получаем

– уравнение гиперболы.

Ответ.

Задача 12

Найти уравнение
гиперболы, фокусы которой находятся в
точках

и

,
а длина мнимой оси равна 6.

Решение.

Центр гиперболы
лежит на прямой

,
параллельной оси

.
Уравнение гиперболы имеет вид

.
По условию

,

.
Расстояние между фокусами равно 14, т.е.

,

.
Используя соотношение

,
находим

:

,

.
Центр гиперболы делит расстояние между
фокусами пополам. Поэтому

,

.
Записываем уравнение гиперболы:

.

Ответ.

Задача 13

Найти угол между
асимптотами гиперболы, если ее
эксцентриситет равен 2.

Решение.

Уравнения асимптот
гиперболы имеют вид

.
Найдем отношение

,
воспользовавшись формулами

и условием

:

.
Отсюда

,
т.е.

.
Имеем:

.
Следовательно, уравнения асимптот
гиперболы есть

и

.

Угол

между асимптотами найдем через угловые
коэффициенты по формуле

,

.

Ответ.

Задача 14

Дан эллипс

.
Найти уравнение гиперболы, вершины
которой находятся в фокусах эллипса, а
фокусы гиперболы – в вершинах данного
эллипса.

Рисунок 86

Решение.

Найдем координаты
вершин

и фокусов эллипса, записав его уравнение
в канонической форме

.
Имеем

,

;

,

.
Из соотношения

находим

:

,

.
Можно записать:

,

,

,

.
Обозначим через

,

,

– соответственно полуоси гиперболы и
половину расстояния между ее фокусами.
Тогда, согласно условиям задачи, можно
записать:

,
т.е.

и

,
т.е.

.
Из соотношения

находим

,
поэтому

,

.
Подставляя найденные значения

в уравнение

,
находим

– искомое уравнение гиперболы.

Ответ.

Задача 15

Дано уравнение
гиперболы

.

Найти:

а) длины его
полуосей;

б) координаты
фокусов;

в) эксцентриситет
гиперболы;

г) уравнения
асимптот и директрис;

д) сделать чертеж.

Решение.

– каноническое
уравнение гиперболы. Центр гиперболы
находится в точке

.

а) длины полуосей
гиперболы.

;

.

б) координаты
фокусов. Так как

.

и

.

в) эксцентриситет
гиперболы.

г) уравнения
асимптот и директрис.

– уравнения асимптот.

;

– уравнения директрис.

д) сделать чертеж

Рисунок 87

Задача 16

Составить уравнение
гиперболы, если известны ее эксцентриситет

,
фокус

и уравнение соответствующей директрисы

.

Решение.

При решении
используем теорему.
Отношение расстояний от любой точки
гиперболы до фокуса и соответствующей
директрисы равно эксцентриситету.

Так как точка

принадлежит гиперболе, то

,
где

– расстояние от точки

до

,

– расстояние от точки

до прямой

.
Таким образом

;

.

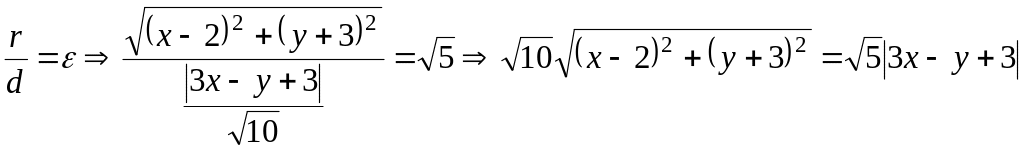
Ответ.

Задача 17

У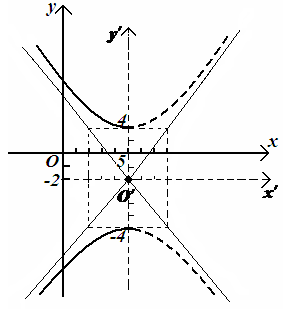
становить
и нарисовать линию, которая определяется
уравнением

.

Решение.

Рисунок
88

.
Уравнение гиперболы, центр в точке

.

З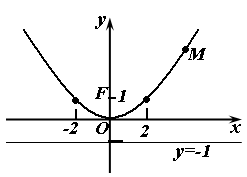
адача
18

Дана парабола

.
Найти координаты ее фокуса, уравнение
директрисы, длину фокального радиуса
точки

.

Решение.

Парабола задана
каноническим уравнением:

.
Следовательно,

,

.
Используя формулы, координаты фокуса

;
Рисунок 89

уравнение директрисы
есть

;
фокальный радиус

точки

равен

.

Ответ.

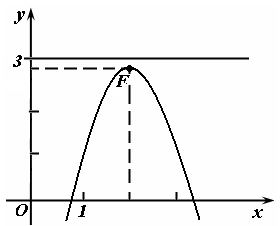
Задача 19

Найти вершину,
фокус и директрису параболы

,
построить эскиз параболы.

Решение.

Преобразуем
уравнение

,
выделив в правой части полный квадрат:

т.е.

или

– уравнение параболы с вершиной в точке

:

,

.
Прямая

является осью симметрии параболы.
Рисунок
90

Координаты фокуса

,

,
т.е.

.

Уравнение директрисы

,
т.е.

.
График изображен

на рисунке 90.

Ответ.

,

Задача 20

Составить уравнение
параболы, если даны ее фокус

и директриса

.

Решение.

Точка

лежит на параболе, если она

равноудалена от фокуса

и директрисы

Таким образом,
точка

лежит на параболе, если

:

и

.

Возведем в квадрат
правую и левую части уравнения.

Ответ.

З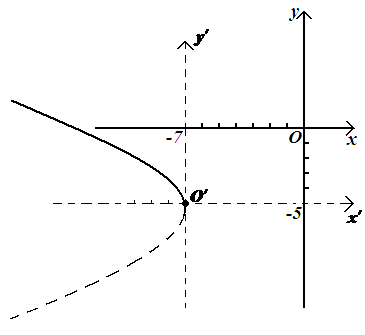
адача
21 Установить
и изобразить линию, которая определяется
уравнением:

.

Решение.
.

.Получили уравнение
параболы в каноническом виде, центр
которой находится в точке

.

.
Рисунок
91

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Парабола — это график функции описанный определённой формулой. Чтобы построить параболу нужно следовать формуле, определениям и уравнениям.

Парабола

Парабола – это множество точек плоскости, которые равноотделённые от заданной точки, что называется фокусом и заданной прямой под названием директриса.

Чтобы получить каноническое уравнение параболы, расположим директрису перпендикулярно оси , а фокус на оси так, чтобы начало координат помещался на одинаковом расстоянии от них (см. рис. 1). Обозначим через расстояние от фокуса к директрисе, тогда у фокуса будут координаты , .

Для произвольной точки параболы расстояний , а расстояние к директрисе . По определению из рис. 1 видим, что , а ${r} = sqrt{x - {pover{2}}^2} + y^2$ и поэтому:

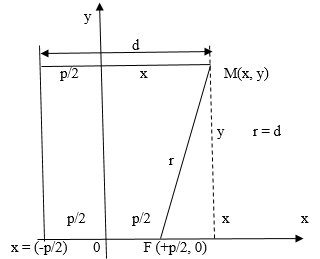
Парабола

Рис. 1

$sqrt{(x - {pover{2}})^2 + y^2} = x + {pover{2}}to{x}^2 - 2 * {pover2}}x + {p^2over{4}} + y^2 = x^2 + 2 * {pover{2}}x + {p^2over{4}}$

(1)

– каноническое уравнение параболы.

Нужна помощь в написании работы?

Мы – биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.

Заказать работу

Что такое вершина параболы

Вершина параболы – это парабола, которая проходит через точки . Если точка $M_{1}(x , y)$ принадлежит параболе, то и $M_{2}(x , -y)$ тоже принадлежит параболе, так как из:

$y^2 = 2pxto{(-y)^2 = 2px}$ .

Значит, парабола симметрична относительно оси , её график достаточно построить в первой четверти, где из канонического уравнения параболы получается, что:

Чтобы найти вершину параболы, необходимо знать формулу: .

Давайте посмотрим, как данная формула действует, допустим дано уравнение:

Тогда:

, , . Чтобы найти величины , и , в квадратном уравнении коэффициент при , при , постоянная (коэффициент без переменной) = . Если взять тот же пример, , получается, что:

, , .

Форма и характеристики параболы

Исследуем за каноническим уравнением форму и расположение параболы:

1. В уравнении переменная входит в парной степени откуда получается, что парабола симметрична относительно оси . Ось – это ось, которая симметрична параболе.

2. Так как , тогда , откуда получается, что парабола расположена справа от оси .

3. При мы имеем , то есть парабола проходит через начало координат. Точка – это вершина параболы.

4. При увеличении значений переменной модуль тоже возрастает. Изобразим параболу на рисунке:

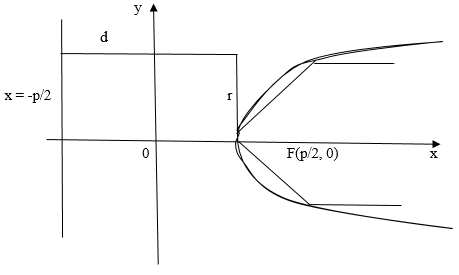
Возрастание параболы

Рис. 2

5. В полярной системе координат, у канонического уравнения параболы такой вид:

6. Уравнение , , , тоже описывают параболы:

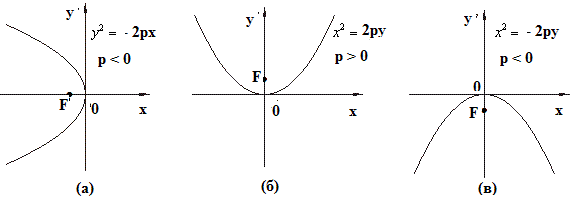
Парабола

Рис. 3

Оптическое свойство параболы

У параболы “оптическое” свойство, если: в фокусе параболы поместить источник света, тогда отбитые от параболы лучи будут параллельными оси . Это свойство учитывают при изготовлении прожекторов, зеркальных телескопов, теле- и радио антенн.

При положительном уравнении:

описывают параболу симметричную относительно с вершиной в точке , ветви которой направлены влево (рис. 3 (а)).

Аналогично изложенному, уравнение и описывают параболы с вершиной в точке симметрично относительно , ветви которой направлены соответственно вверх и вниз (см. рис. 3 (б) и (в)). Если например, уравнение решить относительно

$y = {1over{2p}}x^2$ и обозначить , тогда получим известное со школьного курса уравнение параболы . Теперь её фокусное расстояние .

Примеры решения

Задача

Найти координаты фокуса и составить уравнение директрисы параболы .

Решение

Сравнивая каноническое уравнение и данное , получим , , тогда. Так как уравнение директрисы , тогда в данном случае .

Ответ

координаты фокуса: , а уравнение директрисы параболы: .

Задача

Составить каноническое уравнение параболы:

а) с фокусом в точке ;

б) с фокусом в точке .

Решение

а). Так как фокус на положительной полуоси , тогда парабола симметрична относительно с вершиной в точке и , поэтому и согласно формуле (1) .

б). Фокус лежит на отрицательной полуоси с вершиной в точке , ветви направлены вниз, каноническое уравнение следует искать в виде . Фокусное расстояние параболы и уравнение запишется .

Ответ

а) каноническое уравнение параболы с фокусом в точке : ;

б) каноническое уравнение с фокусом в точке : .

Задача

Показать путём выделения полного квадрата, что уравнение – это уравнение параболы. Привести его к каноническому виду. Найти вершину, фокус, ось и директрису этой параболы.

Решение

Выделим относительно переменной полный квадрат

= $0to{4(x^2 - 3x)} + y + 6$ = $0to{4((x^2 - 2 * {3over{2}}x + {9over{4}}) - {9over{4}}) + y + 6$ = $0}to{4((x - {3over{2}}})^2 - 9 + y + 6$ = = $-4(x - {3over{2}})^2}to{(x - {3over{2}})^2}$ = .

Обозначим $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Тогда в результате параллельного переноса координатных осей в новое начало, то есть в точку $O_{1}({3over{2}}, 3)$ , получим каноническое уравнение параболы ${x_{1}^2} = -{1over{4}}y_{1}$ .

Ветви этой параболы направлены вниз симметрично относительно оси $O_{1}Y_{1}$ , , – фокусное расстояние. В новой системе координат фокус находится в точке , уравнение директрисы в новой системе $y_{1} = {1over{16}}$ .

Повернёмся к старым координатам при помощи замены $y_{1} = y - 3$ , $x_{1} = x - {3over{2}}$ . Уравнение оси в новой системе $x_{1} = 0$ , а в старой – уравнение оси параболы.

Уравнение директрисы в новой системе координат $y_{1} = {1over{16}}$ , а в старой .

В новой системе $X_{1}O_{1}Y_{1}$ для фокуса $F(0, -{1over{16}}) x_{1} = 0$ , $y_{1} = -{1over{16}}$ , а в старой системе $x_{F} - {3over{2}} = 0to{x_{F}} = {3over{2}}$ , $y_{F} - 3 = -{1over{16}}to{y_{F} = -{1over{16}} + 3to{y_{F}} = {47over{16}}$ , то есть .