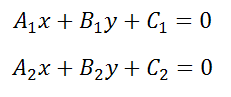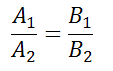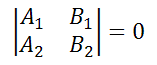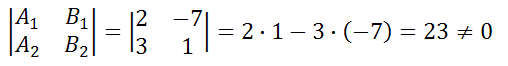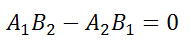Уравнение плоскости, которая проходит через две пересекающиеся или две параллельные прямые.
В этой статье собрана информация, необходимая для нахождения уравнения плоскости, проходящей через две заданные пересекающиеся или параллельные прямые. Сначала разобран принцип составления уравнения плоскости, которая проходит через две заданные прямые, после этого приведены подробные решения характерных примеров.
Навигация по странице.
Нахождение уравнения плоскости, проходящей через две пересекающиеся прямые.
Прежде чем приступать к нахождению уравнения плоскости, проходящей через две заданные пересекающиеся прямые, напомним одну теорему: в трехмерном пространстве через две пересекающиеся прямые проходит единственная плоскость. Это утверждение является следствием из двух аксиом геометрии:
- через три различные и не лежащие на одной прямой точки проходит единственная плоскость;
- если две несовпадающие точки прямой лежат в некоторой плоскости, то все точки этой прямой лежат в этой плоскости.
Таким образом, конкретную плоскость в трехмерном пространстве можно задать, указав две пересекающиеся прямые, лежащие в этой плоскости.
Теперь покажем, что плоскость, проходящая через две заданные пересекающиеся прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных прямых, а третья – на другой прямой.
Пусть заданные прямые a и b пересекаются в точке М . Отметим на прямой a две различные точки М1 и М2 (одна из них может совпадать с точкой M ), а на прямой b точку М3 , отличную от точки М . Покажем, что плоскость М1М2М3 есть плоскость, проходящая через заданные пересекающиеся прямые a и b .
Так как в плоскости М1М2М3 лежат две точки прямой a (точки М1 и М2 ), то из озвученной в начале этого пункта аксиомы следует, что все точки прямой a лежат в плоскости М1М2М3 , в частности, точка М . Тогда в плоскости М1М2М3 лежат все точки прямой b , так как две несовпадающие точки прямой b (точки М и М3 ) лежат в указанной плоскости. Следовательно, плоскость, проходящая через пересекающиеся прямые a и b , и плоскость, проходящая через три точки М1 , М2 и М2 , совпадают.
Итак, поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , заданы две пересекающиеся прямые a и b , и требуется написать уравнение плоскости, проходящей через пересекающиеся прямые a и b .
Сведем решение этой задачи к нахождению уравнения плоскости, проходящей через три точки. Для этого нужно определить координаты двух различных точек M1 и M2 , лежащих на одной из заданных пересекающихся прямых, и координаты точки M3 , лежащей на другой прямой и не являющейся точкой пересечения заданных прямых. Для нахождения координат точек М1 , М2 и М3 все средства хороши. Например, можно получить параметрические уравнения прямой a в пространстве вида . Из них видны координаты точки М1 (они получаются при ), а координаты точки М2 можно вычислить, придав параметру любое ненулевое действительное значение (к примеру, ). После этого можно получить параметрические уравнения прямой b и при некотором значении параметра вычислить координаты точки М3 , не забыв удостовериться, что она не является точкой пересечения заданных прямых (что она не лежит на прямой a ).
Будем считать, что координаты точек М1 , М2 и М3 найдены. После этого мы можем написать уравнение плоскости, проходящей через три точки и в виде . Вычислив определитель матицы вида , мы получим общее уравнение плоскости М1М2М3 , которое и будет уравнением плоскости, проходящей через две пересекающиеся прямые a и b .
Нахождение уравнения плоскости, проходящей через две параллельные прямые.
Прежде чем получить уравнение плоскости, проходящей через две заданные параллельные прямые, вспомним теорему: через две параллельные прямые проходит единственная плоскость. Эта теорема доказывается на основе аксиомы о единственной плоскости, проходящей через три заданные точки, с использованием утверждения: если одна из двух параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость.
Таким образом, мы можем задать конкретную плоскость в трехмерном пространстве, указав две параллельные прямые, лежащие в этой плоскости.
Очевидно, что плоскость, проходящая через две заданные параллельные прямые, совпадает с плоскостью, проходящей через три различные точки, две из которых лежат на одной из заданных параллельных прямых, а третья лежит на другой прямой.
Теперь можно приступать к нахождению уравнения плоскости, проходящей через две заданные параллельные прямые.
Пусть в трехмерном пространстве введена прямоугольная система координат Oxyz , заданы две параллельные прямые a и b и требуется составить уравнение плоскости, которая проходит через параллельные прямые a и b .
Эта задача, также как и задача о нахождении уравнения плоскости, проходящей через две заданные пересекающиеся прямые, сводится к составлению уравнения плоскости, проходящей через три точки. Действительно, мы можем определить координаты двух точек М1 и М2 , лежащих на одной из заданных параллельных прямых, и координаты точки М3 , лежащей на другой прямой. После этого нам лишь нужно написать уравнение плоскости, проходящей через три точки и , в виде . Это уравнение является искомым уравнением плоскости, проходящей через две заданные параллельные прямые.
Примеры составления уравнения плоскости, проходящей через две прямые.
Итак, чтобы написать уравнение плоскости, проходящей через две заданные параллельные или пересекающиеся прямые, нужно найти координаты трех различных точек, две из которых лежат на одной из заданных прямых, а третья точка – на другой прямой, после чего записать уравнение плоскости, проходящей через три точки. Покажем применение этого алгоритма при решении примеров.
Известно, что прямая a в прямоугольной системе координат Oxyz в трехмерном пространстве проходит через точку и пересекает координатную прямую Oy в точке . Напишите уравнение плоскости, проходящей через пересекающиеся прямые a и Oy .
Из условия нам известны координаты двух точек М1 и М2 , лежащих на прямой a . Очевидно, что точка лежит на координатной прямой Oy и не совпадает с точками М1 и М2 . Тогда плоскость, проходящая через три точки , и , есть плоскость, проходящая через пересекающиеся прямые a и Oy . Напишем ее уравнение:
.
Рассмотрим еще один пример, в котором координаты точек, лежащих на заданных пересекающихся прямых, не так очевидны.
Составьте уравнение плоскости, которая проходит через две пересекающиеся прямые a и b , заданные уравнениями и соответственно.
Сначала найдем координаты двух точек, лежащих на прямой a , и координаты точки, лежащей на прямой b .
Прямая, которую в прямоугольной системе координат Oxyz задают канонические уравнения прямой в пространстве вида , проходит через точку . Перейдем к параметрическим уравнениям этой прямой, чтобы определить координаты еще одной точки (обозначим ее М2 ), лежащей на ней. Имеем , примем и из параметрических уравнений прямой вычислим координаты точки М2 : . Следовательно, .
Очевидно, что прямая проходит через точку . Проверим, не является ли точка точкой пересечения заданных прямых, подставив ее координаты в уравнения прямой a : . Канонические уравнения прямой a обратились в тождества, следовательно, точка М3 лежит на прямой a и является точкой пересечения заданных прямых. Таким образом, нам нужно взять другую точку М3 , лежащую на прямой b , так как сейчас найденные точки М1 , М2 и М3 лежат на одной прямой. Для этого мы также переходим к параметрическим уравнениям прямой b : , и вычисляем координаты точки М3 , приняв : .
Теперь мы можем получить уравнение плоскости, проходящей через три точки , и , которое является искомым уравнением плоскости, проходящей через две заданные пересекающиеся прямые:
.
Не правда ли, что нахождение координат точек, лежащих на заданных прямых, является самым трудоемким процессом при составлении уравнения плоскости, проходящей через две пересекающиеся прямые?
Осталось рассмотреть пример составления уравнения плоскости, проходящей через две заданные параллельные прямые.
Напишите уравнение плоскости, проходящей через две параллельные прямые и .
По параметрическим уравнениям прямой при и вычислим координаты двух точек М1 и М2 :
Очевидно, что прямая проходит через точку .
Найдем уравнение плоскости, проходящей через три точки М1 , М2 и М3 :
Это уравнение и есть искомое уравнение плоскости, проходящей через две заданные параллельные прямые.
.
Уравнение параллельной прямой
Альтернативная формула:
Прямая, проходящая через точку M1(x1; y1) и параллельная прямой Ax+By+C=0 , представляется уравнением
назначение сервиса . Онлайн-калькулятор предназначен для составления уравнения параллельной прямой (см. также как составить уравнение перпендикулярной прямой).
Пример №2 . Написать уравнение прямой, параллельной прямой 2x + 5y = 0 и образующей вместе с осями координат треугольник, площадь которого равна 5.
Решение. Так как прямые параллельны, то уравнение искомой прямой 2x + 5y + C = 0. Площадь прямоугольного треугольника , где a и b его катеты. Найдем точки пересечения искомой прямой с осями координат:
;
.
Итак, A(-C/2,0), B(0,-C/5). Подставим в формулу для площади: . Получаем два решения: 2x + 5y + 10 = 0 и 2x + 5y – 10 = 0 .
Пример №3 . Составить уравнение прямой, проходящей через точку (-2; 5) и параллельной прямой 5x-7y-4=0 .
Решение. Данную прямую можно представить уравнением y = 5 /7x – 4 /7 (здесь a = 5 /7). Уравнение искомой прямой есть y – 5 = 5 / 7(x – (-2)), т.е. 7(y-5)=5(x+2) или 5x-7y+45=0 .
Пример №4 . Решив пример 3 (A=5, B=-7) по формуле (2), найдем 5(x+2)-7(y-5)=0.
Пример №5 . Составить уравнение прямой, проходящей через точку (-2;5) и параллельной прямой 7x+10=0.
Решение. Здесь A=7, B=0. Формула (2) дает 7(x+2)=0, т.е. x+2=0. Формула (1) неприменима, так как данное уравнение нельзя разрешить относительно y (данная прямая параллельна оси ординат).
Параллельные прямые, признаки и условия параллельности прямых
В этой статье мы расскажем о параллельных прямых, дадим определения, обозначим признаки и условия параллельности. Для наглядности теоретического материала будем использовать иллюстрации и решение типовых примеров.
Параллельные прямые: основные сведения
Параллельные прямые на плоскости – две прямые на плоскости, не имеющие общих точек.
Параллельные прямые в трехмерном пространстве – две прямые в трехмерном пространстве, лежащие в одной плоскости и не имеющие общих точек.
Необходимо обратить внимание, что для определения параллельных прямых в пространстве крайне важно уточнение «лежащие в одной плоскости»: две прямые в трехмерном пространстве, не имеющие общих точек и не лежащие в одной плоскости, являются не параллельными, а скрещивающимися.
Чтобы обозначить параллельность прямых, общепринято использовать символ ∥ . Т.е., если заданные прямые a и b параллельны, кратко записать это условие нужно так: a ‖ b . Словесно параллельность прямых обозначается следующим образом: прямые a и b параллельны, или прямая а параллельна прямой b , или прямая b параллельна прямой а .
Сформулируем утверждение, играющее важную роль в изучаемой теме.
Через точку, не принадлежащую заданной прямой проходит единственная прямая, параллельная заданной. Это утверждение невозможно доказать на базе известных аксиом планиметрии.
В случае, когда речь идет о пространстве, верна теорема:
Через любую точку пространства, не принадлежащую заданной прямой, будет проходить единственная прямая, параллельная заданной.
Эту теорему просто доказать на базе вышеуказанной аксиомы (программа геометрии 10 – 11 классов).
Параллельность прямых: признаки и условия параллельности
Признак параллельности есть достаточное условие, при выполнении которого гарантирована параллельность прямых. Иначе говоря, выполнения этого условия достаточно, чтобы подтвердить факт параллельности.
В том числе, имеют место необходимые и достаточные условия параллельности прямых на плоскости и в пространстве. Поясним: необходимое – значит то условие, выполнение которого необходимо для параллельности прямых; если оно не выполнено – прямые не являются параллельными.
Резюмируя, необходимое и достаточное условие параллельности прямых – такое условие, соблюдение которого необходимо и достаточно, чтобы прямые были параллельны между собой. С одной стороны, это признак параллельности, с другой – свойство, присущее параллельным прямым.
Перед тем, как дать точную формулировку необходимого и достаточного условия, напомним еще несколько дополнительных понятий.
Секущая прямая – прямая, пересекающая каждую из двух заданных несовпадающих прямых.
Пересекая две прямые, секущая образует восемь неразвернутых углов. Чтобы сформулировать необходимое и достаточное условие, будем использовать такие типы углов, как накрест лежащие, соответственные и односторонние. Продемонстрируем их на иллюстрации:
Если две прямые на плоскости пересекаются секущей, то для параллельности заданных прямых необходимо и достаточно, чтобы накрест лежащие углы были равными, либо были равными соответственные углы, либо сумма односторонних углов была равна 180 градусам.
Проиллюстрируем графически необходимое и достаточное условие параллельности прямых на плоскости:
Доказательство указанных условий присутствует в программе геометрии за 7 – 9 классы.
В общем, эти условия применимы и для трехмерного пространства при том, что две прямые и секущая принадлежат одной плоскости.
Укажем еще несколько теорем, часто используемых при доказательстве факта параллельности прямых.
На плоскости две прямые, параллельные третьей, параллельны между собой. Этот признак доказывается на основе аксиомы параллельности, указанной выше.
В трехмерном пространстве две прямые, параллельные третьей, параллельны между собой.
Доказательство признака изучается в программе геометрии 10 класса.
Дадим иллюстрацию указанных теорем:
Укажем еще одну пару теорем, являющихся доказательством параллельности прямых.
На плоскости две прямые, перпендикулярные третьей, параллельны между собой.
Сформулируем аналогичное для трехмерного пространства.
В трехмерном пространстве две прямые, перпендикулярные третьей, параллельны между собой.
Все указанные выше теоремы, признаки и условия позволяют удобно доказать параллельность прямых методами геометрии. Т.е., чтобы привести доказательство параллельности прямых, можно показать, что равны соответственные углы, или продемонстрировать факт, что две заданные прямые перпендикулярны третьей и т.д. Но отметим, что зачастую для доказательства параллельности прямых на плоскости или в трехмерном пространстве удобнее использовать метод координат.
Параллельность прямых в прямоугольной системе координат
В заданной прямоугольной системе координат прямая определяется уравнением прямой на плоскости одного из возможных видов. Так и прямой линии, заданной в прямоугольной системе координат в трехмерном пространстве, соответствуют некоторые уравнения прямой в пространстве.
Запишем необходимые и достаточные условия параллельности прямых в прямоугольной системе координат в зависимости от типа уравнения, описывающего заданные прямые.
Начнем с условия параллельности прямых на плоскости. Оно базируется на определениях направляющего вектора прямой и нормального вектора прямой на плоскости.
Чтобы на плоскости две несовпадающие прямые были параллельны, необходимо и достаточно, чтобы направляющие векторы заданных прямых были коллинеарными, или были коллинеарными нормальные векторы заданных прямых, или направляющий вектор одной прямой был перпендикулярен нормальному вектору другой прямой.
Становится очевидно, что условие параллельности прямых на плоскости базируется на условии коллинеарности векторов или условию перпендикулярности двух векторов. Т.е., если a → = ( a x , a y ) и b → = ( b x , b y ) являются направляющими векторами прямых a и b ;
и n b → = ( n b x , n b y ) являются нормальными векторами прямых a и b , то указанное выше необходимое и достаточное условие запишем так: a → = t · b → ⇔ a x = t · b x a y = t · b y или n a → = t · n b → ⇔ n a x = t · n b x n a y = t · n b y или a → , n b → = 0 ⇔ a x · n b x + a y · n b y = 0 , где t – некоторое действительное число. Координаты направляющих или прямых векторов определяются по заданным уравнениям прямых. Рассмотрим основные примеры.
- Прямая a в прямоугольной системе координат определяется общим уравнением прямой: A 1 x + B 1 y + C 1 = 0 ; прямая b – A 2 x + B 2 y + C 2 = 0 . Тогда нормальные векторы заданных прямых будут иметь координаты ( А 1 , В 1 ) и ( А 2 , В 2 ) соответственно. Условие параллельности запишем так:
A 1 = t · A 2 B 1 = t · B 2
- Прямая a описывается уравнением прямой с угловым коэффициентом вида y = k 1 x + b 1 . Прямая b – y = k 2 x + b 2 . Тогда нормальные векторы заданных прямых будут иметь координаты ( k 1 , – 1 ) и ( k 2 , – 1 ) соответственно, а условие параллельности запишем так:
k 1 = t · k 2 – 1 = t · ( – 1 ) ⇔ k 1 = t · k 2 t = 1 ⇔ k 1 = k 2
Таким образом, если параллельные прямые на плоскости в прямоугольной системе координат задаются уравнениями с угловыми коэффициентами, то угловые коэффициенты заданных прямых будут равны. И верно обратное утверждение: если несовпадающие прямые на плоскости в прямоугольной системе координат определяются уравнениями прямой с одинаковыми угловыми коэффициентами, то эти заданные прямые параллельны.
- Прямые a и b в прямоугольной системе координат заданы каноническими уравнениями прямой на плоскости: x – x 1 a x = y – y 1 a y и x – x 2 b x = y – y 2 b y или параметрическими уравнениями прямой на плоскости: x = x 1 + λ · a x y = y 1 + λ · a y и x = x 2 + λ · b x y = y 2 + λ · b y .
Тогда направляющие векторы заданных прямых будут: a x , a y и b x , b y соответственно, а условие параллельности запишем так:
a x = t · b x a y = t · b y
Заданы две прямые: 2 x – 3 y + 1 = 0 и x 1 2 + y 5 = 1 . Необходимо определить, параллельны ли они.
Решение
Запишем уравнение прямой в отрезках в виде общего уравнения:
x 1 2 + y 5 = 1 ⇔ 2 x + 1 5 y – 1 = 0
Мы видим, что n a → = ( 2 , – 3 ) – нормальный вектор прямой 2 x – 3 y + 1 = 0 , а n b → = 2 , 1 5 – нормальный вектор прямой x 1 2 + y 5 = 1 .
Полученные векторы не являются коллинеарными, т.к. не существует такого значения t , при котором будет верно равенство:
2 = t · 2 – 3 = t · 1 5 ⇔ t = 1 – 3 = t · 1 5 ⇔ t = 1 – 3 = 1 5
Таким образом, не выполняется необходимое и достаточное условие параллельности прямых на плоскости, а значит заданные прямые не параллельны.
Ответ: заданные прямые не параллельны.
Заданы прямые y = 2 x + 1 и x 1 = y – 4 2 . Параллельны ли они?
Решение
Преобразуем каноническое уравнение прямой x 1 = y – 4 2 к уравнению прямой с угловым коэффициентом:
x 1 = y – 4 2 ⇔ 1 · ( y – 4 ) = 2 x ⇔ y = 2 x + 4
Мы видим, что уравнения прямых y = 2 x + 1 и y = 2 x + 4 не являются одинаковыми (если бы было иначе, прямые были бы совпадающими) и угловые коэффициенты прямых равны, а значит заданные прямые являются параллельными.
Попробуем решить задачу иначе. Сначала проверим, совпадают ли заданные прямые. Используем любую точку прямой y = 2 x + 1 , например, ( 0 , 1 ) , координаты этой точки не отвечают уравнению прямой x 1 = y – 4 2 , а значит прямые не совпадают.
Следующим шагом определим выполнение условия параллельности заданных прямых.
Нормальный вектор прямой y = 2 x + 1 это вектор n a → = ( 2 , – 1 ) , а направляющий вектором второй заданной прямой является b → = ( 1 , 2 ) . Скалярное произведение этих векторов равно нулю:
n a → , b → = 2 · 1 + ( – 1 ) · 2 = 0
Таким образом, векторы перпендикулярны: это демонстрирует нам выполнение необходимого и достаточного условия параллельности исходных прямых. Т.е. заданные прямые параллельны.
Ответ: данные прямые параллельны.
Для доказательства параллельности прямых в прямоугольной системе координат трехмерного пространства используется следующее необходимое и достаточное условие.
Чтобы две несовпадающие прямые в трехмерном пространстве были параллельны, необходимо и достаточно, чтобы направляюще векторы этих прямых были коллинеарными.
Т.е. при заданных уравнениях прямых в трехмерном пространстве ответ на вопрос: параллельны они или нет, находится при помощи определения координат направляющих векторов заданных прямых, а также проверки условия их коллинеарности. Иначе говоря, если a → = ( a x , a y , a z ) и b → = ( b x , b y , b z ) являются направляющими векторами прямых a и b соответственно, то для того, чтобы они были параллельны, необходимо существование такого действительного числа t , чтобы выполнялось равенство:
a → = t · b → ⇔ a x = t · b x a y = t · b y a z = t · b z
Заданы прямые x 1 = y – 2 0 = z + 1 – 3 и x = 2 + 2 λ y = 1 z = – 3 – 6 λ . Необходимо доказать параллельность этих прямых.
Решение
Условиями задачи заданы канонические уравнения одной прямой в пространстве и параметрические уравнения другой прямой в пространстве. Направляющие векторы a → и b → заданных прямых имеют координаты: ( 1 , 0 , – 3 ) и ( 2 , 0 , – 6 ) .
1 = t · 2 0 = t · 0 – 3 = t · – 6 ⇔ t = 1 2 , то a → = 1 2 · b → .
Следовательно, необходимое и достаточное условие параллельности прямых в пространстве выполнено.
Ответ: параллельность заданных прямых доказана.
[spoiler title=”источники:”]
http://math.semestr.ru/line/parallel.php
http://zaochnik.com/spravochnik/matematika/prjamaja-ploskost/parallelnye-prjamye-priznaki-i-uslovija-parallelno/
[/spoiler]
Загрузить PDF
Загрузить PDF
Параллельными прямыми называются прямые, которые лежат в одной плоскости и никогда не пересекаются (на протяжении бесконечности).[1]
У параллельных прямых одинаковый угловой коэффициент.[2]
Угловой коэффициент равен тангенсу угла наклона прямой к оси абсцисс, а именно отношению изменения координаты y к изменению координаты х.[3]
Зачастую параллельные прямые обозначаются значком «ll». Например, запись ABllCD означает, что прямая АВ параллельна прямой CD.
-
1
Запишите формулу для вычисления углового коэффициента. Формула имеет вид k = (y2 – y1)/(x2 – x1), где x и y — координаты двух точек (любых), лежащих на прямой. Координаты первой точки, которая находится ближе к началу координат, обозначьте как (x1, y1); координаты второй точки, которая находится дальше от начала координат, обозначьте как (x2, y2).[4]
- Приведенную формулу можно сформулировать так: отношение вертикального расстояния (между двумя точками) к горизонтальному расстоянию (между двумя точками).
- Если прямая возрастает (направлена вверх), ее угловой коэффициент положительный.
- Если прямая убывает (направлена вниз), ее угловой коэффициент отрицательный.
-
2
Определите координаты двух точек, которые лежат на каждой прямой. Координаты точек записываются в виде (х,у), где х — координата по оси Х (оси абсцисс), y — координата по оси Y (оси ординат). Чтобы вычислить угловой коэффициент, отметьте по две точки на каждой прямой.[5]
- Точки легко отметить, если прямые нарисовать на координатной плоскости.
- Чтобы определить координаты точки, проведите от нее перпендикуляры (пунктиром) к каждой оси. Точка пересечения пунктирной линии с осью Х — это координата х, а точка пересечения с осью Y — координата у.
- Например: на прямой l лежат точки с координатами (1, 5) и (-2, 4), а на прямой r — точки с координатами (3, 3) и (1,-4).
-
3
Подставьте координаты точек в формулу. Затем вычтите соответствующие координаты и найдите отношение полученных результатов. При подстановке координат в формулу не перепутайте их порядок.
- Вычисление углового коэффициента прямой l: k = (5 – (-4))/(1 – (-2))
- Вычитание: k = 9/3
- Деление: k = 3
- Вычисление углового коэффициента прямой r: k = (3 – (-4))/(3 – 1) = 7/2
-
4
Сравните угловые коэффициенты. Помните, что у параллельных прямых угловые коэффициенты равны. На рисунке прямые могут казаться параллельными, но если угловые коэффициента не равны, такие прямые не параллельны друг другу.[6]
- В нашем примере 3 не равно 7/2, поэтому данные прямые не являются параллельными.
Реклама
-
1
Запишите линейное уравнение. Линейное уравнение имеет вид y = kx + b, где k — угловой коэффициент, b — координата у точки пересечения прямой с осью Y, х и у — переменные, определяемые координатами точек, которые лежат на прямой. По этой формуле можно с легкостью вычислить угловой коэффициент k.[7]
- Например: представьте уравнения 4y – 12x = 20 и у = 3x -1 в форме линейного уравнения. Уравнение 4y – 12x = 20 нужно представить в требуемой форме, а вот уравнение у = 3x – 1 уже записано как линейное уравнение.
-
2
Перепишите уравнение в виде линейного уравнения. Иногда дается уравнение, которое не представлено в форме линейного уравнения. Чтобы переписать такое уравнение, нужно выполнить ряд несложных математических операций.
- Например: перепишите уравнение 4y – 12x = 20 в форме линейного уравнения.
- К обеим сторонам уравнения прибавьте 12x: 4y – 12x + 12x = 20 + 12x
- Обе стороны уравнения разделите на 4, чтобы обособить у: 4y/4 = 12х/4 +20/4
- Уравнение в виде линейного: у = 3x + 5
-
3
Сравните угловые коэффициенты. Помните, что у параллельных прямых угловые коэффициенты равны. При помощи уравнения y = kx + b, где k — угловой коэффициент, можно найти и сравнить угловые коэффициенты двух прямых.
- В нашем примере первая прямая описывается уравнением у = 3x + 5, поэтому угловой коэффициент равен 3. Вторая прямая описывается уравнением у = 3x – 1, поэтому угловой коэффициент тоже равен 3. Так как угловые коэффициенты равны, данные прямые параллельны.
- Обратите внимание, что если у прямых с равным угловым коэффициентом коэффициент b (координата у точки пересечения прямой с осью Y) тоже одинаковый, такие прямые совпадают, а не являются параллельными.[8]
Реклама
-
1
Запишите уравнение. Следующее уравнение позволит найти уравнение параллельной (второй) прямой, если дано уравнение первой прямой и координаты точки, которая лежит на искомой параллельной (второй) прямой: y – y1= k(x – x1), где k — угловой коэффициент, x1 и y1 — координаты точки, лежащей на искомой прямой, х и у — переменные, определяемые координатами точек, которые лежат на первой прямой.[9]
- Например: найдите уравнение прямой, которая параллельна прямой у = -4x + 3 и которая проходит через точку с координатами (1, -2).
-
2
Определите угловой коэффициент данной (первой) прямой. Чтобы найти уравнение параллельной (второй) прямой, сначала нужно определить ее угловой коэффициент. Убедитесь, что уравнение дано в форме линейного уравнения, а затем найдите значение углового коэффициента k.
- Вторая прямая должна быть параллельной данной прямой, которая описывается уравнением у = -4x + 3. В этом уравнении k = -4, поэтому у второй прямой будет такой же угловой коэффициент.
-
3
В представленное уравнение подставьте координаты точки, которая лежит на второй прямой. Этот метод применим только в том случае, если даны координаты точки, лежащая на второй прямой, уравнение которой нужно найти. Не перепутайте координаты такой точки с координатами точки, которая лежит на данной (первой) прямой. Помните, что если у прямых с равным угловым коэффициентом коэффициент b (координата у точки пересечения прямой с осью Y) тоже одинаковый, такие прямые совпадают, а не являются параллельными.
- В нашем примере точка, лежащая на второй прямой, имеет координаты (1, -2).
-
4
Запишите уравнение второй прямой. Для этого известные значения подставьте в уравнение y – y1= k(x – x1). Подставьте найденный угловой коэффициент и координаты точки, лежащей на второй прямой.
- В нашем примере k = -4, а координаты точки (1, -2): у – (-2) = -4(х – 1)
-
5
Упростите уравнение. Упростите уравнение и запишите его в виде линейного уравнения. Если нарисовать вторую прямую на координатной плоскости, она будет параллельна данной (первой) прямой.
- Например: у – (-2) = -4(х – 1)
- Два минуса дают плюс: ‘у + 2 = -4(х -1)’
- Раскройте скобки: у + 2 = -4x + 4
- Из обеих сторон уравнения вычтите -2: у + 2 – 2 = -4x + 4 – 2
- Упрощенное уравнение: у = -4x + 2
Реклама
Об этой статье
Эту страницу просматривали 52 847 раз.
Была ли эта статья полезной?
Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
y1=k1x+b1
y2=k2x+b2
служит равенство их угловых коэффициентов, то есть
k1=k2
Если прямые заданы уравнениями в общем виде, то есть
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
или в другом представлении
Также это равенство можно записать в виде
Если свободные члены пропорциональны, то есть,
то прямые не только параллельны, но и совпадают.
Пример 1
Уравнения
4x+2y-8=0 и 8x+4y-16=0
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 (на графике синего цвета) и y=4x+7 (прямая красного цвета) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю
$left| {begin{array}{*{20}{c}} {{A_1}}&{{B_1}} \ {{A_2}}&{{B_2}}end{array}} right| = left| {begin{array}{*{20}{c}} 2&4 \ 3&6 end{array}} right| = 2 cdot 6 — 3 cdot 4 = 0$
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю
18677
Как составить уравнение прямой параллельной данной прямой и проходящей через данную точку?
Пусть y = k1x+b1 — данная прямая. С учётом условия параллельности прямых уравнение прямой, параллельной данной, имеет вид y = k1x+b2.
Так как эта прямая проходит через точку M(xo; yo), то её координаты удовлетворяют уравнению прямой. Подставив в уравнение xo и yo, мы найдем b:
yo= k1∙xo+ b2, откуда b2 = yo — k1∙xo.
Примеры.
1) Составить уравнение прямой, которая проходит через точку A(4;21) и параллельна прямой y=3x-8.
Решение:
Так как угловые коэффициенты у параллельных прямых равны, то k2=k1=3 и уравнение прямой, параллельной прямой y=3x-8, имеет вид y=3x+b. Так как искомая прямая проходит через точку A(4;21), подставляем в уравнение прямой координаты A (x=4; y=21):
21=3·4+b, откуда находим b: b= 21-12= 9.
Итак, уравнение прямой, параллельной прямой y=3x-8, проходящей через точку A(4;21) — y=3x+9.
Ответ: y=3x+9.
2) Написать уравнение прямой, параллельной прямой x=5, проходящей через точку B(-3; 5).
Решение:
Так как прямая x=5 параллельна оси Oy, то и параллельная ей прямая также параллельна Oy, а значит, уравнение этой прямой имеет вид x=a.
Так как эта прямая проходит через точку B(-3; 5), то её абсцисса удовлетворяет уравнению прямой: a= -3.
Итак, уравнение прямой, параллельной прямой x=5 и проходящей через точку B(-3; 5) — x= -3.
Ответ: x= -3.
3) Написать уравнение прямой, параллельной прямой y= -11, проходящей через точку K(2; 4).
Решение:
Так как прямая y= -11 параллельна оси Ox, то и параллельная ей прямая также параллельна оси Ox. Поэтому уравнение прямой имеет вид y=b.
Поскольку эта прямая проходит через точку K(2; 4), то её ордината удовлетворяет уравнению прямой: b=4.
Уравнение прямой, параллельной прямой y= -11 и проходящей через точку K(2; 4) — y=4.
Ответ: y=4.
Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
Если свободные члены пропорциональны, то есть,
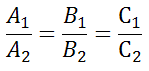
то прямые не только параллельны, но и совпадают.
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 ( на графике синего цвета ) и y=4x+7 ( прямая красного цвета ) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
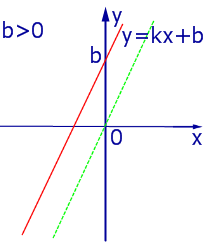
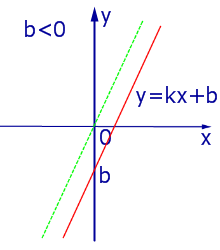
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
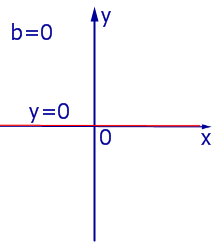
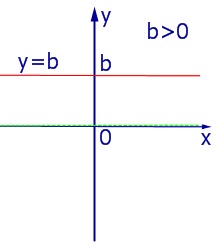
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
имеющие одинаковые угловые коэффициенты и разные свободные члены 
имеющие разные угловые коэффициенты 
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
 |
| Рис.10 |
 |
| Рис.11 |
 |
| Рис.12 |
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .
При 
Прямые, параллельные оси ординат
Прямые, параллельные оси Oy , задаются формулой
где c – произвольное число, и изображены на рис. 13, 14, 15.
 |
| Рис.13 |
 |
| Рис.14 |
 |
| Рис.15 |
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
где p, q, r – произвольные числа.
В случае, когда 
что и требовалось.
В случае, когда 
откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
и при r = 0 его решением являются точки всей плоскости:
В случае, когда 
Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
параллельна прямой, заданной уравнением (4) .
Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
перпендикулярна прямой, заданной уравнением (4) .
Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
- перпендикулярной к прямой (8).
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
График уравнения две параллельные прямые
Условие параллельности прямых
Необходимым и достаточным условием параллельности двух прямых, заданных уравнением:
служит равенство их угловых коэффициентов, то есть
Если прямые заданы уравнениями в общем виде, то есть
то условие параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны:
или в другом представлении
Также это равенство можно записать в виде
Если свободные члены пропорциональны, то есть,
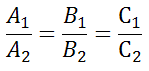
то прямые не только параллельны, но и совпадают.
4x+2y-8=0 и 8x+4y-16=0
представляют одну и ту же прямую, то есть совпадают.
Пример 2
Прямые у=4x-3 ( на графике синего цвета ) и y=4x+7 ( прямая красного цвета ) параллельны, так как у них угловые коэффициенты равны k1=k2=4
Пример 3
Прямые у=5x+1 и y=3x-4 не параллельны, так как у них угловые коэффициенты не равны, т.е. k1=5, k2=3
Пример 4
Прямые 2x+4y+7=0 и 3x+6y-5=0 параллельны, так как выражение равно нулю
Пример 5
Прямые 2x-7y+7=0 и 3x+y-5=0 не параллельны, так как выражение не равно нулю
Прямые на координатной плоскости
Линейная функция
Линейной функцией называют функцию, заданную формулой
где k и b – произвольные (вещественные) числа.
При любых значениях k и b графиком линейной функции является прямая линия .
Число k называют угловым коэффициентом прямой линии (1), а число b – свободным членом .
График линейной функции
При k > 0 линейная функция (1) возрастает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 1, 2 и 3.
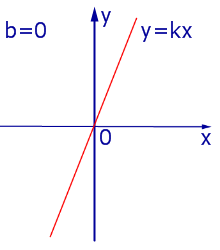 |
| Рис.1 |
 |
| Рис.2 |
 |
| Рис.3 |
При k = 0 линейная функция (1) принимает одно и тоже значение y = b при всех значениях x , а её график представляет собой прямую линию, параллельную оси абсцисс, и изображен на рис. 4, 5 и 6.
 |
| Рис.4 |
 |
| Рис.5 |
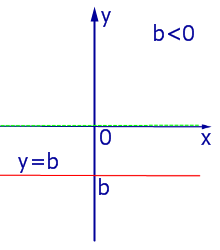 |
| Рис.6 |
При k линейная функция (1) убывает на всей числовой прямой, а её график ( прямая линия ) имеет вид, изображенный на рис. 7, 8 и 9.
имеющие одинаковые угловые коэффициенты и разные свободные члены 
имеющие разные угловые коэффициенты 
y = kx + b1 и
перпендикулярны при любых значениях свободных членов.
Угловой коэффициент прямой линии
| y = kx | (2) |
равен тангенсу угла φ , образованному (рис. 10) при повороте положительной полуоси абсцисс против часовой стрелки вокруг начала координат до прямой (2).
 |
| Рис.10 |
 |
| Рис.11 |
 |
| Рис.12 |
Прямая (1) пересекает ось Oy в точке, ордината которой (рис. 11) равна b .
При 
Прямые, параллельные оси ординат
Прямые, параллельные оси Oy , задаются формулой
| x = c , | (3) |
где c – произвольное число, и изображены на рис. 13, 14, 15.
 |
| Рис.13 |
 |
| Рис.14 |
 |
| Рис.15 |
Замечание 1 . Из рис. 13, 14, 15 вытекает, что зависимость, заданная формулой (3), функцией не является, поскольку значению аргумента x = c соответствует бесконечное множество значений y .;
Уравнение вида px + qy = r . Параллельные прямые. Перпендикулярные прямые
| px + qy = r , | (4) |
где p, q, r – произвольные числа.
В случае, когда 
что и требовалось.
В случае, когда 
откуда вытекает, что уравнение (4) задает прямую линию вида (3).
В случае, когда q = 0, p = 0, уравнение (4) имеет вид
| 0 = r , | (5) |
и при r = 0 его решением являются точки всей плоскости:
В случае, когда 
Замечание 2 . При любом значении r1 , не совпадающем с r прямая линия, заданная уравнением
| px + qy = r1 , | (6) |
параллельна прямой, заданной уравнением (4) .
Замечание 3 . При любом значении r2 прямая линия, заданная уравнением
| – qx + py = r2 , | (7) |
перпендикулярна прямой, заданной уравнением (4) .
Пример . Составить уравнение прямой, проходящей через точку с координатами (2; – 3) и
- параллельной к прямой
4x + 5y = 7 ; (8) - перпендикулярной к прямой (8).
В соответствии с формулой (6), будем искать уравнение прямой, параллельной прямой (8), в виде
| 4x + 5y = r1 , | (9) |
где r1 – некоторое число. Поскольку прямая (9) проходит через точку с координатами (2; – 3), то справедливо равенство
Итак, уравнение прямой, параллельной к прямой
В соответствии с формулой (7), будем искать уравнение прямой, перпендикулярной прямой (8), в виде
| – 5x + 4y = r2 , | (10) |
где r2 – некоторое число. Поскольку прямая (10) проходит через точку с координатами (2; – 3), то справедливо равенство
График линейной функции, его свойства и формулы
О чем эта статья:
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие функции
Функция — это зависимость «y» от «x», где «x» является переменной или аргументом функции, а «y» — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
- Табличный способ — помогает быстро определить конкретные значения без дополнительных измерений или вычислений.
- Графический способ — наглядно.
- Аналитический способ — через формулы. Компактно, и можно посчитать функцию при произвольном значении аргумента из области определения.
- Словесный способ.
График функции — это объединение всех точек, когда вместо «x» можно подставить произвольные значения и найти координаты этих точек.
Понятие линейной функции
Линейная функция — это функция вида y = kx + b, где х — независимая переменная, k, b — некоторые числа. При этом k — угловой коэффициент, b — свободный коэффициент.
Геометрический смысл коэффициента b — длина отрезка, который отсекает прямая по оси OY, считая от начала координат.
Геометрический смысл коэффициента k — угол наклона прямой к положительному направлению оси OX, считается против часовой стрелки.
Если известно конкретное значение х, можно вычислить соответствующее значение у.
Нам дана функция: у = 0,5х — 2. Значит:
- если х = 0, то у = -2;
- если х = 2, то у = -1;
- если х = 4, то у = 0;
- и т. д.
Для удобства результаты можно оформлять в виде таблицы:
| х | 0 | 2 | 4 |
| y | -2 | -1 | 0 |
Графиком линейной функции является прямая линия. Для его построения достаточно двух точек, координаты которых удовлетворяют уравнению функции.
Угловой коэффициент отвечает за угол наклона прямой, свободный коэффициент — за точку пересечения графика с осью ординат.
Буквенные множители «k» и «b» — это числовые коэффициенты функции. На их месте могут стоять любые числа: положительные, отрицательные или дроби.
Давайте потренируемся и определим для каждой функций, чему равны числовые коэффициенты «k» и «b».
| Функция | Коэффициент «k» | Коэффициент «b» |
|---|---|---|
| y = 2x + 8 | k = 2 | b = 8 |
| y = −x + 3 | k = −1 | b = 3 |
| y = 1/8x − 1 | k = 1/8 | b = −1 |
| y = 0,2x | k = 0,2 | b = 0 |
Может показаться, что в функции «y = 0,2x» нет числового коэффициента «b», но это не так. В данном случае он равен нулю. Чтобы не поддаваться сомнениям, нужно запомнить: в каждой функции типа «y = kx + b» есть коэффициенты «k» и «b».
Еще не устали? Изучать математику веселее с опытным преподавателем на курсах по математике в Skysmart!
Свойства линейной функции
- Область определения функции — множество всех действительных чисел.
- Множеством значений функции является множество всех действительных чисел.
- График линейной функции — прямая. Для построения прямой достаточно знать две точки. Положение прямой на координатной плоскости зависит от значений коэффициентов k и b.
- Функция не имеет ни наибольшего, ни наименьшего значений.
- Четность и нечетность линейной функции зависят от значений коэффициентов k и b:
b ≠ 0, k = 0, значит y = b — четная;
b = 0, k ≠ 0, значит y = kx — нечетная;
b ≠ 0, k ≠ 0, значит y = kx + b — функция общего вида;
b = 0, k = 0, значит y = 0 — как четная, так и нечетная функция. - Свойством периодичности линейная функция не обладает, потому что ее спектр непрерывен.
- График функции пересекает оси координат:
ось абсцисс ОХ — в точке (-b/k, 0);
ось ординат OY — в точке (0; b). - x=-b/k — является нулем функции.
- Если b = 0 и k = 0, то функция y = 0 обращается в ноль при любом значении переменной х.
Если b ≠ 0 и k = 0, то функция y = b не обращается в нуль ни при каких значениях переменной х. - Функция монотонно возрастает на области определения при k > 0 и монотонно убывает при k 0: функция принимает отрицательные значения на промежутке (-∞, — b /k) и положительные значения на промежутке (- b /k, +∞)
При k b /k, +∞) и положительные значения на промежутке (-∞, — b /k). - Коэффициент k характеризует угол, который образует прямая с положительным направлением Ох. Поэтому k называют угловым коэффициентом.
Если k > 0, то этот угол острый, если k
Построение линейной функции
В геометрии есть аксиома: через любые две точки можно провести прямую и притом только одну. Исходя из этой аксиомы следует: чтобы построить график функции вида «у = kx + b», достаточно найти всего две точки. А для этого нужно определить два значения х, подставить их в уравнение функции и вычислить соответствующие значения y.
Например, чтобы построить график функции y = 1 /3x + 2, можно взять х = 0 и х = 3, тогда ординаты этих точек будут равны у = 2 и у = 3. Получим точки А (0; 2) и В (3; 3). Соединим их и получим такой график:
В уравнении функции y = kx + b коэффициент k отвечает за наклон графика функции:
- если k > 0, то график наклонен вправо;
- если k 0, то график функции y = kx + b получается из y = kx со сдвигом на b единиц вверх вдоль оси OY;
- если b 1 /2x + 3, y = x + 3.
Проанализируем рисунок. Все графики наклонены вправо, потому что во всех функциях коэффициент k больше нуля. Причем, чем больше значение k, тем круче идет прямая.
В каждой функции b = 3, поэтому все графики пересекают ось OY в точке (0; 3).
Теперь рассмотрим графики функций y = -2x + 3, y = — 1 /2x + 3, y = -x + 3.
В этот раз во всех функциях коэффициент k меньше нуля, и графики функций наклонены влево. Чем больше k, тем круче идет прямая.
Коэффициент b равен трем, и графики также пересекают ось OY в точке (0; 3).
Рассмотрим графики функций y = 2x + 3, y = 2x, y = 2x — 2.
Теперь во всех уравнениях функций коэффициенты k равны. Получили три параллельные прямые.
При этом коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
- график функции y = 2x + 3 (b = 3) пересекает ось OY в точке (0; 3);
- график функции y = 2x (b = 0) пересекает ось OY в точке начала координат (0; 0);
- график функции y = 2x — 2 (b = -2) пересекает ось OY в точке (0; -2).
Прямые будут параллельными тогда, когда у них совпадают угловые коэффициенты.
Подытожим. Если мы знаем знаки коэффициентов k и b, то можем представить, как выглядит график функции y = kx + b.
Если k 0, то график функции y = kx + b выглядит так:
0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc1049363f94987951092.png» style=»height: 600px;»>
Если k > 0 и b > 0, то график функции y = kx + b выглядит так:
0 и b > 0″ src=»https://user84060.clients-cdnnow.ru/uploads/5fc104b2640e6151326286.png» style=»height: 600px;»>
Точки пересечения графика функции y = kx + b с осями координат:
- С осью ОY. Абсцисса любой точки, которая принадлежит оси ОY равна нулю. Поэтому, чтобы найти точку пересечения с осью ОY, нужно в уравнение функции вместо х подставить ноль. Тогда получим y = b.
Координаты точки пересечения с осью OY: (0; b). - С осью ОХ. Ордината любой точки, которая принадлежит оси ОХ равна нулю. Поэтому, чтобы найти точку пересечения с осью ОХ, нужно в уравнение функции вместо y подставить ноль. И получим 0 = kx + b. Значит x = — b /k.
Координаты точки пересечения с осью OX: (- b /k; 0)
Решение задач на линейную функцию
Чтобы решать задачи и строить графики линейных функций, нужно рассуждать и использовать свойства и правила выше. Давайте потренируемся!
Пример 1. Построить график функции y = kx + b, если известно, что он проходит через точку А (-3; 2) и параллелен прямой y = -4x.
- В уравнении функции y = kx + b два неизвестных параметра: k и b. Поэтому в тексте задачи нужно найти два условия, которые характеризуют график функции.
Из того, что график функции y = kx + b параллелен прямой y = -4x, следует, что k = -4. То есть уравнение функции имеет вид y = -4x + b.
Осталось найти b. Известно, что график функции y = -4x + b проходит через точку А (-3; 2). Подставим координаты точки в уравнение функции и мы получим верное равенство:
2 = -4(-3) + b
b = -10 - Таким образом, нам надо построить график функции y = -4x — 10
Мы уже знаем точку А (-3; 2), возьмем точку B (0; -10).
Поставим эти точки в координатной плоскости и соединим прямой:
Пример 2. Написать уравнение прямой, которая проходит через точки A (1; 1); B (2; 4).
- Если прямая проходит через точки с заданными координатами, значит координаты точек удовлетворяют уравнению прямой y = kx + b.
Следовательно, если координаты точек подставить в уравнение прямой, то получим верное равенство. - Подставим координаты каждой точки в уравнение y = kx + b и получим систему линейных уравнений.
- Вычтем из второго уравнения системы первое, и получим k = 3.
Подставим значение k в первое уравнение системы, и получим b = -2.
источники:
http://www.resolventa.ru/spr/algebra/degree1.htm
http://b4.cooksy.ru/articles/grafik-uravneniya-dve-parallelnye-pryamye