В статье рассмотрим такой тип уравнений плоскости как общее уравнение, получим его вид и разберем на практических примерах. Рассмотрим частные случаи и понятие общего неполного уравнения плоскости.
Общее уравнение плоскости: основные сведения
Перед началом разбора темы вспомним, что такое уравнение плоскости в прямоугольной системе координат в трёхмерном пространстве. Пусть нам дана прямоугольная система координат Oxyz в трехмерном пространстве, уравнением плоскости в заданной системе координат будет такое уравнение с тремя неизвестными x, y, и z, которому отвечали бы координаты всех точек этой плоскости и не отвечали бы координаты никаких прочих точек. Иначе говоря, подставив в уравнение плоскости координаты некоторой точки этой плоскости, получаем тождество. Если же в уравнение подставить координаты какой-то другой точки, не принадлежащей заданной плоскости, равенство станет неверным.
Также вспомним определение прямой, перпендикулярной к плоскости: прямая является перпендикулярной к заданной плоскости, если она перпендикулярна любой прямой, принадлежащей этой плоскости.
Любую плоскость, заданную в прямоугольной системе координат Oxyz трехмерного пространства, можно определить уравнением Ax + By + Cz + D = 0. В свою очередь, любое уравнение Ax + By + Cz + D = 0 определяет некоторую плоскость в данной прямоугольной системе координат трехмерного пространства. A, B, C, D – некоторые действительные числа, и числа A, B, C не равны одновременно нулю.
Теорема состоит из двух частей. Разберем доказательство каждой из них.
- Первая часть теоремы гласит, что любую заданную плоскость возможно описать уравнением вида Ax + By + Cz + D = 0. Допустим, задана некоторая плоскость и точка M0(x0, y0, z0), через которую эта плоскость проходит. Нормальным вектором этой плоскости является n→= (A, B, C). Приведем доказательство, что указанную плоскость в прямоугольной системе координат Oxyz задает уравнение Ax + By + Cz + D = 0.
Возьмем произвольную точку заданной плоскости M(x, y, z).В таком случае векторы n→= (A, B, C) и M0M→=(x-x0, y-y0, z-z0) будут перпендикулярны друг другу, а значит их скалярное произведение равно нулю:
n→, M0M→=Ax-x0+B(y-y0)+C(z-z0)=Ax+By+Cz-(Ax0+By0+Cz0)
Примем D=-(Ax0+By0+Cz0) , тогда уравнение преобразуется в следующий вид: Ax + By + Cz + D = 0. Оно и будет задавать исходную плоскость. Первая часть теоремы доказана.
- Во второй части теоремы утверждается, что любое уравнение вида Ax + By + Cz + D = 0 задает некоторую плоскость в прямоугольной системе координат Oxyz трехмерного пространства. Докажем это.
В теореме также указано, что действительные числа А, B, C одновременно не являются равными нулю. Тогда существует некоторая точка M0(x0, y0, z0), координаты которой отвечают уравнению Ax + By + Cz + D = 0, т.е. верным будет равенство Ax0 + By0 + Cz0 + D = 0. Отнимем левую и правую части этого равенства от левой и правой частей уравнения Ax + By + Cz + D = 0. Получим уравнение вида
A(x-x0) + B(y-y0) + C(z-z0) + D = 0, и оно эквивалентно уравнению Ax + By + Cz + D = 0. Докажем, что уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает некоторую плоскость.
Уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 являет собой условие, необходимое и достаточное для перпендикулярности векторов n→=(A, B, C) и M0M→=x-x0, y-y0, z-z0. Опираясь на утверждение, указанное перед теоремой, возможно утверждать, что при справедливом равенстве A(x-x0) + B(y-y0) + C(z-z0) + D = 0 множество точек M(x, y, z) задает плоскость, у которой нормальный вектор n→=(A, B, C). При этом плоскость проходит через точку M(x0, y0, z0). Иначе говоря, уравнение A(x-x0) + B(y-y0) + C(z-z0) + D = 0 задает в прямоугольной системе координат Oxyz трехмерного пространства некоторую плоскость. Таким, образом, эквивалентное этому уравнению уравнение Ax + By + Cz + D = 0 также определяет эту плоскость. Теорема доказана полностью.
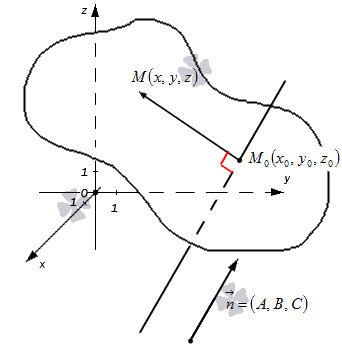
Уравнение вида Ax + By + Cz + D = 0 называют общим уравнением плоскости в прямоугольной системе координат Oxyz трехмерного пространства.
Допустим, задано некоторое общее уравнение плоскости λ·Ax+λ·By+λ·Cz+λ·D=0, где λ – некое действительное число, не равное нулю. Это уравнение также задает в прямоугольной системе координат некоторую плоскость, совпадающую с плоскостью, определяемую уравнением Ax+By+Cz+D=0, поскольку описывает то же самое множество точек трехмерного пространства. Например, уравнения x-2·y+3·z-7=0 и -2·x+4·y-23·z+14=0 задают одну и ту же плоскость, поскольку им обоим отвечают координаты одних и тех же точек трехмерного пространства.
Раскроем чуть шире смысл теорем.
В пределах заданной системы координат плоскость и общее уравнение, ее определяющее, неразрывно связаны: каждой плоскости отвечает общее уравнение плоскости вида Ax+By+Cz+D=0( при конкретных значениях чисел A, B, C, D). В свою очередь, этому уравнению отвечает заданная плоскость в заданной прямоугольной системе координат.
Укажем пример как иллюстрацию этих утверждений.
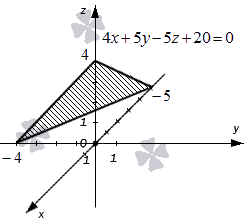
Ниже приведен чертеж, на котором изображена плоскость в фиксированной прямоугольной системе координат трехмерного пространства. Заданной плоскости отвечает общее уравнение вида 4x + 5y – 5z + 20 = 0, и ему соответствуют координаты любой точки этой плоскости. В свою очередь, уравнение 4x + 5y – 5z + 20 = 0 описывает в заданной системе координат множество точек, которые составляют изображенную плоскость.
Общее уравнение плоскости, проходящей через точку
Повторимся: точка M0(x0, y0, z0) лежит на плоскости, заданной в прямоугольной системе координат трехмерного пространства уравнением Ax+By+Cz+D=0 в том случае, когда подставив координаты точки M0(x0, y0, z0) в уравнение Ax+By+Cz+D=0, мы получим тождество.
Заданы точки M0(1, -1, -3) и N0(0, 2, -8) и плоскость, определяемая уравнением 2x+3y-z-2=0. Необходимо проверить, принадлежат ли заданные точки заданной плоскости.
Решение
Подставим координаты точки М0 в исходной уравнение плоскости:
2·1+3·(-1)-(-3)-2=0⇔0=0
Мы видим, что получено верное равенство, значит точка M0(1, -1, -3) принадлежит заданной плоскости.
Аналогично проверим точку N0. Подставим ее координаты в исходное уравнение:
2·0+3·2-(-8)-2=0⇔12=0
Равенство неверно. Таким, образом, точка N0(0, 2, -8) не принадлежит заданной плоскости.
Ответ: точка М0 принадлежит заданной плоскости; точка N0 – не принадлежит.
Приведенное выше доказательство теоремы об общем уравнении дает нам возможность использовать важный факт: вектор n→=(A, B, C) – нормальный вектор для плоскости, определяемой уравнением Ax+By+Cz+D=0. Так, если нам известен вид общего уравнения, то возможно записать координаты нормального вектора заданной плоскости.
В прямоугольной системе координат задана плоскость 2x+3y-z+5=0. Необходимо записать координаты всех нормальных векторов заданной плоскости.
Решение
Мы знаем, что заданные общим уравнением коэффициенты при переменных x, y, z служат координатами нормального вектора заданной плоскости. Тогда, нормальный вектор n→ исходной плоскости имеет координаты 2, 3, -1 . В свою очередь, множество нормальных векторов запишем так:
λ·n→=λ·2, λ·3, -λ, λ∈R, λ≠0
Ответ: λ·2, λ·3, -λ, λ∈R, λ≠0
Разберем обратную задачу, когда требуется составить уравнение плоскости по заданным координатам нормального вектора.
Очевидным фактом является то, что нормальный вектор n→=(A, B, C)является нормальным вектором бесконечного множества параллельных плоскостей. Поэтому для обозначения конкретной плоскости введем дополнительное условие: зададим некоторую точку M0(x0, y0, z0), принадлежащую плоскости. Так, задавая в условии нормальный вектор и некоторую точку плоскости, мы ее зафиксировали.
Общее уравнение плоскости с нормальным вектором n→=(A, B, C) будет выглядеть так: Ax+By+Cz+D=0. По условию задачи точка M0(x0, y0, z0) принадлежит заданной плоскости, т.е. ее координаты отвечают уравнению плоскости, а значит верно равенство:Ax0+By0+Cz0+D=0
Вычитая соответственно правые и левые части исходного уравнения и уравнения Ax0+By0+Cz0+D=0, получим уравнение вида A(x-x0)+B(y-y0)+C(z-z0)=0. Оно и будет уравнением плоскости, проходящей через точку M0(x0, y0, z0) и имеющей нормальный вектор n→=(A, B, C).
Возможно получить это уравнение другим способом.
Очевидным фактом является то, что все точки М (x, y, z) трехмерного пространства задают данную плоскость тогда и только тогда, когда векторы n→=(A, B, C) и M0M→=(x-x0, y-y0, z-z0) перпендикулярны или, иначе говоря, когда скалярное произведение этих векторов равно нулю:
n→, M0M→=A(x-x0)+B(y-y0)+C(z-z0)=0
Задана точка М0(-1, 2, -3), через которую в прямоугольной системе координат проходит плоскость, а также задан нормальный вектор этой плоскости n→=(3, 7, -5). Необходимо записать уравнение заданной плоскости.
Решение
Рассмотрим два способа решения.
- Исходные условия позволяют получить следующие данные:
x0=-1, y0=2, z0=-3, A=3, B=7, C=-5
Подставим их в общее уравнение плоскости, проходящей через точку, т.е. в A(x-x0)+B(y-y0)+C(z-z0)=0
И получим:
3(x-(-1))+7(y-2)-5(z-(-3))=0⇔3x+7y-5z-26=0
- Допустим, М (x, y, z) – некоторая точки заданной плоскости. Определим координаты вектора M0M→ по координатам точек начала и конца:
M0M→=(x-x0, y-y0, z-z0)=(x+1, y-2, z+3)
Чтобы получить искомое общее уравнение плоскости, необходимо также воспользоваться необходимым и достаточным условием перпендикулярности векторов и тогда:
n→, M0M→=0⇔3(x+1)+7(y-2)-5(z+3)=0⇔⇔3x+7y-5z-26=0
Ответ: 3x+7y-5z-26=0
Неполное общее уравнение плоскости
Выше мы говорили о том, что, когда все числа А, B, C, D отличны от нуля, общее уравнение плоскости Ax+By+Cz+D=0 называют полным. В ином случае общее уравнение плоскости является неполным.
Разберем все возможные варианты общих неполных уравнений в прямоугольной системе координат трехмерного пространства.
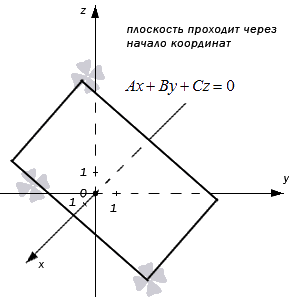
- В случае, когда D = 0, мы получаем общее неполное уравнение плоскости: Ax+By+Cz+D=0⇔Ax+By+Cz=0
Такая плоскость в прямоугольной системе координат проходит через начало координат. В самом деле, если подставим в полученное неполное уравнение плоскости координаты точки О (0, 0, 0), то придем к тождеству:
A·0+B·0+C·0=0⇔0≡0
- Если А = 0, В ≠ 0, С ≠ 0, или А ≠ 0, В = 0, С ≠0, или А ≠ 0, В ≠ 0, С = 0, то общие уравнения плоскостей имеют вид соответственно: By+Cz+D=0, или Ax+Cz+D=0, или Ax+By+D=0. Такие плоскости параллельны координатным осям Оx, Oy, Oz соответственно. Когда D=0, плоскости проходят через эти координатные оси соответственно. Также заметим, что неполные общие уравнения плоскостей By+Cz+D=0, Ax+Cz+D=0 и Ax+By+D=0 задают плоскости, которые перпендикулярны плоскостям Oyz, Oxz, Ozy соответственно.
- При А=0, В=0, С≠0, или А=0, В≠0, С=0, или А≠0, В=0, С=0 получим общие неполные уравнения плоскостей: Cz+D=0 ⇔z+DC=0⇔z=-DC⇔z=λ, λ∈R или By+D=0⇔y+DB=0⇔y=-DB⇔y=λ, λ∈R или Ax+D=0⇔x+DA=0⇔x=-DA⇔x=λ, λ∈R соответственно.
Эти уравнения определяют плоскости, которые параллельны координатным плоскостям Oxy, Oxz, Oyz соответственно и проходят через точки 0, 0, -DC, 0, -DB, 0 и -DA, 0, 0 соответственно. При D=0 уравнения самих координатных плоскостей Oxy, Oxz, Oyz выглядят так: z=0, y=0, x=0
соответственно.
Задана плоскость, параллельная координатной плоскости Oyz и проходящая через точку М0(7, -2, 3). Необходимо составить общее уравнение заданной плоскости.
Решение
Условием задачи определено, что заданная плоскость параллельна координатной плоскости Oyz, а, следовательно, может быть задана общим неполным уравнением плоскости Ax+D=0, A≠0⇔x+DA=0. Поскольку точка M0(7, -2, 3) лежит на плоскости по условию задачи, то очевидно, что координаты этой точки должны отвечать уравнению плоскости x+DA=0, иначе говоря, должно быть верным равенство 7+DA=0 . Преобразуем: DA=-7, тогда требуемое уравнение имеет вид: x-7=0.
Задачу возможно решить еще одним способом.
Вновь обратим внимание на заданную условием задачи параллельность данной плоскости координатной плоскости Oyz. Из этого условия понятно, что возможно в качестве нормального вектора заданной плоскости использовать нормальный вектор плоскости Oyz: i→=(1, 0, 0). Так, нам известны и точка, принадлежащая плоскости (задана условием задачи) и ее нормальный вектор. Таким образом, становится возможно записать общее уравнение заданной плоскости:
A(x-x0)+B(y-y0)+C(z-z0)=0⇔⇔1·(x-7)+0·(y+2)+0·(z-3)=0⇔⇔x-7=0
Ответ: x-7=0
Задана плоскость, перпендикулярная плоскости Oxy и проходящая через начало координат и точку М0(-3, 1, 2).
Решение
Плоскость, которая перпендикулярна координатной плоскости Oxy определяется общим неполным уравнением плоскости Ax+By+D=0 (А≠0, В≠0). Условием задачи дано, что плоскость проходит через начало координат, тогда D=0 и уравнение плоскости принимает вид Ax+By=0⇔x+BAy=0.
Найдем значение BA. В исходных данных фигурирует точка М0(-3, 1, 2), координаты которой должны отвечать уравнению плоскости. Подставим координаты, получим верное равенство: -3+BA·1=0, откуда определяем BA=3.
Так, мы имеем все данные, чтобы записать требуемое общее уравнение плоскости: x+3y=0.
Ответ: x+3y=0.
Для того, чтобы однозначно построить плоскость, необходимы три точки, которые не лежат на одной прямой.
Общее уравнение плоскости принимает вид:
Ax+By+Cz+D=0Ax+By+Cz+D=0,
где A,B,C,DA, B, C, D — коэффициенты, задающие плоскость. Они не могут быть одновременно равны нулю.
Здесь будет калькулятор
Составление уравнения плоскости по трем точкам
Текст цитаты
Заголовок Текст цитаты
В случае, когда известны координаты всех трех точек, уравнение плоскости, проходящей через эти точки составляется с помощью определителя:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0,
где (x1;y1;z1),(x2;y2;z2),(x3;y3;z3)(x_1;y_1;z_1), (x_2;y_2;z_2), (x_3;y_3;z_3) — координаты точек, через которые проходит данная плоскость, а (x;y;z)(x; y; z) — всевозможные координаты точек этой плоскости.
Составить уравнения плоскости проходящей через три точки с координатами (1;3;0),(5;6;4),(−1;−4;0)(1;3;0), (5;6;4), (-1;-4;0).
Решение
Пусть:
x1=1x_1=1
y1=3y_1=3
z1=0z_1=0
x2=5x_2=5
y2=6y_2=6
z2=4z_2=4
x3=−1x_3=-1
y3=−4y_3=-4
z3=0z_3=0
Составляем определитель:
∣x−x1x2−x1x3−x1y−y1y2−y1y3−y1z−z1z2−z1z3−z1∣=0begin{vmatrix}
x-x_1 & x_2-x_1 & x_3-x_1 \
y-y_1 & y_2-y_1 & y_3-y_1 \
z-z_1 & z_2-z_1 & z_3-z_1 \
end{vmatrix}=0
∣x−15−1−1−1y−36−3−4−3z−04−00−0∣=0begin{vmatrix}
x-1 & 5-1 & -1-1 \
y-3 & 6-3 & -4-3 \
z-0 & 4-0 & 0-0 \
end{vmatrix}=0
∣x−14−2y−33−7z40∣=0begin{vmatrix}
x-1 & 4 & -2 \
y-3 & 3 & -7 \
z & 4 & 0 \
end{vmatrix}=0
28x−8y−22z−4=028x-8y-22z-4=0 — уравнение искомой плоскости.
Ответ
28x−8y−22z−4=028x-8y-22z-4=0
Уравнение плоскости по точке и вектору нормали
Если дана точка, лежащая на плоскости и вектор нормали к этой плоскости, то сама плоскость задается уравнением:
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0,
где (x0;y0;z0)(x_0;y_0;z_0) — координаты точки, принадлежащей плоскости, а (n1;n2;n3)(n_1;n_2;n_3) — координаты вектора нормали к этой плоскости.
Выпишите уравнение плоскости, если даны: координата точки плоскости (8;−2;9)(8;-2;9) и вектор нормали (1;3;5)(1;3;5).
Решение
x0=8x_0=8
y0=−2y_0=-2
z0=9z_0=9
n1=1n_1=1
n2=3n_2=3
n3=5n_3=5
(x−x0)⋅n1+(y−y0)⋅n2+(z−z0)⋅n3=0(x-x_0)cdot n_1+(y-y_0)cdot n_2+(z-z_0)cdot n_3=0
(x−8)⋅1+(y−(−2))⋅3+(z−9)⋅5=0(x-8)cdot 1+(y-(-2))cdot 3+(z-9)cdot 5=0
x−8+3y+6+5z−45=0x-8+3y+6+5z-45=0
x+3y+5z−47=0x+3y+5z-47=0 — уравнение плоскости.
Проверка
Чтобы убедиться в том, что задача решена правильно, без ошибок, необходимо в полученное уравнение подставить координаты точки, которые даны в условии задачи:
8+3⋅(−2)+5⋅9−47=08+3cdot(-2)+5cdot9-47=0
0=00=0 — верно, значит ответ правильный.
Ответ
x+3y+5z−47=0x+3y+5z-47=0
1. Общее уравнение плоскости
Определение. Плоскостью называется поверхность, все точки которой удовлетворяют общему уравнению: Ax + By + Cz + D = 0 , где А, В, С – координаты вектора
N = Ai + Bj + Ck -вектор нормали к плоскости. Возможны следующие частные случаи:
A = 0 – плоскость параллельна оси Ох
B = 0 – плоскость параллельна оси Оу C = 0 – плоскость параллельна оси Оz
D = 0 – плоскость проходит через начало координат
A = B = 0 – плоскость параллельна плоскости хОу A = C = 0 – плоскость параллельна плоскости хОz B = C = 0 – плоскость параллельна плоскости yOz A = D = 0 – плоскость проходит через ось Ох
B = D = 0 – плоскость проходит через ось Оу C = D = 0 – плоскость проходит через ось Oz
A = B = D = 0 – плоскость совпадает с плоскостью хОу A = C = D = 0 – плоскость совпадает с плоскостью xOz B = C = D = 0 – плоскость совпадает с плоскостью yOz
2. Уравнение поверхности в пространстве
Определение. Любое уравнение, связывающее координаты x, y, z любой точки поверхности является уравнением этой поверхности.
3. Уравнение плоскости, проходящей через три точки
Для того, чтобы через три какиелибо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.
Рассмотрим точки М1(x1, y1, z1), M2(x2, y2, z2), M3(x3, y3, z3) в общей декартовой системе
|
координат. |
||||||
|
Для того, чтобы произвольная точка M (x, y, z) |
лежала в одной плоскости с точками |
|||||
|
M1, M2 , M3 необходимо, чтобы векторы M1M 2 , M1M 3 , M1M были компланарны, т.е |
||||||
|
M1M = {x − x1 ; y − y1 ; z − z1} |
||||||
|
( M1M 2 , M1M 3 , M1M ) = 0. Таким образом, M1M 2 |
= {x2 − x1 ; y2 |
− y1 ; z2 − z1} |
||||
|
M1M 3 |
= {x3 − x1 ; y3 − y1 ; z3 − z1} |
|||||
|
x − x1 |
y − y1 |
z − z1 |
||||
|
Уравнение плоскости, проходящей через три точки: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||
|
x3 − x1 |
y3 − y1 |
z3 − z1 |
35
4. Уравнение плоскости по двум точкам и вектору, коллинеарному плоскости
Пусть заданы точки М1(x1, y1, z1), M2(x2, y2, z2) и векторa = (a1, a2 , a3 ) .
Составим уравнение плоскости, проходящей через данные точки М1 и М2 и произвольную
|
точку М(х, у, z) параллельно вектору a . |
||||||||||
|
Векторы M1M = {x − x1 ; y − y1 ; z − z1} |
и вектор a = (a , a |
2 |
, a |
3 |
) |
должны быть |
||||
|
M1M 2 = {x2 − x1 ; y2 − y1 ; z2 − z1} |
1 |
|||||||||
|
x − x1 |
y − y1 |
z − z1 |
||||||||
|
компланарны, т.е. ( M1M , M1M 2 , a ) = 0.Уравнение плоскости: |
x2 − x1 |
y2 − y1 |
z2 − z1 |
= 0 |
||||||
|
a1 |
a2 |
a3 |
5. Уравнение плоскости по одной точке и двум векторам, коллинеарным плоскости
Пусть заданы два вектора a = (a1, a2 , a3 ) и b = (b1,b2 ,b3 ) , коллинеарные плоскости. Тогда для произвольной точки М(х, у, z), принадлежащей плоскости, векторы a,b, MM1 должны быть компланарны.
|
x − x1 |
y − y1 |
z − z1 |
|||
|
Уравнение плоскости: |
a1 |
a2 |
a3 |
= 0 . |
|
|
b1 |
b2 |
b3 |
6. Уравнение плоскости по точке и вектору нормали
Теорема. Если в пространстве задана точка M0 (x0 , y0 , z0 ) , то уравнение плоскости, проходящей через точку M0 перпендикулярно вектору нормали N ( A, B,C) имеет вид: A(x − x0 ) + B ( y − y0 ) + C (z − z0 ) = 0 .
7. Уравнение плоскости в отрезках
Если в общем уравнении Ax + By + Cz + D = 0 поделить обе части на (-D)
|
− |
A |
x − |
B |
y − |
C |
z − 1 = 0 , заменив − |
D |
= a, |
− |
D |
= b, |
− |
D |
= c , получим уравнение плоскости |
||||||||
|
A |
B |
C |
||||||||||||||||||||
|
D |
D |
D |
||||||||||||||||||||
|
в отрезках: |
x |
+ |
y |
+ |
z |
= 1 . Числа a, b, c являются точками пересечения плоскости соответственно |
||||||||||||||||
|
a |
b |
c |
||||||||||||||||||||
с осями х, у, z.
8. Уравнение плоскости в векторной форме
r n = p, где r = xi + yj + zk – радиусвектор текущей точки M (x, y, z) ,
n = i cosα + j cos β + k cosγ – единичный вектор, имеющий направление, перпендикуляра,
опущенного на плоскость из начала координат. α, β и γ – углы, образованные этим вектором с осями х, у, z. p – длина этого перпендикуляра. В координатах это уравнение имеет вид:
x cosα + y cos β + z cosγ − p = 0
36
9. Расстояние от точки до плоскости
Расстояние от произвольной точки M0 (x0 , y0 , z0 ) до плоскости Ax + By + Cz + D = 0 равно:
d = Ax0 + By0 + Cz0 + D
A2 + B2 + C 2
Пример. Найти уравнение плоскости, проходящей через точки А(2,-1,4) и В(3,2,-1) перпендикулярно плоскости x + y + 2z − 3 = 0 .
Искомое уравнение плоскости имеет вид: Ax + By + Cz + D = 0 , вектор нормали к этой плоскости n1 (A,B,C). Вектор AB (1,3,-5) принадлежит плоскости. Заданная нам плоскость,
перпендикулярная искомой имеет вектор нормали n2 (1,1,2). Т.к. точки А и В принадлежат обеим плоскостям, а плоскости взаимно перпендикулярны, то
|
n = AB × n |
i |
j |
k |
= i |
3 |
− 5 |
− j |
1 |
− 5 |
+ k |
1 |
3 |
= 11i − 7 j − 2k. |
||||||||
|
2 |
= |
1 |
3 |
− 5 |
|||||||||||||||||
|
1 |
1 |
2 |
1 |
2 |
1 |
1 |
|||||||||||||||
|
1 |
1 |
2 |
|||||||||||||||||||
Таким образом, вектор нормали n1 (11,-7,-2). Т.к. точка А принадлежит искомой плоскости, то ее координаты должны удовлетворять уравнению этой плоскости, т.е.
11.2+ 7.1− 2.4 + D = 0; D = −21. Итого, получаем уравнение плоскости: 11x − 7 y − 2z − 21 = 0
10.Уравнение линии в пространстве
Как на плоскости, так и в пространстве, любая линия может быть определена как совокупность точек, координаты которых в некоторой выбранной в пространстве системе координат удовлетворяют уравнению:
F(x, y, z) = 0 . Это уравнение называется уравнением линии в пространстве.
Кроме того, линия в пространстве может быть определена и иначе. Ее можно рассматривать как линию пересечения двух поверхностей, каждая из которых задана какимлибо уравнением.
Пусть F(x, y, z) = 0 и Ф(x, y, z) = 0 – уравнения поверхностей, пересекающихся по линии L.
F(x, y, z) = 0
Тогда пару уравнений Ф(x, y, z) = 0 назовем уравнением линии в пространстве.
11. Уравнение прямой в пространстве по точке и направляющему вектору
Возьмем произвольную прямую и вектор S (m, n, p), параллельный данной прямой. Вектор S называется направляющим вектором прямой.
На прямой возьмем две произвольные точки M0 (x0 , y0 , z0 ) и M (x, y, z) .
z
37
z
S M1
M0
r0 r
Обозначим радиусвекторы этих точек как r0 и r , очевидно, что r − r0 = M0 M .
Т.к. векторы М0 М и S коллинеарны, то верно соотношение М0 М = St , где t – некоторый параметр. Итого, можно записать: r = r0 + St .
Т.к. этому уравнению удовлетворяют координаты любой точки прямой, то полученное уравнение – параметрическое уравнение прямой.
x = x0 + mt
Это векторное уравнение может быть представлено в координатной форме: y = y0 + nt
z = z0 + pt
Преобразовав эту систему и приравняв значения параметра t, получаем канонические
|
уравнения прямой в пространстве: |
x − x0 |
= |
y − y0 |
= |
z − z0 |
. |
|
m |
n |
|||||
|
p |
Определение. Направляющими косинусами прямой называются направляющие косинусы вектора S , которые могут быть вычислены по формулам:
|
cosα = |
m |
; cos β = |
n |
; cosγ = |
p |
. |
||
|
+ n2 |
+ p2 |
+ n2 + p2 |
m2 + n2 + p2 |
|||||
|
m2 |
m2 |
Отсюда получим: m : n : p = cosα : cos β : cosγ .
Числа m , n , p называются угловыми коэффициентами прямой. Т.к. S – ненулевой вектор, то m, n и p не могут равняться нулю одновременно, но одно или два из этих чисел могут равняться нулю. В этом случае в уравнении прямой следует приравнять нулю соответствующие числители.
12. Уравнение прямой в пространстве, проходящей через две точки
Если на прямой в пространстве отметить две произвольные точки M1 (x1, y1, z1 ) и
M2 (x2 , y2 , z2 ), то координаты этих точек должны удовлетворять полученному выше уравнению прямой:
|
x2 − x1 |
= |
y2 − y1 |
= |
z2 − z1 |
. |
|
m |
n |
||||
|
p |
38
Две пересекающиеся плоскости
Пло́скость — одно из фундаментальных понятий в геометрии. При систематическом изложении геометрии понятие плоскости обычно принимается за одно из исходных понятий, которое лишь косвенным образом определяется аксиомами геометрии. В тесной связи с плоскостью принято рассматривать принадлежащие ей точки и прямые; они также, как правило, вводятся как неопределяемые понятия, свойства которых задаются аксиоматически[1].
Некоторые характеристические свойства плоскости[править | править код]
- Плоскость — поверхность, содержащая полностью каждую прямую, соединяющую любые её точки;
- Две различные плоскости либо являются параллельными, либо пересекаются по прямой.
- Прямая либо параллельна плоскости, либо пересекает её в одной точке, либо содержится в плоскости.
- Две прямые, перпендикулярные одной и той же плоскости, параллельны друг другу.
- Две плоскости, перпендикулярные одной и той же прямой, параллельны друг другу.
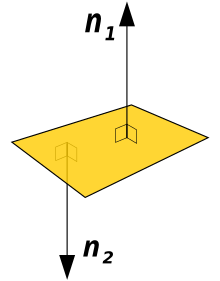
Плоскость и два её нормальных вектора: n1 и n2
Уравнения плоскости[править | править код]
Впервые встречается у А. К. Клеро (1731).
Уравнение плоскости в отрезках, по-видимому, впервые встречается у Г. Ламе (1816—1818).
Нормальное уравнение ввёл Л. О. Гессе (1861).
Плоскость — алгебраическая поверхность первого порядка: в декартовой системе координат плоскость может быть задана уравнением первой степени.
- Общее уравнение (полное) плоскости
где 
и 
— постоянные, причём 
и 
одновременно не равны нулю; в векторной форме:
где 
— радиус-вектор точки 
, вектор 
перпендикулярен к плоскости (нормальный вектор). Направляющие косинусы вектора 
:
Если один из коэффициентов в уравнении плоскости равен нулю, уравнение называется неполным. При 
плоскость проходит через начало координат, при 
(или 
, 
) плоскость параллельна оси 
(соответственно 
или 
). При 
(
, или 
) плоскость параллельна плоскости 
(соответственно 
или 
).
- Уравнение плоскости в отрезках:
где 
, 
, 
— отрезки, отсекаемые плоскостью на осях 
и .
в векторной форме:
- Уравнение плоскости, проходящей через три заданные точки
, не лежащие на одной прямой:
(смешанное произведение векторов), иначе
- Нормальное (нормированное) уравнение плоскости
в векторной форме:
где 
– единичный вектор, 
— расстояние П. от начала координат. Уравнение (2) может быть получено из уравнения (1) умножением на нормирующий множитель
(знаки 
и противоположны).
Определение по точке и вектору нормали[править | править код]
В трёхмерном пространстве одним из важнейших способов определения плоскости является указание точки на плоскости и вектора нормали к ней.
Допустим, 
является радиусом-вектором точки 
, заданной на плоскости, и допустим, что n — это ненулевой вектор, перпендикулярный к плоскости (нормаль). Идея состоит в том, что точка 
с радиусом-вектором r находится на плоскости тогда и только тогда, когда вектор, проведённый от к , перпендикулярен n.
Вернёмся к тому, что два вектора являются перпендикулярными тогда и только тогда, когда их скалярное произведение равно нулю. Отсюда следует, что нужная нам плоскость может быть выражена как множество всех точек r таких, что:
- (Здесь точка означает скалярное произведение, а не умножение.)
Развернув выражение, мы получим:
что является знакомым нам уравнением плоскости.
Например:
Дано: точка на плоскости 
и вектор нормали 
.
Уравнение плоскости записывается так:
Расстояние от точки до плоскости[править | править код]
Расстояние от точки до плоскости — это наименьшее из расстояний между этой точкой и точками плоскости. Известно, что расстояние от точки до плоскости равно длине перпендикуляра, опущенного из этой точки на плоскость.
-
- ,если и начало координат лежат по разные стороны плоскости, в противоположном случае . Расстояние от точки до плоскости равно
Расстояние между параллельными плоскостями[править | править код]
![d={frac {mid [{bar r}_{2}-{bar r}_{1},{bar n}]mid }{mid {bar n}mid }}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cf3b79c1fa73b510197080a2db0d744b6d48080)
Типы взаимного расположения трёх или менее плоскостей. В частности, 4 тип — пересечение двух плоскостей, 11 тип — плоскость E3 проходит через линию пересечения плоскостей E1 и E2, 12 тип — пересечение трёх плоскостей в точке
Связанные понятия[править | править код]
- Угол между двумя плоскостями. Если уравнения П. заданы в виде (1), то
Если в векторной форме, то
- Плоскости параллельны, если
- или (Векторное произведение)
![[{mathbf {N_{1}}},{mathbf {N_{2}}}]=0.](https://wikimedia.org/api/rest_v1/media/math/render/svg/36c4d8baa08e5ef8fcbb9a88761b1d6a6232517f)
- Плоскости перпендикулярны, если
- или . (Скалярное произведение)
- Пучок плоскостей — все плоскости, проходящие через линию пересечения двух плоскостей. Уравнение пучка плоскостей, то есть любой плоскости, проходящей через линию пересечения двух плоскостей, имеет вид[2]:222:
- где и — любые числа, не равные одновременно нулю. Уравнение самой этой линии можно найти из уравнения пучка, подставляя α=1, β=0 и α=0, β=1.
- Связка плоскостей — все плоскости, проходящие через точку пересечения трёх плоскостей[2]:224. Уравнение связки плоскостей, то есть любой плоскости, проходящей через точку пересечения трёх плоскостей, имеет вид:
- где , и — любые числа, не равные одновременно нулю. Саму эту точку можно найти из уравнения связки, подставляя α=1, β=0, γ=0; α=0, β=1, γ=0 и α=0, β=0, γ=1 и решая получившуюся систему уравнений.
Вариации и обобщения[править | править код]
Плоскости в неевклидовом пространстве[править | править код]
Метрика плоскости не обязана быть евклидовой. В зависимости от введенных отношений инцидентности точек и прямых, различают проективные, аффинные, гиперболические и эллиптические плоскости[1].
Многомерные плоскости[править | править код]
Пусть дано n-мерное аффинное-конечномерное пространство 
, над полем действительных чисел. В нём выбрана прямоугольная система координат 
. m-плоскостью называется множество точек 
, радиус векторы которых удовлетворяют следующему соотношению 
— матрица, столбцы которой образует направляющие подпространство плоскости, 
— вектор переменных, 
— радиус-вектор одной из точек плоскости.
Указанное соотношение можно из матрично-векторного вида перевести в векторный:
— векторное уравнение m-плоскости.
Вектора 
образуют направляющее подпространство. Две m-плоскости 
называются параллельными, если их направляющие пространства совпадают и 
.
(n-1)-плоскость в n-мерном пространстве называется гиперплоскостью или просто плоскостью. Для гиперплоскости существует общее уравнение плоскости. Пусть 
— нормальный вектор плоскости, 
— вектор переменных, 
— радиус вектор точки, принадлежащей плоскости, тогда:
— общее уравнение плоскости.
Имея матрицу направляющих векторов, уравнение можно записать так: 
, или:
.
Углом между плоскостями называется наименьший угол между их нормальными векторами.
Примером 1-плоскости в трёхмерном пространстве (n=3) служит прямая. Её векторное уравнение имеет вид: 
. В случае n = 2 прямая является гиперплоскостью.
Гиперплоскость в трёхмерном пространстве соответствует привычному понятию плоскости.
См. также[править | править код]
- Сагиттальная плоскость
- Полуплоскость
- Пространство
Примечания[править | править код]
- ↑ 1 2 Математическая энциклопедия, 1984.
- ↑ 1 2 Гусятников П.Б., Резниченко С.В. Векторная алгебра в примерах и задачах. — М.: Высшая школа, 1985. — 232 с.
Литература[править | править код]
- Ильин В. А., Позняк Э. Г. Аналитическая геометрия. — М.: Физматлит, 2002. — 240 с.
- Плоскость // Математическая энциклопедия (в 5 томах). — М.: Советская Энциклопедия, 1984. — Т. 4. — С. 318—319.
Ссылки[править | править код]
На Викискладе есть медиафайлы по теме Плоскость
На Викискладе есть медиафайлы по теме Плоскость23 ноября 2012
В этом уроке мы рассмотрим, как с помощью определителя составить уравнение плоскости. Если вы не знаете, что такое определитель, зайдите в первую часть урока — «Матрицы и определители». Иначе вы рискуете ничего не понять в сегодняшнем материале.
Уравнение плоскости по трем точкам
Зачем вообще нужно уравнение плоскости? Все просто: зная его, мы легко высчитаем углы, расстояния и прочую хрень в задаче C2. В общем, без этого уравнения не обойтись. Поэтому сформулируем задачу:
Задача. В пространстве даны три точки, не лежащие на одной прямой. Их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3);Требуется составить уравнение плоскости, проходящей через эти три точки. Причем уравнение должно иметь вид:
Ax + By + Cz + D = 0
где числа A, B, C и D — коэффициенты, которые, собственно, и требуется найти.
Ну и как получить уравнение плоскости, если известны только координаты точек? Самый простой способ — подставить координаты в уравнение Ax + By + Cz + D = 0. Получится система из трех уравнений, которая легко решается.
Многие ученики считают такое решение крайне утомительным и ненадежным. Прошлогодний ЕГЭ по математике показал, что вероятность допустить вычислительную ошибку действительно велика.
Поэтому наиболее продвинутые учителя стали искать более простые и изящные решения. И ведь нашли! Правда, полученный прием скорее относится к высшей математике. Лично мне пришлось перерыть весь Федеральный перечень учебников, чтобы убедиться, что мы вправе применять этот прием без каких-либо обоснований и доказательств.
Уравнение плоскости через определитель
Хватит лирики, приступаем к делу. Для начала — теорема о том, как связаны определитель матрицы и уравнение плоскости.
Теорема. Пусть даны координаты трех точек, через которые надо провести плоскость: M = (x1, y1, z1); N = (x2, y2, z2); K = (x3, y3, z3). Тогда уравнение этой плоскости можно записать через определитель:
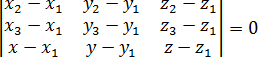
Для примера попробуем найти пару плоскостей, которые реально встречаются в задачах С2. Взгляните, как быстро все считается:
Задача. Составьте уравнение плоскости, проходящей через точки:
A1 = (0, 0, 1);
B = (1, 0, 0);
C1 = (1, 1, 1);
Составляем определитель и приравниваем его к нулю:
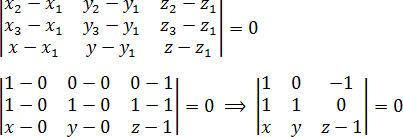
Раскрываем определитель:
a = 1 · 1 · (z − 1) + 0 · 0 · x + (−1) · 1 · y = z − 1 − y;
b = (−1) · 1 · x + 0 · 1 · (z − 1) + 1 · 0 · y = −x;
d = a − b = z − 1 − y − (−x) = z − 1 − y + x = x − y + z − 1;
d = 0 ⇒ x − y + z − 1 = 0;
Как видите, при расчете числа d я немного «причесал» уравнение, чтобы переменные x, y и z шли в правильной последовательности. Вот и все! Уравнение плоскости готово!
Задача. Составьте уравнение плоскости, проходящей через точки:
A = (0, 0, 0);
B1 = (1, 0, 1);
D1 = (0, 1, 1);
Сразу подставляем координаты точек в определитель:
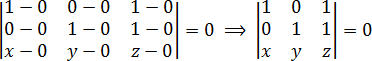
Снова раскрываем определитель:
a = 1 · 1 · z + 0 · 1 · x + 1 · 0 · y = z;
b = 1 · 1 · x + 0 · 0 · z + 1 · 1 · y = x + y;
d = a − b = z − (x + y) = z − x − y;
d = 0 ⇒ z − x − y = 0 ⇒ x + y − z = 0;
Итак, уравнение плоскости снова получено! Опять же, на последнем шаге пришлось поменять в нем знаки, чтобы получить более «красивую» формулу. Делать это в настоящем решении совсем не обязательно, но все-таки рекомендуется — чтобы упростить дальнейшее решение задачи.
Как видите, составлять уравнение плоскости теперь намного проще. Подставляем точки в матрицу, считаем определитель — и все, уравнение готово.
На этом можно было бы закончить урок. Однако многие ученики постоянно забывают, что стоит внутри определителя. Например, в какой строчке стоит x2 или x3, а в какой — просто x. Чтобы окончательно разобраться с этим, давайте проследим, откуда берется каждое число.
Откуда берется формула с определителем?
Итак, разбираемся, откуда возникает такое суровое уравнение с определителем. Это поможет вам запомнить его и успешно применять.
Все плоскости, которые встречаются в задаче C2, задаются тремя точками. Эти точки всегда отмечены на чертеже, либо даже указаны прямо в тексте задачи. В любом случае, для составления уравнения нам потребуется выписать их координаты:
M = (x1, y1, z1);
N = (x2, y2, z2);
K = (x3, y3, z3).
Рассмотрим еще одну точку на нашей плоскости с произвольными координатами:
T = (x, y, z)
Берем любую точку из первой тройки (например, точку M) и проведем из нее векторы в каждую из трех оставшихся точек. Получим три вектора:
MN = (x2 − x1, y2 − y1, z2 − z1);
MK = (x3 − x1, y3 − y1, z3 − z1);
MT = (x − x1, y − y1, z − z1).
Теперь составим из этих векторов квадратную матрицу и приравняем ее определитель к нулю. Координаты векторов станут строчками матрицы — и мы получим тот самый определитель, который указан в теореме:
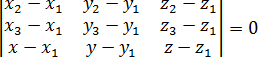
Эта формула означает, что объем параллелепипеда, построенного на векторах MN, MK и MT, равен нулю. Следовательно, все три вектора лежат в одной плоскости. В частности, и произвольная точка T = (x, y, z) — как раз то, что мы искали.
Замена точек и строк определителя
У определителей есть несколько замечательных свойств, которые еще более упрощают решение задачи C2. Например, нам неважно, из какой точки проводить векторы. Поэтому следующие определители дают такое же уравнение плоскости, как и приведенный выше:
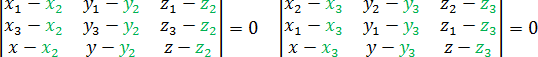
Также можно менять местами строчки определителя. Уравнение при этом останется неизменным. Например, многие любят записывать строчку с координатами точки T = (x; y; z) в самом верху. Пожалуйста, если вам так удобно:
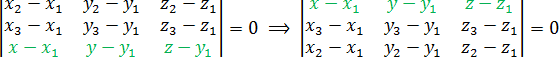
Некоторых смущает, что в одной из строчек присутствуют переменные x, y и z, которые не исчезают при подстановке точек. Но они и не должны исчезать! Подставив числа в определитель, вы должны получить вот такую конструкцию:
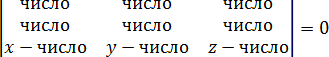
Затем определитель раскрывается по схеме, приведенной в начале урока, и получается стандартное уравнение плоскости:
Ax + By + Cz + D = 0
Взгляните на пример. Он последний в сегодняшнем уроке. Я специально поменяю строчки местами, чтобы убедиться, что в ответе получится одно и то же уравнение плоскости.
Задача. Составьте уравнение плоскости, проходящей через точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1).
Итак, рассматриваем 4 точки:
B1 = (1, 0, 1);
C = (1, 1, 0);
D1 = (0, 1, 1);
T = (x, y, z).
Для начала составим стандартный определитель и приравниваем его к нулю:
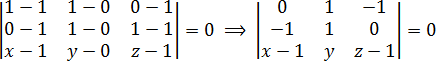
Раскрываем определитель:
a = 0 · 1 · (z − 1) + 1 · 0 · (x − 1) + (−1) · (−1) · y = 0 + 0 + y;
b = (−1) · 1 · (x − 1) + 1 · (−1) · (z − 1) + 0 · 0 · y = 1 − x + 1 − z = 2 − x − z;
d = a − b = y − (2 − x − z) = y − 2 + x + z = x + y + z − 2;
d = 0 ⇒ x + y + z − 2 = 0;
Все, мы получили ответ: x + y + z − 2 = 0.
Теперь давайте переставим пару строк в определителе и посмотрим, что произойдет. Например, запишем строчку с переменными x, y, z не внизу, а вверху:
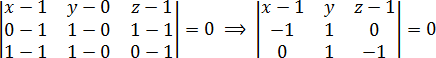
Вновь раскрываем полученный определитель:
a = (x − 1) · 1 · (−1) + (z − 1) · (−1) · 1 + y · 0 · 0 = 1 − x + 1 − z = 2 − x − z;
b = (z − 1) · 1 · 0 + y · (−1) · (−1) + (x − 1) · 1 · 0 = y;
d = a − b = 2 − x − z − y;
d = 0 ⇒ 2 − x − y − z = 0 ⇒ x + y + z − 2 = 0;
Мы получили точно такое же уравнение плоскости: x + y + z − 2 = 0. Значит, оно действительно не зависит от порядка строк. Осталось записать ответ.
Итак, мы убедились, что уравнение плоскости не зависит от последовательности строк. Можно провести аналогичные вычисления и доказать, что уравнение плоскости не зависит и от точки, координаты которой мы вычитаем из остальных точек.
В рассмотренной выше задаче мы использовали точку B1 = (1, 0, 1), но вполне можно было взять C = (1, 1, 0) или D1 = (0, 1, 1). В общем, любую точку с известными координатами, лежащую на искомой плоскости.
Смотрите также:
- Видеоурок по задачам C2: уравнение плоскости через определитель
- Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
- Тест к уроку «Что такое числовая дробь» (легкий)
- Сводный тест по задачам B15 (1 вариант)
- Однородные тригонометрические уравнения: общая схема решения
- Задача B4: тарифы на сотовую связь
