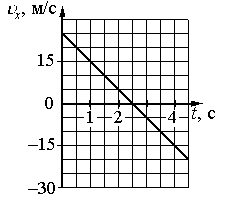Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-
1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк – vн и Δt = tк – tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк – vн)/(tк – tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с2.
Реклама
-
1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется – → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → – (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -
2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-
3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 189 989 раз.
Была ли эта статья полезной?
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:
v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:
Проекция ускорения
Проекция ускорения на ось ОХ
vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.
График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.
Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.
Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.
В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774
На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.
Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:
Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:
Подставим известные данные и вычислим ускорение автомобиля:
Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
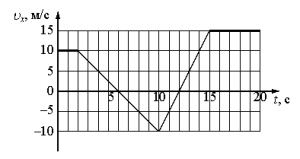
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?
Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:
Подставим в нее известные данные и сделаем вычисления:
Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:
По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:
Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:
Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.6k
Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.94 (Голосов: 35)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Ускорение автомобиля
Одним из важнейших показателей
динамических качеств автомобиля является
интенсивность разгона – ускорение.
При изменении
скорости движения возникают силы
инерции, которые автомобилю необходимо
преодолеть для обеспечения заданного
ускорения. Эти силы вызваны как
поступательно движущимися массами
автомобиля m, так и моментами инерции
вращающихся деталей двигателя, трансмиссии
и колес.
Для удобства
проведения расчетов пользуются
комплексным показателем – приведенными
силами инерции:
где δвр
– коэффициент учета вращающихся масс.
Величина
ускорения j = dv/dt, которое может
развить автомобиль при движении по
горизонтальному участку дороги на
заданной передаче и с заданной скоростью,
находится в результате преобразования
формулы для определения запаса мощности,
которая расходуется на разгон:
,
или по
динамической характеристике:
D = f +
.
Отсюда:
j = 
.
Для определения
ускорения на подъеме или спуске пользуются
формулой:
.
Способность
автомобиля к быстрому разгону особенно
важна в условиях городской езды.
Увеличенные ускорения для автомобиля
могут быть получены за счет увеличения
передаточного числа u0главной передачи и соответствующего
выбора характеристики изменения
крутящего момента двигателя.
Максимальное
ускорение при разгоне находится в
пределах:
– для легковых автомобилей на первой
передаче 2,0…3,5 м/с2;
– для легковых
автомобилей на прямой передаче 0,8…2,0
м/с2;
– для грузовых
автомобилей на второй передаче 1,8…2,8
м/с2;
– для грузовых
автомобилей на прямой передаче 0,4…0,8
м/с2.
Время и путь разгона автомобиля
Величина ускорения в ряде случаев не
является достаточно наглядным показателем
способности автомобиля к разгону. Для
этой цели удобно применять такие
показатели, как время и путь разгонадо заданной скорости и графики,
отображающие зависимость скорости от
времени и пути разгона.
Так как j
= 
, тоdt =
.
Отсюда путем
интегрирования полученного уравнения
находим время разгона tв заданном
интервале изменения скоростей отv1доv2:
.
Определение
пути разгона Sв заданном интервале
изменения скоростей осуществляют
следующим образом. Так как скорость
является первой производной пути по
времени, то дифференциал путиdS=v·dt,
или путь разгона в интервале изменения
скоростей отv1доv2равен:
.
В условиях
реальной эксплуатации автомобиля
затраты времени на операции переключения
передач и буксование сцепления увеличивают
время разгона по сравнению с теоретическим
(расчетным) его значением. Время,
затрачиваемое на переключение передач,
зависит от конструкции коробки передач.
При применении автоматической коробки
передач это время практически равно
нулю.
Кроме того,
разгон не все время происходит при
полной подаче топлива, как это
предполагается в изложенном методе.
Это также увеличивает реальное время
разгона.
При применении
механической коробки передач важным
моментом является правильный выбор
наиболее выгодных скоростей переключения
передач v1-2, v2-3и т.д. (см. раздел «Тяговый расчет
автомобиля»).
Для оценки
способности автомобиля к разгону в
качестве показателя используют также
время разгона после трогания с места
на пути в 100 и 500 м.
Построение графиков ускорений
В практических
расчетах принимают, что разгон происходит
на горизонтальной дороге с твердым
покрытием. Сцепление включено и не
пробуксовывает. Орган управления режимом
работы двигателя находится в положении
полной подачи топлива. При этом обеспечено
сцепление колес с дорогой без
пробуксовывания. Предполагается также,
что изменение параметров двигателя
происходит по внешней скоростной
характеристике.
Полагают,
что разгон для легковых автомобилей
начинается с минимально устойчивой
скорости на низшей передаче порядка v0= 1,5…2,0м/сдо значенийvт= 27,8м/с(100км/ч). Для грузовых
автомобилей принимают:vт= 16,7м/с(60км/ч).
Последовательно,
начиная со скорости v0=
1,5…2,0м/сна первой передачи и
последующих передачах, на динамической
характеристике (рис.1) для выбранных по
оси абсциссvрасчетных точек (не
менее пяти) определяют запас динамического
фактора при разгоне как разность ординат
(D – f)на различных передачах.
Коэффициент учета вращающихся масс
(δвр) для каждой передачи
подсчитывают по формуле:
δвр= 1,04 + 0,05·iкп2.
Ускорения
автомобиля определяют по формуле:
j = 
.
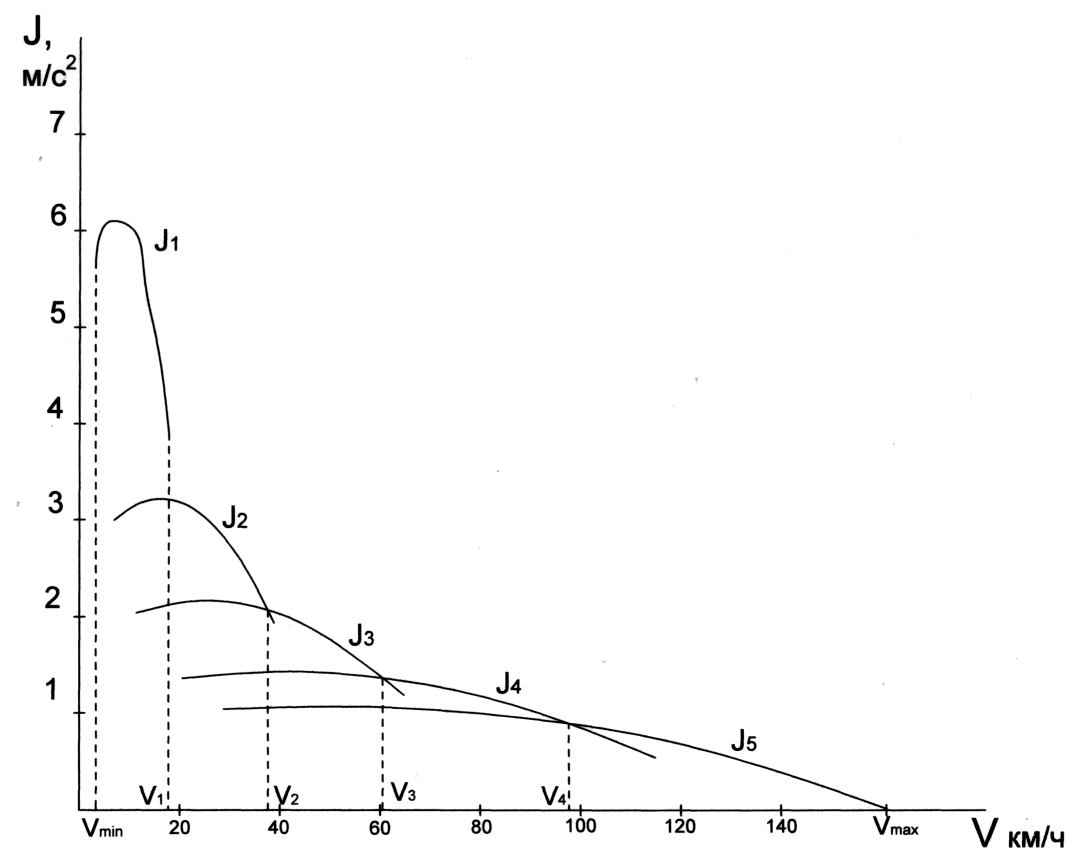
По полученным
данным строят графики ускорений j=f(v)(рис.2).
Рис.2.
Характеристика ускорений автомобиля.
При правильном расчете и построении
кривая ускорений на высшей передаче
пересечет абсциссу в точке максимальной
скорости. Достижение максимальной
скорости происходит при полном
использовании запаса динамического
фактора: D – f = 0.
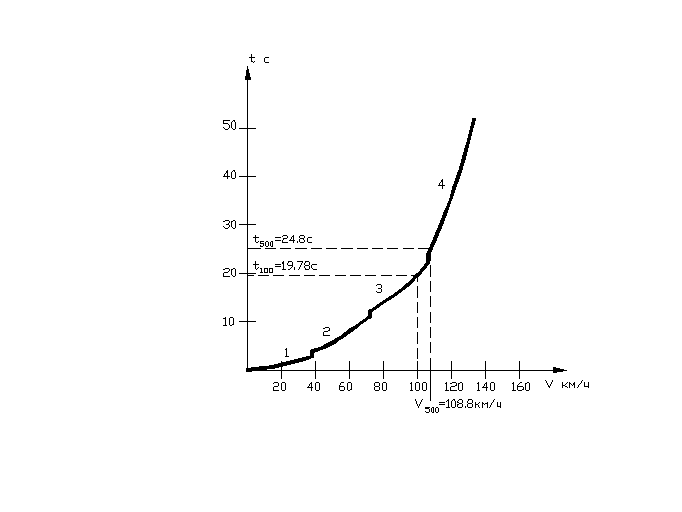
Построение графика времени разгона
t = f(v)
Этот график
строят, используя график ускорения
автомобиля j=f(v)(рис.2). Шкалу скоростей
графика разгона разбивают на равные
участки, например, через каждый 1м/с,
и из начала каждого участка проводят
перпендикуляры до пересечения с кривыми
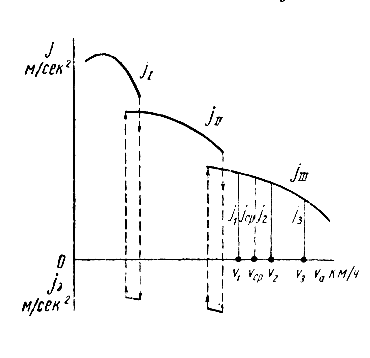
ускорения (рис.3).
Площадь каждой из полученных элементарных
трапеций в принятом масштабе равна
времени разгона для данного участка
скорости, если считать, что на каждом
участке скорости разгон происходит с
постоянным (средним) ускорением:
jср= (j1
+ j2)/2,
где j1
, j2– ускорения соответственно
в начале и в конце рассматриваемого
участка скоростей,м/с2.
В данном расчете не учитывается время
на переключение передач и другие факторы,
приводящие к завышению времени разгона.
Поэтому вместо среднего ускорения
принимают ускорение jiв
начале произвольно взятого участка
(определяют по шкале).
С учетом
сделанного допущения время разгонана каждом участке приращения скоростиΔvопределится как:
ti=Δv/ji,с.
Рис. 3. Построение
графика времени разгона
По полученным
данным строят график времени разгона
t = f(v). Полное время разгона отv0до значенийvтопределяют
как сумму времени разгона (с нарастающим
итогом) по всем участкам:
t1=Δv/j1 ,t2=t1 +(Δv/j2),t3= t2 +(Δv/j3)и так далее доtтконечного
времени разгона:
.
При построении
графика времени разгона удобно
пользоваться таблицей и принять Δv= 1м/с.
|
Участки скорости |
||||||||
|
№ участков |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
и |
|
ji |
||||||||
|
ti |
||||||||
|
Врем |
Напомним,
что построенный (теоретический) график
разгона (рис.4) отличается от действительного
тем, что не учтено реальное время на
переключение передач. На рис.4 время
(1,0 с) на переключение передач
отображено условно для иллюстрации
момента переключения.
При
использовании механической (ступенчатой)
трансмиссии на автомобиле действительный
график времени разгона характеризуется
потерей скорости в моменты переключения
передач. Это также увеличивает время
на разгон. У автомобиля с коробкой
передач с синхронизаторами интенсивность
разгона выше. Наибольшая интенсивность
у автомобиля с автоматической
бесступенчатой трансмиссией.
Время разгона отечественных легковых
автомобилей малого класса с места до
скорости 100 км/ч(28м/с) составляет
порядка 13…20с. Для автомобилей
среднего и большого класса оно не
превышает 8…10с.
Рис.
4. Характеристика разгона автомобиля
по времени.
Время разгона грузовых автомобилей до
скорости 60 км/ч(17м/с) составляет
35…45си выше, что свидетельствует
о недостаточной их динамичности.
Путь разгона для легковых автомобилей
до скорости 100 км/чсоставляет 500…800м.
Сравнительные данные по времени разгона
автомобилей отечественного и зарубежного
производства приведены в табл. 3.4.
Таблица 3.4.
Время разгона
легковых автомобилей до скорости 100км/ч
(28 м/с)
|
Автомобиль |
Время, |
Автомобиль |
Время, |
|
ВАЗ-2106 |
17,5 |
Alfa |
9,0 |
|
ВАЗ-2121 |
25 |
Audi |
9,5 |
|
Москвич |
11,5 |
BMW-320i |
9,9 |
|
ЗИЛ-117 |
13 |
Cadillac |
7,2 |
|
ГАЗель-3302 |
24 |
Mercedes |
11,0 |
|
ЗАЗ-1102 |
16,2 |
Peugeot-406 |
7,9 |
|
ВАЗ-2110 |
12,0 |
Porsche-911 |
5,2 |
|
Ford |
9,2 |
VW |
17,4 |
|
Fiat |
8,8 |
Honda |
8,0 |
Примечание:
Рядом с типом автомобиля указан рабочий
объем (л)
и мощность (в скобках) двигателя (л.с.).
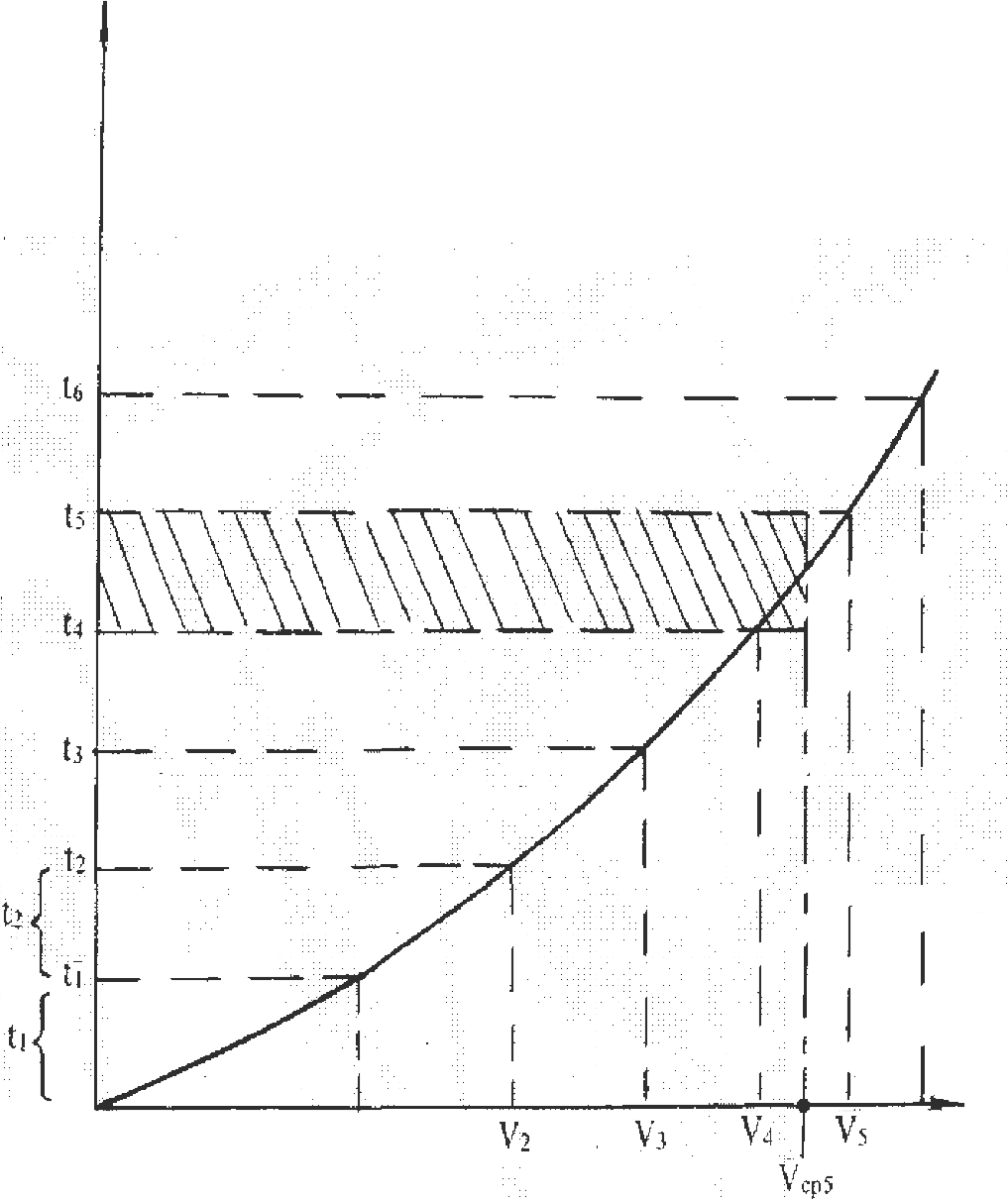
Построение графика пути разгона
автомобиля S
= f(v)
Аналогичным
образом проводится графическое
интегрирование раннее построенной
зависимости
t
= f(V)
для получения зависимости пути разгона
S
от скорости автомобиля.
В
данном случае кривая графика
времени разгона автомобиля
(рис. 5) разбивается на интервалы по
времени,
для каждого из которых находятся
соответствующие значения Vcр
k.
Рис.5. Схема,
поясняющая использование графика
времени разгона автомобиля
t
= f(V)
для
построения графика пути разгона S
= f(V).
Площадь
элементарного прямоугольника, например,
в интервале Δt5
есть
путь, который проходит автомобиль от
отметки t4
до отметки t5,
двигаясь
с постоянной скоростью Vcр
5.
Величина
площади элементарного прямоугольника
определяется следующим
образом:
ΔSk
= Vcр
k
(t
k
– t
k-1)
= Vcр
k
·
Δt
k
.
где k
= l…m
– порядковый номер интервала, m
выбирается произвольно, но считается
удобным для расчета, когда m
= n.
Например (рис. 5), если Vср5
=12,5 м/с;
t
4 =10 с;
t5
=14 с,
то ΔS5
= 12,5(14 – 10) = 5 м.
Путь разгона от скорости
V0
до скорости V1
: S1
= ΔS1;
до скорости V2
: S2
= ΔS1
+ ΔS2;
…
до скорости Vn
: Sn
= ΔS1
+ ΔS2
+ … + ΔSn
=
.
Результаты расчета заносятся
в таблицу и представляются в виде
графика (рис. 6).
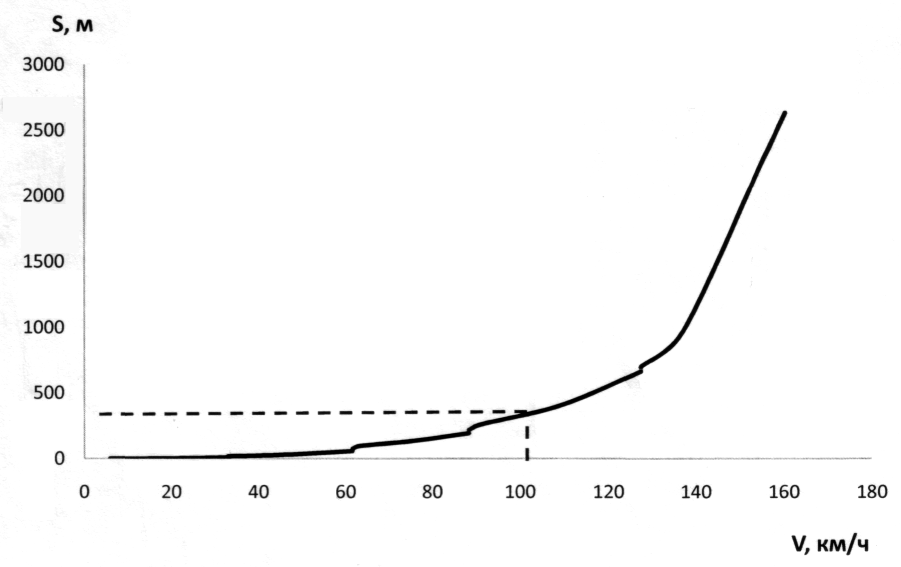
Путь разгона для легковых автомобилей
до скорости 100 км/чсоставляет 300…600м. Для грузовых автомобилей путь
разгона до скорости 50км/чравен
150…300м.
Рис.6. Графика
пути
разгона автомобиля.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Download Article
Download Article
If you’ve ever watched a bright red Ferrari fly ahead of your Honda Civic after a stoplight, you’ve experienced differing rates of acceleration firsthand. Acceleration is the rate of change in the velocity of an object as it moves. You can calculate this rate of acceleration, measured in meters per second, based on the time it takes you to go from one velocity to another, or based on the mass of an object.[1]
-
1
Define Newton’s Second Law of Motion. Newton’s second law of motion states that when the forces acting on an object are unbalanced, the object will accelerate. This acceleration is dependent upon the net forces that act upon the object and the object’s mass.[2]
Using this law, acceleration can be calculated when a known force is acting on an object of known mass.- Newton’s law can be represented by the equation Fnet = m x a, where Fnet is the total force acting on the object, m is the object’s mass, and a is the acceleration of the object.
- When using this equation, keep your units in the metric system. Use kilograms (kg) for mass, newtons (N) for force, and meters per second squared (m/s2) for acceleration.
-
2
Find the mass of your object. To find the mass of an object, simply place it on a balance or scale and find its mass in grams. If you have a very large object, you may need to find a reference that can provide you with the mass.[3]
Larger objects will likely have a mass with the unit of kilograms (kg).- For this equation, you will want to convert the mass into kilograms. If the mass you have is in grams simply divide that mass by 1000 to convert to kilograms.
Advertisement
-
3
Calculate the net force acting on your object. A net force is an unbalanced force. If you have two forces opposing each other and one is larger than the other, you will have a net force in the direction of the larger force.[4]
Acceleration happens when an unbalanced force acts on an object, causing it to change speeds towards the direction the force is pushing or pulling it.- For example: Let’s say you and your big brother are playing tug-of-war. You pull the rope to the left with a force of 5 newtons while your brother pulls the rope in the opposite direction with a force of 7 newtons. The net force on the rope is 2 newtons to the right, in the direction of your brother.
- In order to properly understand the units, know that 1 newton (N) is equal to 1 kilogram X meter/second squared (kg X m/s2).[5]
-
4
Rearrange the equation F = ma to solve for acceleration. You can change this formula around to solve for acceleration by dividing both sides by the mass, so: a = F/m.[6]
To find the acceleration, simply divide the force by the mass of the object being accelerated.- Force is directly proportional to the acceleration, meaning that a greater force will lead to a greater acceleration.
- Mass is inversely proportional to acceleration, meaning that with a greater mass, the acceleration will decrease.
-
5
Use the formula to solve for acceleration. Acceleration is equal to the net force acting on an object divided by the mass of the object. Once you’ve established the values for your variables, do the simple division to find the acceleration of the object.
- For example: A 10 Newton force acts uniformly on a mass of 2 kilograms. What is the object’s acceleration?
- a = F/m = 10/2 = 5 m/s2
Advertisement
-
1
Define the equation for average acceleration. You can calculate the average acceleration of an object over a period of time based on its velocity (its speed traveling in a specific direction), before and after that time. To do this you need to know equation for acceleration: a = Δv / Δt where a is acceleration, Δv is the change in velocity, and Δt is the amount of time it took for that change to occur.[7]
- The unit for acceleration is meters per second per second or m/s2.[8]
- Acceleration is a vector quantity, meaning it has both a magnitude and a direction.[9]
The magnitude is the total amount of acceleration whereas the direction is the way in which the object is moving. If it is slowing down the acceleration will be negative.
- The unit for acceleration is meters per second per second or m/s2.[8]
-
2
Understand the variables. You can further define Δv and Δt: Δv = vf – vi and Δt = tf – ti where vf is the final velocity, vi is the initial velocity, tf is the ending time, and ti is the starting time.[10]
- Because acceleration has a direction, it is important to always subtract the initial velocity from the final velocity. If you reverse them, the direction of your acceleration will be incorrect.
- Unless otherwise stated in the problem, the starting time is usually 0 seconds.
-
3
Use the formula to find acceleration. First write down your equation and all of the given variables. The equation is a = Δv / Δt = (vf – vi)/(tf – ti). Subtract the initial velocity from the final velocity, then divide the result by the time interval. The final result is your average acceleration over that time.
- If the final velocity is less than the initial velocity, acceleration will turn out to be a negative quantity or the rate at which an object slows down.
- Example 1: A race car accelerates uniformly from 18.5 m/s to 46.1 m/s in 2.47 seconds. What is its average acceleration?
- Write the equation: a = Δv / Δt = (vf – vi)/(tf – ti)
- Define the variables: vf = 46.1 m/s, vi = 18.5 m/s, tf = 2.47 s, ti = 0 s.
- Solve: a = (46.1 – 18.5)/2.47 = 11.17 meters/second2.
- Example 2: A biker traveling at 22.4 m/s comes to halt in 2.55 s after applying brakes. Find his deceleration.
- Write the equation: a = Δv / Δt = (vf – vi)/(tf – ti)
- Define the variables: vf = 0 m/s, vi = 22.4 m/s, tf = 2.55 s, ti = 0 s.
- Solve: a = (0 – 22.4)/2.55 = -8.78 meters/second2.
Advertisement
-
1
Understand the Direction of Acceleration. The physics concept of acceleration doesn’t always match how we would use the term in everyday life. Every acceleration has a direction, usually represented as positive if it’s UP or RIGHT, and negative if DOWN or LEFT. See if your answer makes sense based on this breakdown:
Behavior of a Car How is Velocity Changing? Direction of Acceleration Driver moving right (+) hits gas pedal + → ++ (more positive)
positive
Driver moving right (+) hits brakes ++ → + (less positive)
negative
Driver moving left (-) hits gas pedal – → — (more negative)
negative
Driver moving left (-) hits brakes — → – (less negative)
positive
Driver moves at constant velocity remains the same
acceleration is zero
-
2
Understand the Direction of Force. Remember, a force only causes acceleration in the direction of the force. Some problems may try to trick you with irrelevant values.
- Example Problem: A toy boat with mass 10kg is accelerating north at 2 m/s2. A wind blowing due west exerts a force of 100 Newtons on the boat. What is the boat’s new northward acceleration?
- Solution: Because the force is perpendicular to the direction of motion, it does not have an effect on motion in that direction. The boat continues to accelerate north at 2 m/s2.
-
3
Understand Net Force. If more than one force acts on an object, combine them into a net force before you calculate acceleration. For a problem in two dimensions, this looks something like this:
- Example Problem: April is pulling a 400 kg container right with a force of 150 newtons. Bob stand on the left of the container and pushes with a force of 200 newtons. A wind blowing left exerts a force of 10 newtons. What is the acceleration of the container?
- Solution: This problem uses tricky language to try and catch you. Draw a diagram and you’ll see the forces are 150 newtons right, 200 newtons right, and 10 newtons left. If “right” is the positive direction, the net force is 150 + 200 – 10 = 340 newtons. Acceleration = F / m = 340 newtons / 400 kg = 0.85 m/s2.
Advertisement
Calculator, Practice Problems, and Answers
Add New Question
-
Question
How do you solve acceleration word problems?
Sean Alexander is an Academic Tutor specializing in teaching mathematics and physics. Sean is the Owner of Alexander Tutoring, an academic tutoring business that provides personalized studying sessions focused on mathematics and physics. With over 15 years of experience, Sean has worked as a physics and math instructor and tutor for Stanford University, San Francisco State University, and Stanbridge Academy. He holds a BS in Physics from the University of California, Santa Barbara and an MS in Theoretical Physics from San Francisco State University.
Academic Tutor
Expert Answer
-
Question
What is the SI unit for acceleration?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
SI units are standardized units that are used internationally in scientific writing. When describing acceleration, use the SI units meters per seconds squared (m/s^2).
-
Question
How do you calculate acceleration without time?
This answer was written by one of our trained team of researchers who validated it for accuracy and comprehensiveness.
wikiHow Staff Editor
Staff Answer
If you know that acceleration is constant, you can solve for it without time if you have the initial and final velocity of the object as well as the amount of displacement. Use the formula v^2=u^2+2as where v is the final velocity, u is the initial velocity, a is acceleration, and s is displacement. Solve for a to find acceleration.
See more answers
Ask a Question
200 characters left
Include your email address to get a message when this question is answered.
Submit
Advertisement
References
About This Article
Article SummaryX
To calculate acceleration, use the equation a = Δv / Δt, where Δv is the change in velocity, and Δt is how long it took for that change to occur. To calculate Δv, use the equation Δv = vf – vi, where vf is final velocity and vi is initial velocity. To caltulate Δt, use the equation Δt = tf – ti, where tf is the ending time and ti is the starting time. Once you’ve calculated Δv and Δt, plug them into the equation a = Δv / Δt to get the acceleration. To learn how to calculate acceleration from a force, read the article!
Did this summary help you?
Thanks to all authors for creating a page that has been read 1,759,585 times.
Reader Success Stories
-
DrDave Alpenschnee
Mar 5, 2018
“I am an Alpine ski instructor, and was interested in how unbalanced forces cause one ski to accelerate more than…” more
