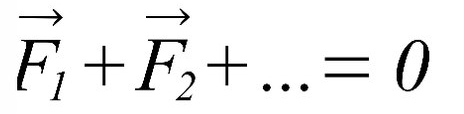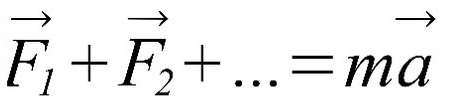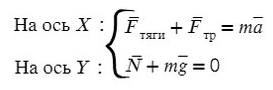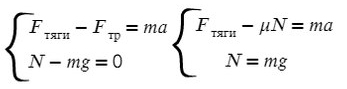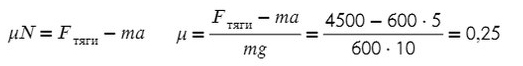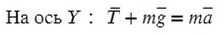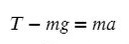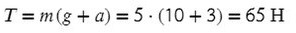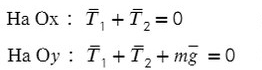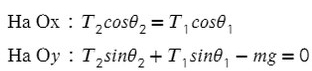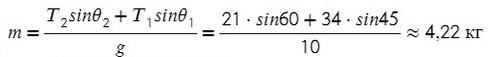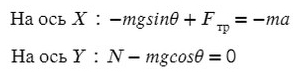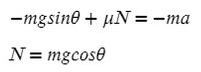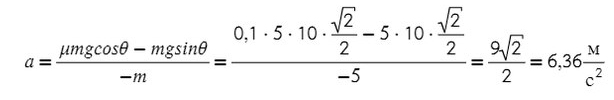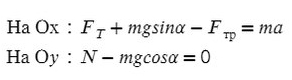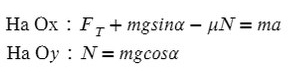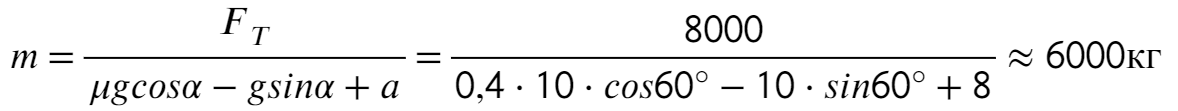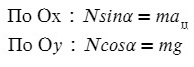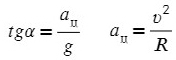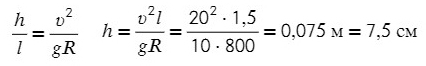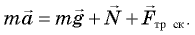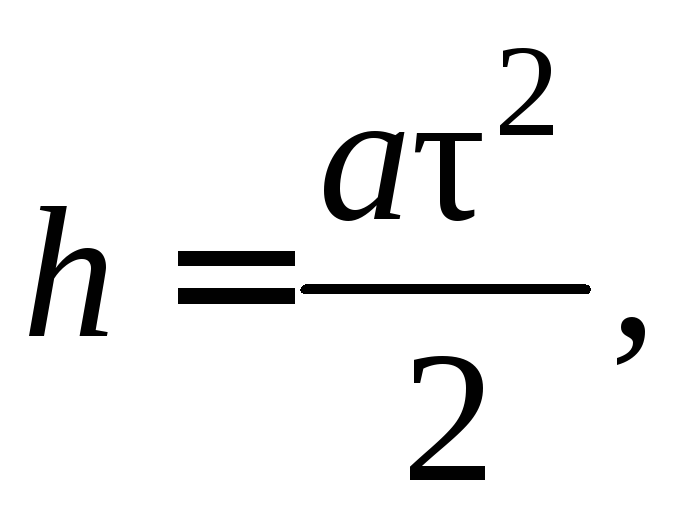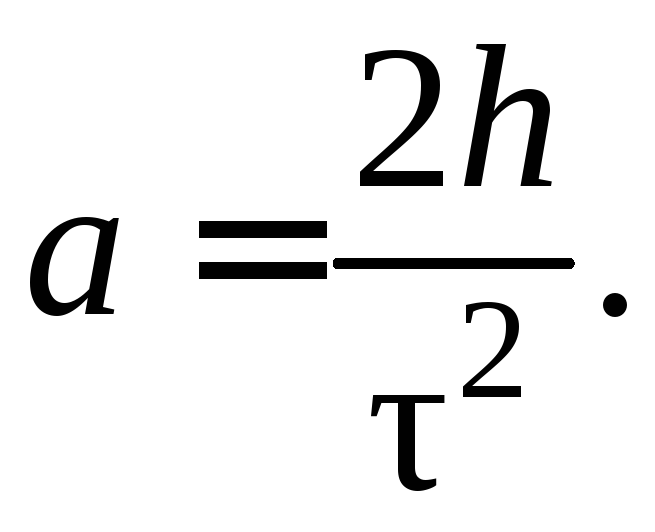Как найти ускорение бруска по наклонной плоскости

Цель этой
работы: с помощью экспериментальной установки определить ускорение
скольжения бруска по наклонной плоскости.

Для выполнения этой работы мы будем использовать оборудование
из комплекта № 5 в составе: штатив с креплением для наклонной плоскости,
направляющая со шкалой, деревянный брусок с пусковым магнитом, электронный
секундомер с датчиками, линейка и транспортир.

Прежде чем приступить к работе давайте с вами вспомним, что неравномерное
движение — это такое движение, при котором тело, за любые равные промежутки
времени совершает разные перемещения.

Из всех видов неравномерного движения в школе изучают самое
простое — прямолинейное равноускоренное движение. Так называют движение,
при котором за любые равные промежутки времени скорость тела изменяется на одну
и туже величину, а траекторией движения тела является прямая линия.

Для того,
чтобы описать насколько быстро меняется скорость тела, в физике ввели величину,
которую назвали ускорением тела. Ускорение — это физическая векторная
величина, равная отношению изменения скорости к промежутку времени, в течение
которого это изменение произошло:

Именно ускорение тела нам и предстоит определить в данной
работе. Однако очевидно, что данная формула нам не подходит, так как в ней
фигурирует скорость тела, измерить которую прямыми измерения в классе мы не
можем. А анализ оборудования нам говорит о том, что для определения ускорения
мы с вами должны воспользоваться формулой, для определения перемещения тела при
его равноускоренном движении:

Так как мы будем изучать прямолинейное равноускоренное
движение без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, то мы с вами можем записать, что модуль вектора
перемещения прямо пропорционален квадрату промежутка времени, в течение
которого это перемещение было совершено:

Отсюда, зная пройденный телом путь и время его движения, мы с
вами легко можем определить модуль ускорения, с которым двигалось тело:

Теперь
приступим к выполнению работы. Итак, для начала давайте соберём экспериментальную
установку. Для этого на штативе закрепим наклонную плоскость. После этого,
используя транспортир, установим направляющую под углом 45° к поверхности
стола.

Далее
установим на направляющей датчики секундомера: первый расположим в точке 0, а
второй — в точке 40 см. При пуске бруска пусковой магнит мы установим на пол
сантиметра выше первого датчика.

Далее мы
сделаем рисунок нашей установки. Для этого схематически изобразим штатив с
прикреплённой к нему направляющей. На направляющей расположим брусок так, как
это показано на экране. Также на рисунке мы должны будем указать перемещение
тела и направление вектора ускорения. Не лишним будет показать и угол, под
которым установлена направляющая.

Запишем формулы, которыми будем пользоваться при выполнении
данной работы. Как мы уже вспоминали, при прямолинейном равноускоренном
движении без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, модуль вектора перемещения (путь) прямо пропорционален
квадрату промежутка времени, в течение которого это перемещение было совершено:

С формулами разобрались, теперь запишем результат измерения
пути, пройденного бруском, с учётом абсолютной погрешности измерения (путь нам
дан в условии задания):

Теперь приступим непосредственно к выполнению работы. Итак,
подключаем электронные датчики к секундомеру, а брусок устанавливаем так, чтобы
пусковой магнит находился на пол сантиметра выше первого датчика. Отпускаем
брусок.

Значение промежутка времени, за которое брусок преодолел
заданный отрезок пути, записываем в бланке ответов с учётом погрешности
измерения:

Опыт повторяем ещё два раза, каждый раз записывая результаты
измерений.

Прямы измерения мы с вами завершили. Теперь давайте определим
среднее значение промежутка времени, как среднее арифметическое значение всех
трёх опытов:

Найденное среднее значение времени мы должны записать также с
учётом погрешности измерения:

И, наконец, мы определяем ускорение бруска. Для чего в
расчётную формулу подставляем значения пути и среднего времени движения бруска
на этом отрезке пути:

В выводе напишем: ускорение бруска при его движении по
наклонной плоскости равно 4,76 м/с².

Задачи по динамике.

I и II закон Ньютона.

Ввод и направление осей.

Неколлинеарные силы.

Проецирование сил на оси.

Решение систем уравнений.

Самые типовые задачи по динамике

---

Начнем с I и II законов Ньютона.

Откроем учебник физики и прочтем. I закон Ньютона: существуют такие инерциальные системы отсчета в которых… Закроем такой учебник, я тоже не понимаю. Ладно шучу, понимаю, но объясню проще.

I закон Ньютона: если тело стоит на месте либо движется равномерно (без ускорения), сумма действующих на него сил равна нулю.

Вывод: Если тело движется с постоянной скоростью или стоит на месте векторная сумма сил будет ноль.

II закон Ньютона: если тело движется равноускоренно или равнозамедленно (с ускорением), сумма сил, действующих на него, равна произведению массы на ускорение.

Вывод: Если тело двигается с изменяющейся скоростью, то векторная сумма сил, которые как-то влияют на это тело ( сила тяги, сила трения, сила сопротивления воздуха), равна массе этого тело умножить на ускорение.

При этом одно и то же тело чаще всего движется по-разному (равномерно или с ускорением) в разных осях. Рассмотрим именно такой пример.

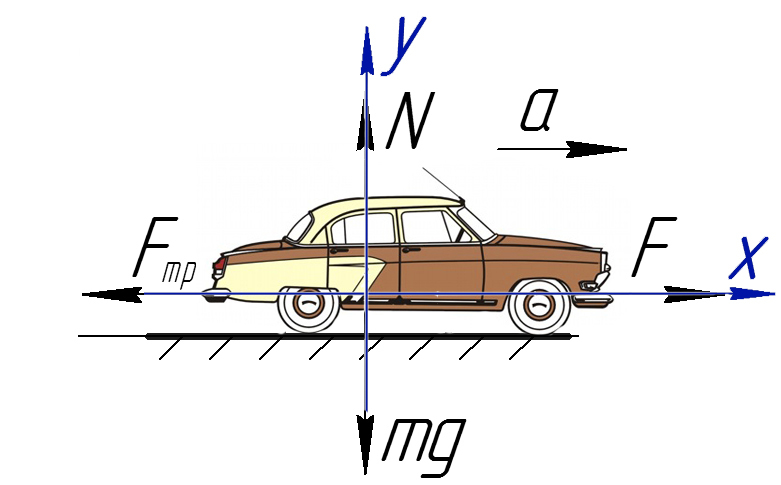
Задача 1. Определите коэффициент трения шин автомобиля массой 600 кг, если сила тяги двигателя 4500 Н вызывает ускорение 5 м/с².

Обязательно в таких задачах делать рисунок, и показывать силы, которые дествуют на машину:

На Ось Х: движение с ускорением 

На Ось Y: нет движения (здесь координата, как была ноль так и останется, машина не поднимает в горы или спускается вниз)

Те силы, направление которых совпадает с направлением осей, будут с плюсом, в противоположном случае — с минусом.

По оси X: сила тяги направлена вправо, так же как и ось X, ускорение так же направлено вправо.

Fтр = μN, где N — сила реакции опоры. На оси Y:  N = mg, тогда в данной задаче Fтр = μmg.

Получаем, что: 

Коэффициент трения — безразмерная величина. Следовательно, единиц измерения нет.

Ответ: 0,25

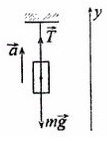
Задача 2. Груз массой 5кг, привязанный к невесомой нерастяжимой нити, поднимают вверх с ускорением 3м/с². Определите силу натяжения нити.

Сделаем рисунок, покажем силы, которые дествуют на груз

T – сила натяжения нити

На ось X: нет сил

Разберемся с направлением сил на ось Y:

Выразим T (силу натяжения) и подставим числительные значения:

Ответ: 65 Н

Самое главное не запутаться с направлением сил (по оси или против), все остальное сделает калькулятор или всеми любимый столбик.

Далеко не всегда все силы, действующие на тело, направлены вдоль осей.

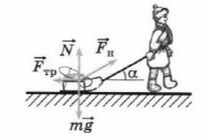
Простой пример: мальчик тянет санки

Если мы так же построим оси X и Y, то сила натяжения (тяги) не будет лежать ни на одной из осей. 

Чтобы спроецировать силу тяги на оси, вспомним прямоугольный треугольник.

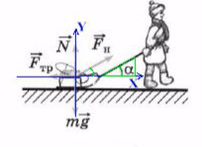
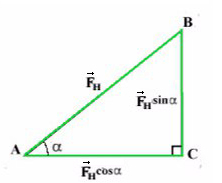
Отношение противолежащего катета к гипотенузе — это синус.

Отношение прилежащего катета к гипотенузе — это косинус.

Сила тяги на ось Y — отрезок (вектор) BC.

Сила тяги на ось X — отрезок (вектор) AC.

Если это непонятно, посмотрите задачу №4.

Чем длинее будет верека и, соответсвенно, меньше угол α, тем проще будет тянуть санки. Идеальный вариант, когда веревка параллельна земле, ведь сила, которая действуют на ось X— это Fнcosα. При каком угле косинус максимален? Чем больше будет этот катет, тем сильнее горизонтальная сила.

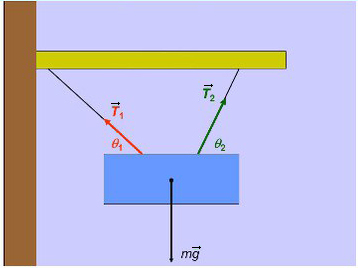
Задача 3. Брусок подвешен на двух нитях. Сила натяжения первой составляет 34 Н, второй — 21Н, θ1 = 45°, θ2 = 60°. Найдите массу бруска.

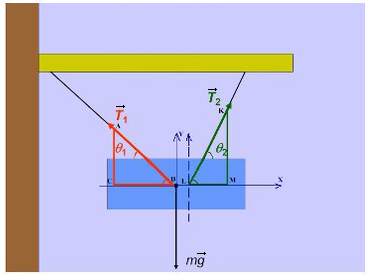
Введем оси и спроецируем силы:

Получаем два прямоугольных треугольника. Гипотенузы AB и KL — силы натяжения. LM и BC — проекции на ось X, AC и KM — на ось Y.

Ответ: 4,22 кг

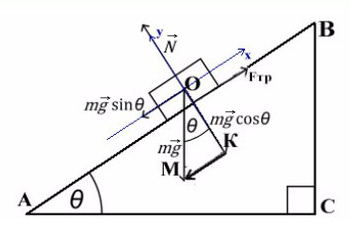
Задача 4. Брусок массой 5 кг (масса в этой задаче не нужна, но, чтобы в уравнениях все было известно, возьмем конкретное значение) соскальзывает с плоскости, которая наклонена под углом 45°, с коэффициентом трения μ = 0,1. Найдите ускорение движения бруска? 

Когда же есть наклонная плоскость, оси (X и Y) лучше всего направить по направлению движения тела. Некоторые силы в данном случае ( здесь это mg) не будут лежать ни на одной из осей. Эту силу нужно спроецировать, чтобы она имела такое же направление, как и взятые оси.
Всегда ΔABC подобен ΔKOM в таких задачах (по прямому углу и углу наклона плоскости).

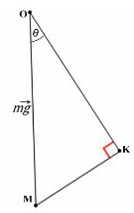
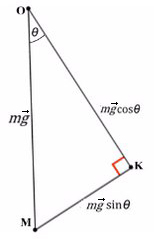
Рассмотрим поподробнее ΔKOM: 

Получим, что KO лежит на оси Y, и проекция mg на ось Y будет с косинусом. А вектор MK коллинеарен (параллелен) оси X, проекция mg на ось X будет с синусом, и вектор МК направлен против оси X (то есть будет с минусом).

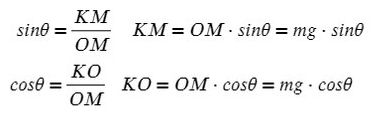
Не забываем, что, если направления оси и силы не совпадают, ее нужно взять с минусом!

Из оси Y выражаем N и подставляем в уравнение оси X, находим ускорение:

Ответ: 6,36 м/с²

Как видно, массу в числителе можно вынести за скобки и сократить со знаменаталем. Тогда знать ее не обязательно, получить ответ реально и без нее.
Да-да, в идеальных условиях (когда нет силы сопротивления воздуха и т.п.), что перо, что гиря скатятся (упадут) за одно и тоже время. 

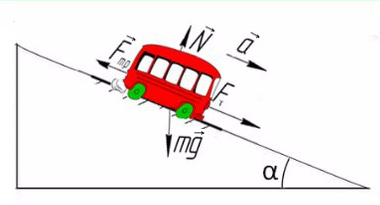
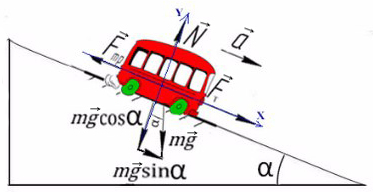
Задача 5. Автобус съезжает с горки под уклоном 60° с ускорением 8 м/с²  и с силой тяги 8 кН. Коэффициент трения шин об асфальт равен 0,4. Найдите массу автобуса.

Сделаем рисунок с силами:

Введем оси X и Y. Спроецируем mg на оси:

Запишем второй закон Ньютона на X и Y:

Ответ: 6000 кг

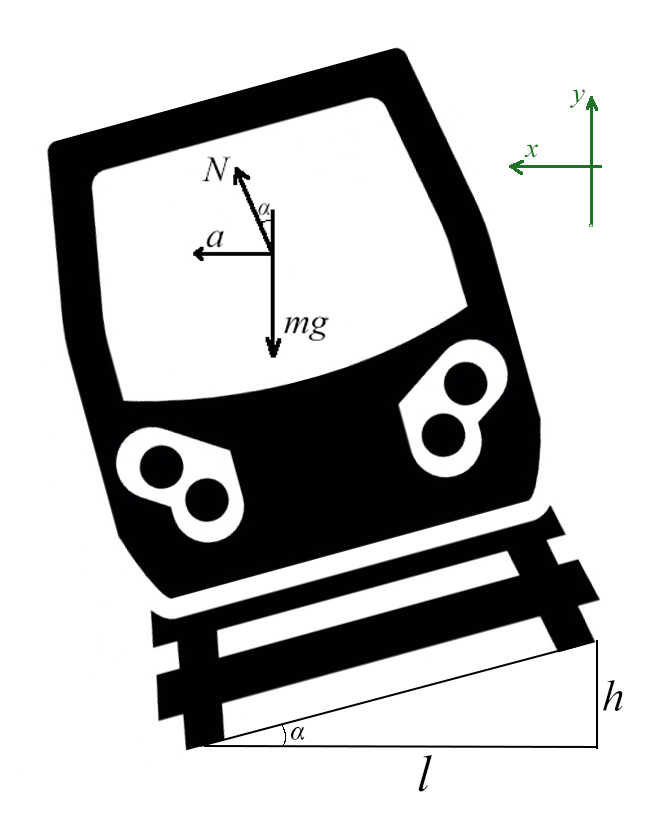
Задача 6. Поезд движется по закруглению радиуса 800 м со скоростью 72 км/ч. Определить, на сколько внешний рельс должен быть выше внутреннего. Расстояние между рельсами 1,5 м.

Самое сложное – понять, какие силы куда действуют, и как угол влияет на них.

Вспомни, когда едешь по кругу на машине или в автобусе, куда тебя выталкивает? Для этого и нужен наклон, чтобы поезд не упал набок!

Угол α задает отношение разницы высоты рельсов к расстоянию между ними (если бы рельсы находились горизонтально)

Запишем какие силы действуют на оси:

Ускорение в данной задачи центростремительное!

Поделим одно уравнение на другое:

Тангенс – это отношение противолежащего катета к прилежащему:

Ответ: 7,5 см

Как мы выяснили, решение подобных задач сводится к расстановке направлений сил, проецированию их на оси и к решению систем уравнений, почти сущий пустяк.

В качестве закрепления материала решите несколько похожих задач с подсказками и ответами. 

Будь в курсе новых статеек, видео и легкого технического юмора.



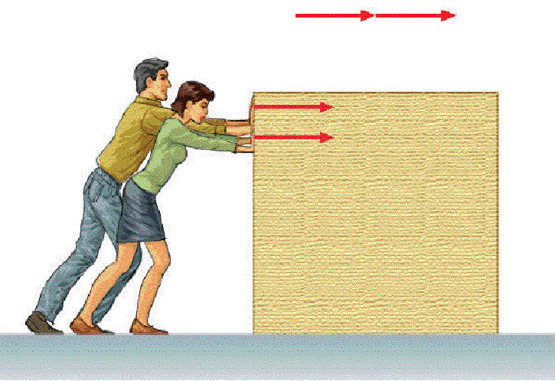
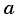
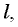
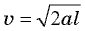
Чтобы ответить на поставленный вопрос, надо определить сначала, с каким ускорением будет двигаться брусок вдоль наклонной плоскости. Зная ускорение и пройденный путь можно будет найти скорость бруска в конце спуска, воспользовавшись уже выведенной нами формулой для равноускоренного движения (см. § 3. Ускорение. Прямолинейное равноускоренное движение).

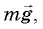
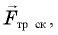
На брусок, скользящий по наклонной плоскости, действуют три силы: сила тяжести сила нормальной реакции и сила трения скольжения направленная вдоль наклонной плоскости вверх.

Чтобы найти ускорение тела, надо воспользоваться вторым законом Ньютона

Выбирая оси координат так же, как в рассмотренном выше примере, получаем:

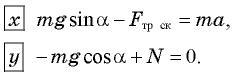
Кроме того, выполняется соотношение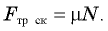

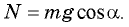
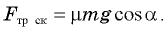
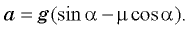
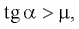
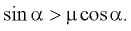
Из второго уравнения системы следует, что Обратите внимание: для тела, находящегося на наклонной плоскости, сила нормальной реакции меньше силы тяжести. Отсюда следует, что Подставляя это соотношение в первое уравнение системы, находим, что ускорение бруска Мы можем быть уверены в том, что это величина положительная, поскольку, согласно условию, брусок начал соскальзывать с наклонной плоскости — а это означает, в соответствии с предыдущим примером, что то есть

Подставляя найденное выражение для ускорения в формулу для скорости в конце спуска, получаем

Механика.
2014

 

Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.

Основная формула динамики

Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:

F¯ = m*a¯

Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.

В случае движения вращения второй закон Ньютона записывается в виде:

M = I*α

Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.

Формулы кинематики

Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:

a = Δv/Δt;

v = v₀ ± a*t;

S = v₀*t ± a*t²/2

Здесь v₀ – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.

Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:

α = Δω/Δt;

ω = ω₀ ± α*t;

θ = ω₀*t ± α*t²/2

Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.

Линейные и угловые характеристики друг с другом связаны формулами:

a = α*r;

v = ω*r

Здесь r – радиус вращения.

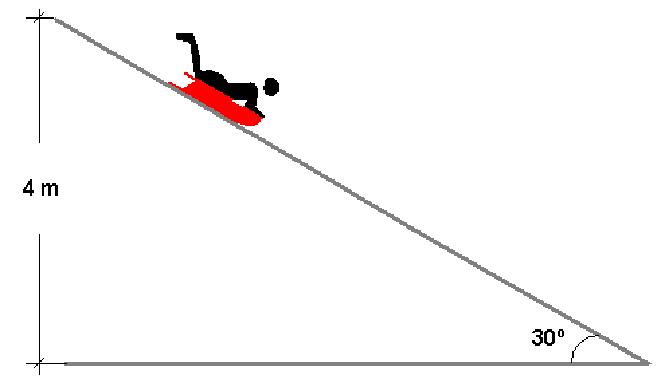
Движение по наклонной плоскости: силы

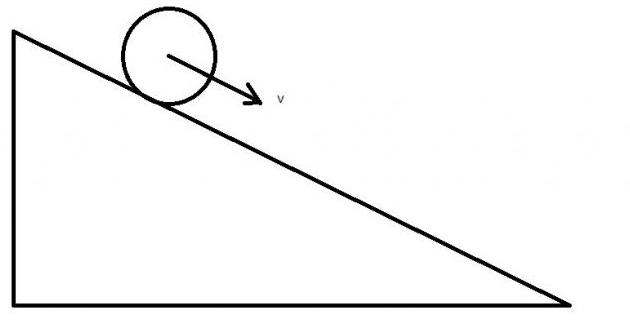
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.

Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:

• тяжести;
• реакции опоры;
• трения качения и/или скольжения;
• натяжение нити;
• сила внешней тяги.

Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.

Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения

Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.

Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:

F_f = µ*N

Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.

Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:

F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a

Здесь φ – это угол наклона плоскости к горизонту.

Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.

В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:

F = m*g*sin(φ) – F_r = m*a

Где F_r – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, F_r создает следующий момент:

M = F_r*r = I*α

Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.

Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.

Задача на движение бруска по наклонной плоскости

Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45^o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.

Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:

m*g*(sin(φ) – µ*cos(φ)) = m*a =>

a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с²

Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:

S = a*t²/2

Откуда следует выразить время, и подставить известные значения:

t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с

Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.

Задача со скатывающимся по плоскости цилиндром

Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30^o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.

Запишем соответствующие уравнения:

m*g*sin(φ) – F_r = m*a;

F_r*r = I*α = I*a/r

Момент инерции I цилиндра вычисляется по формуле:

I = 1/2*m*r²

Подставим это значение во вторую формулу, выразим из нее силу трения F_r и заменим полученным выражением ее в первом уравнении, имеем:

F_r*r = 1/2*m*r²*a/r = >

F_r = 1/2*m*a;

m*g*sin(φ) – 1/2*m*a = m*a =>

a = 2/3*g*sin(φ)

Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.

Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:

S = a*t²/2 =>

t = √(2*S/a)

Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:

v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))

Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.

Лабораторная
работа № 129

Изучение динамики поступательного движения твердого тела по наклонной плоскости

Цель
работы –
экспериментальное определение работы
силы трения при скольжении груза по
наклонной плоскости.

1. Теоретическая часть

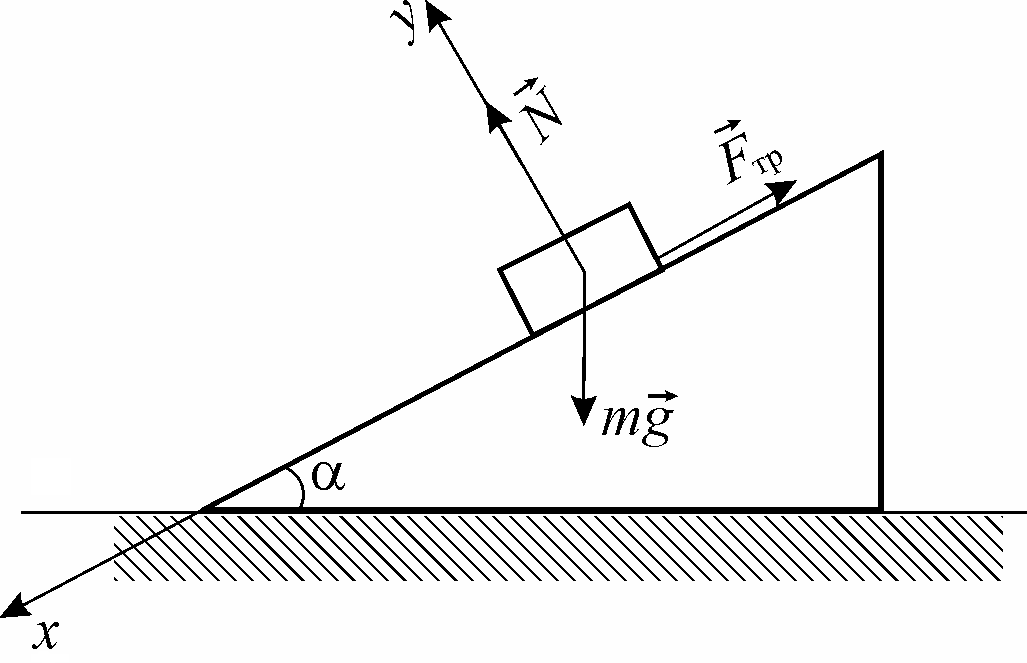
Рис.1. Брусок на
наклонной плоскости

На брусок массой
m,
находящийся на наклонной плоскости,
действуют несколько сил (рис.1) – сила
тяжести
,
сила нормальной реакции опорыи сила трения.
Под действием этих сил брусок может
двигаться или находиться в состоянии
покоя.

Рассмотрим
сначала состояние покоя, когда
равнодействующая всех сил равна нулю:

(1)

где
– сила трения покоя. Введем оси координат
так, как показано на рис. 1. Посколькуто проекция уравнения (1) на осьдает

Откуда

Т.о. в состоянии
покоя сила трения покоя уравновешивает
скатывающую силу

Если увеличивать
угол наклона
то при некотором его предельном значенииэтот баланс нарушится, и брусок начнет
соскальзывать с наклонной плоскости.
В момент начала соскальзывания сила
трения покоя
принимает
максимальное значение, равное силе
трения скольжения

.

По закону Амонтона
– Кулона сила трения скольжения по модулю
равна

,

где 
– коэффициент
трения.

Скольжение бруска
по наклонной плоскости описывается
уравнением динамики

(2)

Проекция уравнения
(2) на ось y
дает

или

.

Поэтому

.

На
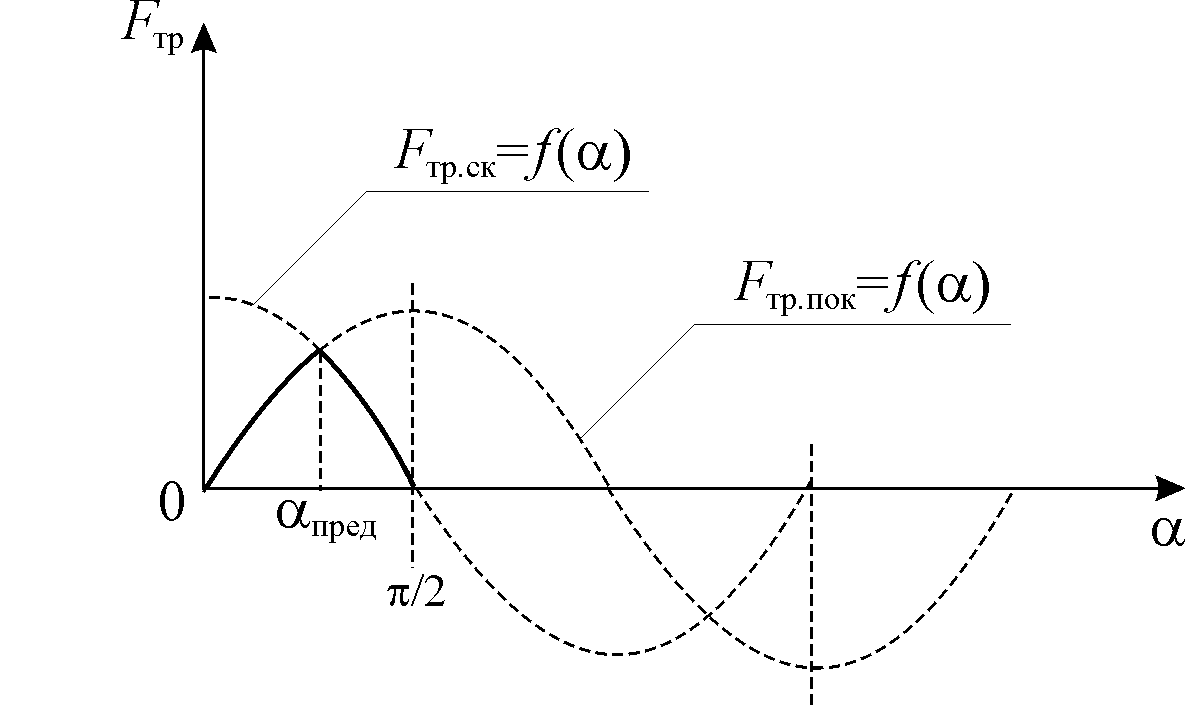
рис.2 показана зависимость сил трения
покоя и трения скольжения от угла наклонаКаждая их этих зависимостей имеет свою
область определения. Для функцииона лежит в пределах.
Область определения функциилежит в интервале.
Вне этих областей обе функции не имеют
физического смысла.

Рис.2. Зависимости
ив функции от угла

Как видно из рис.
2, с ростом угла
сила трения покоя изменяется по
синусоидальному закону, а сила трения
скольжения изменяется по закону косинуса.
Пересечение этих двух функций происходит
при угле,
при достижении которого брусок начнет
скользить вниз по наклонной плоскости.
Значениенаходится из равенства

,

откуда можно найти
коэффициент трения

(3)

Измерив длину пути
l
бруска по наклонной плоскости и угол
ее наклона
,
можно определить работу силы трения
по предельному углуи соответствующему коэффициенту трения

.
(4)

Теперь заставим
брусок массы m₁
скользить не вниз, а вверх по наклонной
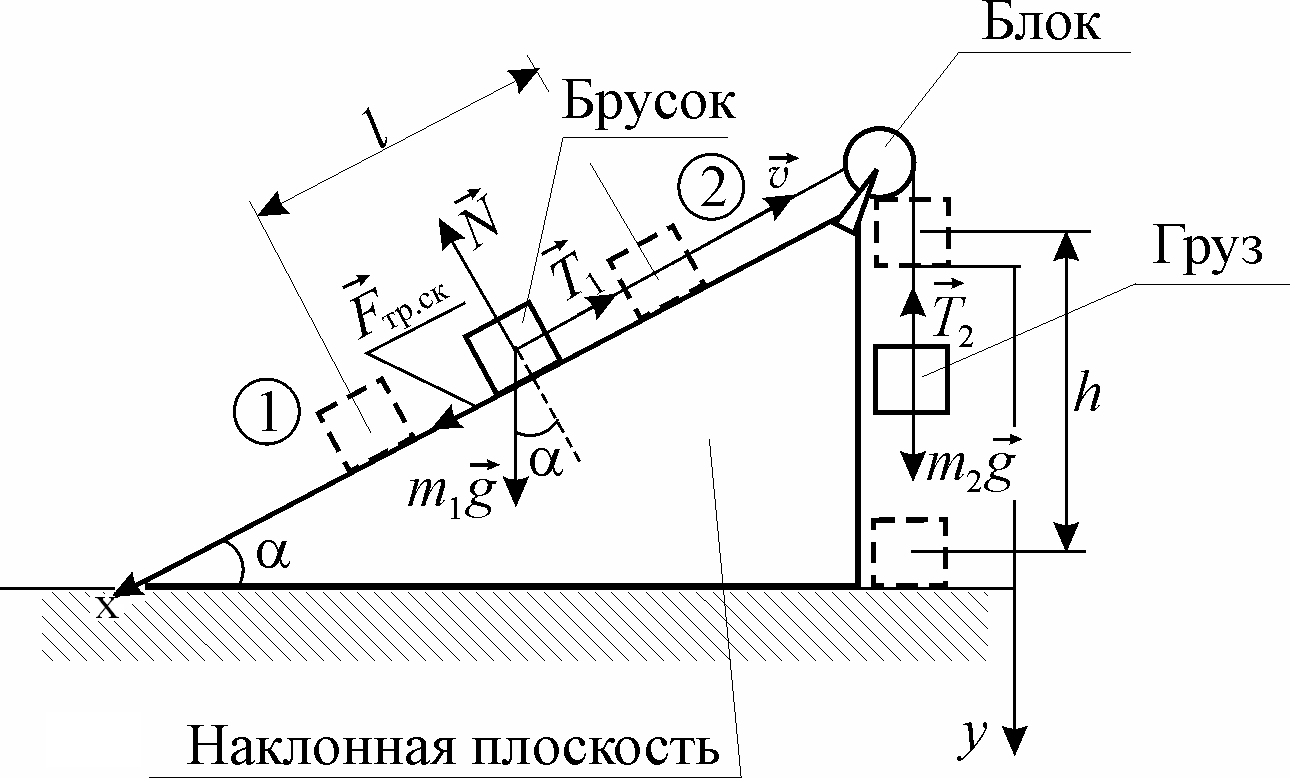
плоскости. Для этого (см. рис. 3) привяжем
к бруску конец нити, перекинутой через
блок; на другом конце нити привяжем груз
массы m₂,
при опускании которого нить будет тянуть
брусок вверх по наклонной плоскости с
ускорением а.

Рис. 3. Схема системы
наклонная плоскость – брусок-груз.

На длине пути l
вдоль наклонной плоскости (координата
)
брусок массойm₁,
при перемещении из т. 1- состояния покоя
в т. 2 приобретает некоторую скорость
и соответственно кинетическую энергиюКинетическая энергия может быть
рассчитана как суммарная работа всех
сил, приложенных к бруску:

(5)

где

.
–работа скатывающей силы,

так как

-работа силы
натяжения нити.

Далее будем
считать, что нить и блок невесомы, поэтому
натяжение нити по обе стороны от блока
одинаково: Т₁
= Т₂
= Т.
Уравнение движения (второй закон Ньютона)
груза m₂
в проекции на ось у
дает

откуда имеем
значение Т

Высота опускания
груза по законам кинематики равна:

Поэтому ускорение
груза можно выразить через измеряемые
величины – высоту h
и время 
спуска груза m₂
–

Все тела
рассматриваемой системы связаны
нерастяжимой нитью и, следовательно,
движутся с одинаковой скоростью и
ускорением. Поэтому скорость бруска
массы m₁
в конце отрезка пути длиной
l
(положение 2) равна

.

С учетом измеренных
и рассчитанных величин уравнение (5)
перепишется в виде

,

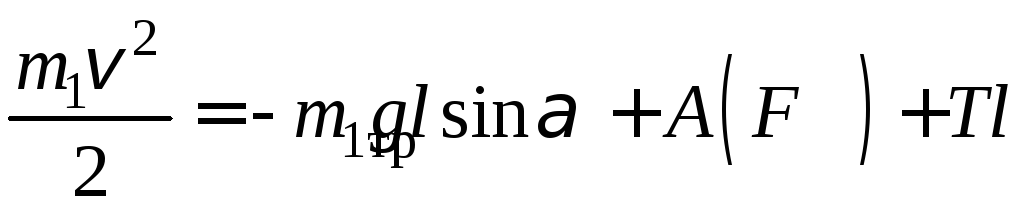
или

откуда

. (6)

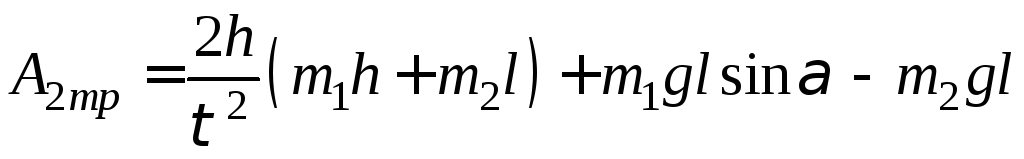
Учтем, что длина
участка 1-2 подъема бруска по наклонной
плоскости равна высотеопускания груза (),
тогда из (5) получимвыражение
для определения работы силы трения
по
кинематическим параметрам (углу наклона

,длине

и времени
)перемещения
бруска по наклонной плоскости

. (7)

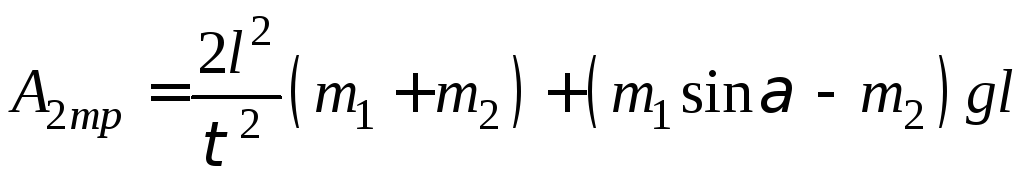
Приборы и
пренадлежности:

1. Лабораторная
установка.

2. Набор грузов.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #