Прямолинейное равноускоренное движение — это прямолинейное движение, при котором скорость тела изменяется (увеличивается или уменьшается) на одну и ту же величину за равные промежутки времени.
Ускорение — физическая величина, характеризующая быстроту изменения скорости тела. То есть, показывает, на какую величину изменяется скорость за единицу времени.
Примеры равноускоренного движения:
- разгон самолета перед взлетом;
- падающая с крыши сосулька;
- торможение лыжника на горном склоне;
- разгоняющийся на склоне сноубордист;
- свободное падение в результате прыжка с парашютом;
- камень брошенный под углом к горизонту;
Равномерное прямолинейное движение является частным случаем равноускоренного движения, при котором ускорение равно нулю.
Равноускоренное движение: формулы
Формула для скорости при равноускоренном движении:
Vк=Vн+at
где: Vк — конечная скорость тела,
Vн — начальная скорость тела,
a=const — ускорение (a>0 при ускорении, a<0 при замедлении)
t — время.
Формула для ускорения при равноускоренном движении:
a=(Vк-Vн)/t
Во время движения тела ускорение остается постоянным.
Задача 1
Кирилл ехал на велосипеде со скоростью 6 м/с, затем начал разгоняться на горке. Чему будет равна его скорость через 10 секунд, если ускорение равно 0,5 м/с?
Решение. Vн=6м/с, ускорение a=0,5м/с, время разгона t=10 секунд.
Получаем: Vн= 6 + 0,5 · 10 = 11 м/с.
Ответ: за 10с Кирилл разгонится до скорости 11 м/с.
Формула расстояния при равноускоренном движении
- Если известны время, скорость начальная и скорость конечная
S = t*(Vн+ Vк)/2
- Если известны время, скорость начальная и ускорение
S = Vнt + at2/2 = t*(Vн + at/2)
где: S — путь, пройденный за время t,
Vн — начальная скорость,
Vк — конечная скорость,
a — ускорение тела,
t — время.
В случае равноускоренного движения с неизвестным временем движения, но с заданными начальной и конечной скоростями пройденный путь можно найти с помощью следующей формулы:
2аS = Vк2−Vн2
где S — путь, пройденный за время t ,
V0 — начальная скорость,
V — скорость в момент времени t,
a — ускорение тела.
Задача 2
Таксист получил заказ и начал движение с ускорением 0,1 м/с2. На каком расстоянии от начала движения его скорость станет равной 15м/с?
Решение. Так как таксист начал движение, начальная скорость равна нулю (Vн=0), Vк=15м/с, ускорение a=0,1м/с2.
Получаем:
S = 15^2 — 0^2 =1125 м.
Ответ: на расстоянии 1 125 м от начала движения скорость такси станет равной 15 м/с.
Перемещение при равноускоренном движении
Важно напомнить разницу между путем и перемещением тела.
- Путь — длина траектории. Если тело движется в любом направлении, то его путь увеличивается. Путь — всегда положительное значение.
- Перемещение — вектор, соединяющий начальное и конечное положение тела. Проекция перемещения может принимать отрицательное значение.
Например, если путник прошел в одну сторону расстояние S1, а обратно — S2, то: путь тела равен S1 + S2, а перемещение равно S1 − S2. В некоторых задачах путь и перемещение могут совпадать, но не всегда.
Равноускоренное движение: графически
График зависимости ускорения от времени:
Во время движения тела ускорение остается постоянным.
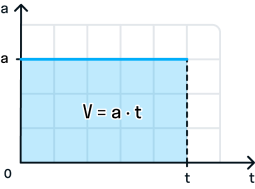
Взаимосвязь скорости, времени и расстояния:
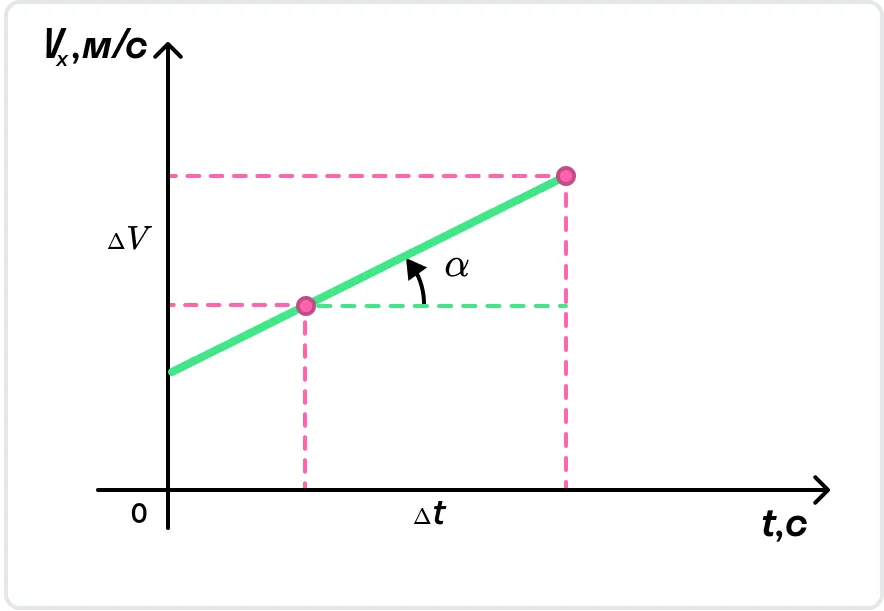
На рисунке показан график, в котором скорость равномерно увеличивается.
С помощью графика скорости можно определить ускорение тела как тангенс угла наклона графика к оси времени.
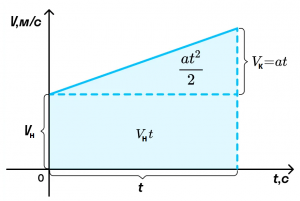
Из графика скорости получим формулу пути при равноускоренном движении тела.
Пройденный телом путь при равноускоренном движении численно равен площади фигуры под графиком зависимости скорости от времени. Вычислим площадь трапеции как сумму площадей прямоугольника Vнt и треугольника at2/2. Получим: S = Vнt + at2/2.
Математически зависимость координаты от времени при равноускоренном движении представляет собой квадратичную функцию, ее график — парабола.
Задача 3
Лыжник подъехал со скоростью 3 м/с к спуску длиной 36 м и съехал с него за несколько секунд, при этом его конечная скорость составила 15 м/с. Определите местонахождение лыжника спустя 2с после начала движения из начала координат.
Дано:
Vн = 3 м/с, начальная координата (t) равна нулю,
Vк = 15м/с,
a — скорость лыжника увеличивается, поэтому ускорение — положительное число,
S = 36м — путь с горы,
t — 2с.
Решение:
Найдем ускорение из формулы пути при равноускоренном движении: 2аS = Vк2−Vн2
Получим: а = (Vк2−Vн2 )/2S = (225-9)/(2*36) = 3 м/с2.
Составим уравнение движения лыжника исходя из формулы: S = Vнt + at2/2.
Получаем: x(t) = 3t + 1,5t2
По уравнению определим координату лыжника в момент времени t = 2с:
Получаем: x(2) = 3*2 + 1,5*22 =6+6=12 м.
Ответ: через 2 с после начала движения координата лыжника будет равна 12 м.
Для того, чтобы проверить правильность решения задач на равноускоренное движение, воспользуйтесь калькулятором равноускоренного движения.
Для того, чтобы перевести единицы измерения, воспользуйтесь конвертерами единиц измерения:
- Конвертер единиц измерения расстояния (длины)
- Конвертер единиц измерения скорости
- Конвертер единиц измерения времени
Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-

1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-

2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк – vн и Δt = tк – tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-

3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк – vн)/(tк – tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 – 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк – vн)/(tк – tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 – 22,4)/2,55 = -8,78 м/с2.
Реклама
-

1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-

2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-

3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-

4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-

5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется – → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → – (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -

2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-

3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 – 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 190 101 раз.
Была ли эта статья полезной?
Темп изменения скорости называется ускорением. Другими словами, если скорость возрастала на одну и ту же величину в единицу времени, то такое движение называется движение с равномерным ускорением.
.
Найти ускорение движения тела
Расстояние, ускорение, скорость
Какое бывает ускорение
Ускорение бывает равномерное, положительное и отрицательное.
- Если скорость изменяется (возрастает или убывает) равномерно, то ускорение называется равномерным;
- Если скорость возрастает, то ускорение положительно;
- Если скорость убывает, то ускорение отрицательно.
Формула для нахождения ускорения: a=v/t
Путь, скорость и ускорение
Формула v=at дает соотношение между скоростью, ускорением и временем, а формула S = at2/2 дает соотношение между путем, ускорением и временем. До сих пор, однако, мы не имели соотношения между путем S, скоростью и и ускорением а. Один из способов вывести это соотношение заключается в подстановке t2, выраженного через v и а, в формулу S = at2/2. Решая относительно t формулу v=at, мы получим t=v/a. Возведя обе части в квадрат: t2=v2/a2, подставляя v2/a2 вместо t2, имеем
v2 = 2aS
Задача:
Скорость автомобиля 90 см/сек. Через 3 сек его скорость равна нулю. Найдите его отрицательное ускорение (темп равномерного уменьшения скорости).
Решение:
a=-v/t
Подстановка значений:
a=-90/3=-30 см/сек. за 1 сек.
Ответ можно записать и так: 30 см/сек2, это будет означать, что автомобиль уменьшает свою скорость на 30 см/сек за каждую секунду.
Валентина Вавилова(Серкова)
Гений
(62183)
12 лет назад
Из формулы перемещения при равноускоренном движении
S=( v^2 – v0^2 ) / 2a . ( S -расстояние, v – конечная скорость, v0 – начальная скорость, а – ускорение ). Отсюда ускорение a=( v^2 – v0^2 ) / 2S .
Leonid
Высший разум
(388685)
12 лет назад
Посмотреть в учебнике. В главе про равноускоренное движение есть формулы, связывающие пройденный путь, время, скорость и ускорение движения. В том числе есть и формула, напрямую показывающая путь как функцию скорости и ускорения
Все мы знаем, что расстояние, скорость и ускорение — физические сущности, неразрывно связанные между собой. В результате мы собираемся обсудить, как найти ускорение со скоростью и расстоянием в этом посте.
Когда ускорение является постоянным в кинематике, уравнение постоянного ускорения можно использовать для нахождения ускорения, даже если вы не знаете время. Его можно найти, используя начальную скорость, конечную скорость и расстояние, пройденное объектом или телом.
Прежде чем перейти к поиску ускорение со скоростью и расстоянием, давайте рассмотрим некоторые уравнения постоянного ускорения, которые могут помочь нам найти ускорение.
Кинематика — это дисциплина физики, изучающая основы движения. Вы можете найти эту одну точную величину, если известны несколько величин. Уравнения постоянного ускорения, также известные как формулы кинематики, представляют собой тип задачи, в которой ускорение вычисляется с использованием различных переменных, таких как расстояние, скорость и время. Для определения ускорения объекта или тела в уравнении движения с постоянным ускорением можно использовать три уравнения.
Уравнения постоянного ускорения ИЛИ формулы кинематики:
Формулы кинематики, которые имеют значение только тогда, когда объект или тело движется с постоянным ускорением в течение заданного интервала времени, известны как уравнения постоянного ускорения. Когда дело доходит до постоянного ускорения, ускорение, вызванное силой тяжести, является лучшим примером из реальной жизни. Обычно его обозначают буквой «g», значение которой на поверхности земли составляет 9.8 м/с.2.
Кинематические формулы, часто известные как уравнения постоянного ускорения, представляют собой ряд формул, связывающих пять кинематических переменных, приведенных ниже.
- постоянное ускорение
- v0 Начальная скорость
- v Финальная скорость
- t Временной интервал
- 𝛥x Расстояние, пройденное объектом в одном направлении
Предположим, что объект или тело испытывает постоянное ускорение, и три из этих пяти кинематических переменных (a, v, v0, t, x) известны. В этом случае мы можем использовать кинематические уравнения, приведенные ниже, для решения одной из неизвестных переменных.
1. v = v0 + в
2. 𝛥х = v0t + (1/2) при2
3. V2 = V02 + 2а𝛥х
Как выбрать и применить формулу постоянного ускорения?
В кинематике у нас есть три уравнения постоянного ускорения. Из пяти кинематических переменных в каждом уравнении присутствуют четыре.
Мы должны выбрать уравнение постоянного ускорения, которое включает в себя как искомую неизвестную переменную, так и три известные кинематические переменные. Вводя известные значения переменных в уравнение, мы можем найти неизвестную переменную, которая неизвестна только в уравнении.
Рассмотрим случай перетаскивания коробки, которая изначально была устойчивой. Через 5 секунд его скорость увеличилась до 10 м/с. Рассмотрим постоянное ускорение в течение 5 секунд. Потому что у нас есть v0, v и t можно найти значение неизвестного постоянного ускорения, применяя уравнение v = v0 + в.
Но наша основная задача в этой статье — выяснить, как рассчитать ускорение, используя скорость и расстояние. Итак, давайте теперь поговорим о том, как найти ускорение через скорость и расстояние.
Как найти ускорение через скорость и расстояние?
Уравнение постоянного ускорения используется в кинематике для нахождения ускорения с использованием скорости и расстояния.
Если у нас есть начальная скорость, конечная скорость и расстояние, но не известен временной интервал, мы можем применить уравнение постоянного ускорения v2 = V02 + 2a𝛥x, чтобы получить ускорение.
У нас есть три известные величины и одна неизвестная величина в приведенном выше уравнении. Мы можем рассчитать постоянное ускорение, поместив все три известных значения в уравнение и сделав ускорение предметом уравнения. В результате ускорение определяется преобразованием приведенного выше уравнения и определяется как:
Мы можем найти ускорение со скоростью и расстоянием, используя приведенное выше уравнение. Имейте в виду, что уравнения постоянного ускорения работают только в том случае, если ускорение постоянно (как следует из названия) и в одном направлении. При работе с двухмерным или трехмерным движением все становится сложнее. Однако, применяя приведенные выше уравнения для постоянного ускорения, можно построить уравнения движения для каждого направления отдельно. Эти простые уравнения не используются при изменении ускорения; вместо этого используется комплексное исчисление.
Давайте рассмотрим некоторые проблемы нахождения ускорения с использованием скорости и расстояния.
Задача: Велосипед постоянно разгоняется из состояния покоя до скорости 10 м/с на пути 20 м. Определить ускорение велосипеда.
Данный:
Начальная скорость велосипеда v0 = 0 м/с (первоначально велосипед покоится)
Конечная скорость велосипеда v = 10 м/с.
Расстояние, пройденное велосипедом 𝛥x = 20 м
Найти:
Постоянное ускорение велосипеда a = ?
Решение:
Подставляя значения в приведенное выше уравнение:
∴ а = 2.5 м/с2
В результате ускорение велосипеда равно 2.5 м/с.2.
Задача: С высоты 1.40 метра на Луну падает перо. Если скорость пера 2.135 м/с, то определите ускорение свободного падения на Луне.

Изображение Кредиты: Википедия
Данный:
Начальная скорость пера v0 = 0 м/с (Поскольку при свободном падении начальная скорость равна нулю)
Конечная скорость пера v = 2.135 м/с
Путь, пройденный пером 𝛥x = 1.40 м
Найти:
Ускорение из-за гравитация на поверхности луны а =?
Решение:
Подставляя значения в приведенное выше уравнение:
∴ а = 1.625 м/с2
В результате получаем постоянное значение гравитационное ускорение на поверхности Луны, что составляет 1.625 м/с.2.
Задача: Гоночный катер со скоростью 12 м/с пересекает финишную черту и продолжает движение прямо. Он остановился в 18 метрах от финиша. Чему равно ускорение гоночной лодки, если она мгновенно затормозится до полной остановки?
Данный:
Начальная скорость гоночного катера v0 = 12 м / с
Конечная скорость гоночной лодки v = 0 м/с (при остановке)
Расстояние, пройденное гоночной лодкой 𝛥x = 18 м
Найти:
Постоянное ускорение гоночной лодки a = ?
Решение:
Подставляя значения в приведенное выше уравнение:
∴ а = -4 м/с2
Знак минус указывает на то, что ускорение гоночного катера уменьшается и его значение равно 4 м/с.2.
Мы надеемся, что ответили на все ваши вопросы о том, как найти ускорение через скорость и расстояние.
Исследуйте передовая наука и исследования сообщения, чтобы узнать больше.
