Как найти ускорение грузов физика

Как найти ускорение — определение и формулы расчета в физике

Содержание:

• Что такое ускорение
  • Единица измерения
• Как рассчитать ускорение: формулы
  • Для прямолинейного движения
  • Для равноускоренного движения
  • Для равнозамедленного движения
  • Нахождение ускорения через массу и силу
• Мгновенное ускорение
• Максимальное ускорение
• Среднее ускорение
• Проекция ускорения

Что такое ускорение

Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.

Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.

Единица измерения

В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

Как рассчитать ускорение: формулы

Для прямолинейного движения

Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.

В этом случае ускорение находится по следующим формулам:

(a;=;frac{mathrm V}t)

(a;=;frac{2S}{t^2})

(a;=;frac{V^2}{2S})

Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.

Время отсчитывается от начала движения тела.

При прямолинейном равномерном движении ускорение по модулю равняется нулю.

Для равноускоренного движения

Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).

При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.

Для равнозамедленного движения

Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).

При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V₀ и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.

Нахождение ускорения через массу и силу

Принцип инерции Галилея:

Если не действовать на тело, то его скорость не будет меняться.

Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.

Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).

II закон Ньютона:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

или

(overrightarrow a=frac{overrightarrow F}m)

Мгновенное ускорение

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.

Выражается по формуле:

( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})

Максимальное ускорение

(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.

Среднее ускорение

Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.

(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.

Проекция ускорения

Определение проекции ускорения на ось (х):

(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.

Текст с ошибкой:

Расскажите, что не так

Использование простых механизмов в физике позволяет изучать различные природные процессы и законы. Одним из этих механизмов является машина Атвуда. Рассмотрим в статье, что она собой представляет, для чего используется, и какие формулы описывают принцип ее работы.

Что такое машина Атвуда?

Названная машина представляет собой простой механизм, состоящий из двух грузов, которые соединены переброшенной через неподвижный блок нитью (веревкой). В данном определении следует пояснить несколько нюансов. Во-первых, массы грузов в общем случае являются разными, что обеспечивает наличие у них ускорения под действием силы тяжести. Во-вторых, нить, связывающая грузы, считается невесомой и нерастяжимой. Эти предположения значительно облегчают последующие расчеты уравнений движения. Наконец, в-третьих, неподвижный блок, через который переброшена нить, также считается невесомым. Кроме того, во время его вращения пренебрегают силой трения. Ниже на схематическом рисунке показана эта машина.

Вам будет интересно:Пространственная экономика: описание специальностей и структура

Вам будет интересно:Что такое подполье? Подпольная организация “Молодая гвардия”. Антифашистское движение

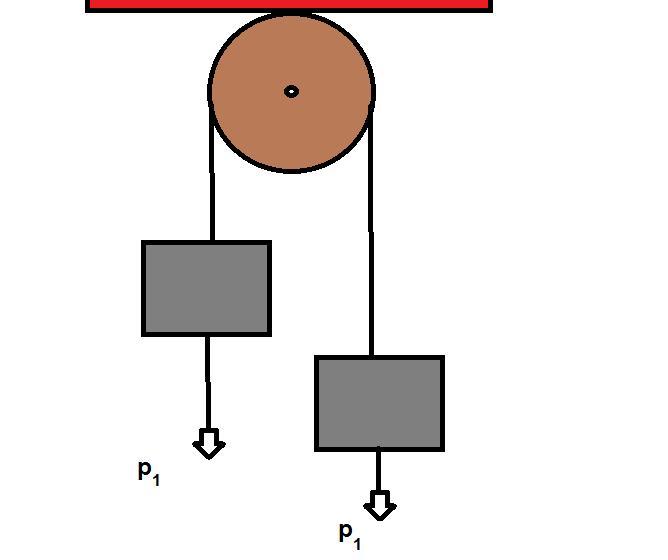
Машина Атвуда была изобретена английским физиком Джорджем Атвудом в конце XVIII века. Служит она для изучения законов поступательного движения, точного определения ускорения свободного падения и экспериментальной проверки второго закона Ньютона.

Уравнения динамики

Каждый школьник знает, что ускорение у тел появляется только в том случае, если на них оказывают действие внешние силы. Данный факт был установлен Исааком Ньютоном в XVII веке. Ученый изложил его в следующем математическом виде:

F = m*a.

Где m – инерционная масса тела, a – ускорение.

Изучение законов поступательного движения на машине Атвуда предполагает знание соответствующих уравнений динамики для нее. Предположим, что массы двух грузов равны m1 и m2, причем m1>m2. В таком случае первый груз будет перемещаться вниз под действием силы тяжести, а второй груз будет двигаться вверх под действием силы натяжения нити.

Рассмотрим, какие силы действуют на первый груз. Их две: сила тяжести F1 и сила натяжения нити T. Силы направлены в разных направлениях. Учитывая знак ускорения a, с которым перемещается груз, получаем следующее уравнение движения для него:

F1 – T = m1*a.

Что касается второго груза, то на него действуют силы той же природы, что и на первый. Поскольку второй груз движется с ускорением a, направленным вверх, то уравнение динамики для него принимает вид:

T – F2 = m2*a.

Таким образом, мы записали два уравнения, в которых содержатся две неизвестных величины (a и T). Это означает, что система имеет однозначное решение, которое будет получено далее в статье.

Расчет уравнений динамики для равноускоренного движения

Как мы видели из записанных выше уравнений, результирующая сила, действующая на каждый груз, остается неизменной в процессе всего движения. Масса каждого груза также не меняется. Это означает, что ускорение a будет постоянным. Такое движение называют равноускоренным.

Изучение равноускоренного движения на машине Атвуда заключается в определении этого ускорения. Запишем еще раз систему динамических уравнений:

F1 – T = m1*a;

T – F2 = m2*a.

Чтобы выразить значение ускорения a, сложим оба равенства, получаем:

F1 – F2 = a*(m1 + m2) =>

a = (F1 – F2)/(m1 + m2).

Подставляя явное значение сил тяжести для каждого груза, получаем конечную формулу для определения ускорения:

a = g*(m1 – m2)/(m1 + m2).

Отношение разницы масс к их сумме называют числом Атвуда. Обозначим его na, тогда получим:

a = na*g.

Проверка решения уравнений динамики

Выше мы определили формулу для ускорения машины Атвуда. Она является справедливой только в том случае, если справедлив сам закон Ньютона. Проверить этот факт можно на практике, если провести лабораторную работу по измерению некоторых величин.

Лабораторная работа с машиной Атвуда является достаточно простой. Суть ее заключается в следующем: как только грузы, находящиеся на одном уровне от поверхности, отпустили, необходимо засечь время движения грузов секундомером, а затем, измерить расстояние, на которое переместился любой из грузов. Предположим, что соответствующие время и расстояние равны t и h. Тогда можно записать кинематическое уравнение равноускоренного движения:

h = a*t2/2.

Откуда ускорение определяется однозначно:

a = 2*h/t2.

Отметим, что для увеличения точности определения величины a, следует проводить несколько экспериментов по измерению hi и ti, где i – номер измерения. После вычисления значений ai, следует рассчитать среднюю величину acp из выражения:

acp = ∑i=1mai/m.

Где m – количество измерений.

Приравнивая это равенство и полученное ранее, приходим к следующему выражению:

acp = na*g.

Если данное выражение оказывается справедливым, то таковым также будет и второй закон Ньютона.

Расчет силы тяжести

Выше мы предположили, что значение ускорения свободного падения g нам известно. Однако при помощи машины Атвуда определение силы тяжести также оказывается возможным. Для этого вместо ускорения a из уравнений динамики следует выразить величину g, имеем:

g = a/na.

Чтобы найти g, следует знать, чему равно ускорение поступательного перемещения. В пункте выше мы уже показали, как его находить экспериментальным путем из уравнения кинематики. Подставляя формулу для a в равенство для g, имеем:

g = 2*h/(t2*na).

Вычислив значение g, несложно определить силу тяжести. Например, для первого груза ее величина будет равна:

F1 = 2*h*m1/(t2*na).

Определение силы натяжения нити

Сила T натяжения нити является одним из неизвестных параметров системы динамических уравнений. Выпишем еще раз эти уравнения:

F1 – T = m1*a;

T – F2 = m2*a.

Если в каждом равенстве выразить a, и приравнять оба выражения, тогда получим:

(F1 – T)/m1 = (T – F2)/m2 =>

T = (m2*F1 + m1*F2)/(m1 + m2).

Подставляя явные значения сил тяжести грузов, приходим к конечной формуле для силы натяжения нити T:

T = 2*m1*m2*g/(m1 + m2).

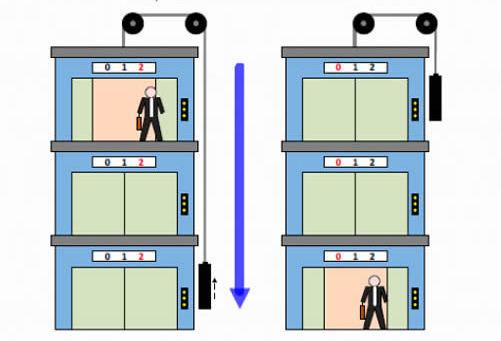
Машина Атвуда имеет не только теоретическую пользу. Так, подъемник (лифт) использует при своей работе контргруз с целью подъема на высоту полезного груза. Такая конструкция значительно облегчает работу двигателя.

Решение.
Покажем силы которые действуют на груз и ускорение. Применим второй закон Ньютона

[ vec{F}={{m}_{1}}cdot vec{a}.{{vec{F}}_{H}}+{{m}_{1}}cdot vec{g}={{m}_{1}}cdot vec{a}.,Oy:,{{m}_{1}}cdot g-{{F}_{H}}={{m}_{1}}cdot a,{{F}_{H}}={{m}_{1}}cdot g-{{m}_{1}}cdot a(1). ]

Рассмотрим барабан. Барабан вращается вокруг своей оси, возникает крутящий момент который равен произведению силы которая действует на барабан на радиус барабана

М = F_H∙R   (2).

Барабан вращается с угловым ускорением, уравнение динамики вращательного движения имеет вид

М = J∙ε   (3).

Где: J – момент инерции цилиндра, ε – угловое ускорение цилиндра.
Момент инерции цилиндра определяется по формуле

[ J=frac{mcdot {{R}^{2}}}{2} (4). ]

Ускорение с которым движется груз, равно тангенциальному ускорению цилиндра, выразим угловое ускорение цилиндра через ускорение груза

[ varepsilon =frac{a}{R}(5). ]

(5) и (4) подставим в (3), (3) подставим в (2) выразим силу натяжения нити, и силу натяжения нити подставим в (1) определим ускорение груза

[ begin{align}
  & M=frac{mcdot {{R}^{2}}}{2}cdot frac{a}{R},frac{mcdot {{R}^{2}}}{2}cdot frac{a}{R}={{F}_{H}}cdot R,{{F}_{H}}=frac{mcdot a}{2},frac{mcdot a}{2}={{m}_{1}}cdot g-{{m}_{1}}cdot a, \
 & frac{mcdot a}{2}+{{m}_{1}}cdot a={{m}_{1}}cdot g,acdot (frac{m}{2}+{{m}_{1}})={{m}_{1}}cdot g,a=frac{{{m}_{1}}cdot g}{frac{m}{2}+{{m}_{1}}}=frac{2cdot {{m}_{1}}cdot g}{m+2cdot {{m}_{1}}}. \
 & a=frac{2cdot 3cdot 10}{12+2cdot 3}=3,33. \
end{align} ]

Ответ: 3,33 м/с².

Блоки, нити, грузы и перегрузки

Задача 1.  К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .

Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона

Откуда найдем ускорение системы:

Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего  и нижнего грузов:

Откуда

Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:

Ответ: Н, Н, Н.

Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н. Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?

Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:

Теперь можно написать уравнения:

Вычитаем уравнения:

Ответ: м/с.

Задача 3.

Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.

Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:

Сложим уравнения:

Откуда

Теперь можно найти и силу натяжения нити:

Сила давления на блок равна :

Ответ: , ,
.

Задача 4.

Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа  массой , слева (рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.

Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:

Сложение уравнений даст нам

Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:

Определим силу давления меньшего перегрузка массой на груз :

Для большего перегрузка

Ответ: , , , .

Задача 5.

Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.

Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:

Для правого грузика

Складываем уравнения:

Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:

Определяем путь грузиков за 4 с:

Ответ: м/с, Н, м.

Задача 6.

Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.

Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это  груз массой  справа и слева. Силу натяжения основной нити обозначим :

Складываем уравнения:

Тогда

Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа

Осталось определить и . Для верхнего грузика слева

Откуда

А для нижнего грузика слева

Ответ: , , , , .

Задача 7.

Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.

Записываем уравнение по второму закону:

Тогда

Ответ: .

Задача 8.

Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.

Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение  по второму закону с учетом наличия силы трения:

Складывая уравнения, имеем:

Откуда

Но, если бы , тогда

Тогда, чтобы учесть обе возможности, запишем ответ так:

Ответ: .

Задача 9.

Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.). С каким ускорением движется кольцо, если груз  неподвижен?

Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза

А для кольца

Ответ: 6 м/с.

4 комментария

У многих учащихся возникают трудности с решением задач, связанных со вращательным движением тел. Также вызывают стопор задачи с блоками. В основном я это понял во время занятий физикой со своими школьниками и студентами. Поэтому я решил написать статью, в которой рассматриваю 7 случаев с небольшими задачами по динамике блоков. Это те основные кирпичики, из которых складываются все типы задач с блоками. В том числе и олимпиадные. Все примеры представлены от простого к сложному. Приятного чтения 🙂

А пока попрошу подписаться на канал в telegram IT mentor . Автор пишет краткие заметки и наблюдения по физике, математике, программированию, железу и технике 💡

Случай 1

Рассмотрим самый простой случай. Идеальная веревка перекидывается через неподвижный идеальный блок. Мы пытаемся удержать груз, прикрепленный на одном конце веревки, с помощью прикладывания силы F на другом конце веревки. Сначала рассмотрим статическое равновесие. Будем определять силу F, которую нам необходимо прикладывать.

Пожалуй, что из задач с блоками этот пример является самым простым. Допущения, принятые здесь, вполне согласуются с реальной жизнью. Но всё таки это сильно упрощенная модель.
1. Выигрыша в силе мы не имеем;
2. На какое расстояние сдвинули веревку, на такое же расстояние поднимется груз;
3. Удобство поднятия груза заключается в выборе направления тяги.

Случай 2

Немного усложним нашу ситуацию, добавив в систему ускорение. Какую силу нужно приложить, чтобы поднять груз с ускорением? Здесь также будем учитывать, что веревка идеальная:
нерастяжимая — поэтому все ускорения равны
невесомая — поэтому для правого конца выполняется условие F = T (для нулевой массы веревки).

Случай 3

Будем продолжать усложнение конфигурации из грузов и блоков. Что если в систему добавить второй блок, который будет висеть на веревке, один конец которой будет подвешен к потолку, а другой конец протянут через неподвижный блок и в итоге удержан нашей силой F. Рассмотрим статической равновесие системы и попробуем найти силу F. Теперь в задаче появляются две веревки:
Первая короткая нить удерживает груз (на рисунке изображена желтым цветом). Вторая длинная нить протянута через блоки, один конец закреплен в потолке, а другой конец удерживается силой F (на рисунке нить обозначена оранжевым цветом).

Мы получили выигрыш в силе в два раза. Простыми словами объяснить это можно так: 50 кг мы сможем удержать, тянув за свободный конец оранжевой веревки так, как будто мы бы удерживали 25 кг в ситуации с одним неподвижным блоком (Случай 1).

Как-то раз, занимаясь в тренажерном зале, я обратил внимание на разговор двух своих друзей. Они рассуждали, что поднимали на бицепс 70 кг в тренажере (так было написано на плитках, когда вставляешь штырек в определенный вес). Мне было интересно и я спросил: «Если в тренажере вы поднимаете 70 кг на бицепс, то почему же не можете поднять штангу в 70 кг также на бицепс?». Вопрос вызвал замешательство… Действительно, они не обращали на это внимание раньше. Вы, мои дорогие читатели, уже наверняка догадались в чем подвох. Конечно же в тренажере был подвижный ролик, тот самый блок, который катался вверх-вниз, удерживываемый тросиком, и давал выигрыш в силе в 2 раза. То есть по факту человек поднимает в этом тренажере 35 кг, а не 70 кг, как написано на плитках. Многие об этом не задумываются 🙂

Подвижный блок можно считать воистину крутым изобретением человечества. Ведь он дает возможность поднять груз, который мы бы никогда не подняли своими силами без этого хитрого приспособления.

Но во всём ли мы выигрываем? Нет, не во всём. Как и любой рычаг, подвижный блок помогает выиграть в силе, но проиграть в расстоянии. Это можно понять, если считать, что работа, выполняемая нами по мерещению груза (изменению его потенциальной энергии в случае подъема) является величиной постоянной ( *здесь мы пока не учитываем трение, которое есть в любых блоках, подшипниках и других механизмах ).

Как видите по рисункам, выиграть можно и в 4 раза, используя только два блока. Такая конструкция часто применяется в подъемных кранах. Однако, чем тяжелее груз, тем медленнее его будут поднимать. Такой же принцип наблюдается в коробке передач автомобиля, такой же принцип работает в переключении скоростей велосипеда. Чем быстрее, тем труднее. Или наоборот, чем легче, тем медленее.

Случай 4

Что если мы усложним наш пример, включив в него ускорение? Здесь важно не забыть учесть тот момент, который мы уже обсуждали в предыдущем пункте. Ускорение центра масс подвижного блока будет в два раза меньше, чем ускорение свободного конца длинной нити, протянутой через два блока. Почему? Попытаюсь это продемонстрировать на рисунке ниже.

Определить соотношение сил и перемещений можно с помощью метода виртуальных перещений. Однажды во время строительства одного из соборов в Швейцарии его архитектору понадобились блоки, позволяющие поднимать на большую высоту особо тяжелые грузы. Он сконструировал сложный полиспаст ( это грузоподъемное устройство, которое натягивается несколькими тросами. подробнее ), но запутался в многочисленных силах натяжения тросов и не смог рассчитать, сколько рабочих будет нужно нанимать для обслуживания грузоподъемного устройства. Архитектор обратился за помощью к известному ученому того времени Иоганну Бернулли (1667 – 1748). Едва взглянув на чертеж, Бернулли сразу же дал ответ. Разумеется, архитектор был очень удивлен и попросил объяснить ему суть решения…

Часто в задаче нужно учесть условия равновесия системы. Для этого определяются силы реакций механических связей. Связи — это ограничения, наложенные на положение отдельных частей системы или их возможные перемещения. Связями могут быть нити, шарниры, блоки. Чем больше связей, тем сложнее проследить за возникающими в них реакциями.

В большинстве случаев мехнические связи обладают интересным свойством, которое Бернулли положил в основу своего простого и изящного способа нахождения условий равновесия механической системы. Напишем это свойство:

Полная работа всех сил реакции, возникающих в связях системы при любых достаточно малых возможных отклонениях системы от положения равновесия, равна нулю.

Замечание: любые возможные отклонения не должны противоречить механическим связям: нити не должны рваться, шарниры не должны ломаться, блоки не должны деформироваться. Это и есть возможные или виртуальные перемещения.

Бернулли сформулировал этот принцип в 1717 году. Получается, что для исследования равновесия системы, достаточно выбрать удобные виртуальные перемещения (мы рисовали это выше), вычислить соответствующую им работу только внешних сил, а затем приравнять её к нулю.

Хотите простейший пример на применение данного метода? Давайте представим, что некоторый груз массой m подвешивают на пружину, и он её растягивает с силой тяжести m•g. При этом в самой пружине возникает сила упругости T. Допустим, груз сместился вниз на маленькую величину Δx. Тогда работа силы тяжести будет равна ΔA₁ = m•g•Δx, а работа силы упругости пружины будет ΔA₂ = − T•Δx. Знак минус здесь стоит потому что сила упругости всегда направлена против перемещения (вспоминайте закон Гука). Тогда, согласно принципу возможных перемещений, сумма работ обеих сил должна быть равна нулю:

ΔA₁ + ΔA₂ = m•g•Δx − T•Δx = 0 откуда получаем T = m•g

Замечание: Конечно же эту задачу можно решить обычным способом. Более того, оба метода будут примерно одинаковы по степени сложности. НО, существуют случаи, когда применение метода возможных перемещений дает более быстрое и простое решение. Иногда позволяет решать задачи, которые не разрешаются на основе обычнх уловий равновесия. Этот метод можно применяться не только для задач механики, но и для задач электростатики или молекулярной физики.

Итак, ускорение повлияет на силы, но не сильно. Мы же помним, что в нашем случае блоки по-прежнему идеальные, то есть их массу мы принимает за ноль (соответственно, момент инерции тоже).

Вот на этом моменте уже хочется обозначить несколько общих принципов решения таких задач.

Алгоритм, общие принципы, замечания

1. При решении нужно выяснить, какие силы действуют на тело, движение которого мы рассматриваем в конкретный момент времени. Все известные силы надо изобразить, сделать рисунок. Понимать со стороны каких тел действуют рассматриваемые силы. Действие одного тело на другое является взаимным (третий закон Ньютона). Бывает такое, что направление силы заранее неизвестно. Здесь не стоит переживать. Выберите то направление, которое вам кажется верным. При проецировании второгой закона Ньютона вы сможете получить численные значения для проекций. И если они будут положительные, то вы угадали с направлением. А если будут отрицательные, то вы не угадали, значит рисунок нужно подкорректировать, инвертировал стрелку, обозначающую силу. Если в задаче рассматривается несколько тел, то разумеется нужно расставить силы, действующие на все тела.

2. Далее осуществляется выбор системы отсчета. Оси (базис XOY) нужно выбирать так, что проекции был как можно более простыми, то есть чтобы как можно большее количество сил были параллельны или перпендикулярны выбранным осям.

3. Для каждого тела в системе записывается второй закон Ньютона. Затем этот закон проецируется на оси выбранного базиса (см 2 пункт). По началу вы можете сразу подставлять в полученную систему уравнений известные вам силы, углы, массы и проекции сил. Однако хорошим тоном является доведения решения до конца в буквенном виде. Если вы сейчас учитесь в школе, то обязательно научитесь оперировать буквами без подстановки чисел.

4. Для решения задач о движении системы тел одних уравнений движения (проекций второго закона Ньютона) может быть недостаточно. Нужна записать ещё все кинематические условия. Эти условия определяют соотношения между ускорениями различных объектов системы, обусловленные связями между ними.
Пример для неподвижных блоков: тела, связанные нерастяжимой нитью (идеальная нить), имеют вдоль этой нити одинаковые по модулю ускорения. И не важно через сколько неподвижных блоков перекинута нить.
Пример для подвижных блоков: При наличии подвижных блоков, ускорение тела (или свободного конца нити), перекинутой через неподвижный блок в два раза больше ускорения тела, прикрепленного к подвижному блоку. Так как за одинаковое время пройденные пути отличаются в два раза (мы это разбирали выше в статье).

5. Во множестве простых задач теоретической механики массой нитей, связывающих тела, пренебрегают. Только тогда натяжение таких нитей одинаково, какое бы мы не взяли сечение на всей длине.

6. Массой блоков также пренебрегают во множестве задач. В этих случаях натяжение нити, перекинутой через такой идеальный блок, можно считать одинаковым по обе стороны блока. В противном случае, если учитывать массу, то натяжения будут разными, угловая скорость будет меняться, то есть у нас появится вращающий момент сил, угловое ускорение и момент инерции реального блока.

7. Очень полезно попытаться понять как будут изменяться искомые величины при изменениях заданных величин. Если вы построите графики таких зависимостей, то сможете лучше разобраться в задаче.

Случай 5

Давайте рассмотрим задачу, в которой мы имеем два разных груза и два разных блока (подвижный и неподвижный.

Задача

Найдите силы натяжения T₁ и T₂ нитей abcd и ce в устройстве с подвижным блоком, изображенном на рисунке. Массы тел соответственно равны m₁ = 2 кг и m₂ = 3 кг.

Решение:

Обратите внимание, что сила натяжения оранжевой длинной веревки abcd меньше, чем сила натяжения короткой желтой веревки ce, хотя на короткой веревке груз висит более легкий, чем на длинной веревке. Получается, что сила натяжения уменьшается при постоянном движении троса.

Случай 6

В задачах на блоки грузы необязательно могут быть подвешены. Бывает так, что грузы скользят по плоскостям, потому как блок опускается под действием силы тяжести груза, прикрепленного к нему. Рассмотрим такой случай.

Задача

На рисунке изображена система движущихся тел, имеющих массы m₁ = m, m₂ = 4m, m₃ = m. Наклонная плоскость составляет с горизонтом угол α = 30°. Трение отсутствует. Определите силы натяжения нитей.

Решение:

Случай 7

Встречаются и более редкие задачи, которые вводят учащихся в замешательство. Это задачи связанные с реальными блоками. Основное отличие заключается в том, что мы учитываем массу блока, а следовательно учитываем его момент инерции. Для раскрутки блока с массой (реального блока) нужен ненулевой момент сил (в сторону вращения). Значит такие задачи отличаются тем, что силы натяжения одной и той же нити на таком блоке будут разные по обе стороны от перегиба нити на блоке. Звучит сложно? Понимаю… Сейчас мы разберемся как это работает на практике.

При описании движения по окружности (другими словами при описании вращения тела) удобно использовать величины угла поворота φ, угловой скорости ω, углового ускорения ε и момента сил M.

Роль массы при вращении тела (или движении по окружности) играет величина J = m·R². Будем называть эту величину моментом инерции. Тогда уравнение вращательного движения по окружности для точки можно записать в виде: J·ε = M. По своей сути последнее уравнение является удобной записью второго закона Ньютона в проекциях на тангенциальное (касатальное) направление при движении по окружности.

Момент инерции является мерой инертности тела. К примеру, камень на длинной верёвке будет раскрутить сложнее, чем на короткой.

Вопрос читателям канала: Почему велосипедной колесо до одной и той же угловой скорости легче раскрутить пацльцем, если прикладывать силу к ободу колеса, чем если прикладывать силу к спицам возле втулки?

Блоки из наших задач выше не являются материальными точками. Поэтому момент инерции для них выводится с помощью суммирования моментов инерции всех частичек (материальных точек), из которых состоит блок.

Наш блок мы будем представлять в виде сплошного диска, сделанного из однородного материала. Момент инерции такого блока J = 1/2·m·R². Возможно, вам непонятно откуда взялась 1/2 ? Тогда выведем формулу…

Вывод формулы для момента инерции кольца и диска (блока) при вращении вокруг оси, проходящей через центр симметрии диска (блока):

Задача с реальным блоком

Через блок, представляющий собой сплошной диск радиусом R, перекинута нить. На нити подвешены грузы массами m₁ и m₂ ( m₂ > m₁). Масса блока m. Определите разность сил натяжения нитей с обеих сторон блока и ускорение грузов. Считать, что нить нерастяжима и не может скользить по блоку.

Решение:

Как видно из решения, больше натягивается та часть нити, в сторону которой происходит вращение блока, то есть та часть, которая разматывает блок. Именно она и может порваться, ведь натяжение в ней больше. Обратим внимание, что разница натяжений в частях нити пропорциальна ускорение грузов и массе блока.

В этой статье разобрано 7 основных случаев, из которых состоят задачи на блоки. И я очень надеюсь, что вам было интересно почитать эту статью. Ибо время на неё было потрачено очень много.

💾 Метод виртуальных перемещений (скачать полезные задачи в pdf)

Ладно, пора заканчивать эту бесконечную статью… А то, боюсь, что до этого момента уже никто не дочитает. Тяжело читать статьи, в которых много математики. Есть и более приятный контент для расслабления.

📚 На Дзен недавно появился интересный канал «Читающий Лингвист». Автор канала пишет замечательные рецензии на зарубежную литературу, рассказывает о прочитанном и делает заметки на околокнижные лингвистические наблюдения.

Советую подписаться на этот авторский канал «Читающего Лингвиста»

Понравилась статья? Поставьте лайк, подпишитесь на канал! Вам не сложно, а мне очень приятно 🙂

Если Вам нужен репетитор по физике, математике или информатике/программированию, Вы можете написать мне или в мою группу Репетитор IT mentor в VK
Библиотека с книгами для физиков, математиков и программистов
Репетитор IT mentor в telegram