Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.
| Земля | 9,81 м/с2 | 1,00 g | Солнце | 273,1 м/с2 | 27,85 g |
| Луна | 1,62 м/с2 | 0,165 g | Меркурий | 3,70 м/с2 | 0,378 g |
| Венера | 8,88 м/с2 | 0,906 g | Марс | 3,86 м/с2 | 0,394 g |
| Юпитер | 24,79 м/с2 | 2,528 g | Сатурн | 10,44 м/с2 | 1,065 g |
| Уран | 8,86 м/с2 | 0,903 g | Нептун | 11,09 м/с2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Физическая сущность[править | править код]
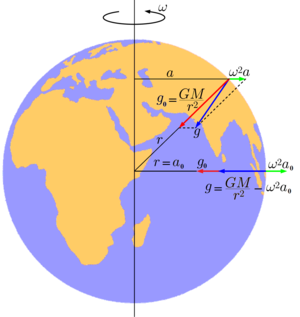
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центростремительное ускорение[править | править код]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
На стыке XVII и XVIII веков жил в Британии один ученый, Исаак Ньютон, отличавшийся большой наблюдательностью. Так случилось, что вид сада, где с веток на землю падали яблоки, помог ему открыть закон всемирного тяготения. Какая же сила заставляет плод все быстрее двигаться к поверхности планеты, по каким законам происходит это перемещение? Попытаемся ответить на эти вопросы.
А если бы эти яблони, как обещала в свое время советская пропаганда, росли на Марсе, каким бы тогда было это падение? Ускорение свободного падения на Марсе, на нашей планете, на других телах Солнечной системы… От чего оно зависит, каких величин достигает?
Ускорение свободного падения
Чем замечательна знаменитая Пизанская башня? Наклоном, архитектурой? Да. А еще с нее удобно бросать вниз различные предметы, чем и занимался в начале XVII века знаменитый итальянский исследователь Галилео Галилей. Бросая вниз всякие вещицы, он заметил, что тяжелый шар в первые мгновения падения двигается медленно, затем скорость его возрастает. Исследователя интересовал математический закон, по которому происходит изменение скорости.
Измерения, произведенные в дальнейшем, в том числе другими исследователями, показали, что скорость падающего тела:
- за 1 секунду падения становится равной 9,8 м/с;
- за 2 секунды – 19,6 м/с;
- 3 – 29,4 м/с;
- …
- n секунд – n∙9,8 м/с.
Эта величина 9,8 м/с∙с получила название «ускорение свободного падения». На Марсе (Красной планете) или другой планете это ускорение такое же или нет?
Почему на Марсе по-другому
Исаак Ньютон, рассказавший миру, что такое всемирное тяготение, смог сформулировать и закон ускорения свободного падения.

С развитием технологий, поднявших на новый уровень точность лабораторных измерений, ученые смогли подтвердить, что ускорение свободного падения на планете Земля – не такая уж и постоянная величина. Так, на полюсах она больше, на экваторе – меньше.
Ответ на эту загадку кроется в вышеуказанном уравнении. Дело в том, что земной шар, строго говоря, не совсем шар. Это эллипсоид, слегка приплюснутый с полюсов. Расстояние до центра планеты на полюсах меньше. А уж как отличается и массой, и размерами от земного шара Марс… Ускорение свободного падения на нем также будет иным.
Используя уравнение Ньютона и общеизвестные данные:
- масса планеты Марс − 6,4171·1023 кг;
- средний диаметр − 3389500 м;
- гравитационная константа − 6,67∙10-11 м3∙с-2∙кг-1.
Не составит труда найти ускорение свободного падения на Марсе.

g Марса = G∙M Марса / RМарса2.
g Марса = 6,67∙10-11∙6,4171·1023/ 33895002 = 3,71 м/с2.
Для проверки полученного значения можно заглянуть в любой справочник. Оно совпадает с табличным, значит, расчет произведен правильно.
Как ускорение свободного падения связано с весом
Вес – это сила, с которой любое тело, обладающее массой, давит на поверхность планеты. Измеряется он в ньютонах и равен произведению массы на ускорение свободного падения. На Марсе и любой другой планете оно, разумеется, будет отличаться от земного. Так, на Луне сила тяжести в шесть раз меньше, чем на поверхности нашей планеты. Это даже создавало определенные трудности у астронавтов, высадившихся на естественный спутник. Перемещаться оказалось удобнее, подражая кенгуру.

Итак, как было рассчитано, ускорение свободного падения на Марсе составляет 3,7 м/с2, или 3,7 / 9,8 = 0,38 от земного.
А означает это, что вес любого предмета на поверхности Красной планеты будет составлять лишь 38% от веса этого же предмета на Земле.
Как и где это работает
Попутешествуем мысленно по Вселенной и найдем ускорение свободного падения на планетах и других космических телах. Астронавты НАСА планируют уже в течение ближайших десятилетий высадиться на одном из астероидов. Возьмем Весту – самый большой астероид в Солнечной системе (Церера была побольше, но ее недавно перевели в разряд карликовых планет, «повысили в звании»).

g Весты = 0,22 м/с2.
Все массивные тела станут легче в 45 раз. При такой маленькой гравитации проблемой станут любые работы на поверхности. Неосторожный рывок или прыжок сразу подбросит астронавта на несколько десятков метров вверх. Что уж говорить про планы по добыче на астероидах полезных ископаемых. Экскаватор или бурильную установку придется в прямом смысле слова привязывать к этим космическим скалам.
А теперь другая крайность. Представим себя на поверхности нейтронной звезды (тело с массой солнца, имеющее при этом диаметр около 15 км). Так вот, если каким-то непостижимым образом астронавт не погибнет от зашкаливающего радиационного излучения всех возможных диапазонов, то его взору предстанет следующая картина:
g н.звезды = 6,67∙10-11∙1,9885·1030/ 75002 = 2 357 919 111 111 м/с2.

Монетка массой в 1 грамм весила бы на поверхности этого уникального космического объекта 240 тысяч тонн.
Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))

Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Ускорение свободного падения тел на Луне (естественный и единственный спутник планеты Земля) рассчитывается по формуле:
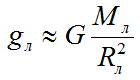
G — гравитационная постоянная, находится из закона всемирного тяготения и равна 6,67·10-11 Н м2/кг2
Mл — масса Луны;
Rл — радиус Луны.
Приведённая формула применима для расчёта ускорения свободного падения тела на планетах солнечной системы, в том числе и на планете Земля.
| Наименование планеты солнечной системы | Значение ускорения свободного падения, м/с2 |
| Солнце | 274 |
| Юпитер | 25,8 |
| Нептун | 11,6 |
| Сатурн | 11,3 |
| Земля | 9,8 |
| Уран | 9 |
| Венера | 8,9 |
| Меркурий | 3,7 |
| Марс | 3,7 |
| Луна | 1,62 |
![]() 21121
21121

История открытия
Учёные Древней Греции разделяли любое движение на два типа: естественное и принудительное. Перемещение тела под воздействием гравитации считалось естественным, так как не имело видимой причины и происходило само собой.

Аристотель считал, что скорость падения напрямую зависит от массы. Это ошибочное утверждение родилось в результате примитивных наблюдений. Философ приводил в пример движение к земле яблок и листьев. Очевидно, что последние летели гораздо медленнее. Исследователи тех времён ещё очень мало понимали в физике. Такие понятия, как сопротивление воздуха и ускорение были неизвестны.
Утверждения Аристотеля считались неоспоримым постулатом вплоть до начала XVII века. Галилео Галлилей решительно отверг древнюю классификацию движения. В результате проведения нескольких опытов с движением тела по наклонной плоскости, учёный ввёл понятие ускорения.
Определение ускорения свободного падения в физике
Основное внимание Галлилей уделял изучению процесса свободного падения. Самым знаменитым стал эксперимент, проведённый на Пизанской башне.
С сооружения высотой 60-м были одновременно сброшены два предмета:
- маленький металлический шарик весом в пол фунта;
- большая круглая бомба, весившая 100 фунтов.

Результат был просто ошеломляющим. Оба тела достигли земли практически одновременно, а небольшая разница была объяснена силой сопротивления воздушной среды. Надо заметить, что наука тех лет существенно отличалась от сегодняшней. Считалось, что воздух не мешает падению, а, напротив, увеличивает его скорость.
Ещё одним заблуждением того времени было утверждение о том, что любое движение со временем прекращается, даже если на его пути нет преград. Галлилей опроверг и этот ошибочный закон физики, введя определение инерции.
В XVI веке ещё не существовало точных хронометров. Из-за этого ускорение падения тел с Пизанской башни было рассчитано довольно грубо. Для более точного измерения учёный изучал равноускоренное движение шарика по наклонной плоскости. А более или менее правильное значение ускорения сумел вычислить Гюйгенс в 1660 г.
Физическая сущность

Свободным падением может называться равноускоренное движение тела в результате действующей на него силы тяжести, происходящее в вакууме. Атмосфера Земли способна тормозить ускорение и замедлять падающие предметы. Однако, если величина сопротивления воздуха небольшая, ей можно пренебречь. К примеру, в опыте Галилея на башне в Пизе использовались шарообразные предметы, обладающие аэродинамичной формой. В результате этого коэффициент торможения удалось свести к минимуму.
Ускорение у поверхности Земли не зависит от массы предмета — это постоянная величина, обозначающаяся латинской буквой g и составляющая 9,80665 м/с.^2. Из-за воздействия центробежных сил на экваторе его значение немного меньше, а на полюсах, соответственно, больше.
Величина ускорения свободного падения зависит от нескольких факторов:
- географических координат, точнее, широты;
- расстояния до поверхности планеты;
- времени суток;
- геомагнитных аномалий.
Вектор свободного падения всегда направлен вниз. Это можно наглядно увидеть, подбросив какой-либо предмет. Благодаря воздействию ускорения, его движение будет постепенно замедляться. Затем оно полностью остановится и направится в обратную сторону.
Формулы для расчёта
Галилей понимал, что исследование падения тел с Пизанской башни является несовершенным. Был поставлен новый эксперимент, в котором учёному удалось увеличить время движения и уменьшить сопротивление воздуха. Отполированные латунные шарики скатывались по желобам, расположенным под определённым углом наклона. В результате были выведен физический закон, согласно которому все падающие тела движутся с одинаковой, постоянно увеличивающейся скоростью.
Формула для нахождения: g=G (M/R ^ 2), где:
- G — гравитационная постоянная;
- M — масса планеты;
- R — радиус планеты.
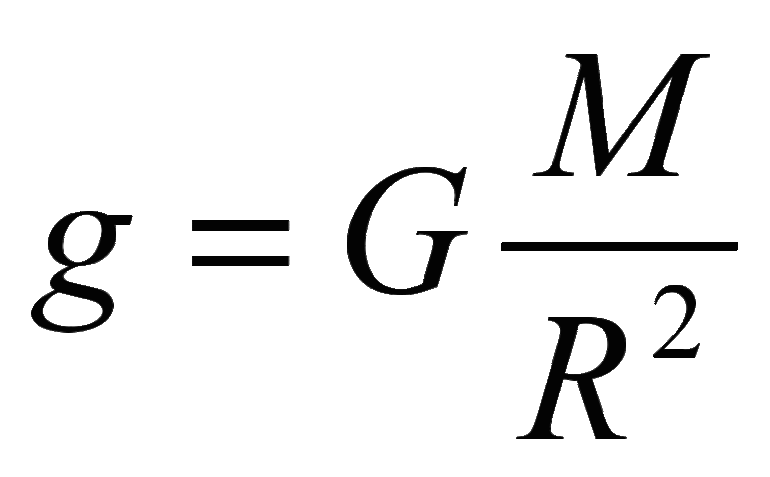
При помощи этой зависимости можно рассчитать значение g на поверхности любой планеты во вселенной.
Существуют задачи, для решения которых необходим более точный расчёт. В таком случае используется другая, расширенная формула: g=G (M/(R2+h)), где h — это высота над поверхностью планеты.
Стоит помнить, что для максимальной точности расчётов придётся учитывать большое количество факторов. Ускорение может измеряться при помощи специального прибора — гравиметра.
Ускорение на других планетах
Как видно из формулы, гравитационное ускорение напрямую зависит от массы и радиуса планеты. Из этого следует, что значение g на других планетах будет отличаться от земного.
Таблица показателя ускорения g для основных объектов Солнечной системы.
| Наименование | Ускорение, м/с. 2 |
| Солнце | 274,01 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,72 |
| Юпитер | 25,8 |
| Сатурн | 11,54 |
| Уран | 9,04 |
| Меркурий | 3,73 |
| Нептун | 11,33 |
| Луна | 1,69 |
Солнце является самым большим объектом в солнечной системе, его масса почти в 300 тыс. раз больше земной. Но как можно заметить из таблицы, ускорение на поверхности звезды превышает земное всего в 28 раз. Это объясняется огромным радиусом светила.
Во вселенной существуют очень компактные объекты с невероятной плотностью и чудовищным притяжением. Если взять среднюю нейтронную звезду с радиусом 13 км и массой 2,5*10 30 кг, то ускорение на её поверхности превысит земное в 100 млрд раз и составит довольно внушительное число — 9,87*10^11м/с.2
Воздействие перегрузок на человека
Благодаря научно-техническому прогрессу и стремительному развитию технологий, современный человек имеет возможность пользоваться довольно быстрыми средствами передвижения. Чтобы попасть в любую точку планеты на самолёте, потребуется не более суток. Быстрая скорость передвижения неминуемо связана с таким понятием, как перегрузка.
Любая перегрузка являет собой отношение двух ускорений:
- негравитационного;
- свободного падения.

За единицу измерения принято брать гравитационное ускорение на Земле — 9,80665 м/с². Таким образом, нулевую перегрузку можно ощутить на себе лишь в невесомости.
Перегрузка является векторной величиной. Для людей и других живых организмов огромное значение имеет её направление. Это связано с тем, что организм приспособлен к постоянному воздействию гравитационного ускорения.
Характер положительной перегрузки заключается в том, что её вектор направлен вниз — от головы к ногам. Кровь оттекает от мозга и при показателе более 10 g человек может потерять сознание за считаные секунды. При отрицательном значении кровь, напротив, бьёт в голову. Это переносится гораздо хуже и может привести к кровоизлиянию и смерти.
Показатель перегрузки для различных ситуаций:
| Пример | Показатель, g |
| Статичное положение, | 1 |
| Взлёт пассажирского авиалайнера | 1,5 |
| Приземление на парашюте | 1,8 |
| Раскрытие купола | 10−16 |
| Спуск космического аппарата «Союз» | 3−4 |
| Высший пилотаж на спортивном самолёте | от -7 до +12 |
| Максимальная длительная перегрузка, переносимая человеком | 8−10 |
| Аварийный спуск из космоса | 20−26 |
| Рекордная не смертельная перегрузка при автокатастрофе | 214 |
| Торможение автоматического аппарата в атмосфере Венеры | 350 |
| Предел прочности твердотельного накопителя информации | 1500 |
| Снаряд в момент выстрела | 47 тыс. |
Военным и спортивным лётчикам приходится постоянно испытывать большие перегрузки. Для уменьшения вредного воздействия на организм существуют специальные защитные костюмы.
Переносить перегрузку лучше всего лёжа на спине. Именно в таком положении находятся космонавты при взлёте ракет.
>

