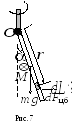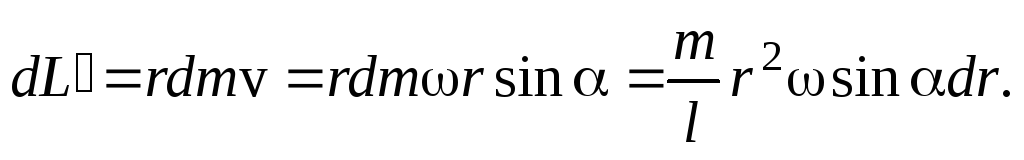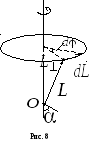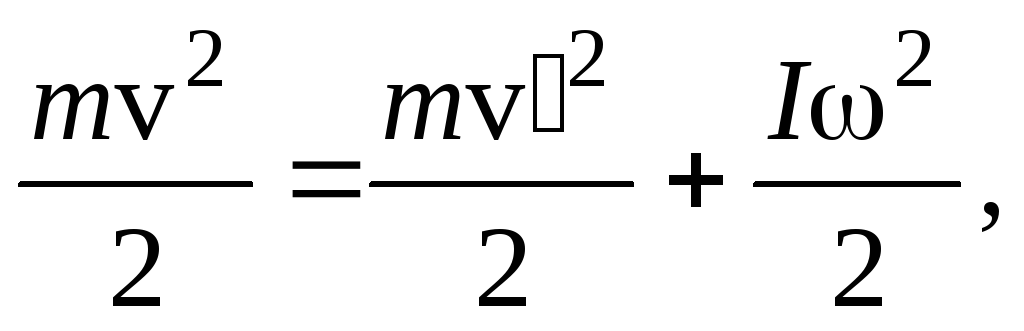Как найти ускорение оси цилиндра

Решение.
Линейное ускорение цилиндра определим по формуле

[ a=frac{{{upsilon }^{2}}-upsilon _{0}^{2}}{2cdot h},{{upsilon }_{0}}=0,a=frac{{{upsilon }^{2}}}{2cdot h}(1). ]

Где: h – высота с которой опустится цилиндр за некоторый промежуток времени, υ – скорость которую приобретет цилиндр за это время.
Для решения задачи применим закон сохранения энергии. Потенциальная энергия переходит в кинетическую энергию. Кинетическая энергия состоит из энергии поступательного движения и энергии вращательного движения.

[ mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{Icdot {{omega }^{2}}}{2} (2).
 ]

Где: J – момент инерции цилиндра, ω – угловая скорость вращения цилиндра.
Момент инерции цилиндра определяется по формуле

[ J=frac{mcdot {{R}^{2}}}{2} (3),
 ]

угловая скорость по формуле

[ omega =frac{upsilon }{R}(4). ]

Подставим (4) и (3) в (2) выразим линейное ускорение цилиндра

[ begin{align}
  & mcdot gcdot h=frac{mcdot {{upsilon }^{2}}}{2}+frac{mcdot {{R}^{2}}cdot {{upsilon }^{2}}}{2cdot 2cdot {{R}^{2}}},gcdot h=frac{{{upsilon }^{2}}}{2}+frac{{{upsilon }^{2}}}{2cdot 2}, gcdot h=frac{{{upsilon }^{2}}}{2}cdot frac{3}{2} , \
 & frac{{{upsilon }^{2}}}{2cdot h} =frac{gcdot 2}{3}=a(5). \
 & a=frac{2cdot 10}{3}=6,67. \
end{align}
 ]

Ускорение с которым движется цилиндр, равно тангенциальному ускорению цилиндра, зная тангенциальное ускорение определим угловое ускорение цилиндра

[ a=varepsilon cdot R,varepsilon =frac{a}{R}(5).varepsilon =frac{6,67}{0,1}=66,7.
 ]

Ответ: 6,67 м/с², 66,7 рад/с².

2018-06-15   

На цилиндр намотана тонкая гибкая нерастяжимая лента, массой которой по сравнению с массой цилиндра можно пренебречь. Свободный конец ленты прикрепили к кронштейну и предоставили цилиндру опускаться под действием силы тяжести. Определить линейное ускорение $a$ оси цилиндра, если цилиндр: 1) сплошной; 2) полый тонкостенный.

Решение:

Пусть момент инерции цилиндра в обобщенном случае равен $J$

Запишем второй закон Ньютона в проекции на вертикальную ось:

$mg – T = ma$ (1)

Сила натяжения нити, помимо прочего, еще и раскручивает цилиндр с угловым ускорением:

$epsilon = frac{TR}{J}$ (2)

Ускорение точки А рано нулю т.к. нить закреплена и натянута:

$a_{A} = a – epsilon R = 0$

$a – epsilon R = 0$ (3)

Из системы трех уравнений можем найти ускорение:

$a = g frac{1}{ frac{J}{mR^{2} } + 1 }$

а) Сплошной цилиндр:

$J = frac{mR^{2}}{2}$

$a = g frac{2}{3}$

$a = 6,533 м/с^{2}$

б) Полый тонкостенный цилиндр:

$J = mR^{2}$

$a = frac{g}{2}$

$a = 4,9 м/с^{2}$

Рассмотрим понятия угловой скорости и углового ускорения при вращении твердого тела в теории и на примерах решения задач.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющуюся приращением угла поворота тела за некоторый промежуток (единицу) времени.

Обозначение угловой скорости: ω (омега).

Рассмотрим некоторое твердое тело, вращающееся относительно неподвижной оси.

С этим телом свяжем воображаемую плоскость П, которая совершает вращение вместе с заданным телом.

Вращательное движение определяется двугранным углом φ между двумя плоскостями, проходящими через ось вращения. Изменение этого угла с течением времени есть закон вращательного движения:

Положительным считается угол, откладываемый против хода часовой стрелки, если смотреть навстречу выбранному направлению оси вращения Oz. Угол измеряется в радианах.

Быстрота изменения угла φ (перемещения плоскости П из положения П₁ в положение П₂) – это и есть угловая скорость:

Приняв вектор k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

1. если известно количество оборотов n за единицу времени t:
   
2. если задан угол поворота φ за единицу времени:
   
3. если известна окружная скорость точки тела v и расстояние от оси вращения до этой точки r:
   

Размерности угловой скорости:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Определение угловой скорости

Пример: Диск вращается относительно своего центра.
Известна скорость v некоторой точки A, расположенной на расстоянии r от центра вращения диска.

Определить величину и направление угловой скорости диска ω, если v = 5 м/с, r = 70 см.

Таким образом, угловая скорость диска составляет 7,14 оборотов в секунду. Направление угловой скорости можно определить по направлению скоростей её точек.

Вектор скорости точки A стремится повернуть диск относительно центра вращения против хода часовой стрелки, следовательно, направление угловой скорости вращения диска имеет такое же направление.

Другие примеры решения задач >

Угловое ускорение

Угловое ускорение характеризует величину изменения угловой скорости при вращении твердого тела:

Обозначение: ε (Эпсилон)

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает (вращение ускоряется), а при отрицательном — уменьшается (вращение замедляется).

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

Расчет углового ускорения

Пример: По заданному значению касательной составляющей полного ускорения a_τ точки B, расположенной на расстоянии r от центра вращения колеса.

Требуется определить величину и направление углового ускорения колеса ε, если a_τ = 10 м/с², r = 50 см.

Угловое ускорение колеса в заданный момент времени составляет 20 оборотов за секунду в квадрате. Направление углового ускорения определяется по направлению тангенциального ускорения точки.

Здесь, угловое ускорение направлено противоположно направлению угловой скорости вращения колеса. Это означает, что вращение колеса замедляется.

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω = 1,5 с^-1 = 9,42 рад/с.

Смотрите также:

• Примеры расчета угловой скорости и ускорения
• Скорости и ускорения точек вращающегося тела

Примеры решения задач

Пример
1. Найти
момент инерции тонкого однородного
диска массой
и радиусаотносительно: а) оси симметрии,
перпендикулярной к плоскости диска; б)
оси, совпадающей с диаметром диска.

Р
е ш е н и е. а)Выберем
на диске цилиндрический слой радиуса
и шириной(см.
рис. 3а). Так как все элементы цилиндрического
слоя находятся на одном расстоянии
от центра кольца, его момент инерции
равен

(14)

где
– масса кольца, которую можно найти,
определив поверхностную плотность
материала дискаи умножив ее на площадь поверхности
кольцат.е.

П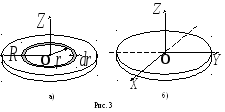одставляя
это значение в (14) интегрируя пов пределах от 0 до,
найдем момент инерции диска относительно
оси симметрии

(15)

б)
Для нахождения момента инерции диска
относительно диаметра, например оси
воспользуемся соотношением (6). Проведем
три взаимно перпендикулярные осипересекающиеся в центре диска (рис. 3б).
Очевидно, что,
тогда из уравнения (6) следует

Подставляя
в это выражение значение
из уравнения (15), найдем момент инерции
диска относительно диаметра

Пример
2. Найти
момент инерции однородного шара массы
и радиусаотносительно оси, совпадающей с центром
шара.

Р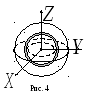е ш е н и е. Вычисление момента инерции
шара прямым методом, т.е. с использованием
уравнения (1) довольно трудоемкая
математическая задача, поэтому для
нахождения этого момента инерции
воспользуемся соотношением (5). Проведем
три взаимно перпендикулярные осипересекающиеся в центре шара (см. рис.
4). Очевидно, что

поэтому
соотношение (5) перепишем в виде

(16)

где
– искомый момент инерции,– момент инерции шара относительно
центра шара.

Для
нахождения момента инерции
выберем тонкий сферический слой радиусаи толщинойцентр
которого совпадает с центром шара (на
рис. 4 он выделен цветом). Все элементы
этого слоя находятся на одинаковом
расстоянии от центра шара, поэтому его
момент инерции относительно центра
шара равен

.
(17)

Объемная
плотность шара равна
,
умножая ее на объем тонкого сферического
слоянайдем массу сферического слоя

Подставляя
это выражение в (17) и интегрируя в пределах
от 0 до
,
найдем момент инерции шара относительно
центра

С учетом этого из
уравнения (16) находим искомый момент
инерции шара

Пример
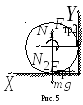
3. Однородный
цилиндр радиуса
раскрутили вокруг его оси до угловой
скоростии поместили затем в угол (рис.5) Коэффициент
трения между стенками угла и цилиндром
равенСколько оборотов сделает цилиндр до
остановки?

Р
е ш е н и е. Расставим силы, действующие
на цилиндр. Запишем уравнение, описывающее
выражение цилиндра относительно его
оси

(18)

где
– момент инерции цилиндра относительно
этой оси. Знак “–” в левой части этого
уравнения обусловлен тем, что при
замедленном движении модуль углового
ускоренияТак как нам необходимо найти число
оборотов, которое сделает цилиндр до
остановки, исключим из уравнения (18)
время. Для этого умножим и разделим
левую часть уравнения (18) на

где
– угловая скорость вращения цилиндра
в некоторый момент времени. После
преобразований получим

.
(19)

Прежде
чем решать это уравнение, найдем выражения
для сил трения. Так как центр цилиндра
покоится,

Запишем
это уравнение в проекциях на оси
и(см. рис. 5)

Решая
эту систему уравнений, учитывая, что
аполучим
выражения для сил трения

Подставляя эти
выражения в уравнение (19) и интегрируя
левую часть этого уравнения в пределах
от
до 0, а правую часть в пределах от 0 до,
найдем число оборотов,
которое сделает цилиндр до остановки

Пример
4. Однородный
шар скатывается без скольжения по
наклонной плоскости, составляющей угол
с горизонтом. Найти ускорениецентра шара и кинетическую энергию шара
через времяпосле начала движения.

Р е ш е н и е. Решим
задачу двумя способами.

а) Шар совершает
плоское движение. Свяжем подвижную
систему отсчета с центром шара. Эта
система движется поступательно
относительно наклонной плоскости, а
шар в этой системе вращается вокруг
оси, проходящей через его центр. Расставим
силы, действующие на шар в
процессе движения (см. рис.6). Запишем
теорему о движении центра масс в проекции
на ось
(см.
рис.6)

(20)

У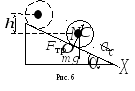равнение
вращательного движения шара вокруг
оси, проходящей через центр масс имеет
вид

(21)

где
– угловое ускорение шара,– момент инерции шара относительно оси
вращения. Решая совместно уравнения
(20) и (21), найдем ускорение центра шараи его угловое ускорение

(22)

Используя формулу
(13) для кинетической энергии тела,
совершающего плоское движение, и
учитывая, что в интересующий нас момент
времени
и(т.к.ипостоянные), найдем кинетическую энергию
шара через времяпосле начала движения

б) Так как шар
катится без проскальзывания, точка
соприкосновения шара
с наклонной плоскостью имеет скорость
равную нулю. Поэтому прямая, перпендикулярная
плоскости рисунка и проходящая через
точкуявляется мгновенной осью вращения.
Относительно этой оси шар совершает
вращательное движение, поэтому для
описания движения достаточно записать
уравнение (12) в виде

(23)

где
– момент инерции шара относительно
мгновенной оси вращения. Согласно
теореме Штейнера момент инерцииравен

Подставляя это
выражение в уравнение (23), находим
ускорение центра шара
и его угловое ускорение(см. уравнения (22)).

Кинетическая
энергия шара, в этом случае, определяется
только вращательным движением

Заметим, что при
любом способе решения, кинетическую
энергию шара можно найти из закона
сохранения энергии (сила трения работы
не совершает, т.к. эта сила – сила трения
покоя). Пусть за время
высота центра шара изменилась на(см. рис.6), тогда

(24)

где
– расстояние, пройденное центром шара
за времяПодставляя
в (24) выражение дляи,
находим кинетическую энергию шара

Пример
5. Однородный
стержень длины
может вращаться вокруг горизонтальной
оси, перпендикулярной к стержню и
проходящей через один из его концов
(рис. 7). Систему равномерно вращают с
угловой скоростьювокруг вертикальной оси. Пренебрегая
трением, найти уголмежду стержнем и вертикалью.

Р е ш е н и е. Решим
задачу двумя способами. Первое решение
приведем в инерциальной системе отсчета,
т.е. в системе, в которой стержень
вращается. Второе решение – в неинерциальной
системе отсчета, жестко связанной со
стержнем.

а) Система отсчета,
в которой будем решать задачу, на рис.
7 не показана. Решение задачи относительно
вертикальной оси вращения не даст
желаемого результата, т.к. моменты сил,
действующих на стержень (сила тяжести
и сила реакции в точке
),
относительно этой оси равны нулю, и
величина момента импульса остается
постоянной.

Поэтому
будем решать задачу относительно точки
подвеса стержня. Напомним, что уравнение
моментов относительно точки имеет вид

откуда видно, что
направление изменения момента импульса
совпадает по направлению с направлением
момента силдействующих на стержень, поэтому в
дальнейшем это уравнение будем записывать
для модулейи

(25)

Момент силы реакции
в точке
равен нулю, т.к. плечо этой силы равно
нулю. Направление момента силы тяжести
показано на рис.7, а величина равна

(26)

Найдем величину
и направление момента импульса
стержня относительно точкиДля этого выделим на стержне небольшой
участок длинойи массойположение которого относительно точкизададим радиус-вектором(см.
рис. 7). Обозначим величину момента
импульса этого участка какТак как стержень вращается вокруг
вертикальной оси, так как показано на
рисунке, скоростьэтого участка будет направлена за
плоскость рисунка, поэтому как следует
из определения момента импульса

,

он будет направлен
перпендикулярно стержню, как показано
на рис. 7. Очевидно, что направления всех
моментов импульса остальных участков
стержня будут иметь такое же направление,
поэтому результирующий момент импульса
будет также перпендикулярен стержню.
Учитывая, что векторы
ивзаимно перпендикулярны, величинаравна

Интегрируя это
уравнение

найдем величину
момента импульса стержня относительно
точки

Момент
импульса поворачивается вместе со
стержнем, и за время
повернется на некоторый угол,
получив приращение(см. рис.8).
Найдем величину этого приращения

или

.
(27)

Подставляя уравнение
(26) и (27) в уравнением моментов (25), получим

где
.
Преобразуем это уравнение к виду

.
(28)

Если величина

уравнение (28) имеет
одно решение
,
и это положение устойчивое, т.е. стержень
будет занимать вертикальное положение
и будет вращаться вокруг собственной
оси.

Если
то уравнение (28) будет иметь два решение

и
,

причем можно
показать, что первое решение перестает
быть устойчивым, и стержень отклонится
на угол, определяемый вторым решением.

б) Решим теперь
задачу в неинерциальной системе отсчета,
жестко связанной со стержнем. В этой
системе отсчета на стержень, кроме сил
взаимодействия действует центробежная
сила инерции. Так как стержень находится
в равновесии, сумма моментов сил,
действующих на стержень, должна равняться
нулю, т.е.

где
– величина момента силы тяжести,– величина момента центробежной силы
инерции относительно точкиВеличина момента силы тяжести определяется
уравнением (26).
Для нахождения момента центробежной
силы инерции воспользуемся рис. 7, считая,
что стержень покоится.

На выделенный
участок стержня действует центробежная
сила инерции

величина момента
которой, относительно точки
равна

Интегрируя это
выражение по всей длине стержня, получим

.

Подставляя
это выражение и соотношение (26) в уравнение
моментов (25), получим уравнение

,

в точности
совпадающее с уравнением (28).

Надо заметить,
что решение этой задачи в неинерциальной
системе отсчета много проще, чем в
инерциальной.

Пример
6. Однородная
тонкая квадратная пластинка массы
может свободно вращаться вокруг
неподвижной вертикальной оси, совпадающей
с одной из ее сторон. В центр пластины
по нормали к ней упруго ударяется шарик
массылетевший со скоростьюНайти величину скорости шарикасразу после удара.

Р
е ш е н и е. Система “пластина-шарик”
незамкнута, так как для удержания оси
пластины в неподвижном состоянии к ней
необходимо приложить внешние силу.
Однако надо заметить, что момент этих
внешних сил относительно оси равны
нулю, т.к. они приложены непосредственно
к оси.

Для
решения задачи воспользуемся законами
сохранения энергии (удар упругий) и
законом сохранения момента импульса
(сумма момента внешних сил относительно
оси равен нулю). Будем считать, что длина
стороны пластины равна
и шарик после удара будет лететь в
прежнем направлении, тогда

,

где
– момент инерции пластины относительно
оси,– угловая скорость, с которой пластина
будет вращаться после удара вокруг оси.

Для
простоты решения этой системы перепишем
ее в виде

(29)

Разделив первое
уравнение не второе, получим

(30)

Решая
совместно уравнения (29) и(30) и учитывая,
что момент инерции пластины относительно
оси, совпадающей с одной из ее сторон
равен
(докажите это самостоятельно), найдем
скорость шарика после удара

Заметим,
что если
,
скорость шарика после удара становится
отрицательной. Это означает, что пришарик полетит в обратную сторону.

Пример
7. Однородный
диск радиуса
и массылежит на гладкой горизонтальной
поверхности. На боковую поверхность
диска плотно намотана нить, к свободному
концукоторой приложили постоянную горизонтальную
силуПосле начала движения диска точкапереместилась на расстояниеНайти угловую скорость диска к этому
моменту времени.

Р
е ш е н и е. Под действием силы
диск будет совершать плоское движение.
Свяжем подвижную систему отсчета с
центром масс диска. Величину ускорения
центра масснайдем из второго закона Ньютона,
записанного в проекции на направление
движения

.
(31)

В
системе отсчета, связанной с центром
масс, диск вращается с угловым ускорением
,
которое найдем из уравнения вращательного
движения диска

(32)

где
– момент инерции диска, относительно
оси вращения.

Найдем
величины скорости
центра масс диска и угловой скорости
его вращения к моменту времени,
когда точка приложения силысовершит перемещениеТак как в начальный момент времени диск
покоился, а величины ускоренийине меняются с течением времени (см.
уравнения (31) и (32)), получим

Исключая
из этих уравнений время
найдем связь между скоростью центра
масс и угловой скоростью вращения диска

(33)

Запишем теорему
об изменении кинетической энергии для
диска

(34)

где
– работа всех сил, действующих на диск.
Силы тяжести и сила реакции опоры работу
на совершают, работу совершает только
постоянная силаПо определению работа постоянной силы
равна произведению модуля силы наперемещение
точки приложения силы,
таким образом

.
(35)

Подставляя
выражения (33) и (35) в уравнение (34), найдем
величину угловой скорости диска к
моменту времени, когда точка приложения
силы совершит перемещение

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #