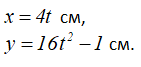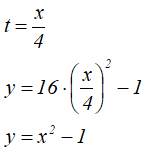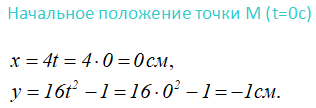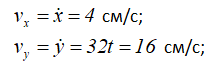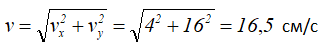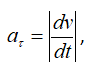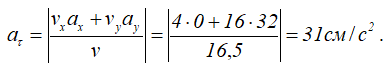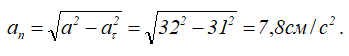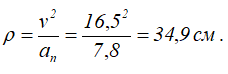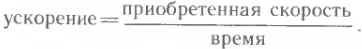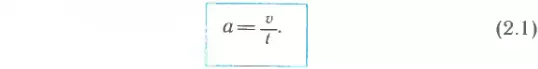Как найти ускорение по таблице - Сайт, где вы сможете решить свои вопросы

Решение задачи (РГР) К1 «Определение скорости и ускорения точки по заданным уравнениям ее движения» по разделу «кинематика» теоретической механики.

Пример определения для заданного момента времени положения точки на траектории, скорости, полного, касательного и нормального ускорения, радиуса кривизны траектории и вида траектории движения точки, если движение точки задано уравнениями.

Задача
Движение точки M задано уравнениями:

Требуется:
Установить вид траектории движения точки M, и для момента времени t = t₁ = 0,5 с найти:

положение точки на траектории,
скорость, полное, касательное и нормальное ускорения,
радиус кривизны траектории.

Другие примеры решений >
Помощь с решением задач >

Решение

Расчет траектории движения точки

Уравнения движения можно рассматривать как параметрические уравнения траектории точки.

Другие видео

Чтобы узнать вид траектории в координатной форме, надо получить прямую зависимость между переменными x и y, для этого избавимся от параметра времени t, выразив его, например, из первого уравнения и подставив во второе.

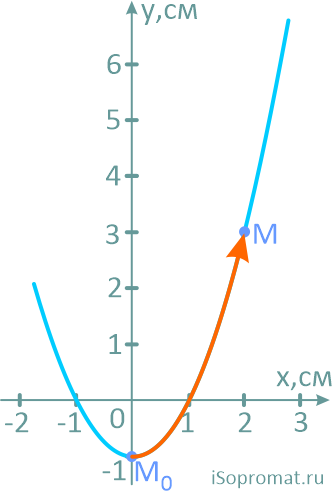
Получилось квадратное уравнение. То есть точка движется по параболе.
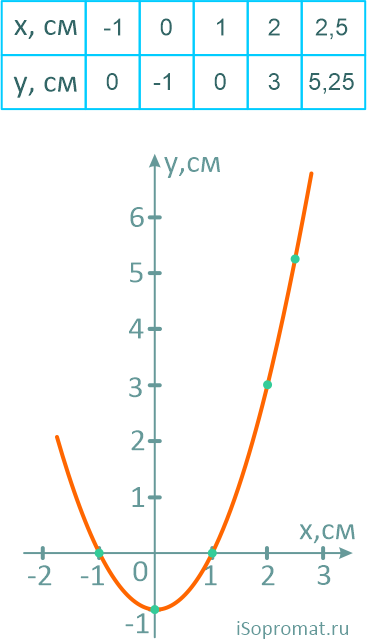
Построим траекторию движения, рассчитав несколько её точек.

Положение точки на траектории

Определим положения точки в начале движения и в заданный момент времени.
Для этого в исходные уравнения подставляем соответственно сначала 0

а затем, половину секунды.

Положение точки на ее траектории в заданный момент обозначим буквой M, и все остальные параметры будем рассчитывать для неё.

Расчет скорости точки

Направление и величину скорости точки определим как векторную сумму её проекций на оси координат.

Здесь i, j — орты осей x и y.
v_x, v_y — проекции вектора скорости на оси координат.

Проекции вектора скорости получим, взяв первые производные по времени t от соответствующих заданных уравнений движения точки.

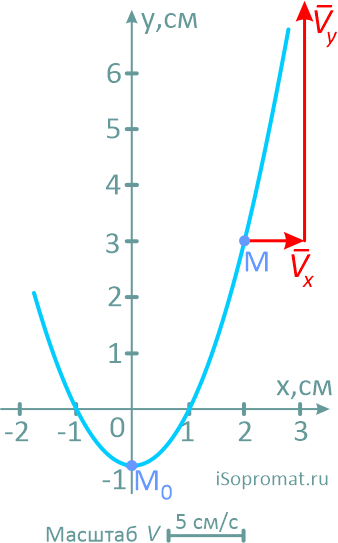
Далее выбрав масштаб, из точки M последовательно и с учетом знака, откладываем оба вектора.

Сам вектор скорости получим, соединив точку M с концом второго вектора и направив его по ходу движения точки.

Здесь надо отметить, что вектор скорости всегда должен располагаться по касательной к траектории. Любое другое положение будет указывать на ошибки в расчетах.

Рассчитаем модуль вектора скорости

Расчет ускорений точки

Проекции полного ускорения точки на оси координат определяются как вторая производная от исходных уравнений движения точки.

Здесь, a_x, a_y – проекции ускорения точки на оси координат.

В этом примере, горизонтальная проекция ускорения оказалась равной нулю, поэтому его модуль и направление будут совпадать с вертикальной.

Касательная составляющая полного ускорения это производная скорости точки по времени.

Ее можно рассчитать по этой формуле.

Вектор касательного ускорения всегда направлен по линии вектора скорости.

Положительная величина говорит об ускоренном движении точки и тогда направления скорости и касательного ускорения совпадают.
В противном случае они разнонаправлены, и движение точки замедляется.

Модуль нормального ускорения определим по формуле Пифагора, так как векторы касательного и центростремительного ускорений всегда взаимно перпендикулярны.

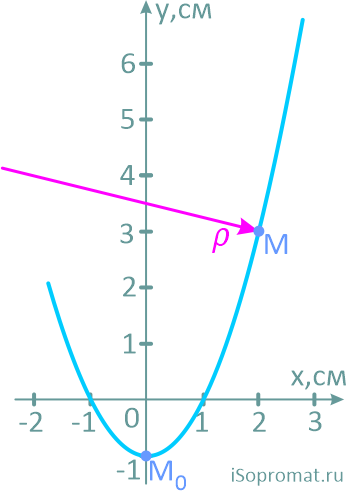
Расчет радиуса кривизны траектории

Осталось найти только радиус кривизны траектории в точке M, который равен отношению квадрата скорости к модулю нормального ускорения.

Результаты расчетов

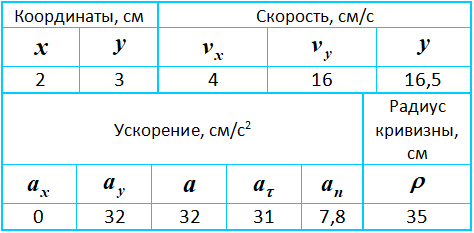
Результаты вычислений для заданного момента времени t₁=0,5c приведены в таблице:

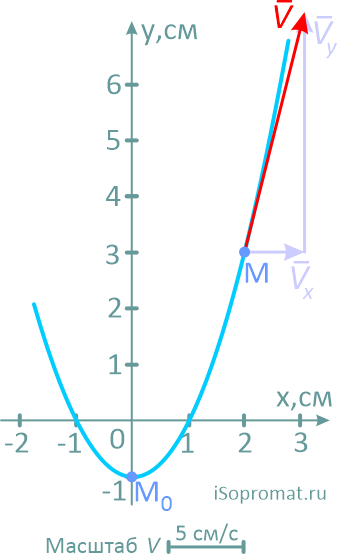
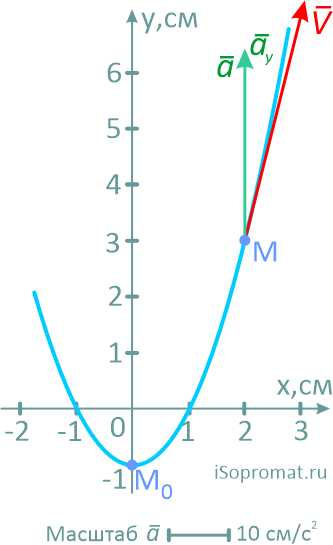
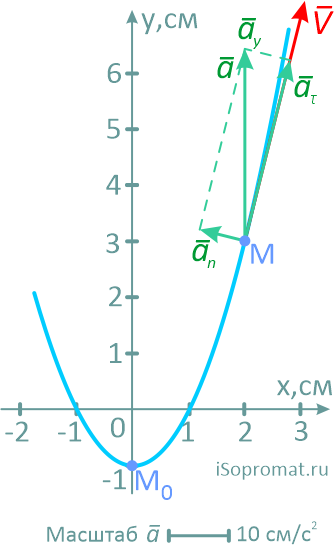
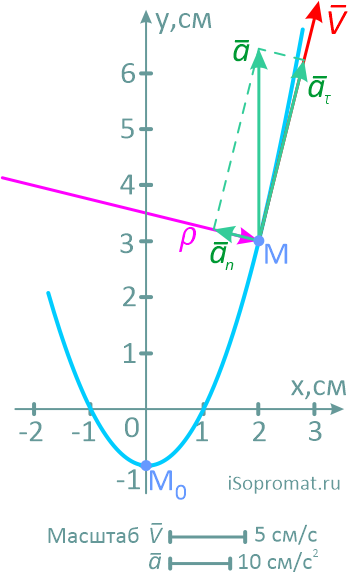
На рисунке показано положение точки M в заданный момент времени и векторы скорости и ускорений в выбранном масштабе.

Вектор v строим по составляющим v_x и v_y, причем этот вектор должен по направлению совпадать с касательной к траектории.

Вектор a строим по составляющим a_x и a_y и затем раскладываем на составляющие векторы a_τ и a_n. Совпадение величин a_τ и a_n, найденных из чертежа, с их значениями, полученными аналитически, служит критерием правильности решения.

Другие примеры решения задач >

Источник

В курсе физики VII класса вы изучали самый простой вид движения — равномерное движение по прямой линии. При таком движении скорость тела была постоянной и тело за любые равные промежутки времени проходило одинаковые пути.

Большинство движений, однако, нельзя считать равномерными. На одних участках тела могут иметь меньшую скорость, на других — большую. Например, поезд, отходящий от станции, начинает двигаться все быстрее и быстрее. Подъезжая к станции, он, наоборот, замедляет свое движение.

Проделаем опыт. Установим на тележку капельницу, из которой через одинаковые промежутки времени падают капли окрашенной жидкости. Поместим эту тележку на наклонную доску и отпустим. Мы увидим, что расстояние между следами, оставленными каплями, по мере движения тележки вниз будет становиться все больше и больше (рис. 3). Это означает, что за равные промежутки времени тележка проходит неодинаковые пути. Скорость тележки возрастает. Причем, как можно доказать, за одни и те же промежутки времени скорость тележки, съезжающей по наклонной доске, возрастает все время на одну и ту же величину.

Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным.

Так, например, опытами установлено, что скорость любого свободно падающего тела (при отсутствии сопротивления воздуха) за каждую секунду возрастает примерно на 9,8 м/с, т. е. если вначале тело покоилось, то через секунду после начала падения оно будет иметь скорость 9,8 м/с, еще через секунду — 19,6 м/с, еще через секунду — 29,4 м/с и т. д.

Физическая величина, показывающая, на сколько изменяется скорость тела за каждую секунду равноускоренного движения, называется ускорением.

a — ускорение.

Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с² и называют «метр на секунду в квадрате».

Ускорение характеризует быстроту изменения скорости. Если, например, ускорение тела равно 10 м/с², то это означает, что за каждую секунду скорость тела изменяется на 10 м/с, т. е. в 10 раз быстрее, чем при ускорении 1 м/с².

Примеры ускорений, встречающихся в нашей жизни, можно найти в таблице 1.

Как рассчитывают ускорение, с которым тела начинают двигаться?

Пусть, например, известно, что скорость отъезжающего от станции электропоезда за 2 с увеличивается на 1,2 м/с. Тогда, для того чтобы узнать, на сколько она возрастает за 1 с, надо 1,2 м/с разделить на 2 с. Мы получим 0,6 м/с². Это и есть ускорение поезда.

Итак, чтобы найти ускорение тела, начинающего равноускоренное движение, надо приобретенную телом скорость разделить на время, за которое была достигнута эта скорость:

Обозначим все величины, входящие в это выражение, латинскими буквами:

a — ускорение; v — приобретенная скорость; t — время.

Тогда формулу для определения ускорения можно записать в следующем виде:

Эта формула справедлива для равноускоренного движения из состояния покоя, т. е. когда начальная скорость тела равна нулю. Начальную скорость тела обозначают Формула (2.1), таким образом, справедлива лить при условии, что v₀ = 0.

Если же нулю равна не начальная, а конечная скорость (которая обозначается просто буквой v), то формула ускорения принимает вид:

В таком виде формулу ускорения применяют в тех случаях, когда тело, имеющее некоторую скорость v₀, начинает двигаться все медленнее и медленнее, пока наконец не остановится (v = 0). Именно по этой формуле, например, мы будем рассчитывать ускорение при торможении автомобилей и других транспортных средств. Под временем t при этом мы будем понимать время торможения.

Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.

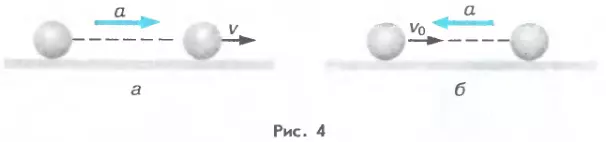
Если скорость тела при равноускоренном прямолинейном движении возрастает, то ускорение направлено в ту же сторону, что и скорость (рис. 4, а); если же скорость тела при данном движении уменьшается, то ускорение направлено в противоположную сторону (рис. 4, б).

При равномерном прямолинейном движении скорость тела не изменяется. Поэтому ускорение при таком движении отсутствует (a = 0) и на рисунках изображено быть не может.

Экспериментальное задание. Используя линейку в качестве наклонной плоскости, положите на ее верхний край монету и отпустите. Будет ли двигаться монета? Если будет, то как — равномерно или равноускоренно? Как это зависит от угла наклона линейки?

Источник

I. Механика

Тестирование онлайн

Механическое движение представляют графическим способом. Зависимость физических величин выражают при помощи функций. Обозначают

Графики равномерного движения

Зависимость ускорения от времени. Так как при равномерном движении ускорение равно нулю, то зависимость a(t) – прямая линия, которая лежит на оси времени.

Зависимость скорости от времени. Скорость со временем не изменяется, график v(t) – прямая линия, параллельная оси времени.

Правило определения пути по графику v(t): Численное значение перемещения (пути) – это площадь прямоугольника под графиком скорости.

Зависимость пути от времени. График s(t) – наклонная линия.

Правило определения скорости по графику s(t): Тангенс угла наклона графика к оси времени равен скорости движения.

Графики равноускоренного движения

Зависимость ускорения от времени. Ускорение со временем не изменяется, имеет постоянное значение, график a(t) – прямая линия, параллельная оси времени.

Зависимость скорости от времени. При равномерном движении путь изменяется, согласно линейной зависимости . В координатах . Графиком является наклонная линия.

Правило определения пути по графику v(t): Путь тела – это площадь треугольника (или трапеции) под графиком скорости.

Правило определения ускорения по графику v(t): Ускорение тела – это тангенс угла наклона графика к оси времени. Если тело замедляет движение, ускорение отрицательное, угол графика тупой, поэтому находим тангенс смежного угла.

Зависимость пути от времени. При равноускоренном движении путь изменяется, согласно квадратной зависимости . В координатах зависимость имеет вид . Графиком является ветка параболы.

График движения при . График движения при

Сравнительная таблица графиков

Источник

Рассмотрим поступательное движение. Когда тело движется поступательно, его координаты изменяются.

Прямолинейное движение – это когда тело движется по прямой. Прямую, вдоль которой движется тело, назовем осью Ox.

Будем отдельно рассматривать:

движение без ускорения (равномерное), и
движение с ускорением (неравномерное).

1). Равномерное движение — скорость тела остается одной и той же (т. е. не изменяется). При таком движении ускорения нет: (vec{a} =0).

2). Неравномерное движение — скорость меняется и появляется ускорение.

Пусть ускорение есть и, оно не изменяется: (vec{a} =const). Такое неравномерное движение называют равнопеременным. Чтобы уточнить, увеличивается ли скорость, или уменьшается, вместо слова «равнопеременное» говорят:

Равноускоренное движение — скорость тела увеличивается.
Равнозамедленное движение — скорость уменьшается.

Примечание: Когда изменяется скорость, всегда появляется ускорение!

Движение будем изображать графически, используя две перпендикулярные оси.

На графиках будем откладывать:

по горизонтали — время в секундах.
по вертикали — координаты тела, или проекции скорости и ускорения.

Для каждого вида движения получим три графика. Графики будем называть так:

x(t) – зависимость координаты от времени;
v(t) – зависимость проекции скорости от времени;
a(t) – зависимость проекции ускорения от времени.

Прочитайте вначале, что такое проекция вектора на ось, это поможет лучше усвоить материал.

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Пусть тело покоится на оси Ox – (рис 1а).
Точкой (x_{0}) обозначена координата этого тела. Когда тело неподвижно, его координата не меняется. На графике неизменную координату обозначают горизонтальной линией, расположенной параллельно оси времени (рис. 1б).
[x=x_{0}]

Рис.1. Тело покоится, график координаты x(t) — горизонтальная прямая рис. б).
Скорость «v» и ускорение «a» — это прямые, лежащие на оси Ox. График скорости – рис. в). График ускорения – рис. г)

Скорость и ускорение неподвижного тела равны нулю:

[vec{v}=0]

[vec{a}=0]

Из-за этого, графики скорости (рис. 1в) и ускорения (рис. 1г) – это горизонтальные линии, лежащие на оси t времени.

Скорость не меняется — движение равномерное

Разберём равномерное движение в направлении оси (рис. 2а).

Начальная координата тела – это точка (x_{0}), а конечная координата — точка (x) на оси Ox. В точку «x» тело переместится к конечному времени «t».

Красной стрелкой обозначено направление, в котором тело движется.

Примечание: Тело движется туда, куда направлен вектор его скорости.

Рис.2. Тело движется равномерно в направлении оси Ox – рис а). Зависимость координаты от времени – это возрастающая прямая x(t) – рис. б). График скорости в) – это горизонтальная прямая, а график ускорения г) лежит на оси времени, так как ускорение равно нулю

Координата возрастает со временем, так как тело движется туда же, куда указывает ось. Поэтому график координаты от времени — это возрастающая прямая x(t) – рис. б).

Уравнение, описывающее изменение координаты выглядят так:

[ x = x_{0} + v cdot t ]

Скорость на графике рис. в) изображена горизонтальной прямой линией, потому, что скорость остается одной и той же (не изменяется). Уравнение скорости записывается так:

[ v = v_{0} = const ]

Ускорение рис. г) изображается прямой, лежащей на оси времени, так как ускорения нет. Математики посмотрят на такой график и скажут: «Ускорение равно нулю и не изменяется». Эту фразу они запишут формулой:

[ a = 0 ]

Равномерное движение в направлении противоположном оси

Пусть теперь тело движется с одной и той же скоростью в направлении, противоположном оси (рис. 3а).

Рис.3. Тело движется равномерно противоположно направлению оси Ox – рис. а). Такому движению соответствуют: убывающая зависимость координаты от времени – рис б), отрицательная проекция скорости на ось – рис. в) и, нулевое ускорение – рис. г)

Так как тело теперь движется против направления оси, то координата тела будет уменьшаться. График (рис 3б) координаты x(t) выглядит, как убывающая прямая линия.

Так как скорость не изменяется, то график v(t) – это горизонтальная прямая.

Тело движется против оси, его вектор скорости направлен противоположно оси Ox. Поэтому проекция скорости будет отрицательной (рис 3в) и на графике v(t) скорость — это горизонтальная прямая, лежащая ниже оси времени.

А график ускорения (рис 3г) лежит на оси времени, так как ускорение нулевое.

Равноускоренное движение в направлении оси, скорость увеличивается

Следующий набор графиков – это случай, когда тело движется вдоль оси Ox с возрастающей скоростью (рис. 4). То есть, мы рассматриваем равноускоренное движение.

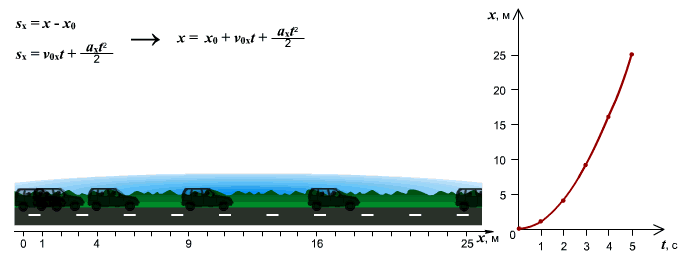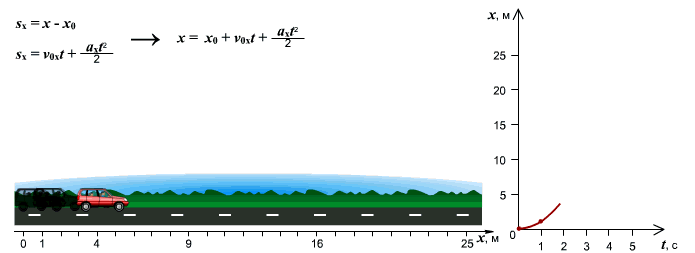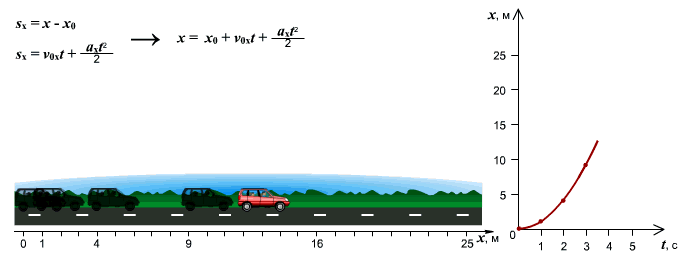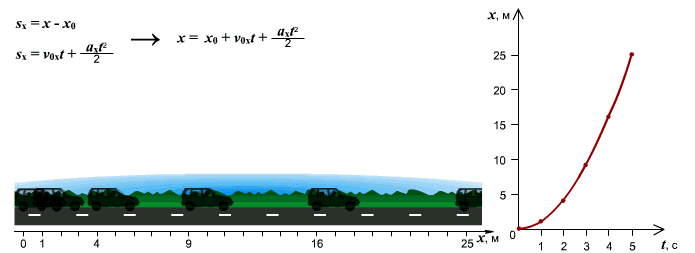
Рис.4. Тело движется равноускорено – рис. а) по направлению оси Ox. Изменение координаты от времени x(t) описывается правой ветвью параболы – рис. б), график v(t) скорости изображен наклонной возрастающей прямой – рис. в), а график неизменного ускорения a(t) – рис. г) изображается горизонтальной прямой, лежащей выше оси времени

Координата «x» теперь изменяется не по линейному, а по квадратичному закону. На графике квадратичное изменение выглядит, как ветвь параболы (рис. 4б). Тело движется по оси и скорость его растет. Такое движение описывается правой ветвью параболы, направленной вверх.

Уравнение, которое описывает квадратичное изменение координаты, выглядит так:

[ x = frac{a}{2}cdot t^{2} + v_{0} cdot t + x_{0} ]

Скорость, так же, растет (рис. 4в). Рост скорости описан наклонной прямой линией – то есть, линейной зависимостью:

[ v = v_{0} + a cdot t ]

Ускорение есть (рис. 4г) и оно не меняется:

[ a = const ]

Скорость и ускорение сонаправлены с осью Ox, поэтому их проекции на ось положительны, а их графики лежат выше оси времени.

Примечания:

1). Координата «x» будет изменяться:

по линейному закону, когда скорость не меняется — остается одной и той же.
по квадратичному закону, когда скорость будет изменяться (расти, или убывать).

2). Линейный закон – это уравнение первой степени, на графике – наклонная прямая линия.

3). Квадратичный закон – это уравнение второй степени, на графике — парабола.

4). Когда скорость увеличивается, для графика координаты x(t) выбираем правую ветвь параболы, а когда скорость уменьшается – то левую ветвь.

Равноускоренное движение против оси

Если тело будет увеличивать свою скорость, двигаясь в направлении, противоположном оси (рис. 5а), то ветвь параболы, описывающая изменение координаты тела, будет направлена вниз (рис. 5б).

Скорость направлена против оси и увеличивается в отрицательную область. Такое изменение скорости изображаем прямой, направленной вниз (рис. 5в).

Рис.5. Тело движется равноускорено противоположно оси Ox – рис. а). Координата меняется параболически – рис. б), ветвь правая, так как скорость растет. Скорость — рис. в), и ускорение — рис. г), направлены против оси Ox, их графики лежат ниже оси времени

Примечание: Чтобы скорость увеличивалась (по модулю), нужно, чтобы векторы скорости и ускорения были сонаправленными (ссылка).

Так как скорость увеличивается, то векторы скорости и ускорения сонаправлены. Но при этом, они направлены против оси, поэтому проекции векторов (vec{v}) и (vec{a}) на ось Ox будут отрицательными. Значит, графики скорости и ускорения будут лежать ниже горизонтальной оси времени.

Ускорение (рис. 5г) не изменяется, поэтому изображается горизонтальной прямой. Но эта прямая будет лежать ниже горизонтальной оси времени, так как ускорение имеет отрицательную проекцию на ось Ox.

Скорость уменьшается — движение равнозамедленное

Когда скорость тела уменьшается с постоянным ускорением, движение называют равнозамедленным. Координата в этом случае изменяется по квадратичному закону. График координаты – это ветвь параболы. Когда скорость уменьшается, координату описываем с помощью левой ветви параболы, с вершиной вверху (рис. 6б).

Рис.6. Тело движется равнозамедленно по оси Ox – рис. а), его координата растет по левой ветви параболы – рис. б), график скорости — убывающая наклонная прямая – рис. в), ускорение направлено против оси Ox, горизонтальный график ускорения — рис. г) лежит ниже оси времени

Примечание: Чтобы скорость уменьшалась по модулю, нужно, чтобы векторы скорости и ускорения были направлены в противоположные стороны (ссылка).

Скорость уменьшается, при этом, скорость направлена по оси. Поэтому, график скорости – это убывающая прямая линия, лежащая выше оси времени (рис. 6в).

А ускорение есть, оно не изменяется и направлено против оси. Поэтому, ускорение отрицательное, его график – это горизонтальная прямая, лежащая ниже оси времени (рис. 6г).

Равнозамедленное движение против оси

Если тело будет двигаться против оси, замедляясь, то график координаты — это левая ветвь параболы, вершиной вниз (рис. 7б).

Скорость вначале была большой, но так как тело замедляется, она падает до нуля. Но тело двигается против оси Ox, поэтому график скорости лежит ниже оси времени (рис. 7в).

Рис.7. Тело движется равнозамедлено против оси Ox – рис. а), его координата убывает по левой ветви параболы – рис. б), скорость отрицательная и уменьшается к нулю, график скорости — наклонная прямая – рис. в), ускорение направлено по оси Ox, горизонтальный график ускорения — рис. г) лежит выше оси времени

Скорость отрицательная. А чтобы она уменьшалась, нужно, чтобы ускорение было направлено противоположно скорости. Поэтому ускорение будет положительным. Значит, график ускорения будет лежать выше оси времени. Так как ускорение не меняется, то его график изображен горизонтальной прямой линией (рис. 7г).

Примечание: Можно вычислить перемещение тела по графику скорости v(t), не пользуясь для этого графиком функции x(t) для координат тела.

Выводы

1). Все, что лежит:

выше оси t – положительное;
ниже оси t – отрицательное;
на горизонтальной оси t – равно нулю.

2). Когда ускорение, или скорость направлены против оси, они будут отрицательными, т. е. будут лежать ниже горизонтальной оси t. Если график ускорения лежит на горизонтальной оси, то ускорение отсутствует (т. е. равно нулю, нулевое).

3). Если скорость не меняется, ускорения нет.

График x(t) координаты – это прямая линия.
График v(t) скорости – горизонтальная прямая.
График a(t) ускорения лежит на оси t.

4). Если скорость растет, ускорение и скорость направлены в одну и ту же сторону.

График x(t) координаты – это правая ветвь параболы.
График v(t) скорости – наклонная прямая.
График a(t) ускорения – горизонтальная прямая.

5). Если скорость уменьшается, ускорение и скорость направлены в противоположные стороны.

График x(t) координаты – это левая ветвь параболы.
График v(t) скорости – наклонная прямая.
График a(t) ускорения – горизонтальная прямая.

Источник

Три этих физических величины взаимосвязаны между собой процессом движения. Если известны две из этих величин, можно найти третью.
Скорость тела при условии равноускоренного прямолинейного движения определяем по формуле:

V = V0 + а*t

V0 — начальная скорость (при t = 0);
а — ускорение;
t — время.

Итак, чтобы найти скорость, к начальной скорости прибавляем произведение ускорения на время.
Если V0 = 0, то V = а*t.

Чтобы найти время, нужно вначале найти разность между скоростью в данный момент и начальной скоростью, затем полученный результат разделить на ускорение.

t = (V — V0) / а

Ускорение показывает изменение скорости движущегося тела, рассчитывается по двум скоростям и времени. Чтобы вычислить ускорение, следует найти разницу между скоростью в данный момент и начальной скоростью, затем все это разделить на время.
При ускорении:

а = (V — V0) / t

а = (V0 — V) / t

Ускорение — величина векторная, которая задается не только числом, но и направлением, измеряется в метрах в секунду (м/с2).

Чтобы рассчитать среднее ускорение, находим разницу между начальной и конечной скоростями Δ v, полученный результат делим на разницу между временем Δ t.(начальным и конечным) :

а = Δ v / Δ t

Быстро и правильно рассчитать величину скорости, ускорения или найти время вам поможет онлайн калькулятор.

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, – это векторная величина).

> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:

где – вектор ускорения .

Направление вектора ускорения совпадает с направлением изменения скорости Δ = — 0 (здесь 0 – это начальная скорость, то есть скорость, с которой тело начало ускоряться).

В момент времени t1 (см. рис 1.8) тело имеет скорость 0 . В момент времени t2 тело имеет скорость . Согласно правилу вычитания векторов найдём вектор изменения скорости Δ = — 0 . Тогда определить ускорение можно так:

Рис. 1.8. Среднее ускорение.

В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с 2 , то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:

Направление ускорения также совпадает с направлением изменения скорости Δ при очень малых значениях промежутка времени, за который происходит изменение скорости. Вектор ускорения может быть задан проекциями на соответствующие оси координат в данной системе отсчёта (проекциями а Х, a Y , a Z).

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

Если скорость тела по модулю уменьшается, то есть

V 2 то направление вектора ускорения противоположно направлению вектора скорости 2 . Иначе говоря, в данном случае происходит замедление движения , при этом ускорение будет отрицательным (а

Рис. 1.9. Мгновенное ускорение.

При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).

Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.

Рис. 1.10. Тангенциальное ускорение.

Направление вектора тангенциального ускорения τ (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.

Нормальное ускорение

Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой n . Вектор нормального ускорения направлен по радиусу кривизны траектории.

Полное ускорение

Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:

(согласно теореме Пифагора для прямоугольно прямоугольника).

При прямолинейном равноускоренном движении тело

двигается вдоль условной прямой линии,
его скорость постепенно увеличивается или уменьшается,
за равные промежутки времени скорость меняется на равную величину.

Например, автомобиль из состояния покоя начинает двигаться по прямой дороге, и до скорости, скажем, в 72 км/ч он двигается равноускоренно. Когда заданная скорость достигнута, то авто движется без изменения скорости, т. е. равномерно. При равноускоренном движении его скорость возрастала от 0 до 72 км/ч. И пусть за каждую секунду движения скорость увеличивалась на 3,6 км/ч. Тогда время равноускоренного движения авто будет равно 20 секундам. Поскольку ускорение в СИ измеряется в метрах на секунду в квадрате, то надо ускорение 3,6 км/ч за секунду перевести в соответствующие единицы измерения. Оно будет равно (3,6 * 1000 м) / (3600 с * 1 с) = 1 м/с 2 .

Допустим, через какое-то время езды с постоянной скоростью автомобиль начал тормозить, чтобы остановиться. Движение при торможении тоже было равноускоренным (за равные промежутки времени скорость уменьшалась на одинаковую величину). В данном случае вектор ускорения будет противоположен вектору скорости. Можно сказать, что ускорение отрицательно.

Итак, если начальная скорость тела нулевая, то его скорость через время в t секунд будет равно произведению ускорения на это время:

При падении тела «работает» ускорение свободного падения, и скорость тела у самой поверхности земли будет определяться по формуле:

Если известна текущая скорость тела и время, которое понадобилось, чтобы развить такую скорость из состояния покоя, то можно определить ускорение (т. е. как быстро менялась скорость), разделив скорость на время:

Однако тело могло начать равноускоренное движение не из состояния покоя, а уже обладая какой-то скоростью (или ему придали начальную скорость). Допустим, вы бросаете камень с башни вертикально вниз с приложением силы. На такое тело действует ускорение свободного падения, равное 9,8 м/с 2 . Однако ваша сила придала камню еще скорости. Таким образом, конечная скорость (в момент касания земли) будет складываться из скорости, развившийся в результате ускорения и начальной скорости. Таким образом, конечная скорость будет находиться по формуле:

Однако, если камень бросали вверх. То начальная его скорость направлена вверх, а ускорение свободного падения вниз. То есть вектора скоростей направлены в противоположные стороны. В этом случае (а также при торможении) произведение ускорения на время надо вычитать из начальной скорости:

Получим из этих формул формулы ускорения. В случае ускорения:

at = v – v 0
a = (v – v 0)/t

В случае торможения:

at = v 0 – v
a = (v 0 – v)/t

В случае, когда тело равноускоренно останавливается, то в момент остановки его скорость равна 0. Тогда формула сокращается до такого вида:

Зная начальную скорость тела и ускорение торможения, определяется время, через которое тело остановится:

Теперь выведем формулы для пути, которое тело проходит при прямолинейном равноускоренном движении . Графиком зависимость скорости от времени при прямолинейном равномерном движении является отрезок, параллельный оси времени (обычно берется ось x). Путь при этом вычисляется как площадь прямоугольника под отрезком. То есть умножением скорости на время (s = vt). При прямолинейном равноускоренном движении графиком является прямая, но не параллельная оси времени. Эта прямая либо возрастает в случае ускорения, либо убывает в случае торможения. Однако путь также определяется как площадь фигуры под графиком.

При прямолинейном равноускоренном движении эта фигура представляет собой трапецию. Ее основаниями являются отрезок на оси y (скорость) и отрезок, соединяющий точку конца графика с ее проекцией на ось x. Боковыми сторонами являются сам график зависимости скорости от времени и его проекция на ось x (ось времени). Проекция на ось x — это не только боковая сторона, но еще и высота трапеции, т. к. перпендикулярна его основаниям.

Как известно, площадь трапеции равна полусумме оснований на высоту. Длина первого основания равна начальной скорости (v 0), длина второго основания равна конечной скорости (v), высота равна времени. Таким образом получаем:

Выше была дана формула зависимости конечной скорости от начальной и ускорения (v = v 0 + at). Поэтому в формуле пути мы можем заменить v:

s = ½ * (v 0 + v 0 + at) * t = ½ * (2v 0 + at) * t = ½ * t * 2v 0 + ½ * t * at = v 0 t + 1/2at 2

Итак, пройденный путь определяется по формуле:

s = v 0 t + at 2 /2

(К данной формуле можно прийти, рассматривая не площадь трапеции, а суммируя площади прямоугольника и прямоугольного треугольника, на которые разбивается трапеция.)

Если тело начало двигаться равноускоренно из состояния покоя (v 0 = 0), то формула пути упрощается до s = at 2 /2.

Если вектор ускорения был противоположен скорости, то произведение at 2 /2 надо вычитать. Понятно, что при этом разность v 0 t и at 2 /2 не должна стать отрицательной. Когда она станет равной нулю, тело остановится. Будет найден путь торможения. Выше была приведена формула времени до полной остановки (t = v 0 /a). Если подставить в формулу пути значение t, то путь торможения приводится к такой формуле.

Тела была постоянной и тело за любые равные промежутки времени проходило одинаковые пути.

Если скорость тела при неравномерном движении за любые равные промежутки времени изменяется одинаково, то движение называют равноускоренным .

Так. например, опытами установлено, что скорость любого свободно падающего тела (при отсутствии сопротивления воздуха) за каждую секунду возрастает примерно на 9,8 м/с, т.е. если вначале тело покоилось, то через секунду после начала падения оно будет иметь скорость 9,8 м/с, еще через секунду- 19,6 м/с, еще через секунду — 29,4 м/с и т.д.

Физическая величина, показывающая, на сколько изменяется скорость тела за каждую секунду равноускоренного движения, называется ускорением .
а — ускорение.

Единицей ускорения в СИ является такое ускорение, при котором за каждую секунду скорость тела изменяется на 1 м/с, т. е. метр в секунду за секунду. Эту единицу обозначают 1 м/с 2 и называют “метр на секунду в квадрате”.

Ускорение характеризует быстроту изменения скорости. Если, например, ускорение тела равно 10 м/с 2 , то это означает, что за каждую секунду скорость тела изменяется на 10 м/с, т. е. в 10 раз быстрее, чем при ускорении 1 м/с 2 .

Примеры ускорений, встречающихся в нашей жизни, можно найти в таблице 1.

Как рассчитывают ускорение, с которым тела начинают двигаться?

Пусть, например, известно, что скорость отъезжающего от станции электропоезда за 2 с увеличивается на 1,2 м/с Тогда, для того чтобы узнать, на сколько она возрастает за 1 с, надо 1,2 м/с разделить на 2 с. Мы получим 0,6 м/с2. Это и есть ускорение поезда.

Обозначим все величины, входящие в это выражение, латинскими буквами:
а — ускорение; V — приобретенная скорость; t — время

Тогда формулу для определения ускорения можно записать в следующем виде:

Эта формула справедлива для равноускоренного движения из состояния покоя , т. е. когда начальная скорость тела равна нулю. Начальную скорость тела обозначаютV 0 — Формула (2.1), таким образом, справедлива лишь при условии, что V 0 = 0.

Если же нулю равна не начальная, а конечная скорость (которая обозначается просто буквой V ), то формула ускорения принимает вид:

В таком виде формулу ускорения применяют в тех случаях, когда тело, имеющее некоторую скорость V 0 , начинает двигаться все медленнее и медленнее, пока наконец не остановится (v = 0). Именно по этой формуле, например, мы будем рассчитывать ускорение при торможении автомобилей и других транспортных средств. Под временем t при этом мы будем понимать время торможения.

Как и скорость, ускорение тела характеризуется не только числовым значением, но и направлением. Это означает, что ускорение тоже является векторной величиной. Поэтому на рисунках его изображают в виде стрелки.

При равномерном прямолинейном движении скорость тела не изменяется. Поэтому ускорение при таком движении отсутствует (а = 0) и на рисунках изображено быть не может.

1. Какое движение называют равноускоренным? 2. Что такое ускорение? 3. Что характеризует ускорение? 4. В каких случаях ускорение равно нулю? 5. По какой формуле находится ускорение тела при равноускоренном движении из состояния покоя? 6. По какой формуле находится ускорение тела при уменьшении скорости движения до нуля? 7. Как направлено ускорение при равноускоренном прямолинейном движении?

Экспериментальное задание . Используя линейку в качестве наклонной плоскости, положите на ее верхний край монету и отпустите. Будет ли двигаться монета? Если будет, то как — равномерно или равноускоренно? Как это зависит от угла наклона линейки?

С.В. Громов, Н.А. Родина, Физика 8 класс

Отослано читателями из интернет-сайтов

Задание и ответы с физики по классам, физика тесты ответы , планирование уроков физики 8 класс, наибольшая библиотека рефератов онлайн, домашние задание и работа

Содержание урока конспект урока опорный каркас презентация урока акселеративные методы интерактивные технологии Практика задачи и упражнения самопроверка практикумы, тренинги, кейсы, квесты домашние задания дискуссионные вопросы риторические вопросы от учеников Иллюстрации аудио-, видеоклипы и мультимедиа фотографии, картинки графики, таблицы, схемы юмор, анекдоты, приколы, комиксы притчи, поговорки, кроссворды, цитаты Дополнения рефераты статьи фишки для любознательных шпаргалки учебники основные и дополнительные словарь терминов прочие Совершенствование учебников и уроков исправление ошибок в учебнике обновление фрагмента в учебнике элементы новаторства на уроке замена устаревших знаний новыми Только для учителей идеальные уроки календарный план на год методические рекомендации программы обсуждения Интегрированные уроки

Ускорение – это величина, которая характеризует быстроту изменения скорости.

Рис. 1.8. Среднее ускорение. В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть

При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть

а направление вектора ускорения совпадает с вектором скорости

Если скорость тела по модулю уменьшается, то есть

Равноускоренное движение

Равноускоренное движение — это движение с ускорением, вектор которого не меняется по модулю и направлению. Примеры такого движения: велосипед, который катится с горки; камень брошенный под углом к горизонту.

Рассмотрим последний случай более подробно. В любой точке траектории на камень действует ускорение свободного падения g → , которое не меняется по величине и всегда направлено в одну сторону.

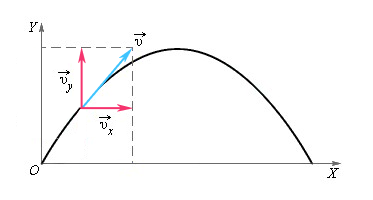
Движение тела, брошенного под углом к горизонту, можно представить в виде суммы движений относительно вертикальной и горизонтальной осей.

Вдоль оси X движение равномерное и прямолинейное, а вдоль оси Y — равноускоренное и прямолинейное. Будем рассматривать проекции векторов скорости и ускорения на оси.

Формулы для равноускоренного движения

Формула для скорости при равноускоренном движении:

Здесь v 0 — начальная скорость тела, a = c o n s t — ускорение.

Покажем на графике, что при равноускоренном движении зависимость v ( t ) имеет вид прямой линии.

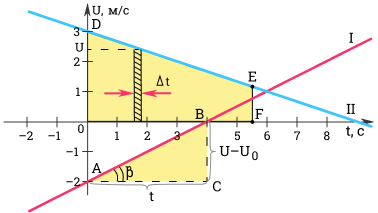
Ускорение можно определить по углу наклона графика скорости. На рисунке выше модуль ускорения равен отношению сторон треугольника ABC.

a = v — v 0 t = B C A C

Чем больше угол β , тем больше наклон (крутизна) графика по отношению к оси времени. Соответственно, тем больше ускорение тела.

Для первого графика: v 0 = — 2 м с ; a = 0 , 5 м с 2 .

Для второго графика: v 0 = 3 м с ; a = — 1 3 м с 2 .

По данному графику можно также вычислить перемещение тела за время t . Как это сделать?

Выделим на графике малый отрезок времени ∆ t . Будем считать, что он настолько мал, что движение за время ∆ t можно считать равномерным движением со скоростью, равной скорости тела в середине промежутка ∆ t . Тогда, перемещение ∆ s за время ∆ t будет равно ∆ s = v ∆ t .

Разобьем все время t на бесконечно малые промежутки ∆ t . Перемещение s за время t равно площади трапеции O D E F .

s = O D + E F 2 O F = v 0 + v 2 t = 2 v 0 + ( v — v 0 ) 2 t .

Мы знаем, что v — v 0 = a t , поэтому окончательная формула для перемещения тела примет вид:

s = v 0 t + a t 2 2

Для того, чтобы найти координату нахождения тела в данный момент времени, нужно к начальной координате тела добавить перемещение. Изменение координаты при равноускоренном движении выражает закон равноускоренного движения.

Закон равноускоренного движения

y = y 0 + v 0 t + a t 2 2 .

Еще одна распространенная задача, которая возникает при анализе равноускоренного движения — нахождение перемещения при заданных значениях начальной и конечной скоростей и ускорения.

Исключая из записанных выше уравнений t и решая их, получаем:

s = v 2 — v 0 2 2 a .

По известным начальной скорости, ускорению и перемещению можно найти конечную скорость тела:

v = v 0 2 + 2 a s .

При v 0 = 0 s = v 2 2 a и v = 2 a s

Величины v , v 0 , a , y 0 , s , входящие в выражения, являются алгебраическими величинами. В зависимости от характера движения и направления координатных осей в условиях конкретной задачи они могут принимать как положительные, так и отрицательные значения.

Источник

Расчет траектории движения точки

Положение точки на траектории

Расчет скорости точки

Расчет ускорений точки

Расчет радиуса кривизны траектории

Результаты расчетов

I. Механика

Тестирование онлайн

Графики равномерного движения

Графики равноускоренного движения

Сравнительная таблица графиков

Тело покоится, его координата не меняется, а скорость и ускорение отсутствуют

Скорость не меняется — движение равномерное

Равномерное движение в направлении противоположном оси

Равноускоренное движение в направлении оси, скорость увеличивается

Равноускоренное движение против оси

Скорость уменьшается — движение равнозамедленное

Равнозамедленное движение против оси

Выводы

Нормальное ускорение

Полное ускорение

Равноускоренное движение

Формулы для равноускоренного движения

Закон равноускоренного движения

Вам также может понравиться

Матрицы как найти значение матричного многочлена

Как можно найти поиск по картинке

Как найти фамилии деда воевавшего в войну

Добавить комментарий Отменить ответ