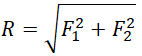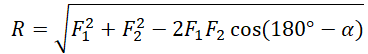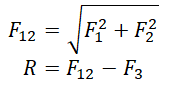Как найти ускорение по второму закону ньютона – Сайт, где вы сможете решить свои вопросы

Классическая механика
История…
Фундаментальные понятия Пространство Время Масса Скорость Сила Механическая работа Энергия Импульс
Формулировки Ньютоновская механика Лагранжева механика Гамильтонова механика Формализм Гамильтона — Якоби Уравнения Рауса Уравнения Аппеля Теория Купмана — фон Неймана
Разделы Прикладная механика Небесная механика Механика сплошных сред Геометрическая оптика Статистическая механика
Учёные Галилей Кеплер Ньютон Эйлер Лаплас Д’Аламбер Лагранж Гамильтон Коши
См. также: Портал:Физика

Второ́й зако́н Нью́то́на — дифференциальный закон механического движения, описывающий зависимость ускорения тела от равнодействующей всех приложенных к телу сил и массы тела. Один из трёх законов Ньютона. Основной закон динамики^[1]^[2]^[3].

Объектом, о котором идёт речь во втором законе Ньютона, является материальная точка, обладающая неотъемлемым свойством — инерцией^[4], величина которой характеризуется массой. В классической (ньютоновской) механике масса материальной точки полагается постоянной во времени и не зависящей от каких-либо особенностей её движения и взаимодействия с другими телами^[5]^[6]^[7]^[8].

Второй закон Ньютона в его наиболее распространённой формулировке, справедливой для скоростей, много меньших скорости света, утверждает: в инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, не зависит от её природы^[9], совпадает с ней по направлению и обратно пропорционально массе материальной точки^[10].

Второй закон Ньютона в классической механике[править | править код]

Возможные формулировки[править | править код]

В своём труде «Математические начала натуральной философии» Исаак Ньютон приводит следующую формулировку^[11] своего закона:

Изменение количества движения пропорционально приложенной движущей силе и происходит по направлению той прямой, по которой эта сила действует.

Современная формулировка:

В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.

Обычно этот закон записывается в виде формулы

${vec {a}}={frac {{vec {F}}}{m}},$

где ${vec {a}}$ — ускорение тела, $vec{F}$ — сила, приложенная к телу, а $m$ — масса тела.

Или в ином виде:

$m{vec {a}}={vec {F}}$

Формулировка второго закона Ньютона с использованием понятия импульса:

В инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на неё силе^[12]:

${frac {d{vec {p}}}{dt}}={vec {F}},$

где ${vec p}=m{vec v}$ — импульс (количество движения) точки, ${vec {v}}$ — её скорость, а $t$ — время.

Область применения закона[править | править код]

Второй закон Ньютона в классической механике сформулирован применительно к движению материальной точки. Предполагается, что масса материальной точки неизменна во времени^[13]^[14]^[15]. Уравнения, соответствующие данному закону, называются уравнениями движения материальной точки или основными уравнениями динамики материальной точки.

Иногда в рамках классической механики предпринимались попытки распространить сферу применения уравнения ${displaystyle d{vec {p}}/dt={vec {F}}}$ и на случай тел переменной массы. Однако вместе с таким расширительным толкованием уравнения приходилось существенным образом модифицировать принятые ранее определения и изменять смысл таких фундаментальных понятий, как материальная точка, импульс и сила^[16]^[17].

В случае, когда на материальную точку действует несколько сил, каждая из них сообщает точке ускорение, определяемое вторым законом Ньютона так, как если бы других сил не было (принцип суперпозиции сил). Поэтому результирующее ускорение материальной точки можно определить по второму закону Ньютона, подставив в него равнодействующую силу^[18].

Уравнение второго закона Ньютона ${displaystyle {vec {F}}=m{vec {a}}}$ предполагает скалярную аддитивность масс^[19].

Помимо материальной точки, уравнение второго закона Ньютона применимо также для описания механического движения центра масс механической системы. Центр масс движется, как материальная точка, имеющая массу, равную массе всей системы, и находящаяся под действием всех внешних сил, приложенных к точкам системы (теорема о движении центра масс системы).

Уравнение второго закона Ньютона может быть записано в виде ${displaystyle dmcdot d{vec {v}}/dt=d{vec {F}}}$ для распределённой силы, где ${displaystyle dm=rho dV}$ — элемент массы ( $rho$ — плотность вещества, $dV$ — элементарный объём), а ${displaystyle d{vec {F}}}$ — бесконечно малая действующая на него сила ( ${displaystyle {vec {f}}=d{vec {F}}/dV}$ — плотность силы). Отталкиваясь от такой записи, получают^[20] гидродинамический вариант закона — уравнение Эйлера.

Второй закон Ньютона выполняется только в инерциальных системах отсчёта^[21]^[22]. Тем не менее, добавляя к силам, действующим со стороны других тел, силы инерции, для описания движения в неинерциальных системах отсчёта можно пользоваться уравнением второго закона Ньютона^[23]. В таком случае для неинерциальной системы отсчёта уравнение движения записывается в той же форме, что и для инерциальной системы: масса тела, умноженная на его ускорение относительно неинерциальной системы отсчёта, равна по величине и направлению равнодействующей всех сил, включая и силы инерции, приложенные к телу^[24]^[25].

Логическая роль второго закона Ньютона[править | править код]

В ньютоновском изложении классической механики законы Ньютона ниоткуда не «выводятся», они имеют статус аксиом, базирующихся на совокупности экспериментальных фактов. Как и аксиомы математики, аксиомы ньютоновской динамики можно сформулировать немного по-разному.

При одном подходе второй закон Ньютона позиционируется как экспериментально проверяемое утверждение о пропорциональности ускорения вызывающей его силе и, одновременно, определение инертной массы тела через отношение величин силы и ускорения^[26]^[27]. Тогда основная идея второго закона состоит в декларации линейности соотношения «сила—ускорение», то есть что именно эти величины (а не, скажем, сила и скорость) и именно таким образом (а не квадратично и т. п.) связаны между собой.

При другом подходе можно ввести инертную массу независимо от второго закона Ньютона, через массу определённого тела, принимаемого за эталон. Тогда второй закон содержит два независимо экспериментально проверяемых утверждения: о пропорциональности ускорения силе и обратной пропорциональности массе^[28].

Во многих практических и учебных задачах второй закон Ньютона позволяет вычислять силу. Но данный закон не является дефиницией силы^[29] (высказывание типа «по определению, сила есть произведение массы на ускорение» неуместно), иначе он превратился бы в тавтологию.

В случае отсутствия воздействия на тело со стороны других тел ( ${displaystyle {vec {F}}=0}$ ), из второго закона Ньютона следует, что ускорение тела равно нулю. Отсюда может показаться, что первый закон Ньютона входит во второй как его частный случай. Однако, это не так, поскольку именно первым законом постулируется существование инерциальных систем отсчёта, что является самостоятельным содержательным утверждением. Соответственно, первый закон Ньютона формулируется независимо от второго^[30].

Второй закон Ньютона устанавливает связь между динамическими и кинематическими величинами^[31]. Кроме того, уравнение закона ${displaystyle {vec {F}}=m{vec {a}}}$ может рассматриваться как уравнение связи между физическими величинами при определении единиц силы в системах СИ, СГС и других^[32]. Единица силы определяется как такая сила, которая материальной точке с массой, равной единице массы, принимаемой в качестве основной, сообщает ускорение, равное единице ускорения, определённой ранее в качестве производной единицы^[33]. (При независимом выборе единиц массы, силы и ускорения выражение второго закона нужно писать в виде ${displaystyle m{vec {a}}=k{vec {F}}}$ , где $k$ — коэффициент пропорциональности, определяющийся выбором единиц измерения^[34]^[35]^[36]^[37]).

Сила $vec{F}$ во втором законе Ньютона зависит только от координат ${vec {r}}$ и скорости $vec{v}$ материальной точки: ${displaystyle {dot {vec {p}}}={vec {F}}({vec {r}},{vec {v}})}$ . Основная задача физической механики сводится к нахождению функции ${displaystyle {vec {F}}({vec {r}},{vec {v}})}$ ^[38].

Формула второго закона Ньютона ${displaystyle {vec {a}}={vec {F}}/m}$ выражает принцип причинности классической механики. Координаты и скорости материальной точки в момент времени ${displaystyle t+Delta t}$ (где $Delta tto 0$ ) непрерывно и однозначно определяются через их значения в момент времени $t$ и заданную силу $vec{F}$ , действующую на материальную точку. Разлагая в ряд Тейлора и ограничиваясь малыми первого порядка по $t$ , получаем^[39]: ${displaystyle {vec {r}}(t+Delta t)={vec {r}}(t)+{vec {v}}Delta t}$ , ${displaystyle {vec {v}}(t+Delta t)={vec {v}}(t)+{vec {a}}Delta t}$ . Форма, в которой в механике реализуется причинность, называется механистическим или лапласовским детерминизмом^[40].

Уравнение второго закона Ньютона ${displaystyle {vec {F}}=m{vec {a}}}$ инвариантно относительно преобразований Галилея. Это утверждение называется принципом относительности Галилея^[41].

В классической механике закон сохранения энергии, закон сохранения импульса и закон сохранения момента импульса являются следствиями второго закона Ньютона, однородности времени, однородности и изотропности пространства, а также некоторых предположений относительно характера действующих сил^[42].

В случае, когда сила $vec{F}$ постоянна, интегрирование уравнения второго закона Ньютона ${displaystyle {frac {d{vec {v}}}{dt}}={frac {vec {F}}{m}}}$ приводит к равенству ${displaystyle {vec {v}}_{2}-{vec {v}}_{1}={frac {vec {F}}{m}}(t_{2}-t_{1})}$ . Это соотношение показывает, что под действием заданной силы $vec{F}$ определённое изменение скорости ${displaystyle Delta {vec {v}}={vec {v}}_{2}-{vec {v}}_{1}}$ у тела с большей массой происходит за более продолжительный промежуток времени. Поэтому говорят, что все тела обладают инерцией, а массу $m$ называют мерой инерции тела^[43].

Запись закона в разных системах координат[править | править код]

Основной источник: ^[18]

Векторная запись второго закона Ньютона ${displaystyle m{vec {a}}={vec {F}}}$ верна для любой инерциальной системы координат, относительно которой определяются входящие в этот закон величины (сила, масса, ускорение)^[44]. Однако, разложение на компоненты (проекции) будет различным для декартовой, цилиндрической и сферической систем. Интерес также представляет разложение на нормальную и тангенциальную составляющие.

Декартова прямоугольная система координат

${displaystyle m{ddot {x}}=F_{x}}$ , ${displaystyle m{ddot {y}}=F_{y}}$ , ${displaystyle m{ddot {z}}=F_{z}}$ ,
где ${displaystyle {vec {F}}=F_{x}{vec {i}}+F_{y}{vec {j}}+F_{z}{vec {k}}}$ , а орты декартовой системы $vec{i}$ , $vec{j}$ , $vec{k}$ направлены по осям координат (в сторону возрастания конкретной координаты),

Цилиндрическая система координат

${displaystyle m({ddot {rho }}-rho {dot {varphi }}^{2})=F_{rho }}$ , ${displaystyle m(rho {ddot {varphi }}+2{dot {rho }}{dot {varphi }})=F_{varphi }}$ , ${displaystyle m{ddot {z}}=F_{z}}$ ,
где ${displaystyle {vec {F}}=F_{rho }{vec {e}}_{rho }+F_{varphi }{vec {e}}_{varphi }+F_{z}{vec {e}}_{z}}$ , а орты ${displaystyle {vec {e}}_{rho }}$ , ${displaystyle {vec {e}}_{varphi }}$ , ${displaystyle {vec {e}}_{z}}$ цилиндрической системы берутся в точке приложения силы и направлены, соответственно, от оси $z$ под 90⁰ к ней, по окружности в плоскости $xy$ с центром на оси, и вдоль $z$ (в сторону возрастания конкретной координаты),

Сферическая система координат

${displaystyle m({ddot {r}}-r{dot {varphi }}^{2}sin ^{2}theta -r{dot {theta }}^{2})=F_{r}}$ ,
${displaystyle m([r{ddot {varphi }}+2{dot {r}}{dot {varphi }}]sin theta +2r{dot {varphi }}{dot {theta }}cos theta )=F_{varphi }}$ ,
${displaystyle m(2{dot {r}}{dot {theta }}+r{ddot {theta }}-r{dot {varphi }}^{2}sin theta cos theta )=F_{theta }}$ ,
где ${displaystyle {vec {F}}=F_{r}{vec {e}}_{r}+F_{varphi }{vec {e}}_{varphi }+F_{theta }{vec {e}}_{theta }}$ , а орты ${displaystyle {vec {e}}_{r}}$ , ${displaystyle {vec {e}}_{varphi }}$ , ${displaystyle {vec {e}}_{theta }}$ сферической системы берутся в точке приложения силы и направлены, соответственно, от центра $O$ , по «параллелям», и по «меридианам» (в сторону возрастания конкретной координаты).

Разложение в соприкасающейся плоскости

В соприкасающейся плоскости ускорение ${displaystyle {vec {a}}={vec {a}}_{n}+{vec {a}}_{tau }}$ материальной точки массой $m$ и действующую на неё силу ${displaystyle {vec {F}}={vec {F}}_{n}+{vec {F}}_{tau }}$ можно разложить на нормальную (перпендикулярную касательной к траектории в соприкасающейся плоскости) ${displaystyle {vec {F}}_{n}=m{vec {a}}_{n}}$ и тангенциальную (параллельную касательной к траектории в соприкасающейся плоскости) ${displaystyle {vec {F}}_{tau }=m{vec {a}}_{tau }}$ составляющие.

Абсолютная величина нормальной силы равна ${displaystyle F_{n}=ma_{n}=mv^{2}/R}$ , где $R$ — радиус кривизны траектории материальной точки, $v$ — абсолютная величина её скорости. Нормальная сила направлена к центру кривизны траектории материальной точки. В случае круговой траектории радиуса $R$ абсолютная величина нормальной силы ${displaystyle F_{n}=momega ^{2}R}$ , где $omega$ — угловая скорость обращения точки. Нормальную силу также называют центростремительной.

Тангенциальная составляющая силы равна ${displaystyle F_{tau }=ma_{tau }=m{frac {d^{2}s}{dt^{2}}}}$ , где ${displaystyle s=s(t)}$ — дуговая координата по траектории точки^[45]. Если ${displaystyle {frac {d^{2}s}{dt^{2}}}>0}$ , то сила ${displaystyle {vec {F}}_{tau }}$ совпадает по направлению с вектором скорости $vec{v}$ и её называют движущей силой. Если ${displaystyle {frac {d^{2}s}{dt^{2}}}<0}$ , то сила ${displaystyle {vec {F}}_{tau }}$ противоположна по направлению вектору скорости $vec{v}$ и её называют тормозящей силой.

Второй закон за пределами классической механики[править | править код]

В релятивистской динамике[править | править код]

Второй закон Ньютона в виде $m{vec {a}}={vec {F}}$ приближённо справедлив только для скоростей, много меньших скорости света, и в инерциальных системах отсчёта.

В виде ${frac {d{vec {p}}}{dt}}={vec {F}}$ второй закон Ньютона точно справедлив также в инерциальных системах отсчёта специальной теории относительности и в локально инерциальных системах отсчёта общей теории относительности, однако при этом вместо прежнего выражения для импульса используется равенство ${vec p}={frac {m{vec v}}{{sqrt {1-{frac {displaystyle v^{2}}{displaystyle c^{2}}}}}}}$ , где $c$ — скорость света^[46].

Существует и четырёхмерное релятивистское обобщение второго закона Ньютона. Производная четырёхимпульса ${displaystyle {vec {mathrm {P} }}}$ по собственному времени $tau$ материальной точки равна четырёхсиле ${displaystyle {vec {Phi }}}$ ^[47]:

${displaystyle {vec {Phi }}={frac {d{vec {mathrm {P} }}}{dtau }}}$ .

В релятивистской динамике вектор трёхмерного ускорения ${vec {a}}$ уже не параллелен вектору трёхмерной силы $vec{F}$ ^[48].

В квантовой механике[править | править код]

Законы ньютоновской динамики, в том числе второй закон Ньютона, неприменимы, если длина волны де Бройля рассматриваемого объекта соизмерима с характерными размерами области, в которой изучается его движение. В этом случае необходимо пользоваться квантовомеханическими законами^[49].

Тем не менее, второй закон Ньютона при определённых условиях актуален применительно к движению волнового пакета в квантовой механике. Если потенциальная энергия волнового пакета пренебрежимо мало изменяется в области нахождения пакета, то производная по времени среднего значения импульса пакета будет равна силе, понимаемой как градиент потенциальной энергии, взятый с обратным знаком (теорема Эренфеста).

Для описания движения частицы в потенциальном поле, в квантовой механике справедливо операторное уравнение, по форме совпадающее с уравнением второго закона Ньютона: ${displaystyle m{frac {d{hat {v}}}{dt}}=-nabla {hat {U}}}$ . Здесь: $m$ — масса частицы, ${displaystyle {hat {v}}={frac {hat {p}}{m}}}$ — оператор скорости, ${hat {p}}$ — оператор импульса, ${displaystyle {hat {U}}=U(x,y,z)}$ — оператор потенциальной энергии^[50].

Видоизменённый второй закон Ньютона используется и при квантовомеханическом описании движения электронов в кристаллической решётке. Взаимодействие электрона с периодическим электромагнитным полем решётки при этом учитывается введением понятия эффективной массы.

Научно-историческое значение закона[править | править код]

Оценивая значение второго закона Ньютона, А. Эйнштейн писал:

Дифференциальный закон является той единственной формой причинного объяснения, которая может полностью удовлетворять современного физика. Ясное понимание дифференциального закона есть одно из величайших духовных достижений Ньютона… Только переход к рассмотрению явления за бесконечно малое время (т. е. к дифференциальному закону) позволил Ньютону дать формулировку, пригодную для описания любого движения… Так Ньютон пришёл… к установлению знаменитого закона движения:

Вектор ускорения × Масса = Вектор силы.

Это — фундамент всей механики и, пожалуй, всей теоретической физики.

— Эйнштейн А. Собрание научных трудов. — М.: Наука, 1967. — Т. 4. — С. 82, 92. — 599 с. — 31 700 экз.

Все законы природы для сил в зависимости от свойств тел, их состояний и движений получаются из опытов и устанавливаются всегда и только на основе решения уравнения ${displaystyle {vec {F}}=m{vec {a}}}$ , которое употребляется для выражения силы^[51].

Второй закон Ньютона является важной частью парадигмы, принятой в классической физической картине мира^[52].

Лагранжево и гамильтоново обобщения закона[править | править код]

В аналитической механике существует два аксиоматических подхода. При одном подходе в качестве аксиомы принимается второй закон Ньютона и из него выводятся уравнения Лагранжа. При другом подходе в качестве аксиомы принимаются уравнения Лагранжа. Тогда второй закон Ньютона рассматривается как следствие из них ^[53].

Из уравнений Лагранжа для произвольной голономной системы, на которую действуют как потенциальные ( ${displaystyle Q_{i}^{p}}$ ), так и непотенциальные ( ${displaystyle Q_{i}^{n}}$ ) обобщённые силы, ${displaystyle {frac {d}{dt}}left({frac {partial L}{partial {dot {q}}_{i}}}right)-{frac {partial L}{partial q_{i}}}=Q_{i}^{n}}$ следует, что производная по времени обобщённого импульса ${displaystyle p_{i}={frac {partial L}{partial {dot {q}}_{i}}}}$ равна суммарной обобщённой силе ${displaystyle Q_{i}=Q_{i}^{p}+Q_{i}^{n}={frac {partial L}{partial q_{i}}}+Q_{i}^{n}}$ :

${displaystyle {dot {p}}_{i}=Q_{i}}$ .

Записанные так в декартовых координатах уравнения Лагранжа называются уравнениями движения в форме Ньютона^[54].

Теорема об изменении обобщённого импульса обобщает и включает как частные случаи теоремы ньютоновской динамики об изменении количества движения и об изменении кинетического момента^[55].

В гамильтоновой динамике

${displaystyle {dot {p}}_{i}=-{frac {partial H}{partial q_{i}}}}$ ,

где, как и выше, ${displaystyle p_{i}={frac {partial L}{partial {dot {q}}_{i}}}}$ — обобщённый импульс, через ${displaystyle H=sum _{i=1}^{s}p_{i}{dot {q}}_{i}-L}$ обозначена функция Гамильтона, а ${displaystyle L=L(q_{i},{dot {q}}_{i},t)}$ — лагранжиан, то есть разность кинетической и потенциальной энергий системы.

См. также[править | править код]

Первый закон Ньютона
Уравнение Гейзенберга
Уравнение Мещерского
Уравнение Эренфеста
Теорема о движении центра масс системы
Принцип причинности

Примечания[править | править код]

↑ Г. А. Бугаенко, В. В. Маланин, В. И. Яковлев Основы классической механики. — М., Высшая школа, 1999. — ISBN 5-06-003587-5 — Тираж 3000 экз. — c. 43
↑ Кузнецов Б. Г. Основные принципы физики Ньютона // отв. ред. Григорьян А. Т., Полак Л. С. Очерки развития основных физических идей. — М., АН СССР, 1959. — Тираж 5000 экз. — с. 188;
↑ Тарасов В. Н., Бояркина И. В., Коваленко М. В., Федорченко Н. П., Фисенко Н. И. Теоретическая механика. — М., ТрансЛит, 2012. — ISBN 978-5-94976-455-8. — Тираж 1000 экз. — с. 249
↑ То же, что инертность. См. Инерция // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 146. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
↑ “Дополнительной характеристикой (по сравнению с геометрическими характеристиками) материальной точки является скалярная величина m — масса материальной точки, которая, вообще говоря, может быть как постоянной, так и переменной величиной. … В классической ньютоновской механике материальная точка обычно моделируется геометрической точкой с присущей ей постоянной массой) являющейся мерой её инерции.” стр. 137 Седов Л. И., Цыпкин А. Г. Основы макроскопических теорий гравитации и электромагнетизма. М: Наука, 1989.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 87. — 572 с. «Масса материальной точки считается постоянной величиной, не зависящей от обстоятельств движения».
↑ Голубев Ю. Ф. Основы теоретической механики. — М.: МГУ, 2000. — С. 160. — 720 с. — ISBN 5-211-04244-1. «Аксиома 3.3.1. Масса материальной точки сохраняет своё значение не только во времени, но и при любых взаимодействиях материальной точки с другими материальными точками независимо от их числа и от природы взаимодействий».
↑ Тарг С. М. Краткий курс теоретической механики. — М.: Высшая школа, 1995. — С. 287. — 416 с. — ISBN 5-06-003117-9. «В классической механике масса каждой точки или частицы системы считается при движении величиной постоянной»
↑ Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы. — М.: Наука, 1982. — С.39.
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 107
↑ Исаак Ньютон. Математические начала натуральной философии. — М.: Наука, 1989. — С. 40. — 690 с. — («Классики науки»). — 5000 экз. — ISBN 5-02-000747-1.
↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; изд-во МФТИ, 2005. — Т. I. Механика. — С. 76. — 560 с. — ISBN 5-9221-0225-7.
↑ Маркеев А. П. Теоретическая механика. — М.: ЧеРО, 1999. — С. 254. — 572 с. «…второй закон Ньютона справедлив только для точки постоянного состава. Динамика систем переменного состава требует особого рассмотрения».
↑ Иродов И. Е. Основные законы механики. — М.: Высшая школа, 1985. — С. 41. — 248 с.«В ньютоновской механике… m=const и dp/dt=ma».
↑ Kleppner D., Kolenkow R. J. An Introduction to Mechanics. — McGraw-Hill, 1973. — P. 112. — ISBN 0-07-035048-5. Архивная копия от 17 июня 2013 на Wayback Machine Архивированная копия. Дата обращения: 9 февраля 2013. Архивировано 17 июня 2013 года. «For a particle in Newtonian mechanics, M is a constant and (d/dt)(Mv) = M(dv/dt) = Ma».
↑ Зоммерфельд А. Механика = Sommerfeld A. Mechanik. Zweite, revidierte Auflage, 1944. — Ижевск: НИЦ «Регулярная и хаотическая динамика», 2001. — С. 45-46. — 368 с. — ISBN 5-93972-051-X.
↑ Кильчевский Н. А. Курс теоретической механики. Том 1. — М.: Наука, 1977. 480 с.
↑ ¹ ² Яворский Б.М., Детлаф А.А., Лебедев А.К. Справочник по физике для инженеров и студентов вузов. — М.: Оникс, 2007. — ISBN 978-5-488-01248-6. — Тираж 5 100 экз. — С. 38 – 39
↑ Орир Дж. Физика // М., Мир, 1981. — Тираж 75 000 экз. — Том 1. — с. 54
↑ Д. В. Александров, А. Ю. Зубарев, Л. Ю. Искакова. Введение в гидродинамику. Изд-во УрФУ, Екатеринбург (2012). — см. стр. 8-11. Дата обращения: 30 апреля 2023.
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 118
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 289
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 118-119
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 291
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 119
↑ Ландсберг Г. С. Элементарный учебник физики. Том 1. Механика. Теплота. Молекулярная физика. — М.: Наука, 1975. — C. 106
↑ Хайкин С. Э. Физические основы механики. — М.: Физматгиз, 1963. — C. 104
↑ Бутиков Е.И., Быков А.А., Кондратьев А.С. Физика для поступающих в вузы. — М.: Наука, 1982. — С. 30.
↑ Р. Ф. Фейнман Фейнмановские лекции по физике. Том I. Современная наука о природе Законы механики. — М.: Наука, 1978. — С. 209-210.
↑ Савельев И. В. Курс общей физики. Том 1. Механика. Молекулярная физика. — М.: Наука, 1987. — C. 54
↑ Селезнев Ю. А. Основы элементарной физики. – М., Наука, 1966. – Тираж 100 000 экз. – с. 40
↑ Г. Д. Бурдун, Б. Н. Марков Основы метрологии. — М.: Издательство стандартов, 1972. — Тираж 30 000 экз. — С. 49.
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1977. — С. 24.
↑ Савельев И. В. Курс общей физики / 2-е изд., перераб. — М.: Наука, 1982. — Т. 1. Механика. Молекулярная физика. — С. 54. — 432 с. Архивная копия от 4 февраля 2014 на Wayback Machine
↑ Сена Л. А. Единицы физических величин и их размерности. — М.: Наука, 1969. — С. 22. — 304 с. Архивная копия от 1 февраля 2014 на Wayback Machine
↑ Мултановский В.В. Курс теоретической физики: Классическая механика. Основы специальной теории относительности. Релятивистская механика. — М.: Просвещение, 1988. — С. 73. — 304 с. — ISBN 5-09-000625-3. Архивная копия от 5 июля 2014 на Wayback Machine
↑ «Не следует смешивать понятия силы и произведения массы на ускорение, которому она равна» (Фок В.А. Механика. Рецензия на книгу: Л. Ландау и Л. Пятигорский. Механика. (Теоретическая физика под общей редакцией проф. Л.Д. Ландау, т. I). Гостехиздат. Москва — Ленинград, 1940 // УФН. — 1946. — Т. 28, вып. 2–3. — С. 377–383. Архивировано 31 октября 2015 года.).
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 71-72
↑ Р. Ф. Фейнман Фейнмановские лекции по физике. Том I. Современная наука о природе Законы механики. — М.: Наука, 1978. — С. 164.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. ISBN 5-06-003587-5 — Тираж 3 000 экз. — С. 47.
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 94
↑ Сивухин Д. В. Общий курс физики. Механика. – М., Наука, 1979. – Тираж 50 000 экз. – с. 199
↑ Жирнов Н. И. Классическая механика. – М., Просвещение, 1980. – с. 34-35
↑ Р. Неванлинна Пространство, время и относительность. – М., Мир, 1966. – c. 202
↑ Тарасов В. Н., Бояркина И. В., Коваленко М. В. Теоретическая механика. – М., ТрансЛит, 2012. – ISBN 978-5-94976-455-8. – с. 254
↑ Савельев И. В. Курс общей физики. Т. 1. Механика. Молекулярная физика.
— М.: Наука, 1987. — С. 237.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 347. — ISBN 5-06-003587-5
↑ Кычкин И. С., Сивцев В. И. Школьная физика: второй закон Ньютона Архивная копия от 30 мая 2019 на Wayback Machine // Международный журнал экспериментального образования. – 2016. № 3-2. – С. 194-197.
↑ Бутиков Е. И., Быков А. А., Кондратьев А. С. Физика для поступающих в вузы. — М.: Наука, 1982. — С. 544.
↑ Ландау Л. Д., Лившиц Е. М. Квантовая механика. — М., Наука, 1972. — с. 76
↑ Седов Л.И.Методы подобия и размерности в механике. — М.: Гостехтеориздат, 1954. — С. 21 – 28.
↑ Томас Кун Структура научных революций. — М., АСТ, 2020. — ISBN 978-5-17-122824-8. — с. 280-282
↑ Айзерман М.А. Классическая механика. — М.: Наука, 1980. — Тираж 17 500 экз. — С. 164-165
↑ Медведев Б. В. Начала теоретической физики. Механика, теория поля, элементы квантовой механики. — М.: Физматлит, 2007. — ISBN 978-5-9221-0770-9 — С. 38.
↑ Бугаенко Г. А., Маланин В. В., Яковлев В. И. Основы классической механики. — М.: Высшая школа, 1999. — С. 247. — ISBN 5-06-003587-5

Ссылки[править | править код]

Gundlach J. H., Schlamminger S., Spitzer C. D., Choi K.-Y., Woodahl B. A., Coy J. J., Fischbach E. Laboratory Test of Newton’s Second Law for Small Accelerations (англ.). Phys. Rev. Lett., Vol. 98. American Physical Society (13 апреля 2007). Дата обращения: 7 апреля 2017. Архивировано 30 марта 2021 года.

Источник

Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».

Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.

(Эпиграмма 18-го века)

Но сатана недолго ждал реванша –
Пришел Эйнштейн, и стало все как раньше.

(Эпиграмма 20-го века)

Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.

Первый закон Ньютона

Первый закон Ньютона гласит:

Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.

Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.

Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.

До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих “Математических началах натуральной философии”.

Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.

Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.

Инерция - способность тела продолжать движение

Второй закон Ньютона

Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.

В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.

Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.

Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:

Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.

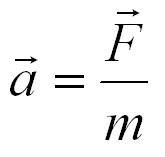
второй закон ньютона сила

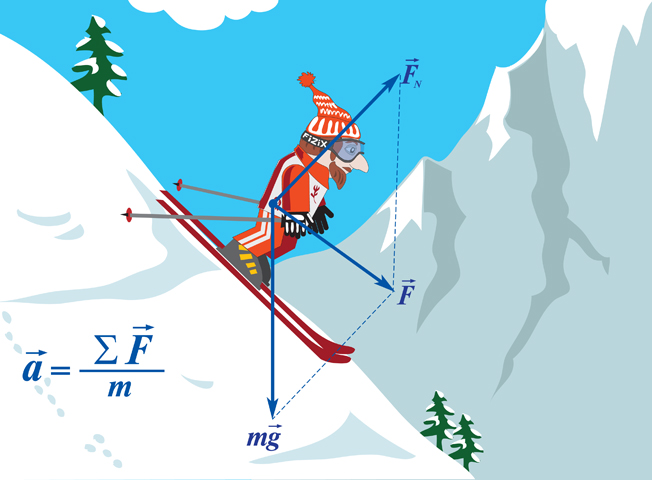
Рисунок - второй закон Ньютона

Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.

В такой формулировке второй закон Ньютона применим только для движения со скоростью, много меньшей, чем скорость света.

Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.

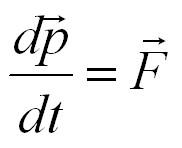
второй закон ньютона сила

В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.

Третий закон Ньютона

В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.

3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:

Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.

Формула, выражающая третий закон Ньютона:

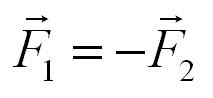
третий закон движения ньютона

Другими словами, третий закон Ньютона – это закон действия и противодействия.

Третий закон Ньютона

Пример задачи на законы Ньютона

Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.

Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.

Решение:

Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.

На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.

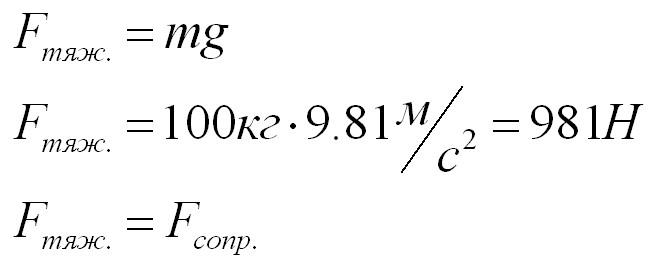
задача на законы Ньютона

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.

Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.

Решение:

По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.

Исаак Ньютон: мифы и факты из жизни

На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.

Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.

Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.

Факт. Исаак Ньютон был очень скромным и застенчивым человеком. Он увековечил себя благодаря своим открытиям, однако сам никогда не стремился к славе и даже пытался ее избежать.
Миф. Существует легенда, согласно которой Ньютона осенило, когда на наго в саду упало яблоко. Это было время чумной эпидемии (1665-1667), и ученый был вынужден покинуть Кембридж, где постоянно трудился. Точно неизвестно, действительно ли падение яблока было таким роковым для науки событием, так как первые упоминания об этом появляются только в биографиях ученого уже после его смерти, а данные разных биографов расходятся.
Факт. Ньютон учился, а потом много работал в Кембридже. По долгу службы ему нужно было несколько часов в неделю вести занятия у студентов. Несмотря на признанные заслуги ученого, занятия Ньютона посещались плохо. Бывало, что на его лекции вообще никто не приходил. Скорее всего, это связано с тем, что ученый был полностью поглощен своими собственными исследованиями.
Миф. В 1689 году Ньютон был избран членом Кембриджского парламента. Согласно легенде, более чем за год заседания в парламенте вечно поглощенный своими мыслями ученый взял слово для выступления всего один раз. Он попросил закрыть окно, так как был сквозняк.
Факт. Неизвестно, как бы сложилась судьба ученого и всей современной науки, если бы он послушался матери и начал заниматься хозяйством на семейной ферме. Только благодаря уговорам учителей и своего дяди юный Исаак отправился учиться дальше вместо того, чтобы сажать свеклу, разбрасывать по полям навоз и по вечерам выпивать в местных пабах.

Дорогие друзья, помните – любую задачу можно решить! Если у вас возникли проблемы с решением задачи по физике, посмотрите на основные физические формулы. Возможно, ответ перед глазами, и его нужно просто рассмотреть. Ну а если времени на самостоятельные занятия совершенно нет, специализированный студенческий сервис всегда к вашим услугам!

В самом конце предлагаем посмотреть видеоурок на тему “Законы Ньютона”.

Источник

Ньютон для многих (Лагранжа, Азимова и др.) важнейший ученый в истории.

Исаак Ньютон и яблоко

Можно многое рассказать о его биографии, но, поскольку для этого предназначена Википедия, достаточно просто сказать, что он был английским физиком, философом, теологом, изобретателем, алхимиком и математиком XVII и XVIII веков. Анекдот о яблоке, которое ударило его по голове и заставило задуматься о Законе всемирного тяготения, хорошо известен.

Существуют противоречивые исследования относительно того, существовало ли то яблоко, которое изменило историю человечества или нет. Есть исследования, которые утверждают, что яблоко упало, но не на голову бедному Ньютону, он просто увидел это. Исследования, в которых говорится, что яблока не существовало, утверждают, что это просто легкая для понимания история для распространения учения о гравитации.

В этой статье будет рассказано об одном из самых важных открытий: трех законах классической механики, позже названных тремя законами Ньютона.

Первый закон Ньютона

Первый закон или закон инерции гласит: «Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано». Если бросить в космосе молот, он будет двигаться с той же скоростью вечно, пока не столкнется с метеоритом, куском космического мусора или чем-то еще, что остановит его. На Земле, поскольку всегда существует трение (которое представляет собой силу, действующую между двумя поверхностями), объекты замедляются, и нет ничего, что двигалось бы вечно.

Первый закон Ньютона содержит выводы о фундаментальной симметрии Вселенной, в которой состояние движения по прямой следует считать таким же естественным, как состояние покоя.

Формулы первого закона Ньютона не существует.

Второй закон Ньютона

Второй закон Ньютона или закон силы гласит: «Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе». Это означает, что если пнуть мяч, он будет ускоряться, и чем сильнее его толкнуть, тем больше он будет ускоряться. Очень распространенная ошибка — думать, что при приложении силы объект «набирает скорость», потому что то, что действительно происходит, вызывает ускорение, с которым, очевидно, связана скорость. Когда мяч движется, ускорение, вызванное силой трения о землю или воздух, будет «противодействовать» ускорению, которое было дано и при ударе, до тех пор, пока ускорение, вызванное силой трения, не станет больше, чем ускорение при ударе и мяч замедляется.

Закон не применяется непосредственно в ситуациях, когда масса изменяется, теряется или набирается, или если объект движется со скоростью, близкой к скорости света, и в этом случае необходимо учитывать релятивистские эффекты. Закон также не применим к очень маленьким масштабам на уровне атома, где должна использоваться квантовая механика.

фото с интернета

Третий закон Ньютона

Третий закон Ньютона гласит: «При каждом действии всегда происходит равное и противоположное противодействие: это означает, что взаимные действия двух тел всегда равны и направлены в противоположном направлении». Можно соблюдать этот закон на практике, когда, например, человек толкает очень тяжелый блок (который, как очевидно, не перемещается) и замечает, что немного сдвигается назад. Это потому, что с той же силой, с которой человек толкает блок, блок толкает человека, и, поскольку блок имеет большую массу, он вызывает небольшое обратное ускорение.

Это полезный инструмент для анализа ситуаций, которые несколько противоречат здравому смыслу. Например, когда маленький грузовик сталкивается с большим, интуиция подсказывает, что сила, действующая на меньший грузовик, больше. Это не так!

Формула, выражающая третий закон Ньютона

Ньютон был кульминацией научной революции, начатой Коперником в 16 веке, и его исследования в области механики объясняли движения Земли и небесных тел до тех пор, пока его теории не были заменены общей теорией относительности Альберта Эйнштейна в 20 веке. Есть цитата Ньютона, которая гласит: «То, что мы знаем, есть капля воды; мы игнорируем океан». Несомненно, он внес большой вклад в уменьшение океана невежества.

Примеры задачи на законы Ньютона

Вот один физический пример, чтобы понять действие третьего закона Ньютона.

Комар попадает в лобовое стекло автомобиля. Нужно сравнить силы, действующие на машину и комара.

Решение:

Согласно третьему закону Ньютона силы, с которыми тела действуют друг на друга, равны и противоположны по величине. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.

Во-вторых, действие этих сил на тела сильно различается из-за разницы в массе и ускорении.

Парашютист открывает парашют и спускается в постоянном темпе. Насколько сильно сопротивление воздуху? Парашютист весит 100 кг.

Решение:

Движение парашютиста равномерное и прямое, поэтому согласно первому закону Ньютона действие сил на него компенсируется.

На парашютиста действует сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.

Согласно второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу парашютиста.

Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и направлена в обратном направлении.

Законы Ньютона простыми словами: объяснение 1, 2, 3 закона, пример с формулами

Исаак Ньютон: мифы и факты из жизни

25 декабря христиане отмечают рождение Иисуса из Назарета. Но наука тоже празднует, потому что в тот же день, хотя и много столетий спустя, родился сэр Исаак Ньютон. Он пришел в этот мир не для того, чтобы спасти людей, но он принес человечеству три важнейших закона физики. Кроме того, он способствовал развитию большого количества научных областей, от астрономии до биологии.

Но это не единственное, что интересно в жизни английского ученого. Сегодня его также помнят из-за большого количества мифов и легенд, которые циркулируют вокруг его жизни. У некоторых действительно есть доказательства их правдивости.

Если посмотреть на биографию Исаака Ньютона, можно увидеть, что в подавляющем большинстве средств массовой информации говорится, что он родился 4 января 1643 года. Однако его день рождения отмечают 25 декабря. Как это может быть?

Ньютон родился 25 декабря 1643 года. В то время в Англии все еще использовался юлианский календарь, который в других европейских странах был заменен григорианским в 1582 году. Однако в 1752 году англичане присоединились к этой инициативе, поэтому некоторые даты того времени создают определенную путаницу. Можно сказать, что у Ньютона два дня рождения.

История науки изобилует фразами, которые никогда не произносились, или сценами, которых никогда не было. Ярким примером первого является знаменитое «И все же она вертится!», которое Галилей якобы выпалил после того, как его заставили отказаться от своих гелиоцентрических теорий . Сегодня многие думают, что он никогда ничего подобного не говорил. Эта фраза не встречается ни в биографии, написанной его учеником Винченцо Вивиани, ни в протоколах судебного заседания. Было бы действительно очень рискованно ляпнуть что-то подобное в суде. В любом случае, легенда это или нет, эта фраза вошла в историю, став изречением о важности верить в знания и не поддаваться устоявшимся взглядам.

Что касается сцен, которые никогда не происходили, одна из самых известных — про Ньютона и яблоко, якобы заставившие его сделать одно из самых важных открытий в физике. Однако нет никаких данных о том, что это падение произошло. Но откуда тогда взялась эта история?

Все началось в 1665 году, когда из-за вспышки бубонной чумы Кембриджский университет был закрыт. Тогда еще молодой Исаак должен был забрать свои вещи и вернуться в дом своей семьи. Так началось самое плодотворное время его жизни, когда он начал некоторые из своих самых важных занятий. Возле дома росли три яблони, к которым Ньютон иногда выходил размышлять о науке и жизни. Но ни в одном из своих произведений он никогда не заявлял, что падение яблока ему на голову имело какое-либо отношение к началу его исследований гравитации. Фактически, первым, кто упомянул об этом, был писатель Уильям Стьюкли, опубликовавший рассказ об ученом незадолго до его смерти. В нем он описал, как сам Ньютон сказал ему, что, когда он увидел, как яблоки падают, то задался вопросом, почему они падают перпендикулярно, а не вверх или вбок. С тех пор многие другие биографы изменили это событие, создав настоящую легенду, достоверность которой совершенно неизвестна. В любом случае, как утверждают специалисты, закон всемирного тяготения не мог быть открытым из-за внезапного падения фрукта. И уж тем более удара по голове.

Хотя Ньютон особенно известен своими тремя законами и яблоком, которого никогда не существовало, любопытство ученого и стремление узнать побудили его заняться исследованиями во многих других областях. Его работы в области оптики выделяются не только с физической, но и с биологической точки зрения. Его очень интересовало, как глаза могут преобразовывать свет в изображения. Он мог бы изучить, что происходит с животными или трупами, но он хотел знать механизмы, происходящие с живыми людьми. И зная, что никто не станет добровольцем для его экспериментов, он решил стать подопытным кроликом. Для этого он вставил длинную иглу в глазницу, очень близко к кости, так что концом этого она могла прижать глаз, выгибая его. Как он позже записал в своих рабочих тетрадях, когда он прижал иглу к передней части глаза, то увидел белые и темные круги , которые менялись по мере того, как он двигал глазным яблоком. Судя по всему, его зрение после этого эксперимента не пострадало.

Источник

Теория: Если сумма всех сил не равна нулю, то тело будет двигаться с ускорением.
Второй закон Ньютона: Ускорение тела прямо пропорционально равнодействующей всех сил, и обратно пропорциональна массе.
Ускорение направлена в ту же сторону что и равнодействующая всех сил. F↑↑a
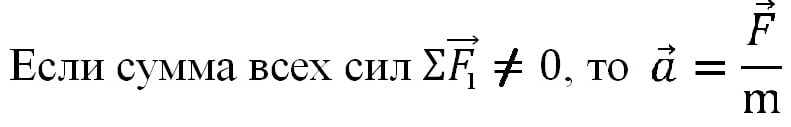
второй закон Ньютона

равнодействующая всех сил находится по формуле : F=ma

Вес тела – сила с которой тело действует на точку опоры или подвеса.
второй закон Ньютона
В инерциальной системе вес тела равен силе тяжести P=F_тяж=mg. В случае неинерциальной системы, например в лифте, когда лифт движется вертикально вверх(вниз) с ускорением, вес тела возрастает (уменьшается) P=m(g±a).

Задание: Чему равна работа силы тяги, действующей на вагон, массой 20 т, если, начав двигаться из состояния покоя с постоянным ускорением 3м/с², вагон прошел путь 100 м? Трением пренебречь.

Дано:	СИ	Решение:
a=3м/с² S=100м m=20т	20000кг	по второму закону Ньютона F=ma, получим F=20000·3= 60000Н = 60кН Работу силы тяги найдем по формуле: A=F·S A=60000·100=6000000=6000кДж Ответ: 6000кДж.
A – ?

Задание: В инерциальной системе отсчёта брусок из состояния покоя начинает скользить с ускорением вниз по наклонной плоскости. Равнодействующая всех сил, действующих на брусок, сонаправлена вектору
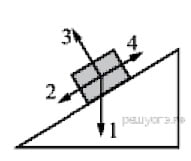
второй закон Ньютона
1) 1
2) 2
3) 3
4) 4
Решение: Ускорение направлена в ту же сторону что и равнодействующая всех сил. F↑↑a, брусок скользит с ускорением вниз по наклонной плоскости.
Ответ: 2

Задание:
Одна и та же горизонтальная сила F действует вначале на тело 1 массой 0,5 кг, а затем на тело 2 массой 3 кг. Оба тела до начала действия силы покоились на гладком горизонтальном столе. С каким по модулю ускорением будет двигаться тело 2 под действием силы F, если тело 1 движется с ускорением, модуль которого равен 1,8 м/с²?
1) 0
2) 0,3 м/с²
3) 0,6 м/с²
4) 0,9 м/с²

Решение: 1 способ. Найдем силу F=m₁a₁=0,5·1,8=0,9 Н. Затем вычислим ускорение 2 тела a₂=F/m₂=0,9/3=0,3м/с²
2 способ. Масса больше в 6 раз, так как силы равны то ускорение в 6 раз меньше.

Ответ: 2

Задание: В инерциальной системе отсчета брусок начинает скользить с ускорением вниз по наклонной плоскости. Модуль равнодействующей сил, действующих на брусок, равен
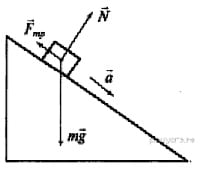
второй закон Ньютона
1) mg
2) ma
3) F_тр
4) N
Решение: Модуль равнодействующей сил F=ma по второму закону Ньютона.
Ответ: 2

Задание огэ по физике: Брусок массой 200г, подвешенный на легкой пружинке, поднимают вверх с ускорением, равным по модулю 0,5 м/с² и
направленным вверх. Чему равен модуль силы упругости пружинки?
Решение: Во время подъема сила упругости равна весу тела, тело движется вверх с ускорением, вес тела находим по формуле: P=m(g+a), получим F_упр=m(g+a)=0,2·(10+0,5)=2,1 Н.
Ответ: 2,1 Н
Задание огэ по физике (фипи): Тело массой 6 кг движется вдоль оси OX инерциальной системы отсчёта. В таблице приведена зависимость проекции скорости υ_х этого тела на ось OX от времени t. Чему равна проекция на ось OX силы, действующей на тело?

Решение: из таблицы видно, что тело движется равноускоренно, найдем ускорение по формуле: a=(υ-υ₀)/t=(1,5-0)/3=0,5 м/с²
используя второй закон Ньютона вычислим силу действующую на тело массой 6 кг. F=ma=6·0,5=3 Н.
Ответ: 3 Н

Задание демонстрационного варианта ОГЭ 2019: На покоящееся тело, находящееся на гладкой горизонтальной плоскости, в момент времени t = 0 начинают действовать две горизонтальные силы (см. рисунок). Определите, как после этого изменяются со временем модуль скорости тела и модуль ускорения тела.
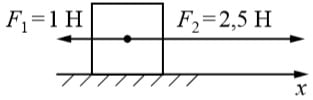
На покоящееся тело, находящееся на гладкой горизонтальной плоскости.
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Модуль скорости	Модуль ускорения

Решение: Силы направлены вдоль одной прямой в противоположные стороны. Результирующая сил F=F₂-F₁=2,5-1=1,5 Н. не равна нулю, следовательно тело будет двинаться равноускоренно a=const (т.к. равнодейстующая сил постоянна). Поэтому скорость тела будет увеличиваться.
Ответ: 13

Предыдущая тема Следующая тема

Источник

Три закона Ньютона

Динамика — раздел механики, изучающий причины движения тел и способы определения их ускорения. В нем движение тел описывается с учетом их взаимодействия.

Большой вклад в развитие динамики внес английский ученый Исаак Ньютон. Он первым смог выделить законы движения, которым подчиняются все макроскопические тела. Эти законы называют законами Ньютона, законами механики, законами динамики или законами движения тел.

Внимание! Законы Ньютона нельзя применять к произвольным телам. Они применимы только к точке, обладающей массой — к материальной точке.

Основное утверждение механики

Для описания движения тела можно взять любую систему отсчета. Обычно для этого используется система отсчета, связанная с Землей. Если какое-то тело меняет свою скорость, рядом с ним всегда можно обнаружить другое тело, которое на него действует. Так, если поднять камень и отпустить, он не останется висеть в воздухе, а упадет вниз. Следовательно, на него что-то подействовало. В данном случае сама Земля притянула камень к себе. Отсюда следует основное утверждение механики:

Основное утверждение механики

Изменение скорости (ускорение) тела всегда вызывается воздействием на него других тел.

Согласно утверждению, если на тело не действуют никакие силы, его ускорение будет нулевым, и оно будет либо покоиться, либо двигаться равномерно и прямолинейно (с постоянной скоростью).

Но в нашем мире мы не всегда это наблюдаем. И этому есть объяснение. Если тело покоится, оно действительно не меняет свою скорость. Так, мяч лежит на траве до тех пор, пока его не пнут. После того, как его пнут, он начинает катиться, но затем останавливается. Пока мяч катится, к нему больше не прикасаются. Казалось бы, согласно основному утверждению механики, мяч должен катиться вечно. Но этого не происходит, потому что на мяч действует сила трения, возникающая между его поверхностью и травой.

Основное утверждение механики можно проиллюстрировать в открытом космосе в месте, где сила притяжения космических тел пренебрежимо мала. Если в космосе придать телу скорость и отпустить, оно будет двигаться с такой скоростью по прямой линии до тех пор, пока на него не подействуют другие силы. Ярким примером служат межгалактические звезды, или звезды-изгои. Гравитационно они не связаны ни с одной из галактик, а потому движутся с постоянной скоростью. Так, звезда HE 0437-5439 удаляется от нашей галактики с постоянной скоростью 723 км/с.

Свободное тело — тело, на которое не действуют другие тела. Свободное тело либо покоится, либо движется прямолинейно и равномерно.

Первый закон Ньютона

Исаак Ньютон, изучая движение тел, заметил, что относительно одних систем отсчета свободные тела сохраняют свою скорость, а относительно других — нет. Он разделил их на две большие группы: инерциальные системы отсчета и неинерциальные. В этом кроется первый закон динамики.

Первый закон Ньютона

Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано.

Примером инерциальной системы отсчета служит система отсчета, связанная с Землей (геоцентрическая). Другой пример — гелиоцентрическая система отсчета (связанная с Солнцем).

Неинерциальная система отсчета — система отсчета, в которой тела могут менять свою скорость при отсутствии на них действия других тел.

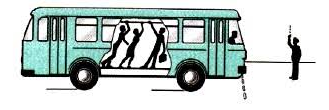
Примером неинерциальной системы отсчета служит автобус. Когда он движется равномерно и прямолинейно, стоящие внутри пассажиры находятся относительно него в состоянии покоя. Но когда автобус останавливается, пассажиры падают вперед, т. е. меняют свою скорость, хотя на них не действуют другие тела.

Второй закон Ньютона

В примере с автобусом видно, что пассажиры стараются сохранить свою скорость относительно Земли — инерциальной системы отсчета. Такое явление называется инерцией.

Инерция — явление, при котором тело сохраняет состояние покоя или равномерного прямолинейного движения.

Инертность — физическое свойство, заключающееся в том, что любое тело оказывает сопротивление изменению его скорости (как по модулю, так и по направлению).

Не все тела одинаково инертны. Вы можете взять мячик и придать ему большое ускорение. Но вы не можете придать такое же ускорение гире, хотя она обладает похожим размером. Но мячик и гиря различаются между собой массой.

Масса — скалярная физическая величина, являющаяся мерой инертности тела. Чем больше масса, тем больше инертность тела.

Масса обозначается буквой m. Единица измерения массы — кг. Прибор для измерения массы — весы.

Чтобы придать одинаковую скорость двум телам с разной инертностью, к телу с большей инертностью придется приложить больше силы. Попробуйте сдвинуть с места стол, а затем — шкаф. Сдвинуть с места стол будет проще.

Если же приложить две одинаковые силы к телам с разной инертностью, будет видно, что тело с меньшей инертностью получает большее ускорение. Если приставить к пружине теннисный шарик, а затем сжать ее и резко отпустить, шарик улетит далеко. Если вместо теннисного шарика взять железный, он лишь откатится на некоторое расстояние.

Описанные выше примеры показывают, что между силой, прикладываемой к телу, и ускорением, которое оно получает в результате прикладывания этой силы, и массой этого тела есть взаимосвязь. Она раскрывается во втором законе Ньютона.

Второй закон Ньютона

Сила, действующая на тело, равна произведению массы этого тела на ускорение, которое сообщает эта сила.

F = ma

где F — сила, которую прикладывают к телу, a — ускорение, которое сообщает эта сила, m — масса тела

Сила — количественная мера действия тел друг на друга, в результате которого тела получают ускорения.

Сила — векторная физическая величина. Обозначается F. Единица измерения — Н (Ньютон). Прибор для измерения силы — динамометр.

Пример №1. Определить, с какой силой действует Земля на яблоко, если, упав с ветки, оно получило ускорение 9,8 м/с². Масса яблока равна 200 г.

Сначала переведем массу яблока в кг. 200 г = 0,2 кг. Теперь найдем силу, действующую на яблоко со стороны Земли, по второму закону Ньютона:

F = ma = 0,2 ∙ 9,8 = 1,96 (Н)

Равнодействующая сила

Иногда на тело действуют несколько сил. Тогда при описании его движения вводится понятие равнодействующей силы.

Определение

Равнодействующая сила — векторная сумма всех сил, действующих на тело одновременно.

R = F₁ + F₂ + F₃ + …

В этом случае второй закон Ньютона формулируется так:

Второй закон Ньютона через равнодействующие силы

Если на тело действует несколько сил, то их равнодействующая R будет равна произведению массы на ускорение этого тела.

ma = R = F₁ + F₂ + F₃ + …

Правила сложения сил и их проекций

Сложение двух сил, направленных вдоль одной прямой в одну сторону
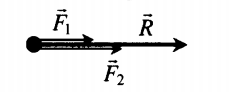	Если F₁↑↑F₂, то: R = F₁ + F₂ Равнодействующая сила сонаправлена с обеими силами.
Сложение двух сил, направленных вдоль одной прямой во взаимно противоположных направлениях
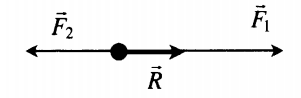	Если F₁↑↓F₂, то: R = \|F₁ – F₂\| Равнодействующая сила направлена в сторону направления большей по модулю силы.
Сложение двух сил, перпендикулярных друг к другу
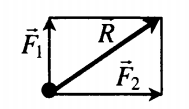	Если F₁ перпендикулярна F₂, то равнодействующая сила вычисляется по теореме Пифагора:
Сложение двух сил, расположенных под углом α друг к другу
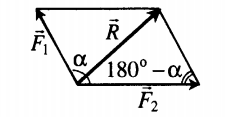	Если F₁ и F₂ расположены под углом α друг к другу, равнодействующая сила вычисляется по теореме косинусов:
Сложение трех сил
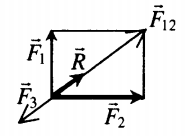	Способ сложения определяется правилами сложения векторов. В данном случае:
Сложение проекций сил
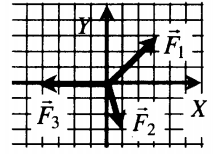	Проекция на ось ОХ: F_1x + F_2x– F_3x = 0 Проекция на ось OY: F_1y– F_2y= 0

Третий закон Ньютона

Когда одно тело действует на другое, начинается взаимодействие этих тел. Это значит, если тело А действует на тело В и сообщает ему ускорение, то и тело В действует на тело А, тоже придавая ему ускорение. К примеру, если сжать пружину руками, то руки будут чувствовать сопротивление, оказываемое силой упругости пружины. Если же, находясь в лодке, начать тянуть за веревку вторую лодку, то обе лодки будут двигаться навстречу друг другу. То есть, вы, находясь в своей лодке, тоже будете двигаться навстречу второй лодке.

Иногда на тело действует сразу несколько сил, но тело продолжает покоиться. В этом случае говорят, что силы друг друга компенсируют, то есть их равнодействующая равна нулю.

Две силы независимо от их природы считаются равными по модулю и противоположно направленными, если их одновременное действие на тело не меняет его скорости.

Примером такого явления служит ситуация, когда при перетягивании каната его никто не может перетянуть в свою сторону. Если взять два каната и присоединить между ними два динамометра, а затем начать игру в перетягивание, выяснится, что показания динамометра всегда будут одинаковыми. Это значит, что независимо от масс и придаваемых ускорений два взаимодействующих тела оказывают друг на друга равные по модулю силы. В этом заключается смысл третьего закона Ньютона.

Третий закон Ньютона

Силы, с которыми тела действуют друг на друга, равны по модулям и направлены по одной прямой в противоположные стороны.

F_A = –F_B

Используя второй закон Ньютона, третий закон механики можно переписать иначе:

m₁a₁ = –m₂a₂

Отсюда следует:

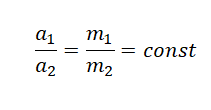
Отношение модулей ускорений a₁ и a₂ взаимодействующих друг с другом тел определяется обратным отношением их масс и совершенно не зависит от характера действующих между ними сил.

Пример №2. Определить ускорение, с которым движется Земля к падающему на нее яблоку. Масса яблока равна 0,2 кг. Ускорение свободного падения принять равной за 10 м/с². Массу Земли принять равно 6∙10²⁴ кг.

Согласно третьему закону Ньютона модули сил, с которыми взаимодействуют Земли и яблоко, равны. Поэтому:

F₁ = F₂

Отсюда:

m₁a₁ = m₂a₂

Пусть тело 1 будет яблоко, а тело 2 — Земля. Тогда a₁ будет равно g. Отсюда ускорение, с которым движется Земля к падающему на нее яблоку, равна:

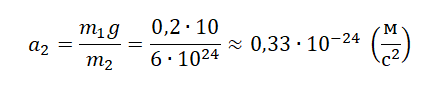
Задание EF17993

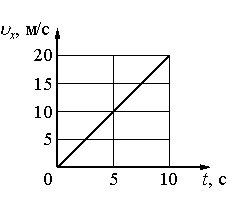Скорость тела массой 5 кг, движущегося вдоль оси Ох в инерциальной системе отсчёта, изменяется со временем в соответствии с графиком (см. рисунок). Равнодействующая приложенных к телу сил в момент времени t=2,5 с равна…

а) 2Н

б) 8 Н

в) 10 Н

г) 20 Н

Алгоритм решения

1.Записать исходные данные.

2.Проанализировать задачу.

3.Записать второй закон Ньютона.

4.Определить ускорение по графику проекции скорости от времени.

5.Подставить найденное ускорение в формулу второго закона Ньютона и произвести вычисления.

Решение

Запишем исходные данные:

Так как графиком скорости является прямая, непараллельная ось времени, тело движется с постоянным ускорением. Если ускорение постоянно, равнодействующая сил тоже будет постоянной в любой момент времени. Поэтому нам достаточно использовать координаты любой, более удобной для их определения точки. К примеру, в точке, соответствующей моменту времени 10 с.

Запишем второй закон Ньютона:

F = ma

Ускорение тела определяется как отношение изменения скорости ко времени, в течение которого эта скорость менялась. Согласно графику, за 10 секунд скорость изменилась на 20 м/с. Следовательно, ускорение равно:

a = 20/10 = 2 (м/с²)

Теперь можем вычислить равнодействующую сил:

F = ma = 5∙2 = 10 (Н)

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18915

Необходимо собрать экспериментальную установку, с помощью которой можно определить коэффициент трения скольжения стали по дереву. Для этого школьник взял стальной брусок с крючком. Какие два предмета из приведённого ниже перечня оборудования необходимо дополнительно использовать для проведения этого эксперимента?

а) деревянная рейка

б) динамометр

в) мензурка

г) пластмассовая рейка

д) линейка

Алгоритм решения

1.Проанализировать задачу. Выяснить, какие предметы необходимы для проведения опыта.

2.Вывести формулу для коэффициента трения.

3.Определить, какую величину нужно измерить, чтобы рассчитать коэффициент трения, и какой прибор для этого нужен.

Решение

Для определения коэффициента трения стали по дереву, нужен не только стальной груз, но и деревянная поверхность. То есть, понадобится деревянная рейка.

Сила трения определяется формулой:

Отсюда коэффициент трения равен:

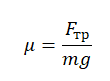
Ускорение свободного падения известно. Массу можно измерить на весах, но весов в вариантах ответа нет. Силу трения можно измерить динамометром. Следовательно, для опыта нужны только динамометр и деревянная рейка. Рейка из пластика не понадобится, так как цели расчета коэффициента трения стали по пластику нет. Мензурка используется для определения объема жидкости. В данном опыте она тоже не нужна.

Ответ: аб

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17589

Система отсчёта, связанная с Землёй, считается инерциальной. В этом случае систему отсчёта, связанную с самолётом, можно считать инерциальной, если самолёт движется:

а) равномерно и прямолинейно, набирая высоту

б) с постоянным ускорением по горизонтали

в) равномерно, выполняя поворот

г) по взлетной полосе при взлете

Алгоритм решения

Сформулировать первый закон Ньютона об инерциальных системах отсчета.
На основании закона сделать вывод, при каких условиях система отсчета, связанная с самолетом, может считаться инерциальной.
Проанализировать все 4 ситуации, приведенные в вариантах ответа.
Выбрать тот вариант, который описывает ситуацию, не противоречащую условию, выведенному в шаге 2.

Решение

Первый закон Ньютона формулируется так:

«Существуют такие системы отсчета, называемые инерциальными, относительно которых тела движутся равномерно и прямолинейно или находятся в состоянии покоя, если на них не действуют другие тела или их действие компенсировано».

Чтобы система отсчета, связанная с самолетом, была инерциальной, она должна быть неподвижной или двигаться относительно Земли — инерциальной системы отсчета — равномерно и прямолинейно.

Когда самолет движется равномерно и прямолинейно, набирая высоту, самолет движется с собственным ускорением, которое компенсируется ускорением свободного падения. И это единственный верный ответ, так как:

Самолет, двигаясь с постоянным ускорением по горизонтали, движется неравномерно, что противоречит условию.
Самолет, двигаясь равномерно во время поворота, движется непрямолинейно (с центростремительным ускорением).
Самолет, двигаясь по взлетной полосе при взлете, движется прямолинейно, но неравномерно, так как он разгоняется из состояния покоя.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22791

Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?

Ответ: ( ± ) Н.

Внимание! Записывать ответ следует последовательностью цифр без запятых.

Алгоритм решения

1.Записать исходные данные.

2.Определить цену деления шкалы.

3.Записать значение измерения с учетом погрешности.

Решение

Из условий задачи известно, что погрешность равна цене деления шкалы. Цена деления шкалы определяется отношением разности двух ближайших числовых обозначений на шкале и количеству делений между ними. Возьмем ближайшие значения 1,0 и 1,5. Между ними 5 делений. Следовательно, цена деления шкалы динамометра равна:

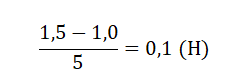
Так как погрешность равна цене деления, она также равна 0,1 Н.

Стрелка динамометра показывает 1,1 Н. Следовательно, вес груза равен: 1,1±0,1. Но по условию задачи ответ нужно записать без запятых и прочих знаков. Следовательно, верный ответ: 1101.

Ответ: 1101

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17484

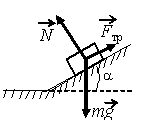Тело массой m скользит по шероховатой наклонной опоре с углом α к горизонту (см. рисунок). На него действуют 3 силы: сила тяжести mg, сила упругости опоры N и сила трения F_тр. Если скорость тела не меняется, то модуль равнодействующей сил F_тр и mg равен:

а) N cosα

б) N

в) N sinα

г) mg + F_тр

Алгоритм решения

Запись второго закона Ньютона в векторном виде.
Вывод формулы равнодействующей силы трения и силы тяжести.
Нахождение модуля равнодействующей силы трения и силы тяжести.

Решение

Записываем второй закон Ньютона в векторном виде с учетом того, сто скорость тела не меняется (ускорение равно 0):

N + mg + F_тр = 0

Отсюда равнодействующая силы трения и силы тяжести равна:

mg + F_тр = –N

Следовательно, равнодействующая силы трения и силы тяжести направлена противоположно силе реакции опоры, но равна ей по модулю. Отсюда:

|mg + F_тр| = N

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18548

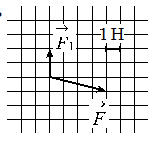На тело действуют две силы: F₁ и F₂. По силе F₁ и равнодействующей двух сил F = F₁+ F₂ найдите модуль второй силы (см. рисунок).

Алгоритм решения

Изобразить на рисунке второй вектор с учетом правил сложения векторов.
Записать геометрическую формулу для расчета модуля вектора по его проекциям.
Выбрать систему координат и построить проекции второй силы на оси ОХ и ОУ.
По рисунку определить проекции второй силы на оси.
Используя полученные данные, применить формулу для расчета вектора по его проекциям.

Решение

Построим вектор второй силы. Его начало должно совпадать с концом вектора первой силы, а его конец — с концов равнодействующей этих сил. Этот вывод следует из сложения векторов правилом треугольника.

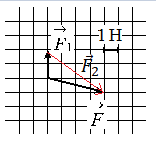
Модуль вектора равен корню из суммы квадратов его проекций на оси ОХ и ОУ:

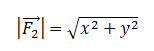
Выберем систему координат и построим проекции второй силы на оси ОХ и ОУ:

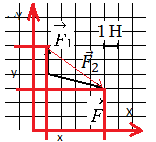
Согласно рисунку, проекция второй силы на ось ОХ равна: x = 4 (Н). Ее проекция на ось ОУ равна: y = 3 (Н).

Подставим известные данные в формулу и вычислим модуль вектора второй силы:

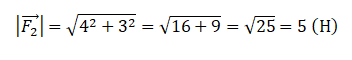
Ответ: 5

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 16.5k

Источник

Второй закон Ньютона в классической механике[править | править код]

Возможные формулировки[править | править код]

Область применения закона[править | править код]

Логическая роль второго закона Ньютона[править | править код]

Запись закона в разных системах координат[править | править код]

Второй закон за пределами классической механики[править | править код]

В релятивистской динамике[править | править код]

В квантовой механике[править | править код]

Научно-историческое значение закона[править | править код]

Лагранжево и гамильтоново обобщения закона[править | править код]

См. также[править | править код]

Примечания[править | править код]

Ссылки[править | править код]

Первый закон Ньютона

Второй закон Ньютона

Третий закон Ньютона

Пример задачи на законы Ньютона

Исаак Ньютон: мифы и факты из жизни

Первый закон Ньютона

Второй закон Ньютона

Третий закон Ньютона

Примеры задачи на законы Ньютона

Исаак Ньютон: мифы и факты из жизни

Три закона Ньютона

Основное утверждение механики

Первый закон Ньютона

Второй закон Ньютона

Равнодействующая сила

Правила сложения сил и их проекций

Третий закон Ньютона

Вам также может понравиться

Как найти историю операций тинькофф

Как найти айфон который потерялся дома

Как составить бюллетень для голосования в тсж

Добавить комментарий Отменить ответ