Как найти ускорение поршня

Ускорение
поршня

,
м/с, определяется путём дифференцирования
уравнения скорости поршня по времени
и рассчитывается по формуле:

(4.6)

Ускорение поршня
в соответствии с выражением (4.6) может
быть представлена как сумма ускорений
первого и второго порядков:

(4.7)

где

–
ускорение поршня первого
порядка,
м/с²;

–
ускорение
поршня второго порядка, м/с².

Результаты расчётов
ускорения первого, второго порядков

и суммарного
заносим в таблицу 5.

Таблица 5 – Результаты
расчёта кинематических параметров КШМ

Угол поворота кривошипа	Перемещение поршня, м	Скорость поршня, м/с	Ускорение лотлиня, м/с3

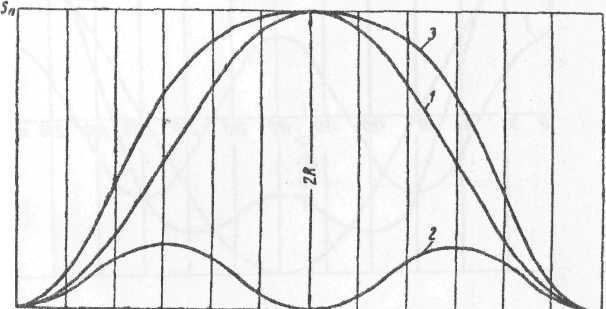
По результатам
таблицы 5 строят графики перемещения,
скорости и ускорения поршня.

0 30
60 90 120 150 180 210 240 270 300 330

в.м.т.
н.м.т.
в.м.т.

Рис. 7 – Кривые
перемещения поршня.

Рис. 8 – Кривые
скорости поршня.

Рис. 9 – Кривые
ускорения поршня.

5 Динамический расчет двигателя

Динамический
расчет KШM
заключается в определении суммарных
сил и моментов, возникающих от давления
газов и сил инерции движущихся масс.

5.1. Определение сил, действующих вдоль оси цилиндра на поршневой палец

На
поршневой палец действуют силы давления
газов

и
силы инерции

возвратно-поступательно движущихся
масс кривошипно-шатунного механизма.

Сила
давления газов

,
кН определяется по формуле:

(5.1)

где

–
текущее
значение давления газов в цилиндре

(определяется по
индикаторной диаграмме);

МПа
– атмосферное давление при нормальных
условиях;

площадь
поршня, м,

Силу

выражают
в функции от угла

°
поворота
коленчатого вала. Для этого под
индикаторной диаграммой строят
вспомогательную
полуокружность радиусом

(рис.
10).

От
центра полуокружности (точка О)
в сторону
НМТ откладывают поправку Бриккса, равную

,
где R
– радиус
кривошипа,
м, а

–
отношение
радиуса кривошипа к длине шатуна,
(таблица 6). Если необходимой марки
двигателя в таблице нет, то

можно
принять для автотракторных двигателей
в интервале
от 0,23 до 0,30 [2].

Таблица
6 – Значения постоянной кривошипно-шатунного
механизма

для автотракторных двигателей.

Марка двигателя	Значение
МеМЗ-965	0,237
МЗМА-412	0,265
ВАЗ-2106	0,295
ЗиЛ-130, ЗиЛ-131, Зил-357	0,257
ЗМЗ-66	0,295
Д-37, Д-144	0,279
СМД-14, СМД-60	0,280
СМД-62	0,274
ЯМЗ-236, ЯМЗ-238, ЯМЗ-240	0,264
ЯМЗ-740, ЯМЗ-743	0,267
Д-240	0,272
А-41, А-0,1	0,264

Рис. 10 – Построение
графика силы газов в зависимости от
угла поворота коленчатого вала

Получают
точку

и
из нее проводят лучи под углами

до
пересечения с полуокружностью. Точки,
полученные на полуокружности, соответствуют
определенным углам

поворота коленчатого вала. Из этих точек
проводят вертикальные линии до пересечения
с линиями индикаторной диаграммы и
полученные величины давлений

подставляют
в ранее приведенную формулу. Подсчитанные
значения

при разных углах поворота коленчатого
вала в течение рабочего цикла заносят
в таблицу.

Силы давления
газов, направленные к оси коленчатого
вала, считают положительными, а от
коленчатого вала -отрицательными.

В
кривошипно-шатунном механизме действуют
две силы инерции: сила инерции
возвратно-поступательно движущихся
масс

;
центробежная сила инерции вращающихся
масс

.

Действующая
на поршневой палец сила инерции
возвратно-поступательно движущихся
масс КШМ может быть
представлена
в виде суммы сил инерции первого –

и второго

порядков:

(5.2)

где

–
сила
инерции первого порядка, период изменения
которой равен одному обороту коленчатого
вала (360° п.к.в.);

–
сила
инерции
второго
порядка, период изменения
которой
равен 0,5
оборота коленчатого
вала
(180°п.к.в.).

Таким
образом:

,Н

(5.3)

Знак
« – » показывает, что действие сил инерции
противоположно направлению действия
ускорения. Сила инерции

действует
по оси цилиндра. Она положительна, если
направлена
к оси коленчатого вала, и отрицательна,
если от оси.

– масса совершающая
возвратно-поступательное движение, кг:

(5.4)

где

–
масса
комплекта поршня, кг;

–
часть массы шатуна, совершающая
возвратно-поступательное движение,

–
масса шатуна, кг.

Значения
масс

и

принимают
по данным двигателей прототипов
(подсчитывают по чертежам, определяют
взвешиванием или другими методами). Для
приближенных расчётов можно пользоваться
данными, приведёнными в таблице 7.

Центробежная
сила инерции

,
кН, от вращающихся масс определяется
по формуле:

(5.5)

где

–
масса,
совершающая вращательное движение,

(5.6)

–
часть
массы шатуна, совершающая вращательное
движение,

.

Значения
масс

также принимают по данным двигателей
прототипов, приведённых в таблице 7.

Центробежная
сила инерции Ps
всегда
постоянна по величине (так как

—
const),
действует по радиусу кривошипа, всегда
отрицательна, так как направлена от оси
коленчатого вала.

Значения угловых
частот вращения коленчатого вала берут
при номинальном скоростном режиме
двигателя, т.е.:

,с

(5.7)

Таблица
7 – Приближенные значения масс элементов
KШM
автотракторных двигателей

Элементы KШM	Конструктивные массы
Дизели D=80…120мм.	Карбюраторные двигатели D=60…100мм.
Поршень ( )	150…300	80…100
Шатун ( )	250…400	100…200
Неуравновешенная часть колена вала без противовесов ( ) Стальной кованный вал со сплошными шейками Чугунный литой вал с полыми шейками	200…400 150…300	150…200 100…200

Примечание:
большие значения m’
относятся
к

двигателям с
большим диаметром цилиндра.

Суммарную
силу

,
действующую на поршень , определяют
алгебраическим сложением силы давления
газов

и
силы инерции возвратно-поступательно
движущихся масс

:

(5.8)

Суммарная сила
направлена по оси цилиндра и приложена
к оси поршневого пальца (рис. 11). Воздействие
от неё передаётся на стенки цилиндра
перпендикулярно его оси и на шатун.

Для
определения сил, действующих в деталях
кривошипно-шатунного механизма,
раскладывают силу

на
составляющие:

N –
нормальную силу, направленную
перпендикулярно оси цилиндра и прижимающую
поршень к стенке цилиндра:

(5.9)

где

–
угол отклонения шатуна, связанный с
углом поворота коленчатого вала

зависимостью:

(5.10)

Рис. 11 – Силы,
действующие в КШМ

Нормальная
сила N
считается
положительной, если создаваемый ею
момент направлен противоположно
направлению вращения вала двигателя.

S
–
сила, направленная по оси шатуна, которая
сжимает или растягивает шатун. Она
считается положительной, если сжимает
шатун, и отрицательной, если его
растягивает:

(5.11)

После
переноса точки приложения силы S
к
оси шатунной её раскладывают на две
составляющие: тангенциальную Т
, касательную
к окружности и радиальную Z,
действующую вдоль кривошипа:

(5.12)

(5.13)

Складывая
силы Z
и
Ps,
получают
суммарную силу

,
действующую
вдоль кривошипа.

Сложив
силы Т
и

по
правилу
параллелограмма, получают силу,
действующую на шатунную шейку:

(5.14)

Крутящий
момент

Н
м,
двигателя данного цилиндра:

(5.15)

Динамический
расчёт рекомендуют вести с интервалом

=
30

, результаты расчётов заносят в таблицы.

По результатам
расчётов строят графики рассмотренных
выше сил (рис. 12).

Рис. 12 –
развёрнутые диаграммы суммарных
сил, действующих в кривошипно-шатунном
механизме

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Кинематика и динамика КШМ



Кривошипно-шатунный механизм (КШМ) является основным механизмом поршневого двигателя внутреннего сгорания (ДВС), который воспринимает и передает значительные по величине нагрузки. Поэтому расчет прочности КШМ имеет важное значение. В свою очередь расчеты многих деталей двигателя зависят от кинематики и динамики КШМ.
Кинематический анализ КШМ устанавливает законы движения его звеньев, в первую очередь поршня и шатуна.

***

Типы КШМ

В поршневых ДВС применяются три типа КШМ:

• центральный (аксиальный);
• смешанный (дезаксиальный);
• с прицепным шатуном.

В центральном КШМ ось цилиндра пересекается с осью коленчатого вала (рис. 1).
Угловая скорость рассчитывается по формуле

ɷ = πn/30.

Важным конструктивным параметром КШМ является отношение радиуса кривошипа R к длине шатуна L:

λ = R/L.

Установлено, что с уменьшением λ (за счет увеличения длины шатуна L) происходит снижение инерционных и нормальных сил. При этом увеличивается высота двигателя и его масса, поэтому в автомобильных двигателях принимают значение λ от 0,23 до 0,3.

В дезаксиальном КШМ (рис. 2) ось цилиндра не пересекает ось коленчатого вала и смещена относительно ее на расстояние а.
Дезаксиальные КШМ имеют некоторые преимущества в сравнении с центральными КШМ:

• увеличенное расстояние между коленчатым и распределительным валами, в результате чего увеличивается пространство для перемещения нижней головки шатуна;
• более равномерный износ цилиндров двигателя из-за уменьшения давления поршня на гильзу во время такта рабочего хода;
• при одинаковых значениях R и λ у дезаксиального двигателя больше ход поршня, что способствует снижению содержания токсичных веществ в отработавших газах;
• увеличенный рабочий объем двигателя.

КШМ с прицепным шатуном применяется на двигателях с большим числом цилиндров, когда хотят уменьшить длину двигателя (рис. 3).
Конструкция такого КШМ содержит главный шатун 12, соединенный непосредственно с шейкой коленчатого вала, и прицепной шатун 3, который соединен с главным шатуном посредством шарнира 11, расположенного на его головке. При этом поршни, соединенные с главным и прицепным шатуном имеют не одинаковый рабочий ход, Так, в V-образном двенадцатицилиндровом двигателе Д-12 разница в ходе поршней составляет 6,7 мм.

***

Кинематика центрального КШМ

При кинематическом анализе КШМ считается, что угловая скорость коленчатого вала постоянна. В задачу кинематического расчета входит определение перемещения поршня, скорости его движения и ускорения.

Перемещение поршня в зависимости от угла поворота кривошипа для двигателя с центральным КШМ рассчитывается по формуле:

x = R[1 – cos φ) + (λ/4)(1 – cos 2φ)].

Перемещение поршня для каждого угла поворота коленчатого вала может быть определено графическим способом, который получил название метод Брикса.

Скорость поршня может быть определена, как производная уравнения (1) по времени.
Максимальных значений скорость достигает при углах поворота коленчатого вала меньше 90˚ и больше 270˚. Точное значение этих углов зависит от величины λ.
Для λ от 0,2 до 0,3 максимальные скорости поршня соответствуют углам поворота коленчатого вала от 70˚ до 80˚ и от 280˚ до 287˚.

Средняя скорость поршня может быть определена по формулам:

V_ср = Sn/30 = 2Rπn/30 = 2Rɷ/π,

где S – ход поршня, м;
n – частота вращения коленчатого вала, об/мин;
R – радиус кривошипа, м;
ɷ – угловая скорость вращения коленчатого вала, с^-1.

Средняя скорость поршня в автомобильных двигателях находится в пределах от 8 до 15 м/с.

Значение максимальной скорости поршня с достаточной степенью точности может быть определено по формулам:

V_max = 1,62V_ср = 1,62Sn/30.

Ускорение поршня определяется, как первая производная скорости по времени или как вторая производная перемещения поршня по времени:

j = Rɷ₂(cos φ + λcos 2φ).

Ускорение достигает максимальных значений в верхней и нижней мертвых точках (ВМТ и НМТ), а в средней части хода поршня уменьшается до нуля. Максимальное ускорение поршня в автомобильных ДВС составляет 10000 м/с².

***



Отношение хода поршня к диаметру цилиндра

Отношение хода поршня S к диаметру цилиндра D является одним из основных параметров, который определяет размеры и массу двигателя. В автомобильных двигателях значения S/D варьируют от 0,8 до 1,2. Двигатели, у которых S/D больше единицы, называют длинноходными, а у которых S/D меньше единицы – короткоходными. Данное соотношение непосредственно влияет на скорость поршня, а значит и на мощность двигателя.
С уменьшением значения S/D очевидны следующие преимущества:

• уменьшается высота двигателя;
• снижаются механические потери и износ деталей (за счет уменьшения средней скорости поршня);
• улучшаются условия размещения клапанов ГРМ и создаются предпосылки для увеличения их размеров;
• появляется возможность увеличения диаметров коренных и шатунных шеек, что повышает жесткость коленчатого вала.

Однако есть и отрицательные моменты:

• увеличивается длина двигателя и длина коленчатого вала;
• повышаются нагрузки на детали от сил давления газов и сил инерции;
• уменьшается высота камеры сгорания и ухудшается ее форма, что в бензиновых двигателях способствует детонации, а в дизелях ухудшает качество смесеобразования.

При выборе значений S/D конструкторы учитывают назначение и конструктивные особенности двигателя. Так, для быстроходных двигателей целесообразно уменьшить значения S/D. Выгодно уменьшать это соотношение и для V-образных двигателей, где благодаря короткоходности можно получить оптимальные массовые и габаритные показатели.
Следует, также, учитывать, что силы, действующие в КШМ, в большей степени зависят от диаметра цилиндра, и в меньшей – от хода поршня.

***

Динамика КШМ

При работе двигателя в КШМ действуют силы и моменты, которые не только воздействуют на детали КШМ и другие узлы, но и вызывают неравномерность работы двигателя.
К таким силам относятся:

• сила давления газов (уравновешивается в самом двигателе и на его опоры не передается);
• сила инерции приложена к центру возвратно-поступательно движущихся масс и направлена вдоль оси цилиндра; эта сила воздействует на корпус двигателя через подшипники коленчатого вала, вызывая вибрацию двигателя на опорах в направлении оси цилиндра;
• центробежная сила от вращающихся масс направлена по кривошипу в средней его плоскости, воздействуя через опоры коленчатого вала на корпус двигателя, вызывает колебания двигателя на опорах в направлении кривошипа.

Кроме того, возникают такие силы, как давление на поршень со стороны картера, и силы тяжести элементов КШМ, которые в расчетах не учитываются в виду относительно малой величины.

Все действующие в двигателе силы взаимодействуют с сопротивлением на коленчатом валу, силами трения и воспринимаются опорами двигателя.
В течение каждого рабочего цикла (720˚ – для четырехтактного и 360˚ – для двухтактного двигателей) силы, действующие в КШМ, непрерывно меняются по величине и направлению. Для установления характера изменения данных сил от угла поворота коленчатого вала их определяют через каждые 10˚ – 30˚ для определенных положений коленчатого вала.
Эти данные необходимы для устранения причин вибраций двигателя во время работы, т. е. для уравновешивания двигателя.

***

Уравновешивание двигателей

Уравновешивание двигателя сводится к созданию такой системы, в которой равнодействующие силы и их моменты постоянны по величине или равны нулю.
Уравновешивание двигателей достигается подбором оптимального числа цилиндров, их расположения, порядка работы, выбором соответствующей схемы коленчатого вала, установкой противовесов на коленчатом валу (иногда – на специальных дополнительных валах), а также равенством масс подвижных деталей КШМ, балансировкой коленчатого вала и т. п.

***

Эксплуатационные свойства автомобиля



1.
Кинематика и динамика

1.1 
Ускорение
поршня. Этот параметр определяется как первая производная от скорости по
времени

.

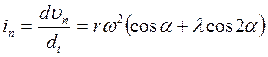В
соответствии с полученным ворожением ускорение поршня можно представить в виде
двух гармонических составляющих

, где  – ускорение
(гармоника) первого порядка; –
ускорение (гармоника) второго порядка.

Первая
составляющая выражает ускорение поршня при бесконечной длине шатуна (), вторая – вносит
поправку на конечную длину шатуна и возрастает с увеличением .

Формула ускорения II порядка:

r_k – радиус кривошипа;

 – угловая
скорость;

,

 –
отношение радиуса кривошипа к длине шатуна;

 –
угол поворота I кривошипа;

n_c – частота вращения коленчатого вала в установившемся режиме;

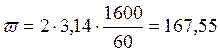рад/с.

Примем  равным 0,24, тогда
радиус кривошипа найдем из отношения:

, где     L_ш – заданная длина шатуна.

м.

Таким образом, зная числовые значения
параметров, входящих в формулу для нахождения ускорения II порядка определены его значения
через каждые 15 градусов за один период работы двигателя. Полученные значения
занесены в таблицу 1.1.

 

Таблица 1.1 – Значения ускорения II порядка

	0	15	30	45	60	75	90	105	120	135	150	165	180
	360,81	312,47	180,41	0,00	-180,41	-312,47	-360,81	-312,47	-180,41	0,00	180,41	312,47	360,81
	195	210	225	240	255	270	285	300	315	330	345	360	375
	312,47	180,41	0,00	-180,41	-312,47	-360,81	-312,47	-180,41	0,00	180,41	312,47	360,81	312,47
	390	405	420	435	450	465	480	495	510	525	540	555	570
	180,41	0,00	-180,41	-312,47	-360,81	-312,47	-180,41	0,00	180,41	312,47	360,81	312,47	180,41
	585	600	615	630	645	660	675	690	705	720
	0,00	-180,41	-312,47	-360,81	-312,47	-180,41	0,00	180,41	312,47	360,81

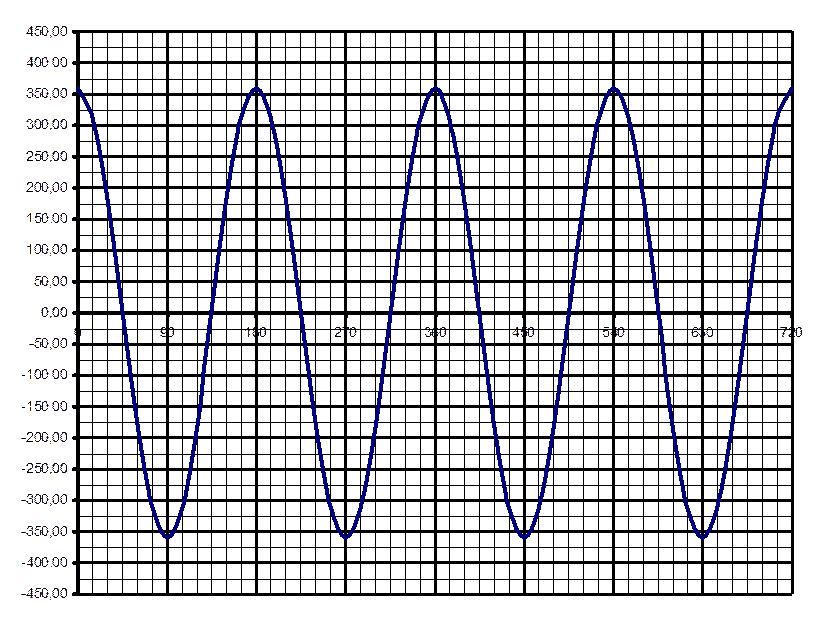
Рисунок 1.1 – График
изменения ускорения II порядка

 

УДК 621.43. 551.31

ОПРЕДЕЛЕНИЕ СКОРОСТИ И УСКОРЕНИЯ ПОРШНЯ С ПОМОЩЬЮ ПРОИЗВОДНЫХ

Ю.П. Макушев, Т.А. Полякова, П.А. Батраков

Аннотация. Рассмотрено понятие «производной» и ее практическое применение в расчетах двигателей внутреннего сгорания. Расчетным путем определен путь поршня; при помощи ««производных» найдены значения скорости и ускорения поршня. Показано практическое применение кинематики поршня в расчетах двигателей.

Ключевые слова: производная, поршень, путь, скорость, ускорение.

Введение

В двигателях внутреннего сгорания процессы наполнения, сжатия, сгорания и выпуска отработавших газов являются неустановившими-ся и протекают за короткое время. Например, процесс сгорания топлива в цилиндре быстроходного двигателя протекает за время менее

0,002 с. Давление газов в цилиндре и его температура изменяются во времени. Скорость изменения любого процесса во времени можно оценить при помощи производной.

Для понятия производной рассмотрим движение толкателя 2 при вращении вала без кулачка и с кулачком (рис. 1). Толкатель применяют, например, для перемещения (открытия и закрытия) клапана механизма газораспределения двигателя.

Из анализа рис. 1а следует, что при вращении вала 1 путь толкателя 2 и его скорость будут равны нулю (наружная поверхность вала симметрична относительно оси вращения). Толкатель неподвижен даже при вращении вала и производная постоянного числа будет равна нулю. На рис. 1б показан вал 1, выполненный с кулачком. При вращении вала кулачок приводит в движение толкатель, изменяя его путь с учетом профиля. При этом изменяется и скорость толкателя 2. Скорость толкателя является первой производной пути по времени. В зоне вала, где нет кулачка, путь не изменяется, скорость толкателя и «производная» равны нулю.

На рис. 2 показано изменение пути и скорости толкателя в зависимости от угла поворота кулачкового вала.

/т, м/с

2,0

1,8

1,6

и

1.2

1,0

0,8

0,6

0А

0,2

л

/ /

/ /

<

/ /

/ / х

/ /

/ / *

/ 7

/ /

Зт.ММ

10

9

8

7

6

5

4

3

2

1

0 5 10 15 20 25 30 35 ІО І5 50 55 60 65

(р.

а) б)

Рис. 1. Механизмы привода толкателя

Рис. 2. Изменение пути и скорости толкателя

Производной функции у=^х) в точке хо называется предел отношения приращения функции (например, перемещение толкателя) Лу =у1-уо к приращению аргумента (например, угла поворота вала) Лх=х1-хо. При этом значение х1 стремится к величине хо. Приращение аргумента стремится к нулю.

Физический смысл производной – это скорость изменения процесса, а геометрический – тангенс острого угла в прямоугольном треугольнике. Тангенс – это отношение противолежащего катета (приращения функции), к прилежащему (приращению аргумента).

На рис. 3 показана схема четырехтактного двигателя, а на рис. 4 схема центрального кривошипно-шатунного механизма (КШМ).

Рис. 3. Схема четырехтактного двигателя: 1 – цилиндр; 2 – поршень; 3 – впускной трубопровод; 4 – впускной клапан; 5 – свеча зажигания бензинового двигателя или форсунка дизельного двигателя; 6 – выпускной клапан; 7 – выпускной трубопровод; 8 – шатун; 9 – коленчатый вал; Vц – рабочий объем цилиндра; VС – объем камеры сгорания; Vп -полный объем цилиндра

1. Определение пути поршня Центральным кривошипным шатунным механизмом (КШМ) называется механизм, у которого ось цилиндра пересекает ось коленчатого вала. При помощи этого механизма работа газов в цилиндре двигателя передается кривошипу, и поступательное движение поршня преобразуется во вращательное движение коленчатого вала (рис. 4). Работа газов (Дж) равна произведению давления в цилиндре (Н/м2) на изменение его объема (м3).

Рис. 4. Схема кривошипно-шатунного механизма

Изменение направления движения поршня в цилиндре происходит в верхней и нижней мертвых точках. В мертвых точках скорость поршня равняется нулю, а ускорение достигает максимальной величины.

Отрезок ОВ является радиусом R кривошипа, ВА равен длине шатуна L, а ф – угол поворота коленчатого вала (рис. 4).

Верхней мертвой точкой (ВМТ) называют крайнее положение поршня, при котором он максимально удален от оси коленчатого вала (рис. 4, точка А).

Нижней мертвой точкой (НМТ) называет крайнее положение поршня в цилиндре, при котором он минимально удалён от оси коленчатого вала (рис. 4, точка А ).

Ходом поршня называется расстояние по оси цилиндра между мертвыми точками. По величине полный ход поршня равен двум радиусам кривошипа 5П = 2^.

Величина в – это угол отклонения оси шатуна от оси цилиндра. Значение 1=R/L – это отношение радиуса кривошипа к длине шатуна (конструктивный параметр двигателя). Для современных двигателей величина А может находиться в пределах 1/3 -И/4.

Зависимость между углом поворота коленчатого вала (град) и соответствующим ему временем ^ (сек) выражается формулой

2п-n 180•n•t

ф = ш • t =——t =———- = 6 • n • t

60 30

(1)

где ш – угловая скорость вращения коленча-

-1

того вала, с , п – частота вращения коленча-

-1

того вала, мин .

Определим зависимость перемещения поршня от угла поворота коленчатого вала. Принимаем за исходное положение КШМ такое, положение, при котором поршень находится ВМТ (рис. 4 точка А).

S = OA – OA , OA = R + L,

OA’ = R ■ cos р + L ■ cos Р, тогда S = (R + L) – (R ■ cos р + L ■ cos в),

RR S = (R + L—) – (R ■ cos р + L — ■ cos в). RR Вынесем значение R за скобку

S = R ■[(1 + L) – (cos P + L cos в)] R R

заменяя, L 1 получим:

R Я

(2)

S = R ■ [(1 + Я) – (совр + ^Ясовв)] ■ (3)

Я Я

Значение выражения

A = (1 + Я) – (cos р + — cos в)

Я Я

для различных значений ф и А приведены в работе [1].

Путь поршня может быть определен графическим способом. Для этого вычерчивают в определенном масштабе (например, 1:1) КШМ при положении кривошипа и шатуна на оси цилиндра. Поворачивают кривошип на угол, соответствующий 100, вычерчивают КШМ в новом положении и определяют пройденный путь поршнем. Затем кривошип поворачивают ещё на 100 (до 3600) и во всех точках определяют путь поршня. Строят график зависимости пути поршня от угла поворота коленчатого вала, который необходим для определения давления в цилиндре по анализу индикаторной диаграммы, построенной в координатах P-

V и перестроения ее в координаты Р-р..

2. Скорость поршня

Скорость поршня для любого угла поворота коленчатого вала является первой производной от его перемещения по времени [3].

dS dS dp dS

V =— =————-— = о—

dt dp dt dp

(4)

dp de (7)

R ■ cos p— = L ■ cos p— dt dt

Из формулы (7) находим, что:

dp cos ф

L — = R • ш —–.

dt cos p

Формулу (5) можно представить в следующем виде:

V = R ■ о ■ sinp + R ■ о ■

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

cos p ■ sin в = cos в (8)

sin p ■ cos в + cos p ■ sin в R ■о ■ (————————————————–) =

= R ■ о ■

cos в sin(p + в) cos в

Численные значения выражения B = sin(p + в) для различных значений А и ф

cos в

приведены в работе [1].

Степень быстроходности двигателей определяется по средней скорости поршня (табл. 1)

V = 2 Sn-n = Sn ‘ П .

ср 60 30

(9)

где ю =^L – угловая скорость вращения ко-

dt

ленчатого вала в рассматриваемый момент

п ■ n = 30

Следует помнить, что производная постоянного числа равна нулю, cos’p = -sinp, а sin’p = cosp.

Так как текущий путь поршня определяется выражением

S = (R + L) – (R ■ cos р + L ■ cos в),

то, подставляя в формулу скорости V значение пути S, получим:

V = R ■ sinр — + L ■sinв —. (5)

dt dt

Из анализа рис. 4 следует, что:

BC = R ■ sin р = L ■ sin в. (6)

Продифференцировав это равенство по t, получим:

Таблица 1 – Степень быстроходности двигателей

Тихоходные 5 – – 6 м/сек

Средней быстроходности 6 – – 9 м/сек

Быстроходные 9 – – 12 м/сек

Сверх быстроходные более 12 м/сек

По средней скорости поршня Уср, площади поршня Fп, выбранной площади впускного трубопровода Fвп (рис. 3), определяют скорость во впускном трубопроводе Vвп:

Vвп = УСр’ Fп/Fвп ■ (10)

Определив величину Увп, определяют потери давления в линии всасывания и величину давления в конце такта впуска.

3. Ускорение поршня

Ускорение поршня является первой производной от его скорости по времени:

. = dV = dV dp= dV dt dp dt dp

(11)

Тогда:

j = Rш

cos(<p + Р) • (1 + <dP) • cos p + sin p • <dP • sin(<p + P) Іф йф

= R • ш2 [

cos2 P

2 vcos(ф + Р) cos фcos2 p — sin фsin P^ cosP

cos P

cos 2 P

sin фsin P- CosP + cosфsin2 P dp

Іф

cos2 P

= R • ш

cos(ф + P) cos ф^ (cos2 P + sin2 P) dP

—————+————–2—————

cosP cos P

= R •ш

cos( ф + P) + cos ф dP cos P cos2 P Іф

іф (12)

Из равенства (7) находим, что

dp . dв R cos р—–= L ■ cos в—-

dt dt

R cosp = dв dt я cosp = dв

L cos в dt dр cos в dp

Подставив полученное выражение для ф/бф в уравнение 12, получим:

j = R ш

cos^ + P)

cos^ + P) cos ф cos ф

—————1—–2—-A———

cos P cos2 P cos P

cos P

+ A

cos2 ф cos3 P

(13)

j = R • ш 2 •C (14)

Численные значения постоянной величи-

ны

С =

cos^ + P) , cos ф

+ A • ■

cos P

cos P

для различных значений ф и А приведены в работе [1].

Численное значение ускорения поршня необходимо для определения сил инерции от поступательных масс КШМ и расчета на прочность деталей двигателя. Для расчета сил инерции от поступательно-движущихся масс (Р) используют выражение

Pj тПОС ‘ j;

(15)

где тпос – масса от поступательных частей, равная массе поршня и 1/3 массы шатуна.

Графики пути, скорости, ускорения поршня удобнее строить, заполнив табл. 2, в которой указаны расчетные коэффициенты А, В, С, абсолютное значение пути, скорости, ускорения поршня и их значения с учетом выбранного масштаба.

В качестве примера рассмотрим двигатель с А= 1/3,8, Я=0,05м, частотой вращения коленчатого вала 6000 мин-1 , угловой скоростью ш=628с-1 и частично заполним табл. 2.

Таблица 2 – Определение пути, скорости, ускорения поршня в зависимости от угла поворота коленчатого вала

путь, м скорость, м/с ускорение, м/с2

ф 0 знак A S S* знак B V знак C j J*

V*

0 + 0,0 0,0 + 0,0 0,0 + 1,26 24850

30 + 0,17 0,008 + 0,61 19 + 1,0 19720

60 + 0,60 0,03 + 0,98 31 + 0,37 7300

90 + 1,13 0,056 + 1,0 32 + 0,27 5324

360

В табл. 3 приведены результаты кинематического расчета на ПЭВМ двигателя на базе ВАЗ-2108 с частотой вращения 4900 мин” , угловой скоростью 513 с , А = 0,26 и радиусом кривошипа 0,035 м. На рис. 5, 6, 7 показаны графики изменения перемещения поршня, его скорости и ускорения [2].

0,080 и

S 0,070 –

х 0,060 -3

0 0,050 -с

® 0,040 -х

1 0,030 –

iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.

4»

І 0,020 -с 0,010 -0,000 –

0 30 60 90 120 150 180 210 240 270 300 330 360

угол поворота коленчатого вала, град

Рис. 5. Изменение перемещения поршня

Таблица 3 – Результаты кинематического расчета двигателя

ф град S, м V, м/с J, м/с

0 0,000 0,000 11765,45

30 0,006 11,153 9300,542

60 0,021 17,817 3454,933

90 0,040 18,207 -2427,79

120 0,057 13,718 -5882,72

150 0,067 7,054 -6872,75

180 0,071 0,000 -6909,87

210 0,067 -7,054 -6872,75

240 0,057 -13,718 -5882,72

270 0,040 -18,207 -2427,79

300 0,021 -17,817 3454,933

330 0,006 -11,153 9300,542

360 0,000 0,000 11765,45

Рис. 6. Изменение скорости поршня

BC = R ■ sin р = L ■sin в

■ в R ■ а •

sin в = L sinp = Яsmр Зная, что sin в + cos в = 1 имеем:

(16)

cos в = 1 – sin в = 1 -а sin в= (17)

:(l -Я2 sin2 вГ.

Рис. 7. Изменение ускорения поршня

4. Приближенные вычисления пути, скорости, ускорения поршня

При расчете коленчатого вала на крутильные колебания и анализе уравновешенности двигателя выражения для определения 5, V, / желательно иметь в виде функции только угла Ф поворота коленчатого вала.

Из анализа рис. 4 следует, что

Разложим выражение (17), в ряд по формуле бинома Ньютона, получим

п л 1 л2 2 1 п4 4

cos в = 1 а sin р — Я sin р.

2 8

При Я=1/4 и ф=900 второй член разложения составляет от первого примерно 3% , а третий 0,05%.

Поэтому с достаточной для практики точностью считаем,что

cos в = 1 – ■“Я2 sin 2 р. (18 )

Подставляем выражение (18) в формулу пути.

R

S = R■ (1-cos р)+L—(1-cosв) ,

R

(приведенная формула является результатом алгебраических преобразований формулы пути (2)), получим:

S=R ■ (1-cos р)+L~

1-| 1- -2 Я sin? р

S = R ■ (1 – cos p) + —

X

1.

Библиографический список

Попык, К.Г. Динамика автомобильных и

с п п R ■ X ■ 2

S = R ■ (1 – cos p) +———sin p .

2 ■ X

О Г. /1 R ■ X ■ 2

S = R-(1 -cosp) + —^sin p.

Так как sin2 p = 1 – cos 2p , то 2

S = R ■(! – cosp) +

R ■ X 4

(1 – cos2p) (19)

Из формулы (19) следует, что перемещение поршня можно условно представить состоящим из двух гармонических перемещений: S=S1+S2, где S1=R ( 1- cosy) – перемещение поршня первого порядка, если бы шатун имел бесконечно большую длину; S2=X R (1-cos2q)/4 – перемещение поршня второго порядка или дополнительное перемещение, зависящее от конечных длин шатуна и определяемое вторым членом бинома.

Определив путь (формула 19), находим скорость и ускорение поршня как первую и вторую производную пути по времени.

V = Ru[sin (ф +(X/2)sin 2ф]. (20)

j = R-ш (cosy +X cos 2ф).

(21)

Выводы по работе

– дано понятие «производной» как скорости изменения процесса, дан вывод формул для определения пути, скорости, ускорения поршня в зависимости от угла поворота коленчатого вала, показано их практическое применение;

– произведен расчет кинематики двигателя, построены графики пути, скорости, ускорения поршня;

– показаны возможности использования знаний, полученных студентами в результате изучения курса «Высшая математика» (раздел «производные»), в расчетах двигателей внутреннего сгорания.

тракторных двигателей / К.Г. Попык. – М.: Высшая школа, 1972. – 327 с.

2. Двигатели внутреннего сгорания. В 3 кн. Кн. 2. Динамика и конструирование: Учебник для вузов / В.Н Луканин и др.; под ред. В.Н Луканина и М.Г Шатрова. – М.: Высшая школа, 2005. – 400 с.

3. Письменный, Д.Т. Конспект лекций по высшей математике: полный курс / Д.Т. Письменный -М.: Айрис-пресс, 2007. – 608 с.

Determination of piston’s velocity and speedup by means of derived

Y.P. Makushev, T.A. Polyakova,

P.A. Batrakov

In the article is considered the notion “derived” and its practical application in the calculation of the engines of internal combustion. By the accounting method it is determined the way of piston; by means of “derived” it was founded the values of the piston’s velocity and its speedup. The practical application of the piston’s kinematics has been shown in the calculation of the engines.

Макушев Юрий Петрович – канд. техн. наук, доцент кафедры «Теплотехника и тепловые двигатели» Сибирской государственной автомобильно-дорожной академии. Основное направление научных исследований – расчет и проектирование двигателей и их систем. Имеет более 100 опубликованных работ. E-mail makushev321@mail.ru Полякова Татьяна Анатольевна – канд. пед. наук, доцент кафедры ««Высшая математика» Сибирской государственной автомобильнодорожной академии. Основное направление научных исследований – методика преподавания математики в школе и в вузе; методика преподавания теории вероятностей и математической статистики посредством реализации прикладной направленности. Имеет 12 опубликованных работ. E-mail: ta_polyakova@mail.ru

Батраков Петр Андреевич – студент группы ДВС-05-А1 Сибирской государственной автомобильно-дорожной академии. Основное направление научных исследований – совершенствование двигателей. Имеет 3 опубликованные работы.

Статья поступила 20.05.2010 г.