Как найти ускорение при перегрузке

В данной статье репетитор по физике и математике рассказывает о том, как рассчитать перегрузку, которую испытывает тело в момент разгона или торможения. Данный материал очень плохо рассматривается в школе, поэтому школьники очень часто не знают, как осуществлять расчёт перегрузки, а ведь соответствующие задания встречаются на ЕГЭ и ОГЭ по физике. Так что дочитайте эту статью до конца или посмотрите прилагающийся видеоурок. Знания, которые вы получите, пригодятся вам на экзамене.

Начнём с определений. Перегрузкой называется отношение веса тела к величине силы тяжести, действующей на это тело у поверхности земли. Вес тела — это сила, которая действует со стороны тела на опору или подвес. Обратите внимание, вес — это именно сила! Поэтому измеряется вес в ньютонах, а не в килограммах, как некоторые считают.

Таком образом, перегрузка — это безразмерная величина (ньютоны делятся на ньютоны, в результате ничего не остаётся). Однако, иногда эту величину выражают в ускорениях свободного падения. Говорят, к примеру, что перегрузка равна , имея ввиду, что вес тела вдвое больше силы тяжести.

Примеры расчёта перегрузки

Покажем, как осуществлять расчёт перегрузки на конкретных примерах. Начнём с самых простых примеров и перейдём далее к более сложным.

Пример 1. Чему равна перегрузка человека, стоящего на земле? Чему равна перегрузка человека, свободно падающего с некоторой высоты?

Очевидно, что человек, стоящий на земле, не испытывает никаких перегрузок. Поэтому хочется сказать, что его перегрузка равна нулю. Но не будем делать поспешных выводов. Нарисуем силы, действующие на этого человека:

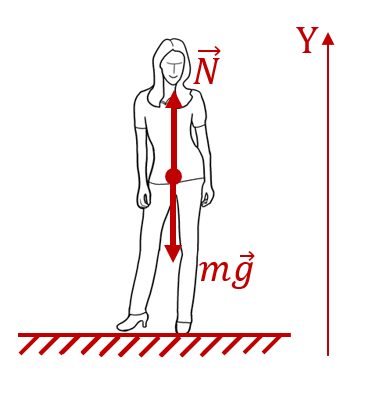
К человеку приложены две силы: сила тяжести , притягивающая тело к земле, и противодействующая ей со стороны земной поверхности сила реакции , направленная  вверх. На самом деле, если быть точным, то эта сила приложена к подошвам ног человека. Но в данном конкретном случае, это не имеет значения, поэтому её можно отложить от любой точки тела. На рисунке она отложена от центра масс человека.

Вес человека приложен к опоре (к поверхности земли), в ответ в соответствии с 3-м законом Ньютона со стороны опоры на человека действует равная по величине и противоположно направленная сила . Значит для нахождения веса тела, нам нужно найти величину силы реакции опоры.

Поскольку человек стоит на месте и не проваливается сквозь землю, то силы, которые на него действуют скомпенсированы. То есть , и, соответственно, . То есть расчёт перегрузки в этом случае даёт следующий результат:

   

Запомните это! При отсутствии перегрузок перегрузка равна 1, а не 0. Как бы странно это не звучало.

Определим теперь, чему равна перегрузка человека, который находится в свободном падении.

Если человек пребывает в состоянии свободного падения, то на него действует только сила тяжести, которая ничем не уравновешивается. Силы реакции опоры нет, как нет и веса тела. Человек находится в так называемом состоянии невесомости. В этом случае перегрузка равна 0.

Пример 2. Определите перегрузку космонавтов, находящихся в ракете, движущейся на небольшой высоте вверх с ускорением 40 м/с².

Космонавты находятся в горизонтальном положении в ракете во время её старта. Только так они могут выдержать перегрузки, которые они испытывают, не потеряв при этом сознания. Изобразим это на рисунке:

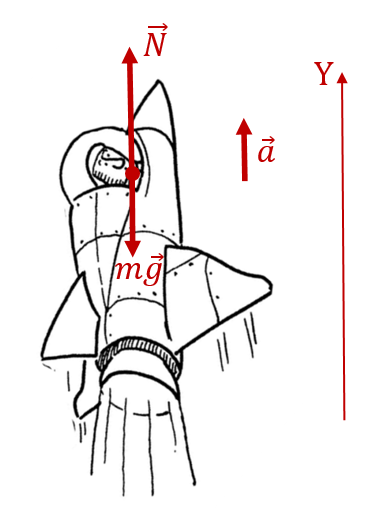
В этом состоянии на них действует две силы: сила реакции опоры и сила тяжести . Как и в прошлом примере, модуль веса космонавтов равен величине силы реакции опоры: . Отличие будет состоять в том, что сила реакции опоры уже не равна силе тяжести, как в прошлый раз, поскольку ракета движется вверх с ускорением . С этим же ускорением синхронно с ракетой ускоряются и космонавты.

Тогда в соответствии со 2-м законом Ньютона в проекции на ось Y (см. рисунок), получаем следующее выражение: , откуда . То есть искомая перегрузка равна:

   

Надо сказать, что это не самая большая перегрузка, которую приходится испытывать космонавтам во время старта ракеты. Перегрузка может доходить до 7. Длительное воздействие таких перегрузок на тело человека неминуемо приводит к летальному исходу.

Пример 3. Рассчитайте перегрузку, которую испытывает пилот самолёта, выполняющего «мёртвую петлю» в нижней точке траектории. Скорость самолёта в этой точке составляет 360 км/ч. Радиус «мёртвой петли» составляет 200 м.

В нижней точке «мёртвой петли» на пилота будут действовать две силы: вниз — сила , вверх, к центру «мёртвой петли», — сила (со стороны кресла, в котором сидит пилот):

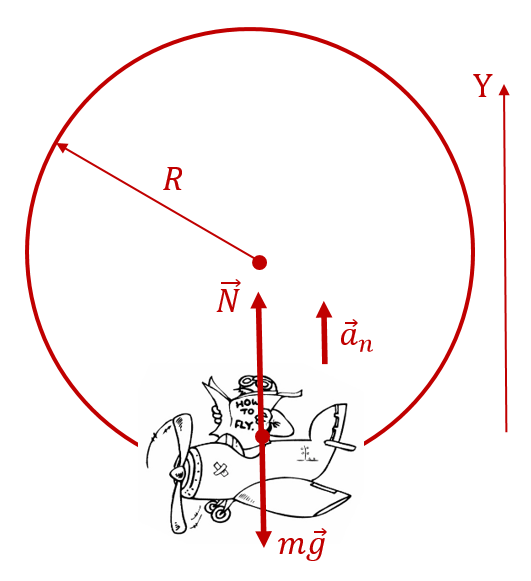
Туда же будет направлено центростремительное ускорение пилота , где км/ч м/с — скорость самолёта, — радиус «мёртвой петли». Тогда вновь в соответствии со 2-м законом Ньютона в проекции на ось, направленную вертикально вверх, получаем следующее уравнение:

   

Тогда вес равен . Итак, расчёт перегрузки даёт следующий результат:

   

Весьма существенная перегрузка. Спасает жизнь пилота только то, что действует она не очень длительно.

Ну и напоследок, рассчитаем перегрузку, которую испытывает водитель автомобиля при разгоне.

Пример 4. Рассчитайте перегрузку, которую испытывает водитель автомобиля, разгоняющегося с места до скорости 180 км/ч за 10 с.

Итак, конечная скорость автомобиля равна км/ч м/с. Если автомобиль ускоряется до этой скорости из состояния покоя за c, то его ускорение равно м/с².

На водителя в процессе ускорения действуют две составляющие силы реакции опоры: со стороны седушки кресла (вертикальная составляющая) и со стороны спинки кресла (горизонатльная составляющая) :

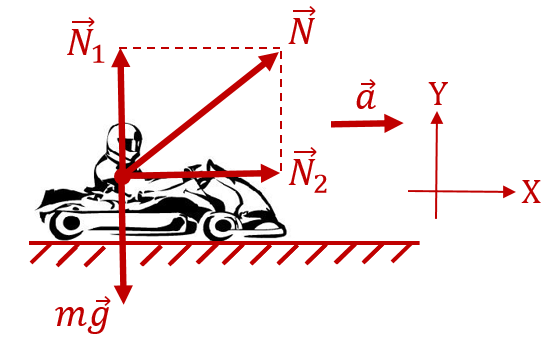
Автомобиль движется горизонтально, следовательно, вертикальная составляющая силы реакции опоры уравновешена силой тяжести, то есть . В горизонтальном направлении водитель ускоряется вместе с автомобилем. Следовательно, по 2-закону Ньютона в проекции на ось, сонаправленную с ускорением, горизонтальная составляющая силы реакции опоры равна .

Величину общей силы реакции опоры найдём по теореме Пифагора: . Она будет равна модулю веса. То есть искомая перегрузка будет равна:

   

Сегодня мы научились рассчитывать перегрузку. Запомните этот материал, он может пригодиться при решении заданий из ЕГЭ или ОГЭ по физике, а также на различных вступительных экзаменах и олимпиадах.

Материал подготовил репетитор по физике в Москве, Сергей Валерьевич

Смотрите также:

• Как рассчитать скорость спутника, вращающегося вокруг земли
• Как легко решить сложную задачу на относительность движения

Enter the total number of G-forces into the calculator to determine the G-Force to Acceleration. 

• All Acceleration Calculators
• G-Force To Velocity Calculator
• Joules to G Force Calculator
• Newtons to G Force Calculator
• Near Force to Acceleration Calculator
• Tidal Acceleration Calculator
• Power to Acceleration Calculator

The following equation is used to calculate the G-Force to Acceleration.

• Where A is the G-Force to Acceleration (m/s^2)
• G is the total number of G-forces ((g-forces))

To calculate acceleration from G-force, multiply the number of g-forces by 9.81.

What are the units for G-Force to Acceleration?

The most common units for G-Force to Acceleration are m/s^2.

How to Convert G-Force to Acceleration?

Example Problem:

The following example problem outlines the steps and information required to calculate the G-Force to Acceleration.

First, determine the total number of G-forces. In this example, the total number of G-forces is measured to be 6 ((g-forces)).

Finally, calculate the G-Force to Acceleration using the formula above: 

A = G * 9.81

Inserting the values from above and solving the equation gives us: 

A = 6 * 9.81 = 58.86 (m/s^2)

При какой максимальной скорости разгона автомобиля с 0-100 км/ч может выжить водитель

Какая скорость разгона с 0 до 100 км/час угрожает жизни человека?

По какой-то особой причине в мире большое внимание уделяется именно скорости разгона автомобиля с 0 до 100 км/час (в США с 0 до 60 миль в час). Эксперты, инженеры, любители спортивных автомобилей а также и простые автолюбители с какой-то одержимостью постоянно следят за технической характеристикой автомобилей, которая как правило раскрывает динамику разгона автомобиля с 0 до 100 км/час. Причем весь этот интерес наблюдается не только к спортивным автомобилям для которых динамика разгона с места является очень важным значением, но и к совсем обычным автомобилям эконом-класса.

В наши дни наибольший интерес к динамике разгона с 0 до 100 км/час направлен на электрические современные автомобили, которые начали потихоньку вытеснять из авто ниши спортивные суперкары с их невероятной скоростью разгона. Вот например, еще несколько лет назад казалось просто фантастикой, что автомобиль может разгоняться до 100 км/час чуть-более чем за 2 секунды. Но сегодня некоторые современные электрокары уже вплотную приблизились к этому показателю.

Это естественно заставляет задуматься: А какая скорость разгона автомобиля с 0 до 100 км/час опасна для здоровья самого человека? Ведь чем быстрее разгоняется автомобиль, тем больше нагрузки испытывает водитель, что находится (сидит) за рулем.

Согласитесь с нами, что человеческий организм имеет свои определенные пределы и не может выдержать бесконечные нарастающие нагрузки, которые действуют и оказывают на него при быстром разгоне транспортного средства, определенное воздействие. Давайте вместе с нами узнаем, а какой предельный разгон автомобиля может теоретически ну и практически выдержать человек.

Согласно законам физики установлено, что при движении объекта возникает перегрузка (G), которая зависит от ускорения. То есть, чем быстрее происходит ускорение движущего объекта, тем больше возникает перегрузка, образуемая из-за силы тяжести. Например, когда человек стоит неподвижно на месте, то он испытывает перегрузку в 1g, так как по сути, мы движемся в пространстве вместе с нашей планетой и в связи с гравитацией, которая нас и удерживает на поверхности земли.

Такая же перегрузка в 1g действует и на наше тело, когда, мы допустим сидим на стуле. 1g это количество силы, которая оказывается (давит) на нашу поясницу и нижнюю часть спины, все для того, чтобы помешать нам уйти в свободное падение в пространстве. Ведь согласитесь, если бы сила тяжести оказываемая свое давление на нас была бы меньше, то мы просто не смогли бы устоять на поверхности нашей планеты. В этом случае мы бы отправились в свободное падение.

Когда же мы сидим в автомобиле и начинаем ускоряться, то эти G-силы начинают действовать на линейно-горизонтальной оси. Естественно, что перегрузка при разгоне машины будет совершенно иной по сравнению с той, которая воздействует на человека в стоящем автомобиле.

Давайте же выясним, какая перегрузка оказывается на человека при разгоне автомобиля.

Начнем мы с относительно медленной динамики этого ускорения (по современным меркам), с 0 до 100 км/час в периодике 10 секунд.

Для этого можно воспользоваться специальным онлайн-конвектором преобразования величин. Так, с помощью этого калькулятора мы с вами высчитали, что при разгоне автомобиля с 0 до 100 км/час за 10 секунд перегрузка, воздействующая на водителя, составляет 0.28325450 = 0.28. То есть разгон с места с 0 до 100 км/час в течение десяти секунд будет оказывать на человека перегрузку в 0.28g.

Как вы видите, при ускорении за рулем автомобиля линейно горизонтальные G-силы воздействуют на человека гораздо меньше, чем эти силы оказывают воздействие на тело человека в состоянии покоя.

Соответственно, для того, чтобы добиться той же перегрузки в 1g, которая воздействует на человека когда он стоит или сидит неподвижно на стуле необходимо, чтобы автомобиль с 0 до 100 км/час разгонялся за 2,83 секунды. Это можно вычислить и с помощью простого калькулятора.

Если мы хотим быть совсем уж точными, то перегрузка человека в 1g сидящего за рулем автомобиля образуется при ускорении машины с 0 до 100 км/час за 2,83254504 секунды.

И так, мы знаем, что при перегрузке в 1g человек не испытывает на себе ни каких проблем. Например, серийный автомобиль Tesla Model S (дорогая спецверсия) с 0 до 100 км/час может разгоняться за 2,5 секунды (согласно спецификации). Соответственно, водитель находящийся за рулем этого автомобиля при разгоне будет испытывать перегрузку в 1.13g.

Это уже как мы видим, больше чем перегрузка, которая испытывается человеком в обычной жизни и которая возникает из-за гравитации а также из-за движения планеты в пространстве. Но это совсем немного и перегрузка не представляет для человека никакой опасности. Но, если мы сядем за руль мощного драгстера (спортивного автомобиля), то картина здесь уже получается совершенно иная, так как мы с вами наблюдаем уже иные цифры перегрузки.

Приведем пример, человек на американских горках в парке аттракционов может испытывать перегрузки до 6g, но их длительность настолько мала, что это не опасно для жизни. Летчики пилотируемых истребителей в компрессионных костюмах могут выжить при длительных перегрузках в 8g или 9g. Но это все не те виды перегрузок, которые испытывает человек, находясь за рулем автотранспортного средства с ускорением в пространстве на земле.

Кстате, мы заодно сразу вспомнили, что офицер ВВС США Джон Стапп участвовал в эксперименте по воздействию перегрузки на человека во время ускорения. Джона Стаппа посадили в специальные сани установленные на платформе, которые с помощью тяги ракетных двигателей разогнали до 1017 км/час. Во время этого ускорения Джон выдержал перегрузку в 46.2g.

Таким образом убеждаемся, зная, что человек способен выдержать перегрузку в 46.2g, выяснить с какой скоростью должен разгоняться автомобиль, чтобы перегрузка составляла такое значение, которое выдержал офицер ВВС США Джон Стапп, мы должны снова воспользоваться калькулятором преобразования величин, подставив в соответствующем поле полученное значение в 46.2g.

В итоге, калькулятор помог нам установить следующее, чтобы водитель за рулем автомобиля испытывал перегрузку в 46.2g, необходимо разогнать транспортное средство с места до 100 км/час с ускорением, всего за 0,06131050 = 0,06 секунды.

Хотим вам сказать, что Джон Стапп также участвовал и во многих других подобных экспериментах, где перегрузка во время ускорения составляла тоже до 35g. Во многих этих испытаниях Джон не раз получал травмы. Например, в одном эксперименте у него, от силы тяжести оказываемое на его тело, лопнуло одно ребро. Также, не редко во время проведения экспериментов у офицера вылетали пломбы из зубов.

Таким образом мы с вами убедились, что перегрузка выше 30g все-таки для человека запредельная. Не думаем, что покупатели премиальных дорогих суперкаров были бы довольны такими последствиями разгона своего автомобиля.

И так, на основании выше представленной информации давайте вместе с вами установим, что перегрузка в 30g при ускорении за рулем автомобиля является нашим (человеческим) пределом при котором, ни- каких особых последствий от разгона машины не будет. То есть, не будет травм.

Соответственно от сюда делаем вывод, что максимально безопасная динамика разгона автомобиля с 0 до 100 км/час составляет (составит) 0,09441817 = 0,09 секунды.

Если же мы (Вы) согласны разгоняться на машине с риском получить для себя травмы рёбер или готовы распрощаться с пломбами в зубах, то нам (Вам) нужен автомобиль способный разгоняться с места до 100 км/час за 0,08092986 = 0,08 секунды.

Но, если же мы готовы повторить мировой рекорд по перегрузке организма человека, который был установлен Джоном Стаппом, то ваше транспортное средство должно ускориться с 0 до 100 км/час за 0,06 секунды.

Источник

Расчёт минимально возможного времени разгона

На написание данной статьи меня подтолкнуло следующее видео:

Используемые в нём расчёты основаны на школьном курсе физики.
Начнём с того, что время t разгона до заданной скорости v (например, до 100 км/ч) определяется по формуле

Вообще говоря, в силу разных причин ускорение меняется по мере разгона, но мы можем оценить его максимальную величину a_max, тем самым найдя минимально возможное время разгона t_min.

Согласно второму закону Ньютона ускорение a любого тела прямо пропорционально приложенной к телу силе F и обратно пропорционально его массе m:

Как известно, на ровной дороге автомобиль ускоряется за счёт силы трения между шинами и поверхностью дороги. Максимальная величина силы трения F_max определяется по формуле

F_max = μ∙N, (3)
где
μ — коэффициент трения покоя (для большинства летних гражданских шин μ ≈ 1);
N — нормальная сила давления.

Заметим, что при пробуксовке ведущих колёс коэффициент трения покоя меняется на коэффициент трения скольжения, который приблизительно вдвое меньше. Поэтому при пробуксовке тяга, а в след за ней и ускорение, падают не менее чем вдвое.

Таким образом, зная силу N, приходящуюся на ведущие колёса автомобиля, можно определить максимальную тягу, создаваемую шинами, а уже по ней найти ускорение и время разгона.

1 ПОЛНОПРИВОДНЫЕ АВТОМОБИЛИ

Для полноприводных автомобилей эта сила N равна весу P автомобиля:

N = P = m∙g, (4)
где
m — масса автомобиля, кг;
g — ускорение свободного падения (9.81 м/с²).

Если подставить (2), (3) и (4) в (1), то получится

что для v = 100 км/ч = 27.78 м/c даёт

t_min ≈ 27.78/9.81 = 2.83 с

2 МОНОПРИВОДНЫЕ АВТОМОБИЛИ

С моноприводными автомобилями ситуация иная. У них за счёт продольного переноса веса во время разгона сила N будет определяться по формуле

N = δ∙P ± m∙a∙H/B = m∙(δ∙g ± a∙H/B), (6)
где
δ — статическая доля веса автомобиля, приходящаяся на ведущую ось;
a — ускорение (2), с которым разгоняется автомобиль, м/с²;
H — высота центра тяжести автомобиля, мм;
B — колёсная база, мм.

При этом в случае заднеприводных автомобилей в формуле (6) используется знак «+», а в случае переднеприводных — знак «−».

Если подставить (3) и (6) в (2), то получится

откуда находим максимально возможное ускорение автомобиля:

Осталось подставить (7) в (1):

В формулах (7) и (8) знак «−» уже используется для заднеприводных автомобилей, а знак «+» — для переднеприводных.

Из выражения (8) видно, что при равномерной загрузке осей заднеприводный автомобиль потенциально будет разгоняться быстрее переднеприводного.

Оценим минимально возможное время разгона а/м Lada Granta. Для этого автомобиля известно, что статическая развесовка составляет 60/40, а база равна 2476 мм. В качестве высоты центра тяжести примем ⅓ от полной высоты автомобиля, т.е. 500 мм. Тогда по формуле (8) получаем

Видно, что по сравнению с полноприводным автомобилем это время оказалось вдвое дольше.

Теперь занизим центр тяжести нашей Гранты на 100 мм:

t_min ≈ (1 + 400/2476)∙27.78/(0.6∙9.81) = 5.48 с

С помощью такого занижения время разгона удалось сократить всего на 0.2 с

Посмотрим, что будет, если мы поставим гоночные шины с коэффициентом трения μ = 1.2:

t_min = (1 + 1.2∙400/2476)∙27.78/(0.6∙1.2∙9.81) = 4.70 с

Разница с исходным вариантом составляет уже почти 1 с, т.е. такая модификация сильнее влияет на сокращение времени разгона.

Найдём оценку минимальной мощности, выдаваемой двигателем, при которой рассчитанное время разгона становится достижимым.

Кинетическая энергия T автомобиля (как и любого другого тела) определяется по формуле

Тогда мощность с колёс во время разгона не должна быть меньше:

Здесь мы пренебрегли силами сопротивления качения и сопротивления воздуха.

Для рассмотренной выше Гранты со снаряженной массой 1160 кг на штатных шинах получается

W_min ≥ 1160∙27.78²/(2∙5.48) = 81.7 кВт = 110 л.с.

Обычно потери в трансмиссии составляют около 25%, что даёт оценку на минимальную мощность двигателя почти 140 л.с. К этому надо добавить мощность сил сопротивления, которые можно оценить в 10% от рассчитанной минимальной мощности с колёс.

Таким образом, если во время разгона мощность с колёс не будет падать ниже 120 л.с. (а мощность двигателя не будет падать ниже 150 л.с.), то минимально возможное время разгона становится достижимым.

Обычно во время разгона обороты двигателя не опускаются ниже 3000 об/мин. При таких оборотах мощность мотора составляет приблизительно половину от максимальной. Следовательно, минимально возможное время разгона можно ожидать на Гранте с двигателем не менее 300 л.с.

P.P.S. Дополнение, касающееся минимально возможного времени заезда на четверть мили

При равноускоренном движении пройденный путь S вычисляется по формуле

откуда легко выражается время

По этой формуле для полноприводного автомобиля получается

Источник

Какой разгон до 100 км/ч может выдержать человек

Как известно, ускорение — это физическая величина, определяющая изменение скорости со временем. Обычно мы измеряем его с точки зрения ускорения свободного падения, которое численно равно силе тяжести на поверхности Земли. Ускорение свободного падения обозначается буквой g и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Стандартное значение g, определённое как «среднее» по всей планете, составляет 9,8 м/с².

Соответственно, 1 g считается эквивалентом силы земной гравитации. Когда мы говорим об ускорении в автомобиле, мы подразумеваем силу g, действующую на пассажиров в линейной горизонтальной оси. Давайте же выясним, сколько именно g мы испытываем в тех или иных машинах. Для того, чтобы продемонстрировать ускорение в 1 g, автомобиль должен разогнаться до 100 км/ч за 2,8 секунды. Ускорение до «сотни» за 10 секунд, довольно медленное по нынешним временам, составляет лишь 0,28 g.

Например, «американские горки» могут обеспечить вам до 6 g, но длительность ускорения настолько мала, что это совершенно не опасно для здоровья. Лётчики в специальных костюмах переносят 9 g, но абсолютный рекорд принадлежит офицеру ВВС США Джону Стаппу, который испытал ужасающие 46,2 g, пилотируя ракетные сани на авиабазе Эдвардс в Калифорнии. Впрочем, едва ли обычный человек выдержал такую перегрузку без подготовки.

Источник

Какой разгон до 100 км/ч может выдержать человек

По неизвестной нам причине производители автомобилей буквально одержимы временем разгона с места до 100 км/ч, словно это самый важный параметр на свете. И это заставляет всерьёз задуматься — насколько быстрый разгон способно выдержать человеческое тело? Вдруг мы уже находимся на пределе возможностей?

Как известно, ускорение — это физическая величина, определяющая изменение скорости со временем. Обычно мы измеряем его с точки зрения ускорения свободного падения, которое численно равно силе тяжести на поверхности Земли.

Ускорение свободного падения обозначается буквой g и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах. Стандартное значение g, определённое как «среднее» по всей планете, составляет 9,8 м/с².

Соответственно, 1 g считается эквивалентом силы земной гравитации. Когда мы говорим об ускорении в автомобиле, мы подразумеваем силу g, действующую на пассажиров в линейной горизонтальной оси.

Давайте же выясним, сколько именно g мы испытываем в тех или иных машинах. Для того, чтобы продемонстрировать ускорение в 1 g, автомобиль должен разогнаться до 100 км/ч за 2,8 секунды. Ускорение до «сотни» за 10 секунд, довольно медленное по нынешним временам, составляет лишь 0,28 g.

В принципе, можно потерять сознание или даже умереть, если испытать ускорение порядка 6 g продолжительностью несколько секунд, но известны случаи, когда человек выживал и при воздействии 100 g — правда, чрезвычайно кратковременном.

Например, «американские горки» могут обеспечить вам до 6 g, но длительность ускорения настолько мала, что это совершенно не опасно для здоровья.

Лётчики в специальных костюмах переносят 9 g, но абсолютный рекорд принадлежит офицеру ВВС США Джону Стаппу, который испытал ужасающие 46,2 g, пилотируя ракетные сани на авиабазе Эдвардс в Калифорнии. Впрочем, едва ли обычный человек выдержал такую перегрузку без подготовки.

К тому же подполковник Стапп в ходе испытаний реактивных саней успел перенести и несколько значительно менее удачных для здоровья заездов.

Однажды при ускорении в 35 g Джон потерял несколько пломб, сломал рёбра и испытал некоторые другие пикантные неудобства, на которые вряд ли согласятся покупатели дорогих и мощных автомобилей. Имея это в виду, давайте установим 30 g как предел для ускорения без телесных повреждений.

В привычных нам величинах это означает разгон с 0 до 100 км/ч за невероятные пока 0,093 секунды. Если мы готовы пойти на выпавшие пломбы, сломанные рёбра и испорченный салон автомобиля, можно рискнуть катапультироваться до «сотни» за 0,08 секунды.

Наконец, в ходе рекордного заезда бывалый испытатель Джон Стапп перенёс ускорение в 0,06 секунды до 100 км/ч. Что ж, на сегодняшний день мы весьма далеки от опасного для жизни разгона. Хорошая новость, не так ли?

Источник

Наука собственными силами

Расчет перегрузок, возникающих при использовании «реактивного якоря»

Пусть транспортное средство массы m движется со скоростью v₀.

Рассмотрим торможение с помощью реактивного якоря(идея изобретателя Сергея Братченко).
Этот способ экстренного торможения состоит в том, что в дорожное покрытие «выстреливается» металлический штырь с раскрывающимися лопастями, к штырю прикреплен упругий элемент, другой конец упругого элемента прикреплен к автомобилю. Тогда автомобиль тормозится не силой трения, а силой упругости, которая подчиняется закону Гука – сила упругости пропорциональна растяжению упругого элемента.

Эта сила по ходу торможения не постоянна, она возрастает по мере растяжения упругого элемента, и, очевидно, будет максимальной при максимальном растяжении x_макс
Рассчитаем, какая максимальная перегрузка возникает при таком торможении. Силу трения между колесами и дорогой и силу сопротивления воздуха для простоты не будем принимать в расчет.

По закону сохранения энергии кинетическая энергия автомобиля переходит в потенциальную энергию упругого элемента:

откуда максимальная сила торможения

Здесь m – масса автомобиля, а x_М – тормозной путь, определяемый максимальной длиной упругого элемента.
При этом максимальное тормозное ускорение (отрицательное) автомобиля

Определим также горизонтальную перегрузку, которая показывает, во сколько раз сила торможения превышает вес автомобиля

где g≈10м/с 2 – ускорение свободного падения.

Подставив (4), получим

Полное время торможения можно определить, рассматривая машину, прикрепленную к упругому элементу, как пружинный маятник. Период такого маятника

а время торможения соответствует четверти периода, т.е.

При этом время торможения, определяется формулой (8), где коэффициент жесткости k можно определить с помощью формул (1) и (2):

Подставляя в (8), получим время торможения

Для сравнения приведем таблицу типичных перегрузок из Википедии и фотографии людей, подвергшихся перегрузкам. Из этих материалов можно сделать вывод, что перегрузка 18 g переносима на пределе физиологических возможностей человека.
И она, предотвращая аварию, представляет собой заведомо меньшее зло, чем разрушительные перегрузки, возникающие при авариях.

Источник

Нормальная
перегрузка

вычисляется по формуле:

,

где

кН
– сила тяги двигателя летательного
аппарата;

– нормальная
аэродинамическая сила;

–
угол
поворота двигателя;

m=11483,3
кг

– масса летательного аппарата на
расчётный момент времени;

м/с²
– ускорение свободного падения.

Полная
нормальная аэродинамическая сила
рассчитывается по формуле

,

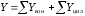где

– суммарное значение всех полных
нормальных аэродинамических сил на
конических участках;

– суммарное
значение всех полных нормальных
аэродинамических сил на цилиндрических
участках.

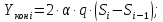
где

– удлинение цилиндра;

–
площади основания конуса.

На
рисунке 1.8 изображена схема ЛА с
обозначением необходимых для определения
нормальной аэродинамической силы
участков и расположение оснований,
необходимых для расчета и приведенных
для наглядности.

Рисунок
1.8 – Схема ЛА с обозначением расположения
участков и оснований конусов

Н,

где


– площади основания конуса.

Н,

где

–
площади основания конуса.

Н,

где

– удлинение цилиндрического участка
1-5,

–
площадь
основания цилиндрического участка 1-5.

Н,

где

– удлинение цилиндрического участка
7-12,

–
площадь
основания цилиндрического участка
7-12.

Полная
нормальная аэродинамическая сила:

Нормальная
перегрузка

в этом случае:

Угловое
ускорение

можно найти из уравнения вращательного
движения летательного аппарата вокруг
оси z

,

где

– момент всех внешних сил;

кгм²
– массовый
момент инерции летательного аппарата
относительно оси z.

Момент
всех внешних сил определяется по формуле:

,

где
м
– расстояние от носка до центра масс
летательного аппарата для расчётного
момента времени;

=
12,4 м
– координата точки приложения тяги
двигательной установки;

–
координата
точки приложения равнодействующей
нормальной аэродинамической силы.

Координата
точки приложения равнодействующей
нормальной аэродинамической силы
определяется по формуле:

где
–
координата центра давления i-го
конического
участка от носка аппарата;

где
–
координата центра давления i-го
цилиндрического
участка от носка аппарата.

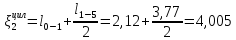м;

м;

м;

м,

где

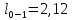
м
– длина участка 0-1,

=
3,77 м
– длина участка 1-5,

=
1,8 м
– длина
участка 5-7,

=
5,29 м
– длина
участка 7-12,

м,
м
– радиусы
оснований конусов.

Получаем
координату приложения
:

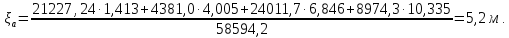
_{Момент
внешних сил}

Угловое
ускорение:

Значения
эпюр M
и Q
по длине летательного аппарата находим
с помощью программы QM.exe.
Распечатка результатов работы программы
приведена на странице 18. Эпюры представлены
на рисунке 1.9 и рисунке 1.10.

Рисунок
1.9 — Эпюра перерезывающей силы Q

Рисунок
1.10 — Эпюра изгибающего момента М

Suhov

KУPCOBOЙ
ПPOEKT ПO PACЧETУ

Л.A.
HA ПPOЧHOCTЬ

PACЧET
HAГPУЗOK

ЗHAЧEHИE
CEKУHДЫ ПOЛETA 56.00000

CKOPOCTЬ
ПOЛETA, M/C 600.0000

CKOPOCTЬ
BETPA, M/C 60.00000

УГOЛ
OTKЛOHEHИЯ TЯГИ, ГPAД 4.800000

ПЛOTHOCTЬ
BOЗДУXA, KГ/M**3 .4000000

ЧИCЛO
MAXA 2.004000

ЗHAЧEHИE
ПEPEPEЗЫB. CИЛЫ, KH .0000000

ИЗГИБAЮЩИЙ
MOMEHT, KH*M .0000000

KOHTPOЛЬHOE
CEЧEHИE 0

HOMEP
BAPИAHTA 7

MACCA
ЛETATEЛЬHOГO AППAPATA, KГ 11483.260

KOOPДИHATA
ЦEHTPA MACC, M 8.770

MACCOBЫЙ
MOMEHT ИHEPЦИИ, KГ*M**2 9.8636E+04

ПOПEPEЧHAЯ
AЭPOДИHAMИЧECKAЯ CИЛA, KH 58.59

KOOPДИHATA
ЦEHTPA ДABЛEHИЯ, M 5.200

ПOПEPEЧHAЯ
ПEPEГPУЗKA .6852

УГЛOBOE
УCKOPEHИE, 1 / C**2 1.4366

**********************************************************************************************

*
* * *
*

*
* * ПEPEPEЗЫBAЮЩAЯ CИЛA Q, KH *
ИЗГИБAЮЩИЙ MOMEHT M, KH*M *

*
HOMEPA * ДЛИHA * *
*

*
CEЧ. * УЧ.,M * CЛEBA * B CEPEДИHE* CПPABA *
CЛEBA * B CEPEДИHE* CПPABA *

*
* * * * * *
* *

**********************************************************************************************

*
* * * * * *
* *

*
0, 1 * 2.120E+00 * 0.000E+00 * 5.045E+00 * 2.024E+01 * 0.000E+00
*-1.777E+00 *-1.428E+01 *

*
1, 2 * 1.650E+00 * 1.352E+01 * 1.409E+01 * 1.469E+01 *-1.428E+01
*-2.566E+01 *-3.753E+01 *

*
2, 3 * 5.300E-01 * 9.221E+00 * 9.420E+00 * 9.622E+00 *-3.753E+01
*-4.000E+01 *-4.252E+01 *

*
3, 4 * 5.300E-01 * 8.926E+00 * 9.131E+00 * 9.339E+00 *-4.252E+01
*-4.491E+01 *-4.736E+01 *

*
4, 5 * 1.060E+00 * 9.128E+00 *-3.135E+00 *-1.458E+01 *-4.736E+01
*-4.891E+01 *-4.418E+01 *

*
5, 6 * 1.120E+00 *-1.945E+01 *-1.313E+01 *-5.950E+00 *-4.545E+01
*-3.628E+01 *-3.090E+01 *

*
6, 7 * 6.800E-01 *-5.950E+00 *-1.169E+00 * 3.931E+00 *-3.090E+01
*-2.968E+01 *-3.014E+01 *

*
7, 8 * 2.163E-01 * 3.559E+00 * 3.682E+00 * 3.806E+00 *-3.014E+01
*-3.053E+01 *-3.094E+01 *

*
8, 9 * 1.370E-02 * 3.806E+00 * 3.670E+00 * 3.535E+00 *-3.094E+01
*-3.096E+01 *-3.099E+01 *

*
9,10 * 1.050E+00 * 1.290E-02 * 6.334E-01 * 1.281E+00 *-3.126E+01
*-3.143E+01 *-3.193E+01 *

*
10,11 * 1.102E+00 *-8.023E-02 * 7.383E-01 * 1.572E+00 *-3.144E+01
*-3.162E+01 *-3.225E+01 *

*
11,12 * 1.328E+00 * 1.572E+00 *-9.811E+00 *-1.847E+01 *-3.225E+01
*-2.937E+01 *-1.983E+01 *

*
12,13 * 1.580E+00 *-2.482E+00 *-1.272E+00 *-4.929E-06 *-1.993E+00
*-5.065E-01 * 5.721E-05 *

*
* * * * * *
* *

**********************************************************************************************

Перегрузка в динамике.

Увеличение веса тела, вызванное ускоренным движением опоры или подвеса, называется перегрузкой.

При перегрузке не только тело начинает сильнее давить на опору, но и его отдельные части начинают сильнее давить друг на друга.

Если тело движется с ускорением, направленным вертикально вверх, вес тела увеличивается. Такое состояние тела называется перегрузкой. По второму закону Ньютона

.

Будучи отношением двух сил, перегрузка – безразмерная величина, однако, часто она выражается в единицах ускорения свободного падения g. Перегрузка в одну единицу (1 g) численно равна весу тела, покоящемуся в поле тяжести Земли.

Перегрузки испытывают космонавты при взлете и торможении космического корабля, летчики при выполнении фигур высшего пилотажа, пассажиры лифта при его подъеме или торможении и т. д.

В состоянии перегрузки у человека затрудняется дыхание, ухудшается сердечная деятельность, перераспределяется кровь – приливает к голове или отливает и т. д.

Перегрузка – векторная величина. Для живого организма важно направление ее действия. При перегрузке органы человека стремятся остаться в прежнем состоянии. При перегрузке голова-ноги (положительная перегрузка) кровь отливает от головы в ноги, желудок опускается вниз. При отрицательной перегрузке кровь приливает к голове. Положение тела человека, при котором он может выдерживать наибольшие перегрузки – лежа на спине, лицом к направлению ускорения движения.

I. Механика

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T – это время, за которое тело совершает один оборот.

Частота вращение – это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено – это есть период T. Путь, который преодолевает точка – это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Вращение Земли

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Связь со вторым законом Ньютона

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Как вывести формулу центростремительного ускорения

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение – изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

Движение по циклоиде*

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Равномерное движение по окружности

Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.

При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (a_r = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) a_n или а_ЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.

Модуль центростремительного ускорения равен

Где v – линейная скорость, R – радиус окружности

Рис. 1.22. Движение тела по окружности.

Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то

Так как длина окружности равна

360 о = 2πR / R = 2π рад.

1 рад. = 57,2958 о = 57 о 18’

Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:

Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:

Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением

где R – радиус окружности.

Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:

v = l / t = Rφ / t = Rω или v = Rω

Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.

За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда

То есть угловая скорость равна

Центростремительное ускорение можно выразить через период Т и частоту обращения n:

a_ЦС = (4π 2 R) / T 2 = 4π 2 Rn 2

[spoiler title=”источники:”]

http://fizmat.by/kursy/kinematika/okruzhnost

[/spoiler]