Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.92 (Голосов: 36)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Основные понятия и законы кинематики
Часть механики, в которой изучают движение, не рассматривая причины, вызывающие тот или иной характер движения, называют кинематикой.
Механическим движением называют изменение положения тела относительно других тел
Системой отсчёта называют тело отсчёта, связанную с ним систему координат и часы.
Телом отсчёта называют тело, относительно которого рассматривают положение других тел.
Материальной точкой называют тело, размерами которого в данной задаче можно пренебречь.
Траекторией называют мысленную линию, которую при своём движении описывает материальная точка.
По форме траектории движение делится на:
а) прямолинейное — траектория представляет собой отрезок прямой;
б) криволинейное — траектория представляет собой отрезок кривой.
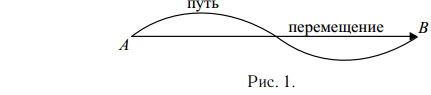
Путь — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.
Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).
Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение – это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь – это, наборот, скалярная величина, отражающая длину пройденной траектории.
Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещения
Скоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:
Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:
Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.
Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину
Ускорением называют отношение изменения мгновенной скорости тела ко времени, за которое это изменение произошло:
Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x0 + Vxt, где x0 — начальная координата тела, Vx — скорость движения.
Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.
Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:
Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением
где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:
Основные понятия и законы динамики
Часть механики, изучающая причины, вызвавшие ускорение тел, называется динамикой
Первый закон Ньютона:
Cуществуют такие системы отсчёта, относительно которых тело сохраняет свою скорость постоянной или покоится, если на него не действуют другие тела или действие других тел скомпенсировано.
Свойство тела сохранять состояние покоя или равномерного прямолинейного движения при уравновешенных внешних силах, действующих на него, называется инертностью. Явление сохранения скорости тела при уравновешенных внешних силах называют инерцией. Инерциальными системами отсчёта называют системы, в которых выполняется первый закон Ньютона.
Принцип относительности Галилея:
во всех инерциальных системах отсчёта при одинаковых начальных условиях все механические явления протекают одинаково, т.е. подчиняются одинаковым законам
Масса — это мера инертности тела
Сила — это количественная мера взаимодействия тел.
Второй закон Ньютона:
Сила, действующая на тело, равна произведению массы тела на ускорение, сообщаемое этой силой:
$F↖{→} = m⋅a↖{→}$
Сложение сил заключается в нахождении равнодействующей нескольких сил, которая производит такое же действие, как и несколько одновременно действующих сил.
Третий закон Ньютона:
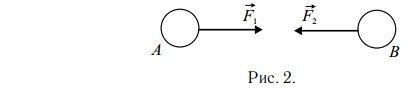
Силы, с которыми два тела действуют друг на друга, расположены на одной прямой, равны по модулю и противоположны по направлению:
$F_1↖{→} = -F_2↖{→} $
III закон Ньютона подчёркивает, что действие тел друг на друга носит характер взаимодействия. Если тело A действует на тело B, то и тело B действует на тело
A (см. рис.).
Или короче, сила действия равна силе противодействия. Часто возникает вопрос: почему лошадь тянет сани, если эти тела взаимодействуют с равными силами? Это возможно только за счёт взаимодействия с третьим телом — Землёй. Сила, с которой копыта упираются в землю, должна быть больше, чем сила трения саней о землю. Иначе копыта будут проскальзывать, и лошадь не сдвинется с места.
Если тело подвергнуть деформации, то возникают силы, препятствующие этой деформации. Такие силы называют силами упругости.
Закон Гука записывают в виде
где k — жёсткость пружины, x — деформация тела. Знак «−» указывает, что сила и деформация направлены в разные стороны.
При движении тел друг относительно друга возникают силы, препятствующие движению. Эти силы называются силами трения. Различают трение покоя и трение скольжения. Сила трения скольжения подсчитывается по формуле
где N — сила реакции опоры, µ — коэффициент трения.
Эта сила не зависит от площади трущихся тел. Коэффициент трения зависит от материала, из которого сделаны тела, и качества обработки их поверхности.
Трение покоя возникает, если тела не перемещаются друг относительно друга. Сила трения покоя может меняться от нуля до некоторого максимального значения
Гравитационными силами называют силы, с которыми любые два тела притягиваются друг к другу.
Закон всемирного тяготения:
любые два тела притягиваются друг к другу с силой, прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния между ними.
Здесь R — расстояние между телами. Закон всемирного тяготения в таком виде справедлив либо для материальных точек, либо для тел шарообразной формы.
Весом тела называют силу, с которой тело давит на горизонтальную опору или растягивает подвес.
Сила тяжести — это сила, с которой все тела притягиваются к Земле:
При неподвижной опоре вес тела равен по модулю силе тяжести:
Если тело движется по вертикали с ускорением, то его вес будет изменяться.
При движении тела с ускорением, направленным вверх, его вес
Видно, что вес тела больше веса покоящегося тела.
При движении тела с ускорением, направленным вниз, его вес
В этом случае вес тела меньше веса покоящегося тела.
Невесомостью называется такое движение тела, при котором его ускорение равно ускорению свободного падения, т.е. a = g. Это возможно в том случае, если на тело действует только одна сила — сила тяжести.
Искусственный спутник Земли — это тело, имеющее скорость V1, достаточную для того, чтобы двигаться по окружности вокруг Земли
На спутник Земли действует только одна сила — сила тяжести, направленная к центру Земли
Первая космическая скорость — это скорость, которую надо сообщить телу, чтобы оно обращалось вокруг планеты по круговой орбите.
где R — расстояние от центра планеты до спутника.
Для Земли, вблизи её поверхности, первая космическая скорость равна
1.3. Основные понятия и законы статики и гидростатики
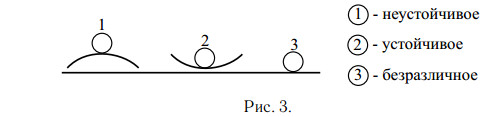
Тело (материальная точка) находится в состоянии равновесия, если векторная сумма сил, действующих на него, равна нулю. Различают 3 вида равновесия: устойчивое, неустойчивое и безразличное. Если при выведении тела из положения равновесия возникают силы, стремящиеся вернуть это тело обратно, это устойчивое равновесие. Если возникают силы, стремящиеся увести тело ещё дальше из положения равновесия, это неустойчивое положение; если никаких сил не возникает — безразличное (см. рис. 3).
Когда речь идёт не о материальной точке, а о теле, которое может иметь ось вращения, то для достижения положения равновесия помимо равенства нулю суммы сил, действующих на тело, необходимо, чтобы алгебраическая сумма моментов всех сил, действующих на тело, была равна нулю.
Здесь d —плечо силы. Плечом силы d называют расстояние от оси вращения до линии действия силы.
Условие равновесия рычага:
алгебраическая сумма моментов всех вращающих тело сил равна нулю.
Давлением называют физическую величину, равную отношению силы, действующей на площадку, перпендикулярную этой силе, к площади площадки:
Для жидкостей и газов справедлив закон Паскаля:
давление распространяется по всем направлениям без изменений.
Если жидкость или газ находятся в поле силы тяжести, то каждый вышерасположенный слой давит на нижерасположенные и по мере погружения внутрь жидкости или газа давление растёт. Для жидкостей
где ρ — плотность жидкости, h — глубина проникновения в жидкость.
Однородная жидкость в сообщающихся сосудах устанавливается на одном уровне. Если в колена сообщающихся сосудов залить жидкость с разными плотностями, то жидкость с большей плотностью устанавливается на меньшей высоте. В этом случае
Высоты столбов жидкости обратно пропорциональны плотностям:
Гидравлический пресс представляет собой сосуд, заполненный маслом или иной жидкостью, в котором прорезаны два отверстия, закрытые поршнями. Поршни имеют разную площадь. Если к одному поршню приложить некоторую силу, то сила, приложенная ко второму поршню, оказывается другой.
Таким образом, гидравлический пресс служит для преобразования величины силы. Поскольку давление под поршнями должно быть одинаковым, то
Тогда A1 = A2.
На тело, погружённое в жидкость или газ, со стороны этой жидкости или газа действует направленная вверх выталкивающая сила, которую называют силой Архимеда
Величину выталкивающей силы устанавливает закон Архимеда: на тело, погружённое в жидкость или газ, действует выталкивающая сила, направленная вертикально вверх и равная весу жидкости или газа, вытесненного телом:
где ρжидк — плотность жидкости, в которую погружено тело; Vпогр — объём погружённой части тела.
Условие плавания тела — тело плавает в жидкости или газе, когда выталкивающая сила,действующая на тело, равна силе тяжести, действующей на тело.
1.4. Законы сохранения
Импульсом тела называют физическую величину, равную произведению массы тела на его скорость:
Импульс — векторная величина. [p] =кг·м/с. Наряду с импульсом тела часто пользуются импульсом силы. Это произведение силы на время её действия
Изменение импульса тела равно импульсу действующей на это тело силы. Для изолированной системы тел (система, тела которой взаимодействуют только друг с другом) выполняется закон сохранения импульса: сумма импульсов тел изолированной системы до взаимодействия равна сумме импульсов этих же тел после взаимодействия.
Механической работой называют физическую величину, которая равна произведению силы, действующей на тело, на перемещение тела и на косинус угла между направлением силы и перемещения:
Мощность — это работа, совершённая в единицу времени:
Способность тела совершать работу характеризуют величиной, которую называют энергией. Механическую энергию делят на кинетическую и потенциальную. Если тело может совершать работу за счёт своего движения, говорят, что оно обладает кинетической энергией. Кинетическая энергия поступательного движения материальной точки подсчитывается по формуле
Если тело может совершать работу за счёт изменения своего положения относительно других тел или за счёт изменения положения частей тела, оно обладает потенциальной энергией. Пример потенциальной энергии: тело, поднятое над землёй, его энергия подсчитывается по формуле
где h — высота подъёма
Энергия сжатой пружины:
где k — коэффициент жёсткости пружины, x — абсолютная деформация пружины.
Сумма потенциальной и кинетической энергии составляет механическую энергию. Для изолированной системы тел в механике справедлив закон сохранения механической энергии: если между телами изолированной системы не действуют силы трения (или другие силы, приводящие к рассеянию энергии), то сумма механических энергий тел этой системы не изменяется (закон сохранения энергии в механике). Если же силы трения между телами изолированной системы есть, то при взаимодействии часть механической энергии тел переходит во внутреннюю энергию.
1.5. Механические колебания и волны
Колебаниями называются движения, обладающие той или иной степенью повторяемости во времени. Колебания называются периодическими, если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени.
Гармоническими колебаниями называются такие колебания, в которых колеблющаяся физическая величина x изменяется по закону синуса или косинуса, т.е.
Величина A, равная наибольшему абсолютному значению колеблющейся физической величины
x, называется амплитудой колебаний. Выражение α = ωt + ϕ определяет значение x в данный момент времени и называется фазой колебаний. Периодом T называется время, за которое
колеблющееся тело совершает одно полное колебание. Частотой периодических колебаний называют число полных колебаний, совершённых за единицу времени:
Частота измеряется в с-1. Эта единица называется герц (Гц).
Математическим маятником называется материальная точка массой m, подвешенная на невесомой нерастяжимой нити и совершающая колебания в вертикальной плоскости.
Если один конец пружины закрепить неподвижно, а к другому её концу прикрепить некоторое тело массой m, то при выведении тела из положения равновесия пружина растянется и возникнут колебания тела на пружине в горизонтальной или вертикальной плоскости. Такой маятник называется пружинным.
Период колебаний математического маятника определяется по формуле
где l — длина маятника.
Период колебаний груза на пружине определяется по формуле
где k — жёсткость пружины, m — масса груза.
Распространение колебаний в упругих средах.
Среда называется упругой, если между её частицами существуют силы взаимодействия. Волнами называется процесс распространения колебаний в упругих средах.
Волна называется поперечной, если частицы среды колеблются в направлениях, перпендикулярных к направлению распространения волны. Волна называется продольной, если колебания частиц среды происходят в направлении распространения волны.
Длиной волны называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе:
где v — скорость распространения волны.
Звуковыми волнами называют волны, колебания в которых происходят с частотами от 20 до 20 000 Гц.
Скорость звука различна в различных средах. Скорость звука в воздухе равна 340 м/c.
Ультразвуковыми волнами называют волны, частота колебаний в которых превышает 20 000 Гц. Ультразвуковые волны не воспринимаются человеческим ухом.
Skip to content
Равномерное движение (движение тела с постоянной скоростью)
Формула скорости движения при равномерном движении:
v=const
a=0
v — скорость, м/с
s — перемещение, м
t — время, с
Формула перемещения при равномерном движении:
Координата вычисляются через кинематическое уравнение равномерного прямолинейного движения по формуле:
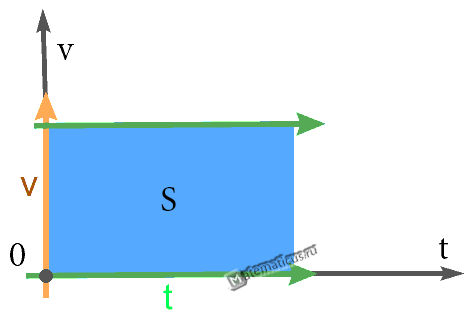
График — Равномерного прямолинейного движения
Равноускоренное движение
Формула скорости при равноускоренном движении:
a=const
v0 — начальная скорость, м/с
a — ускорение, м/с2
Формула для нахождения перемещения при равноускоренном движении:
или
Уравнение равноускоренного движения в проекции на оси координат:
Формула для определения ускорения при равноускоренном прямолинейном движении:
v0 — начальная скорость, м/с
v — мгновенная скорость, м/с
Формула для определения средней скорости движения:
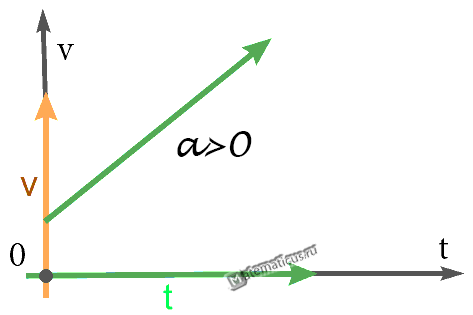
График — Равноускоренное движение при a>0
Равнозамедленное движение
Равнозамедленное движение — это движение тела, при котором модуль скорости равномерно уменьшается с течением времени, а вектор ускорения остается постоянным как по модулю, так и по направлению.
Формула скорости при равнозамедленном движении:
Формула перемещения при равнозамедленном движении:
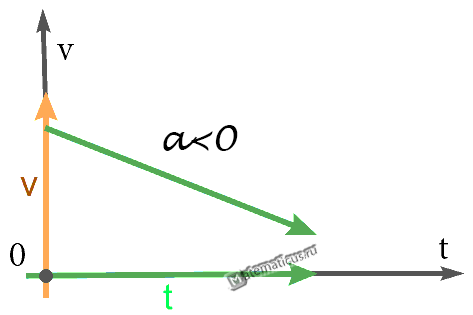
График — Равнозамедленное движение при a<0
Свободное падение
Постоянная величина скорости свободного падения тела равна g=9,8 м/с2
Формула для вычисления скорости при свободном падении тела:
Формула для вычисления перемещения при свободном падении тела:
Формула координаты при свободном падении тела:
Формула высоты с которой тело свободно падает:
Формула для определения скорости тела в конце свободного падения:
Время свободного падения тела равно:
61654
| Ускорение | |
|---|---|
 |
|
| Размерность | LT−2 |
| Единицы измерения | |
| СИ | м/с² |
| СГС | см/с² |
| Примечания | |
| векторная величина |
Падающий мяч при отсутствии сопротивления воздуха ускоряется, то есть движется все быстрее и быстрее.
Ускоре́ние (обычно обозначается латинскими буквами a (от лат. acceleratio) или w) — физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени. Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости 
Например, тела, свободно падающие вблизи поверхности Земли вдоль вертикали, в случаях, когда испытываемое ими сопротивление воздуха мало, увеличивают свою скорость примерно на 9,8 м/с за секунду, то есть их ускорение примерно равно 9,8 м/с². При непрямолинейном движении учитывается изменение не только величины скорости, но и её направления: скажем, ускорение тела, движущегося по окружности с постоянной по модулю скоростью, не равно нулю: имеется постоянное по модулю (и переменное по направлению) ускорение, направленное к центру окружности.
Единицей ускорения в Международной системе единиц (СИ) служит метр в секунду за секунду (русское обозначение: м/с2; международное: m/s2).
Ускорение в кинематике точки[править | править код]
Наиболее общий случай[править | править код]
Ускорение и связанные величины[править | править код]
Вектор ускорения материальной точки в любой момент времени находится путём однократного дифференцирования по времени вектора скорости материальной точки (или двукратного дифференцирования радиус-вектора):
Если на траектории точки известны координаты 


Производная ускорения по времени, то есть величина, характеризующая скорость изменения ускорения, называется рывок:
где
— вектор рывка.
Анализ движения по кривой[править | править код]
Траекторию движения материальной точки на малом участке можно считать плоской. Вектор ускорения 

где
— величина скорости,
— единичный касательный к траектории вектор, направленный вдоль скорости (касательный орт),
— орт главной нормали к траектории, который можно определить как единичный вектор в направлении
— орт бинормали к траектории, перпендикулярный одновременно ортам
и
(то есть ортогональный к мгновенной плоскости траектории),
— радиус кривизны траектории.
Слагаемое 

Векторы 

Итак, учитывая сказанное выше, вектор ускорения при движении по любой траектории можно записать как:
Важные частные случаи[править | править код]
Равноускоренное движение[править | править код]
Если вектор 
Частным случаем равноускоренного движения является случай, когда ускорение равно нулю в течение всего времени движения. В этом случае скорость постоянна, а движение происходит по прямолинейной траектории (если скорость тоже равна нулю, то тело покоится), поэтому такое движение называют прямолинейным и равномерным.
Равноускоренное движение точки всегда является плоским, а твёрдого тела — плоскопараллельным (поступательным). Обратное, вообще говоря, неверно.
Равноускоренное движение при переходе в другую инерциальную систему отсчёта остаётся равноускоренным.
Случай равноускоренного движения, когда ускорение (постоянное) и скорость направлены по одной прямой, но в разных направлениях, называется равнозамедленным движением. Равнозамедленное движение всегда одномерно. Движение можно рассматривать как равнозамедленное лишь до того момента, пока скорость не станет равной нулю. Кроме того, всегда существуют инерциальные системы отсчёта, в которых движение не является равнозамедленным.
Прямолинейное движение[править | править код]
Важным частным случаем движения с ускорением является прямолинейное движение, когда ускорение в любой момент времени коллинеарно скорости (например, случай падения тела с вертикальной начальной скоростью). В случае прямолинейного движения можно выбрать одну из координатных осей вдоль направления движения и заменить радиус-вектор и векторы ускорения и скорости на скаляры. При этом, при постоянном ускорении из приведённых выше формул вытекает, что
Здесь v0 и v — начальная и конечная скорость тела, a — его ускорение, s — пройденный телом путь.
Ряд практически важных формул связывают затраченное время, пройденный путь, достигнутую скорость и ускорение при равноускоренном прямолинейном движении с нулевой (
так что любые две из этих величин определяют две другие (здесь предполагается, что время отсчитывается от начала движения: t0 = 0).
Движение по окружности[править | править код]
Равномерное движение по окружности. Ускорение всегда перпендикулярно скорости и направлено к центру.
Пример неравномерного движения по окружности (математический маятник). Ускорение, складывающееся из тангенциальной и центростремительной компонент, в разные моменты изменяется от полностью касательного до полностью нормального к траектории.
Вектор ускорения
при движении точки по окружности можно разложить на два слагаемых (компоненты):
Тангенциальное или касательное ускорение 


Центростремительное или нормальное ускорение 


а модуль равен
где ω — угловая скорость относительно центра вращения, а r — радиус окружности.
Кроме этих двух компонент, используется также понятие угловое ускорение, показывающее, на сколько изменилась угловая скорость за единицу времени, и, аналогично линейному ускорению, вычисляемое следующим образом:
Направление вектора здесь показывает, увеличивается или уменьшается модуль скорости. Если векторы углового ускорения и угловой скорости сонаправлены (или хотя бы их скалярное произведение положительно), значение скорости растёт, и наоборот.
В частном случае равномерного движения по окружности векторы углового ускорения и тангенциального ускорения равны нулю, а центростремительное ускорение постоянно по модулю.
Ускорение при сложном движении[править | править код]
Говорят, что материальная точка (тело) совершает сложное движение, если она движется относительно какой-либо системы отсчёта, а та, в свою очередь, движется относительно другой, «лабораторной», системы отсчёта. Тогда абсолютное ускорение тела в лабораторной системе равно сумме относительного, переносного и кориолисова ускорений:
Последний член содержит векторное произведение угловой скорости вращения движущейся системы отсчёта и скорости материальной точки в этой движущейся системе.
Ускорения в кинематике твёрдого тела[править | править код]
Связь ускорений двух точек абсолютно твёрдого тела A и B можно получить из формулы Эйлера для скоростей этих точек:
где 
где 
Второе слагаемое называется осестремительным ускорением, а третье — вращательным ускорением[1].
Создание ускорения. Динамика точки[править | править код]
Первый закон Ньютона постулирует существование инерциальных систем отсчёта. В этих системах отсчёта равномерное прямолинейное движение имеет место в том случае, когда тело (материальная точка) не подвергается никаким внешним воздействиям в процессе своего движения. На основе этого закона возникает ключевое для механики понятие силы как такого внешнего воздействия на тело, которое выводит его из состояния покоя или влияет на скорость его движения. Таким образом, постулируется, что причиной возникновения ненулевого ускорения в инерциальной системе отсчёта всегда является некоторое внешнее силовое воздействие[4].
Классическая механика[править | править код]
Второй закон Ньютона применительно к нерелятивистскому движению (то есть к движению со скоростями, много меньшими скорости света) утверждает, что ускорение материальной точки всегда пропорционально приложенной к ней и порождающей ускорение силе, причём коэффициент пропорциональности всегда один и тот же независимо от вида силового воздействия (он называется инертной массой материальной точки):
Если известны масса материальной точки и (как функция времени) сила, действующая на неё, то из второго закона Ньютона известно и её ускорение: 
Релятивистская механика[править | править код]
В релятивистской физике второй закон Ньютона записывается в форме
что делает нахождение ускорения более сложной задачей, чем в классическом случае. В частности, длительное движение с постоянным ускорением принципиально невозможно (иначе скорость точки в конце концов превысит скорость света), а неизменность силы не означает неизменности ускорения: оно будет стремиться к нулю при нарастании скорости. Тем не менее, если зависимость 


Ускорение в теории относительности[править | править код]
В теории относительности движение тела с переменной скоростью вдоль мировой линии в 4-мерном пространстве-времени характеризуется определённой величиной, аналогичной ускорению. В отличие от обычного (трёхмерного) вектора ускорения, 4-вектор ускорения (называемый 4-ускорением) ai является второй производной от 4-вектора координат xi не по времени, а по пространственно-временному интервалу τ (или, что то же самое, по собственному времени) вдоль мировой линии тела:
В любой точке мировой линии 4-вектор ускорения всегда ортогонален к 4-скорости:
Это означает, в частности, что 4-скорости меняются не по модулю, а лишь по направлению: независимо от направления в пространстве-времени 4-скорость любого тела равна по модулю скорости света. Геометрически, 4-ускорение совпадает с кривизной мировой линии и является аналогом нормального ускорения в классической кинематике.
В классической механике значение ускорения не изменяется при переходе от одной инерциальной системы отсчета к другой, то есть ускорение инвариантно относительно преобразований Галилея. В релятивистской механике 4-ускорение является 4-вектором, то есть при преобразованиях Лоренца изменяется аналогично пространственно-временным координатам.
“Обычный” трёхмерный вектор ускорения 





Измерения ускорений[править | править код]
Используемые единицы[править | править код]
- метр на секунду в квадрате (метр в секунду за секунду), м/с², производная единица системы СИ;
- сантиметр на секунду в квадрате (сантиметр в секунду за секунду), см/с², производная единица системы СГС, имеет также собственное наименование гал, или галилео (применяется преимущественно в гравиметрии);
- g (произносится «же»), стандартное ускорение свободного падения на поверхности Земли, равное по определению 9,80665 м/с². В технических расчётах, не требующих точности выше 2 %, часто используется приближение g ≈ 10 м/с².
| м/с2 | фут/с2 | g | см/с2 | |
|---|---|---|---|---|
| 1 м/с² = | 1 | 3,28084 | 0,101972 | 100 |
| 1 фут/с² = | 0,304800 | 1 | 0,0310810 | 30,4800 |
| 1 g = | 9,80665 | 32,1740 | 1 | 980,665 |
| 1 см/с² = | 0,01 | 0,0328084 | 0,00101972 | 1 |
Технические средства[править | править код]
Приборы для измерения ускорения называются акселерометрами. Они не «детектируют» ускорение непосредственно, а измеряют силу реакции (укр.) (рус. опоры, возникающую при ускоренном движении. Поскольку аналогичные силы сопротивления возникают в поле тяготения, с помощью акселерометров можно измерять также гравитацию.
Акселерографы — приборы, измеряющие и автоматически записывающие (в виде графиков) значения ускорения поступательного и вращательного движения.
Значения ускорения в некоторых случаях[править | править код]
Значения ускорений различных движений:[5]
| Вид движения | Ускорение, м/с2 |
|---|---|
| Центростремительное ускорение Солнечной системы при орбитальном движении в Галактике | 2,2⋅10−10 |
| Центростремительное ускорение Земли при орбитальном движении вокруг Солнца | 0,0060 |
| Центростремительное ускорение Луны при орбитальном движении вокруг Земли | 0,0027 |
| Пассажирский лифт | 0,9—1,6 |
| Поезд метро | 1 |
| Автомобиль «Жигули» | 1,5 |
| Бегун на коротких дистанциях | 1,5 |
| Велосипедист | 1,7 |
| Конькобежец | 1,9 |
| Мотоцикл | 3—6 |
| Аварийное торможение автомобиля | 4—6 |
| Усэйн Болт, максимальное ускорение | 8[6] |
| Гоночный автомобиль | 8—9 |
| Торможение при открытии парашюта | 30 (3 g) |
| Запуск и торможение космического корабля | 40—60 (4—6 g) |
| Манёвр реактивного самолёта | до 100 (до 10 g) |
| Свая после удара копром | 300 (30 g) |
| Поршень двигателя внутреннего сгорания | 3×103 |
| Пуля в стволе винтовки | 2,5×105 |
| Микрочастицы в ускорителе | (2—50)×1014 |
| Электроны между катодом и анодом трубки цветного телевизора (20 кВ, 0,5 м) | ≈7×1015 |
| Электроны при соударении с люминофором трубки цветного телевизора (20 кВ) | ≈1022 |
| Альфа-частицы в атомном ядре | ≈1027 |
Примечание: здесь g ≈ 10 м/с2.
Понятие “обобщённое ускорение”[править | править код]
Если динамика механической системы описывается не в декартовых, а в обобщённых координатах 


См. также[править | править код]
- Ускорение свободного падения
- Собственное ускорение
- Релятивистски равноускоренное движение
- Приливное ускорение
- Кориолисово ускорение
- Рывок (кинематика)
Примечания[править | править код]
- ↑ 1 2 Маркеев А. П. Теоретическая механика. — М.: ЧеРо, 1999. — С. 59. — 572 с.
- ↑ Обзор результатов Ривальса: Appendice au Mémoire de M. Bresse // Journal de l’École polytechnique. — 1853. — Т. 20. — С. 109—115. Архивировано 9 марта 2016 года.
- ↑ Joulin L. Notice biographique sur M. le commandant Rivals // Mémoires de l’Académie royale des sciences, inscriptions et belles-lettres de Toulouse. — 1891. — Т. 3, вып. 9. — С. 535—539. Архивировано 8 марта 2016 года.
- ↑ Для того, чтобы использовать уравнение движения в форме, совпадающей с формой уравнения второго закона Ньютона, применительно к ускорениям, возникающим в неинерциальных системах отсчёта даже в отсутствие каких-либо воздействий на тело, вводят фиктивные силы инерции. Например, пусть тело массой m покоится в инерциальной системе отсчёта на некотором расстоянии R от оси. Если привести систему отсчёта во вращение с угловой скоростью ω вокруг этой оси, то система становится неинерциальной, а тело будет совершать видимое вращательное движение с линейной скоростью v=ωR по окружности вокруг оси. Для его описания во вращающейся системе отсчёта необходимо ввести центростремительное ускорение, которое можно формально считать результатом действия одной из сил инерции — силы Кориолиса, равной по модулю 2mvω и направленной к оси, перпендикулярно оси и скорости тела; при этом она наполовину компенсируется действием другой силы инерции — центробежной силы, равной по модулю mvω и направленной от оси вращения.
- ↑ Кошкин Н.И., Ширкевич М.Г. Справочник по элементарной физике. — 10-е, испр. и доп.. — М.: Наука, 1988. — С. 61. — 256 с. — ISBN 5-02-013833-9.
- ↑ График зависимости ускорения У. Болта от времени Архивная копия от 10 мая 2013 на Wayback Machine — забег на 100 м на летних Олимпийских играх 2008 года в Пекине
Ссылки[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 5-е, стереотипное. — М.: Физматлит, 2004. — 224 с. — («Теоретическая физика», том I). — ISBN 5-9221-0055-6.
- David C. Cassidy, Gerald James Holton, and F. James Rutherford. Understanding physics. — Birkhäuser (англ.) (рус., 2002. — ISBN 978-0-387-98756-9.
- Pauli W. Theory of Relativity. — Dover, 1981. — ISBN 978-0-486-64152-2.
Алексей Алексеевич Ивахно
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Определение 1
Движение, при котором за одинаковые интервалы времени тело проходит неравное расстояние, называют неравномерным (или переменным).
При переменном движении скорость тела с течением времени меняется, по этой причине для характеристики подобного перемещения применяются определения средней и моментальной скоростей.
Средней скоростью переменного движения $v_{cp}$ называют векторную величину, равную отношению перемещения тела $s$ к промежутку времени $t$, в течении которого оно совершило перемещение:
$v_{cp} = limleft(frac{Ds}{Dt}right)$.
Переменное перемещение внедряет в процесс только лишь тот интервал времени, для которого эта скорость установлена. Мгновенной скоростью является скорость, какой тело обладает в определенный период времени (и значит, в конкретной точке траектории). Мгновенная скорость $v$ является пределом, к которому устремляется средняя скорость точки $v_{cp}$, в то время как промежуток времени движения точки стремится к 0:
$v = limleft(frac{Ds}{Dt}right)$.
Из курса математики известно, что предел отношения приращения функции к приращению аргумента, когда последний стремится к 0 (если этот порог существует), выступает главной производной этой функции по данному аргументу.
Изучим, как скатывается шарик с наклонной плоскости. Шар перемещается неровно: пути, проходимые им за последовательные одинаковые интервалы периода, увеличиваются. Таким образом, темп передвижения шарика возрастает. Перемещение объекта, скатывающегося с косой плоскости, считается классическим примером прямолинейного равноускоренного перемещения.
Рассмотрим определение равноускоренного движения.
Определение 2
Прямолинейным равноускоренным движением именуют прямолинейное перемещение, при котором скорость тела за любые одинаковые интервалы времени меняется на одну и ту же величину.
Прямо равноускорено способен передвигаться, к примеру, транспорт в период разгона. Но необычным может представиться в таком случае, то что во время торможения машина также способна передвигаться прямолинейно равноускорено! Так как в определении равноускоренного перемещения речь никак не идет не о росте стремительности, а только лишь об изменении скорости.
«Равномерное и равноускоренное движение» 👇
Суть в том, что представление ускорения в физике обширнее, нежели в обыденном понимании. В повседневной речи под ускорением подразумевают как правило только лишь повышение быстроты. Мы в физике станем говорить, то что тело перемещается с ускорением постоянно, если быстрота тела меняется любым способом (возрастает либо снижается согласно модулю, меняется согласно направленности и т.п.).
Может возникнуть вопрос: по какой причине мы уделяем внимание непосредственно прямолинейному равноускоренному перемещению? Забегая немножко вперед, скажем, что с этим перемещением мы будем часто иметь дело при рассмотрении законов механики.
Напомним, что под воздействием стабильной силы тело перемещается прямо равноускорено. (В случае если первоначальная скорость тела равна нулю либо ориентирована по линии воздействия силы.) А в многочисленных задачах из сферы механики рассматривается непосредственно такая ситуация, в которой применяются уравнения прямолинейного равноускоренного движения, формулы конечной скорости и формулы пути без времени.
Равноускоренное движение тела
Определение 3
Равноускоренное движение – это перемещение тела, при каком его скорость за всевозможные одинаковые интервалы времени меняется (способна расти либо снижаться) одинаково.
Равноускоренное перемещение никак не обладает равной скоростью в течении всего пути прохождения. В этом случае имеется убыстрение, что отвечает за непрерывное повышение скорости. Ускорение перемещения остается постоянным, а темп регулярно и одинаково увеличивается.
Кроме равноускоренного имеется также равнозамедленное перемещение, где модуль темп одинаково уменьшается. Таким образом, равноускоренное перемещение способно проходить в некоторых измерениях. Оно бывает:
- одномерным;
- многомерным.
В случае первого — перемещение осуществляется по одной оси местоположение. В случае второго могут добавляться и прочие замеры.
Ускорение тела
Применять формулы перемещений при равноускоренном движении, а также формулы ускорения без времени возможно в абсолютно различных плоскостях. К примеру, с целью расчета падения жестких тел в свободном падении, места падения. В частности, для различных точных и геометрических расчетов.
Исходя из противопоставления равномерному перемещению, неравномерное – это движение с разной скоростью согласно каждой траектории. В чем его особенность? Это неравномерное передвижение, но оно “равно ускоряется”.
Ускорение мы ассоциируем с увеличением скорости. Так как она ускоряется одинаково, получается равное увеличение скорости. Как понять, скорость равно увеличивается или нет? Нам нужно засечь время, оценить скорость через одинаковый промежуток времени, используя формулы ускорения при равноускоренном движении.
Пример 1
Например, автомобиль начал движение, за первые 2 сек он развил скорость до 10 м/с, за последующие 2 сек 20 м/с. Еще через 2 сек он уже едет со скоростью 30 м/с. Каждые 2 секунды темп возрастает и каждый раз на 10 м/с.
Такое передвижение и является равноускоренным. Ускорением называется величина, определяющая, насколько каждый раз увеличивается скорость. Кроме этого необходимо обратить внимание на формулу скорости при равноускоренном движении.
Перемещение с убывающей скоростью – замедленное передвижение. Однако физики каждое перемещение с изменяющейся быстротой называют ускоренным перемещением. Трогается ли автомобиль с участка (темп увеличивается), либо притормаживает – скорость снижается, в каждом случае он перемещается с ускорением.
Быстроту изменения скорости характеризует ускорение. Это число, на которое меняется скорость за каждую секунду. Если ускорение точки по модулю большое, значит точка стремительно набирает скорость (при разгоне) или быстро сбрасывает ее (при торможении). Ускорение $a$ – это физическая векторная величина, которая равна отношению перемены скорости $delta V$ к промежутку времени $delta t$, за которое оно произошло
$vec{a} = frac{delta V}{delta t}$
Равномерное движение
Механическое передвижение, при котором тело за всевозможные одинаковые интервалы времени проходит одну и ту же дистанцию является равномерным. При равномерном перемещении значение скорости точки остаётся стабильной (формула равномерного и равноускоренного движения).
$υ = frac{l}{delta t}$, где:
- $υ$– скорость равномерного движения (м/с)
- $l$– пройденный телом путь (м)
- $ delta t$– интервал времени движения (с)
Равномерное перемещение присутствует, если скорость предмета остается равной в каждом интервале пройденного пути, к этом случае период прохождения различных двух одинаковых участков будет одинаково.
В случае если перемещение является не только лишь равномерным, а и прямолинейным, в таком случае путь тела одинаковый с модулем передвижения. По этой причине, воспользовавшись аналогией с предшествующей формулой равноускоренного движения, в физике определяют скорость равномерного прямолинейного перемещения:
$ vec{v} = frac{vec s}{vecdelta t}$, где:
- $ vec{v}$ – скорость равно прямолинейного движения, м/с
- $ vec{s}$ – перемещение тела, м
- ${vecdelta t}$ – интервал времени движения, с
Скорость равномерного прямолинейного движения является вектором, так как перемещение – величина векторная. А значит, имеет не только числовое значение, но и пространственное направление.
Замечание 1
Равноускоренное перемещение отлично от равномерного тем, что быстрота в этом перемещении регулярно и одинаково увеличивается, вплоть до конкретного предела. В равномерном же перемещении скорость не изменяется ни в коем случае, другим образом подобное перемещение никак не станет называться равномерным.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме

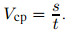
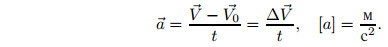





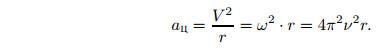
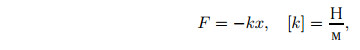


























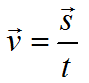
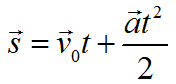
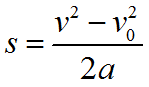
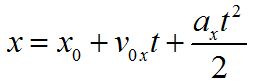
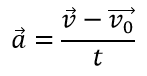
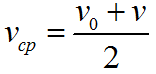
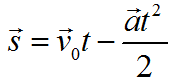
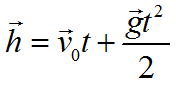
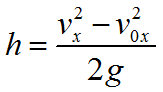
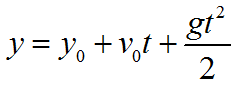
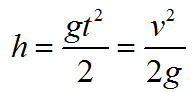
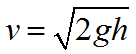
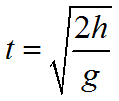






























![{displaystyle {vec {a}}={vec {a}}_{r'}+{vec {a}}_{e}+2left[{vec {omega }}times {vec {v}}_{r'}right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/14c94b28221af9efd57db669ebd5baabb5db5e85)
![vec{v}_B = vec{v}_A + left[vec{omega}timesvec{AB}right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/674393e427cf0812f2a78e9593820b0f5f0dd0a7)
![vec{a}_B = vec{a}_A + left[vec{omega}times left[ vec{omega}times vec{AB}right] right] + left[ vec{varepsilon}times vec{AB} right],](https://wikimedia.org/api/rest_v1/media/math/render/svg/73ba130aeb13035b7b570db42daa1c2bf8bd55f0)




