Как найти ускорение при равнопеременном движении - Сайт, где вы сможете решить свои вопросы

Равномерное прямолинейное движение – это частный случай неравномерного движения.

Неравномерное движение – это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение – это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

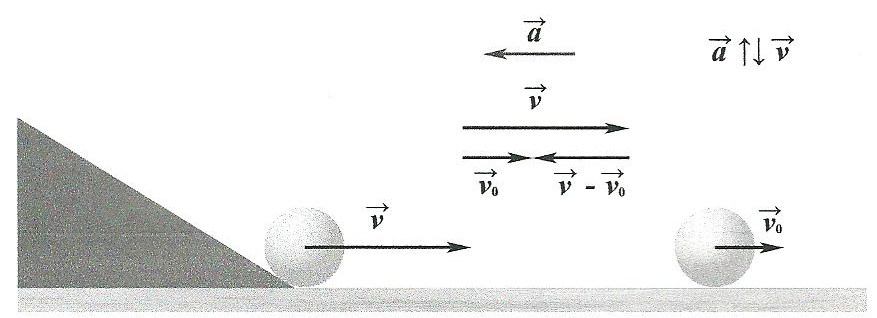
Равноускоренное движение – это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение – это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости – м/с.

v_cp = s / t

Мгновенная скорость – это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

Проекция вектора скорости на ось ОХ:

v_x = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Ускорение – это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

v_x = v_0x ± a_xt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения – это прямая, параллельная оси 0t (оси времени, рис. 1.15).

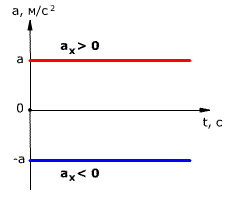
Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени – это линейная функция, графиком которой является прямая линия (рис. 1.16).

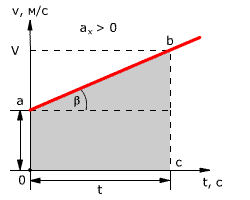
Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v₀
bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

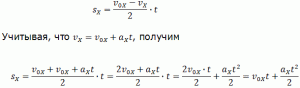
В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «–» (минус).

Общая формула для определения проекции перемещения:

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

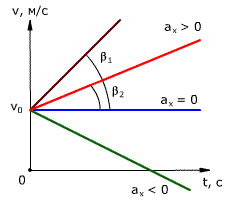
Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

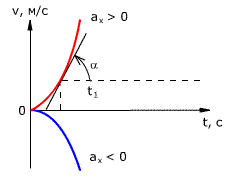
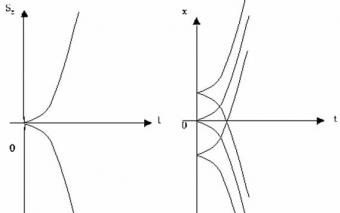
Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t₁ равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

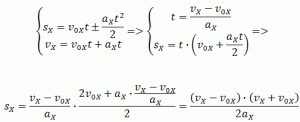
Формула сокращённого умножения разности квадратов поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то уравнение движения тела будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а_x < 0 и х₀ = 0 ветви параболы направлены вниз (рис. 1.18).

Источник

Равнопеременное движение. Ускорение.

Движение, при котором скорость тела изменяется одинаково за любые равные промежутки времени, называется равнопеременным движением.

Обозначим: – вектор начальной скорости, – изменение скорости, а Δt – промежуток времени.

Пусть Δt₁= Δt₂=Δt₃=…, тогда по определению

Следовательно,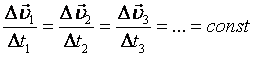

Т.о., это характеристика движения.

Если t₀=0, то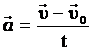

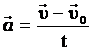
УСКОРЕНИЕ – физическая величина, характеризующая быстроту изменения скорости и (при равнопеременном движении) численно равная отношению вектора изменения скорости к промежутку времени, в течение которого это изменение произошло.

Ускорение при равнопеременном движении показывает, насколько меняется мгновенная скорость движения тела за единицу времени. Единица ускорения в СИ – м/с².

Например, ускорение равно 5 м/с² – это значит, что, двигаясь равноускоренно, тело изменяет скорость на 5 м/с за каждую секунду своего движения.

В случае не равнопеременного движения:

тогда мгновенное ускорение

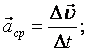
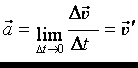
Равнопеременное движение называется равноускоренным, если модуль скорости возрастает.

Условие р.у.д. –.

Равнопеременное движение называется равнозамедленным, если модуль скорости уменьшается.

Условие р.з.д. – .

Графики равнопеременного движения.

или – в проекциях;

или – через модули.

Линейная функция. График – прямая.

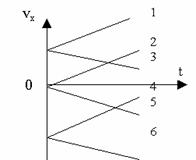
Движения, совпадающие с направлением координатной оси:

1. равноускоренноес начальной скоростью

2. равноускоренное без начальной скорости

3. равнозамедленное

Движения против координатной оси.

4. равнозамедленное

5. равноускоренное без начальной скорости

6. равноускоренное с начальной скоростью

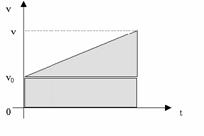
Перемещение при равнопеременном движении.

Площадь под графиком скорости численно равна перемещению.

Следовательно, площадь трапеции численно равна перемещению.

Решение основной задачи механики для р.у.д. :

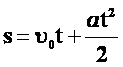
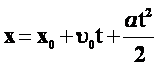
Графики перемещения и координаты.

Функци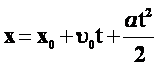и и 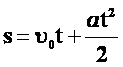– квадратичные. График – парабола!

Источник

Прямолинейное равнопеременное движение — движение тела вдоль прямой, характеризующееся постоянным по модулю и направлению линейным ускорением.

Траектория такого движения — прямая, поэтому в задачах равнозначными являются понятия пути и модуля перемещения. Такое движение может быть описано несколькими соотношениями:

вектор скорости тела при равнопеременном движении

$displaystyle vec{upsilon }={{vec{upsilon }}_{0}}+vec{a}t$ (1)

$displaystyle Delta vec{r}={{vec{upsilon }}_{0}}t+frac{vec{a}{{t}^{2}}}{2}$ (2)

где
- — вектор перемещения тела

Однако это векторные уравнения, с которыми работать достаточно сложно, а иногда, просто не хочется. Попробуем, анализируя условия задачи, составить уравнения скалярного вида, спроецировав вектора на некую ось.

Рис. 1. Равноускоренное движение 1

Пример 1. Тело движется прямо с начальной скоростью $displaystyle {{upsilon }_{0}}$ и ускоряется. По задаче выставляем вектора на ось OX (движение прямолинейное) (рис. 1). Сказано, что тело движется вдоль оси (вектор направлен по оси) и ускоряется (вектор displaystyle vec{a} также направлен вдоль оси). Осталось зафиксированные вектора спроецировать:

В общем случае, мы не можем предугадать направления векторов $displaystyle {{vec{upsilon }}_{0}}$ и $displaystyle {{vec{upsilon }}_{0}}$ , соответственно, мы не можем указать точный знак проекции этих векторов на выбранную ось. Но не заморачиваемся: в результате решения задачи мы получим одно и то же по модулю число, даже если ошибёмся. Т.е. выбираем направления как хотим, а потом анализируем ответ.

Рис. 2. Равноускоренное движение-2

Пример 2. Тело движется в положительном направлении оси и затормаживает. По задаче тело движется вдоль оси (вектор направлен по оси), а торможение говорит о том, что вектор ускорения ( displaystyle {vec{a}} ) направлен против оси OX (рис. 2). Проецируем:

Рис. 3. Равноускоренное движение-3

Пример 3. Тело движется в отрицательном направлении оси и затормаживает. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а торможение говорит о том, что вектор ускорения ( displaystyle {vec{a}} ) направлен против движения, а значит, по оси OX (рис. 3). Проецируем:

Рис. 4. Равноускоренное движение-4

Пример 4. Тело движется в отрицательном направлении оси и ускоряется. По задаче тело движется в обратную сторону оси OX (вектор направлен против оси), а ускорение говорит о том, что вектор ускорения ( displaystyle {vec{a}} ) направлен в сторону движения, а значит, против оси OX (рис. 4). Проецируем:

Вывод: только что мы получили восемь различных формул, применимых для решения задач. Очень не хотелось бы их помнить. К счастью, есть выход: запомнить и понять векторный вид этих уравнений (1) и (2), а далее, применительно к данной вам задаче, просто адаптировать их, используя проекции.

Кроме формул (1) и (2), имеется ещё одна расчётная формула, которая чаще всего используется, когда в задаче на нужно найти время или его не дано. Воспользуемся уже имеющимися (1) и (2), считая движение тела равноускоренным. Выделим из (1) время:

$displaystyle t=frac{upsilon -{{upsilon }_{0}}}{a}$ (3)

Подставим (3) в (2) при условии displaystyle left| Delta vec{r} right|=S :

$displaystyle frac{upsilon {{upsilon }_{0}}-upsilon _{0}^{2}}{a}+frac{a({{upsilon }^{2}}-2upsilon {{upsilon }_{0}}+upsilon _{0}^{2})}{2{{a}^{2}}}$ = $displaystyle frac{2upsilon {{upsilon }_{0}}-2upsilon _{0}^{2}+{{upsilon }^{2}}-2upsilon {{upsilon }_{0}}+upsilon _{0}^{2}}{2a}$ = $displaystyle frac{{{upsilon }^{2}}-upsilon _{0}^{2}}{2a}$ = displaystyle Rightarrow

$displaystyle {{upsilon }^{2}}-upsilon _{0}^{2}=2aS$ (4)

Таким образом, мы получили формулу, в которой нет параметра времени.

Источник

Рассмотрим один
из видов неравномерного движения –
равноускоренное
движение.
Предположим, что в начальный момент
времени мы движемся в автомобиле со
скоростью v₀.
Автомобиль начинает увеличивать
скорость, и через некоторое время его
скорость становиться равной v.
Если за любые промежутки времени скорость
этого автомобиля увеличилась на одно
и то же значение, то в течение времени
t
автомобиль двигался равноускоренно.
Прямолинейным
равнопеременным движением
называется движение, при котором
траекторией тела является прямая линий,
и за любые промежутки времени проекция
вектора скорости тела изменяется
(увеличивается или уменьшается) на одно
и то же значение.

В физике существует
величина, характеризующая быстроту
изменения скорости тела при равнопеременном
движении. Она называется ускорением
(a,
м/c²).
Для того чтобы найти ускорение, необходимо
найти отношение изменения скорости ко
времени, в течение которого это изменение
произошло.

Ускорение – это
векторная величина. Направление ускорения
совпадает с направлением вектора
изменения скорости.

Тело увеличивает скорость	Тело тормозится
Модуль скорости движения тела возрастает, направление вектора ускорения совпадает с направлением движения тела (с направлением вектора скорости)	Модуль скорости движения тела уменьшается, направление вектора ускорения противоположно направ-лению движения тела (направлению вектора скорости)

Скорость и
перемещение при прямолинейном
равнопеременном движении

Преобразовав
формулу для вычисления ускорения при
прямолинейном равнопеременном движении,
можно получить формулу
для нахождения скорости тела в любой
момент времени:

Если в начальный
момент тело покоилось, т.е. ₀=0,
то формула принимает вид: =

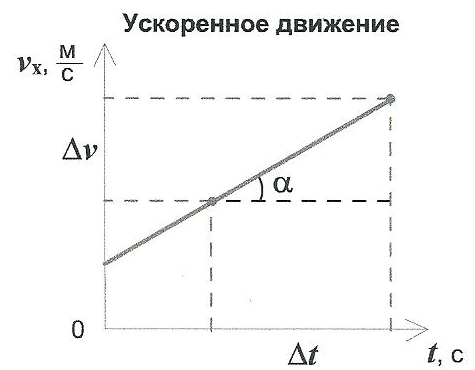
Наклон графика
скорости показывает, как быстро изменяется
скорость с течением времени. Таким
образом, по графику скорости можно
определить проекцию ускорения на ось
X.
Для этого
на графике выбирают две точки, находят
изменение скорости и времени на этом
участке. Как известно, проекция ускорения
равна отношению изменения скорости ко
времени, за которое это изменение
произошло.

Используя график
зависимости скорости от времени можно
найти перемещение при прямолинейном
равнопеременном движении. Перемещение
тела при равномерном и неравномерном
движении численно равно площади под
графиком скорости.

Если начальная
скорость равна нулю, то перемещение
численно равно площади треугольника
под графиком скорости. Площадь
треугольника, равна половине произведения
основания на высоту. Получим, что
перемещение
пропорционально квадрату времени.

Если тело движется
с начальной скоростью v₀,
то перемещение численно равно сумме
площадей треугольника и прямоугольника.

Из
формулы проекции перемещения тела при
равнопеременном движении, можно найти
положение (координату) тела в любой
момент времени.

s_x=x-x₀

x=x₀+v_0xt+

s_x=v_0xt+

График
зависимости координаты равноускоренного
движения от времени

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Конспект по физике для 8 класса «Ускорение и скорость при равнопеременном движении». О том, что ускорение — это векторная физическая величина. Как вычислить скорость прямолинейного равнопеременного движения. Что собой представляет график скорости прямолинейного равнопеременного движения.

Конспекты по физике Учебник физики Тесты по физике

Ускорение и скорость
при равнопеременном движении

Примеров неравномерного движения в окружающем нас мире огромное количество. Давайте подробнее остановимся на движении, которое называется равнопеременным.

РАВНОУСКОРЕННОЕ И РАВНОЗАМЕДЛЕННОЕ ДВИЖЕНИЕ

Предположим, в начале определённого отрезка времени мы движемся в автомобиле со скоростью υ₀. Автомобиль начинает увеличивать скорость, и через некоторое время она становится равной υ. Если за любые одинаковые промежутки времени скорость этого автомобиля увеличивалась на одно и то же значение, то в течение времени t автомобиль двигался равноускоренно.

При прямолинейном равноускоренном движении не только сама скорость, но и проекции вектора скорости за любые равные промежутки времени увеличиваются на одно и то же значение. Если за любые одинаковые промежутки времени скорость тела уменьшается на одно и то же значение, то говорят, что тело движется равнозамедленно.

УСКОРЕНИЕ — ВЕКТОРНАЯ ФИЗИЧЕСКАЯ ВЕЛИЧИНА

Для того чтобы понять, как именно изменяется скорость тела при равнопеременном движении, необходимо найти его ускорение:
В числителе формулы определения ускорения находится векторная величина (υ – υ₀), в знаменателе — скалярная (время t). Поэтому ускорение является векторной величиной, и для его определения необходимо найти его проекцию. Вычислить проекцию ускорения можно при помощи проекций векторов скорости:

Пусть автомобиль начинает своё движение в момент времени t = 0. В таблице приведены значения скорости движения автомобиля через равные промежутки времени. Видно, что за каждые 2 с движения скорость увеличивается на 10 м/с. Значит, автомобиль движется равноускоренно. Найдём ускорение, с которым движется автомобиль.

Направим ось X по направлению движения. Так как направления оси и вектора скорости совпадают, то значения проекции скорости на эту ось будут положительны и равны модулю вектора скорости.

Полученное положительное значение проекции ускорения говорит о том, что вектор ускорения имеет то же направление, что и вектор скорости.

Если тело ускоряется, т. е. модуль скорости движения тела возрастает, то направление вектора ускорения совпадает с направлением движения тела (с направлением вектора скорости). Если тело замедляет своё движение, т. е. модуль скорости движения тела уменьшается, то в этом случае направление вектора ускорения противоположно направлению движения тела (направлению вектора скорости).

СКОРОСТЬ РАВНОПЕРЕМЕННОГО ДВИЖЕНИЯ

Преобразовав формулу для вычисления ускорения при прямолинейном равнопеременном движении, можно получить формулу для нахождения скорости в любой момент времени:

Если в начальный момент тело покоилось (υ₀ = 0), то формула принимает вид

Используя значения проекций скорости и ускорения, получаем υ_x = υ_0x + a_xt.

ГРАФИК ЗАВИСИМОСТИ ПРОЕКЦИИ СКОРОСТИ ОТ ВРЕМЕНИ

Функция υ_x = υ_0x + a_xt — линейная. Её аргументом является время t, угловой коэффициент равен а_х, а свободный член — это υ_0x.

Графиком данной функции является прямая линия, расположение которой по отношению к осям координат определяется значениями а_х и υ_0x.

Вы смотрели Конспект по физике для 8 класса «Ускорение и скорость при равнопеременном движении».

Вернуться к Списку конспектов по физике (Оглавление).

Источник

Ускорение и скорость при равнопеременном движении

РАВНОУСКОРЕННОЕ И РАВНОЗАМЕДЛЕННОЕ ДВИЖЕНИЕ

УСКОРЕНИЕ — ВЕКТОРНАЯ ФИЗИЧЕСКАЯ ВЕЛИЧИНА

СКОРОСТЬ РАВНОПЕРЕМЕННОГО ДВИЖЕНИЯ

ГРАФИК ЗАВИСИМОСТИ ПРОЕКЦИИ СКОРОСТИ ОТ ВРЕМЕНИ

Вам также может понравиться

Как найти объем по плотности пример

Как найти велосипед бесплатно

Как правильно писать слово не нашла

Добавить комментарий Отменить ответ

Ускорение и скорость
при равнопеременном движении