Как найти ускорение при торможении тела

Перейти к содержимому

ускорение. по какой формуле найти ускорение при торможении?

Рома

Ученик

(84),
закрыт

7 месяцев назад

I. Механика

Тестирование онлайн

Равноускоренное движение

В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению, неравномерное движение – это движение с неодинаковой скоростью, по любой траектории. В чем особенность равноускоренного движения? Это неравномерное движение, но которое “равно ускоряется”. Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово “равно”, получим равное увеличение скорости. А как понимать “равное увеличение скорости”, как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую – 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).

Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью – замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.

Равноускоренное движение – это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково

Ускорение тела

Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение – это физическая векторная величина, численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй – 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды – 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Формула записана не в векторном виде, поэтому знак “+” пишем, когда тело ускоряется, знак “-” – когда замедляется.

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на “-2м/с”. 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком “минус”.

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение – вектор. Если тело разгоняется ускорение положительное, если замедляется – ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ

Упражнения

Два поезда идут навстречу друг другу: один – ускоренно на север, другой – замедленно на юг. Как направлены ускорения поездов?

Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго – противоположное движению (он замедляется).

Поезд движется равноускоренно с ускорением a (a>0). Известно, что к концу четвертой секунды скорость поезда равна 6м/с. Что можно сказать о величине пути, пройденном за четвертую секунду? Будет ли этот путь больше, меньше или равен 6м?

Так как поезд движется с ускорением, то скорость его все время возрастает (a>0). Если к концу четвертой секунды скорость равна 6м/с, то в начале четвертой секунды она была меньше 6м/с. Следовательно, путь, пройденный поездом за четвертую секунду, меньше 6м.

Какие из приведенных зависимостей описывают равноускоренное движение?

Уравнение скорости движущегося тела . Каково соответствующее уравнение пути?

*Автомобиль прошел за первую секунду 1м, за вторую секунду 2м, за третью секунду 3м, за четвертую секунду 4м и т.д. Можно ли считать такое движение равноускоренным?

В равноускоренном движении пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел. Следовательно, описанное движение не равноускоренное.

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – “>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Ускорение при равноускоренном движении

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Управление общеобразовательной организацией:
новые тенденции и современные технологии»

Свидетельство и скидка на обучение каждому участнику

Конспект урока по физике в 9 классе.

Тема урока: Прямолинейное равноускоренное движение. Ускорение.

Тип урока: изучение и первичное закрепление новых знаний

Цель урока: сформировать понятие прямолинейного равноускоренного движения, ускорения

рассмотреть основные характеристики равноускоренного движения;

построить графики скорости равномерного и равнопеременного движения;

развивать практические умения учащихся: умение анализировать, обобщать, выделять главную мысль из рассказа учителя и делать выводы;

развивать умение применять полученные знания в новых условиях.

расширить кругозор учащихся о видах механического движения (в частности, о прямолинейном равнопеременном (равноускоренном) движении);

отрабатывать навыки по составлению опорного конспекта (схемы) материала.

Учитель: На предыдущих уроках с каким движ ением мы знакомились? ( равномерным прямолинейным движением. )

Какое же движение называется равномерным?

Ученики: Движение, при котором тело, за любые равные промежутки времени проходит одинаковые расстояния.

Движение с постоянной скоростью.

Учитель: Что называ ю т скоростью прямолинейного равномерного движения?

Ученики: Постоянная векторная величина равная отношению перемещения к промежутку времени, за которое это изменение произошло. V = s / t .

Учитель: Тогда скажите, как вы понимаете: скорость автомобиля 60 км/ч?

Ученики: За каждый час автомобиль проезжает 60 км.

Учитель: Скорость скалярная или векторная величина?

Ученики: Векто рная. Поэтому характеризуется направлением и модулем (численным значением).

Учитель: В каких случаях проекция вектора скорости положительна, в каких отрицательна?

Ученики: Положительна, если проекция вектора скорости сонаправлена с осью.

Отрицательно, если проекция скорости и выбранная ось противоположно направлены.

Изучение нового материала

Н ам приходилось иметь дело с равномерным движением. Движение с постоянной скоростью, не очень часто встречается на практике. Гораздо чаще приходится иметь дело с таким движением, при котором скорость со временем изменяется. Такое движение называется неравно ме р ным.

При неравномерном движении скорость тела непрерывно изменяется: от точки к точке, от одного момента времени к другому. Как же вычислить скорость в любой момент времени?

Допустим, по дороге движется автомобиль и из бака капает бензин через одинаковые промежутки времени и оставляет следы.

Время, через каждые 2сек.

Найдём скорость через каждые 2 секунды.

Мы видим , что через одинаковые промежутки времени скорость меняется одинаково.
Самым простым видом неравномерного движения является равноускоренное. При котором тело движется вдоль прямой линии, а проекция вектора скорости тела за любые равные промежутки времени меняется одинаково.

Учитель: Давайте запишем в тетрадях определение равноускоренного движения.

Опр. Движение тела, при котором его скорость за любые равные промежутки времени изменяется одинаково, называется равноускоренным .

При рассмотрении равноускоренного движения вводится понятие мгновенной скорости.

Опр. Мгновенная скорость- скорость в каждой конкретной точке траектории, в соответствующий момент времени. ( скорость в данный момент времени или в данной точке траектории).

Рассмотрим движение, при котором в начальный момент времени скорость тела была равно V _0, а через промежуток времени t она оказалась равной V , то за каждую единицу времени скорость изменяется на  –  _{0 =∆}  изменение скорости, м/с
Величина характеризует быстроту изменения скорости. Ее называют ускорением и обозначают буквой : (1) (от лат. аcceleratio – ускорение – ускоренное развитие живого организма)

V ₀ – начальная скорость, скорость в момент времени t =0 или в начале наблюдения.

V – скорость, которую тело имело к концу промежутка времени t .

О. Ускорением движущегося тела называют величину, равную отношению изменения скорости тела к промежутку времени, в течение которого это изменение произошло.
Если ускорение тела по абсолютному значению велико, то это значит, что тело быстро набирает скорость (когда тело разгоняется), или быстро теряет ее (при торможении).
Равноускоренное движение это движение с постоянным ускорением.

За единицу ускорения принимают ускорение такого движения, при котором за единицу времени скорость изменяется на единицу скорости. [а]=м/с 2

В системе единиц СИ скорость измеряется в метрах в секунду, а время — в секундах, так что ускорение измеряется в метрах в секунду за секунду или в метрах на секунду в квадрате м/с 2 .

Т.к. ускорение это векторная величина, значит она имеет направление.

Как определить, куда направлен вектор ускорения?

Допустим, прямолинейно движется тело и с течением времени его скорость увеличивается. Изобразим это на чертеже.

₀

В этом случае вектор ускорения направлен в ту же скорость, что и вектор скорости.

Если тело движется и его скорость с течением времени уменьшается (тормозит), в этом случае вектор ускорения направлен противоположно вектору скорости.

₀

Если векторы скорости и ускорения движущегося тела направлены в одну сторону, то модуль вектора скорости увеличивается.

Если в противоположные стороны, то модуль вектора скорости уменьшается.

Учитель: Давайте еще раз повторим, что такое ускорение.

Ученики: Ускорением тела при его равноускоренном движении называется величина, равная отношению изменения скорости к промежутку времени за которое это изменение произошло.

Ответим на вопросы:

1.Ускорение тела равно 0,6 м/с 2 . На сколько изменится скорость этого тела за 1 с?

2.Ускорение тела равно 2 м/с 2 . Как это понимать?

3. Ускорение тела равно – 3 м/с 2 . Как это понимать?

4.Поезд начинает тормозить. Как направлены его скорость и ускорение?

5.Поезд отходит от станции. Как направлено его ускорение?

Учитель: Хорошо. А теперь решим задачу.

Задача : Автомобиль, движущийся со скоростью 10м/с начал тормозить с ускорением 1м/с . Сколько времени пройдет до остановки автомобиль?

Делаем чертеж. Указываем на нем направление скоростей. Куда будет направлен вектор ускорения, если автомобиль тормозит?

₀

t = t = = 10 С

Скорость движения автомобиля за 40 с возросла от 5 м/с до 15 м/с. Определите ускорение автомобиля.

Запишем Д/З. §5, упр.5 (2).

Заполните, пожалуйста, бланк. Полное заполнение которого, даст вам возможность покинуть кабинет сразу после звонка с урока:

[spoiler title=”источники:”]

http://infourok.ru/uskorenie-pri-ravnouskorennom-dvizhenii-475143.html

[/spoiler]

Может ли быть ускорение отрицательным при торможении. Что такое ускорение? Связь со средней скоростью

При прямолинейном движении векторы и направлены вдоль одной прямой, которая является в то же время и траекторией движения. Вдоль этой же прямой в направлении движения телами условились направлять и координатную ось (ось X). В таком случае вектор разности а значит и вектор ускорения а, лежш на той же прямой (см. § 6). Но куда он направлен — в сторону движения (так же как ось X) или против него?

В § 6 мы видели, что проекция разности двух векторов на какую-нибудь ось равна разности их проекций на ту же ось. Следовательно, для проекций векторов и на ось X можно написать

Здесь а — проекция вектора а на ось проекции векторов и на ту же ось.

Так как все три вектора лежат на одной прямой (оси X), то абсолютные значения их проекций равны абсолютным значениям самих векторов.

Рассмотрим 2 случая ускоренного движения тела.

Первый случай. Скорость тела по абсолютному значению растет (тело «разгоняется»). Это значит, что Тогда из формулы (1) видно, что проекция ускорения а положительна и равна Вектор а, следовательно, направлен так же, как ось X, т. е. в сторону движения. Когда, например, бронебойный снаряд движется при выстреле в стволе орудия, его скорость растет и ускорение направлено так же, как и скорость (рис. 39).

Второй случай. Тело тормозится, т. е. абсолютное значение его скорости уменьшается Из формулы (1) видно, что проекция ускорения а в этом случае отрицательна:

Из формулы (1) можно получить выражение для скорости :

В этой формуле, повторяем, — проекции векторов на ось X, которые могут быть как положительными, так и отрицательными.

При решении задач выражение для скорости (2) удобно записывать так, чтобы из него сразу было видно, как направлен вектор ускорения.

Если скорость тела растет (разгон), то и

Когда же скорость тела уменьшается (торможение),

Понятно, что тело, которое тормозится, должно когда-то остановиться. Это произойдет, как это видно из формулы (26), тогда, когда станет равным т. е. в момент времени Но если ускорение остается постоянным (по модулю и направлению) и после этого момента, то тело, остановившись, начнет двигаться в противоположную сторону. Это видно из того, что при станет больше, чем скорость изменит свой знак на обратный. Так

движется, например, тело, брошенное вертикально вверх: долетев до высшей точки траектории, тело начинает движение вниз.

Если и вектор ускорения направлен так же, как и ось координат, то из формулы (2а) следует, что

Если же ось координат выбрана так, что направление вектора ускорения противоположно направлению оси координат, то из формулы (26) следует, что

Знак в этой формуле означает, что вектор скорости, так же как и вектор ускорения, направлен противоположно направлению оси координат. Модуль скорости, конечно, и в этом случае увеличивается со временем.

Обычно мы называем движение с возрастающей по абсолютной величине скоростью ускоренным движением, а движение с убывающей скоростью медленным движение Но в механике любое неравномерное движение является ускоренным движением. Трогается ли автомобиль с места или тормозит, в обоих случаях он движется с ускорением. Ускоренное прямолинейное движение отличается от замедленного только знаком проекции вектора ускорения.

Мы знаем, что и перемещение, и скорость, и траектория движения различны относительно разных тел отсчета, движущихся друг относительно друга.

А ускорение? Относительно ли оно?

Ускорение тела, как мы теперь знаем, определяется векторной разностью двух значений его скорости в различные моменты времени. При переходе от одной системы координат к другой, движущейся относительно первой равномерно и прямолинейно, изменятся оба значения скорости. Но изменятся они на одну и ту же величину. Разность же их останется неизменной. Поэтому и ускорение останется неизменным.

Во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно, ускорение тела одинаково.

Но ускорения тела будут различными в системах отсчета, движущихся с ускорением друг относительно друга. В этом случае ускорения складываются так же, как скорости (см. § 10).

Задача. Автомобиль проезжает мимо наблюдателя, двигаясь со скоростью 10 м/сек. В этот момент водитель нажимает на тормоз, и автомобиль начинает двигаться с ускорением Сколько времени пройдет с того момента, когда водитель нажал на тормоз, до остановки автомобиля?

Решение. Выберем за начало отсчета то место, в котором находится наблюдатель, и направим координатную ось в сторону движения автомобиля. Тогда проекция скорости автомобиля на эту ось будет положительной. Так как скорость автомобиля

уменьшается, то проекция ускорения отрицательна и мы должны воспользоваться формулой (26):

Подставляя в эту формулу численные значения заданных величин, получим:

За положительное направление координатной оси можно принять и направление, противоположное движению. Тогда проекция начальной скорости автомобиля будет отрицательной а проекция ускорения — положительной, и применять тогда нужно формулу (2а):

Результат получился тот же. Да он и не может зависеть от того, как выбрано направление оси координат!

1. Что такое ускорение и для чего его нужно знать?

2. При любом неравномерном движении изменяется скорость. Как ускорение характеризует это изменение?

3. Чем отличается замедленное прямолинейное движение от ускоренного?

4. Что такое равноускоренное движение?

5. Троллейбус, трогаясь с места, движется с постоянным ускорением Через сколько времени он приобретет скорость 54 км/ч?

6. Автомобиль, движущийся со скоростью 36 км/ч, останавливается при торможении в течение 4 сек. С каким ускорением движется автомобиль при торможении?

7. Грузовик, двигаясь с постоянным ускорением, на некотором участке пути увеличил свою скорость с 15 до 25 м/сек. За какое время произошло это увеличение скорости, если ускорение грузовика равно

8. Какая скорость движения была бы достигнута, если бы тело двигалось прямолинейно с ускорением в течение 0,5 ч при начальной скорости, равной нулю?

Ускорение точки — это пространственно-временная мера изме­нения движения. Она характеризует быстроту и направление изменения вектора скорости точки в данный момент времени. Ускорение измеряется пределом отношения изменения скорости к соответствующему промежутку времени (в данной системе от­счета), когда этот промежуток стремится к нулю: a=lim Dv /Dt

Скорость точки как вектор может изменяться по модулю , по направлению или одновременно и по модулю и по направлению. Соответственно различают ускорения точки:

а) положительное , имеющее одинаковое направление со ско­ростью,- скорость возрастает; б) отрицательное , имеющее направление, противоположное направлению скорости,- скорость убывает; в) нормальное — направление его перпендикулярно направлению скорости и вектор скорости изменяет только направле­ние, не изменяя своей величины (криволинейное движение).

При поступательном движении линейное ускорение тела равно линейному ускорению любой его точки.

При вращательном движении положительное и отрицательное ускорения, направленные по касательной, называются тангенциальными, а направленные по радиусу (нормали) — радиаль­ными или нормальными . Каждое из этих ускорений может проявляться независимо. Сочетание тангенциального ускорения с нор­мальным бывает при одновременном изменении скорости и по модулю, и по направлению. Векторная сумма нормального и тангенциального ускорений определяет полное ускорение.

При вращательном движении угловое ускорение тела характери­зует изменение скорости вращения.

Угловое ускорение — это мера изменения скорости вращатель­ного движения тела в данный момент времени. Угловое ускорение определяется как предел отношения изменения угловой скорости к соответствующему промежутку времени в данной системе отсчёта1, когда этот промежуток стремится к нулю:

Среднее ускорение за время всего движения, особенно в тех случаях, когда оно меняет знак, обычно не определяется, поскольку оно не характеризует подробности (детали) движения.

Угловое ускорение может быть либо положительным (убыстрение вращения), либо отрицательным (замедление вращения). Для вращающегося твердого тела отношения линейных ускорений точек к их радиусам вращения (расстояниям до оси) одинаковы; они равны угловому ускорению тела: a/r=e

Линейное ускорение точки вращающегося тела равно произведению углового ускорения и радиуса вращения: a=er(в радианном измере­нии);

В сложном движении тела (одновременно поступательном и враща­тельном) изменения скорости измеряют линейным ускорением ОЦТ и угловым ускорением тела относительно его ОЦТ.

Определение угловых ускорений биомеханической системы еще бо­лее затруднено, чем определение угловых скоростей.

Таким образом, ускорение характеризует непостоянство скорости.

Скорости точек звеньев тела человека изменяются по модулю и направлению. Значит, всегда есть нормальные ускорения и почти всегда — тангенциальные (положительные и отрицательные). Движений тела человека без ускорений не бывает , но ускорения иногда могут оказаться настолько малыми, что практиче­ски не будут иметь значения.

В этой теме мы рассмотрим очень особенный вид неравномерного движения. Исходя из противопоставления равномерному движению , неравномерное движение — это движение с неодинаковой скоростью, по любой траектории . В чем особенность равноускоренного движения? Это неравномерное движение, но которое «равно ускоряется» . Ускорение у нас ассоциируется с увеличением скорости. Вспомним про слово «равно», получим равное увеличение скорости. А как понимать «равное увеличение скорости», как оценить скорость равно увеличивается или нет? Для этого нам потребуется засечь время, оценить скорость через один и тот же интервал времени. Например, машина начинает двигаться, за первые две секунды она развивает скорость до 10 м/с, за следующие две секунды 20 м/с, еще через две секунды она уже двигается со скоростью 30 м/с. Каждые две секунды скорость увеличивается и каждый раз на 10 м/с. Это и есть равноускоренное движение.

Физическая величина, характеризующая то, на сколько каждый раз увеличивается скорость называется ускорением.

Можно ли движение велосипедиста считать равноускоренным, если после остановки в первую минуту его скорость 7км/ч, во вторую — 9км/ч, в третью 12км/ч? Нельзя! Велосипедист ускоряется, но не одинаково, сначала ускорился на 7км/ч (7-0), потом на 2 км/ч (9-7), затем на 3 км/ч (12-9).

Обычно движение с возрастающей по модулю скоростью называют ускоренным движением. Движение же с убывающей скоростью — замедленным движением. Но физики любое движение с изменяющейся скоростью называют ускоренным движением. Трогается ли автомобиль с места (скорость растет!), или тормозит (скорость уменьшается!), в любом случае он движется с ускорением.

Равноускоренное движение — это такое движение тела, при котором его скорость за любые равные промежутки времени изменяется (может увеличиваться или уменьшаться) одинаково

Ускорение тела

Ускорение характеризует быстроту изменения скорости. Это число, на которое изменяется скорость за каждую секунду. Если ускорение тела по модулю велико, это значит, что тело быстро набирает скорость (когда оно разгоняется) или быстро теряет ее (при торможении). Ускорение — это физическая векторная величина , численно равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло.

Определим ускорение в следующей задаче. В начальный момент времени скорость теплохода была 3 м/с, в конце первой секунды скорость теплохода стала 5 м/с, в конце второй — 7м/с, в конце третьей 9 м/с и т.д. Очевидно, . Но как мы определили? Мы рассматриваем разницу скоростей за одну секунду. В первую секунду 5-3=2, во вторую секунду 7-5=2, в третью 9-7=2. А как быть, если скорости даны не за каждую секунду? Такая задача: начальная скорость теплохода 3 м/с, в конце второй секунды — 7 м/с, в конце четвертой 11 м/с.В этом случае необходимо 11-7= 4, затем 4/2=2. Разницу скоростей мы делим на промежуток времени.

Эту формулу чаще всего при решении задач применяют в видоизмененном виде:

Формула записана не в векторном виде, поэтому знак «+» пишем, когда тело ускоряется, знак «-» — когда замедляется.

Направление вектора ускорения

Направление вектора ускорения изображено на рисунках

На этом рисунке машина движется в положительном направлении вдоль оси Ox, вектор скорости всегда совпадает с направлением движения (направлен вправо). Когда вектор ускорение совпадает с направлением скорости, это означает, что машина разгоняется. Ускорение положительное.

При разгоне направление ускорения совпадает с направлением скорости. Ускорение положительное.

На этом рисунке машина движется в положительном направлении по оси Ox, вектор скорости совпадает с направлением движения (направлен вправо), ускорение НЕ совпадает с направлением скорости, это означает, что машина тормозит. Ускорение отрицательное.

При торможении направление ускорения противоположно направлению скорости. Ускорение отрицательное.

Разберемся, почему при торможении ускорение отрицательное. Например, теплоход за первую секунду сбросил скорость с 9м/с до 7м/с, за вторую секунду до 5м/с, за третью до 3м/с. Скорость изменяется на «-2м/с». 3-5=-2; 5-7=-2; 7-9=-2м/с. Вот откуда появляется отрицательное значение ускорения.

При решении задач, если тело замедляется, ускорение в формулы подставляется со знаком «минус».

Перемещение при равноускоренном движении

Дополнительная формула, которую называют безвременной

Формула в координатах

Связь со средней скоростью

При равноускоренном движении среднюю скорость можно рассчитывать как среднеарифметическое начальной и конечной скорости

Из этого правила следует формула, которую очень удобно использовать при решении многих задач

Соотношение путей

Если тело движется равноускоренно, начальная скорость нулевая, то пути, проходимые в последовательные равные промежутки времени, относятся как последовательный ряд нечетных чисел.

Главное запомнить

1) Что такое равноускоренное движение;
2) Что характеризует ускорение;
3) Ускорение — вектор. Если тело разгоняется ускорение положительное, если замедляется — ускорение отрицательное;
3) Направление вектора ускорения;
4) Формулы, единицы измерения в СИ

Упражнения

Два поезда идут навстречу друг другу: один — ускоренно на север, другой — замедленно на юг. Как направлены ускорения поездов?

Одинаково на север. Потому что у первого поезда ускорение совпадает по направлению с движением, а у второго — противоположное движению (он замедляется).

К примеру, автомобиль, который трогается с места, движется ускоренно, так как наращивает скорость движения. В точке начала движения скорость автомобиля равняется нулю. Начав движение, автомобиль разгоняется до некоторой скорости. При необходимости затормозить, автомобиль не сможет остановиться мгновенно, а за какое-то время. То есть скорость автомобиля будет стремиться к нулю — автомобиль начнет двигаться замедленно до тех пор, пока не остановится полностью. Но физика не имеет термина «замедление». Если тело двигается, уменьшая скорость, этот процесс тоже называется ускорением , но со знаком «-».

Средним ускорением называется отношение изменения скорости к промежутку времени, за который это изменении произошло. Вычисляют среднее ускорение при помощи формулы:

где — это . Направление вектора ускорения такое же, как у направления изменения скорости Δ = — 0

где 0 является начальной скоростью. В момент времени t 1 (см. рис. ниже) у тела 0 . В момент времени t 2 тело имеет скорость . Исходя из правила вычитания векторов, определим вектор изменения скорости Δ = — 0 . Отсюда вычисляем ускорение:

.

В системе СИ единицей ускорения называется 1 метр в секунду за секунду (либо метр на секунду в квадрате):

.

Метр на секунду в квадрате — это ускорение прямолинейно движущейся точки, при котором за 1 с скорость этой точки растет на 1 м/с. Другими словами, ускорение определяет степень изменения скорости тела за 1 с. К примеру, если ускорение составляет 5 м/с 2 , значит, скорость тела ежесекундно растет на 5 м/с.

Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина , которая равна пределу, к которому стремится среднее ускорение при стремлении промежутка времени к 0. Другими словами — это ускорение, развиваемое телом за очень маленький отрезок времени:

.

Ускорение имеет такое же направление, как и изменение скорости Δ в крайне маленьких промежутках времени, за которые скорость изменяется. Вектор ускорения можно задать при помощи проекций на соответствующие оси координат в заданной системе отсчета (проекциями а Х, a Y , a Z).

При ускоренном прямолинейном движении скорость тела увеличивается по модулю, т.е. v 2 > v 1 , а вектор ускорения имеет такое же направление, как и у вектора скорости 2 .

Если скорость тела по модулю уменьшается (v 2

Источник

При кажущемся изобилии задач на прямолинейное равноускоренное движение все они могут быть сведены к задачам двух типов. Для этого необходимо выбрать ось X таким образом, чтобы ее положительное направление совпадало с направлением движения тела. В этом случае все задачи сводятся либо к задаче «разгон» (если a > 0), либо к задаче «торможение» (если a

Задача «Разгон»

Гоночный автомобиль трогается с места, набирая скорость 30 м/с (108 км/ч) за время t = 6 с. Определите пройденный автомобилем за это время путь, считая движение автомобиля равноускоренным.

Решение.

Используем известную нам схему решения кинематических задач.

Шаг 1. Свяжем координатную ось X с дорогой, по которой разгоняется автомобиль. Начало отсчета поместим в то место, откуда автомобиль начинает разгон. Ось X направим по ходу движения автомобиля, как показано на рис. 59. В качестве единицы выберем 1 м. Включим часы (секундомер) в момент начала разгона.

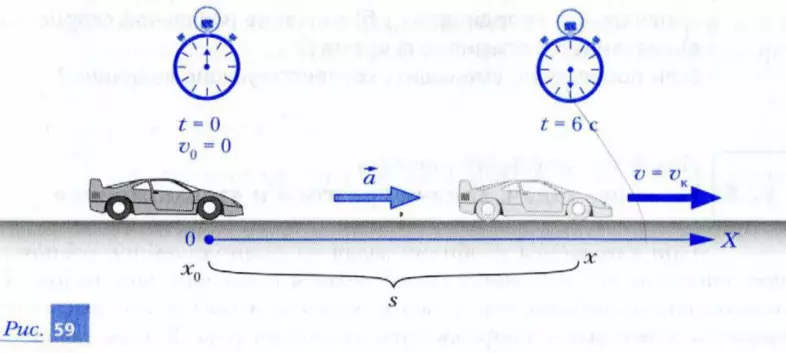
Шаг 2. Определим в выбранной нами системе отсчета начальную координату автомобиля – x₀ = 0.

Шаг 3. По условию начальная скорость автомобиля v₀ = 0. Так как направление ускорения совпадает с положительным направлением оси X, то значение ускорения a будет положительным.

Шаг 4. Запишем зависимость координаты от времени при прямолинейном равноускоренном движении автомобиля с учетом данных задачи:

x = x₀ + v₀ · t + (a · t²) / 2 = 0 + 0 + (a · t²) / 2 = (a · t²) / 2.

Шаг 4* (новый). Запишем зависимость значения скорости автомобиля от времени:

v = v₀ + a · t = 0 + a · t = a · t.

Из этого выражения видно, что при положительном значении ускорения скорость автомобиля увеличивается со временем. При этом за каждую секунду значение скорости возрастает на величину, равную a · 1 (м/с).

Шаг 5. Условие окончания разгона до скорости v_к имеет вид:

v = v_к.

Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:

x = (a · t²) / 2, (1) (закон движения автомобиля)
v = a · t, (2) (зависимость скорости от времени)
v = v_к. (3) (условие окончания разгона)

Шаг 7. Решение уравнений. Чтобы ответить на вопрос задачи, необходимо решить уравнение (1), подставив в него время разгона 6 с и значение ускорения a. Однако значение ускорения нам пока не известно. Зато нам известны значения начальной и конечной скоростей автомобиля. Следовательно, мы можем найти значение ускорения. Для этого в условие окончания разгона (3) подставим из уравнения (2) значение скорости a · t в момент t = 6 с:

v_к = a · t,
a = v_к/t; a = 30/6 = 5 (м/с²).

Подставив полученное значение a в уравнение (1), находим:

x = (a · t²) / 2 = (5 · 6²) / 2 = 90 (м).

Ясно, что s = x – x₀ = 90 – 0 = 90 (м).

Как вы заметили, в отличие от задач о равномерном движении, в шаге 4 появилось дополнение, связанное с тем, что скорость равноускоренно движущегося тела изменяется со временем. В результате появилось новое уравнение – зависимость значения скорости от времени.

Задача «Торможение»

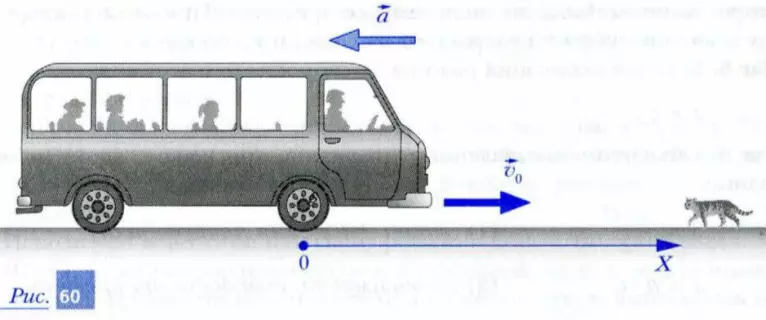
Автобус движется со скоростью, модуль которой равен 20 м/с (72 км/ч). Водитель автобуса замечает на дороге кошку и нажимает на педаль тормоза. Определите длину тормозного пути автобуса, если модуль ускорения при торможении |a| = 4 м/с².

Решение.

Шаг 1. Систему отсчета выберем так, как показано на рис. 60.

Шаг 2. Начальная координата автобуса x₀ = 0.

Шаг 3. Значение начальной скорости автобуса v₀ = 20 м/с.

Шаг 4. С учетом шагов 1, 2 и 3 зависимость координаты автобуса от времени будет иметь вид:

x = x₀ + v₀ · t + (a · t²) / 2 = 0 + 20 · t – (4 · t²) / 2.

Внимание! Значение скорости автобуса уменьшается. Значит, направление вектора ускорения автобуса противоположно положительному направлению оси X. Поэтому мы подставили в формулу отрицательное значение ускорения (a = -4 м/с²). При этом направление вектора начальной скорости совпадает с положительным направлением оси X. Поэтому значение скорости v0 положительно. Такие же знаки у величин v0 и a будут и в шаге 4*.

Шаг 4* (новый). Зависимость значения скорости от времени имеет вид:

v = v₀ + a · t = 20 – 4 · t.

Видно, что при отрицательном значении ускорения a = -4 м/с² скорость автобуса со временем уменьшается. При этом за каждую секунду значение скорости изменяется на величину -4 м/с, т. е. уменьшается на 4 м/с.

Шаг 5. Запишем условие окончания торможения: v = 0, так как в искомый момент времени t автобус должен остановиться.

Шаг 6. Объединим составленные уравнения, присвоив каждому номер и название:

x = 0 + 20 · t – (4 · t²) / 2, (1) (закон движения автобуса)
v = v₀ + a · t = 20 – 4 · t, (2) (зависимость скорости от времени)
v = 0. (3) (условие окончания торможения)

Шаг 7. Решение уравнений. Чтобы найти тормозной путь, необходимо подставить в уравнение (1) время торможения автобуса. Эта величина нам неизвестна, но ее можно найти из уравнений (2) и (3). Для этого необходимо подставить в зависимость скорости от времени значение скорости в момент окончания торможения v = 0, после чего решить полученное уравнение:

20 – 4 · t = 0, t = 5 c.

Таким образом, автобус остановится через время t = 5 с.

Подставим найденное время торможения t = 5 с в уравнение (1) и найдем тормозной путь:

x = 20 · 5 – (4 · 5²) / 2 = 50 (м).

Таким образом, длина тормозного пути автобуса равна 50 м.

Итоги
Если положительное направление оси X выбрать совпадающим с направлением движения тела, то все задачи на равноускоренное движение можно свести к двум типам:
1) задача «разгон» (a > 0, скорость тела увеличивается с течением времени);
2) задача «торможение» (a
Если тело меняет направление своего движения, то рассматриваемый промежуток времени нужно разделить на интервалы, в течение каждого из которых тело движется только в одном направлении. При этом задача разделяется на несколько задач.

Упражнения

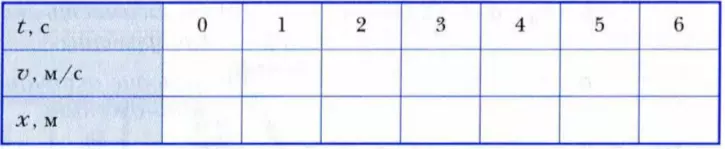
1. Заполните таблицу для разгоняющегося автомобиля, используя условия задачи 1 («разгон»). Как изменяются со временем: значение скорости; координата разгоняющегося автомобиля?

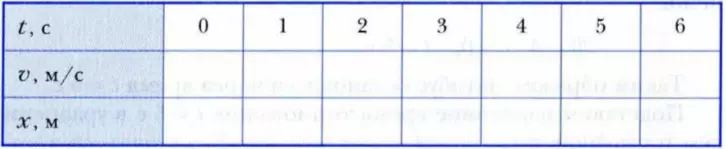
2. Заполните таблицу для тормозящего автобуса, используя условия задачи 2 («торможение»). Ответьте на вопросы: как изменяются со временем: значение скорости; координата тормозящего автобуса?

3. Найдите координату x автомобиля (см. рис. 57) в моменты времени 3, 5 и 8 с, если его начальная координата x₀ = 30 м, значение начальной скорости v₀ = 10 м/с, а значение ускорения a = 3 м/с².

4. Решите задачу 2 («торможение») в общем виде. Представьте полученный ответ в виде
s = v₀² / (2 · a).
Проведите анализ полученного ответа. Определите тормозной путь автобуса, если: а) v₀ = 16 м/с; б) v₀ = 115,2 км/ч.

5. Найдите путь, пройденный автомобилем, движение которого задано в упражнении 3, за промежуток времени от t₁ = 2 с до t₂ =5 с.

6. Два мотоциклиста, двигавшиеся прямолинейно, начинают одновременно тормозить перед светофором и так же одновременно останавливаются, проехав расстояние s = 100 м. Первый мотоциклист перед торможением двигался со скоростью, имеющей значение v₁ = 72 км/ч, второй – со скоростью, имеющей значение v₂ = 108 км/ч. Найдите значения ускорений мотоциклистов.