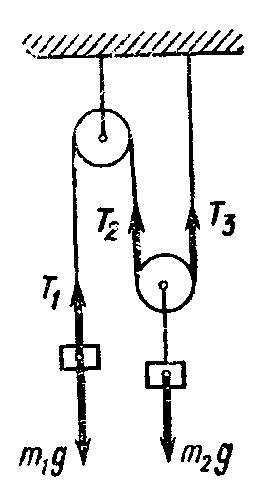
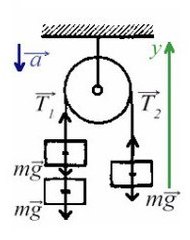
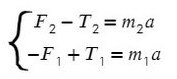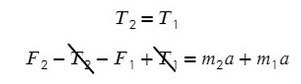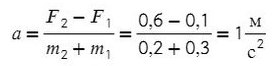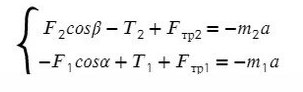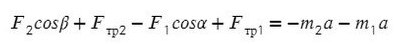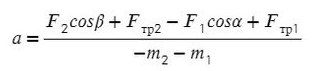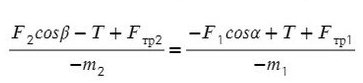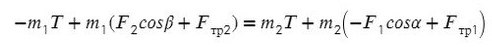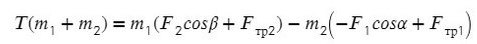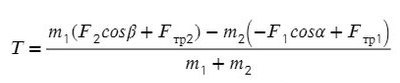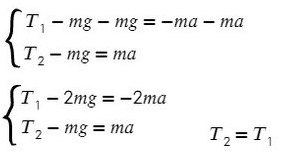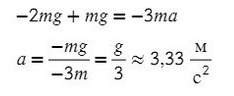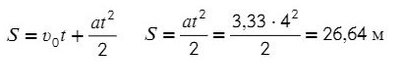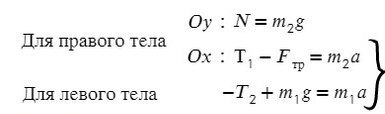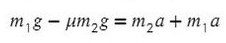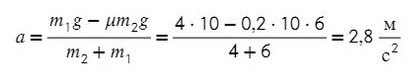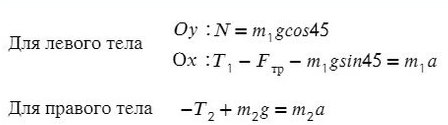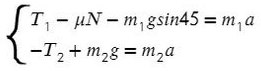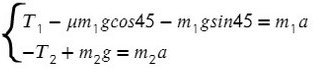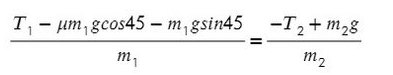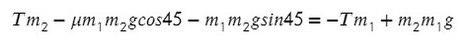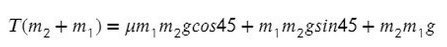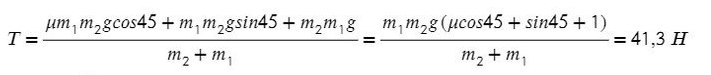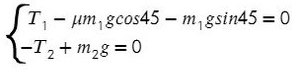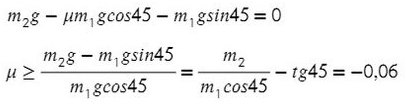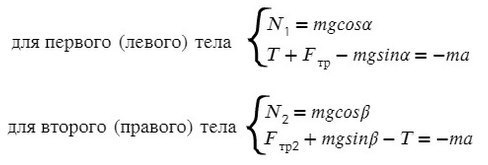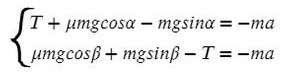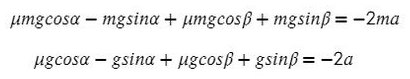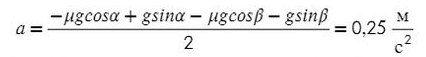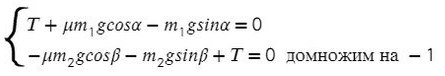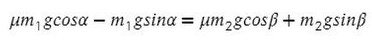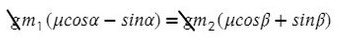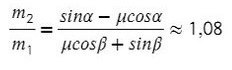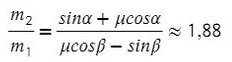Как найти ускорение с которой движутся грузы - Сайт, где вы сможете решить свои вопросы

Мячик, брошенный с балкона в вертикальном направлении, через t = 3,0 с упал на Землю... Решение задачи

Задача. Определить ускорения $a_{1}$ и $a_{2}$ , с которыми движутся грузы $m_{1}$ и $m_{2}$ в установке, изображенной на рис. 1, а также силу натяжения textbf{T} нити. Трением и массой блоков пренебречь. Нить считать невесомой и нерастяжимой.
Решение. На груз $m_{1}$ действуют силы тяжести $m_{1}textbf{g}$ и сила натяжения $textbf{T}_{1}$ нити, на груз $m_{2}$ — сила тяжести $m_{2}textbf{g}$ и силы натяжения $textbf{T}_{2},textbf{T}_{3}$ нитей. При этом $T_{1}=T_{2}=T_{3}=T$ . Поскольку все силы направлены по вертикали, запишем уравнения, выражающие второй закон Ньютона, применительно к грузам сразу в скалярном виде, выбрав положительным направление вниз и предположив, что ускорение груза $m_{1}$ направлено вниз и, следовательно, ускорение груза $m_{2}$ — вверх:

$m_{1}g-T=m_{1}a_{1},; ; ; ; ; ; (1)$

$m_{2}g-2T=-m_{2}a_{2},; ; ; ; ; ; (2)$

Рис.1

Рассматривая кинематическую схему установки и учитывая условие нерастяжимости нити, запишем соотношение между модулями перемещений грузов, происходящих за одно и то же время: $s_{1}=2s_{2}$ . Очевидно, такое же соотношение существует и между модулями ускорений грузов:

$a_{1}=2a_{2}.$

Решив совместно уравнения (1), (2), (3), получим:

$displaystyle a_{1}=frac{2(2m_{1}-m_{2})}{4m_{1}+m_{2}}g;; a_{2}=frac{2m_{1}-m_{2}}{4m_{1}+m_{2}}g;; T=frac{3m_{1}m_{2}}{4m_{1}+m_{2}}g.$

Отсюда следует: 1) если

Источник

Динамика: движения системы связанных тел.

Проецирование сил нескольких объектов.

Действие второго закона Ньютона на тела, которые скреплены нитью

Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.

А для тех, кто все помнит, поехали!

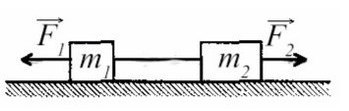
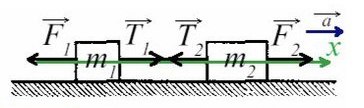
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?

Движение происходит только на оси X.

Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.

По II з. Ньютона спроецируем силы обоих тел на Ох:

Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T₁ и Т₂.

Выразим ускорение:

Ответ: 1 м/с²

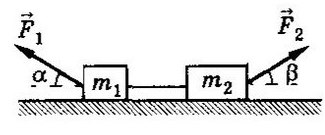
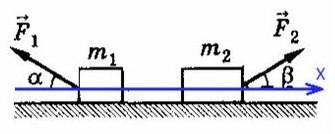
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.

Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).

По II з. Ньютона спроецируем силы обоих тел на Ох:

Сложим уравнения и выразим ускорение:

Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:

Задача 3. Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?

В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.

Вычтем из первого уравнения второе:

Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:

Ответ: 26,64 м

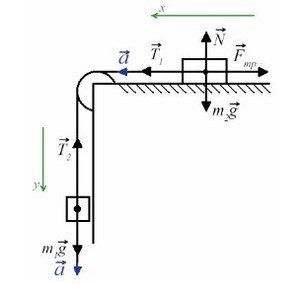
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.

Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):

(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)

Сложим два нижних уравнения для того, чтобы T сократилось:

Выразим ускорение:

Ответ: 2,8 м/с²

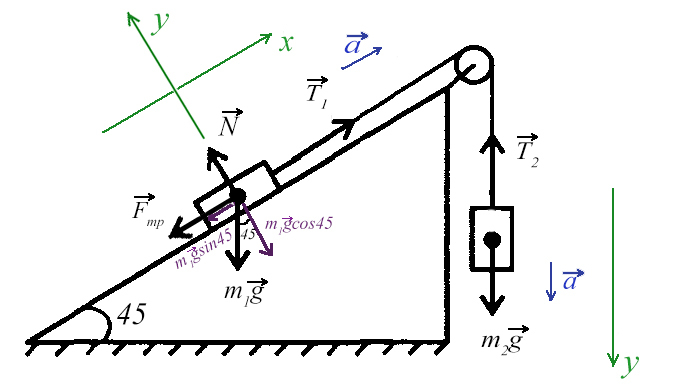
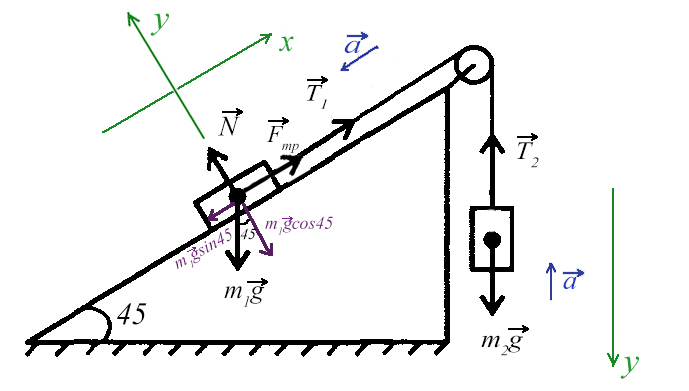
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?

Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.

Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):

Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:

Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:

Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:

Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.

Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.

Ответ: 0,06

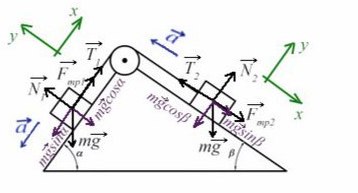
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.

В данной задаче уже потребуются все уравнения на обе оси для каждого тела:

Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:

Сложим уравнения и сократим на массу:

Выразим ускорение:

Подставив в любое уравнение найденное ускорение, найдем Т:

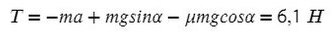
А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:

Сложим уравнения

Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:

Получили, что отношение масс должно быть таким:

Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:

Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.

У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.

В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.

Ответ: от 1,08 до 1,88

Задачи для закрепления.
Система связанных тел.

Будь в курсе новых статеек, видео и легкого технического юмора.

Источник

Условие задачи:

С каким ускорением движутся грузы (m_1=0,5) кг и (m_2=0,6) кг, если высота наклонной плоскости (H=60) см, длина наклонной плоскости (l=1) м и коэффициент трения первого груза о плоскость 0,25? Невесомый блок вращается по часовой стрелке.

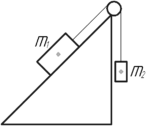
Задача №2.3.15 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

(m_1=0,5) кг, (m_2=0,6) кг, (H=60) см, (l=1) м, (mu=0,25), (a-?)

Решение задачи:

Сделав схему к задаче, введем координатные оси для каждого груза и покажем все силы, действующие на них (смотрите схему). Грузы движутся ускоренно, причем первый груз поднимается по плоскости, а второй – опускается вниз, так как блок вращается по часовой стрелке. Запишем второй закон Ньютона для второго груза в проекции на ось (y):

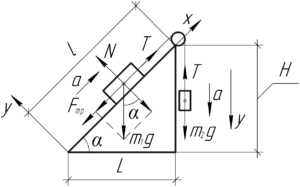
[{m_2}g – T = {m_2}a;;;;(1)]

Для первого груза запишем второй закон Ньютона в проекции на ось (x) и первый закон Ньютона в проекции на ось (y):

[left{ begin{gathered}
T – {m_1}gsin alpha – {F_{тр}} = {m_1}a ;;;;(2)hfill \
N = {m_1}gcos alpha ;;;;(3)hfill \
end{gathered} right.]

Силу трения скольжения определяют по следующей формуле:

[{F_{тр}} = mu N]

Так как мы уже определили силу реакции опоры (формула (3)), то:

[{F_{тр}} = mu {m_1}gcos alpha ]

Полученное подставим в (2), тогда:

[T – {m_1}gsin alpha – mu {m_1}gcos alpha = {m_1}a;;;;(4)]

Теперь сложим равенства (1) и (4), в итоге получим:

[{m_2}g – {m_1}gsin alpha – mu {m_1}gcos alpha = left( {{m_1} + {m_2}} right)a;;;;(5)]

Вы должны заметить, что нам неизвестен угол наклонной плоскости (alpha) и тригонометрические функции этого угла. Но их можно выразить через геометрические параметры наклонной плоскости, что мы сейчас и сделаем. Для начала определим длину основания наклонной плоскости по теореме Пифагора:

[L = sqrt {{l^2} – {H^2}} ]

Тогда синус и косинус угла (alpha) по определению равны:

[sin alpha = frac{H}{l}]

[cos alpha = frac{L}{l} = frac{{sqrt {{l^2} – {H^2}} }}{l}]

Полученное подставим в (5), далее домножим обе части равенства на (l) и выразим искомое ускорение (a):

[{m_2}g – {m_1}gfrac{H}{l} – mu {m_1}gfrac{{sqrt {{l^2} – {H^2}} }}{l} = left( {{m_1} + {m_2}} right)a]

[{m_2}gl – {m_1}gH – mu {m_1}gsqrt {{l^2} – {H^2}} = left( {{m_1} + {m_2}} right)al]

[a = frac{{gleft( {{m_2}l – {m_1}H – mu {m_1}sqrt {{l^2} – {H^2}} } right)}}{{left( {{m_1} + {m_2}} right)l}}]

Переведем высоту (H) в систему СИ:

[60; см = frac{{60}}{{100}}; м = 0,6; м]

Посчитаем численный ответ:

[a = frac{{10 cdot left( {0,6 cdot 1 – 0,5 cdot 0,6 – 0,25 cdot 0,5 cdot sqrt {{1^2} – {{0,6}^2}} } right)}}{{left( {0,5 + 0,6} right) cdot 1}} = 1,82; м/с^2]

Ответ: 1,82 м/с².

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.14 Ледяная горка составляет с горизонтом угол 10 градусов. По ней пускают вверх камень
2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами

Источник

Блоки, нити, грузы и перегрузки

Задача 1. К телу массой кг подвешено на веревке тело массой кг. Масса веревки кг. Вся система движется ускоренно вверх под действием силы Н, приложенной к верхнему телу (рис.1). Найти натяжение веревки в ее центре и в точках крепления тел и .

Рисунок 1

Представим всю систему единым телом массой . Будем действовать на эту систему с силой . Тогда по второму закону Ньютона

Откуда найдем ускорение системы:

Теперь вернемся к первому рисунку и запишем уравнения по второму закону Ньютона для верхнего и нижнего грузов:

Откуда

Очевидно, что посередине веревки сила ее натяжения будет средним арифметическим найденных двух сил:

Ответ: Н, Н, Н.

Задача 2. Маляр массой кг работает в подвесном кресле. Ему понадобилось срочно подняться вверх. Он начинает тянуть веревку с такой силой, что сила давления на кресло уменьшается до Н. Масса кресла кг. Чему равно ускорение маляра? Чему равна нагрузка на блок?

Рисунок 2

Расставим силы. Отметим все силы, действующие не маляра, и силы, действующие на люльку:

Теперь можно написать уравнения:

Вычитаем уравнения:

Ответ: м/с.

Задача 3.

Через легкий неподвижный блок перекинута невесомая нерастяжимая нить с двумя грузами на концах, массы которых и , . Система приходит в движение, причем нить не проскальзывает относительно блока. Определить ускорение грузов, силу натяжения нити и силу давления на ось блока.

Рисунок 3

Понятно, что больший груз перетянет и начнет двигаться вниз, а меньший – подниматься. Запишем для них уравнение по второму закону:

Сложим уравнения:

Откуда

Теперь можно найти и силу натяжения нити:

Сила давления на блок равна :

Ответ: , ,
.

Задача 4.

Через блок перекинута нить, на концах которой висят два груза с одинаковыми массами . Одновременно на каждый из грузов кладут по перегрузку: справа массой , слева (рис. 2). Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.

Рисунок 4

Запишем уравнение по второму закону Ньютона для обоих грузов с учетом массы перегрузков:

Сложение уравнений даст нам

Сила натяжения нити найдется подстановкой найденного ускорения в любое уравнение системы:

Определим силу давления меньшего перегрузка массой на груз :

Для большего перегрузка

Ответ: , , , .

Задача 5.

Через неподвижный блок перекинута нить, к которой подвешены три одинаковых груза массой кг каждый (рис. 3). Найти ускорение системы и силу натяжения нити между грузами 1 и 2. Какой путь пройдут грузы за первые с движения? Трением пренебречь.

Рисунок 5

Сначала мысленно объединим два груза слева в один и запишем уравнение по второму закону:

Для правого грузика

Складываем уравнения:

Определим силу натяжения нити между грузиками. Обозначим ее . Тогда для самого нижнего грузика слева:

Определяем путь грузиков за 4 с:

Ответ: м/с, Н, м.

Задача 6.

Определить ускорение грузов и силы натяжения всех нитей в системе, изображенной на рисунке. Масса каждого груза , массой блока пренебречь.

Рисунок 6

Сначала определяем ускорение. Для этого записываем уравнение по второму закону для грузиков справа и слева, пока не вспоминая о том, что их там несколько. Для нас сейчас это груз массой справа и слева. Силу натяжения основной нити обозначим :

Складываем уравнения:

Тогда

Рассмотрим теперь грузы, висящие справа. Обозначим натяжение нити между ними . Для нижнего груза справа

Осталось определить и . Для верхнего грузика слева

Откуда

А для нижнего грузика слева

Ответ: , , , , .

Задача 7.

Два груза массами г и г соединены нерастяжимой нитью, перекинутой через невесомый блок (рис.). Грузы прижимаются друг к другу с постоянными силами Н. Коэффициент трения между ними . Найти ускорение, с которым движутся грузы.

Рисунок 7

Записываем уравнение по второму закону:

Тогда

Ответ: .

Задача 8.

Невесомая нить, перекинутая через неподвижный блок, пропущена через щель (рис.). При движении нити на нее действует постоянная сила трения . На концах нити подвешены грузы, массы которых и . Определить ускорение грузов.

Рисунок 8

Давайте предположим, что . Тогда левый груз начинает движение вверх, правый – вниз. Записываем для них уравнение по второму закону с учетом наличия силы трения:

Складывая уравнения, имеем:

Откуда

Но, если бы , тогда

Тогда, чтобы учесть обе возможности, запишем ответ так:

Ответ: .

Задача 9.

Через невесомый блок перекинута легкая нерастяжимая нить, к одному концу которой привязан груз массой г, а по другому
скользит кольцо массой г (рис.). С каким ускорением движется кольцо, если груз неподвижен?

Рисунок 9

Сила трения кольца в данном случае и порождает силу натяжения нити, то есть это одна и та же сила. Поэтому для неподвижного груза

А для кольца

Ответ: 6 м/с.

Источник

Два груза массами 300 г и 200 г соединены нитью, перекинутой через блок, подвешенный на пружинных весах. Определите ускорение грузов, показание пружинных весов и силу упругости нити. Массой блока и трением в нем пренебречь.

Спрятать решение

Решение.

Изобразим силы, действующие на каждый груз и на блок. Нить невесома и нерастяжима, поэтому силы натяжения Т₁ и Т₂ равны по модулю и ускорения обоих грузов одинаковы. Запишем второй закон Ньютона для каждого тела и для блока

В проекции на ось Оy:

Решая систему уравнений, найдем ускорение, с которым движутся грузы, силу натяжения нити и силу упругости:

Ответ: 1,96 м/с²; 4,7 Н; 2,35 Н.

Источник: Кирик Л. А. Самостоятельные и контрольные работы для 9 класса, Х.: «Гимназия», 2002 (№ 8 (дост.) стр. 88)

Источник

Условие задачи:

Дано:

Решение задачи:

Ответ: 1,82 м/с2.

Смотрите также задачи:

Блоки, нити, грузы и перегрузки

Вам также может понравиться

Как найти поиск на телефоне самсунг

0х80070035 не найден сетевой путь windows 10 0x80070035 как исправить

Как найти паблик по ссылке

Добавить комментарий Отменить ответ

Ответ: 1,82 м/с².