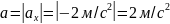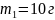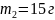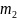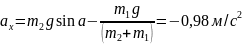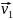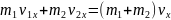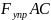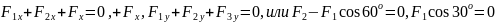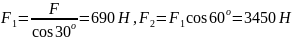Как найти ускорение шайбы

• Комментировать
• Жалоба
• Ссылка

Спрятать решение

Спрятать критерии

Классификатор: Ме­ха­ни­ка. Дви­же­ние по окруж­но­сти

2018-03-10   

Однородный стержень массы $M$ подвешен при помощи легких нерастяжимых веревок одинаковой длины к потолку и находится в положении устойчивого равновесия. Расстояние между точками крепления веревок равно длине стержня. По стержню без трения может перемещаться небольшая шайба массы $m$. В начальный момент времени натянутые веревки отводят на угол $alpha$ от вертикали, так что стержень и точки крепления веревок к потолку лежат в вертикальной плоскости, а шайба находится посередине стержня (рис.). Найти ускорение шайбы сразу после того, как веревки отпустят.

Решение:

Так как в процессе движения (рис.) фигура, образованная веревками, стержнем и отрезком потолка между точками крепления веревок представляет собой параллелограмм, то при любом своем положении стержень будет оставаться параллельным своему первоначальному положению, т. е. стержень движется поступательно. Рассмотрим нашу систему, спустя некоторый интервал времени после того, как веревки отпустили. Концы веревок совершат одинаковые перемещения $Delta s$, высота стержня над горизонтом уменьшится на $Delta h$. Под действием вертикально направленных сил тяжести и реакции со стороны стержня (трения нет!) шайба совершит вертикальное перемещение $Delta h$.

Тогда потенциальная энергия системы уменьшится на величину

$Delta U = (m+M)g Delta h$,

где $m$ и $M$ — массы шайбы и стержня соответственно. Пусть к концу интервала $Delta t$ скорость шайбы станет равной $v$, а стержня $u$. Так как перемещения стержня $Delta s$ и шайбы $Delta h$ связаны соотношением $Delta h = Delta s sin alpha$, где $alpha$ – угол первоначального отклонения нитей от вертикали, то $v = u sin alpha$ и закон сохранения энергии запишем в виде

$(m + M)g Delta h = frac{mv^{2} }{2} + frac{Mu^{2}}{2}$,

или

$v^{2} = 2g Delta h frac{M + m}{M / sin^{2} alpha + m}$.

Мы считаем, что интервал времени $Delta t$ настолько мал, что ускорения стержня и шайбы на этом интервале можно считать постоянными. Тогда так как

$v^{2} = 2a Delta h$,

то

$a = g frac{M + m}{m + M/ sin^{2} alpha }$.

Образцы решения задач Кинематика

Ударом клюшки
хоккейной шайбе сообщили скорость v₀
=20 м/с. Через
время t₁=2с
скорость
шайбы, движущейся прямолинейно, стала
равна 16м/с. Найдите ускорение шайбы,
считая его постоянным.

Решение:

Выберем
оси координат так, чтобы движение шайбы
происходило вдоль какой-либо координатной
оси Ох. За продолжительное направление
оси Ох примем направление вектора
начальной скорости (рис.) Так как шайба
движется с постоянным ускорением, то
проекцию

ускорения
на ось Ох найдём из формулы

. учитывая, что при выбранном положительном
направлении оси Ох

,
а при

,
получаем

.
Отсюда

.
Знак

означает, что вектор ускорения направлен
в сторону, противоположную положительному
направлению оси Ох. Модуль же ускорения
равен

.

Динамика

Два
тела с массами

связанны нитью, перекинутой через блок,
установленный на наклонной плоскости
(рис.). плоскость образуется с горизонтом
угол а=
.
Найдите ускорение, с которым будут
двигаться эти тела. Трением пренебречь.

Решение:

Е
сли
предположить, что перетягивает груз
массой

(рис.),
то уравнение движения грузов запишутся
в виде

исключая силу натяжения Т, найдём
проекцию ускорения на направление
движения:

.

Знак
“минус” означает, что движение в
действительности происходит в направлении,
обратному тому, которое мы предположили.

Законы сохранения

Два
шара с массами m₁
= 0,5кг и m₂
= 0,2кг движутся по гладкой горизонтальной
поверхности навстречу друг другу со
скоростями v₁
= 1м/с и v₂
= 4м/с. Найдите их скорость

после центрального абсолютно неупругого
удара.

Решение:

Ось
Ох направим вдоль линии, проходящей
через центры движущихся шаров по
направлению скорости

.
Так как вдоль оси Ох силы не действуют
(трения нет), то сумма проекций импульсов
на эту ось сохраняется:

.
Здесь учтено, что после неупругого удара
шары движутся с одной и той же скоростью.
Так как

После удара шары будут двигаться в
отрицательном направлении оси Ох со
скоростью 0,4 м/с.

Статика

Груз
висит на двух тросах (рис.). угол АСВ
равен

.
сила тяжести, действующая на груз, равна
600 Н. определите силы упругости тросов
АС и СВ.

Решение:

Силы
упругости тросов силы направлены вдоль
тросов от точки С (рис. б). кроме этих
сил, на точку С действует сила

,
равная сила тяжести. Точка С находится
в равновесии. Следовательно, сумма сил,
действующих на неё, равна нулю:

.
Оси координат выбираем так, как показано
на рис. В. При равновесии сумма проекций
всех сил на оси координат равна нулю:

.

Отсюда

.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

F=m*a=250*0,4=100 H
……………………………………….

X=45:9            
<span>X=5</span>
9*5=45
Держи

<em>N=A/t=mgh/t —-> h=Nt/mg</em>

В пасмурный день (когда на небе облачка)  происходит рассеивание и отражение  солнечных лучей  и тень будет не такая резкая как при ясном дне.