Голосование за лучший ответ
Сергей Логинов
Оракул
(87321)
10 лет назад
Ускорение свободного падения g домножь на синус заданного угла:
a = g * sin(fi)
Это если задан угол в основании наклонной плоскости. Если он отсчитывается от вертикали, вычти его из 90° или примени косинус, что то же самое.
Трудное детство
Оракул
(70151)
10 лет назад
обозначим угол наклонной плоскости А, направим ось ОХ вдоль наклонной плоскости, тогда уравнение движения шарика: ma(x)=mgsinA, ma(y)=mgcosA=0, т. к. а (у) =0. итак a=a(x)=gsinA и от массы не зависит, т. е. при одинаковом угле тела разной массы скатываются одинаково. это тот самый опыт на основании которого Галилей сделал вывод о постоянстве ускорения свободного падения для всех тел.
Mikhail Levin
Искусственный Интеллект
(614570)
10 лет назад
надеюсь, вам это задали в университете, а не в школе?
катящийся шарик принципиально отличается от катящихся санок, у него большАя часть энергии уходит не в линейное движение, а во вращение.
то есть, не как в школе с санками:
mgh=mv^2/2
а
mgh=mv^2/2 + Iw^2/2
Цель работы: вычислить ускорение, с которым скатывается шарик по наклонному желобу. Для этого измеряют длину перемещения s шарика за известное время t. Так как при равноускоренном движении без начальной скорости
то, измерив s и t, можно найти ускорение шарика. Оно равно:
Никакие измерения не делаются абсолютно точно. Они всегда производятся с некоторой погрешностью, связанной с несовершенством средств измерения и другими причинами. Но и при наличии погрешностей имеется несколько способов проведения достоверных измерений. Наиболее простой из них — вычисление среднего арифметического из результатов нескольких независимых измерений одной и той же величины, если условия опыта не изменяются. Это и предлагается сделать в работе.
Средства измерения: 1) измерительная лента; 2) метроном.
Материалы: 1) желоб; 2) шарик; 3) штатив с муфтами и лапкой; 4) металлический цилиндр.
Порядок выполнения работы
1. Укрепите желоб с помощью штатива в наклонном положении под небольшим углом к горизонту (рис. 175). У нижнего конца желоба положите в него металлический цилиндр.
2. Пустив шарик (одновременно с ударом метронома) с верхнего конца желоба, подсчитайте число ударов метронома до столкновения шарика с цилиндром. Опыт удобно проводить при 120 ударах метронома в минуту.
3. Меняя угол наклона желоба к горизонту и производя небольшие передвижения металлического цилиндра, добивайтесь того, чтобы между моментом пуска шарика и моментом его столкновения с цилиндром было 4 удара метронома (3 промежутка между ударами).
4. Вычислите время движения шарика.
5. С помощью измерительной ленты определите длину перемещения s шарика. Не меняя наклона желоба (условия опыта должны оставаться неизменными), повторите опыт пять раз, добиваясь снова совпадения четвертого удара метронома с ударом шарика о металлический цилиндр (цилиндр для этого можно немного передвигать).
6. По формуле
найдите среднее значение модуля перемещения, а затем рассчитайте среднее значение модуля ускорения:
7. Результаты измерений и вычислений занесите в таблицу:
|
Номер опыта |
s, м |
sср, м |
Число ударов метро нома |
t, с |
aср, м/с2 |
При прямолинейном равноускоренном движении без начальной скорости
где S – путь, пройденный телом, t – время прохождения пути. Средства измерения: измерительная лента (линейка), метроном (секундомер).
Лабораторная установка и порядок выполнения работы подробно описаны в учебнике.
|
№ опыта |
t, с |
S, м |
 |
|
1 |
6 |
0,5 |
0,028 |
|
2 |
5,5 |
0,5 |
0,033 |
|
3 |
5 |
0,49 |
0,039 |
|
4 |
5,5 |
0,49 |
0,032 |
|
5 |
6,5 |
0,51 |
0,024 |
|
среднее значение |
5,7 |
0,5 |
0,031 |
Вычисления:
Вычисление погрешностей
Точность приборов: Измерительная лента:
Секундомер:
Вычислим абсолютные погрешности:
Вычислим относительную погрешность:
Абсолютная погрешность косвенного измерения:
Найденное в результате работы ускорение можно записать так:
но при данной абсолютной погрешности последняя цифра в значении аср значения не имеет, поэтому запишем так:
|
По наклонному жёлобу скатывается шарик (трением качения можно пренебречь). Известна высота, с которой катится шарик, известен путь, пройденный шариком за отрезки времени, пока он не скатился вниз. Это обычные данные эксперимента. Как из этих данных найти ускорение свободного падения? (См. задачу “Почему расчет из опыта ускорения свободного падения Фейнман назвал бедой?” и ответ на нее.) Ох, не думаю, что “написать пару формул в состоянии даже троеник-восьмиклассник”. И даже троечник не сможет, а даже не всякий студент технического вуза (про другие умолчу). А решение не вполне элементарное, хотя исходная посылка простая: закон сохранения энергии. Потенциальная энергия шарика на вершине mgh. Эта энергия переходит в кинетическую энергию поступательного движения mv2/2 и энергию вращательного движения, которая выражается аналогичной формулой Jw2/2 (буквой w я обозначил греч. омегу, которая может “слететь”). Пока всё достаточно элементарно. Но чтобы найти момент инерции сплошного шара w, нужно взять тройной интеграл по объему. Мы в 8-м классе это не проходили, и в 10-м тоже. Но проходили на матане. Правда, “знающий троечник”, не знающий интегралов, может подсмотреть в хорошем справочнике и узнать, для для шара w = 2/5 mr2, где r – радиус шара. И тогда окажется, что энергия вращения Jw2/2 = mv2/5, то есть не зависит от радиуса шарика! (И от его диаметра тоже.) Приравнивая потенциальную и кинетическую энергию, получает: gh = 7/10v2 (масса тоже исчезает! – в прямом противоречии и с материализмом, и с эмпириокритицизмом). Из последней формулы и получаем для ускорения свободного падения g = 7/10 v2/h. Ускорение шарика (а) находим по пути, пройденном за определенные промежутки времени. А конечная скорость ко времени t равна at. Грустный Роджер 9 лет назад Ну как, как… Элементарно. Потенциальная энергия тела преобразуется в кинетическую энергия катящегося шарика. Катящегося – означает, что у него есть кинетическая энергия движения и кинетическая энергия вращения. Угловая скорость этого вращения вполне понятным образом связана с линейной скоростью движения. Момент инерции шарика тоже вполне понятно связан с его массой и радиусом. Так что написать пару формул в состоянии даже троеник-восьмиклассник (впрочем, не уверен, что в нынешней школе механику вообще проходят…). Ну а скорость шарика на каждом участке известна “по условию задачки”. Знаете ответ? |
Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.
Основная формула динамики
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
F¯ = m*a¯
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
M = I*α
Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Здесь v0 – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.
Линейные и угловые характеристики друг с другом связаны формулами:
a = α*r;
v = ω*r
Здесь r – радиус вращения.
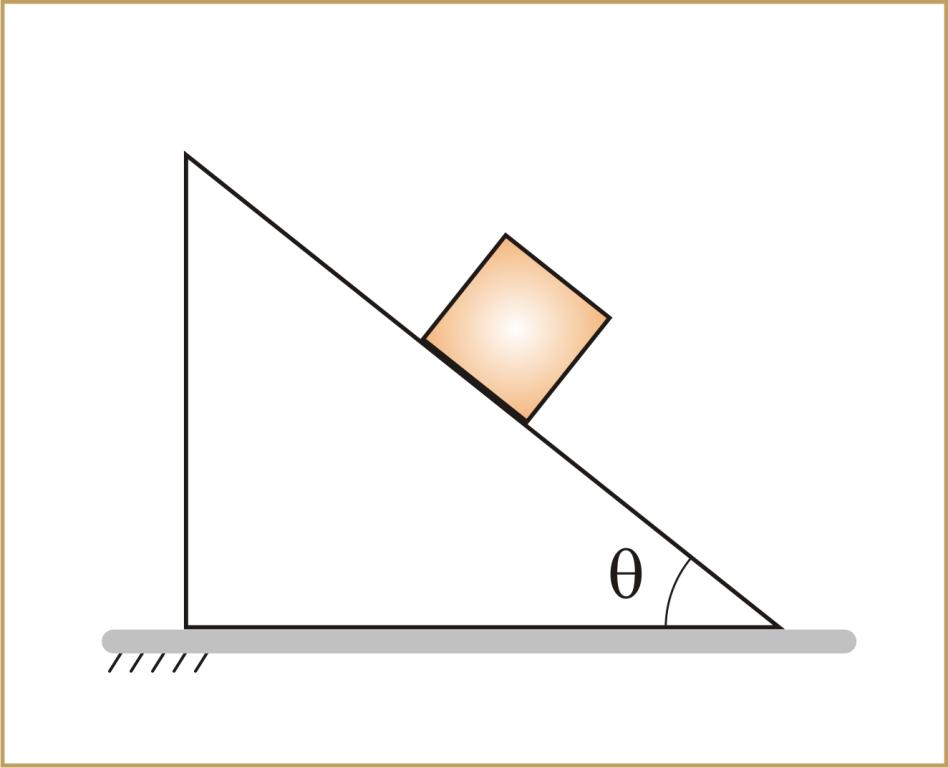
Движение по наклонной плоскости: силы
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
- тяжести;
- реакции опоры;
- трения качения и/или скольжения;
- натяжение нити;
- сила внешней тяги.
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.
Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Ff = µ*N
Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a
Здесь φ – это угол наклона плоскости к горизонту.
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
F = m*g*sin(φ) – Fr = m*a
Где Fr – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, Fr создает следующий момент:
M = Fr*r = I*α
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
m*g*(sin(φ) – µ*cos(φ)) = m*a =>
a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с2
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
S = a*t2/2
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
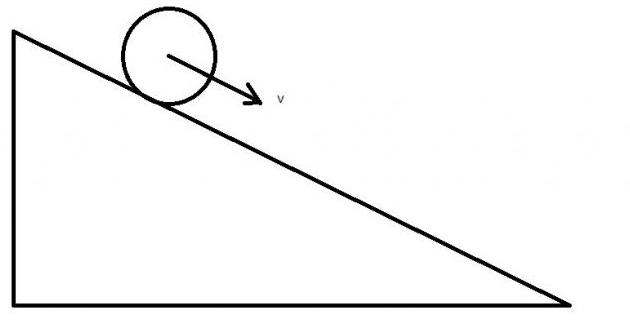
Задача со скатывающимся по плоскости цилиндром
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
m*g*sin(φ) – Fr = m*a;
Fr*r = I*α = I*a/r
Момент инерции I цилиндра вычисляется по формуле:
I = 1/2*m*r2
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) – 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
S = a*t2/2 =>
t = √(2*S/a)
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.
По наклонной к
горизонту доске пустили катиться снизу вверх шарик. На расстоянии 30 см от
начала пути шарик побывал дважды: через 1 с и через 2 с от начала движения.
Определите начальную скорость и ускорение шарика, считая его постоянным.
Решение.
В качестве тела отсчета
выберем доску, ось OX
направим вдоль плоскости доски, начало координат выберем в точке начала
движения, отсчет времени начнем также с момента начала движения. При таком
выборе системы
отсчета x0 = 0, t0 = 0.
Движение шарика будем
считать прямолинейным, а по условию задачи его ускорение постоянно. Это значит,
что мы должны пренебречь взаимодействием шарика с воздухом, а поверхность доски
считать абсолютно гладкой. Поэтому кинематические законы движения шарика в
проекции на ось OX
имеют вид
.
Поскольку в моменты
времени t1 = 1 c и t2 = 2 с шарик находился в одной и той же точке доски, то его
координаты в эти моменты времени были одинаковыми, т.е. x1 = x2
= l. Таким образом
.
Решение этой системы
уравнений относительно v0 и a
приводит к результату
.
Правильность решения
можно проверить, например, путем сравнения наименований правой и левой частей
полученных формул или, исходя из энергетический соображений. Поскольку во время
движения шарика потери энергии отсутствуют, то его кинетическая энергия в
моменты времени t1 = 1 с и t2 = 2 с должна быть одинаковой. Для
проверки этого определим значения проекций скорости шарика на ось OX в эти моменты времени. Если подставить
значений v0 и a в формулы для vx и
v’x , получим:
Поскольку vx = | v’x |, то кинетическая энергия шарика в эти моменты времени
на самом деле одинакова, поэтому можно быть уверенным, что полученные значения v0 и a
являются решениями задачи в общем виде.