Как найти ускорение шарниров

Ускорение – шарнир

Cтраница 1

Ускорение шарнира С находим из теоремы подобия.
 [1]

Определяем ускорение шарнира А, принадлежащего звену О А с известной постоянной угловой скоростью ШОА.
 [2]

Переходим к ускорению шарнира D.
 [3]

При определении скоростей и ускорений шарниров В, D и F значение угла а, при котором выполняется уравнение ( 2), известно.
 [5]

Затруднение при построении плана ускорений возникает в самом начале при определении ускорения шарнира В.
 [6]

Для проверки конструкции УММЧ и определения диапазона положений, угловых скоростей и ускорений шарниров был проведен ряд экспериментов.
 [7]

На рис. 1.36, г показано применение метода. Зная ускорение концевых шарниров и центра качания, определяем на плане механизма линию действия силы инерции Ри при статической замене массы и при динамической.
 [8]

На рис. 1.37 6 показано применение метода. Зная ускорение концевых шарниров и центра качания, определяем на плане механизма линию действия силы инерции Ръ при статической замене массы и то же при динамической.
 [9]

Определение положений, скоростей и ускорении вну-тренннх шарниров ( Е, Г, О) тпехповод-ковой группы пи положениям, скорое.
 [10]

Определение положении, скоростей и ускорений внутренних шарниров ( Е, F, G) трехповод-ковой группы по положениям, скоростям и ускорениям внешних шарниров ( С, D и О3) производится следующим образом.
 [11]

Определение положений, скоростей и ускорений внутренних шарниров ( Е, F, G) трехповод-ковой группы по положениям, скоростям и ускорениям внешних шарниров ( С, D и О3) производится следующим образом.
 [12]

От полюса q ( рис. 237) откладываем Wa С Ло. Wa qa А – Oi и обычным путем – построением плана ускорений для части механизма О АВО – находим точку Ь, конец вектора Wb qb ускорения Wb. Затем переходим к выяснению ускорения шарнира С. С одной стороны, точка С, как принадлежащая ползуну, будет разделять сложное движение ползуна: переносное-вращательное, вместе с кулисой 3, и относительное-поступательное, вдоль кулисы.
 [13]

Страницы:  

   1

Содержание:

Плоское движение тела:

При изучении темы ПЛОСКОЕ ДВИЖЕНИЕ ТЕЛА раздела КИНЕМАТИКА. вы научитесь применять аналитические и графические методы для определения скоростей и ускорений точек тел и механизмов. Хотя эти знания имеют самостоятельную ценность, особенно необходимы они будут для решения задач динамики тела и системы.

Приведены программы расчета кинематики плоского движения в математической системе Maple V. Анимационные возможности этой системы делают решение наглядным, позволяя глубже понять суть задачи.

Методы решения задачи кинематики плоского движения разнообразны. Выбрать оптимальный путь, который может существенно упростить решение, помогут примеры, приведенные в этой главе.

Скорости точек многозвенного механизма

Постановка задачи. Плоский многозвенный механизм с одной степенью свободы находится в движении. Известна угловая скорость какого-либо его звена или скорость одной из точек механизма. Найти скорости точек механизма и угловые скорости его звеньев.

План решения:

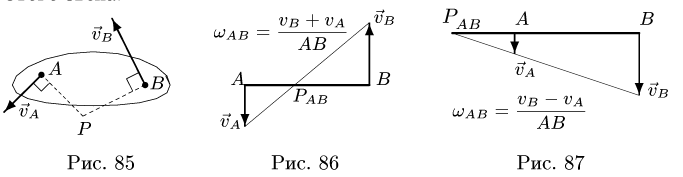
Рассмотрим два простых геометрических способа решения задачи, в которых, в отличие от аналитических методов, определяются модули скоростей и угловых скоростей. Не оговаривая отдельно, всякий раз под угловой скоростью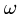

1-й способ. Мгновенные центры скоростей

1. Определяем положение мгновенного центра скоростей (МЦС) каждого звена. МЦС лежит на пересечении перпендикуляров, проведенных

к скоростям точек, принадлежащих звену (рис. 85). У тех звеньев, у которых МЦС не существует (скорости двух точек параллельны и не перпендикулярны отрезку, их соединяющему), угловая скорость равна нулю, а скорости всех точек равны. Если векторы скоростей перпендикулярны отрезку их соединяющем}’, то имеют место два частных случая положения МЦС (рис. 86, 87).

Если тело (колесо, диск, цилиндр) катится по поверхности без проскальзывания, то МЦС этого тела находится в точке касания.

2. Для каждого звена определяем расстояния от его точек до МЦС этого звена.

3. Записываем систему уравнений для скоростей N точек звена 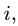 включая точку с известной скоростью:

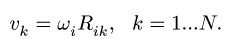
Здесь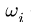 — угловая скорость звена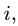 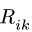— расстояние от МЦС звена 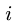до точки 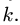Решаем систему, определяем угловую скорость звена, а затем скорости всех его точек.

Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим, для которого угловая скорость найдена или известна.

2-й способ. План скоростей

1.    Как и в методе МЦС ведем расчет, переходя от одного звена к другому, шарнирно с ним соединенном}’.

Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. Этот вектор в заданном масштабе откладываем от некоторой произвольной точки О (рис. 91). Его конец определяет первую точку плана скоростей. Точку плана скоростей (конец вектора) отмечаем строчной буквой, соответствующей точке вектора скорости. Пусть первая точка плана скоростей обозначена как b.

2.    Рассматриваем очередное звено, на котором имеется точка с уже известной скоростью. Необходимо, чтобы на этом звене была

еще одна точка с известным направлением вектора скорости (например, ползун или точка звена, совершающего вращательное движение). Пусть эта точка обозначена как С (рис. 88).

Справедливо правило, согласно которому неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами.

Следующая точка плана скоростей лежит на пересечении двух прямых. Одна прямая определяется направлением скорости точки С, вторая перпендикулярна ВС. Длина полученного отрезка Ос является модулем скорости 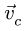(рис. 91).

Скорости остальных точек этого звена (если таковые имеются) найдем по правилу подобия неизменяемых фигур механизма и фигур, обозначенных теми же строчными буквами плана скоростей.

Пункт 2 плана выполняем для всех звеньев механизма (рис. 91-95).

3. После построения плана скоростей определяем угловую скорость каждого звена по простой формул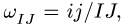е где 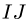расстояние между точками 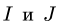звена, 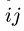— длина отрезка на плане скоростей.

Задача №1

Плоский многозвенный механизм с одной степенью свободы приводится в движение кривошипом АВ, который вращается против часовой стрелки с угловой скоростью 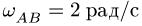(рис. 88).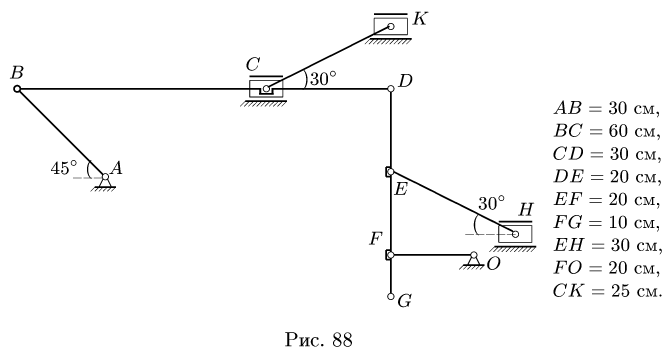

Ползуны С, К, Н движутся горизонтально, 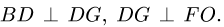Найти скорости точек В, С, D, Е, F, G, Н, К механизма и угловые

8.1.Скорости точек многозвенного механизма скорости его звеньев АВ, BD, DG, EH, FO, СК.

Решение

1-й способ. Мгновенные центры скоростей

1. Определяем положение мгновенного центра скоростей каждого звена АВ, BD, DG, СК, EH, FO.

МЦС звеньев АВ и FO искать не требуется. Они совершают вращательное движение вокруг шарниров А и О соответственно. Можно условно считать, что там находятся их МЦС.

Вектор 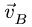скорости точки В направим перпендикулярно радиусу АВ против часовой стрелки (рис. 89). Далее, чтобы узнать положение МЦС следующего звена надо знать направления векторов скоростей двух его точек. Следующим звеном будет стержень BD, имеющий со звеном АВ общую точку В. У него есть три характерные точки В, С и D. Направление вектора скорости точки D пока неизвестно.

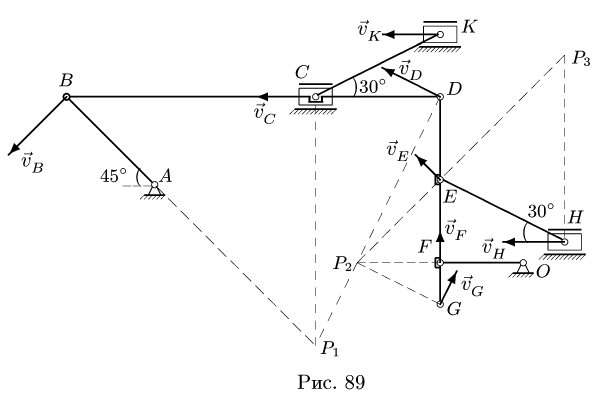
Остается точка С. Ползун С движется строго горизонтально. Вектор скорости 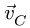направляем по горизонтали налево. Из двух возможных горизонтальных направлений мы выбрали этот вариант, исходя из теоремы о проекции векторов скоростей точек неизменяемого отрезка. Проекции должны быть равны и направлены в одну сторону. Таким образом, известны направления скоростей двух точек тела. Это позволяет определить МЦС звена BCD. Находим точку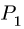пересечения перпендикуляров, проведенных из точек В и С, к векторам 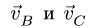(рис. 89). Теперь определяем направление вектора 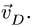Он будет перпендикулярен радиусу 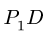и направлен налево, исходя из той же теоремы о проекциях скоростей точек отрезка BD.

Со стержнем BCD имеют общие точки два стержня: СК и DG. Рассмотрим сначала стержень DG. Направление вектора скорости точки D уже известно. Чтобы определить положение МЦС, надо знать направление вектора еще одной точки на этом звене. Такой точкой является F. Вектор ее скорости перпендикулярен радиусу вращения FO и направлен вертикально. Перпендикуляры к векторам 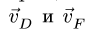задают положение точки 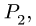вокруг которой звено DEFG совершает мгновенное вращательное движение.

Перпендикулярно радиусам 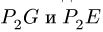проводим вектора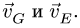

Переходим к звену ЕН, МЦС которого находим на пересечении перпендикуляров к 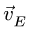(продолжение радиуса 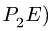и к вектору скорости 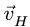ползуна Н, движущегося горизонтально. Получаем точку 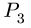— МЦС звена ЕН.

И, наконец, рассматриваем звено СК. Скорости 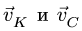параллельны и не перпендикулярны СК. Звено С К совершает мгновенно-поступательное движение. Условно можно сказать, что МЦС звена С К находится в бесконечности.

2. Определяем расстояния от МЦС звеньев до тех точек этих звеньев, скорости которых надо найти.

Звено BCD

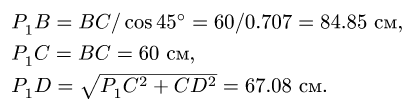
Звено DEFG. Пользуясь подобием 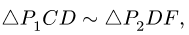находим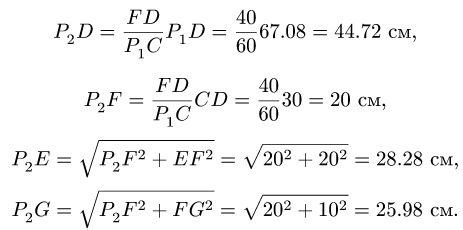

Звено ЕН (рис. 90). Находим расстояния до МЦС:

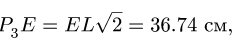
8.1.Скорости точек многозвенного механизма

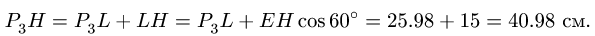
3. Записываем систему уравнений для скоростей трех точек звена BCD, включая точку В с известной скоростью:

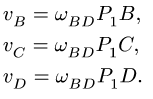
Решаем эту систему. Находим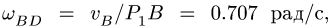

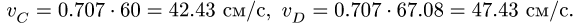
Система уравнений для скоростей точек звена DEFG имеет вид

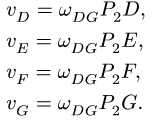
Из первого уравнения вычисляем угловую скорость:

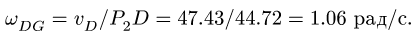
Получаем скорости точек:

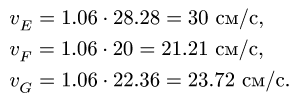
Система уравнений для скоростей точек звена ЕН имеет вид

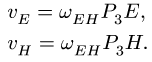
Отсюда

Звено СК совершает мгновенно-поступательное движение. Следовательно, скорости точек С я К равны: 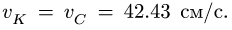Угловая скорость этого звена равна нулю .

Можно считать, что МЦС звена, движущегося мгновенно-поступательно, находится в бесконечности. Поэтому, рассуждая формально, получаем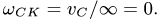

Частично проверить решение можно графически. Известно, что концы векторов скоростей точек неизменяемого отрезка лежат на одной прямой. Убеждаемся в этом, проводя прямую через концы векторов 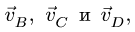отложенных на чертеже в масштабе (рис. 90).

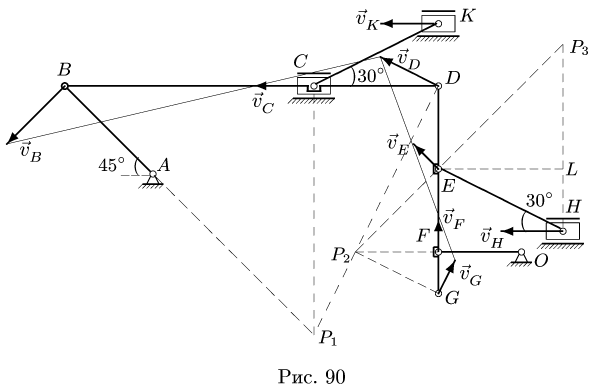
Аналогично, проверяем скорости 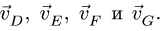Через их концы также можно провести прямую. Остались непроверенными скорости точек Е и Н. Для этого можно воспользоваться методом построения плана скоростей, см. ниже 2-й способ.

Результаты расчетов помещаем в таблицы. Скорости даны в см/с, угловые скорости — в рад/с.

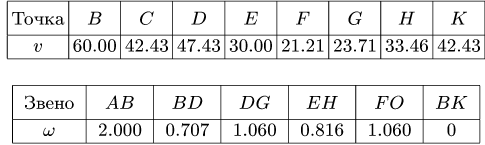
2-й способ. План скоростей

1. Построение начинаем с вектора, величина и направление которого известны или легко вычисляются. В нашем случае это 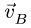. Вектор 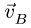в заданном масштабе откладываем от некоторой произвольной точки О (рис. 91). Все остальные вектора также будем откладывать от этой точки.

8.1.Скорости точек многозвенного механизма

Точки плана скоростей (концы векторов) отмечаем соответствующими строчными буквами. Таким образом, положение точки b на плане скоростей известно.

2. Рассматриваем звено BCD (рис. 90), на котором имеется точка В с известной скоростью. Неизменяемые отрезки механизма, обозначенные прописными буквами, перпендикулярны отрезкам плана скоростей, обозначенными теми же строчными буквами,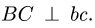Звено механизма ВС горизонтально.

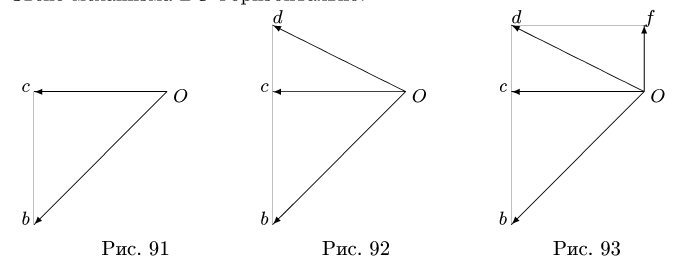
Следовательно, точка с плана скоростей лежит на одной вертикали с точкой b. Известно направление скорости ползуна С. Точку с находим на пересечении двух прямых. Вектор 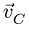изображен отрезком Ос плана скоростей (рис. 91). Из правила подобия фигур механизма и фигур, обозначенных теми же строчными буквами плана скоростей(в данном случае это отрезки BC и CD),имеем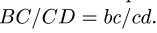 

Так получаем точку d плана скоростей и, следовательно, величину и направление вектора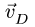 (рис. 92).

Определяем скорость 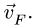Направление этого вектора известно – он перпендикулярен радиусу вращения FO. По свойству плана скоростей 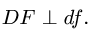Точка d на плане уже есть. Проводим через нее горизонтальную прямую (перпендикулярную DF) до пересечения с вертикальным направлением вектора скорости 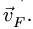Получаем точку 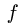(рис. 93). Соединяя ее с центром О, определяем модуль искомой скорости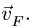

Из соотношения подобия 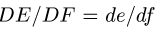на отрезке 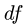находим внутри него конец вектора скорости 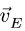и вне отрезка, пользуясь пропорцией 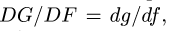точку 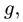определяющую вектор скорости 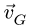(рис. 94).

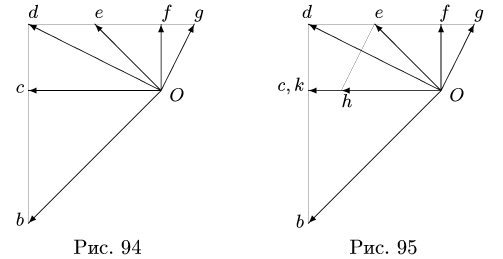
Аналогично, определяем скорость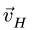 (рис. 95). Здесь 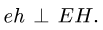Точки 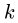и с на плане скоростей совпадают.

3. Угловые скорости звеньев определяем по простым формулам: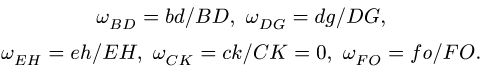

Ускорения точек многозвенного механизма

Постановка Задачи. Плоский шарнирно-стержневой механизм состоит из шарнирно соединенных стержней и ползунов. Механизм приводится в движение кривошипом, который вращается с заданной угловой скоростью. В указанном положении механизма найти ускорения всех его шарниров.
*) Существует еще несколько способов проверки вычисления скоростей точек многозвенного механизма.

8.2. Ускорения точек многозвенного механизма

План решения

1.    Определяем угловые скорости звеньев и скорости точек механизма (см. § 8.1).

2.    Определяем ускорение шарнира, принадлежащего звену с известным законом движения:

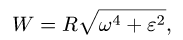
где R — длина звена. Если задан закон изменения утла поворота 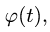то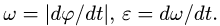

Если угловая скорость звена постоянна, 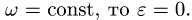Вектор ускорения в этом случае направляем к центру вращения звена.

3.    Для определения ускорения точки В тела, совершающего плоское движение, воспользуемся векторной формулой

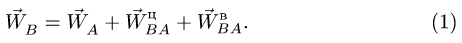
Здесь 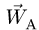— известное ускорение точки, выбранной в качестве полюса, 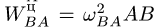— центростремительное ускорение условного движения В вокруг А по окружности с радиусом 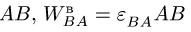— вращательное ускорение.

Возможны три случая определения ускорения по формуле (1). А. Точка В является ползуном, или направление ее вектора ускорения по каким-либо другим причинам известно. В этом случае формула (1) в проекциях на оси координат представляет собой систему двух линейных уравнений для неизвестного модуля ускорения ав и неизвестного углового ускорения звена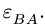

Б. В точке В шарнирно соединены звено АВ и звено ВС, где С — неподвижный шарнир. Таким образом, точка В движется по окружности с центром в С, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорения:

Величину нормального ускорения 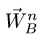находим, зная скорость точки 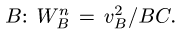Направляем вектор 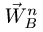по радиусу ВС к центру вращения С. Вектор 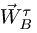неизвестен лишь по модулю, направление его известно — перпендикулярно радиусу ВС.

В результате, система уравнений (1-2), записанная в проекциях, дает четыре уравнения для четырех неизвестных 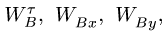 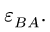Решая ее, находим ускорение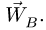

В. Точка В не удовлетворяет случаям А и Б. В этом случае либо она не является шарниром, либо к ней шарнирно присоединено тело, совершающее плоское (не вращательное и не поступательное) движение. Для решения задачи должны быть известны угловая скорость и угловое ускорение звена, на котором находится точка В. Они могут быть найдены при вычислении скорости и ускорения других точек этого звена. При этих условиях уравнение (1) является векторным уравнением для одной неизвестной .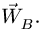

Этот пункт плана выполняем последовательно для всех звеньев механизма. Очередное звено должно иметь общую точку (шарнир) с предыдущим.

Задача №2

Плоский шарнирно-стержневой механизм состоит из четырех шарнирно соединенных стержней и горизонтально движущегося ползуна С (рис. 96). Механизм приводится в движение кривошипом OA, который вращается с постоянной угловой скоростью 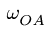= 2 рад/с. В указанном положении механизма найти ускорения шарниров А, В, С и точки М. Даны размеры: АО = 2 см, А В = 5 см,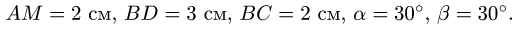 
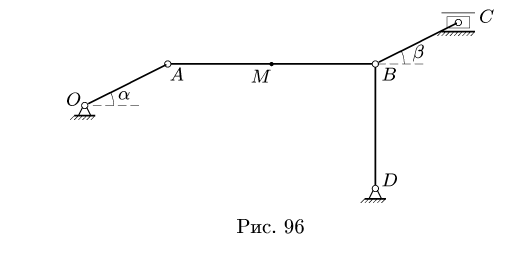
Решение

1. Определяем угловые скорости звеньев и скорости точек механизма. Находим величину скорости точки А:

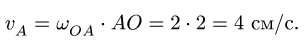
Вектор 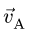направляем перпендикулярно радиусу АО против часовой стрелки. Вектор скорости 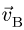направлен горизонтально. Мгновенный центр скоростей Р звена АВ находится на пересечении перпендикуляров к векторам скоростей точек 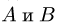(рис. 97). Находим расстояния

8.2. Ускорены точек многозвенного механизма

от точек А, В, М до МЦС: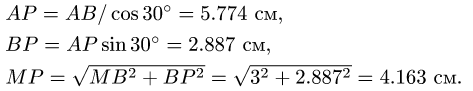

Скорости точек находим из системы уравнений

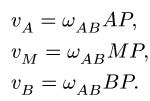
В результате решения получаем

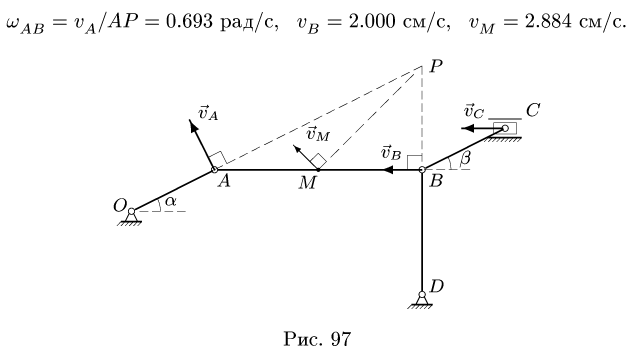
Найти скорость точки С не составит труда. Векторы 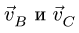параллельны и не перпендикулярны отрезку ВС. Следовательно, звено ВС совершает мгновенно-поступательное движение, и скорости всех его точек в этот момент равны. Отсюда,  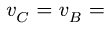2 см/с. Угловая скорость звена ВС равна нулю.

2. Определяем ускорение шарнира А, принадлежащего звену OA с известной постоянной угловой скоростью 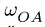. Ускорение точки А состоит только из нормальной составляющей,

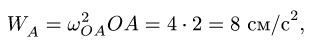 и направлено вдоль О А к центру О (рис. 98).

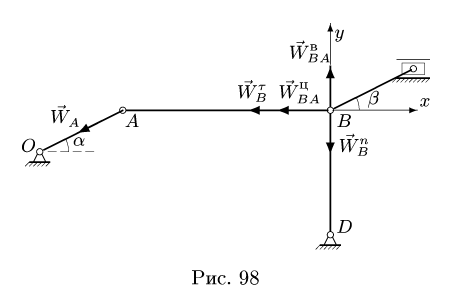
3. Находим ускорение точки В. Точка В движется по окружности с центром в неподвижном шарнире D, и ее ускорение можно представить в виде векторной суммы нормального и тангенциального ускорений:

С другой стороны, ускорение точки В выражается через ускорение точки А, лежащей на том же звене АВ. Рассматривая А в качестве полюса, имеем

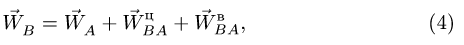
Сравнивая (3) и (4), получаем, что

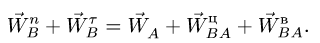
В проекциях на оси х, у (рис. 98) векторное уравнение (3) дает систем}’ двух уравнений относительно неизвестных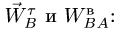

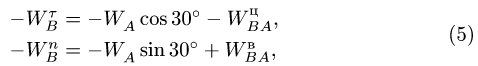
где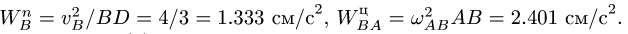

Решаем систему (5):

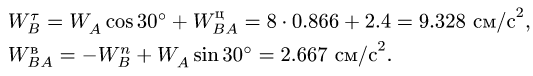
Окончательно, величина ускорения точки В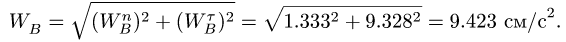

8.2. Ускорены точек многозвенного механизма

Вычисление ускорения точки М выполняем по п.ЗВ плана решения. Действительно, угловая скорость и угловое ускорение звена А В уже известны: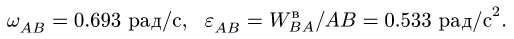

Рассматривая А в качестве полюса (рис. 99), записываем векторное уравнение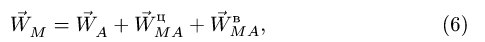

где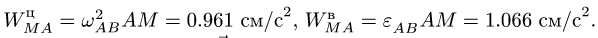 Из (6) определяем проекции 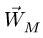на оси координат:

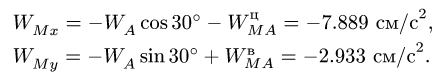
Величина ускорения точки M

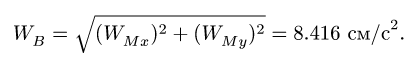
Находим ускорение точки С. Скорости точек В я С звена ВС, совершающего мгновенно – поступательное движение, равны, однако, их ускорения различны.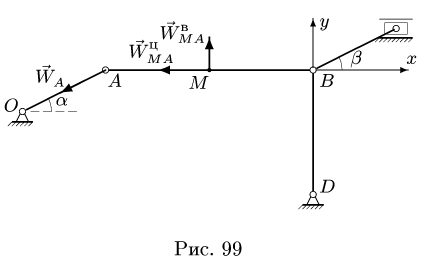

Для определения 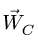воспользуемся векторным равенством (полюс — точка В)

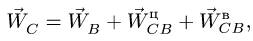
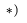В качестве полюса можно также брать точку В, ускорение которой уже найдено.

где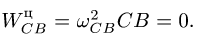 Вектор 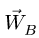раскладываем на составляющие (рис. 100)

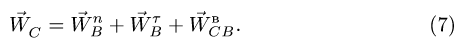
Векторное уравнение (7) содержит две неизвестных величины: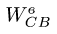и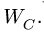 Записывая (7) в проекциях на оси ху, получаем систему двух уравнений с двумя неизвестными. Но можно решить задачу проще.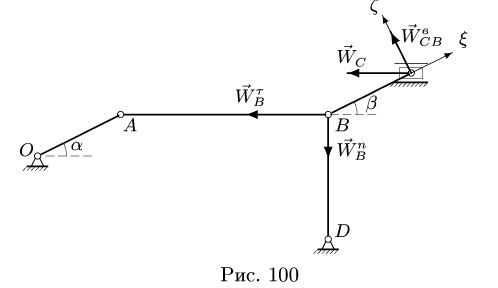
Спроецируем (7) на ось 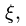 направленную вдоль стержня ВС. При этом в уравнение не войдет модуль неизвестного вектора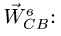 

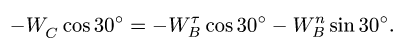
Находим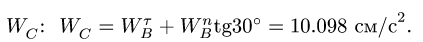

Результаты расчетов помещаем в таблицу (скорости в см/с, ускорения в см/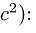

8.3. Уравнение трех угловых скоростей

Постановка задачи. Подобрать длины звеньев шарнирного четырехзвенника так, чтобы в некоторый момент движения угловые скорости его звеньев были бы равны заданным. Положение опорных шарниров четырехзвенника известно.

План решения:

Под угловыми скоростями будем понимать проекции соответствующих векторов на ось 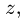перпендикулярную плоскости движения. Индекс 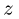дополнительно указывать не будем, принимая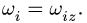

1. Последовательно нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начало в один из шарниров механизма. Определяем координаты шарниров.

2.    Записываем уравнения трех угловых скоростей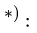

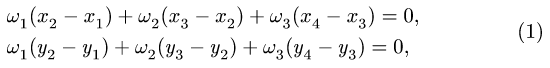
где 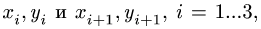— координаты шарниров на концах звена, имеющего угловую скорость  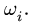Шарниры 1 и 4 — опорные. Все угловые скорости и некоторые координаты даны в условии.

3.    Решаем систему (1) относительно неизвестных координат. Определяем длины звеньев механизма (расстояния между шарнирами) по формулам

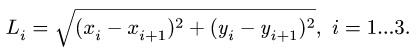
Задача №3

В положении, изображенном на рис. 101, известны угловые скорости шарнирного четырехзвенника О ABC: 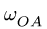= 2 рад/с, 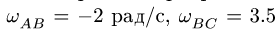рад/с. Найти длины звеньев OA и ВС, 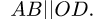. Расстояния даны в см, АВ = 60 см.

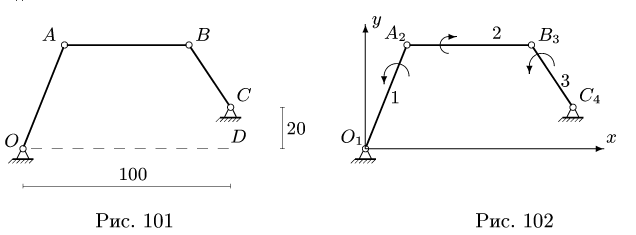
Решение

1.    Последовательно нумеруем шарниры и звенья механизма. Номера шарниров указываем индексами у соответствующих букв. Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров (рис. 102):

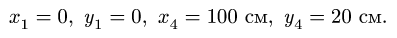
2.    Записываем уравнения трех угловых скоростей (1), где по условию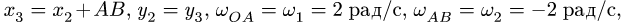

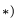Уравнения следуют из координатной формы записи векторной формулы (1), на с. 130, для скоростей точек при плоском движении.

8.3. Уравнение трех угловых скоростей

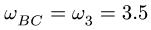рад/с. Система приобретает вид

3. Решаем систему (2) относительно 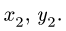Получаем

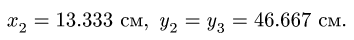
Кроме того, 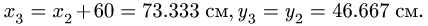Определяем длины звеньев: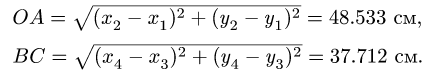

Уравнение трех угловых ускорений

Постановка задачи. Многозвенный механизм приводится в движение кривошипом, вращающимся с известной угловой скоростью и известным угловым ускорением. Найти угловые скорости и угловые ускорения звеньев механизма.

План решения:

Под угловыми скоростями и ускорениями будем понимать проекции соответствующих векторов на ось 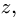перпендикулярную плоскости движения. Индекс  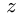дополнительно указывать не будем, принимая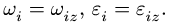

1.    Нумеруем шарниры и звенья механизма. Выбираем систему координат, помещая ее начато в один из шарниров механизма. Определяем координаты шарниров.

2.    Выделяем из механизма шарнирные четырехзвенники. Рассмотрим четырехзвенник, шарниры которого последовательно обозначены номерами 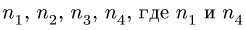— номера неподвижных

Гл. 8. Плоское движение тела

шарниров. Стержни четырехзвенника имеют номера 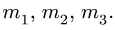Записываем уравнения трех угловых скоростей:

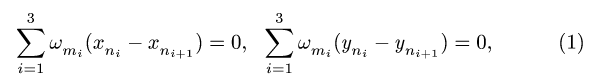
где 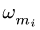( — угловая скорость 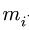-го  звена, 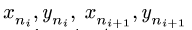— координаты его концов. Номера шарниров 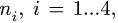как и номера звеньев 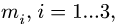не обязательно должны быть последовательными числами.

3.    Из решения (1) получаем все угловые скорости механизма.

4.    Записываем уравнения трех угловых ускорений для каждого четырехзвенника *) :

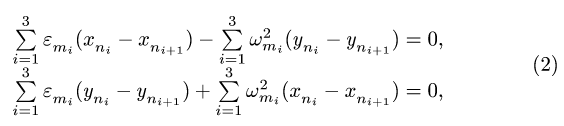
где 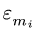— угловое ускорение 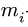-го звена.

5.    Решаем (2) относительно неизвестных угловых ускорений.

Задача №4

Многозвенный механизм приводится в движение кривошипом OA, вращающимся с угловой скоростью 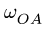= 1 рад/с и угловым ускорением 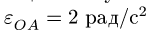(рис. 103).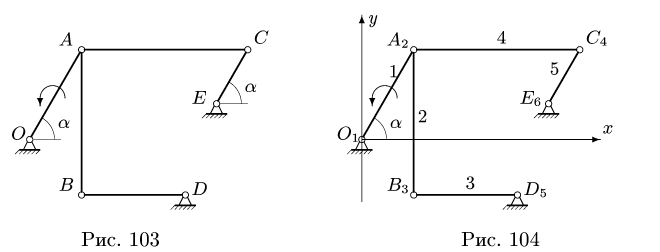
Дано: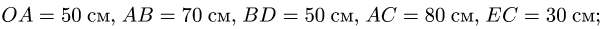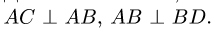Найти угловые скорости и угловые ускорения звеньев механизма.

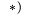Уравнения следуют из координатной формы записи векторной формулы (4), на с. 130, для ускорений точек при плоском движении.

8.4. Уравнение трех угловых ускорений

Решение

1. Нумеруем шарниры и звенья механизма (рис. 104). Выбираем систему координат, помещая ее начало в шарнир О. Определяем координаты шарниров:

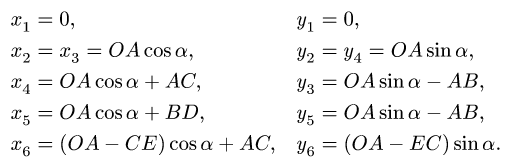
2. Выделяем из механизма шарнирные четырехзвенники (рис. 105, 106). Записываем уравнения трех угловых скоростей для четырехзвенника OABD (рис. 105),

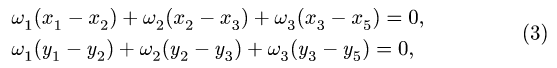
и для четырехзвенника О АСЕ (рис. 106),

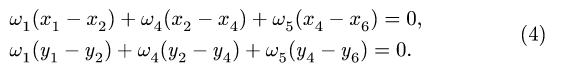
(4)
3. Решаем систему четырех линейных уравнений (3), (4). Получаем угловые скорости звеньев: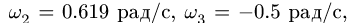 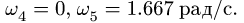Из решения следует, что звено АС движется мгновенно-поступательно. Этот результат очевиден. Его можно было получить сразу из условия задачи, не решая ее. Действительно,  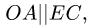следовательно, векторы скоростей шарниров А и С также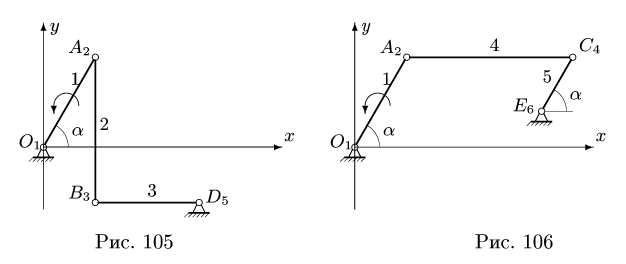

параллельны и но перпендикулярны АС. Мгновенного центра скоростей звена АС не существует (расположен в “бесконечности”), что соответствует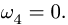

4. Записываем уравнения трех угловых ускорений для четырех-звенника OABD (рис. 105),

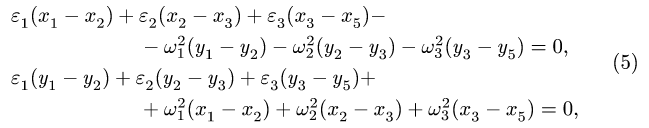
и для четырехзвенника ОАСЕ (рис. 106),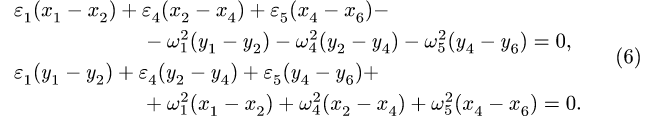
5. Из решения (5,6) получаем угловые ускорения: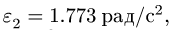

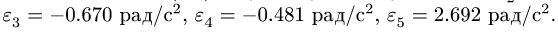
Кинематические уравнения плоского движения

Постановка задачи. Составить кинематические уравнения плоского многозвенного механизма.

План решения:

1. Составляем кинематические графы механизма, выбирая наиболее короткие маршруты. Началом и концом графа должна быть точка с известной скоростью. Кинематические графы должны включать в себя все звенья механизма. Некоторые звенья могут входить в разные графы. Обозначения для графов приведены на с. 130.

8.5. Кинематические уравнения плоского движения

2.    Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа. Получаем систему дифференциальных уравнений.

3.    Упрощаем систему уравнений, используя уравнения связей и тригонометрические формулы приведения.

Задача №5

Механизм состоит из стержней OA, АВ, CD и ползунов С и D. Ползун D движется вверх со скоростью 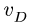(рис. 107); BD = ВС. Составить кинематические уравнения механизма.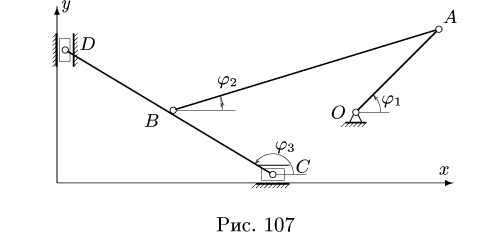
Решение

1.    Составляем кинематические графы:

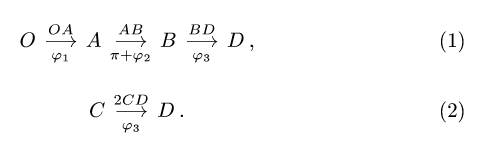
2.    Записываем для каждого графа (1), (2) по два кинематических уравнения в проекциях на оси координат:

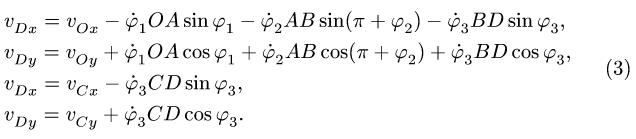
3.    Упрощаем систему (3), используя уравнения связей,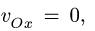 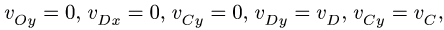и тригонометрические

Гл. 8. Плоское движение тела

формулы приведения:

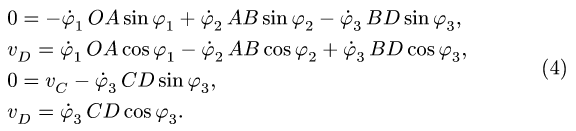
Задача №6

Плоский манипулятор состоит из жесткой детали ОАВ, стержней ВС, AM, колеса С и захвата М. Даны длины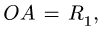 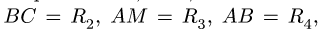и скорость захвата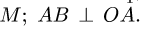

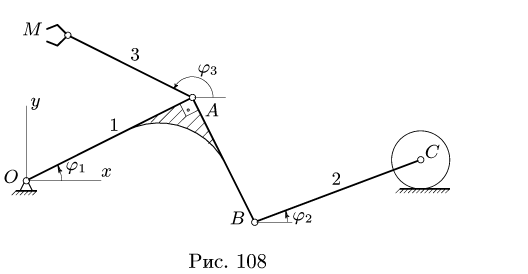
Составить кинематические уравнения манипулятора . Решение

1.    Составляем кинематические графы:

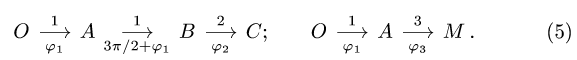
2.    Записываем по два кинематических уравнения в проекциях на оси координат для каждого графа (5):

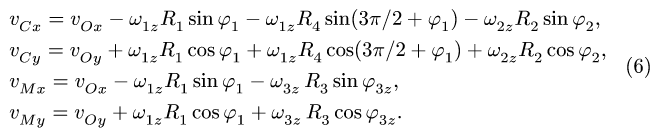
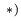Задание K-3 из сборника [15]. В задании К-3 скорость точки М определяется из решения дифференциального уравнения так, чтобы манипулятор захватил деталь, движущуюся по известному закону. В рассматриваемом примере задача захвата не решается, а предполагается, что скорость М известна из других соображений, в том числе из условия захвата детали.

8.5. Кинематические уравнения плоского движения

3. Упрощаем систему (6), используя уравнения связей,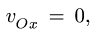 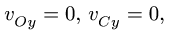 и тригонометрические формулы приведения:

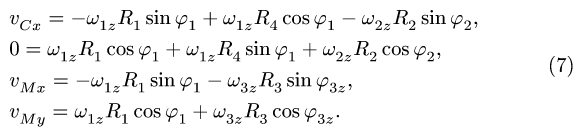
Замечание 1. В данной задаче скорости точек механизма можно найти для некоторого промежутка времени, а не для фиксированного момента времени, как в аналогичных задачах § 8.1, § 8.3. Решая нелинейную систему дифференциальных уравнений (4), получаем полную картину движения механизма . Для решения системы (4) необходимо дополнить ее начальными условиями:

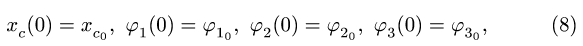
где константы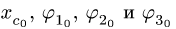 и определяют начальную конфигурацию механизма. В некоторых численных методах для решения систему (4) требуется привести к форме Коши. Уравнения (4) представляют собой систему четырех алгебраических уравнений относительно 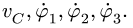Решая систему, получаем, что

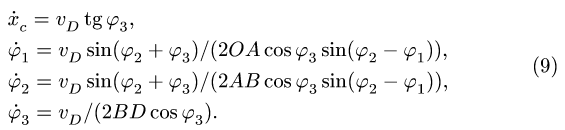
Замечание 2. В решении задачи следует использовать наиболее короткие графы. В данном случае вместо графа (2) можно было бы выбрать граф

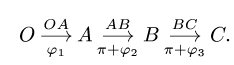
Система дифференциальных уравнений изменится, однако в форме Коши ее вид останется прежним.
На странице Интернет кафедры теоретической механики МЭИ www.termech.mpei.ac.ru можно найти обучающую программу ROBBY2, разработанную Осадченко Н.В. и Корецким А.В. Программа интегрирует уравнения (4), составленные- для задач из сборника [15], анимирует полученное решение и представляет результаты в виде графиков и таблиц.

Замечание 3. Метод графов широко используется для решения задач кинематики и динамики. Примеры составления графов представлены также на с. 243, 244 310, 313, 316, 327, 329.

Замечание 4. Для того, чтобы проинтегрировать полученные кинематические уравнения, необходимо скорости ползунов выразить через соответствующие координаты, например, 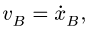 задать одну из пяти функций, входящих в уравнения, и выбрать для остальных функций начальные условия.

Предупреждение типичных ошибок:

1. Кинематические графы являются ориентированными графами. Меняя направление маршрута, меняйте и угол. Следующие два графа
2. эквивалентны:
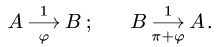
3. Угловая скорость звена, которому принадлежат точки А и В графа 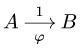, не обязательно равна 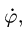см., например, с. 243.

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ГОРОДА КЕРЧИ РЕСПУБЛИКИ КРЫМ «ШКОЛА-ГИМНАЗИЯ №1»

Приемы решения задач с использованием кинематических связей

Подборка задач с примерами решений

Учитель физики Ксенофонтова Л. В.

Приемы решения задач с использованием  кинематических связей

Кинематическими связями называют определенные ограничения свободы передвижения тела или системы тел.

Рассматривая задачи, где такие связи есть, будем придерживаться следующих идей:

1. Идея первая

Известно из определения, что у твердого тела расстояние между любыми двумя его точками сохраняется в случае движения этого тела (жесткий стержень, натянутая нить А это значит, что с какой скоростью первая точка при движении тела удаляется от второй , с такой же скоростью вторая точка приближается к первой. Следовательно, проекции этих скоростей на линию, соединяющую данные точки, должны быть одинаковыми. Иначе твердое тело деформировалось бы.

Пусть таким  твердым телом будет жесткий стержень или натянутая нить. Тогда

1. Идея вторая: использование мгновенного центра вращения. 

Что подразумевает переход в такую систему отсчета, в которой есть неподвижная в данный момент времени точка, относительно которой все остальные точки твердого тела движутся. Тогда проектируя скорость точки С и точки В на прямую СВ получаем уравнение вида:

то есть при движении твердого тела скорости всех его точек направлены перпендикулярно прямым, которые  соединяют точки с мгновенным центром вращения. Фактически тело проворачивается возле мгновенного центра.

Местоположение мгновенного центра вращения можно находить двумя способами:

1. если известны скорости двух точек твердого тела и эти скорости не параллельны, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С  – неподвижна, она является центром вращения, ВС и АС – радиусы окружностей, по которым

вращаются соответственно точки А и В. Скорости υ1 и υ2 перпендикулярны радиусам.

 

1. Так как тело проворачивается возле мгновенного центра, то  это означает, что у всех его точек одинаковая угловая скорость. А так как линейная скорость связана с угловой соотношением

то следует пропорция: во сколько раз больше расстояние между данной точкой и мгновенным центром, во столько раз больше ее линейная скорость. Поэтому в случае параллельных скоростей  мгновенный центр вращения можно находить через пропорцию скоростей и расстояний.

1. Идея третья

Если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине и по направлению.

1. Идея четвертая

Если при движении одного тела по поверхности другого есть проскальзывание, то проекции скоростей соприкасающихся точек на перпендикуляр, восстановленный к этим двум поверхностям, должны быть одинаковы: по оси Y тела должны двигаться только совместно, иначе будет наблюдаться отрыв одного тела от другого.

                 Задача 1

Стержень длиной L шарнирно соединён с муфтами А и В, которые перемещаются по двум взаимно перпендикулярным рейкам. Муфта А движется с постоянной скоростью υ1. Найдите зависимость скорости муфты В от угла α.

Использование первой идеи для решения данной  задачи: проекции скоростей точек А и В на линию АВ должны быть одинаковыми.

Понятно, что точка В скользит вниз, в то время как точка А движется в горизонтальном направлении. Обозначенные на чертеже углы равны как углы, образованные взаимно перпендикулярными сторонами.

Тогда

 

Применение второй идеи для решения данной задачи: использование мгновенного центра вращения.

Представим, что палочка – это элемент, видимая линия, проведенная на большом твердом прозрачном теле. Так как известны скорости двух точек твердого тела, точек А и В,  и эти скорости не параллельны, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С –  мгновенный центр вращения, вокруг которой точка А вращается по окружности радиуса СА, а точка

В вращается по окружности, радиусом ВС. Угловые скорости этих точек равны. Поэтому можно записать:

Еще один способ решения данной задачи:  переход в другую систему отсчета.

Перейдем  в систему отсчета, которая движется вправо со скоростью V0. (Для перехода от скорости каждой точки надо отнять скорость V0)

Тогда точка А неподвижна, а стенка, и вместе с ней точка В, движется влево со скоростью V0. А так как длина палочки ℓ постоянна, то точка В движется по окружности с линейной скоростью u, которая перпендикулярна радиусу окружности  ℓ. Из треугольника скоростей следует:

Задача 2

Палочка АВ длины ℓ движется в плоскости чертежа так, что в данный момент времени скорость её конца А направлена под углом α, а скорость конца В — под углом β к палочке. Величина скорости конца А равна υ. Определить величину скорости u конца В. Начертить распределение скоростей вдоль палочки.

На основании первой идеи можно утверждать, что проекции скоростей точек А и В на линию АВ одинаковы. А значит, можно записать:

Скорость точки А и точки В можно разложить на составляющие вдоль палочки и перпендикулярно ей. Тогда движение палочки можно представить как два движения: каждая точка палочки движется поступательно со скоростью u∙Cos β  и палочка совершает вращательное движение вокруг точки С. Скорости, перпендикулярные палочке –это линейные скорости. Их величина уменьшается при приближении к точке С. И у точки С только скорость поступательного движения.

Второй способ решения состоит в том, что движение полочки можно рассмотреть только как вращательное движение возле мгновенного центра вращения. Для нахождения мгновенного центра вращения точки С проведем перпендикуляры в точку А к скорости u и в точку В к скорости υ. Все точки палочки имеют одинаковую угловую скорость, но линейные скорости у них разные. Чем меньше радиус окружности, по которым они двигаются возле точки С, тем меньше их линейная скорость. То есть для любой точке выполняется υ ~ r и υ ⊥ r

Задача 3

Лодку подтягивают к крутому  берегу высотой h = 3 м с помощью верёвки, выбирая её со скоростью 60 см/с. С какой скоростью двигалась лодка в тот момент, когда верёвка составляла  с горизонтом угол 600? Найти также ускорение лодки в этот момент.

   

На основании первой идеи проекции скорости υ и скорости υ0 на нерастяжимую веревку должны быть одинаковыми.

Задача 4

Рабочие поднимают груз с помощью двух канатов, за концы которых они тянут с одинаковыми скоростями υ. Какую скорость u имеет груз в тот момент, когда угол между канатами, к которым он прикреплён, равен 2α

На основании первой идеи можно утверждать, что проекции скоростей точек А и В на линию АВ одинаковы. Но точка В движется со скоростью υ, так как с этой скоростью движется конец каната. Значит, и точка А движется с этой же скоростью. Аналогично для второго каната: точка А движется вдоль него со скоростью υ.

Казалось бы, что результирующую скорость точки А можно найти, складывая два вектора υ по правилу параллелограмма…

Но этого делать нельзя! Так как в этом случае, если бы α был равен нулю (α=0), тот канаты были бы параллельны, и груз бы двигался со скоростью 2υ. А последнее, при наличии неподвижных блоков, невозможно.

Скорость U такова, что скорости υ являются ее проекциями на канаты. С учетом этого, можно записать:

Задача 5

Тяжёлый ящик перемещают с помощью двух тракторов, движущихся со скоростями υ1 и υ2, составляющими угол α. Как направлена и чему равна скорость ящика в тот момент, когда канаты параллельны векторам υ1 и υ2? 

Понятно, что точка А имеет скорость υ1 вдоль первого каната и скорость  υ2 направленную вдоль второго каната. Но, так же, как и в предыдущей задаче, находить результирующую скорость ящика, складывая выше упомянутые скорости по правилу параллелограмма нельзя. В этом случае, если угол α=0, то ящик должен двигаться со скоростью υ1+ υ1, а это противоречить здравому смыслу.

Следовательно, у результирующей скорости проекции на канаты должны быть равны υ1и υ2. Проводим перпендикуляры из концов этих векторов и в  их пересечение утыкается конец результирующей скорости υ, с которой движется ящик. Теперь, зная υ1 и υ, а так же угол между ними надо найти скорость υ. Это геометрическая задача

Точки А, D, С и В лежат на одной окружности и в этой окружности результирующая скорость υ – диаметр. Эта окружность описана возле  треугольника АВD, в котором известны две стороны  υ1 и υ2, и угол между ними. Тогда по теореме косинусов можно определить сторону ВD:

Известно, что диаметр описанной окружности равен:

Задача 6

Колечки О и О’ надеты на вертикально закреплённые стержни АВ и А’В’. Нерастяжимая нить привязана к кольцу О, пропущена через кольцо О’ и закреплена в точке А’. В тот момент, когда угол AOO’ = α, кольцо О’ движется вниз со скоростью υ. Найти скорость u0 кольца О в этот момент.

Так как в колечке О’ нитка преломляется, то использовать первую идею о том, что проекции скорости точки О’ и скорости точки О (проекции скоростей υ и u) на нить О’О  равны, нельзя.

Используем следующий способ решения:  переход в другую систему отсчета.

Перейдем в СО, которая движется со скоростью υ вниз ( то есть, от каждой скорости вычитаем скорость υ). В такой системе отсчета колечко О’ останавливается, оно неподвижно, а со скоростью υ в точке А’ вытягиваем веревку. Тогда веревка в точке О так же движется со скоростью υ.

Теперь надо перейти в СО, связанную с землей (надо ко всем скоростям теперь прибавить скорость υ, направленную вниз)

Задача 7

Один конец шарнирной конструкции из двух одинаковых звеньев длины 2ℓ закреплён, а другой движется с постоянной скоростью υ по прямой, расстояние до которой от неподвижного конца конструкции равно 3ℓ. Найдите ускорение шарнира в тот момент, когда: 1) левое звено горизонтально, 2) скорость шарнира равна нулю.

1). Так как левый конец звена конструкции закреплен в точке О, то шарнир А будет двигаться по окружности радиуса R=2ℓ и в любой момент времени вектор его скорости будет перпендикулярен ОА. В интересующий нас  момент времени, когда левое звено ОА горизонтально, скорость шарнира А направлена вверх. И конец правого звена, точка 2,  также имеет вертикально направленную скорость υ0 

На основании первой идеи, из-за  не растяжимости правого звена, можно утверждать, что проекции скоростей υ и υ0  на правое звено (то есть вдоль оси у),  равны.  

   

Но это равенство скоростей имеет место только для данного момента времени.    

Центростремительное ускорение шарнира А может быть определено по формуле:

И направлено это ускорение вдоль левого звена, то есть по оси х. Но так как скорость шарнира А меняется по величине, а не только по направлению, есть и тангенциальное (касательное) ускорение. Согласно условию, надо найти полное ускорение шарнира А.

 Используем переход в другую систему отсчета, которая движется вверх со скоростью υ вместе с правым концом правого звена (от каждой скорости надо вычитать υ, направленную вверх). Тогда, в этой системе отсчета, точка О движется вниз со скоростью υ, а шарнир  А неподвижен. Поэтому вектор его ускорения может быть лишь перпендикулярен правому звену.

Вектор полного ускорения шарнира будет точно таким же и в неподвижной системе отсчета. Проекция вектора полного   ускорения   шарнира   на направление левого звена  (на ось х) представляет собой центростремительное ускорение,  и равна:

Значит, вектор полного ускорения шарнира в момент времени, когда левое звено горизонтально, будет равен:

2). В момент времени, когда скорость шарнира А равна нулю, правое звено будет горизонтально. А вектор ускорения шарнира будет перпендикулярен неподвижному левому звену (рис. б).

Составляющая ускорения  шарнира на правое звено будет равна

Таким образом,

                                                                                    Задача 8

Два стержня длины L соединены шарнирно. Свободный конец одного из стержней шарнирно прикреплён к стене, а свободный конец другого стержня двигают перпендикулярно стене с постоянной по величине скоростью υ0. Найти величину и направление вектора ускорения шарнира, соединяющего стержни, в момент, когда угол между стержнями равен 2а.

У левой палочки ее правый конец  движется со скоростью υ, которая перпендикулярно этой палочке. У правой палочки по условию скорость υ0 направлена горизонтально.

На основании первой идеи, из-за  не растяжимости стороны АВ, можно утверждать, что проекции скоростей υ и υ0  на АВ равны.  

Известно, что

Тогда    

Определяем проекции ускорения на координатные оси. На ось х:

Чтобы найти проекцию ускорения на вторую ось, перейдем в СО, которая движется вправо со скоростью υ0.Тогда точка В неподвижна, а стенка  движется влево со скоростью υ0. И для точки А  составляем треугольник скоростей. И в этой системе вектор ускорения шарнира будет перпендикулярен неподвижному левому звену

Задача 9

На неподвижном клине, образующем угол α с горизонтом, лежит груз, прикреплённый к стене перекинутой через закреплённый на клине блок нерастяжимой нитью. В некоторый момент времени клин начинает двигаться вправо с постоянной скоростью υ. С какой скоростью движется груз, пока он находится на клине?

Предположим, что клин движется вправо со скоростью υ. При этом надо понимать, что расстояние между точками А и В все время меняется, несмотря на то, что веревка нерастяжима. Меняется потому, что есть перегиб на блоке. Перейдем в систему отсчета, которая движется вправо со скоростью υ. В этой системе клин неподвижен, а стенка уходит вправо со скоростью υ. Тогда очевидно, что по неподвижному клину груз может двигаться только вдоль наклонной плоскости, то есть вдоль веревки со скоростью υ. Скорость груза относительно земли, согласно классическому закону сложения скоростей равна:

В этом треугольнике скоростей ( см. рис.)      

Определим результирующую скорость по теореме косинусов:

Задача 10

Нитку тянут со скоростью υ0. Найдите угловую скорость катушки и скорость её центра. Катушка по столу и нитка по катушке не проскальзывают. Внутренний радиус катушки r, внешний — R.

На основании второй идеи, используя понятие мгновенного центра вращения, можно утверждать, что результирующая скорость точки А равно 0, то есть точка А  – это мгновенный центр вращения. Следовательно, все остальные точки катушки проворачиваются возле точки А с одинаковой угловой скоростью, но линейная скорость у них разная, так как разный радиус вращения. Угловая скорость точки С равна:

Угловая скорость точки O равна:

Задача 11

Точка А, лежащая на пересечении рельса с внешним ободом колеса поезда, движется в данный момент времени со скоростью и =5,0 м/с (см. рис). Определить, с какой скоростью и в каком направлении движется поезд, если r = 50 см, R = 56 см.

Скорость реборды u, заданная по условию, является результирующей скоростью двух скоростей: скорости поступательного движения  υпоступ  и линейной скорости υкасат  вращательного движения вокруг точки О. Так как точка А лежит на ободе реборды, эти две скорости численно равны.

Используя вторую идею, можно считать точку С мгновенным центром вращения. Тогда скорость u будет линейной скорость точки А, вращающейся вокруг тоски С, а скорость поступательного движения так же будет линейной скоростью для точки О вращающейся вокруг точки С. И у точки А, и у точки О в этом случае будет одна и та же угловая скорость.

Следовательно, можно записать:

Задача 12

Кривошип ОА, вращаясь с угловой скоростью ω, приводит в движение колесо радиуса r, катящееся по неподвижному колесу радиуса R = 3r. Найдите скорость точки В.

Точка С принадлежит всем трем телам: колесу радиусом R, колесу радиусом r, и кривошипу ОА. И скорость точки А такая же, как у кривошипа, вращающегося относительно точки О с угловой скоростью ω. То есть его точка А движется с линейной скоростью, равной:

На основании второй идеи, можно считать точку С мгновенным центром вращения для колеса радиусом r. Тогда точки А и В проворачиваются относительно точки С с одинаковой угловой скоростью:

Задача 13

Тяжёлый диск радиуса R скатывается на двух не растяжимых нитях, намотанных на него. Свободные концы нитей закреплены. Нити при движении диска постоянно натянуты. В некоторый момент угловая скорость диска равна ω, а угол между нитями α. Какова в этот момент скорость центра диска? 

 Нить касается диска в точке А. Тогда, согласно третьей идеи, если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине и по направлению. Величина этой скорости

Нить АА1 натянута, это значит, на основании первой идеи, что проекции скоростей точек А и А1 на нить должны быть равными. Но точка А1 неподвижна и нет у нее проекции на нить, значит не должно быть проекции и скорости в точке А. А это возможно только в том случае, если υА перпендикулярна нити.

Аналогично и для второй нити, то есть υВ перпендикулярно нити ВВ1

Значит, скорости  υА  и υВ направлены по радиусу диска. И после этого про нити можно забыть есть диск, две точки на нем А и В, и скорости в этих точках имеют радиальные направления.

Согласно второй идее о мгновенном центре вращения, если скорости двух точек твердого тела и эти скорости не параллельны, а образуют некоторый угол α, то мгновенный центр вращения лежит на пересечении перпендикуляров, проведенным к этим скоростям. Точка С  – неподвижна, она является центром вращения, ВС и АС – радиусы окружностей, по которым вращаются соответственно точки А и В. Скорости υА и υВ перпендикулярны радиусам. В четырехугольнике угол ОАВ равен углу между нитями α как углы, образованные взаимно перпендикулярными сторонами. В этот момент скорость центра диска, то есть скорость точки О равна:

Задача 14

Цилиндр с намотанной на него нитью, второй конец которой закреплён, находится на горизонтальной подставке, движущейся поступательно с постоянной горизонтальной скоростью V. Найти скорость оси цилиндра в зависимости от угла α, образуемого нитью с вертикалью. Относительно подставки цилиндр не проскальзывает.

Точка С – точка соприкосновения цилиндра с подставкой. Третья идея заключается в том, что если одно тело катится по поверхности другого без проскальзывания, то в точках их соприкосновения и них одинаковая линейная скорость и по величине,  и по направлению. Раз подставка движется со скоростью V. то и у точки С такая же скорость. И про доску можно забыть. То есть рассматриваем цилиндр с намотанной на него нитью. Нить касается цилиндра в точке А. В этой точке, так же как в точке С качение без проскальзывания, а это снова означает, что скорость этой точки нити равно скорости этой точки диска. Нить не растяжима,  на основании первой идеи, проекции скоростей точек А и В на нить должны быть равными. Но точка В неподвижна и нет у нее проекции на нить, значит не должно быть проекции и скорости в точке А. Это возможно только в том случае, если υА перпендикулярна нити.

Определим положение мгновенного центра вращения: он лежит на пересечении перпендикуляров ОС и ОА, проведенным к скоростям υА и υС. Мгновенным центром вращения является точка О. Ось цилиндра описывает вокруг мгновенного центра вращения окружность радиусом R1 

У оси цилиндра и точки С одинаковые угловые скорости ω относительно мгновенного центра вращения.

Но точка С описывает вокруг точки О окружность радиусом (R1 +R) 

Задачи для самостоятельного решения

1. Концы А и В стержня АВ скользят по сторонам прямого угла. Как зависит от угла α скорость υ и ускорение а середины стержня, если конец В движется с постоянной скоростью. Длина стержня равна L.
2. Нерастяжимая нить длины L соединяет две бусинки А и В. Бусинку В передвигают с постоянной скоростью υ0  по прямой спице МО. В результате этого бусинка А движется по спице CD, изогнутой в виде дуги окружности радиуса   Найти ускорение бусинки А в тот момент, когда бусинка В будет на расстоянии L от точки О.
3. Два стержня длины L соединены шарнирно. Свободный конец одного из стержней шарнирно закреплён на вертикальной стене, а свободный конец другого стержня двигают с постоянной по величине вертикальной скоростью υ0. Найти величину и направление вектора ускорения шарнира, соединяющего стержни, в момент, когда их концы окажутся на одной горизонтали, если угол между стержнями в этом момент равен 2α.

1. Два жёстких стержня длины ℓ каждый шарнирно скреплены в точке А. Стержень В А жёстко закреплён в точке В, а точка С стержня АС может скользить по направляющей ВС. Стержень ВА начинают вращать в плоскости рисунка вокруг точки В с постоянной угловой скоростью ω. Чему будут равны максимальная скорость и ускорение точки С, если в начальный момент стержни вытянуты вдоль направляющей ВС (
2. Бусинка может двигаться по кольцу радиуса R подталкиваемая спицей, равномерно вращающейся с угловой скоростью ω вокруг точки О в плоскости кольца. Определите ускорение бусинки.                          
3. Толпа муравьев тащит кусочек коры в форме равностороннего треугольника. В некоторый момент скорость вершины В равна υ и направлена вдоль АВ, а скорость вершины С направлена вдоль СВ. Найти скорости вершин А и С в этот момент.
4. По окружности радиусом R с постоянной скоростью υ бежит лошадь. На расстоянии r от центра окружности стоит человек. Чему равно максимальное значение скорости сближения лошади и человека?
5. На клине с углом α лежит монета. С каким наименьшим ускорением должен двигаться клин по горизонтальной плоскости, чтобы монета свободно падала вниз?
6. Клин, имеющий угол а, лежит на горизонтальной плоскости. Вертикальный стержень, опускающийся со скоростью υ заставляет клин скользить по этой плоскости. Какова скорость клина?
7. Две параллельные рейки движутся со скоростями υ1 и υ2. Между рейками зажат диск радиуса r, катящийся по рейкам без скольжения. Найдите угловую скорость диска и скорость его центра?
8. Катушка, зажатая между двумя параллельными досками, движущимися со скоростями υ1и υ2, катится по ним без проскальзывания. Найдите угловую скорость катушки и скорость её центра. Внутренний радиус катушки r, внешний — R.

1. Конец нити, намотанной на катушку, тянут с горизонтальной скоростью υ. С какой скоростью двигается центр катушки в тот момент, когда нить составляет угол α с горизонтом? Внешний радиус катушки R, внутренний r. Катушка по столу и нить по катушке не проскальзывают.
2. Бревно, упираясь нижним своим концом в угол между стеной и землёй, касается дна кузова грузовика на высоте Н от земли. Найдите угловую скорость бревна в зависимости от угла α между ним и горизонталью, если грузовик отъезжает от стены со скоростью υ.
3. Стержень, одним концом шарнирно закреплённый на горизонтальной плоскости, лежит на цилиндре. Угловая скорость стержня ω. Проскальзывания между цилиндром и плоскостью нет. Найдите зависимость угловой скорости цилиндра от угла α между стержнем и плоскостью

Ответы