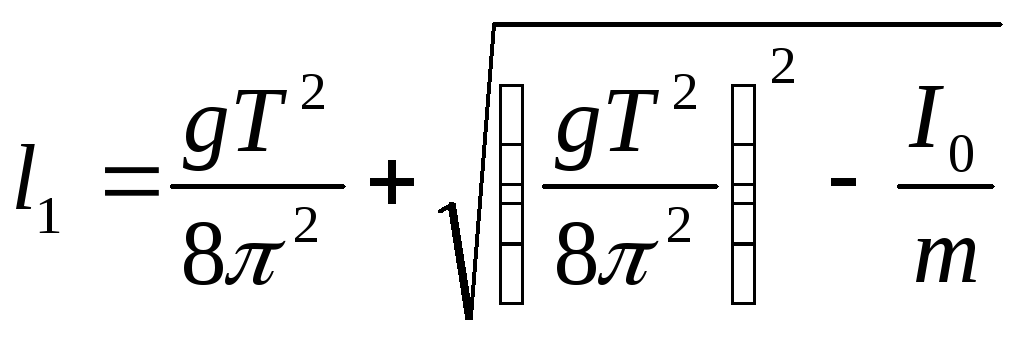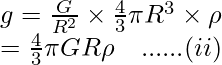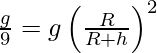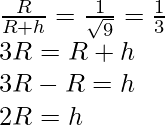Ускорение силы тяжести

3.9
Средняя оценка: 3.9
Всего получено оценок: 104.
3.9
Средняя оценка: 3.9
Всего получено оценок: 104.
Процесс изменения скорости при движении физического тела характеризуется ускорением. Ускорение силы тяжести (обозначается буквой g) возникает в результате влияния силы тяжести, которая действует на любое тело у поверхности Земли или другой планеты. Разберемся от чего зависит значение g и как его определяют.
Основные формулы для равноускоренного движения
Равноускоренное движение — самый простой вид неравномерного движения. Равноускоренным называется движение с ускорением, постоянным по модулю и направлению:
$ a = {Δvover Δt} = const $ (1),
где:
Δv — изменение скорости (“дельта v “), м/с;
Δt — промежуток времени, (“дельта t “)за которое произошло изменение скорости, с.
Из формулы (1) следует, что размерность ускорения будет выражаться в метрах на секунду в квадрате:
$ {1 м/сover 1 c} = 1 м/с^2 $ (2).
Второй закон Ньютона гласит:
$ F = m * a $ (3),
где:
F — сила, действующая на тело, Н;
m — масса тела, кг;
a — ускорение, м/с2.
Сила тяжести и ускорение свободного падения
При свободном падении на Землю все тела, независимо от их массы, движутся одинаково. Свободное движение является равноускоренным движением. Ускорение, с которым падают на Землю тела в пустоте, называется ускорением свободного падения (или ускорением силы тяжести). Условие пустоты или, что тоже самое, вакуума, требуется для исключения влияния сопротивления атмосферного воздуха. Сила притяжения Fт со стороны Земли на тело массой m, называется силой тяжести:
$ F_т = m * g $ (4),
Определением ускорения силы тяжести впервые систематически занимался Галилео Галилей — итальянский математик, физик, астроном. Будучи профессором университета в городе Пиза, Галилей измерял время падения предметов с высоты местной, слегка наклонной, башни.
.
В результате этих наблюдений он пришел к следующим выводам:
- Время падения не зависит от массы тела. Все тела падают одинаково;
- Падение тел представляет собой равноускоренное движение с ускорением $ g = 9,81{ мover c^2} $ .
И хотя это открытие датировано 1589г., современное, общепринятое среднее значение g практически не отличается от этого значения. Когда от расчетов не требуется высокой точности, то принимают, что модуль g равен 10 м/с2.
Последовавшие за Галилеем более точные измерения показали, что значение g не является абсолютной константой, а зависит от местоположения измерений в разных точках Земли. Ответ на этот вопрос нашел английский ученый Исаак Ньютон.
Закон всемирного тяготения
В 1682 г. Ньютон открыл закон всемирного тяготения, из которого следует:
- все тела притягиваются друг к другу;
- сила тяготения прямо пропорциональна произведению масс тел и обратно пропорциональна квадрату расстояния между ними;
- векторы сил тяготения направлены вдоль прямой, соединяющей тела.
Этот закон универсален, и для случая пары тел, одно из которых является произвольным телом массой m, а второй — Земля, в виде формулы выглядит так:
$ F_т = G * {{m * Mз }over {(R_з + h)^2} } $ (5),
где:
Mз — масса Земли, кг;
Rз — радиус Земли, м;
h — высота, на которой находится тело, относительно поверхности Земли, м;
G — гравитационная постоянная, равная 6,6720 * 10-11 Н*м2 * кг-2.
Из формул (4) и (5) следует, что:
$ g = G * {{ Mз }over {(R_з + h)^2 } }$ (6)
Из (6) следует, что ускорение силы тяжести будет зависеть от высоты h и величины радиуса Земли, который для обычных расчетов принимается равным примерно 6400 км. Но поскольку форма Земли не является идеальным шаром, а сплюснута к полюсам, то точные значения g будут отличаться от среднего значения в 9,81 м/с2:
- максимальное значение gмакс = 9,83 м/с2 — на полюсах Земли, где Rз меньше;
- минимальное значение gмин = 9,79 м/с2 — на экваторе Земли, где Rз больше.
Из формулы (6) также следует, что ускорение силы тяжести на других планетах, имеющих массу, отличающуюся от массы Земли, будет для космонавтов значительно отличаться от привычных земных условий. Так, например:
- На Марсе — gМарса = 3,86 м/с2;
- На Меркурии — gМеркурия = 3,7 м/с2;
- На Луне — gЛуны = 1,62 м/с2;
- На Нептуне — gНептуна = 11,0 м/с2.
Как определяют ускорение силы тяжести
Для точного измерения силы тяжести, а значит, и ускорения, используется прибор, называемый гравиметром. Прибор применяется при поиске полезных ископаемых и для сбора информации археологами, палеонтологами, гидрологами и представителями других профессий, изучающих поверхность Земли.
Следует упомянуть еще два фактора, влияющих на значение ускорения свободного падения:
- Известно, что Земля вращается вокруг своей оси, имея при этом так называемое центростремительное ускорение, которое влияет на величину ускорения свободного падения;
- Масса Земли распределена неравномерно, например, в местах расположения больших месторождений металлических руд ускорение силы тяжести будет больше, а там, где есть пустоты (газовые месторождения) ускорение будет несколько меньше.
Эти факторы дают очень малые отклонения от средних значений g , но зато их регистрация позволяет, например, геологам находить новые месторождения полезных ископаемых.
Что мы узнали?
Итак, мы узнали, что такое ускорение силы тяжести. Сила тяжести возникает вследствие действия силы гравитации, подчиняющейся закону Ньютона (формула (5)). На Земле среднее значение ускорения силы тяжести gЗемли равно 9,81 м/с2. Для точного определения ускорения силы тяжести требуется использование современных приборов, называемых гравиметрами.
Тест по теме
Доска почёта

Чтобы попасть сюда – пройдите тест.
-
Александр Коновалов
4/5
Оценка доклада
3.9
Средняя оценка: 3.9
Всего получено оценок: 104.
А какая ваша оценка?
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.
| Земля | 9,81 м/с2 | 1,00 g | Солнце | 273,1 м/с2 | 27,85 g |
| Луна | 1,62 м/с2 | 0,165 g | Меркурий | 3,70 м/с2 | 0,378 g |
| Венера | 8,88 м/с2 | 0,906 g | Марс | 3,86 м/с2 | 0,394 g |
| Юпитер | 24,79 м/с2 | 2,528 g | Сатурн | 10,44 м/с2 | 1,065 g |
| Уран | 8,86 м/с2 | 0,903 g | Нептун | 11,09 м/с2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Физическая сущность[править | править код]
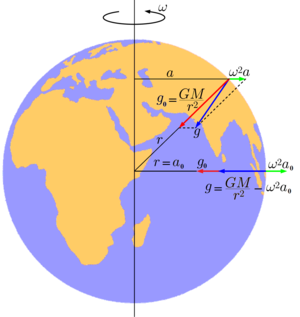
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центростремительное ускорение[править | править код]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
Ускоре́ние свобо́дного паде́ния g (обычно произносится как «Жэ» или «Жи»), — ускорение, сообщаемое телу под действием притяжения планеты или другого астрономического тела в безвоздушном пространстве — вакууме. Его значение для Земли обычно принимают равным 9,8 или 10 м/с². Стандартное (“нормальное”) значение, принятое при построении систем единиц, g = 9,80665 м/с², а в технических расчетах обычно принимают g = 9,81 м/с².
| Луна | 1,62 | Сатурн | 9,74 |
| Меркурий | 3,68 — 3,74 | Земля | 9,81 |
| Марс | 3,86 | Нептун | 11,0 |
| Уран | 7,51 | Юпитер | 23,95 |
| Венера | 8,88 | Солнце | 273,1 |
Значение g было определено как «среднее» в каком-то смысле ускорение свободного падения на Земле, примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
Реальное ускорение свободного падения на поверхности Земли зависит от широты и варьируется от 9,780 м/с² на экваторе до 9,832 м/с² на полюсах[1]. Оно может быть вычислено по эмпирической формуле:
- g = 9,780327(1 + 0,0053024sin2(φ) − 0,0000058sin2(2φ)),
где φ — широта рассматриваемого места.[2]
Содержание
- 1 Вычисление ускорения свободного падения
- 2 Перегрузки
- 3 Примечания
- 4 Литература
Вычисление ускорения свободного падения
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9.8066 | 20 | 9.7452 |
| 1 | 9.8036 | 50 | 9.6542 |
| 2 | 9.8005 | 80 | 9.5644 |
| 3 | 9.7974 | 100 | 9.505 |
| 4 | 9.7943 | 120 | 9.447 |
| 5 | 9.7912 | 500 | 8.45 |
| 6 | 9.7882 | 1000 | 7.36 |
| 8 | 9.7820 | 10 000 | 1.50 |
| 10 | 9.7759 | 50 000 | 0.125 |
| 15 | 9.7605 | 400 000 | 0.0025 |
Ускорение свободного падения состоит из двух слагаемых: гравитационного ускорения и центростремительного ускорения.
Значение гравитационного ускорения на поверхности планеты можно приблизительно подсчитать, представив планету точечной массой M, и вычислив гравитационное ускорение на расстоянии её радиуса R:
,
где G — гравитационная постоянная (6,6742×10-11 м3с-2кг-1).
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли, мы получим
м/с²
Полученное значение приблизительно совпадает с ускорением свободного падения. Отличия обусловлены:
- центростремительным ускорением в системе отсчёта, связанной с вращающейся Землёй;
- неточностью формулы из-за того, что масса планеты распределена по объёму, который, кроме того, имеет нешарообразную форму(см. геоид);
- неоднородностью Земли, что используется для поиска полезных ископаемых по гравитационным аномалиям;
| Город | Географические координаты (по Гринвичу) | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 | |
|---|---|---|---|---|
| Долгота | Широта | |||
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80112 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 655 | 9,79981 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Исторически масса Земли была впервые определена Генри Кавендишем, исходя из известного ускорения свободного падения и радиуса Земли, и впервые измеренной им гравитационной постоянной.
Перегрузки
Термин жэ используется в космонавтике и авиации для обозначения перегрузок — увеличения веса тела, вызванного его ускоренным движением. Допустимое значение перегрузок для гражданских самолетов составляет 4,33 жи. Обычный человек может выдерживать перегрузки до 5 g. Тренированные пилоты в антиперегрузочных костюмах могут переносить перегрузки до 9 g. Сопротивляемость к отрицательным, направленным вверх перегрузкам, значительно ниже. Обычно при 2-3 g в глазах «краснеет» и человек теряет сознание из-за прилива крови к голове.
В этом вопросе существует небольшая терминологическая путаница: к примеру, определение перегрузки выше даёт для стоящего неподвижно человека перегрузку в 0g, но в таблице ниже этот же случай рассматривается как перегрузка в 1g. Похожий казус происходит при измерении давления: мы говорим – давление 0, подразумевая давление в одну атмосферу вокруг нас, учёный скажет – давление 0, подразумевая полное отсутствие молекул в данном объёме.
| Человек, стоящий неподвижно | 1 g |
| Пассажир в самолете при взлете | 1,5 g |
| Парашютист при приземлении со скоростью 6 м/с | 1,8 g |
| Парашютист при раскрытии парашюта (при изменении скорости от 60 до 5 м/с) | 5,0 g |
| Космонавты при спуске в космическом корабле «Союз» | до 3,0—4,0 g |
| Летчик при выполнении фигур высшего пилотажа | до 5 g |
| Летчик при выведении самолета из пикирования | 8,0—9 g |
| Перегрузка (длительная), соответствующая пределу физиологических возможностей человека | 8,0—10,0 g |
| Наибольшая (кратковременная) перегрузка автомобиля, при которой человеку удалось выжить[3] | 179,8 g |
Примечания
- ↑ «Свободное падение тел. Ускорение свободного падения»
- ↑ g-Extractor на сайте Physikalisch-Technische Bundesanstalt (PTB).
- ↑ Авария в предквалификации Гран-при Великобритании
Литература
- А. С. Енохович Краткий справочник по физике. — М.: «Высшая школа», 1976. — 288 с.
Wikimedia Foundation.
2010.
Кафедра общей физики ПГУ
Механическая лаборатория
Лабораторная работа № 109
Лабораторная работа № 109
ОПРЕДЕЛЕНИЕ УСКОРЕНИЯ СИЛЫ ТЯЖЕСТИ ПРИ
ПОМОЩИ УНИВЕРСАЛЬНОГО МАЯТНИКА
Принадлежности: универсальный
маятник FPM-04
Цель данной работы:
1. Изучить работу физического маятника
и связанные с ним основные понятия и
законы,
2. Экспериментально определить ускорение
силы тяжести с помощью физического
маятника,
3. Экспериментально определить момент
инерции тела относительно произвольной
оси вращения.
Введение. Физическим маятником
называется твердое тело, способное
совершать колебания вокруг некоторой
оси. Период малых колебаний физического
маятника определяется формулой
(1)
где I – момент инерции
маятника относительно оси подвеса (или
оси вращения), m – его
масса, l – расстояние
от оси подвеса до центра инерции маятника,
g – ускорение свободного
падения. В формуле (1) величину
называют приведенной длиной lпр
физического маятника, так как
математический маятник длины
будет иметь одинаковый период с данным
физическим маятником. Приведенной
длиной физического маятника называется
длина такого математического маятника,
период колебаний которого одинаков с
периодом физического маятника. Отсюда
получаем формулу для определения
ускорения силы тяжести
(2)
Период колебаний T
физического маятника можно измерить
непосредственно с помощью секундомера,
а приведенную длину lпр
непосредственно измерить нельзя. Поэтому
необходимо выразить приведенную длину
через величины, доступные прямому
измерению. По теореме Гюйгенса-Штейнера
момент инерции I
маятника относительно любой оси подвеса
равен
(3)
где I0 – момент
инерции маятника относительно оси,
параллельной оси подвеса и проходящей
через центр инерции маятника, l
– расстояние от оси подвеса до центра
инерции. Подставив (3) в формулу (1), получим
(4)
График зависимости периода колебаний
T от расстояния l
представляет кривую, имеющую минимум
(рис.1).
l рис.1
Решив уравнение
относительно l, найдем,
что в точке минимума
(5)
где а0 – радиус инерции
маятника относительно оси, проходящей
через его центр инерции. Подставив (5) в
формулу (4), получим выражение для
минимального перехода:
(6)
Таким образом: а) если маятник колеблется
относительно оси, проходящей на расстоянии
радиуса инерции а0 от
центра инерции, то период колебаний
маятника будет наименьшим из всех
возможных; б) если же ось подвеса удаляется
от
,
то период колебаний будет увеличиваться
до бесконечности при приближении оси
подвеса к центру инерции и до некоторой
конечной величины, зависящей от центра
инерции. Прямая T=const
(рис.2) пересечет кривую
в двух точках l1
и l2, т.е.
существуют такие две оси подвеса по
одну сторону от центра инерции, периоды
колебаний которых совпадают. Решая
уравнение (4), найдем, что эти оси находятся
от центра инерции на расстояниях
(7)
Сумма расстояний l1
и l2 равна
приведенной длине физического маятника
(8)
Таким образом, измерив период T
и найдя lпр
из графика, можно вычислить
ускорение силы тяжести по формуле (2).
Перемножая в (7) расстояния l1
и l2 ,
получим формулу для определения момента
инерции маятника относительно оси,
проходящей через его центр инерции
(9)
(откуда
).
Зная I0 , по
теореме Гюйгенса-Штейнера (3) можно
вычислить момент инерции I
относительно любой оси подвеса или
определить его экспериментально,
пользуясь формулой (1).
О
установки. Общий вид универсального
маятника представлен на рис.1.

универсальный включает в свой состав
штатив1, математический и физический
маятники, имеющие узлы подвеса на едином
кронштейне 2
Математический
маятник имеет бифилярный подвес,
выполненный из капроновой нити 3, на
которой подвешен груз в виде металлического
шарика 4, и устройство 5для изменения
длины подвеса маятника.
Физический
(оборотный) маятник имеет жесткий
металлический
стержень 6 с рисками черезкаждые 10 мм
для отсчета длины, две призматические
опоры два груза (для работы с оборотным
маятником, на рисунке не указаны) с
возможностью перемещения и фиксации
по всей длине стержня.
Узлы подвески
математического и физического маятников
расположены на диаметрально противоположных,
относительно вертикальной стойки,
сторонах кронштейна. С помощью фотодатчика
7 колебания маятника фиксируются и
подсчитываются блоком управления 8.
Блок электронный
включает в свой состав корпус 8,на
передней панели которого находится
электронное табло 9 и счетчика колебаний.
Управление блоком осуществляется
кнопками 10 (ПУСК и СТОП). Принцип работы
заключается в подсчете времени между
нажатием кнопки ПУСК и сигналом от
срабатывания фотодатчика, при подсчете
полных колебаний от момента пуска
таймера до нажатия кнопки СТОП
Упражнение №1 Определение ускорения
силы тяжести при помощи математического
маятника.
Измерения.
1. Установить нижний кронштейн с
фотодатчиком 7 в крайнее нижнее положение
шкалы так, чтобы плоскость кронштейна,
окрашенная в синий свет, совпадала с
одной из рисок шкалы.
2. Установить верхний кронштейн таким
образом, чтобы шарик 4 математического
маятника оказался в рабочей зоне
фотодатчика. Вращая ролик устройства
5, добиться такого положения шарика, при
котором его центральная риска будет
совпадать по высоте с риской на
фотодатчике.
3. По шкале вертикальной стойки определить
длину математического маятника. L
.
4. Нажать кнопку «СЕТЬ» блока. При этом
должно включиться табло индикации.
5. Отклонить шарик математического
маятника на угол 5-6 градусов и отпустить.
Нажать кнопку «ПУСК» на блоке. По
показанию таймера определить значение
времени 20 колебаний маятника. Нажать
кнопку «СТОП».
6. Повторить пункт 5 не менее пяти раз
Данные измерений записать в таблицу
№1.
Обработка результатов измерений.
1. По формуле
найти период колебаний математического
маятника.
2. Вычислить значение ускорения силы
тяжести
.
3. Найти среднее значение ускорения
свободного падения.
4. Оценить абсолютную погрешность
измерения ускорения свободного падения
по формуле
,
где ∆L = – погрешность
измерения длины маятника, ∆Т= –
погрешность измерения времени.
5. Окончательный результат записать в
виде
,
с указанием коэффициента доверия.
6. Определить относительную погрешность.
Таблица № 1.
|
№ |
L, |
n |
t, (с) |
T, (c) |
g (м |
(м |
|
Упражнение №2 Определение
ускорения силы тяжести при помощи
физического маятника
1. Взвешиванием на технических весах,
определить массу стержня, используемого
в качестве физического маятника.
2. При помощи кольцевых нарезок на стержне
определить его длину L
и все возможные расстояния l
от центра инерции до каждой кольцевой
метки по одну сторону от центра инерции.
3. Опустить кронштейн с фотоэлектрическим
датчиком в нижнее положение.
4. Закрепить опорную призму на стержне
так, чтобы ее ребро оказалось против
самой удаленной кольцевой метки.
5. Установить маятник-стержень опорной
призмой на вкладыше верхнего кронштейна
6. Нижний кронштейн вместе с фотоэлектрическим
датчиком переместить таким образом,
чтобы стержень маятника пересекал
оптическую ось.
7. Определить период колебаний физического
маятника. Для этого отклонить стержень
на 4-5 градусов от положения равновесия
и отпустить. Нажать клавишу «ПУСК».
После подсчета периода 10 полных колебаний
нажать «Стоп». Записать число полных
колебаний n и время
t, в течение которого
они совершаются в таблицу №2.
8. Произвести измерения периода колебаний
для всех остальных расстояний l
между центром инерции и осью подвеса
(п.п. 4-8).Данные измерений записать в
таблицу №2.
Обработка результатов измерений.
1. По формуле
найти период колебаний.
2. Вычислить момент инерции I
тела по формуле

3. На миллиметровой бумаге построить
график зависимости периода колебаний
от расстояния T =f
(l).
4. На графике провести прямую T=const
и найти l1 и
l2
(прямую следует проводить там, где ветви
кривой являются более надежными). Данные
занести в таблицу 2.
5. Найти приведенную длину физического
маятника по формуле lпр=l1+l2.
6. По формуле (2) вычислить ускорение силы
тяжести
7. Операцию, указанную в п.7 повторить
для трех значений T.
8. Найти среднее значение ускорения
свободного падения.
9. Задать коэффициент доверия р=0,95 и
вычислить погрешность по формуле
10. Окончательный результат записать в
виде
11. При аккуратном выполнении работы
относительная погрешность
не должна превышать 2%.
12. На миллиметровой бумаге построить
график зависимости момента инерции от
квадрата расстояния I
=f (l2)
.Из графика методом экстраполяции
определить момент инерции согласно
формуле (3) при l2=0.
13. Из экспериментальных данных определить
момент инерции I0
. По формуле
определить
момент инерции маятника относительно
оси, проходящей через центр инерции
тела. Сравнить эту величину с теоретически
найденной по формуле
.
14. Записать вывод о проделанной работе.
Указать теоретическое и экспериментальное
значение момента инерции, полученное
значение для ускорения свободного
падения, анализ графиков.
Таблица №1
m стержня=
|
№ |
l, (м) |
n |
t |
T, (с) |
I ,(кг∙м2) |
Таблица №2
|
№ |
T, (с) |
l1, (м) |
l2, (м) |
lпр, (м) |
g, (м/с2) |
|
|
Соседние файлы в папке Методички (мех)
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Take something in your hand and toss it down. Its speed is zero when you free it from your grip. Its pace rises as it descends. It flies faster the longer it goes. This sounds like acceleration.
Acceleration, on the other hand, implies more than just rising speed. Pick up the same object and throw it into the air vertically. It will slow down on the way up until it comes to a halt and reverses course. Acceleration may also be described as a decrease in speed. However, acceleration is more than just a change of height.
Pick up your battered object and give it one last launch. This time, toss it horizontally and see how the horizontal velocity increases as the vertical velocity decrease. This change of direction is often called acceleration since acceleration is the rate of change in velocity with time and velocity is a vector quantity. The acceleration in both of these cases was caused by gravity. Since gravity was dragging the object down, it was speeding up. Even the straight-up object is dropping — and it starts falling the moment it leaves your side. If it hadn’t been, it would have proceeded in a straight line away from you. This is the acceleration due to gravity.
Now, Let’s discuss some basics before understanding the factors affecting acceleration due to gravity.
What is Gravity?
The universal force of attraction among all the entities or matter in this universe is also known as gravity. It can be considered as the driving force which pulls together all the matter. Gravity is measured in terms of the acceleration or movement that it gives to freely falling objects. At Earth’s surface, the value of the acceleration of gravity is about 9.8 m/s2. Thus, for every second an object is in free fall, its speed increases by about 9.8 m/s2.
Some important that one must learn before going on further are:
- There exist a direct correlation between mass and gravity, that is, mass is directly proportional to gravity. The heavier the object, the greater the intensity of pull. For instance, stars and sun, have greater gravity.
- Direct relation also exists between the mass of the object and gravity, that is increase in mass leads to increase in the pull due to gravity.
- Gravity is also inversely proportional to the distance between two objects.
Acceleration due to Gravity
The Earth pulls any particle lying on its surface towards its center with a force known as gravitational pull of gravity. When a force acts on a body, it causes acceleration, and in the case of gravitation, this acceleration caused by gravity is referred to as acceleration due to gravity
Acceleration due to gravity, usually referred by the symbol ‘g‘ is the acceleration attained by any object in the universe due to gravitational force.
The SI unit of acceleration due to gravity is m/s2.
The value of g in SI system is 9.806 ms-2. And the value of g in CGS system is 980 cm s-2.
The Dimensional Formula for g is [ M0 L1 T-2 ].
It has a magnitude as well as direction. Thus it is a vector quantity.
Derivation of the formula for Acceleration due to Gravity
Near the surface of Earth, the acceleration due to gravity is approximately constant. But, at large distances from the Earth, or around other planets or moons, it is varying. The acceleration due to gravity depends on the terms as the following:
- Mass of the body,
- Distance from the center of mass,
- Constant G i.e. Universal gravitational constant.
Let’s consider an object of mass m, on which the acceleration due to gravity g is acting, now suppose F is the force acting on it and is given by:
F = mg ……(1)
where F is the force acting on the object,
g is the acceleration due to gravity and
m is the mass of the object.
According to the universal law of gravitation, the attractive gravitational force is given as:
F = (G × m × M) / (r+h)2
where F is the force between two objects,
G is the universal gravitational constant (6.67 × 10-11 Nm2 / kg2),
M is the mass of the earth,
r is the radius of the earth, and
h is the height at which the body is from the surface of the earth.
Since the height is negligibly small compared to the radius of the earth, so the last equation can be rewritten as:
F = (G × m × M) / r2 ……(2)
Lets equate equation (1) and (2) and solve to evaluate the expression for g as:
mg = (G × m × M) / r2
g = GM / r2
Hence, the formula of acceleration due to gravity is evaluated as shown above.
Factors affecting Acceleration due to Gravity
g is majorly affected by the following four factors:
- The shape of the Earth.
- Rotational motion of the Earth.
- Altitude above the Earth’s surface.
- Depth below the Earth’s surface.
Variation of g due to shape of the Earth
The earth is not perfectly spherical, but is an oblate spheroid. The polar radius (radius near poles) of the earth is 21 km smaller than its equatorial radius (near the equator). As per the formula derived, the acceleration due to gravity is inversely proportional to the square of the radius of the earth
Where, ge and gp are the accelerations due to gravity assumed at the equator and poles, Re and Rp are the radii of earth near the equator and poles, respectively.
From the above equation, it can be easily derived that acceleration due to gravity is more at poles and less at the equator, that is ge < gp . Thus, acceleration due to gravity increases when one moves from the equator to the pole.
Rotational motion of the Earth.
Let us assume, ω is the angular velocity of rotation of earth about its own axis, then the acceleration due to gravity at a place having latitude λ is shown as
g′ = g – Rω² cos² λ
Here, λ at poles is 90° and λ at the equator is 0°.
g’ = g
Thus, there is no effect of rotation of earth about its own axis at poles.
At the equator,
λ = 0° and g’ = g – Rω²
The value of g is minimum at the equator.
If earth stops its rotation about its own axis, then g will remain unchanged at poles but increases by Rω² at the equator.
Hence, we can conclude that;
Acceleration due to gravity is minimum at the equator.
At poles, θ=90°
Acceleration due to gravity is maximum at poles.
Altitude above the Earth’s surface
Assume a mass ‘m’ that is under the effect of earth’s gravity at a height ‘h’ from earth’s surface. The force due to gravitational pull acting on the object is;
Acceleration due to gravity at the height ‘h’ from the Earth’s surface
……..(i)
Here,
M is the mass of earth
R is the radius of the earth.
The acceleration due to gravity at a certain height is given by ‘h’
Therefore,
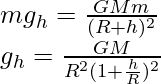
Then, the acceleration due to gravity on the surface of the earth is shown by;
………..(iii)
After dividing equation (iii) and (ii) we will get,
…………(iv)
It is clear that the value of g decreases with an increase in height of an object. Hence, the value of g becomes zero at infinite distance from the earth.
Depth below the Earth’s surface.
The acceleration due to gravity on the surface of the earth is given by
Assume be the density of the material of the Earth
As we know
Mass = volume × density
…….(i)
Thus, if we put the value of (i) in g, we will get
Also, let us assume the body to be taken to the depth ‘d’ below the surface of the earth. Then acceleration due to gravity gd at the depth ‘d’ below the Earth’s surface is shown as;
……..(iii)
Now, divide the equation (iii) by (ii), we will get
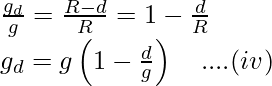
Here, equation (iv) is an expression for the acceleration due to gravity at the depth ‘d’ below the surface of the earth.
From equation (iv) we get to know that acceleration due to gravity decreases as we go down into the Earth.
At the Centre of earth d = R,
Thus, acceleration due to gravity at the Centre of the earth is 0.
Sample Problems
Problem 1: At what height above the surface of the earth value of acceleration due to gravity is reduced to one by ninth of its value on the surface of the earth?
Solution:
From the formula
gh =
Here gh = acceleration due to gravity at height ‘h’
g = acceleration due to gravity
R = radius of the earth
Thus,
From the problem
Hence,
At twice the height of the radius of the Earth value of acceleration due to gravity is reduced to one by ninth of its value on the surface of the earth.
Problem 2. If the radius of the Earth is decreased by 2% while keeping its mass the same, how will the acceleration due to gravity change?
Solution:
As we know that

Where,
g = acceleration due to gravity
R = radius of the Earth
M = mass of the Earth
If R is decreased by 2% it will become

Therefore,
Therefore,
g’ increases by 0.04
therefore increases by 4%.
Problem 3. At what height from the surface of the earth will the value of ‘g’ be reduced by 19% of its value at the surface of the earth.
Solution:
g’ = 81% of g
g’ =

Therefore,
At the height of
from the Earth surface the value of ‘g’ will be reduced to 19% of its value at the surface of earth.
Problem 4. How many times is the acceleration due to gravity on the surface of Jupiter as compared to Earth’s surface?
(Use the following data: mEarth = 5.98 × 1024 kg, rEarth = 6.4 × 106 m, mJupiter = 1.9 × 1027 kg, rJupiter = 6.99 × 107 m)
Solution:
To solve this example we will need to find the ratio of acceleration due to gravity of Jupiter to acceleration due to gravity of Earth
By the relation;
Here,
m = mass of planet
r = radius of planet
Thus, the acceleration due to gravity on Jupiter surface is 2.66 times more than that of Earth’s surface.
Problem 5. Explain acceleration due to gravity increase or decrease with the increase in the altitude?
Solution:
As we know that acceleration due to gravity at the depth of h is shown as;
Here,
Re = Radius of the Earth
g = Acceleration due to gravity on the surface of the Earth
Thus, we can clearly see that from the equation that acceleration due to gravity increases with decrease in height and decreases with increase in height.
Problem 6. Explain that acceleration due to gravity is independent of the mass of earth as well as the mass of the body?
Solution:
As we know that acceleration due to gravity of body of mass m is shown as;
Here,
G = Is the universal gravitational constant
M = Mass of the Earth
R = Radius of the Earth
Thus, we can clearly see here that acceleration due to gravity is independent of the mass.
Problem 7. Explain that acceleration due to gravity is increased or decreases with the increase in depth?
Solution:
As we know that acceleration due to gravity is shown as;
Thus, here we can clearly see that the acceleration due to gravity increases with decrease in depth and decreases with increase in depth.








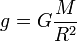 ,
,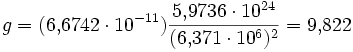 м/с²
м/с²