Как найти ускорение свободного падения тела, зная его плотность и радиус?
Ученик
(162),
на голосовании
11 лет назад
Дополнен 11 лет назад
неправильно сформулировала)
нужно найти ускорение свободного падения тела на поверхности Венеры, зная её плотность и радиус. Затруднения в нахождении массы (м=pV) а отсюда уже не знаю, как найти объём)
Голосование за лучший ответ
1 2
Мастер
(2497)
11 лет назад
Ускорение для всех одинаковое, зная плотность и радиус возможно сможите посчитать сопротивление воздуха, хотя оно также зависит и от скорости, так-что задача тогда не такая простая, на курсовой проект примерно.
Ускорение свободного падения, теория и онлайн калькуляторы
Ускорение свободного падения
Определение ускорения свободного падения
Определение
Ускорением свободного падения называют ускорение, которое телу придает сила тяжести, если другие силы на рассматриваемое тело не действуют или их
действие взаимно компенсируется.
Ускорение свободного падения обозначают буквой $g$. На поверхности Земли оно изменяется пределах от $9,78 frac{м}{с^2}$ до $9,832 frac{м}{с^2}$. На полюсах Земли ускорение свободного падения максимально, на экваторе минимально. Средним (стандартным или нормальным) значением ускорения свободного падения на Земле принято считать его величину, равную $g=9,80665 frac{м}{с^2} $. В задачах величину ускорения свободного падения считают равной $g=9,81frac{м}{с^2}$ или часто даже полагают $g=10frac{м}{с^2}$, если расчеты приблизительные.
В соответствии с обобщенным законом Галилея все тела, находящиеся в одном и том же поле тяготения падают с одинаковыми ускорениями. Это означает, что в данной точке Земли ускорение свободного падения одинаково для всех тел. Изменение величины ускорения свободного падения около поверхности Земли в зависимости от широты связано с суточным вращением нашей планеты вокруг своей оси и тем, что форма Земли отличается от формы шара (Земля сплюснута).
Зависимость ускорения свободного падения от высоты над уровнем Земли
Если суточным вращением Земли пренебречь, то сила тяжести ($P=mg$) равна по величине силе тяготения (F):
[P=mg=F=gamma frac{mM}{R^2}left(1right),]
где $M$ – масса Земли; $R$ – расстояние от центра Земли, до рассматриваемого тела; $gamma $- гравитационная постоянная. Формула (1) справедлива, если тело находится около поверхности Земли, тогда ускорение свободного падения равно:
[g=gamma frac{M}{R^2}left(2right).]
Ускорение, вычисляемое при помощи формулы (2) называют ускорением свободного падения на уровне моря.
Допустим, что тело находится на высоте $h$ над уровнем Земли, тогда сила тяжести, действующая на тело равна:
[P=gamma frac{mM}{{left(R_Z+hright)}^2}left(3right),]
где $R_Z$ – радиус Земли. В таком случае ускорение свободного падения зависит от высоты, на которой находится рассматриваемое тело:
[g=gamma frac{M}{{left(R_Z+hright)}^2}left(4right).]
Изменениями ускорения свободного падения на высотах, которые много меньше, чем радиус Земли обычно пренебрегают. При этом считают, что ускорение свободного падения постоянная величина.
Влияние вращения Земли на ускорение свободного падения
Как уже отмечалось, на ускорение свободного падения оказывает влияние вращение нашей планеты вокруг своей оси. Допустим, что тело массой $m$ находится в точке с географической широтой $varphi $. Вместе в планетой тело движется и при этом траекторией его движения является окружность радиуса $r$, равного:
[r=R_Z{cos varphi left(5right), }]
где $R_Z$ – радиус Земли. Центростремительное ускорение ($a_n$) нашего тела при этом будет составлять величину:
[a_n=frac{v^2}{r}=frac{4{pi }^2R_Z{cos varphi }}{T^2} left(6right),]
где $T$ – период вращения Земли. Силу тяготения ($F$) можно разложить на две составляющие: центростремительную силу ($F_n$) и силу тяжести ($P$). Сила тяжести везде кроме полюсов, меньше силы тяготения. Везде, кроме экватора и полюсов, сила тяжести направлена не точно в центр Земли, а немного в сторону от него.
За счет вращения Земли сила тяжести на полюсах больше, чем у экватора, наша планета сплюснута.
Ускорение свободного падения на полюсе ($g_p$) максимально. Так как центростремительное ускорение равно нулю, полярный радиус ($R_p$) минимален:
[g_p=frac{gamma M}{R^2_p}left(7right).]
Ускорение свободного падения ($g_e$) на экваторе равно разности:
[g_e=frac{gamma M}{R^2_e}-a^e_n=frac{gamma M}{R^2_e}-frac{4{pi }^2R_e}{T^2}left(8right),]
где $R_e$ – экваториальный радиус Земли. Величину $frac{gamma M}{R^2_e}$ называют напряженностью гравитационного поля Земли.
Примеры задач с решением
Пример 1
Задание. Радиус некоторой планеты равен R, ее средняя плотность составляет $rho $, считая, что масса планеты распределена равномерно, определите ускорение свободного падения около поверхности этой планеты.
Решение. Ускорение свободного падения около поверхности планеты можно найти как:
[g=gamma frac{M}{R^2}left(1.1right),]
где $R$ – радиус планеты; $M$ – масса планеты. Массу планеты найдем, считая ее шаром:
[M=frac{4}{3}pi R^3rho left(1.2right).]
Тогда ускорение свободного падения около поверхности этой планеты равно:
[g=gamma frac{frac{4}{3}pi R^3rho }{R^2}=frac{4}{3}gamma pi rho R.]
Ответ. $g=frac{4}{3}gamma pi rho R.$
Пример 2
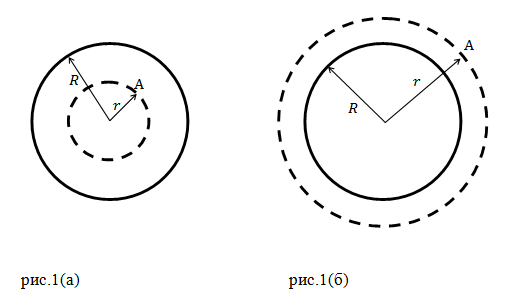
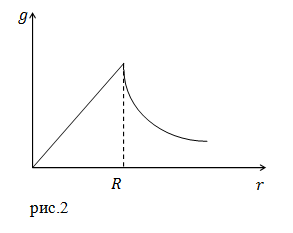
Задание. Какова зависимость ускорения свободного падения от расстояния от центра планеты$ ( r)$, если планета – однородный шар, плотность которого равна $rho ?$ Радиус планеты R. Изобразите график $gleft(rright).$
Решение. Рассмотрим случай, когда расстояние от центра планеты меньше ее радиуса ($r$ меньше $R$) (рис.1 (а)).
Расположим тело массы $m$ на расстоянии $r$ от центра планеты (в точке А). Тогда тело притягивается к планете с силой:
[mg=frac{gamma M’m}{r^2}left(2.1right),]
где $M’=frac{4}{3}pi r^3rho $ – масса планеты, которая ограничена сферической поверхностью радиуса $r$. При этом, ускорение свободного падения равно:
[g_1(r)=frac{gamma frac{4}{3}pi r^3rho }{r^2}=frac{4}{3}pi gamma rho r.]
Расположим материальную точку массы $m$ в точке А за пределами планеты (рис.1 (б)), тогда по закону всемирного тяготения на точечную массу действует сила, равная:
[mg=gamma frac{mM’}{r^2} left(2.2right),]
где $M’=frac{4}{3}pi R^3rho $, в этом случае ускорение свободного падения равно:
[g_2(r)=gamma frac{4}{3}pi R^3frac{rho }{r^2}.]
В результате получаем:
[left{ begin{array}{c}
g_1left(rright)=frac{4}{3}pi gamma rho r при rle R \
g_2left(rright)=gamma frac{4}{3}pi R^3frac{rho }{r^2}при rge R. end{array}
right. ]
Читать дальше: центростремительное ускорение.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.
| Земля | 9,81 м/с2 | 1,00 g | Солнце | 273,1 м/с2 | 27,85 g |
| Луна | 1,62 м/с2 | 0,165 g | Меркурий | 3,70 м/с2 | 0,378 g |
| Венера | 8,88 м/с2 | 0,906 g | Марс | 3,86 м/с2 | 0,394 g |
| Юпитер | 24,79 м/с2 | 2,528 g | Сатурн | 10,44 м/с2 | 1,065 g |
| Уран | 8,86 м/с2 | 0,903 g | Нептун | 11,09 м/с2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Физическая сущность[править | править код]
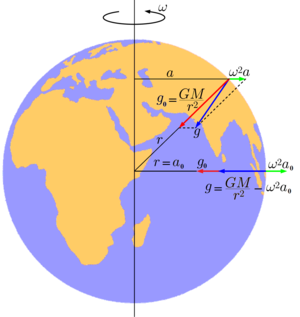
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центростремительное ускорение[править | править код]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
Ускорение свободного падения— ускорение, сообщаемое свободной материальной точке силой тяжести, поднятой на небольшое расстояние над Землей.
Если применить эту формулу для вычисления гравитационного ускорения на поверхности Земли, то мы получим:
В условиях Земли падение тел считается условно свободным, т.к. при падении тела в воздушной среде всегда возникает еще и сила сопротивления воздуха.
Идеальное свободное падение возможно лишь в вакууме, где нет силы сопротивления воздуха, и независимо от массы, плотности и формы все тела падают одинаково быстро, т. е. в любой момент времени тела имеют одинаковые мгновенные скорости и ускорения.
Наблюдать идеальное свободное падение тел можно в трубке Ньютона, если с помощью насоса выкачать из неё воздух.
Вблизи поверхности Земли величина силы тяжести считается постоянной, поэтому свободное падение тела — это движение тела под действием постоянной силы. Следовательно, свободное падение — это равноускоренное движение.
Экспериментально установлено, что ускорение свободного падения не зависит от массы падающего тела, но зависит от географической широты q местности и высоты h подъема над земной поверхностью. При этом зависимость g от q двоякая.
Во-первых, Земля — не шар, а эллипсоид вращения, то есть радиус Земли на полюсе меньше радиуса Земли на экваторе. Поэтому сила тяжести и вызываемое ею ускорение свободного падения на полюсе больше, чем на экваторе (g=9,832 на полюсе и g = 9,780
на экваторе).
Во-вторых, Земля вращается вокруг своей оси и это влияет на ускорение свободного падения, приводя к его зависимости от географической широты местности
В формуле мы использовали :
— Ускорение свободного падения на поверхности Земли
— Гравитационная постоянная
— Масса Земли
— Радиус Земли
— Высота тела над поверхностью Земли
Ускорение свободного падения.
Ускорение свободного падения – это ускорение, с которым движется любое тело во время свободного падения.
Ускорение свободного падения
Формула ускорения свободного падения
Ускорения свободного падения на Земле и планетах Солнечной системы
Состав планеты (иного небесного тела) и ускорение свободного падения
Полезные ископаемые и ускорение свободного падения
Вращение планеты вокруг своей оси и ускорение свободного падения
Ускорение свободного падения:
Ускорение свободного падения – это ускорение, с которым движется любое тело в поле тяготения Земли (или другого небесного тела), если на него действует только сила тяжести.
Ускорение свободного падения – это ускорение, с которым движется любое тело во время свободного падения.
Ускорение свободного падения (ускорение силы тяжести) – ускорение, придаваемое телу только силой тяжести во время свободного падения, в вакууме (т.е. в безвоздушном пространстве и, следовательно, без сопротивления), при исключении взаимодействия с другими телами.
В свою очередь свободное падение – это равноускоренное движение в безвоздушном пространстве, под действием только силы тяжести, когда другие силы, действующие на тело, отсутствуют или пренебрежимо малы.
Ускорение свободного падения обозначается g (обычно произносится как «же») и измеряется м/с².
Все тела ускоряются в вакууме с одинаковой скоростью, независимо от массы или состава тел.
На ускорение свободного падения влияют масса планеты (или другого небесного тела), форма планеты, состав планеты, размер планеты, вращение планеты вокруг своей оси и расстояние между падающим телом и центром планеты.
Ускорение свободного падения на Земле, на других планетах и небесных телах различается.
Ускорение свободного падения на поверхности Земли (g) варьируется в зависимости от высоты, широты и долготы и составляет от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах. Это связанно с тем, что Земля по форме не идеальный шар, она сплюснута с полюсов, вследствие чего на полюсах Земли радиус несколько меньше, чем на экваторе.
Стандартное («нормальное») значение ускорения свободного падения (g) на Земле, принятое при построении систем единиц, составляет 9,80665 м/с². Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря.
В приблизительных расчётах g обычно принимают равным 9,81 м/с², 9,8 м/с² или более грубо 10 м/с².
Ускорение свободного падения (g) направлено к центру Земли.
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра.
Формула ускорения свободного падения:
В соответствии с законом всемирного тяготения величина ускорения свободного падения (g) на поверхности Земли или иного небесного тела связана с его массой M следующим соотношением:
где G – гравитационная постоянная, равная 6,67430(15) · 10−11 м3/ кг · с2 ,
M – масса Земли или иного небесного тела, выраженная в килограммах. Масса Земли равна 5,9726 · 1024 кг,
r – радиус планеты или иного небесного тела, выраженный в метрах. Радиус Земли равен 6371 км или 6 371 000 м.
Подставим значения в формулу и получим:
g = 6,67430(15)·10−11 м3/кг·с2 ⋅ 5,9726·1024 кг / 6 371 0002 м2 = 9,82 м/с².
На экваторе Земли ускорение свободного падения (g) составляет 9,780 м/с².
На полюсах Земли ускорение свободного падения (g) составляет 9,82 м/с².
Таким образом, притяжение (сила тяжести) на полюсе примерно на 0,5% больше, чем на экваторе. Следовательно, если сила тяжести составляет 800 Н на экваторе, то на полюсах Земли она увеличивается до 804,24 Н.
В 1901 году на третьей Генеральной конференции по мерам и весам стандартное значение ускорения свободного падения (g) было установлено равным 9,80665 м/с2 значение для 45,5° (северной или южной) широты и уровня моря.
Данная формула справедлива для вычисления ускорения свободного падения (g) на поверхности Земли (или иного небесного тела).
Поскольку у Земли в разных точках различается радиус, то и ускорение свободного падения (g) также будет различаться.
Если необходимо вычислить ускорения свободного падения (g) над поверхностью Земли (или иного небесного тела) на высоте h, то справедлива следующая формула:
где h – расстояние от тела до поверхности Земли (или иного небесного тела).
Нетрудно подсчитать, то вблизи поверхности Земли ускорение свободного падения (g) уменьшается примерно на 3,1 мкм/с2 на каждый поднятый метр.
Таблица 1.
Ускорение свободного падения для некоторых городов
| Город | Долгота | Широта | Высота над
уровнем моря, м |
Ускорение свободного
падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Ускорения свободного падения на Земле и планетах Солнечной системы:
| Небесное тело | Масса, кг | Средний радиус, км | Ускорение свободного падения | |
| Солнце | 1,9885 · 1030 | 695 700 | 274,0 м/с2 | 27,93 g |
| Меркурий | 3,33022⋅1023 | 2 439,7 | 3,70 м/с2 | 0,377 g |
| Венера | 4,8675⋅1024 | 6 051,8 | 8,87 м/с2 | 0,904 g |
| Земля | 5,9726·1024 | 6 371 | 9,81 м/с2 | 1,00 g |
| Луна | 7,3477·1022 | 1 737,5 | 1,62 м/с2 | 0,165 g |
| Марс | 6,4171⋅1023 | 3 396,2 | 3,711 м/с2 | 0,378 g |
| Юпитер | 1,89813⋅1027 | 69 911 | 24,79 м/с2 | 2,527 g |
| Сатурн | 5,6834⋅1026 | 58 232 | 10,44 м/с2 | 1,064 g |
| Уран | 8,6813⋅1025 | 25 362 | 8,87 м/с2 | 0,904 g |
| Нептун | 1,0243 ⋅ 1026 | 24 622 | 11,15 м/с2 | 1,14 g |
| Плутон | 1,303⋅1022 | 1188,3 | 0,617 м/с2 | 0,063 g |
Состав планеты (иного небесного тела) и ускорение свободного падения (g):
Вышеприведенная формула для определения ускорения свободного падения (g) справедлива для небесного тела, имеющего однородную по плотности сферу.
Однако состав планеты Земля (или иного небесного тела) неоднороден, что оказывает влияние на величину ускорения свободного падения (g).
Если бы Земля была однородной сферой, то ускорение свободного падения (g) линейно возрастало бы от нуля в центре Земли до максимума на поверхности Земли. На самом деле Земля состоит из нескольких слоев с очень разной плотностью. Следовательно, связь между глубиной и ускорением свободного падения более сложна.
Наиболее плотный слой Земли – ядро. Это центральная, наиболее глубокая часть планеты Земля, находящаяся под мантией Земли и, предположительно, состоящая из железо-никелевого сплава с примесью других сидерофильных элементов. Глубина залегания — 2900 км. Средний радиус ядра – 3500 км. Ядро разделяется на твердое внутреннее ядро радиусом около 1300 км и жидкое внешнее ядро толщиной около 2200 км, между которыми иногда выделяется переходная зона. Ядро Земли, состоящее из металла, более чем в два раза плотнее мантии и земной коры.
Далее следует менее плотные слои – мантия и земная кора.
В ядре Земли ускорение свободного падения (g) сначала равномерно увеличивается по мере удаления от центра Земли. На границе ядро-мантия (на глубине примерно 2900 км от поверхности Земли или 3471 км от центра Земли) оно достигает максимума – чуть менее 10,68 м/с2. Далее на расстоянии 4900 км от центра Земли ускорение свободного падения (g) сначала снова медленно уменьшается до 9,93 м/с2, затем снова увеличивается до 10,01 м/с2 на расстоянии 5700 км от центра Земли, а затем монотонно снижается, пока не достигнет значения около 9,82 м/с2 на поверхности Земли.
Полезные ископаемые и ускорение свободного падения (g):
В земной коре залегают различные полезные ископаемые. Они имеют различную плотность и с разной силой притягивают объект в точке наблюдения. Поэтому над достаточно большим телом с повышенной или пониженной плотностью ускорение свободного падения будет отличаться.
Залежи более плотных (и соответственно более тяжелых) полезных ископаемых, например, металлов, увеличивают значение ускорения свободного падения (g). Пустоты или залежи менее плотных (и соответственно более легких) полезных ископаемых, например, нефти уменьшают значение ускорения свободного падения (g).
Известно, что на одной и той же географической широте ускорение свободного падения (g), при прочих равных условиях, одинаково. Измеряя в рамках одной широты значение ускорения свободного падения (g) в разных точках, можно судить о наличии полезных ископаемых или их отсутствии.
Современные гравиразведочные приборы позволяют измерять ускорение свободного падения с точностью до миллионных долей.
Данный способ измерения значения ускорения свободного падения (g) в геологии называется гравиметрической (гравитационной) разведкой и используется для поиска и разведки полезных ископаемых (нефти и газа, угля, руды и других).
Вращение планеты вокруг своей оси и ускорение свободного падения (g):
При расчете ускорения свободного падения (g) Земли или иного небесного тела для упрощения расчетов вращение Земли или иного небесного тела вокруг своей оси не принимается во внимание.
Вращение Земли вокруг своей оси создает центробежную силу и центробежное ускорение, которое влияет на величину ускорения свободного падения (g).
Величину ускорения свободного падения (g) можно представить как векторную сумму двух слагаемых-компонентов: гравитационного ускорения (ускорения силы тяжести), вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центробежное ускорение направлено по нормали от оси вращения Земли, в то время как гравитационное ускорение (ускорение силы тяжести), направлено к центру Земли. На экваторе вектора гравитационного ускорения и центробежного ускорения располагаются на одной прямой линии, но направлены в противоположные стороны.
В точке, находящейся на расстоянии a от оси вращения (земной оси), оно (центробежное ускорение) равно ω2a,
где ω – угловая скорость вращения Земли, определяемая как ω = 2π / T,
а Т – время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки).
На экваторе центробежное ускорение составляет 3,39636 см/с2 или 0,0339636 м/с2.
В итоге получается, что почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты.
Источник: https://ru.wikipedia.org
Примечание: © Фото https://www.pexels.com, https://pixabay.com
Коэффициент востребованности
92