Как найти ускорение свободного падения маятника формула

Как найти ускорение свободного падения маятника формула

Определение ускорения свободного падения при помощи маятника

Ускорение свободного падения можно
определить из формулы периода колебаний
маятника;

откуда

Из последней формулы видно ,
что для определения ускорения свободного
падения необходимо знать длину маятника
и период его колебаний.Длину
маятника можно измерить непосредственно.
Для этого необходимо иметь лишь линейку
. Период колебаний
можно найти по формуле;

где N – число колебаний
за время t.
Оценим возможные погрешности этого
способа определения ускорения свободного
падения. Так как

Длина маятника

L (м)

Частота колебаний маятника

 ( Гц)

Начальное отклонение маятника

0 ( град.)

Интервал времени за который совершается
20 колебаний t ( c
)

Частота колебаний маятника

э = n t
( Гц)

э –
100%

э

1

10

1

20

1

40

1

60

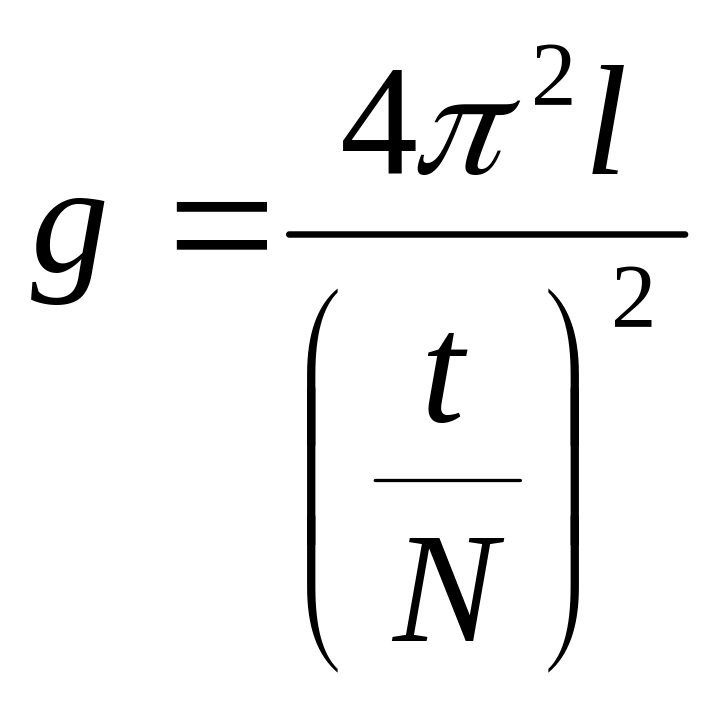
то

Длину маятника с помощью линейки можно
измерить с абсолютной погрешностью
+1 мм

В условиях школьной лаборатории длина
маятника может быть порядка 1- 2 м .Если
l = 1м,
то относительная погрешность
измерения длины маятника

Это обеспечивает достаточно высокую
точность измерения.
Хуже дело обстоит с измерением периода
колебаний. При
длине маятника 1 м период колебаний
примерно 2 с , а
абсолютная погрешность секундомера
примерно + 1 с ;

Точность измерения периода колебаний
можно повысить если измерить время не
одного полного колебания а,
например, 20
полных колебаний. В этом случае
погрешность измерения времени

Порядок выполнения работы

1.
Установите на краю стола штатив.
У его верхнего конца с помощью муфты
укрепите кольцо и подвесьте к нему шарик
на нити. Шарик
должен висеть на расстоянии 1 – 2 см от
пола.

  1. Отклонив шарик на 5 – 8 см ,
    отпустите его.

  2. Заметьте время 20 полных колебаний.

  3. Измерьте длину маятника.

  4. Вычислите ускорение свободного падения
    по формуле

6.Рассчитайте
погрешность измерения и запишите ее в
виде

Изучение зависимости частоты колебаний математического маятника от его длины.

Согласно формуле

частота колебаний математического
маятника должна быть обратно пропорциональна
корню квадратному из его длины.
Отсюда следует ,
что произведение частоты колебаний
математического маятника
на корень квадратный из его длины l
должно быть постоянной величиной;

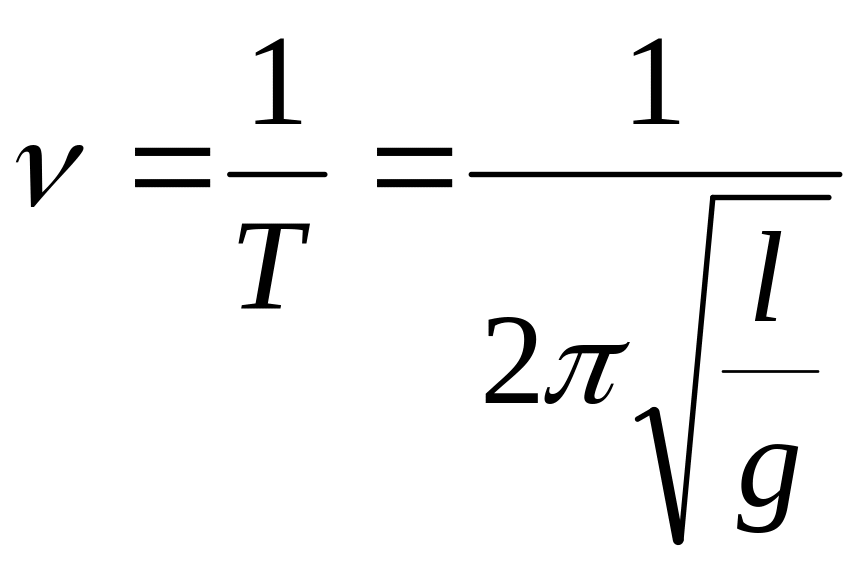
Для проверки этого свойства маятника
произведите измерения частоты его
колебаний при трех различных значениях
длины и небольшом отклонении шарика от
положения равновесия.
Результаты измерений и вычислений
занесите в таблицу.

Длина маятника(м)

Интервал времени,
за который маятник совершил 20 колебаний
t ( с)

Частота колебаний

 ( Гц)

( м12)

( м12 с-1 )

1

0,
9

0,
8

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

Christman

Мастер

(1430)


12 лет назад

Его не нужно искать, оно есть в таблицах: g=9,80665 м/с в кв. – для планеты Земля

KorolevУченик (30)

2 месяца назад

а как тогда это решить? тут вообще не понятно

На другой планете период
колебаний математического
маятника с длиной нити 4 м был
равен 6.28 с. Чему равно ускорение
свободного падения на этой
планете?

ChristmanМастер (1430)

2 месяца назад

Период делим на 2пи, возводим в квадрат. Полученное число равно длина/ускорение св. падения. Отсюда находим ускорение…

Источник

Цель работы: вычислить ускорение свободного падения из формулы для периода колебаний математического маятника:

Для этого необходимо измерить период колебания и длину подвеса маятника. Тогда из формулы (1) можно вычислить ускорение свободного падения:

Средства измерения:

1) часы с секундной стрелкой;

2) измерительная лента (Δл = 0,5 см).

Материалы: 1) шарик с отверстием; 2) нить; 3) штатив с муфтой и кольцом.

Порядок выполнения работы

1. Установите на краю стола штатив. У его верхнего конца укрепите при помощи муфты кольцо и подвесьте к нему шарик на нити. Шарик должен висеть на расстоянии 3—5 см от пола.

2. Отклоните маятник от положения равновесия на 5—8 см и отпустите его.

3. Измерьте длину подвеса мерной лентой.

4. Измерьте время Δt 40 полных колебаний (N).

5. Повторите измерения Δt (не изменяя условий опыта) и найдите среднее значение Δtср.

6. Вычислите среднее значение периода колебаний Tср по среднему значению Δtср.

7. Вычислите значение gcp по формуле:

8. Полученные результаты занесите в таблицу:

Номер

опыта

l, м

N

Δt, с

Δtср, с

9. Сравните полученное среднее значение для gcp со значением g = 9,8 м/с2 и рассчитайте относительную погрешность измерения по формуле:

Изучая курс физики вам часто приходилось использовать в решении задач и других расчетах значение ускорения свободного падения на поверхности земли. Вы принимали значение g = 9,81 м/с2, то есть с той точностью, которой вполне достаточно для производимых вами расчетов.

Целью данной лабораторной работы является экспериментальное установление ускорения свободного падения с помощью маятника. Зная формулу периода колебания математического маятника Т =

можно выразить значение g через величины, доступные простому установлению путем эксперимента и рассчитать g с некоторой точностью. Выразим

где l – длина подвеса, а Т – период колебаний маятника. Период колебаний маятника Т легко определить, измерив время t, необходимое для совершения некоторого количества N полных колебаний маятника

Математическим маятником называют груз, подвешенный к тонкой нерастяжимой нити, размеры которого много меньше длины нити, а масса – много больше массы нити. Отклонение этого груза от вертикали происходит на бесконечно малый угол, а трение отсутствует. В реальных условиях формула

имеет приблизительный характер.

Рассмотрим такое тело (в нашем случае рычаг). На него действуют две силы: вес грузов P и сила F (упругости пружины динамометра), чтобы рычаг находился в равновесии и моменты этих сил должны быть равны по модулю меду собой. Абсолютные значения моментов сил F и P определим соответственно:

В лабораторных условиях для измерения с некоторой степенью точности можно использовать небольшой, но массивный металлический шарик, подвешенный на нити длиной 1-1,5 м (или большей, если есть возможность такой подвес разместить) и отклонять его на небольшой угол. Ход работы целиком понятен из описания ее в учебнике.

Средства измерения: секундомер (Δt = ±0,5 с); линейка или измерительная лента (Δl = ±0,5 см)

Выполнение работы:

№

опыта

1, м

N

t, с

tср, с

Тср

gср, м/с2

1

1,5

40

100

2

1,5

40

98

99

2,475

9,657

3

1,5

40

99

Вычисления:

Погрешность:

Источник

Лабораторная работа

измерение ускорения свободного падения с помощью маятника

Цель работы:

вычислить ускорение свободного падения из формулы для периода колебаний математического маятника.

Оборудование:

часы с секундной стрелкой (или секундомер), измерительная лента, шарик с отверстием, нить, штатив с муфтой и кольцом.

Краткие теоретические сведения

Математическим маятником называют идеализированную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена масса, сосредоточенная в одной точке, и совершающую под действием силы тяжести гармонические колебания в вертикальной плоскости. Как известно, период малых колебаний математического маятника выражается формулой:

Т = 2π√hello_html_3495e65.gif , откуда g = hello_html_me6d6292.gif·l ,

где g – ускорение свободного падения (м/с²);

π = 3,14;

l = длина нити (м);

N – число колебаний за время t.

Из последней формулы видно, что для определения ускорения свободного падения необходимо знать длину маятника и период его колебаний. Длину маятника можно измерить непосредственно с помощью линейки, а период колебаний можно определить по формуле

Тср. = hello_html_6b7613f.gif ,

где

N – число колебаний за время t, измеренное с помощью секундомера.

Тогда для определения ускорения свободного падения получим следующую формулу:

gср. = hello_html_m599423b9.gif·

Ход работы

IMG.jpg

1. На краю стола устанавливаем штатив. У его верхнего конца укрепляем при помощи муфты кольцо и к нему подвешиваем шарик на нити. Шарик должен висеть на расстоянии нескольких сантиметров от пола.

2. Шарик отклоняем в сторону на 5 – 8 см. и отпускаем

3. Замеряем время (t) 30 полных колебаний (N).

4. С помощью мерной ленты замеряем длину маятника.

5. Не изменяя условий опыта, повторяем измерения t.

Опыт проводим 4 раза.

6. Результаты измерений и вычислений заносим в таблицу.

№

опыта

l,м

N

t,с

tср,с

Tср,с

gср, м/с2

1

2

3

4

7. Пользуясь расчетной формулой вычисляем значение gср.

8. Вычислить точность проведенного измерения.

8.1 Относительная погрешность измерения равна:

εg = hello_html_61b4cd70.gif· 100%,

где g =9,8 (м/с²);

8. Вывод.

Контрольные вопросы.

1. Что такое математический маятник?

2. Что такое период колебаний?

3. Определите теорию метода определения ускорения свободного падения.

Источник

Добавить комментарий