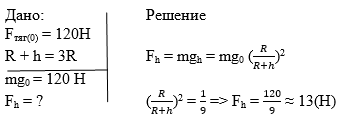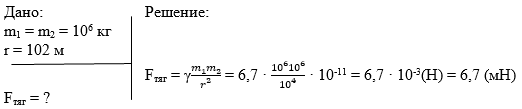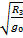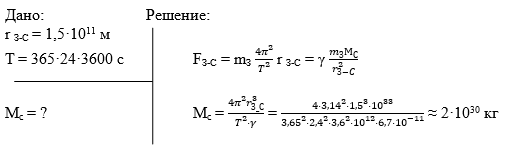Как найти ускорение свободного падения на спутнике

Как найти ускорение свободного падения на спутнике

Сила всемирного тяготения. Искусственные спутники

  1. Гравитационное взаимодействие
  2. Закон всемирного тяготения
  3. Ускорение свободного падения на поверхности для различных планет
  4. Космические скорости
  5. Искусственные спутники Земли
  6. Задачи

п.1. Гравитационное взаимодействие

Согласно современным представлениям, все тела, обладающие массой, притягиваются друг к другу. Это взаимодействие называется гравитационным.

Таким образом, масса проявляется в природе двумя качественно разными способами.

Инертная масса – мера инертности тел (второй закон Ньютона), дающая связь между силой и вызываемым ею ускорением.
Гравитационная масса – мера гравитационного взаимодействия тел (закон всемирного тяготения), определяющая силу взаимного притяжения.

Нужно подчеркнуть, что инертная масса и гравитационная масса возникают в механике при рассмотрении совершенно разных явлений, и ниоткуда не следует, что они должны быть равны.

Тем не менее, уже сам Ньютон доказал равенство этих масс с точностью 10-3.

На сегодняшний день (эксперимент 2009 г.) этот факт подтвержден с точностью 10-13.

Принцип эквивалентности
Значения инертной и гравитационной массы одного и того же тела равны.

п.2. Закон всемирного тяготения

Закон всемирного тяготения
Две материальные точки массами (m_1) и (m_2) притягиваются по направлению друг к другу с силой (F), прямо пропорциональной произведению их масс и обратно пропорциональной квадрату расстояния (r) между ними: $$ F=Gfrac{m_1m_2}{r^2} $$ Коэффициент пропорциональности называется гравитационной постоянной;
она одинакова для всех тел природы и в системе СИ равна $$ G=6,67cdot 10^{-11}frac{text{Н}cdot text{м}^2}{text{кг}^2} $$

Физический смысл гравитационной постоянной
Если два тела массой по 1 кг находятся на расстоянии 1 м друг от друга, сила гравитационного взаимодействия между ними равна $$ F=Gcdot 1frac{text{кг}^2}{text{м}^2}=6,67cdot 10^{-11} text{Н} $$

Закон всемирного тяготения выполняется для тел, размерами которых можно пренебречь, т.е. для материальных точек. Но его применение можно расширить.

При рассмотрении небесных тел (Солнца, планет и их спутников) в первом приближении их можно считать однородными идеальными сферами с одинаковой плотностью вещества внутри. Как показывает теория, в такой модели небесное тело можно заменить материальной точкой, совпадающей с его центром, с массой полностью сосредоточенной в этом центре.

В этом случае для применения закона всемирного тяготения открываются дополнительные возможности. Например, можно описывать движение небольшого тела на поверхности планеты, «сжимая» всю планету в материальную точку, от которой тело удалено на расстояние, равное радиусу планеты.

п.3. Ускорение свободного падения на поверхности для различных планет

Найдем силу, с которой Земля притягивает небольшое тело массой m, расположенное на её поверхности.

Будем считать Землю сферическим однородным телом.
Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}),
радиус Земли (R_oplus=6370 text{км}).
Допущение об однородности позволяет перейти к модели, в которой вся масса Земли сосредоточена в её центре. Расстояние от центра до поверхности, на которой находится тело, – это радиус Земли.

Получаем, что сила притяжения между Землей и телом: $$ F=Gfrac{M_oplus m}{R^2_oplus} $$

По своей природе, полученная сила является ничем иным, как силой тяжести (F=mg), с которой мы уже знакомы (см. §22 данного справочника).

Значит, (Gfrac{M_oplus m}{R^2_oplus}=mg), и ускорение свободного падения begin{gather*} g=Gfrac{M_oplus}{R^2_oplus}\[6pt] g=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}}{(6,37cdot 10^6)^2}approx 9,81 (text{м/с}^2) end{gather*} Что полностью согласуется с многочисленными экспериментами.

Полученный результат можно обобщить и применить к любому другому небесному телу.

Ускорение свободного падения на поверхности сферической однородной планеты или звезды массой (M) и радиусом (R) прямо пропорционально массе и обратно пропорционально квадрату радиуса: $$ g=Gfrac{M}{R^2} $$

Например, для Луны (g_{text{Л}}=1,62frac{text{м}}{text{с}^2}approx 0,165g_0); для Юпитера (g_{text{Ю}}=23,95frac{text{м}}{text{с}^2}approx 2,442g_0); для Солнца (g_{text{С}}=273,1frac{text{м}}{text{с}^2}approx 27,85g_0). Здесь, (g_0) – ускорение свободного падения у поверхности Земли.

Заметим, что в задачах на гравитационное взаимодействие часто оказывается полезной замена (GM=gR^2).

п.4. Космические скорости

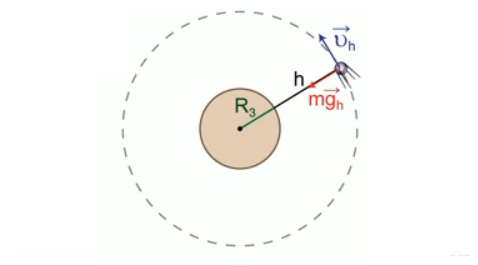
Если тело находится на поверхности Земли, то расстояние между центром планеты, где сосредоточена вся масса, и этим телом равно радиусу Земли (R_oplus).

Если подняться над поверхностью на некоторую высоту (h), расстояние станет равным ((R_oplus+h)). Сила всемирного тяготения (она же – сила тяжести) на этой высоте: $$ F_h=Gfrac{M_oplus m}{(R_oplus+h)^2} $$

Т.к. (GM_oplus=gR^2_oplus), где (g=9,81 (text{м/с})^2), можем также записать удобное на практике выражение: $$ F_h=mgleft(frac{R_oplus}{(R_oplus+h)}right)^2 $$

Пусть мы хотим запустить спутник, который будет летать на высоте (h) по круговой орбите с постоянной скоростью (v). При равномерном движении по окружности ускорение равно отношению квадрата скорости к радиусу орбиты. Получаем: $$ F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=ma=mfrac{v^2_h}{(R_oplus + h)} $$

Скорость вращения спутника на высоте (h): $$ v_h=sqrt{frac{GM_oplus}{R_oplus + h}} $$

Зная ускорение свободного падения у поверхности Земли (g), можем также записать: $$ v_h=sqrt{frac{gR^2_oplus}{R_oplus + h}} $$

В общем случае:

Чтобы запустить тело на круговую орбиту на высоте (h) над поверхностью сферической однородной планеты или звезды массой (M) и радиусом (R), нужно на этой высоте сообщить телу в горизонтальном направлении скорость $$ v_h=sqrt{frac{GM}{R+h}} $$

Скорости, достаточные для запуска околоземного спутника, межпланетной станции и вылета за пределы Солнечной системы, называют космическими скоростями для Земли.

Первая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), стало её искусственным спутником, равна $$ v_1=sqrt{frac{GM_oplus}{R_oplus}}=sqrt{gR_oplus}approx 7,92 text{км/с} $$

Вторая космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело земное притяжение и смогло осуществить межпланетный полет в пределах Солнечной системы, равна $$ v_2=sqrt{frac{2GM_oplus}{R_oplus}}=sqrt{2gR_oplus}approx 11,18 text{км/с} $$

Аналогичные формулы для первой и второй космических скоростей можно получить для любой планеты, как в Солнечной системе, так и за ее пределами.

Нужно только знать массу и радиус планеты.

Можно также рассчитать скорость, необходимую для межзвездных полетов при старте с Земли. Это задача непростая, т.к. необходимо учесть относительное движение трех тел: космического корабля, Земли и Солнца.

Третья космическая скорость
Скорость, достаточная для того, чтобы тело, запускаемое с Земли на уровне моря ((h=0)), преодолело притяжение Земли и Солнца и смогло осуществить межзвездный полет за пределы Солнечной системы, равна $$ v_3=sqrt{(sqrt{2}-1)^2frac{GM_odot}{R_odot}+frac{2GM_oplus}{R_oplus}} approx 16,65 text{км/с} $$

В этой формуле, (M_odot) – масса Солнца, (R_odot) – радиус орбиты вращения Земли вокруг Солнца.

п.5. Искусственные спутники Земли

Искусственный спутник Земли – это космический летательный аппарат, вращающийся вокруг Земли по геоцентрической орбите (эллипсу, в одном из фокусов которого находится Земля).

Круговая орбита спутника в плоскости экватора Земли, двигаясь по которой он находится всё время над одной и той же точкой экватора, называется геостационарной. Такие спутники имеет большое значение для создания систем связи.

Чтобы запустить спутник на орбиту, ему необходимо сообщить скорость, больше чем первая космическая, но меньше чем вторая космическая: $$ 7,92frac{text{км}}{text{с}}lt vlt 11,18frac{text{км}}{text{с}} $$

На практике, получение соответствующей силы тяги ракетного двигателя, способного разогнать ракету до таких скоростей, является сложной технической проблемой.

Вывод спутников на орбиту осуществляется с помощью многоступенчатых ракет-носителей в несколько этапов. На первом этапе ракета стартует и, двигаясь вертикально вверх, проходит плотные слои атмосферы на относительно небольшой скорости, после чего отработавшие двигатели первой ступени отделяются (у Илона Маска – аккуратно возвращаются на Землю). На втором этапе ракета постепенно разворачивается параллельно к поверхности Земли и начинает ускоряться. Когда скорость достигает определенной величины и направления, работа двигателей прекращается, отделяется вторая ступень. Спутник начинает самостоятельное движение по расчетной орбите.

Искусственные спутники Земли используются для решения разнообразных научных и прикладных задач.

В апреле 2020 года на орбите находилось 1388 спутников США, 356 Китая, 167 России, 138 Британии, 78 Японии и 627 других стран. Из них: 1007 спутников связи, 446 спутников для исследования Земли, 97 спутников навигации и GPS, 87 научно-исследовательских спутников и другие космические аппараты.

п.6. Задачи

Задача 1. С какой силой Земля притягивает Луну? Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), масса Луны (m_{text{л}}=7,36cdot 10^{22} text{кг}), средний радиус лунной орбиты (R=384 text{тыс.км}). А с какой силой Луна притягивает Землю?

Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(m_{text{л}}=7,36cdot 10^{22} text{кг})
(R=384 text{тыс.км}=3,84cdot 10^8 text{м})
__________________
(F_{text{ЗЛ}}, F_{text{ЛЗ}}-?)

По закону всемирного тяготения $$ F_{text{ЗЛ}}=Gfrac{M_oplus m_{text{л}}}{R^2} $$ Получаем begin{gather*} F_{text{ЗЛ}}=6,67cdot 10^{-11}cdot frac{5,97cdot 10^{24}cdot 7,36cdot 10^{22}}{(3,84cdot 10^8)^2}approx \[6pt] approx 19,9cdot 10^{-11+24+22-16}=1,99cdot 10^{20} (text{Н}) end{gather*} Эта сила направлена от центра Луны к центру Земли.
По третьему закону Ньютона, Луна притягивает Землю с такой же по величине силой, которая направлена противоположно, от центра Земли к центру Луны: $$ overrightarrow{F_{text{ЗЛ}}}=-overrightarrow{F_{text{ЛЗ}}} $$ Ответ: 1,99·1020 Н

Задача 2. Самая высокая гора на Земле – Эверест (8848 м). Во сколько раз сила тяжести на уровне моря больше силы тяжести на вершине Эвереста? Радиус Земли (R_oplus=6370 text{км}).

Дано:
(R_oplus=6370 text{км}=6,37cdot 10^6 text{м})
(h=8848 text{м})
__________________
(frac{F}{F_h}-?)

Сила тяжести для тела массой (m) на уровне моря begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} На вершине Эвереста begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{(R_oplus +h)^2}= frac{(R_oplus+h)^2}{R^2_oplus}=left(frac{R_oplus+h}{R_oplus}right)^2 =left(1+frac{h}{R_oplus}right)^2 end{gather*} Получаем: begin{gather*} frac{F}{F_h}=left(1+frac{8848}{6,37cdot 10^6}right)^2approx 1,003 end{gather*} Ответ: в 1,003 раза

Задача 3. На поверхности Земли на тело действует силы тяжести (F=54 text{Н}).
Чему будет равна сила тяжести, действующая на это тело на высоте, равной двум радиусам Земли?

Дано:
(F=54 text{Н})
(h=2R_oplus )
__________________
(F_h-?)

Сила тяжести на поверхности Земли begin{gather*} F=Gfrac{M_oplus m}{R_oplus^2} end{gather*} Сила тяжести на высоте (h) begin{gather*} F_h=Gfrac{M_oplus m}{(R_oplus +h)^2}=Gfrac{M_oplus m}{(R_oplus+2R_oplus)^2}=Gfrac{M_oplus m}{9R^2_oplus} end{gather*} Отношение сил: begin{gather*} frac{F}{F_h}=Gfrac{M_oplus m}{R_oplus^2}:Gfrac{M_oplus m}{9R^2_oplus}=9, F_h=frac{F}{9}\[6pt] F_h=frac{54}{9}=6 (text{Н}) end{gather*} Ответ: 6 Н

Задача 4*. Чему равны первая и вторая космические скорости вблизи поверхности Луны? Сравните их со значениями первой и второй космических скоростей у поверхности Земли.
Радиус Луны (R=1740 text{км}), масса Луны (M=7,36cdot 10^{22} text{кг}).

Дано:
(R=1740 text{км}=1,74cdot 10^6 text{м})
(M=7,36cdot 10^{22} text{кг})
__________________
(v_1, v_2-?)
(frac{v_{text{1З}}}{v_{text{1Л}}}, frac{v_{text{2З}}}{v_{text{2Л}}}-?)

Первая и вторая космические скорости $$ v_1=sqrt{frac{GM}{R}}, v_2=sqrt{frac{2GM}{R}}=sqrt{2}v_1 $$ Получаем: begin{gather*} v_1=sqrt{frac{6,67cdot 10^{-11}cdot 7,36cdot 10^{22}}{1,74cdot 10^6}}approx sqrt{2,82cdot 10^6}approx\[6pt] approx 1,68cdot 10^3frac{text{м}}{text{с}}=1,68frac{text{км}}{text{с}}\[6pt] v_2=sqrt{2}cdot 1,68approx 2,37frac{text{км}}{text{с}} end{gather*} Сравним со скоростями для Земли: begin{gather*} frac{v_{text{1З}}}{v_{text{1Л}}}=frac{7,92}{1,68}approx 4,7 text{раз}, frac{v_{text{2З}}}{v_{text{2Л}}}=frac{sqrt{2}v_{text{1З}}}{sqrt{2}v_{text{1Л}}}=frac{v_{text{1З}}}{v_{text{1Л}}}approx 4,7 text{раз} end{gather*} Космические скорости для Луны в 4,7 раз меньше земных.
Ответ: 1,68 км/с; 2,37 км/с; в 4,7 раз меньше

Задача 5*. Рассчитайте радиус геостационарной орбиты спутника и высоту такого спутника над Землей. Масса Земли (M_oplus=5,97cdot 10^{24} text{кг}), радиус Земли (R_oplus =6400 text{км}).
Ответ запишите в км.

Дано:
(M_oplus=5,97cdot 10^{24} text{кг})
(T=24 text{ч}=8,64cdot 10^4 text{с})
(R_oplus =6400 text{км}=6,4cdot 10^6 text{м})
__________________
(R, h-?)

На геостационарной орбите спутник «зависает» над Землей, его линейная скорость равна отношению длины окружности орбиты к периоду вращения (сутки): begin{gather*} v=frac{2pi R}{T}=sqrt{frac{GM_oplus}{R}}Rightarrow frac{4pi ^2R^2}{T^2}=frac{GM_oplus}{R}Rightarrow R^3=frac{GM_oplus T^2}{4pi ^2}\[6pt] R=sqrt[{3}]{frac{GMT^2}{4pi ^2}} end{gather*} Получаем: begin{gather*} R=sqrt[{3}]{frac{6,67cdot 10^{-11}cdot 5,97cdot 10^{24}cdot (8,64cdot 10^4)^2}{4pi ^2}}approx sqrt[{3}]{75,3cdot 10^{-11+24+8}}approx\[6pt] approx 4,22cdot 10^7 (text{м})=42200 (text{км})\[6pt] h=R-R_oplus=42200-6400=35800 (text{км}) end{gather*} Ответ: 42200 км; 35800 км

Источник

Физика Как найти ускорение свободного падения на конкретной планете/ спутнике

Дмитрий Картавый



Знаток

(306),
на голосовании



3 года назад

как найти ускорение свободного падения на спутнике зная радиус орбиты, радиус спутника, среднюю плотность и вторую космическую скорость на этом спутнике

Голосование за лучший ответ

Сновидец

Оракул

(66894)


3 года назад

g=GM/R^2

Дмитрий КартавыйЗнаток (306)

3 года назад

m= p * V ; Vшара=4/3ПиR^3
таким образом у меня M тритона вышла на 21425601600
g= 6,7 * 21425601600/(1350)^2 что выходит на 78766,272
мне кажется это слишком много, нет ?

Сновидец
Оракул
(66894)
6,7*10^-11

Похожие вопросы

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.

Ускорение свободного падения на поверхности[1] некоторых небесных тел, м/с2 и g

Земля 9,81 м/с2 1,00 g Солнце 273,1 м/с2 27,85 g
Луна 1,62 м/с2 0,165 g Меркурий 3,70 м/с2 0,378 g
Венера 8,88 м/с2 0,906 g Марс 3,86 м/с2 0,394 g
Юпитер 24,79 м/с2 2,528 g Сатурн 10,44 м/с2 1,065 g
Уран 8,86 м/с2 0,903 g Нептун 11,09 м/с2 1,131 g
Эрида 0,82 ± 0,02 м/с2 0,084 ± 0,002 g Плутон 0,617 м/с2 0,063 g

Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.

Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².

Физическая сущность[править | править код]

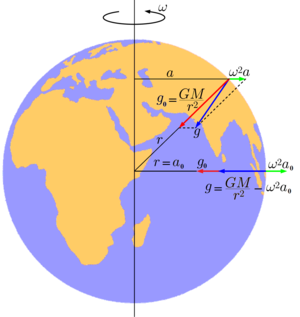
Две компоненты ускорения свободного падения на Земле

g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна

GM/r2 и центробежная, равная

ω2a, где

a — расстояние до земной оси,

ω — угловая скорость вращения Земли.

Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.

Центростремительное ускорение[править | править код]

Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.

Гравитационное ускорение[править | править код]

Гравитационное ускорение на различной высоте h над уровнем моря

h, км g, м/с2 h, км g, м/с2
0 9,8066 20 9,7452
1 9,8036 50 9,6542
2 9,8005 80 9,5644
3 9,7974 100 9,505
4 9,7943 120 9,447
5 9,7912 500 8,45
6 9,7882 1000 7,36
8 9,7820 10 000 1,50
10 9,7759 50 000 0,125
15 9,7605 400 000 0,0025

В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:

g=G{frac {M}{r^{2}}},

где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.

Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.

Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:

g(h)={frac {GM}{(r+h)^{2}}},
где M — масса планеты.

Ускорение свободного падения на Земле[править | править код]

Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:

{displaystyle g=9{,}780318(1+0{,}005302sin ^{2}varphi -0{,}000006sin ^{2}2varphi )-0{,}000003086h,}
где varphi  — широта рассматриваемого места,
h — высота над уровнем моря в метрах.

Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].

Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.

Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].

Ускорение свободного падения для некоторых городов
Город Долгота Широта Высота над уровнем моря, м Ускорение свободного падения, м/с2
Алма-Ата 76,85 в.д. 43,22 с.ш. 786 9.78125
Берлин 13,40 в.д. 52,50 с.ш. 40 9,81280
Будапешт 19,06 в.д. 47,48 с.ш. 108 9,80852
Вашингтон 77,01 з.д. 38,89 с.ш. 14 9,80188
Вена 16,36 в.д. 48,21 с.ш. 183 9,80860
Владивосток 131,53 в.д. 43,06 с.ш. 50 9,80424
Гринвич 0,0 в.д. 51,48 с.ш. 48 9,81188
Каир 31,28 в.д. 30,07 с.ш. 30 9,79317
Киев 30,30 в.д. 50,27 с.ш. 179 9,81054
Мадрид 3,69 в.д. 40,41 с.ш. 667 9,79981
Минск 27,55 в.д. 53,92 с.ш. 220 9,81347
Москва 37,61 в.д. 55,75 с.ш. 151 9,8154
Нью-Йорк 73,96 з.д. 40,81 с.ш. 38 9,80247
Одесса 30,73 в.д. 46,47 с.ш. 54 9.80735
Осло 10,72 в.д. 59,91 с.ш. 28 9,81927
Париж 2,34 в.д. 48,84 с.ш. 61 9,80943
Прага 14,39 в.д. 50,09 с.ш. 297 9,81014
Рим 12,99 в.д. 41,54 с.ш. 37 9,80312
Стокгольм 18,06 в.д. 59,34 с.ш. 45 9,81843
Токио 139,80 в.д. 35,71 с.ш. 18 9,79801

Измерение[править | править код]

Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.

См. также[править | править код]

  • Свободное падение
  • Гравиметрия
  • Гравиразведка
  • Перегрузка (летательные аппараты)

Примечания[править | править код]

  1. ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
  2. ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
  3. ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
  4. ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
  5. ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
  6. ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
  7. ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
  8. ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
  9. ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
  10. ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
  11. ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.

Литература[править | править код]

  • Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
Источник

Закон всемирного тяготения. Движение планет и спутников

 Закон всемирного тяготения

Со­об­ра­же­ния Нью­то­на со­сто­я­ли в сле­ду­ю­щем.

– Если сила при­тя­же­ния тела к Земле про­пор­ци­о­наль­на массе тела Fтяг = mg, а каж­дой силе дей­ствия есть сила про­ти­во­дей­ствия F1,2 = F2,1 и если тело при­тя­ги­ва­ет­ся к Земле, то и Земля при­тя­ги­ва­ет­ся к телу. Тогда сила тя­го­те­ния долж­на быть про­пор­ци­о­наль­на как массе од­но­го тела, так и массе вто­ро­го тела Fтяг ~ m1m2, то есть сила тя­го­те­ния про­пор­ци­о­наль­на про­из­ве­де­нию масс, вза­и­мо­дей­ству­ю­щих тел.

– Нью­тон за­ме­тил, что уско­ре­ние на пла­не­те Земля, уско­ре­ние сво­бод­но­го па­де­ния

g = Fтяг / m – это при­мер­но 10 м/с2, а уско­ре­ние, с ко­то­рым дви­жет­ся Луна по своей ор­би­те ал = Fтяг / Мл = g / 3600, – это цен­тро­стре­ми­тель­ное уско­ре­ние, в 3600 раз мень­ше уско­ре­ния сво­бод­но­го па­де­ния. Нью­тон до­га­дал­ся, по­че­му такая раз­ни­ца в чис­лах: дело в том, что рас­сто­я­ние от Земли до Луны со­став­ля­ет при­мер­но ше­сть­де­сят зем­ных ра­ди­у­сов rз-л ≈ 60Rз. Их, а также уско­ре­ние 3600 Нью­тон объ­еди­нил сле­ду­ю­щим вы­во­дом: сила тя­го­те­ния об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между вза­и­мо­дей­ству­ю­щи­ми те­ла­ми Fтяг ~ 1 / r2.

Учи­ты­вая эти два по­сы­ла, Нью­тон дал общую фор­му­ли­ров­ку: сила все­мир­но­го тя­го­те­ния прямо про­пор­ци­о­наль­на мас­сам вза­и­мо­дей­ству­ю­щих тел и об­рат­но про­пор­ци­о­наль­на квад­ра­ту рас­сто­я­ния между ними.

  = γ (-)

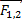
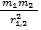
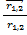
γ – ко­эф­фи­ци­ент про­пор­ци­о­наль­но­сти (гамма), а на­прав­ле­ние силы – это сила при­тя­же­ния друг к другу, и на­прав­ле­ние в этой фор­му­ле да­ет­ся сле­ду­ю­щим об­ра­зом: это еди­нич­ный век­тор, при­ве­ден­ный из пер­во­го тела ко вто­ро­му, то есть от­но­ше­ние са­мо­го век­то­ра к его мо­ду­лю. Знак минус озна­ча­ет, что сила тя­го­те­ния на­прав­ле­на не от пер­во­го тела ко вто­ро­му, а от вто­ро­го тела к пер­во­му.

Ко­эф­фи­ци­ент про­пор­ци­о­наль­но­сти из­ме­рил Ка­вен­диш в своем экс­пе­ри­мен­те:

γ = G = 6,62 · 10-11 Нм2 / кг2

Из за­ко­на все­мир­но­го тя­го­те­ния сле­ду­ют фор­му­лы уско­ре­ния сво­бод­но­го па­де­ния:

1. Уско­ре­ние сво­бод­но­го па­де­ния у по­верх­но­сти пла­не­ты:

g0 = Fтяг / m = γmМз / R2з · m = γ · Мз / R2з.

Зная уско­ре­ние на пла­не­те Земля, ра­ди­ус Земли, зна­че­ние гра­ви­та­ци­он­ной по­сто­ян­ной, можно при необ­хо­ди­мо­сти вы­чис­лить массу Земли.

2. Уско­ре­ние сво­бод­но­го па­де­ния на ка­ком-то рас­сто­я­нии h от по­верх­но­сти пла­не­ты:

gh = γ· Мз / (Rз + h)2 = (γ · Мз / R2з) · R2з / (Rз + h)2.

Так как в такой форме ее труд­но при­ме­нить, то поль­зу­ют­ся при­ве­ден­ной фор­му­лой:

gh = g0 · (Rз / Rз + h)2

3. Уско­ре­ние сво­бод­но­го па­де­ния на глу­бине: gh↓ = g0 · (Rз – h / Rз).

На ос­но­ве за­ко­на все­мир­но­го тя­го­те­ния можно рас­счи­тать ско­рость спут­ни­ков пла­нет (рис. 1).

При­мер рас­че­та ско­ро­сти спут­ни­ка

Рис. 1. При­мер рас­че­та ско­ро­сти спут­ни­ка

m ┴  => gh =  ; g0 = ; Vh =  

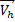
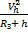
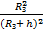
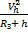
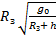
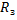
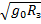
при h <<  Vh =  ≈ 7,9 км/с

В этом слу­чае сила при­тя­же­ния будет пер­пен­ди­ку­ляр­на ско­ро­сти спут­ни­ка при дви­же­нии по кру­го­вой ор­би­те, она вы­зы­ва­ет цен­тро­стре­ми­тель­ное дви­же­ние. Зная уско­ре­ние сво­бод­но­го па­де­ния на вы­со­те h, по­лу­ча­ем фор­му­лу ско­ро­сти спут­ни­ка на вы­со­те h. Оче­вид­но, что с ро­стом вы­со­ты ско­рость будет умень­шать­ся, а у самой по­верх­но­сти Земли при очень малых h по срав­не­нию с ра­ди­у­сом Земли при­ме­ня­ет­ся упро­ще­ние. То есть h пре­не­бре­га­ют, вно­сят ра­ди­ус Земли под ко­рень, про­из­во­дят со­кра­ще­ния и по­лу­ча­ют фор­му­лу пер­вой кос­ми­че­ской ско­ро­сти, ко­то­рая равна 7,9 км/с. При такой ско­ро­сти спут­ник неда­ле­ко от по­верх­но­сти Земли может дви­гать­ся по кру­го­вой ор­би­те.

 Пример решения задачи 1

У по­верх­но­сти Луны на кос­мо­нав­та дей­ству­ет сила тя­го­те­ния 120 Н. Какая сила тя­го­те­ния дей­ству­ет со сто­ро­ны Луны на того же кос­мо­нав­та в кос­ми­че­ском ко­раб­ле, дви­жу­щем­ся по кру­го­вой ор­би­те во­круг Луны на рас­сто­я­нии трех лун­ных ра­ди­у­сов от ее цен­тра?

1. 0 Н; 2. 39 Н; 3. 21 Н; 4. 13 Н.

За­пи­шем крат­кое усло­вие за­да­чи и рас­смот­рим ре­ше­ние:

Какая сила тя­го­те­ния дей­ству­ет со сто­ро­ны Луны на того же кос­мо­нав­та в кос­ми­че­ском ко­раб­ле

Ответ: ва­ри­ант 4. 13 Н.

 Пример решения задачи 2

Два тела мас­сой по 1000 тонн уда­ле­ны на 0,1 км друг от друга. Найти силу их гра­ви­та­ци­он­но­го при­тя­же­ния.

1. 6,7 мН; 2. 0,67 Н; 3. 6,7 Н; 4. 6,7 кН.

За­пи­сы­ва­ем крат­кое усло­вие за­да­чи, пе­ре­во­дя тонны в ки­ло­грам­мы, рас­сто­я­ние в метры, и ре­ше­ние.

Пример решения задачи 2 айти силу их гра­ви­та­ци­он­но­го при­тя­же­ния

Ответ: ва­ри­ант 1. 6,7 мН.

При­ме­няя закон все­мир­но­го тя­го­те­ния, мы по­лу­ча­ем пра­виль­ный ответ 1.

 Пример решения задачи 3

Чему равна ско­рость спут­ни­ка Земли на кру­го­вой ор­би­те на вы­со­те 500 км от ее по­верх­но­сти? Ра­ди­ус Земли при­нять рав­ным 6400 км.

1. 7,6 км/с; 2. 7,8 км/с; 3. 7,9 км/с; 4. 8,2 км/с.

За­пи­сы­ва­ем крат­кое усло­вие за­да­чи и вы­чис­ле­ния.

Чему равна ско­рость спут­ни­ка Земли на кру­го­вой ор­би­те на вы­со­те 500 км от ее по­верх­но­сти

Ответ: ва­ри­ант 1. 7,6 км/с.

Ис­поль­зуя фор­му­лу спут­ни­ка на вы­со­те, мы вно­сим ра­ди­ус пла­не­ты под знак ра­ди­ка­ла и раз­би­ва­ем его на два мно­жи­те­ля. У нас под кор­нем по­лу­чи­лась пер­вая кос­ми­че­ская ско­рость, ко­то­рую мы можем вы­не­сти за знак ра­ди­ка­ла и, под­ста­вив зна­че­ния, по­лу­чим, что ско­рость будет равна 7,6 км/с – это со­от­вет­ству­ет 1 от­ве­ту.

 Движение планет и спутников

На ос­но­ве за­ко­на все­мир­но­го тя­го­те­ния рас­счи­ты­ва­ют пе­ри­од об­ра­ще­ния спут­ни­ков, как есте­ствен­ных, так и ис­кус­ствен­ных. Зная пе­ри­од об­ра­ще­ния, мы можем найти массу спут­ни­ков. Пе­ри­од об­ра­ще­ния на­хо­дит­ся по фор­му­ле: Т = 2πR / V, то есть длина окруж­но­сти, де­лен­ная на ско­рость по ор­би­те. При малых вы­со­тах по срав­не­нию с ра­ди­у­сом Земли для вы­чис­ле­ния ско­ро­сти спут­ни­ка, ко­то­рый летит неда­ле­ко от по­верх­но­сти Земли, пе­ри­од мы на­хо­дим по фор­му­ле:

То = 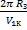 = 2π

Пом­ним о том, что в чис­ли­те­ле у нас длина эк­ва­то­ра, а в зна­ме­на­те­ле пер­вая кос­ми­че­ская ско­рость. Про­из­ве­дя рас­че­ты мы по­лу­чим, что То ≈ 5060 с ≈ 1 ч 24 мин = 1,4 ч – это время, за ко­то­рое ис­кус­ствен­ный спут­ник Земли, дви­га­ю­щий­ся неда­ле­ко от по­верх­но­сти, со­вер­ша­ет пол­ный обо­рот. Если спут­ник летит по ор­би­те, вы­со­та ко­то­рой со­из­ме­ри­ма с ра­ди­у­сом Земли, мы поль­зу­ем­ся фор­му­лой:

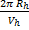
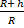
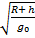
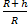
Тh =  = 2π  = То ( )3/2

Эту фор­му­лу мы по­лу­чи­ли, внеся (R + h) под знак ра­ди­ка­ла и ис­поль­зуя уже по­лу­чен­ное зна­че­ние То.

Рас­смот­рим за­да­чу, по ко­то­рой была вы­чис­ле­на масса Солн­ца.

Ра­ди­ус зем­ной ор­би­ты со­став­ля­ет 1,5 · 1011 м. Чему равна масса Солн­ца?

Обыч­но эта за­да­ча вы­зы­ва­ет за­труд­не­ние, так как дан всего лишь один па­ра­метр, но нужно пом­нить, что Земля во­круг Солн­ца со­вер­ша­ет один обо­рот за 365 дней, в сут­ках у нас 24 часа и в каж­дом часе 3600 се­кунд, так что нам из­ве­стен пе­ри­од об­ра­ще­ния Земли как спут­ни­ка Солн­ца. По­это­му за­пи­сы­ва­ем крат­кое усло­вие за­да­чи и ре­ше­ние.

Движение планет и спутников

Ответ: 2·1030 кг.

Сила, с ко­то­рой Земля при­тя­ги­ва­ет­ся к Солн­цу, при­во­дит к цен­тро­стре­ми­тель­но­му уско­ре­нию, по­это­му при­ме­ня­ем фор­му­лу, ко­то­рая вы­ра­жа­ет­ся через пе­ри­од об­ра­ще­ния. С дру­гой сто­ро­ны, это сила тя­го­те­ния, и по за­ко­ну все­мир­но­го тя­го­те­ния вы­ра­жа­ет­ся через гра­ви­та­ци­он­ную по­сто­ян­ную, массу Земли и массу Солн­ца, де­лен­ные на квад­рат рас­сто­я­ния между ними. Со­кра­ща­ем массу Земли в двух по­след­них чле­нах этого ра­вен­ства, неиз­вест­ным оста­ет­ся толь­ко масса Солн­ца, ко­то­рую мы можем вы­чис­лить, под­став­ляя все дан­ные.

Рас­смот­рим еще одну за­да­чу.

В ре­зуль­та­те пе­ре­хо­да с одной кру­го­вой ор­би­ты на дру­гую цен­тро­стре­ми­тель­ное уско­ре­ние спут­ни­ка Земли умень­ша­ет­ся. Как из­ме­ня­ют­ся в ре­зуль­та­те этого пе­ре­хо­да ра­ди­ус ор­би­ты спут­ни­ка, ско­рость его дви­же­ния по ор­би­те и пе­ри­од об­ра­ще­ния во­круг Земли? Для каж­дой ве­ли­чи­ны опре­де­ли­те со­от­вет­ству­ю­щий ха­рак­тер из­ме­не­ния:

1. уве­ли­чи­лась; 2. умень­ши­лась; 3. не из­ме­ни­лась.

При ре­ше­нии задач с вы­бо­ром от­ве­та необ­хо­ди­мо перед ре­ше­ни­ем вы­пи­сать фор­му­лы ве­ли­чин, ко­то­рые фи­гу­ри­ру­ют в усло­вии за­да­чи. Ска­за­но о том, что цен­тро­стре­ми­тель­ное уско­ре­ние умень­ши­лось, а цен­тро­стре­ми­тель­ное уско­ре­ние спут­ни­ка есть не что иное, как уско­ре­ние сво­бод­но­го па­де­ния на его ор­би­те: gh = g0 · (Rз / Rз + h)2, если g умень­ши­лось, зна­чит, h уве­ли­чи­лось.

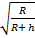
Ско­рость спут­ни­ка на ор­би­те, на­хо­дя­ще­го­ся на вы­со­те, – Vh =  , если h уве­ли­чи­ва­ет­ся, то ско­рость умень­ша­ет­ся.

Фор­му­лу для пе­ри­о­да об­ра­ще­ния при­ме­ня­ем Тh = То (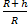)3/2, по ко­то­рой видно без вы­чис­ле­ний, что про­изо­шли из­ме­не­ния.

Ответ: в ре­зуль­та­те пе­ре­хо­да ра­ди­ус ор­би­ты спут­ни­ка уве­ли­чил­ся, ско­рость его дви­же­ния по ор­би­те умень­ши­лась, пе­ри­од об­ра­ще­ния во­круг Земли уве­ли­чил­ся.

 Заключение

На­ли­чие все­мир­но­го тя­го­те­ния объ­яс­ня­ет устой­чи­вость Сол­неч­ной си­сте­мы, дви­же­ние пла­нет и дру­гих небес­ных тел. С от­кры­ти­ем за­ко­на все­мир­но­го тя­го­те­ния к людям при­шло по­ни­ма­ние прин­ци­па стро­е­ния все­лен­ной. Яр­чай­шим при­ме­ром при­ме­не­ния за­ко­на все­мир­но­го тя­го­те­ния яв­ля­ет­ся за­пуск ис­кус­ствен­но­го спут­ни­ка Земли. Спут­ник все время на­хо­дит­ся на рав­ном рас­сто­я­нии над по­верх­но­стью Земли. Земля при­тя­ги­ва­ет оди­на­ко­во во всех на­прав­ле­ни­ях.

Источник

Ускорение свободного падения тел на Луне (естественный и единственный спутник планеты Земля) рассчитывается по формуле:
Ускорение свободного падения на Луне формула
G — гравитационная постоянная, находится из закона всемирного тяготения и равна 6,67·10-11 Н м2/кг2
Mл — масса Луны;
 Rл — радиус Луны.
Приведённая формула применима для расчёта ускорения свободного падения тела на планетах солнечной системы, в том числе и на планете Земля.

Наименование планеты солнечной системы Значение ускорения свободного падения, м/с2
Солнце 274
Юпитер 25,8
Нептун 11,6
Сатурн 11,3
Земля 9,8
Уран 9
Венера 8,9
Меркурий 3,7
Марс 3,7
Луна 1,62

21228


Источник

Добавить комментарий