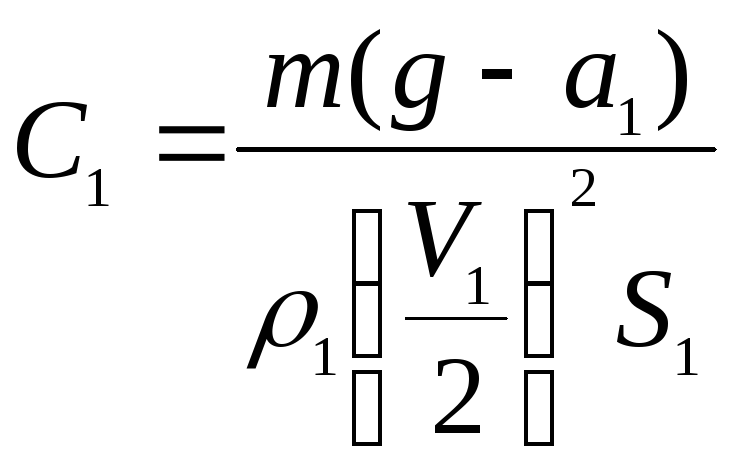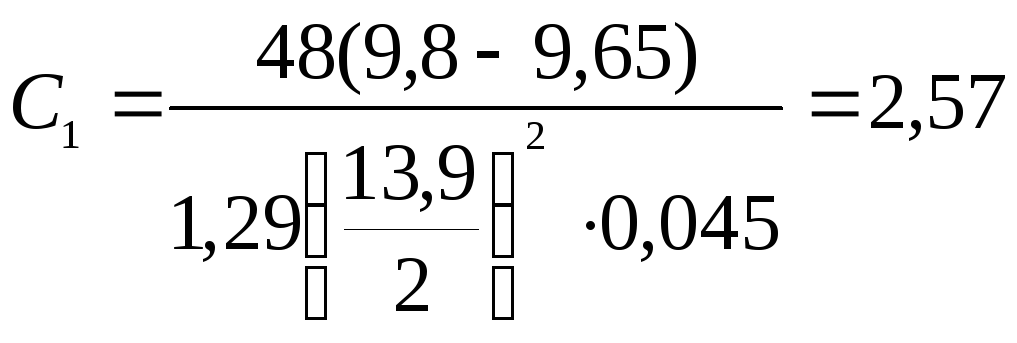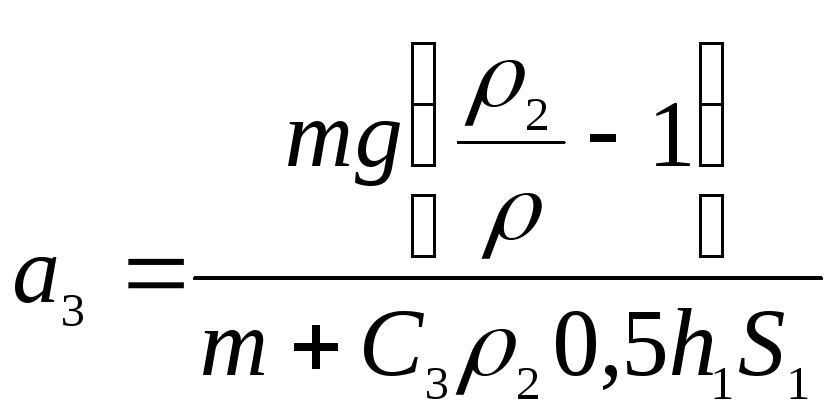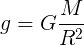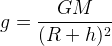|
Понятно, что вопрос чисто теоретический: скважин такой глубины не бывает. Ускорение свободного падения на поверхности планеты определяется соотношением g = GM/R^2. Масса планеты, если её форма сферическая или близка к сфере, будет М = р*4*pi*R^3/3 (p – средняя плотность вещества планеты). Тогда ускорение свободного падения на поверхности планеты gп = G*р*4*pi*R^3/3R^2 = G*р*4*pi*R/3. На любой глубине верхние слои вещества планеты, естественно оказывают гравитационное воздействие на тело, но поскольку вещество расположено со всех сторон, то сумма гравитационных сил внешних слоев вещества, равна нулю. И можно считать, что верхних слоев вещества просто нет. Если допустить, что средняя плотность вещества центральной зоны планеты такая же как у всей планеты,то g на глубине 1000 км g1000 = G*р*4*pi*(R-1000)/3. Ускорение на поверхности Земли деленной на ускорение на глубине 1000 км gп/g1000 = G*р*4*pi*R*3/ G*р*4*pi*(R-1000)*3 = R/(R-1000). Отсюда g1000 = gп*(R-1000)/R = 9,81*(6371-1000)/6371= 8,270…м/с^2 автор вопроса выбрал этот ответ лучшим Анатолий1950 8 лет назад Вопрос у Вас какой-то усеченный. Если Вы имеете ввиду ускорение свободного падения, то оно будет 9,8 м кв в сек, независимо от глубины так как на тело действует только сила притяжения Земли. Знаете ответ? |
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 19 августа 2022 года; проверки требуют 4 правки.
| Земля | 9,81 м/с2 | 1,00 g | Солнце | 273,1 м/с2 | 27,85 g |
| Луна | 1,62 м/с2 | 0,165 g | Меркурий | 3,70 м/с2 | 0,378 g |
| Венера | 8,88 м/с2 | 0,906 g | Марс | 3,86 м/с2 | 0,394 g |
| Юпитер | 24,79 м/с2 | 2,528 g | Сатурн | 10,44 м/с2 | 1,065 g |
| Уран | 8,86 м/с2 | 0,903 g | Нептун | 11,09 м/с2 | 1,131 g |
| Эрида | 0,82 ± 0,02 м/с2 | 0,084 ± 0,002 g | Плутон | 0,617 м/с2 | 0,063 g |
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении взаимодействия с другими телами.
В соответствии с уравнением движения тел в неинерциальных системах отсчёта[2] ускорение свободного падения численно равно силе тяжести, воздействующей на объект единичной массы.
Ускорение свободного падения на поверхности Земли g (обычно произносится как «же») варьируется от 9,780 м/с² на экваторе до 9,82 м/с² на полюсах[3]. Стандартное («нормальное») значение, принятое при построении систем единиц, составляет 9,80665 м/с²[4][5]. Стандартное значение g было определено как «среднее» в каком-то смысле на всей Земле: оно примерно равно ускорению свободного падения на широте 45,5° на уровне моря. В приблизительных расчётах его обычно принимают равным 9,81, 9,8 или более грубо 10 м/с².
Физическая сущность[править | править код]
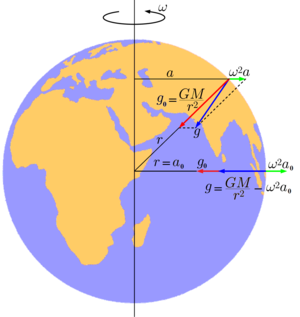
Две компоненты ускорения свободного падения на Земле
g: гравитационная (в приближении сферически симметричной зависимости плотности от расстояния от центра Земли) равна
GM/r2 и центробежная, равная
ω2a, где
a — расстояние до земной оси,
ω — угловая скорость вращения Земли.
Для определённости будем считать, что речь идёт о свободном падении на Земле. Эту величину можно представить как векторную сумму двух слагаемых: гравитационного ускорения, вызванного земным притяжением, и центробежного ускорения, связанного с вращением Земли.
Центростремительное ускорение[править | править код]
Центростремительное ускорение является следствием вращения Земли вокруг своей оси. Именно центростремительное ускорение, вызванное вращением Земли вокруг своей оси, вносит наибольший вклад в неинерциальность системы отсчёта, связанную с Землёй. В точке, находящейся на расстоянии a от оси вращения, оно равно ω2a, где ω — угловая скорость вращения Земли, определяемая как ω = 2π/T, а Т — время одного оборота вокруг своей оси, для Земли равное 86164 секундам (звёздные сутки). Центростремительное ускорение направлено по нормали к оси вращения Земли. На экваторе оно составляет 3,39636 см/с2, причём на других широтах направление вектора его не совпадает с направлением вектора гравитационного ускорения, направленного к центру Земли.
Гравитационное ускорение[править | править код]
| h, км | g, м/с2 | h, км | g, м/с2 |
|---|---|---|---|
| 0 | 9,8066 | 20 | 9,7452 |
| 1 | 9,8036 | 50 | 9,6542 |
| 2 | 9,8005 | 80 | 9,5644 |
| 3 | 9,7974 | 100 | 9,505 |
| 4 | 9,7943 | 120 | 9,447 |
| 5 | 9,7912 | 500 | 8,45 |
| 6 | 9,7882 | 1000 | 7,36 |
| 8 | 9,7820 | 10 000 | 1,50 |
| 10 | 9,7759 | 50 000 | 0,125 |
| 15 | 9,7605 | 400 000 | 0,0025 |
В соответствии с законом всемирного тяготения, величина гравитационного ускорения на поверхности Земли или космического тела связана с его массой M следующим соотношением:
,
где G — гравитационная постоянная (6,67430[15]·10−11 м3·с−2·кг−1)[6], а r — радиус планеты. Это соотношение справедливо в предположении, что плотность вещества планеты сферически симметрична. Приведённое соотношение позволяет определить массу любого космического тела, включая Землю, зная её радиус и гравитационное ускорение на её поверхности, либо, наоборот, по известной массе и радиусу определить ускорение свободного падения на поверхности.
Исторически масса Земли была впервые определена Генри Кавендишем, который провёл первые измерения гравитационной постоянной.
Гравитационное ускорение на высоте h над поверхностью Земли (или иного космического тела) можно вычислить по формуле:
,
- где M — масса планеты.
Ускорение свободного падения на Земле[править | править код]
Ускорение свободного падения у поверхности Земли зависит от широты. Приблизительно оно может быть вычислено (в м/с²) по эмпирической формуле[7][8]:
- где
— широта рассматриваемого места,
— высота над уровнем моря в метрах.
Полученное значение лишь приблизительно совпадает с ускорением свободного падения в данном месте. При более точных расчётах необходимо использовать одну из моделей гравитационного поля Земли[en][9], дополнив её поправками, связанными с вращением Земли, приливными воздействиями.
На ускорение свободного падения влияют и другие факторы, например, атмосферное давление, которое меняется в течение суток: от атмосферного давления зависит плотность воздуха в большом объёме, а следовательно и результирующая сила тяжести, изменение которой могут зафиксировать высокочувствительные гравиметры[10].
Пространственные изменения гравитационного поля Земли (гравитационные аномалии) связаны с неоднородности плотности в её недрах, что может быть использовано для поиска залежей полезных ископаемых методами гравиразведки.
Почти везде ускорение свободного падения на экваторе ниже, чем на полюсах, за счёт центробежных сил, возникающих при вращении планеты, а также потому, что радиус r на полюсах меньше, чем на экваторе из-за сплюснутой формы планеты. Однако места экстремально низкого и высокого значения g несколько отличаются от теоретических показателей по этой модели. Так, самое низкое значение g (9,7639 м/с²) зафиксировано на горе Уаскаран в Перу в 1000 км южнее экватора, а самое большое (9,8337 м/с²) — в 100 км от Северного полюса[11].
| Ускорение свободного падения для некоторых городов | ||||
|---|---|---|---|---|
| Город | Долгота | Широта | Высота над уровнем моря, м | Ускорение свободного падения, м/с2 |
| Алма-Ата | 76,85 в.д. | 43,22 с.ш. | 786 | 9.78125 |
| Берлин | 13,40 в.д. | 52,50 с.ш. | 40 | 9,81280 |
| Будапешт | 19,06 в.д. | 47,48 с.ш. | 108 | 9,80852 |
| Вашингтон | 77,01 з.д. | 38,89 с.ш. | 14 | 9,80188 |
| Вена | 16,36 в.д. | 48,21 с.ш. | 183 | 9,80860 |
| Владивосток | 131,53 в.д. | 43,06 с.ш. | 50 | 9,80424 |
| Гринвич | 0,0 в.д. | 51,48 с.ш. | 48 | 9,81188 |
| Каир | 31,28 в.д. | 30,07 с.ш. | 30 | 9,79317 |
| Киев | 30,30 в.д. | 50,27 с.ш. | 179 | 9,81054 |
| Мадрид | 3,69 в.д. | 40,41 с.ш. | 667 | 9,79981 |
| Минск | 27,55 в.д. | 53,92 с.ш. | 220 | 9,81347 |
| Москва | 37,61 в.д. | 55,75 с.ш. | 151 | 9,8154 |
| Нью-Йорк | 73,96 з.д. | 40,81 с.ш. | 38 | 9,80247 |
| Одесса | 30,73 в.д. | 46,47 с.ш. | 54 | 9.80735 |
| Осло | 10,72 в.д. | 59,91 с.ш. | 28 | 9,81927 |
| Париж | 2,34 в.д. | 48,84 с.ш. | 61 | 9,80943 |
| Прага | 14,39 в.д. | 50,09 с.ш. | 297 | 9,81014 |
| Рим | 12,99 в.д. | 41,54 с.ш. | 37 | 9,80312 |
| Стокгольм | 18,06 в.д. | 59,34 с.ш. | 45 | 9,81843 |
| Токио | 139,80 в.д. | 35,71 с.ш. | 18 | 9,79801 |
Измерение[править | править код]
Ускорение свободного падения у поверхности Земли может быть измерено посредством гравиметра. Различают две разновидности гравиметров: абсолютные и относительные. Абсолютные гравиметры измеряют ускорение свободного падения непосредственно. Относительные гравиметры, некоторые модели которых действуют по принципу пружинных весов, определяют приращение ускорения свободного падения относительно значения в некотором исходном пункте.
Ускорение свободного падения на поверхности Земли или другой планеты может быть также вычислено на основе данных о вращении планеты и её гравитационном поле. Последнее может быть определено посредством наблюдения за орбитами спутников и движения других небесных тел вблизи рассматриваемой планеты.
См. также[править | править код]
- Свободное падение
- Гравиметрия
- Гравиразведка
- Перегрузка (летательные аппараты)
Примечания[править | править код]
- ↑ У планет газовых гигантов и звёзд «поверхность» понимается как область меньших высот в атмосфере, где давление равно атмосферному давлению на Земле на уровне моря (1,013×105 Па). Также у звёзд поверхностью иногда считают поверхность фотосферы.
- ↑ Аналог уравнения второго закона Ньютона, выполняющийся для неинерциальных систем отсчёта.
- ↑ Свободное падение тел. Ускорение свободного падения. Архивировано из оригинала 20101219 года.
- ↑ Декларация III Генеральной конференции по мерам и весам (1901) (англ.). Международное бюро мер и весов. Дата обращения: 9 апреля 2013. Архивировано 8 июля 2018 года.
- ↑ Деньгуб В. М., Смирнов В. Г. Единицы величин. Словарь-справочник. — М. : Изд-во стандартов, 1990. — С. 237.
- ↑ CODATA Value: Newtonian constant of gravitation. physics.nist.gov. Дата обращения: 7 марта 2020. Архивировано 23 сентября 2020 года.
- ↑ Грушинский Н. П. Гравиметрия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 521. — 707 с. — 100 000 экз.
- ↑ Ускорение свободного падения // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Большая российская энциклопедия, 1994. — Т. 4: Пойнтинга — Робертсона — Стримеры. — С. 245—246. — 704 с. — 40 000 экз. — ISBN 5-85270-087-8.
- ↑ ICCEM – table of models (англ.). Дата обращения: 10 ноября 2021. Архивировано из оригинала 24 августа 2013 года.
- ↑ GRAVITY MONITORING AT OIL AND GAS FIELDS: DATA INVERSION AND ERRORS // Геология и геофизика. — 2015. — Т. 56, вып. 5. — doi:10.15372/GiG20150507. Архивировано 2 июня 2018 года.
- ↑ Перуанцам живется легче, чем полярникам? Дата обращения: 21 июля 2016. Архивировано 16 сентября 2016 года.
Литература[править | править код]
- Енохович А. С. Краткий справочник по физике. — М.: Высшая школа, 1976. — 288 с.
Движение тела в жидкости
Основные положения
гидроаэромеханики
Жидкости
являются телами с характерным ближайшим
упорядочением структурной взаимосвязи
молекул. Расстояние между молекулами
жидкости мало, поэтому силы взаимодействия
значительны, что приводит к малой
сжимаемости жидкостей от действия
внешних сил и вызывает появление
значительных сил межмолекулярного
отталкивания.
Молекулы жидкости
колеблются около положения равновесия,
однако эти положения не являются
постоянными. По истечении некоторого
времени, называемого «временем оседлой
жизни», молекула скачком переходит в
новое положение равновесия, равное
среднему расстоянию между соседними
молекулами. Например, для воды это
расстояние составляет:
метра.
Подвижность
молекул объясняет малую вязкость
жидкости. С понижением температуры и
давления подвижность молекул аморфных
тел уменьшается и тела становятся
твердыми.
Силы противодействия
внешней силе, сжимающей жидкость,
определяют упругие свойства жидкости.
Особенностью упругих сил жидкости (сил
давления) является то, что, будучи
векторами, они не имеют определенной
точки приложения. Для характеристики
распределения сил давления вдоль
поверхности введена скалярная
характеристика – давление. Величина
давления измеряется силой, действующей
в направлении нормали на единицу
поверхности:
Паскалем
было
определено, что жидкость или газ передают
производимое на них давление по всем
направлениям одинаково.
В сообщающихся
сосудах, например, давление жидкости
на одной горизонтальной плоскости будет
одинаковым. При этом соотношение высот
столбов установившейся жидкости в
сообщающихся сосудах обратно соотношению
плотностей этих жидкостей:
Давление
в слое жидкости образованное от веса
самой вышерасположенной жидкости
называется гидростатическим и определяется
по формуле:
или, преобразовав,
Разность
гидростатических давлений на верхнюю
и нижнюю поверхности тела обуславливает
появление выталкивающей силы, действующей
со стороны жидкости на погруженное в
нее тело и равной:
где dж
– удельный вес жидкости,
Vт
– объем погруженной части тела.
Движущаяся жидкость
может образовать два вида своего течения
– неразрывное (ламинарное) и разрывное
(турбулентное). Если соотношение скоростей
струй жидкости в потоке остается
постоянным по всему течению, то такое
называется ламинарным в противном
случае -течение турбулентное. Вязкость
– это проявление взаимодействие слоев
жидкости. Силы вязкости направлены
касательно к слоям жидкости. Вязкость
называют еще и внутренним трением
жидкости.
Сила вязкости
изменяется от изменения скорости
жидкости, отнесенной к длине в направлении,
перпендикулярном скорости течения:
где
– коэффициент внутреннего трения или
коэффициент динамической вязкости с
размерностью [кг/м·с];
изменяется в
широких пределах.
Например: для воды
– 0,105 10-2,
для смазочных
масел – 66·10-2,
для глицерина –
139, 3·10-2.
Это различие
объясняется различием связей молекул
– чем сложнее молекула. Тем крепче связи,
тем больше вязкость.
Объем
протекающей
жидкости в выделенном ее сечении (S)
радиуса R
за 1 секунду был определен в 18 веке
Пуазейлем:
.
В случае движения
тела в жидкости с постоянной скоростью,
сила трения со стороны жидкости,
обладающей определенной вязкостью,
находится по формуле Стокса:
где R
– радиус тела, V
– скорость движения.
Определителем
характера движения жидкости (ламинарного
или турбулентного) служит коэффициент,
называемый числом Рейнольдса
(Re):
где V
– скорость течения; D
– диаметр сечения объема жидкости.
Например, если для
течения воды Re
> 2300, то в ней возникает турбулентное
движение, если Re
меньше – ламинарное.
Бернулли
было
установлено, что в стационарном потоке
жидкости полное давление, состоящее из
статистического (p),
динамического (ρ(V)2/2)
и гидростатистического (ρgh)
есть величина постоянная:
Движущаяся
жидкость, обладая кинетической энергией,
образует так называемую силу лобового
сопротивления:
;
S
– площадь поперечного сечения тела в
направлении перпендикулярном вектору
скорости движения потока (миделево
сечения).
Контрольные
вопросы по теории
-
Чем объясняется
свойство текучести жидкости? -
Что такое время
оседлости молекул? -
Что называется
давлением жидкости? -
Напишите формулу
гидростатистического давления. -
Сформулируйте
закон Архимеда и напишите формулу. -
Напишите формулу
лобового сопротивления жидкости. -
Напишите формулу
Стокса величины вязкости жидкости. -
В каком случае
сила давления жидкости на стенку будет
равно силе давления на дно сосуда? -
Сформулируйте
условия плавания тел. -
Почему давление
не векторная величина? -
Напишите уравнение
Бернулли для стационарного потока
жидкости. -
Дайте определение
ламинарного и турбулентного течений
жидкости. -
Каков механизм
подъемной силы крыла? -
Сформулируйте
закон Паскаля. -
Каков принцип
работы гидравлического пресса? -
На поверхности
воды в сосуде плавает лед. Изменится
ли уровень воды, если лед растает? -
Почему возникает
выталкивающая сила в жидкостях и газе? -
Как будут относиться
высоты жидкостей различной плотности
в сообщающихся сосудах? -
Назовите основные
механические свойства жидкости.
Российский
государственный университет физической
культуры,
спорта и туризма
Кафедра
естественно-научных дисциплин
Движение тела в
жидкости и газе
Вычисление глубины
погружения спортсмена при прыжках в
воду
РГР №2
по курсу физики
Вариант №43
Выполнил:
студент I
курса I
потока I
группы
Иванов И.И.
Преподаватель:
доцент (профессор)
кафедры ЕНД
Москва 2010 г.
Содержание:
-
Текст задания.
-
Алгоритм решения.
-
Иллюстрация.
-
Таблица исходных
данных. -
Таблица вычислений.
-
Таблица результатов.
-
Текст задания:
Спортсмен прыгает
в воду с вышки высотой Н=10
м.
Масса тела спортсмена
m.
Коэффициент
обтекаемости тела спортсмена при
погружении в воду C2.
Коэффициент
обтекаемости тела спортсмена при
всплытии
C1.
Плотность тела ρ.
Плотность воздуха
ρ1=1,29
кг/м3.
Плотность воды
ρ2=103
кг/м3.
Коэффициент
вязкости воды j=0,105·10-2
(Па·с).
Ускорение свободного
падения g=9,8
м/с2.
Вычислить:
Глубину погружения
спортсмена в бассейне h1.
Время погружения
t2.
Время всплытия
t3.
Время нахождения
спортсмена под водой t4.
Величину инерционных
перегрузок при входе в воду n.
Импульс силы при
погружении в воду F·t.
Силу сопротивления
воздуха F0.
Коэффициент
обтекания в воздухе C1.
Построить:
График зависимости
глубины погружения h
от массы
тела m
по трём
точкам: m;
m-4;
m+4
(кг).
2. Алгоритм
решения:
2.1. Максимальная
глубина погружения определяется из
условия, что вся потенциальная энергия
тела ПАС
от уровня вышки до уровня погружения
затрачена на работу против силы
динамического (лобового) сопротивления
воды (FЛС),
гидростатической силы выталкивания
(силы Архимеда FАр)
и силы вязкости воды (FВ):
ПАС
= АЛС
+ ААр
+ АВ.
2.2. Сделаем допущение,
что скорость движения тела спортсмена
в воде снижается равнозамедленно под
действием всех приложенных сил, что
допускает расчёт силы динамического
(лобового) сопротивления с использованием
значения квадрата средней скорости
движения.
2.3. Коэффициент
обтекаемости и плотность тела спортсмена
на вдохе примем равными табличным
значениям.
а
Faрх
Fлс
Fв
mg
mg
Fлс
Погружение
Всплытие
H
h1
Faрх
Графическая
интерпретация
условий задачи.
mg
FВ
а
4. Таблица исходных
данных
|
№ |
Параметр |
Обозначение |
Величина |
Единица |
|
1. |
Масса |
m |
48 |
кг |
|
2. |
Высота |
Н |
10 |
м |
|
3. |
Плотность |
ρ |
996 |
кг/м3 |
|
4. |
Плотность |
ρ1 |
1,29 |
кг/м3 |
|
5. |
Плотность |
ρ2 |
1000 |
кг/м3 |
|
6. |
Коэффициент |
C2 |
0,43 |
– |
|
7. |
Коэффициент |
C3 |
0,63 |
– |
|
8. |
Коэффициент |
j |
0,105·10-2 |
Па·с |
|
9. |
Ускорение |
g |
9,8 |
м/с2 |
|
10. |
Время |
t1 |
1,44 |
с |
|
11. |
Обхват |
L |
0,81 |
м |
|
12. |
Площадь |
S1 |
0,045 |
м2 |
5. Таблица
вычислений
|
Параметр |
Формула |
Вычисления |
Результат |
|
1. |
|||
|
1.1. |
|
|
9,65 |
|
1.2. |
|
|
7,2 |
|
1.3. |
|
|
13,9 |
|
1.4. Силу
где |
|
|
2,57 |
|
2. |
|||
|
2.1. |
|
|
934,65 |
|
2.2. |
|
|
0,0177 |
|
Параметр |
Формула |
Вычисления |
Резуль- тат |
|
2.3. |
|
|
472,3 |
|
2.4. |
|
|
5,023 |
|
2.5. |
|
|
0,72 |
|
2.6. |
|
|
1,97 |
|
2.7. |
|
|
667,2 |
|
3. |
|||
|
3.1.
т.к. |
|
|
0,0159 |
|
3.2. |
|
|
25,14 |
|
Параметр |
Формула |
Вычисления |
Резуль- тат |
|
3.3. |
|
|
25,86 |
6. Таблица
результатов
|
№ |
Параметр |
Обозначение |
Величина |
Единица |
|
1. |
Сила |
F0 |
7,2 |
Н |
|
2. |
Коэффициент |
C1 |
2,57 |
– |
|
3. |
Глубина |
h1 |
5,023 |
м |
|
4. |
Время |
t2 |
0,72 |
с |
|
5. |
Время |
t3 |
25,14 |
с |
|
6. |
Время |
t4 |
25,86 |
с |
|
7. |
Инерционные |
n |
1,97 |
|
|
8. |
Импульс |
F·t |
667,2 |
Н·с |
Таблица вариантов
исходных данных РГР №2
|
Параметры |
Номер |
||||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
|
1. |
Масса |
42 |
44 |
46 |
48 |
50 |
52 |
54 |
56 |
58 |
60 |
|
2. |
Высота |
10 |
10 |
||||||||
|
3. |
Плотность |
996 |
994 |
||||||||
|
4. |
Плотность |
1,29 |
1,29 |
||||||||
|
5. |
Плотность |
1000 |
1000 |
||||||||
|
6. |
Коэффициент |
0,40 |
0,41 |
0,42 |
0,43 |
0,44 |
0,45 |
0,46 |
0,47 |
0,48 |
0,49 |
|
7. |
Коэффициент |
0,60 |
0,61 |
0,62 |
0,63 |
0,64 |
0,65 |
0,66 |
0,67 |
0,68 |
0,69 |
|
8. |
Коэффициент |
0,105·10-2 |
0,105·10-2 |
||||||||
|
9. |
Ускорение |
9,8 |
9,8 |
||||||||
|
10. |
Время |
1,44 |
1,44 |
||||||||
|
11. |
Обхват |
0,75 |
0,77 |
0,79 |
0,81 |
0,83 |
0,85 |
0,88 |
0,90 |
0,91 |
0,93 |
|
12. |
Площадь |
0,045 |
0,045 |
0,053 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Свободное падение – это движение тела под действием силы тяжести. В упрощенном виде расчет производится без учета сопротивления воздуха.
На поверхности Земли ускорение свободного падения имеет величину от 9,78 м/с2 на экваторе до 9,82 м/с2 на полюсах.
Кроме того, на планете существуют места с экстремальными значениями, которые не вписываются в математическую модель. Минимум составляет
9,76 м/с2, максимум – 9,83 м/с2. Для расчетов в физике используется усредненная величина – 9,8 м/с2
Формула ускорения свободного падения:
Ускорение свободного падения вычисляется по следующей формуле:
где
G – гравитационная постоянная (постоянная Ньютона), равная 6,6743015·10-11 м3/(кг*с2), или Н*м2/кг2
R – расстояние, на котором находится тело от центра планеты
M – масса планеты
Как видно из вышеприведенной формулы, значение ускорения свободного падения обратно пропорционально квадрату расстояния от центра планеты,
т.е. зависит не только от радиуса самой планеты, но от того, на какой высоте над ее поверхностью находится тело.
Поэтому для расчёта величины “g” на определенной высоте формулу можно скорректировать вот таким образом:
где
G – гравитационная постоянная
R – радиус планеты
h – высота над поверхностью планеты, на которой находится тело
M – масса планеты
Для расчёта можно воспользоваться калькулятором, который приведен ниже.
Калькулятор ускорения свободного падения
Другие формулы
В статье обсуждается несколько подходов к тому, как найти ускорение свободного падения без массы.
Ускорение свободного падения g не зависит от малой массы. Следовательно, при вычислении g им пренебрегают. Формулы и понятия наклонной плоскости, силы выкупа, закона Кеплера и сферически-симметричных тел помогают нам найти ускорение свободного падения без малой массы.
При вычислении значения ускорения свободного падения g в Предыдущая статья, мы узнали, что Значение g зависит только от большой массы M гравитирующих тел. подобно Земле или другим планетам, которые имеют постоянное значение массы для всех других объектов, которые они привлекают. Наоборот, масса объекта, который притягивается к гравитирующему телу, не учитывается.
Давайте найдем значение g с помощью нескольких подходов и задач, используя разные законы, в которых не учитывается малая масса.
Узнайте больше о том, как найти массу по гравитационному ускорению.
Как найти ускорение свободного падения без массы с помощью силы выкупа
Давайте посмотрим, как сила выкупа из жидкости помогает нам найти ускорение свободного падения без массы.
Жидкость оказывает выкупающее усилие на объект, чтобы противостоять его весу «mg», тонет он или плавает. Когда сила выкупа превышает вес или силу тяжести, объект плавает в жидкости. Если сила тяжести больше, объект тонет в жидкости.
без массы
(Кредит: Shutterstock)
Когда мы ныряем в бассейн, вода оказывает на наши тела восходящую силу. То же самое мы испытываем, когда плывем под водой. Сила, направленная вверх, – это давление воды, которое называется ‘сила выкупа.
По мере того, как мы погружаемся в воду, она оказывает высокое давление на нашу нижнюю сторону и низкое давление на нашу верхнюю сторону.
Чтобы рассчитать общую силу выкупа, действующую на объект, сначала рассчитайте силу выкупа на верхней и нижней сторонах по отдельности, а затем вычтите их.
Fb = ФНижний – Fтоп ……………… (*)
Приложенное давление – это сила, приложенная к единице площади, на которую распространяется приложенная сила.
P = F / A
F = PA
В зависимости от веса объект будет плавать или тонуть в воде. Поэтому сила выкупа связана с силой тяжести Fg.
Fg= мг
Подставляя указанную выше силу тяжести в уравнение (1),
Р=мг/А
Принимая во внимание, что масса = объем x плотность, т. Е.
Где высота h = V / A
Приведенная выше формула является формулой Гидростатическое манометрическое давление оказываемое водой из-за силы тяжести.
Согласно уравнению (1) сила выкупа на верхних сторонах равна
Fтоп = PтопA
Подставляя значение манометрического давления (2),
Точно так же сила выкупа на нижней стороне равна
Уравнение (*) становится,
Где (hнижний – чтоп) – это точная высота объекта “h”.
Следовательно,
Где «Ah» – объем вытесненной воды.
Следовательно,
Вот как используется сила выкупа; мы можем вычислить ускорение свободного падения g в терминах плотности и объема.
Узнать больше о Типах сил.
Когда мы поместили кубик в ванну с водой, он вытеснил воду до 1.55 литра. Сила отрыва, испытываемая на кубе, составляет 15 Н для воды, имеющей плотность около 1000 кг / мXNUMX.3. Вычислите ускорение свободного падения куба внутри воды.
Данный:
ρ = 1000 кг / м3
V = 1.53 литра
Поскольку 1 м3 = 1000 литров, значит, 1.53 литра = 0.00153 м.3
Fb = 15 Н
Найти: g =?
Формула:
Решения:
Ускорение свободного падения куба рассчитывается с помощью формула силы выкупа в виде,
Подставляя все значения,
15=1000*г*0.00153
г=15/1.53
г = 9.803
Наблюдения и советы этой статьи мы подготовили на основании опыта команды гравитационное ускорение на кубе 9.80 м/с2.
Как найти ускорение свободного падения без массы, используя сферически-симметричную основуy
Давайте посмотрим, как вычисляется ускорение свободного падения без массы с использованием сферически-симметричного тела.
В сферически-симметричном теле вся его масса сосредоточена в одной точке. Подставляя большое значение Массы M сферически-симметричного тела в силу тяжести, мы можем получить ускорение свободного падения через его плотность ρ0.
для сферически симметричного тела
Мы получили ускорение свободного падения без массы, как если бы сначала подставили значение массы в силу тяжести с помощью закон всемирного тяготения а затем в силу тяжести на Второй закон Ньютона,
Чтобы узнать, как мы получили указанную выше формулу, прочитайте статью здесь.
Рассчитайте ускорение свободного падения космонавта, идущего по Луне. Луна имеет плотность около 104 кг / см3, а расстояние между центром масс космонавта и луны составляет 1.74 x 106m.
Данный:
G = 6.67 х 10-11 Nm2/ кг2
г = 1.74 х 106m
σ = 104 г / см3
Найти: g =?
Формула:
г=(4/3)Gσr
Решения:
Если рассматривать Луну как сферически симметричное тело, затем
Ускорение свободного падения космонавта рассчитывается как
г=(4/3)Gσr
Подставляя все значения,
(46.42 * 10-1) / 3
г = 1.54
Ускорение свободного падения космонавта, идущего по луна составляет 1.54 м/с2.
Подробнее о том, как рассчитать массу по силе и расстоянию.
Как найти ускорение свободного падения без массы с помощью наклонной плоскости
Посмотрим, как наклонная плоскость помогает нам найти ускорение свободного падения без массы.
Из-за треугольной формы требуется меньше усилий для ускорения любого объекта на наклонной плоскости. Следовательно, ускоренный наклонный объект имеет значение, немного отличное от ускорения свободного падения g. Если мы знаем ускорение и угол наклона падающего объекта, мы можем найти значение g без учета массы.
на наклонной плоскости
Когда объект ускоряется горизонтально вдоль поверхности земли, он ускоряется в равной степени до значения g, которое составляет 9.8 м / с.2. Но если мы наклоним горизонтальную поверхность под определенным углом, ее значение ускорения станет немного отличаться от значения g.
Таким образом, сила тяжести mg распадается на парные компоненты на наклонная плоскость без трения. Один компонент действует перпендикулярно плоскости mgcosθ, а другой параллелен плоскости mgsinθ. Двойник нормальной силы ⊥ компоненты силы, действуя противоположно ему.
Так что единственный || Составляющая силы тяжести ускоряет объект на наклонной плоскости.
Согласно Второй закон Ньютона, равнодействующая сила действие на объект,
Fсеть=ма
а=Fсеть/m
Поскольку результирующая сила, действующая на наклонную плоскость,
F|| = mgsinθ
Следовательно, второй закон Ньютона принимает вид
а=мгsinθ/м
а=gsinθ
г=а/sinθ
Приведенное выше уравнение показывает, что В зависимости от угла наклона значение ускорения падающего объекта изменяется от постоянного значения g ускорения свободного падения.
Подробнее о работе на наклонной плоскости.
Рассчитайте ускорение свободного падения шара, ускоряющегося вниз со скоростью 6 м / с.2 на поверхности с наклоном 38 °.
Данный:
a = 6 м / с2
θ = 38°
Найти: g =?
Формула:
г=а/sinθ
Решения:
Ускорение свободного падения шара, падающего на наклонную плоскость, рассчитывается как
г=а/sinθ
Подставляя все значения,
г=6/грех 380
г=6/0.615
г = 9.75
г = 9.75
Ускорение свободного падения падающего шара составляет 9.75 м / с.2.
Рассчитайте ускорение коробки, скользящей вниз по наклонной аппарели под углом 87 °..
Данный:
θ = 87°
g = 9.8 м / с2
Найти: а =?
Формула:
а=gsinθ
Решения:
Ускорение скольжения ящика вниз рассчитывается как
а=gsinθ
а=9.8*sin 870
а=9.8*0.998
а = 9.78
Подставляя все значения,
a = 9.78
Ускорение скольжения ящика вниз – 9.78 м / с.2.