Свободное падение — это движение тела только под действием силы тяжести.
В действительности при падении на тело действует не только сила тяжести, но и сила сопротивления воздуха. Но в ряде задач сопротивлением воздуха можно пренебречь. Воздух не оказывает значимого сопротивления падающему мячу или тяжелому грузу. Но падение пера или листа бумаги можно рассматривать только с учетом двух сил: небольшая масса тела в сочетании с большой площадью его поверхности препятствует свободному падению вниз.
Внимание!
В вакууме все тела падают с одинаковым ускорением, так как в нем отсутствует среда, которая могла бы дать сопротивление. Так, брошенные в условиях вакуума с одинаковой высоты перо и молоток приземлятся в одно и то же время!
Ускорение свободного падения
Ускорение свободного падения — векторная физическая величина. Вектор ускорения свободного падения всегда направлен вниз к центру Земли. Обозначается как g.
Единица измерения ускорения свободного падения — 1 м/с2.
Модуль ускорения свободного падения — скалярная величина. Обозначается как g. Численно равна 9,8 м/с2. При решении задач это значение округляется до целых: g = 10 м/с2.
Свободное падение
Свободное падение — частный случай равноускоренного прямолинейного движения. Если тело отпустить с некоторой высоты, оно будет падать с ускорением свободного падения без начальной скорости. Тогда его кинематические величины можно определить по следующим формулам:
Скорость
v = gt
v — скорость, g — ускорение свободного падения, t — время, в течение которого падало тело
Пример №1. Тело упало без начальной скорости с некоторой высоты. Найти его скорость в конечный момент времени t, равный 3 с.
Подставляем данные в формулу и вычисляем:
v = gt = 10∙3 = 30 (м/с).
Перемещение при свободном падении тела равно высоте, с которой оно начало падать. Высота обозначается буквой h.
Внимание! Перемещение равно высоте, с которой падало тело, только в том случае, если t — полное время падения.
Высота падения
Если известна скорость падения тела в момент времени t, перемещение (высота) определяется по следующей формуле.
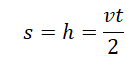
Если скорость тела в момент времени t неизвестна, но для нахождения перемещения (высоты) используется формула:
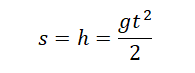
Если неизвестно время, в течение которого падало тело, но известна его конечная скорость, перемещение (высота) вычисляется по формуле:
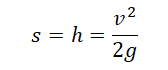
Пример №2. Тело упало с высоты 5 м. Найти его скорость в конечный момент времени.
Так как нам известна только высота, и найти нужно скорость, используем для вычислений последнюю формулу. Выразим из нее скорость:
![]()
Формула определения перемещения тела в n-ную секунду свободного падения:
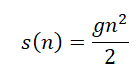
s(n) — перемещение за секунду n.
Пример №3. Определить перемещение свободно падающего тела за 3-ую секунду движения.

Движение тела, брошенного вертикально вверх
Движение тела, брошенного вертикально вверх, описывается в два этапа
Два этапа движения тела, брошенного вертикально вверхЭтап №1 — равнозамедленное движение. Тело поднимается вверх на некоторую высоту h за время t с начальной скоростью v0 и на мгновение останавливается в верхней точке, достигнув скорости v = 0 м/с. На этом участке пути векторы скорости и ускорения свободного падения направлены во взаимно противоположных направлениях (v↑↓g).
Этап №2 — равноускоренное движение. Когда тело достигает верхней точки, и его скорость равна 0, начинается свободное падение с начальной скоростью до тех пор, пока тело не упадет или не будет поймано на некоторой высоте. На этом участке пути векторы скорости и ускорения свободного падения направлены в одну сторону (v↑↑g).
Формулы для расчета параметров движения тела, брошенного вертикально вверхПеремещение тела, брошенного вертикально вверх, определяется по формуле:
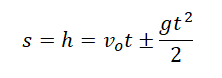
Если известна скорость в момент времени t, для определения перемещения используется следующая формула:
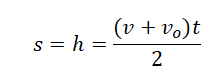
Если время движения неизвестно, для определения перемещения используется следующая формула:
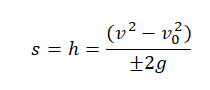
Формула определения скорости:
![]()
Какой знак выбрать — «+» или «–» — вам помогут правила:
- Если движение равнозамедленное (тело поднимается вверх), перед ускорением свободного падения в формуле нужно ставить знак «–», так как векторы скорости и ускорения противоположно направлены.
- Если движение равноускоренное (тело падает вниз), перед ускорением свободного падения в формуле нужно ставить знак «+», так как векторы скорости и ускорения сонаправлены.
Обычно тело бросают вертикально вверх с некоторой высоты. Поэтому если тело упадет на землю, высота падения будет больше высоты подъема (h2 > h1). По этой же причине время второго этапов движения тоже будет больше (t2 > t1). Если бы тело приземлилось на той же высоте, то начальная скорость движения на 1 этапе была бы равно конечной скорости движения на втором этапе. Но так как точка приземления лежит ниже высоты броска, модуль конечной скорости 2 этапа будет выше модуля начальной скорости, с которой тело было брошено вверх (v2 > v01).
Пример №4. Тело подкинули вверх на некотором расстоянии 2 м от земли, придав начальную скорость 10 м/с. Найти высоту тела относительно земли в момент, когда оно достигнет верхней точки движения.
Конечная скорость в верхней точке равна 0 м/с. Но неизвестно время. Поэтому для вычисления перемещения тела с точки броска до верхней точки найдем по этой формуле:
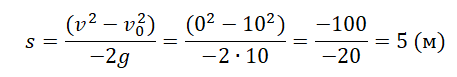
Согласно условию задачи, тело бросили на высоте 2 м от земли. Чтобы найти высоту, на которую поднялось тело относительно земли, нужно сложить эту высоту и найденное перемещение: 5 + 2 = 7 (м).
Уравнение координаты и скорости при свободном падении
Уравнение координаты при свободном падении позволяет вычислять кинематические параметры движения даже в случае, если оно меняет свое направление. Так как при вертикальном движении тело меняет свое положение лишь относительно оси ОУ, уравнение координаты при свободном падении принимает вид:
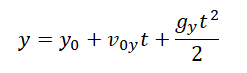
Уравнение скорости при свободном падении:
vy = v0y + gyt
Полезные факты
- В момент падения тела на землю y = 0.
- В момент броска тела от земли y0 = 0.
- Когда тело падает без начальной скорости (свободно) v0 = 0.
- Когда тело достигает наибольшей высоты v = 0.
Построение чертежа
Решать задачи на нахождение кинематических параметров движения тела, брошенного вертикально вверх, проще, если выполнить чертеж. Строится он в 3 шага.
План построения чертежа
- Чертится ось ОУ. Начало координат должно совпадать с уровнем земли или с самой нижней точки траектории.
- Отмечаются начальная и конечная координаты тела (y и y0).
- Указываются направления векторов. Нужно указать направление ускорения свободного падения, начальной и конечной скоростей.
Свободное падение на землю с некоторой высоты
Чертеж:
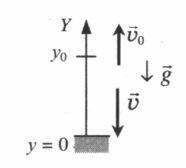
Уравнение скорости:
–v = v0 – gtпад
Уравнение координаты:
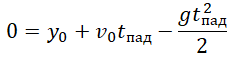
Тело подбросили от земли и поймали на некоторой высоте
Чертеж:
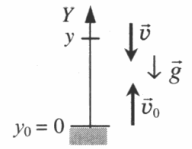 Уравнение скорости:
Уравнение скорости:
–v = v0 – gt
Уравнение координаты:
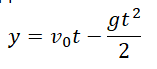
Тело подбросили от земли, на одной и той же высоте оно побывало дважды
Чертеж:
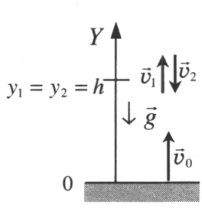
Интервал времени между моментами прохождения высоты h:
∆t = t2 – t1
Уравнение координаты для первого прохождения h:
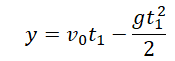
Уравнение координаты для второго прохождения h:
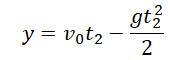
Важно! Для определения знаков проекций скорости и ускорения нужно сравнивать направления их векторов с направлением оси ОУ.
Пример №5. Тело падает из состояния покоя с высоты 50 м. На какой высоте окажется тело через 3 с падения?
Из условия задачи начальная скорость равна 0, а начальная координата — 50.
Поэтому:
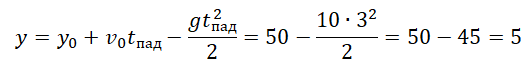
Через 3 с после падения тело окажется на высоте 5 м.
Задание EF17519
С аэростата, зависшего над Землёй, упал груз. Через 10 с он достиг поверхности Земли. На какой высоте находился аэростат? Сопротивление воздуха пренебрежимо мало.
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения искомой величины в векторном виде.
- Записать формулу для определения искомой величины в векторном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 0 м/с.
- Время падения t = 10 c.
Делаем чертеж:
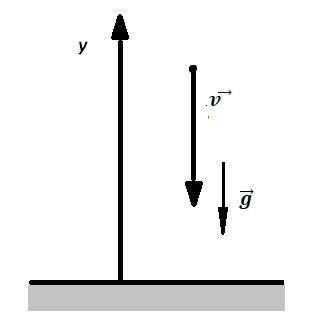
Перемещение (высота) свободно падающего тела, определяется по формуле:
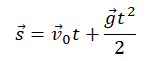
В скалярном виде эта формула примет вид:
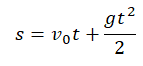
Учтем, что начальная скорость равна нулю, а ускорение свободного падения противоположно направлено оси ОУ:
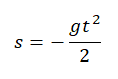
Относительно оси ОУ груз совершил отрицательное перемещение. Но высота — величина положительная. Поэтому она будет равна модулю перемещения:
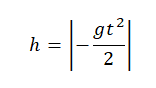
Вычисляем высоту, подставив известные данные:
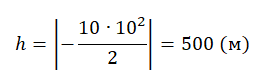
Ответ: 500
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17483
Тело брошено вертикально вверх с начальной скоростью 10 м/с. Если сопротивление воздуха пренебрежимо мало, то через одну секунду после броска скорость тела будет равна…
Алгоритм решения
- Записать исходные данные.
- Сделать чертеж, иллюстрирующий ситуацию.
- Записать формулу для определения скорости тела в векторном виде.
- Записать формулу для определения скорости тела в скалярном виде.
- Подставить известные данные и вычислить скорость.
Решение
Записываем исходные данные:
- Начальная скорость v0 = 10 м/с.
- Время движения t = 1 c.
Делаем чертеж:
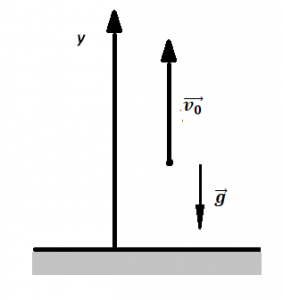
Записываем формулу для определения скорости тела в векторном виде:
v = v0 + gt
Теперь запишем эту формулу в скалярном виде. Учтем, что согласно чертежу, вектор скорости сонаправлен с осью ОУ, а вектор ускорения свободного падения направлен в противоположную сторону:
v = v0 – gt
Подставим известные данные и вычислим скорость:
v = 10 –10∙1 = 0 (м/с)
Ответ: 0
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20.5k
Что такое свободное падение? Это падение тел на Землю при отсутствии сопротивления воздуха. Иначе говоря – падение в пустоте. Конечно, отсутствие сопротивления воздуха – это вакуум, который нельзя встретить на Земле в нормальных условиях. Поэтому мы не будем брать силу сопротивления воздуха во внимание, считая ее настолько малой, что ей можно пренебречь.
Ускорение свободного падения
Проводя свои знаменитые опыты на Пизанской башне Галилео Галилей выяснил, что все тела, независимо от их массы, падают на Землю одинаково. То есть, для всех тел ускорение свободного падения одинаково. По легенде, ученый тогда сбрасывал с башни шары разной массы.
Ускорение свободного падения – ускорение, с которым все тела падают на Землю.
Ускорение свободного падения приблизительно равно 9,81 мс2 и обозначается буквой g. Иногда, когда точность принципиально не важна, ускорение свободного падения округляют до 10 мс2.
Земля – не идеальный шар, и в различных точках земной поверхности, в зависимости от координат и высоты над уровнем моря, значение g варьируется. Так, самое большое ускорение свободного падения – на полюсах (≈9,83 мс2), а самое малое – на экваторе (≈9,78 мс2).
Свободное падение тела
Рассмотрим простой пример свободного падения. Пусть некоторое тело падает с высоты h с нулевой начальной скоростью. Допустим мы подняли рояль на высоту h и спокойно отпустили его.
Свободное падение – прямолинейное движение с постоянным ускорением. Направим ось координат от точки начального положения тела к Земле. Применяя формулы кинематики для прямолинейного равноускоренного движения, можно записать.
h=v0+gt22.
Так как начальна скорость равна нулю, перепишем:
h=gt22.
Отсюда находится выражение для времени падения тела с высоты h:
t=2hg.
Принимая во внимание, что v=gt, найдем скорость тела в момент падения, то есть максимальную скорость:
v=2hg·g=2hg.
Движение тела, брошенного вертикально вверх
Аналогично можно рассмотреть движение тела, брошенного вертикально вверх с определенной начальной скоростью. Например, мы бросаем вверх мячик.
Пусть ось координат направлена вертикально вверх из точки бросания тела. На сей раз тело движется равнозамедленно, теряя скорость. В наивысшей точки скорость тела равна нулю. Применяя формулы кинематики, можно записать:
v=v0-gt.
Подставив v=0, найдем время подъема тела на максимальную высоту:
t=v0g.
Время падения совпадает со временем подъема, и тело вернется на Землю через t=2v0g.
Максимальная высота подъема тела, брошенного вертикально:
h=v022g.
Взглянем на рисунок ниже. На нем приведены графики скоростей тел для трех случаев движения с ускорением a=-g. Рассмотрим каждый из них, предварительно уточнив, что в данном примере все числа округлены, а ускорение свободного падения принято равным 10мс2.
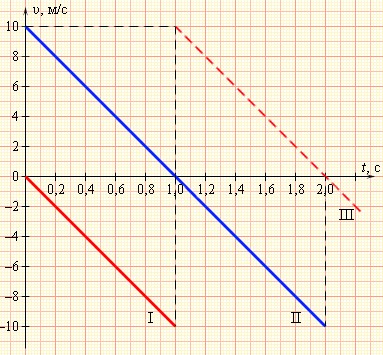
Первый график – это падение тела с некоторой высоты без начальной скорости. Время падения tп=1с. Из формул и из графика легко получить, что высота, с которой падало тело, равна h=5м.
Второй график – движение тела, брошенного вертикально вверх с начальной скоростью v0=10 мс. Максимальная высота подъема h=5м. Время подъема и время падения tп=1с.
Третий график является продолжением первого. Падающее тело отскакивает от поверхности и его скорость резко меняет знак на противоположный. Дальнейшее движение тела можно рассматривать по второму графику.
Движение тела, брошенного под углом к горизонту
С задачей о свободном падении тела тесно связана задача о движении тела, брошенного под определенным углом к горизонту. Так, движение по параболической траектории можно представить как сумму двух независимых движений относительно вертикальной и горизонтальной осей.
Вдоль оси OY тело движется равноускоренно с ускорением g, начальная скорость этого движения – v0y. Движение вдоль оси OX – равномерное и прямолинейное, с начальной скоростью v0x.
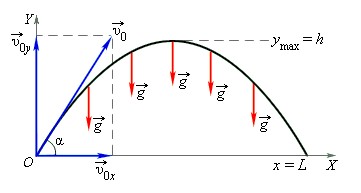
Условия для движения вдоль оси ОХ:
x0=0; v0x=v0cosα; ax=0.
Условия для движения вдоль оси OY:
y0=0; v0y=v0sinα; ay=-g.
Приведем формулы для движения тела, брошенного под углом к горизонту.
Время полета тела:
t=2v0sinαg.
Дальность полета тела:
L=v02sin2αg.
Максимальная дальность полета достигается при угле α=45°.
Lmax=v02g.
Максимальная высота подъема:
h=v02sin2α2g.
Отметим, что в реальных условиях движение тела, брошенного под углом к горизонту, может проходить по траектории, отличной от параболической вследствие сопротивления воздуха и ветра. Изучением движения тел, брошенных в пространстве, занимается специальная наука – баллистика.
Все вы в своей жизни наблюдали за тем, что тела, не имеющие опоры или подвеса, падают вниз. В чем причина такого падения? Конечно же в том, что на все тела у поверхности Земли действует сила тяжести.
Свободным падением тела называется движение тела только под действием силы тяжести.
Проведем мысленный эксперимент. Представьте, что одновременно начинают падение мяч, камень, лист дерева и перо птицы. В какой очередности упадут эти тела?
Первым упадут камень и мяч, затем перо и лист.
Почему? На перо и лист оказывает заметное влияние сила сопротивления воздуха, направленная против силы тяжести.
Падение тела не может считаться свободным, если сила сопротивления воздуха сравнима с силой тяжести.
Еще в конце XVI века знаменитый итальянский ученый Г. Галилей предположил, что все тела падают с одинаковым ускорением и опытным путем доказал, что это предположение верно.

Согласно биографии Галилео Галилея, написанной его учеником Винченцо Вивиани, в 1589 году Галилей провёл эксперимент, сбросив два шара различной массы (ядро и мушкетную пулю) со знаменитой падающей башни в Пизе, чтобы продемонстрировать, что время падения не зависит от массы шара. С помощью этого эксперимента Галилей якобы обнаружил, что тела упали практически одновременно, тем самым доказав, что в отсутствии сопротивления воздуха все тела падают на Землю равноускоренно и что в данной точке Земли ускорение всех тел при падении одно и то же.

Исаак Ньютон доказал справедливость выводов Галилео простым опытом.

В стеклянную трубку он поместил дробинку, пробку и перышко. Если резко перевернуть расположенную вертикально трубку, то быстрее всего упадет дробинка, за ней кусочек пробки и потом плавно опустится перышко. Если же из трубки откачать воздух и опять резко перевернуть её,то все три тела опустятся на дно одновременно.
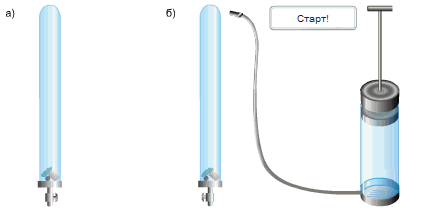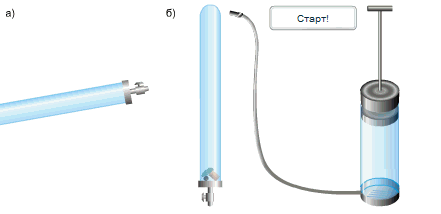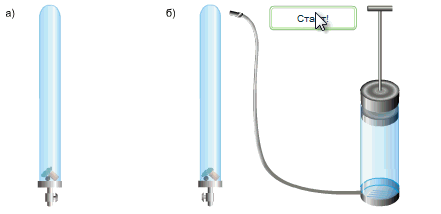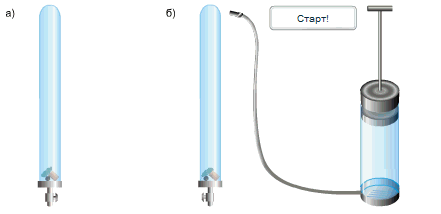
Какие выводы можно сделать из опыта Ньютона?
1. Тела падают с одинаковым ускорением.
2. Существует сила сопротивления воздуха
Ускорение, с которым тела падают на Землю, называется ускорением свободного падения.
Ускорение свободного падения – ускорение, сообщаемое телу, поднятому над Землей, силой тяжести.
Вектор ускорения свободного падения обозначается символом g.
g=9,8 м/с2≈10м/с2
Из закона всемирного тяготения: 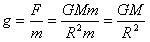
Ускорение свободного падения:
1) Всегда направлено по вертикали вниз
2) Не зависит от массы падающего тела
3) Зависит от географической широты. Так как Земля не шар, а эллипсоид вращения, т.е. радиус Земли на полюсе меньше, чем радиус Земли на экваторе.
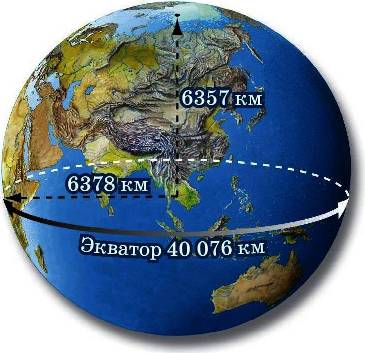
Поэтому сила тяжести и вызвемое ей ускорение больше на полюсе, чем на экваторе. g изменяется примерно от 9,83 м/с2 на полюсах до 9,78 м/с2 на экваторе. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с2 или даже 10 м/с2.
4) Зависит от высоты над уровнем моря
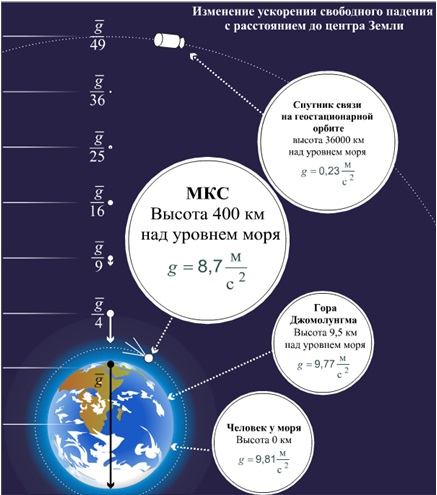
Рассмотрим несколько примеров движения тел под действием силы тяжести. При решении подобных задач очень важно правильно выполнить чертеж, на котором указать направление осей и всех векторных величин.
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости.
Анализируем рисунок.
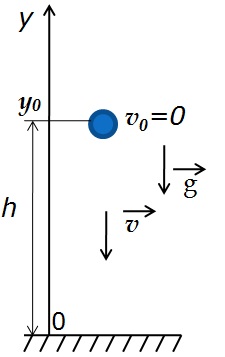
Свободное падение является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело падало s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальная скорость движения равна нулю v0=0
Проекция конечной скорости на ось y отрицательна vу =-v
Начальная координата тела y0=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и vу=-v, получаем -v=0-gt
Упростив выражение, получим формулу для нахождения скорости свободно падающено тела в любой момент времени:
v=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и sу=-h, получаем -h=0-gt2/2
Упростив выражение, получим формулу для нахождения перемещения тела при свободном падении в любой момент времени:
h=gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и y0=h, получаем y=h-gt2/2
То есть, формула для нахождения координаты тела при свободном падении в любой момент времени:
y=h-gt2/2
2. Тело брошено вертикально вверх.
Как будет двигаться тело, брошенное вертикально вверх?
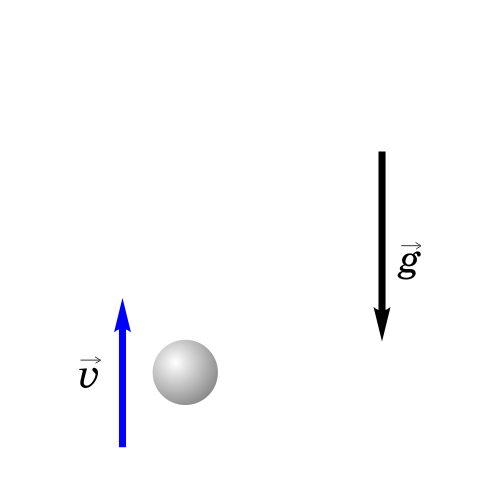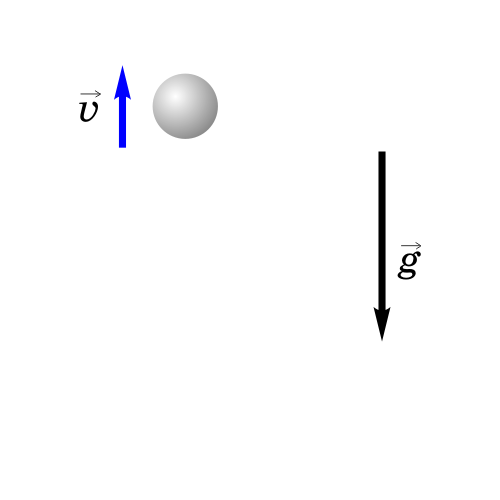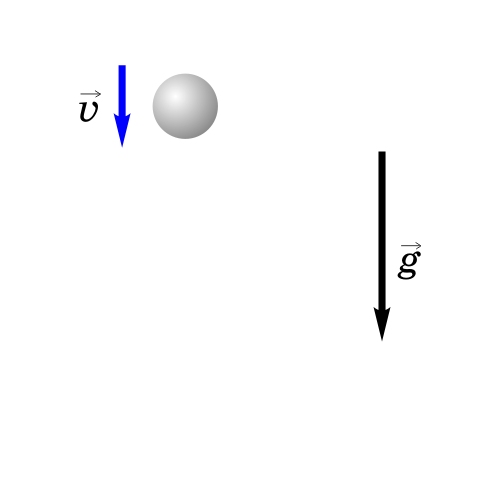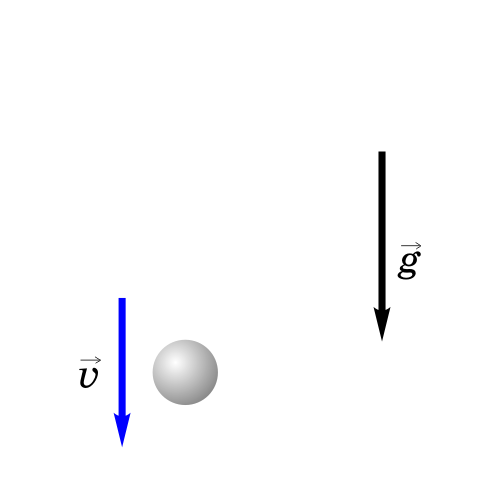
Если бросить тело вертикально вверх, то некоторое время оно будет двигаться вверх. Действующая на него сила тяжести направлена вниз и сообщает ему ускорение g, тоже направленное вниз. Поэтому скорость тела будет уменьшаться со временем и в некоторый момент она станет равной нулю, после чего тело начнет падать вниз с увеличивающейся скоростью.
Анализируем рисунок.
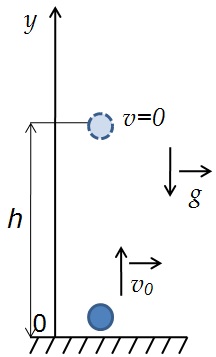
Движение тела, брошенного вертикально вверх тоже является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Проекция начальной скорости движения на ось y положительна v0y=v0
Конечная скорость в верхней точке равна нулю v =0
Начальная координата тела равна нулю y0=0, а конечная координата равна высоте, на которую тело поднимется y=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и vу=v, получаем, что скорость тела, брошенного вертикально в любой момент времени:
v=v0-gt
Если учесть, что в верхней точке v =0, получим 0=v0-gt
Упростив выражение, получим формулу для нахождения начальной скорости тела, брошенного вертикально:
v0=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и sу=h, получим формулу для нахождения перемещения тела, брошенного вертикально, в любой момент времени:
h=v0t-gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 , y0=0 и y=h, получаем формулу для нахождения координаты тела, брошенного вертикально, в любой момент времени:
y=v0t-gt2/2
3. Тело брошено горизонтально.
Как будет двигаться тело, брошенное горизонтально?
Если тело бросить горизонтально, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
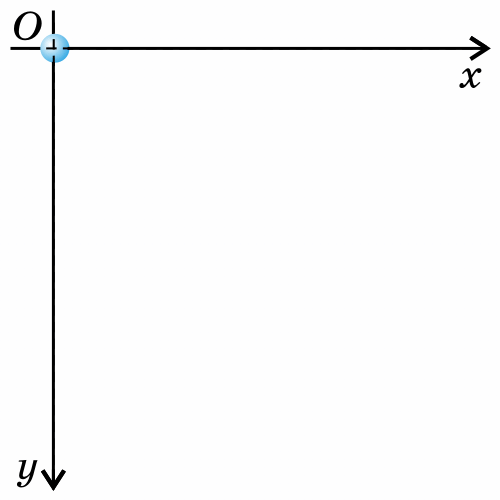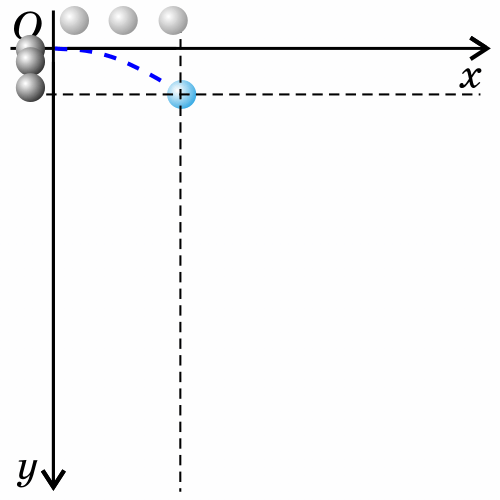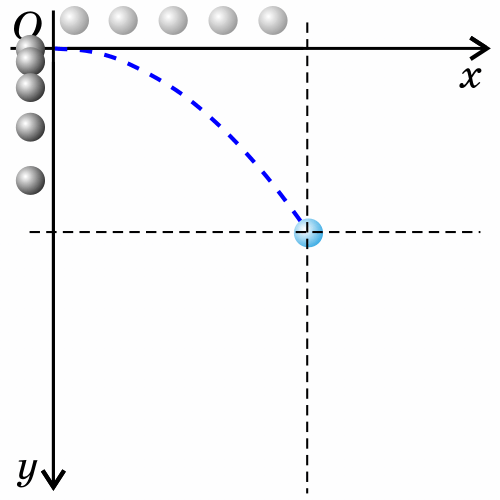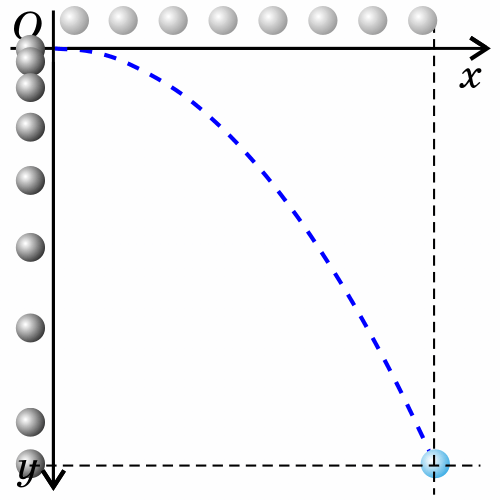
Такое движение тела рассматривают как два движения: по горизонтали – вдоль оси х, и по вертикали – вдоль оси y.
Анализируем рисунок.
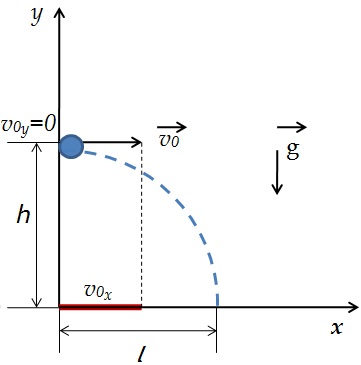
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело бросили s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальные координаты тела х0=0 y0=h
Проекция начальной скорости на ось х равна v0х=v0
Проекция начальной скорости на ось y равна v0y=0
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси х нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0=const
Уравнение перемещения (дальность полета): l=v0х·t= v0·t
Уравнение координаты: x= x0 + v0·t
По вертикали, т.е. вдоль оси y тело свободно падает с высоты h. Поэтому при рассмотрении движения вдоль оси y применимы формулы для свободного падения.
Уравнение скорости: v=g·t
Уравнение перемещения: h=g·t2/2
Уравнение координаты: y= y0-g·t2/2
4. Тело брошено под углом к горизонту.
Как будет двигаться тело, брошенное под углом к горизонту?
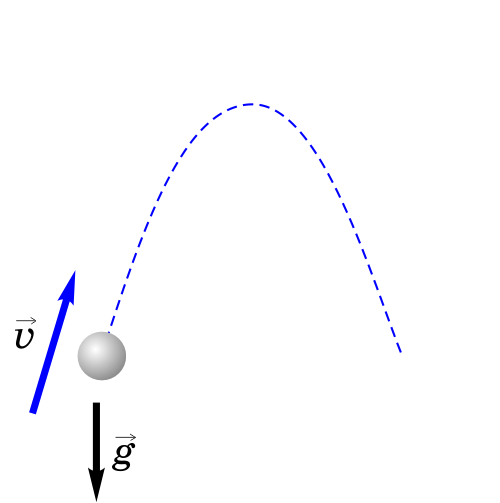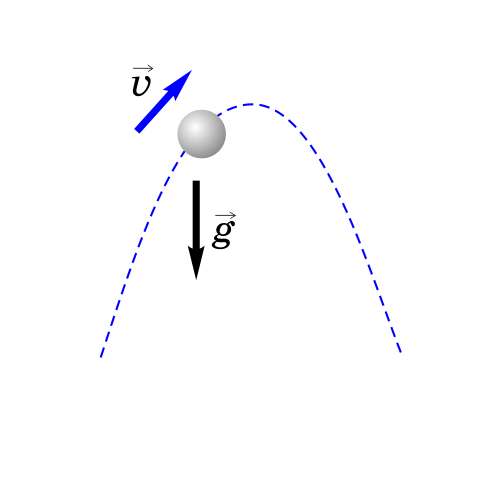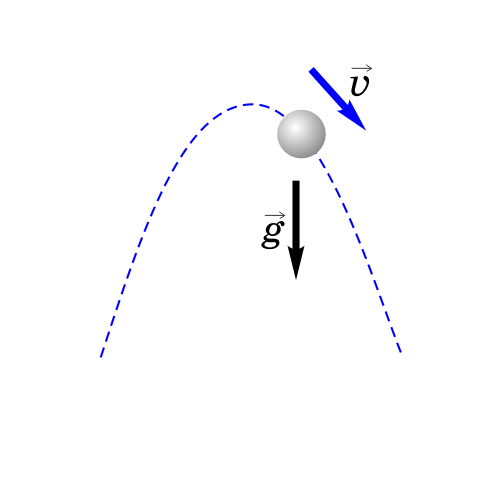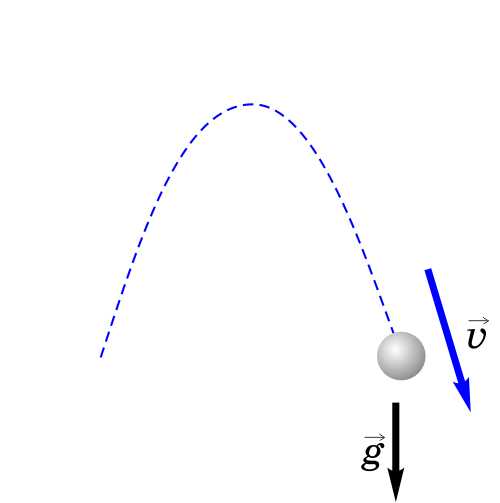
Если тело бросить под углом к горизонту, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
Такое движение тела рассматривают как два движения: по горизонтали – вдоль оси х, и по вертикали – вдоль оси y.
Анализируем рисунок.
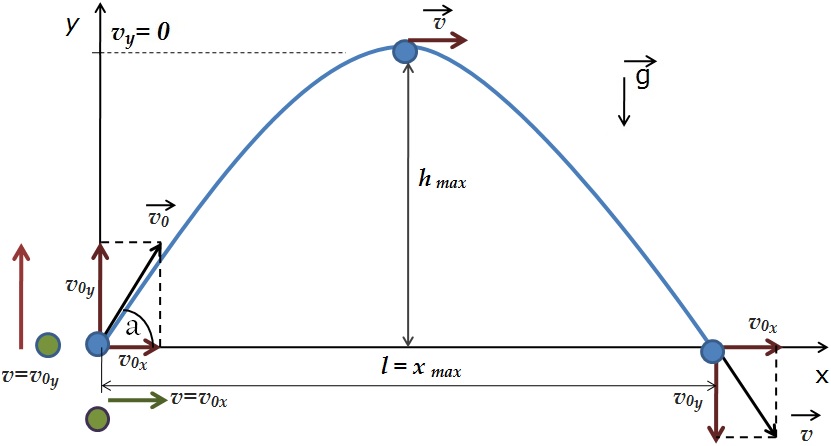
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Начальные координаты тела равны нулю х0=0 y0=0
Проекция начальной скорости на ось х равна v0х=v0·cosa
Проекция начальной скорости на ось y равна v0y=v0·sina
h – максимальная высота, на которую тело поднимется. На этой высоте проекция скорости на ось y равна 0.
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0·cosa=const
Уравнение перемещения (дальность полета): l=vxt= v0·cosa·t
Уравнение координаты: x= x0 + v0·cosa·t
По вертикали, т.е. вдоль оси y тело движется сначало равнозамедленно, подобно телу, брошенному вертикально вверх со скоростью, равной проекции начальной скорости на ось y, а затем равноускоренно (свободно падая).
Проекция ускорения на ось y gy= -g , проекция начальной скорости на ось y v0у=v0·sina, начальная координата y0=0
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали.
Уравнение скорости: vy=v0·sina-g·t
Уравнение перемещения (максимальная высота полета): h=v0·sina·t-g·t2/2
Уравнение координаты: y= v0·sina·t-g·t2/2
Время полета в 2 раза больше времени подъема тела на максимальную высоту
t= 2·tmax = 2·v0·sina/g
Скорость тела находится по теореме Пифагора: ![]()
 .
.
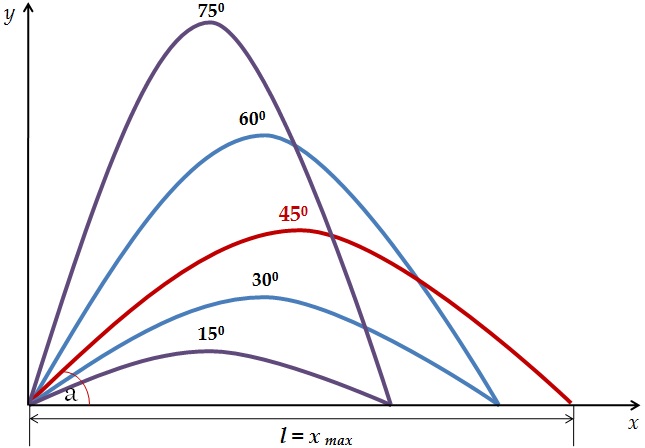
l = x max= v02·sin2a /g
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900, откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова.
Расширения для Joomla
План урока:
Закон сложения скоростей
Мгновенная скорость, направление мгновенной скорости
Ускорение. Касательное ускорение. Центростремительное ускорение
Равноускоренное движение
Свободное падение
Равномерное движение точки по окружности
Закон сложения скоростей
Как уже упоминалось в предыдущем уроке, скорость тела зависит от выбранной наблюдателем системы отсчета. Разберем следующий пример: в безветренную погоду пчела летит со скоростью  относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена
относительно земли. Это будет собственная скорость пчелы. Затем погода меняется и начинает дуть ветер, перпендикулярный скорости пчелы. Скорость ветра обозначена  (см. рисунок 1).
(см. рисунок 1).

Рисунок 1 – Первоначальная скорость пчелы и ветра
Естественно, что ветер начнет сдувать пчелу с первоначального курса. Собственная скорость не изменяется, так как это характеристика самой пчелы, но ее скорость относительно земли (по модулю и направлению) изменится и станет (см. рисунок 2):

Рисунок 2 – Изменившаяся скорость пчелы
Систему отсчета, связанную с землей, можно считать неподвижной. Если же рассматривать движение пчелы относительно воздуха, можно говорить о движущейся со скоростью v2 системе отсчета.


Рисунок 3 – Векторы скорости и перемещений при движении пчелы при ветре
Мгновенная скорость, направление мгновенной скорости
Средняя скорость. Средняя путевая скорость
Так как в реальной жизни тела редко движутся с постоянной скорость, но необходимо как-то описывать их движение и скорость, ввели понятие мгновенной скорости.
Мгновенная скорость – это скорость тела в выбранный конкретный момент времени.

Если по определению скорости разделить перемещение на суммарное время пути, можно получить средняя скорость:

Фактически, это та же формула, которая используется при расчетах для прямолинейного равномерного движения.
То есть средняя скорость движения – это такая скорость, с которой тело должно было бы двигаться, если бы оно перемещалось из начальной точки в конечную равномерно и прямолинейно. Из выражения для вычисления средней скорости можно увидеть, что средняя скорость сонаправлена вектору перемещения.
Касательно же мгновенной скорости, чтобы ее найти, необходимо разделить общее время Δt на одинаковые отрезки Δt1, Δt2,…Δtn, и найти средние скорости за эти отрезки времени:


А куда направлена мгновенная скорость? Из рисунка 5 видно, что при уменьшении отрезков времени Δtb направление вектора перемещения ему соответствующее постепенно приближается к направлению касательной к траектории. Значит, мгновенная скорость направлена по касательной к линии траектории.
Еще одна важная характеристика, использующаяся в кинематике – средняя путевая скорость. Из названия вытекает, что средняя путевая скорость – это отношение пути (S), пройденного телом, к отрезку времени (t), за которое оно этот путь прошло:

Именно о путевой скорости идет речь, когда говорят, что автомобиль ехал из одного города в другой со скоростью 70 км/ч, например.
Ускорение. Касательное ускорение. Центростремительное ускорение
Продолжая речь о телах, движущихся неравномерно, необходимо сказать о такой физической величине, как ускорение.

Единицы измерения ускорения:

Рисунок 6 – Тело перемещается из точки 1 в точку 2 (в верхнем правом углу дана иллюстрация к разности векторов)
Если скорость тела меняется не равномерно на выбранном участке пути, нужно поступить так же, как и в случае с поиском мгновенной скорости: разделить на маленькие отрезки времени и рассматривать ускорение на каждом из них.
Поскольку ускорение получается из разности векторов скорости (конечной и начальной), в общем случае оно будет направлено под некоторым углом к мгновенной скорости (а, следовательно, и к вектору перемещения, и к касательной к траектории).

Рисунок 7 – Полное, касательно и центростремительное ускорение тела, движущегося из точки 1 в точку 2
Равноускоренное движение
Прямолинейное равноускоренное движение. Определение скорости при равноускоренном движении. Уравнения движения при равноускоренном движении
Когда движение тела происходит с постоянным по модулю и направлению ускорением, такой тип движения называют равноускоренным. Для него справедливо выражение:

Частный случай равноускоренного движения – прямолинейное равноускоренное движение. Как следует из названия, это движение вдоль прямой линии с постоянным ускорением.
При условии, что ускорение сонаправлено начальной скорости, формула для вычисления скорости при прямолинейном равноускоренном движении записывается в скалярном виде:
v = v0 + a * t
Если же ускорение противонаправлено начальной скорости, это выражение станет таким:
v = v0 – a * t
Рассмотрим график зависимости скорости от времени при равноускоренном движении (см. рисунок 8). Считаем, что тело совершает движение вдоль оси ОХ, а все величины – начальная скорость (vox) , ускорение (ax) – взяты в проекции на эту ось.

Рисунок 8 – График зависимости скорости от времени при прямолинейном равноускоренном движении
Как известно из предыдущего курса физики, путь, который прошло тело, можно найти как площадь фигуры под графиком зависимости скорости движения от времени. Общую площадь под графиком можно найти как сумму площадей прямоугольника ABCD и треугольника ADE.

Свободное падение
Движение тела, брошенного вертикально вверх. Движение тела, брошенного под углом к горизонту. Криволинейное равноускоренное движение
Примерами движения с постоянным ускорением может служить свободное падение, движение брошенного вертикально вверх тела, движение тела, брошенного под углом к горизонту. Поговорим об этих видах движения подробнее.
- Свободное падение
Представим, что какое-то небольшое, но тяжелое тело подняли на высоту h, а затем отпустили (см. рисунок 9).

Рисунок 9 – Свободное падение тела
Тело начнет падать. Принимаем допущение, что на это тело воздействует одна только сила тяжести (силой сопротивления воздуха и силой ветра пренебрегаем). Тогда тело будет двигаться вертикально вниз, а его ускорение будет равняться ускорению свободного падения:

- Движение тела, брошенного вертикально вверх
Представим, что тело подкинули вертикально наверх с начальной скоростью v0 (см. рисунок 10).

Рисунок 10 – Тело бросили вертикально вверх
Очевидно, что тело сначала будет лететь вверх, постепенно замедляясь, пока его скорость не уменьшится до нуля. Затем тело полетит вниз, постепенно ускоряясь. Получается, что максимальной своей скорости тело будет достигать два раза – у земли, и эта скорость будет равно начальной скорости v0 (вообще нужно было бы писать voy, но так как рассматривается движение вдоль только одной оси OY, опустим индекс y).
Отсюда можно найти полное время полета:

- Движение тела, брошенного под углом к горизонту
Данный тип движения чуть сложнее, чем предыдущие два, так как придется рассматривать движение сразу вдоль двух осей OX и OY (см. рисунок 11). Этот тип движения относится к криволинейному равноускоренному движению. Будем считать, что тело подбросили с начальной скоростью под углом α к горизонту.

Рисунок 11 – Тело брошено под углом к горизонту
Уравнения движения в общем виде по двум осям выглядят так:

Еще время полета можно посчитать, учитывая что в двух моментах – в начале полета и в конце. Значит можно посчитать:

Равномерное движение точки по окружности
Центростремительное ускорение
Представим себе равномерное движение по окружности: во время этого типа движения скорость не меняется по модулю, однако меняется по направлению (см. рисунок 12).

Рисунок 12 – Изменение направления скорости при равномерном движении по окружности
За изменение направления скорости отвечает центростремительное ускорение ( Оно, так же как и скорость, постоянно по модулю, но меняется по направлению – в любой точке окружности оно направлено к ее центру. Центростремительное ускорение можно найти по формуле:

где R – радиус окружности, по которой циклически движется тело.
В данной теме разговор пойдёт о свободном падении тел, также
поговорим об ускорении свободного падения и рассмотрим виды движений тел под
действием силы тяжести.
Ранее говорилось о прямолинейном равноускоренном движении
тел. Прямолинейное равноускоренное движение – это такое движение тела,
при котором его скорость за любые равные промежутки времени изменяется
одинаково, то есть это движение с постоянным по модулю и направлению
ускорением. Ускорение — это векторная физическая величина, равная
отношению изменения скорости к промежутку времени, в течении которого это
изменение произошло.
Одно из наиболее распространенных видов движения с
постоянным ускорением — это свободное падение тел.
Под свободным падением тела понимают движение тела
только под действием силы тяжести.
Долгое время считалось, что ускорение, с которым падает тело,
зависит от размеров и массы этого тела. Действительно, можно с уверенностью
сказать, что листок с дерева или птичье перо падают значительно медленнее, чем
камень или мяч, например.
Аристотель в свое время говорил, что «точно так же,
как направленное вниз движение куска свинца или золота, или любого другого
тела, наделенного весом, происходит тем быстрее, чем больше его размер». А
«одно тело будет тяжелее другого, имеющего тот же объем, если оно движется
вниз быстрее».
Вывод о том, что все тела, независимо от их масс, форм и
размеров, совершают свободное падение совершенно одинаково, на первый
взгляд может показаться противоречащим повседневному опыту.
Люди привыкли к тому, что тяжелые тела достигают земли
быстрее, чем легкие, падающие с той же высоты. На самом деле никакого
противоречия здесь нет. Известно, что дело здесь в том, что существует сила
сопротивления воздуха, которая и препятствует свободному падению. В
большинстве случаев эта сила незначительна, и ею можно пренебречь, за
исключением тех случаев, когда сила сопротивления воздуха становится сравнимой
с силой тяжести. Поэтому в дальнейшем будем рассматривать примеры, в которых
силой сопротивления воздуха можно пренебречь.
Впервые предположение о том, что все тела падают с одинаковым
ускорением, высказал Галилео Галилей. Опытным путем он доказал, что это
предположение верно. Галилей провел один из самых знаменитых физических
экспериментов: он сбросил с Пизанской башни ядро и мушкетную пулю на глазах у
многих людей. Вопреки ожиданиям, и ядро, и пуля упали одновременно.
Исаак Ньютон провел иной опыт, чтобы ещё раз доказать
справедливость предположения Галилея. Он поместил в стеклянную трубку дробинки,
кусочки пробки и пушинку. Перевернув трубку, он наблюдал, как сначала упали
дробинки, потом кусочки пробки и только потом пушинка. Затем он откачал из
трубки воздух и повторил эксперимент. Как и ожидалось, все тела упали
одновременно. Это свидетельствует о том, что ускорение свободного падения
постоянно для любого тела, а различные скорости падения могут быть
обусловлены сопротивлением воздуха.
Таким образом, в данном месте Земли все тела, независимо от их
массы и других физических характеристик, совершают свободное падение с
одинаковым ускорением — ускорением свободного падения. Обозначается оно
малой латинской буквой g. Его значение вблизи
поверхности Земли не постоянно и варьируется от 9,78 м/с2 на
экваторе до 9,83 м/с2 – на полюсах.
Стандартное значение ускорения свободного падения было
определено как «среднее» в каком-то смысле на всей Земле, оно примерно равно
ускорению свободного падения на широте 45,5º на уровне моря. В
приблизительных расчётах его обычно принимают равным
Однако следует помнить о том, что данным значением ускорения
свободного падения можно пользоваться только для вычислений, когда тело
движется вблизи поверхности Земли. Все дело в том, что в соответствии с законом
всемирного тяготения, ускорение свободного падения зависит и от массы
планеты, и от ее радиуса, и от высоты над поверхностью планеты.
Ускорение свободного падения в данной точке земного
шара всегда направлено вертикально вниз к центру Земли.
Рассмотрим свободное падение тел по прямолинейной и
криволинейной траекториям. Сразу обратим внимание на то, что во всех случаях,
которые будут рассматриваться, движение тела будет описываться двумя основными
уравнениями равноускоренного движения — уравнением скорости и кинематическим
уравнением равноускоренного движения.
Рассмотрим тело, которое свободно падает без начальной
скорости с некоторой высоты h над поверхностью
Земли.
В этом случае все время полета можно определить из
кинематического уравнения для равноускоренного движения.
Если данное значение промежутка времени подставить в
уравнение скорости для равноускоренного движения, то можно легко получить
формулу для расчета скорости в последний момент движения.
Следующим вспомним движение тела, брошенного вертикально
вверх с некоторой начальной скоростью.
При таком движении время всего полета определяется формулой:
А время подъема тела на максимальную высоту в два раза меньше
всего времени движения.
Максимальную высоту подъема не трудно определить из уравнения
перемещения для равноускоренного движения, зная время подъема тела и то, что в
верхней точке траектории скорость тела обращается в ноль.
Что касается скорости тела в последний момент движения, то
оказывается, что с какой скоростью тело брошено вертикально вверх, с такой же
по модулю скоростью оно вернется обратно.
Рассмотрим падения тел по криволинейной траектории. Такое
движение возникает в том случае, если вектор начальной скорости тела направлен
не вертикально вверх.
Начнем с рассмотрения движения тела, брошенного в
горизонтальном направлении с некоторой высоты и начальной скоростью.
При рассмотрении такого движения используется две
координатные оси, так как движение происходит в двух плоскостях.
Главное помнить о том, что в горизонтальном направлении
тело движется равномерно, а вот движение в вертикальной плоскости
— равноускоренное, то есть в вертикальной плоскости тело движется также,
как и при свободном падении без начальной скорости.
Зная высоту, с которой брошено тело, можно определить время
всего движения
Как видно, время падения не зависит от начальной скорости
тела и это время равно времени свободного падения тела с некоторой высоты без
начальной скорости. За это время тело в горизонтальном направлении пройдет
некоторое расстояние, которое называют дальностью полета, при этом чем
больше начальная скорость, тем большая дальность полета тела.
Мгновенную скорость тела в любой момент времени можно
рассчитать по формуле:
Рассмотрим последний вид движения под действием силы тяжести
— движение тела, брошенного под углом к горизонту. Для этого решим следующую
задачу.
Задача. Камень бросили под углом α
к горизонту с начальной скоростью υ0.
Определите: скорость и координаты камня через время t после бросания, время полета, максимальную высоту, на
которую поднимется тело, дальность полета и скорость тела в момент падения на
Землю. Сопротивлением воздуха пренебречь.
Таким образом, для движения тела, брошенного
под углом к горизонту
Основные выводы:
Было рассмотрено свободное падение тел. Ускорение, с которым
движется тело во время свободного падения, называют ускорением свободного падения.
Были рассмотрены виды наиболее часто встречающихся движений тел под действием
силы тяжести — это свободное падение тел по прямолинейной и криволинейной
траектории.
