Уравнение ускорения и натяжения нити
Динамика: движения системы связанных тел.
Проецирование сил нескольких объектов.
Действие второго закона Ньютона на тела, которые скреплены нитью
Если ты, дружок, позабыл, как силушку проецировать, советую мыслишки в своей головушке освежить.
А для тех, кто все помнит, поехали!
Задача 1. На гладком столе лежат два связанных невесомой и нерастяжимой ниткой бруска с массой 200 г левого и массой правого 300 г. К первому приложена сила 0,1 Н, к левому — в противоположном направлении сила 0,6 Н. С каким ускорением движутся грузы?
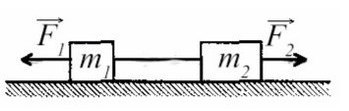
Движение происходит только на оси X.
Т.к. к правому грузу приложена большая сила, движение данной системы будет направлено вправо, поэтому направим ось так же. Ускорение у обоих брусков будет направлено в одну сторону — сторону большей силы.
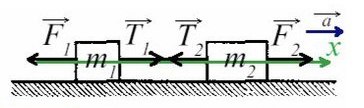
По II з. Ньютона спроецируем силы обоих тел на Ох:
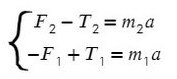
Сложим верхнее и нижнее уравнение. Во всех задачах, если нет каких-то условий сила натяжения у разных тел одинакова T ₁ и Т ₂.
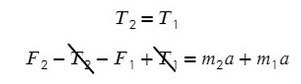
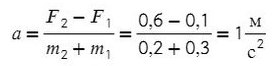
Задача 2. Два бруска, связанные нерастяжимой нитью, находятся на горизонтальной плоскости. К ним приложены силы F₁ и F₂, составляющие с горизонтом углы α и β. Найти ускорение системы и силу натяжения нити. Коэффициенты трения брусков о плоскость одинаковы и равны μ. Силы F₁ и F₂ меньше силы тяжести брусков. Система движется влево.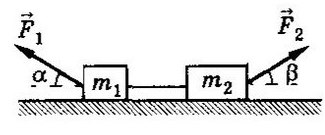 
Cистема движется влево, однако ось можно направить в любую сторону (дело лишь в знаках, можете поэксперментировать на досуге). Для разнообразия направим вправо, против движения всей системы, мы же любим минусы! Спроецируем силы на Ох (если с этим сложности — вам сюда ).
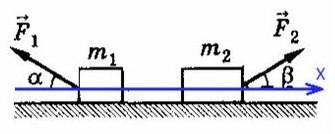
По II з. Ньютона спроецируем силы обоих тел на Ох:
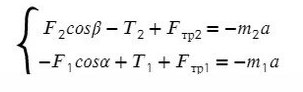
Сложим уравнения и выразим ускорение:
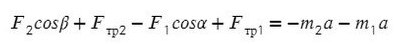
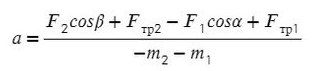
Выразим натяжение нити. Для этого приравняем ускорение из обоих уравнений системы:
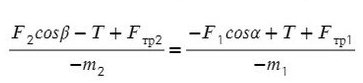
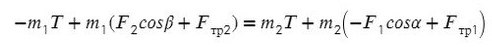
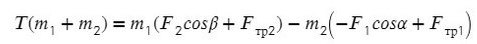
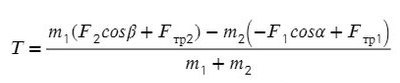
Задача 3 . Через неподивжный блок перекинуты нить, к которой подвешены три одинаковых груза (два с одной стороны и один с другой) массой 5 кг каждый. Найти ускорение системы. Какой путь пройдут грузы за первые 4 с движения?
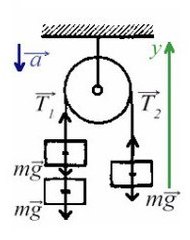
В данной задаче можно представить, что два левых груза скреплены вместе без нити, это избавит нас от проецирования взаимно равных сил.
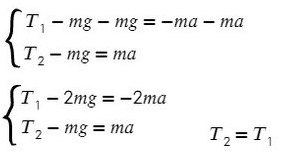
Вычтем из первого уравнения второе:
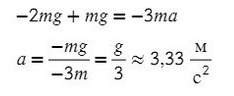
Зная ускорение и то, что начальная скорость равна нулю, используем формулу пути для равноускоренного движения:
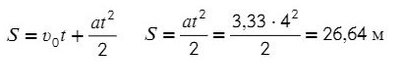
Задача 4. Два груза массами 4 кг и 6 кг соединены легкой нерастяжимой нитью. Коэффициенты трения между грузом и столом μ = 0,2. Определите ускорение, с которым будут двигаться грузы.
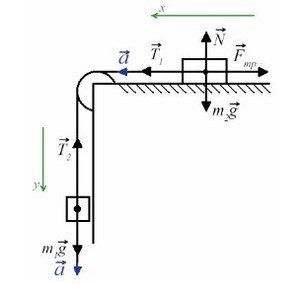
Запишем движение тел на оси, из Oy найдем N для силы трения (Fтр = μN):
(Если сложно понять, какие уравнения понадобятся для решения задачи, лучше запишите все)
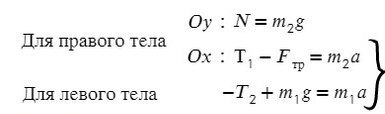
Сложим два нижних уравнения для того, чтобы T сократилось:
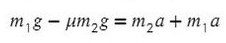
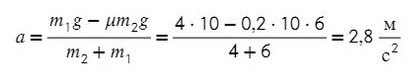
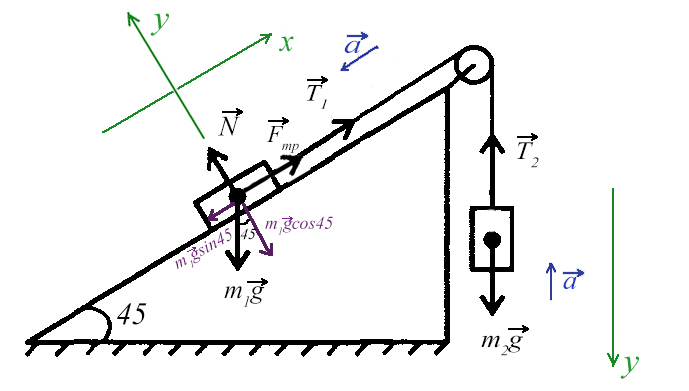
Задача 5. На наклонной поскости с углом наклона 45° лежит брускок массой 6 кг. Груз массой 4 кг присоединен к бруску при помощи нити и перекинут через блок. Определите натяжение нити, если коэффициент трения бруска о плоскость μ = 0,02. При каких значениях μ система будет в равновесии?
Ось направим произвольно и предположим, что правый груз перевешивает левый и поднимает его вверх по наклонной плоскости.
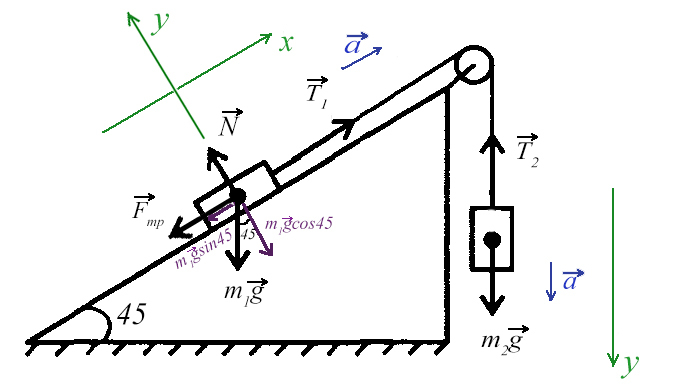
Из уравнения на ось Y выразим N для силы трения на ось Х (Fтр = μN):
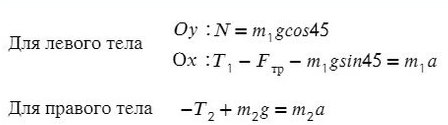
Решим систему, взяв уравнение для левого тела по оси Х и для правого тела по оси Y:
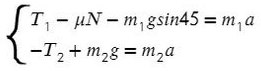
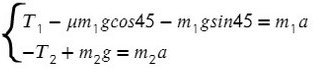
Выразим ускорение, чтобы осталась одна неизвестная T, и найдем ее:
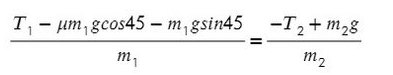
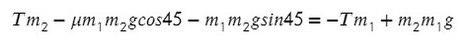
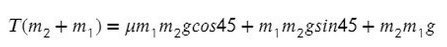
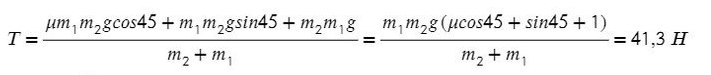
Система будет в равновесии. Это означает, что сумма всех сил, действующих на каждое из тел, будет равна нулю:
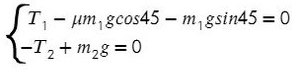
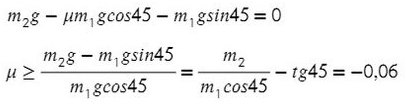
Получили отрицательный коэффициент трения, значит, движение системы мы выбрали неверно (ускорение, силу трения). Можно это проверить, подставив силу натяжения нити Т в любое уравнение и найдя ускорение. Но ничего страшного, значения остаются теми же по модулю, но противоположными по направлению.
Значит, правильное направление сил должно выглядить так, а коэффициент трения, при котором система будет в равновесии, равен 0,06.
Задача 6. На двух наклонных плоскостях находится по грузу массами 1 кг. Угол между горизонталью и плоскостями равен α = 45° и β = 30°. Коэффициент трения у обеих плоскостей μ = 0,1. Найдите ускорение, с которым движутся грузы, и силу натяжения нити. Каким должно быть отношение масс грузов, чтобы они находились в равновесии.
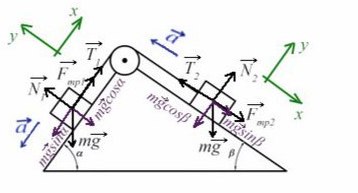
В данной задаче уже потребуются все уравнения на обе оси для каждого тела:
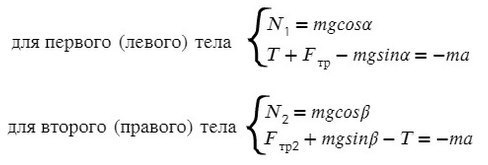
Найдем N в обоих случаях, подставим их в силу трения и запишем вместе уравнения для оси Х обоих тел:
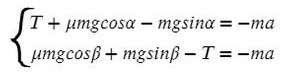
Сложим уравнения и сократим на массу:
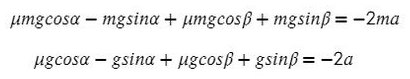
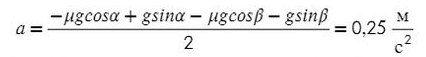
Подставив в любое уравнение найденное ускорение, найдем Т:
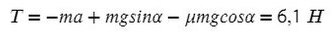А теперь одолеем последний пункт и разберемся с соотношением масс. Сумма всех сил, действующих на любое из тел, равна нулю для того, чтобы система находилась в равновесии:
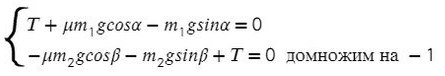
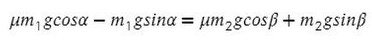
Все, что с одной массой, перенесем в одну часть, все остальное — в другую часть уравнения:
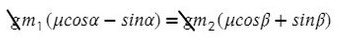
Получили, что отношение масс должно быть таким:
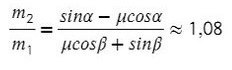
Однако, если мы предположим, что система может двигаться в другом направлении, то есть правый груз будет перевешивать левый, направление ускорения и силы трения изменится. Уравнения останутся такими же, а вот знаки будут другими, и тогда отношение масс получится таким:
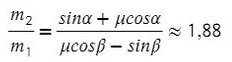
Тогда при соотношении масс от 1,08 до 1,88 система будет находиться в покое.
У многих может сложиться впечатление, что соотношение масс должно быть каким-то конкретным значением, а не промежутком. Это правда, если отстутвует сила трения. Чтобы уравновешивать силы тяжести под разными углами, найдется только один варинт, когда система находится в покое.
В данном же случае сила трения дает диапазон, в котором, пока сила трения не будет преодолена, движения не начнется.
Формула силы натяжения нити
Определение и формула силы натяжения нити
Силу натяжения определяют как равнодействующую сил $(bar)$, приложенных к нити, равную ей по модулю, но противоположно направленную. Устоявшегося символа (буквы), обозначающего силу натяжения нет. Ее обозначают и просто $bar$ и $bar$, и $bar$ . Математически определение для силы натяжения нити можно записать как:
где $bar$ = векторная сумма всех сил, которые действуют на нить. Сила натяжения нити всегда направлена по нити (или подвесу).
Чаще всего в задачах и примерах рассматривают нить, массой которой можно пренебречь. Ее называют невесомой.
Еще одним важной характеристикой нити при расчете силы натяжения является ее растяжимость. Если исследуется невесомая и нерастяжимая нить, то такая нить считается просто проводящей через себя силу. В том случае, когда необходимо учитывать растяжение нити, применяют закон Гука, при этом:
где k – коэффициент жесткости нити, $Delta l$ – удлинение нити при растяжении.
Единицы измерения силы натяжения нити
Основной единицей измерения силы натяжения нити (как и любой силы) в системе СИ является: [T]=Н
Примеры решения задач
Задание. Невесомая, нерастяжимая нить выдерживает силу натяжения T=4400Н. С каким максимальным ускорением можно поднимать груз массой m=400 кг, который подвешивают на эту нить, чтобы она не разорвалась?
Решение. Изобразим на рис.1 все силы, действующие на груз, и запишем второй закон Ньютона. Тело будем считать материальной точкой, все силы приложенными к центру масс тела.
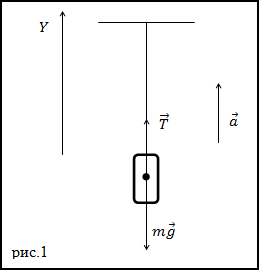
где $bar$ – сила натяжения нити. Запишем проекцию уравнения (1.1) на ось Y:
Из выражения (1.2) получим ускорение:
Все данные в задаче представлены в единицах системы СИ, проведем вычисления:
Ответ. a=1,2м/с 2
Задание. Шарик, имеющий массу m=0,1 кг прикрепленный к нити (рис.2) движется по окружности, расположенной в горизонтальной плоскости. Найдите модуль силы натяжения нити, если длина нити l=5 м, радиус окружности R=3м.
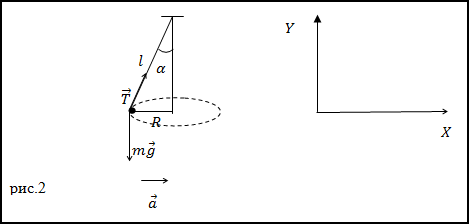
Решение. Запишем второй закон Ньютона для сил, приложенных к шарику, который вращается по окружности с центростремительным ускорением:
Найдем проекции данного уравнения на обозначенные на рис.2 оси X и Y:
$$ begin X: quad T sin alpha=m a=m omega^ <2>R(2.2) \ Y: quad-m g+T cos alpha=0 end $$
Из уравнения (2.3) получим формулу для модуля силы натяжения нити:
Из рис.2 видно, что:
Подставим (2.5) вместо $cos alpha$ в выражение (2.4), получим:
Так как все данные в условиях задачи приведены в единицах системы СИ, проведем вычисления:
iSopromat.ru
Пример расчета ускорения груза и натяжения нитей для заданной механической системы, движущейся из состояния покоя, без учета моментов сопротивления в подшипниках и массы нерастяжимых нитей.
Условие задачи
Для заданной механической системы определить ускорение груза и натяжения нитей.
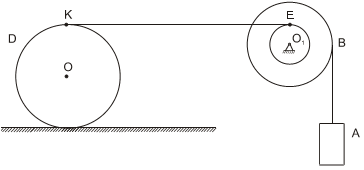
Система движется из состояния покоя, моменты сопротивления в подшипниках не учитывать, массами нитей пренебречь, нити не растяжимы (рис. 2.1).
Пример решения
Определим направление движения системы, указав направление ускорения груза A, покажем на рис. 2.2. задаваемые силы: GA, GB, GD реакции связей NB, ND (направление NB пока неизвестно). Силы инерции для тела A приводятся к главному вектору сил инерции ФА=mA∙aA, для тела B к главному моменту сил инерции MB Ф =JB∙εB, для тела D, совершающего плоское движение к главному вектору сил инерции ФD=mD∙aD и к главному моменту сил инерции MD Ф =JD∙εD. Коэффициент трения качения определяет наличие момента сопротивления
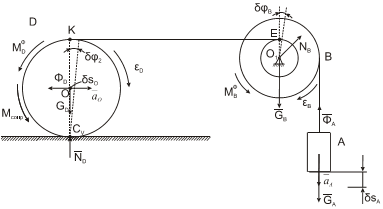
Ускорения и перемещения точек системы получаются дифференцированием и интегрированием зависимостей между линейными и угловыми скоростями точек системы.
Приняв скорость груза VA, получим соотношения
Можно продифференцировать и проинтегрировать выше приведенные формулы и получить выражения
Сообщим системе возможное перемещение в направлении ее действительного движения. Силы и моменты, действующие на систему, совершат элементарную работу. Сумма всех работ должна быть равна нолю. Момент сопротивления отнесем к внешним воздействиям. Это позволит считать данную систему идеальной. Составим общее уравнение динамики (уравнение работ):
Подставим данные задачи и получим:
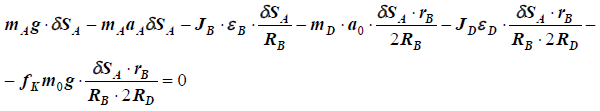
Сократив на δSA — задаваемое нами возможное перемещение груза А получим:
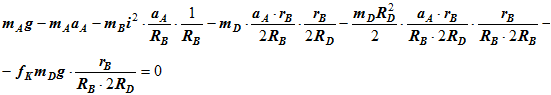
Из этого соотношения определим ускорение груза
Из найденных ранее соотношений можно определить: εB, a0, εD.
При решении задачи этим методом внутренние силы в уравнения не входят. Для определения натяжения нитей нужно сделать эти силы внешними, для чего разделяем систему на части. Рассмотрим отдельно груз А, на который действуют силы ФA, GA и сила TAB, ставшая внешней (рис. 2.3). Для этой системы можно написать или принцип Даламбера или общее уравнение динамики.
Находим натяжение нити:
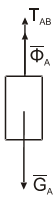
Для определения натяжения нити между телами B и D можно составить общее уравнение динамики (или написать принцип Даламбера) для тела B или D.
Рассмотрим тело D (рис. 2.4). Покажем действующие внешние силы и силы инерции. Натяжение нити ТBD стало внешней силой. Приняв за возможное перемещение угол поворота тела D — δφD составим уравнение работ.
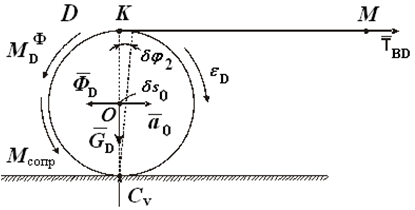
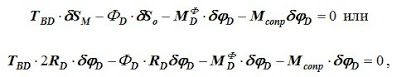
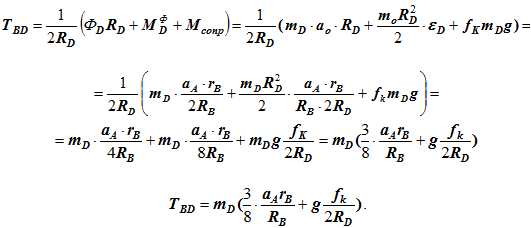
Для проверки результатов можно написать общее уравнение динамики (или принцип Даламбера) для блока B.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
[spoiler title=”источники:”]
http://www.webmath.ru/poleznoe/formules_21_30_sila_natjazhenija_niti.php
[/spoiler]
Иногда в системе движется не одно, а два связанных между собой тела. Тогда описание движения с применением законов Ньютона включает в себя описания движения каждого из этих тел.
Движение тел по горизонтали без трения
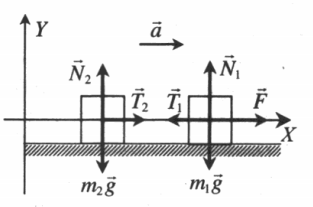
Решение
II закон Ньютона в векторной форме для 1 тела:
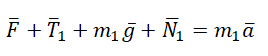
II закон Ньютона в векторной форме для 2 тела:
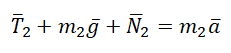
Проекция на ОХ для 1 тела:
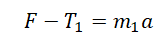
Проекция на ОY для 1 тела:
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
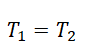
Движение по горизонтали с учетом сил трения
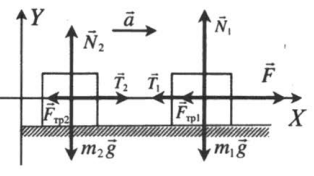
Решение
II закон Ньютона в векторной форме для 1 тела:
II закон Ньютона в векторной форме для 2 тела:
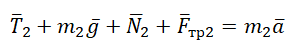
Проекция на ОХ для 1 тела:
Проекция на ОY для 1 тела:
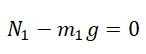
Проекция на ОХ для 2 тела:
Проекция на ОY для 2 тела:
III закон Ньютона:
Вертикальное движение тел (m1 > m2)
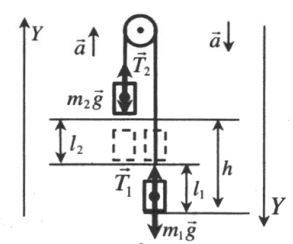
h — расстояние между телами. l1 и l2 — перемещение тела 1 и тела 2 соответственно. Перемещения обоих тел равны, поэтому: l1 = l2 = l.
Решение
Расстояние между телами определяется формулой: h = l1 + l2 = 2l.
II закон Ньютона в векторной форме для 1 тела:
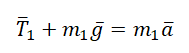
II закон Ньютона в векторной форме для 2 тела:
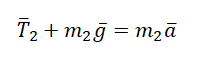
Проекция на ОY для 1 тела:
Проекция на ОY для 2 тела:
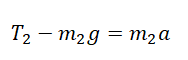
III закон Ньютона:
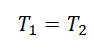
На один из грузов положили довесок
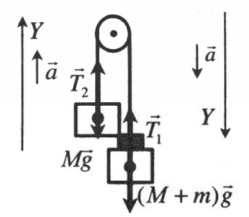
Решение
II закон Ньютона для 1 тела:
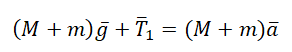
II закон Ньютона для 2 тела:
Проекция на ось ОУ для 1 тела:
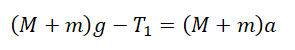
Проекция на ось ОУ для 2 тела:
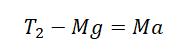
III закон Ньютона:
Вес довеска определяется по формуле:
Пример №1. На нити, переброшенной через неподвижный блок, подвешены грузы массами m и 2m. С каким ускорением будут двигаться грузы, если их отпустить? Трением в блоке пренебречь.
Строим чертеж:
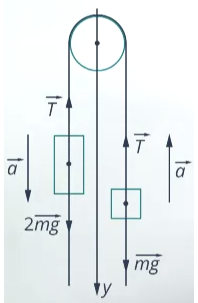
Записываем второй закон Ньютона для каждого из тел. Для первого тела он будет иметь вид:
Для второго тела II закон Ньютона примет следующий вид:
Запишем проекции на ось OУ для каждого из тел:
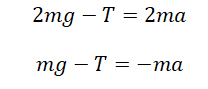
Выразим силы натяжения нити для каждого из тел и приравняем их правые части:
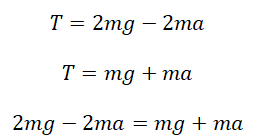
Сделаем несколько преобразований:
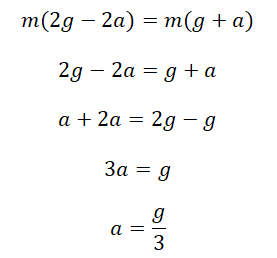
Это значит, если отпустить грузы, они будут двигаться с ускорением, втрое меньшим по сравнению с ускорением свободного падения. Приблизительно оно будет равно 3,33 м/с2.
Задание EF17717
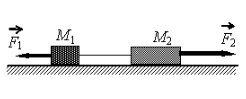Два груза массами соответственно М1 = 1 кг и М2 = 2 кг, лежащие на гладкой горизонтальной поверхности, связаны невесомой и нерастяжимой нитью. На грузы действуют силы F1 и F2, как показано на рисунке. Сила натяжения нити Т = 15 Н. Каков модуль силы F1, если F2 = 21 Н?
а) 6 Н
б) 12 Н
в) 18 Н
г) 21 Н
Алгоритм решения
1.Записать исходные данные.
2.Сделать чертеж. Указать все силы, которые действуют на 1 и 2 тело. Выбрать систему координат.
3.Записать для каждого тела второй закон Ньютона в векторной форме.
4.Записать для каждого тела второй закон Ньютона в виде проекций на оси ОХ и ОУ.
5.Выразить формулу для вычисления силы, действующей на первое тело.
6.Подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные:
• Масса тела 1: m1 = 1 кг.
• Масса тела 2: m2 = 1 кг.
• Сила натяжения нити: Т = 15 Н.
• Сила, действующая на второе тело, равна: F2 = 21 Н.
Сделаем чертеж. Систему координат выберем такую, чтобы ось ОУ была параллельная ускорению свободного падения.
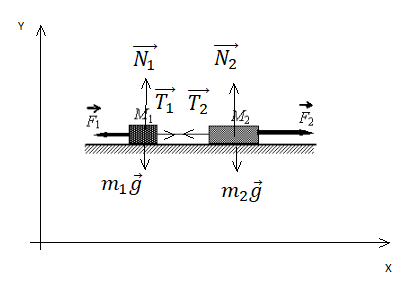
Согласно третьему закону Ньютона, два тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Поэтому модули сил натяжения нити Т1 и T2 равны:
T1 = T2 = T
Учтем это при записи второго закона Ньютона для каждого из тел:
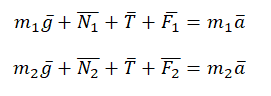
Запишем второй закон Ньютона в проекциях на оси ОХ и ОУ. Сначала для первого тела:
T – F1 = m1a
N1 = m1g
Теперь для второго тела:
F2 – T = m2a
N2 = m2g
Выразим из проекции на ось ОХ для 1 тела модуль первой силы:
F1 = T – m1a
Из проекции на ось ОХ для второго тела выразим ускорение:
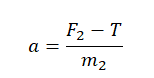
Подставим ускорение в формулу для нахождения силы, действующей на первое тело:
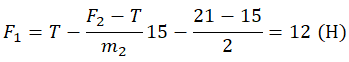
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18920
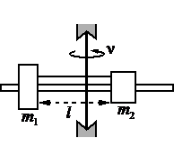На вертикальной оси укреплена гладкая горизонтальная штанга, по которой могут перемещаться два груза массами m1 = 200 г и m2 = 300 г, связанные нерастяжимой невесомой нитью длиной l = 20 см. Нить закрепили на оси так, что грузы располагаются по разные стороны от оси и натяжение нити с обеих сторон от оси при вращении штанги одинаково (см. рисунок). Определите модуль силы натяжения Т нити, соединяющей грузы, при вращении штанги с частотой 600 об/мин.
Алгоритм решения
1.Записать исходные данные. Перевести их в СИ.
2.Сделать чертеж, обозначив все силы, действующие на систему тел, их направления. Выбрать систему координат.
3.Записать второй закон Ньютона в векторной форме для каждого из тел.
4.Записать второй закон Ньютона для каждого из грузов в виде проекций на ось ОХ.
5.Вывести формулу для радиуса окружности, по которой движется любой из грузов.
6.Вывести формулу для вычисления силы натяжения нити, подставить известные данные и произвести вычисления.
Решение
Запишем исходные данные, сразу переведя их в СИ:
• Масса первого груза m1 = 200 г = 0,2 кг.
• Масса первого груза m2 = 300 г = 0,3 кг.
• Длина нити l = 20 см = 0,2 м.
• Натяжение нити с обеих сторон одинаково, следовательно: T1 = T2 = T.
• Частота вращения штанги ν = 600 об./мин. = 10 об./с.
Сделаем чертеж, обозначив все силы. Учтем, что сила натяжения нити равна с обеих сторон. Выберем систему координат, в которой ось ОУ параллельна оси вращения.
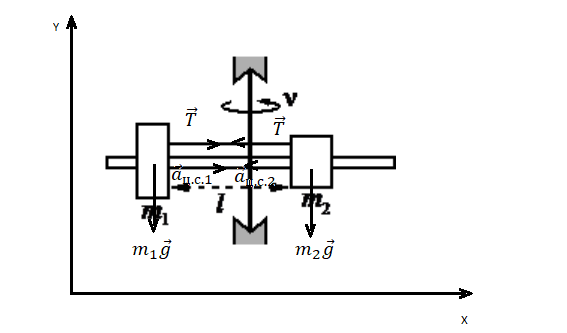
Запишем второй закон Ньютона для первого и второго груза соответственно:
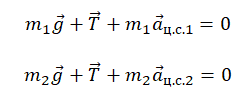
Запишем проекции на ось ОХ для каждого из тел:
T = m1aц.с.1
T = m2aц.с.2
Центростремительное ускорение также определяется формулой:
aц.с. = ω2R
Угловая скорость определяется формулой:
ω = 2πν
Следовательно, центростремительное ускорение равно:
aц.с. = 4π2ν2R
Применим эту формулу для обоих грузов:
aц.с.1 = 4π2ν2R1
aц.с.2 = 4π2ν2R2
Сумма радиусов окружностей, по которым вращаются грузы, есть длина нити:
R1 + R2 = l
Выразим радиус окружности, по которой вращается второй груз:
R2 = l – R1
Так как грузы связаны между собой, и ни один из них не перевешивает другой:
m1gR1 = m2gR2
Ускорение свободного падения взаимоуничтожается. Получаем:
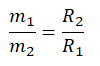
Подставим радиус второй окружности и выразим радиус первой окружности:
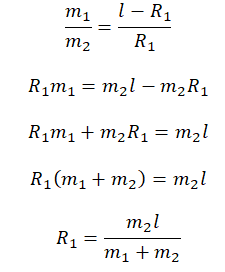
Следовательно, центростремительное ускорение первого груза равно:
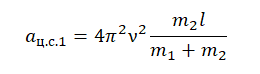
Теперь возьмем проекцию на ось ОХ для первого тела и вставим в формулу найденное центростремительное ускорение для первого тела:
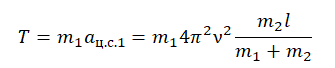
Подставим известные данные и вычислим силу натяжения нити:
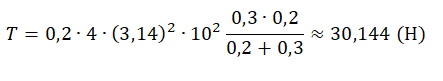
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17647
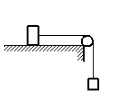По горизонтальному столу из состояния покоя движется брусок массой 0,9 кг, соединённый с грузом массой 0,3 кг невесомой нерастяжимой нитью, перекинутой через гладкий невесомый блок (см. рисунок). Коэффициент трения бруска о поверхность стола равен 0,2. Натяжение вертикальной части нити равно:
а) 2,25 Н
б) 2,7 Н
в) 3 Н
г) 3,6 Н
Алгоритм решения
• Записать исходные данные.
• Сделать чертеж. Указать все силы, действующие на тела, и их направление. Выбрать систему отсчета.
• Записать второй закон Ньютона для бруска и подвешенного к нити груза в векторной форме.
• Записать второй закон Ньютона для обоих тел в виде проекций на оси.
• Вывести формулу для вычисления искомой величины.
• Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса первого тела (движущегося по плоскости) равна: m1 = 0,9 кг.
• Масса второго тела (подвешенного к нити) равна: m2 = 0,3 кг.
• Коэффициент трения первого тела о поверхность плоскости равна: μ = 0,2.
Выполним чертеж и укажем все силы, которые действуют на брусок и груз на нити. Выберем систему координат так, чтобы направление оси ОХ совпадало с направлением движения бруска.
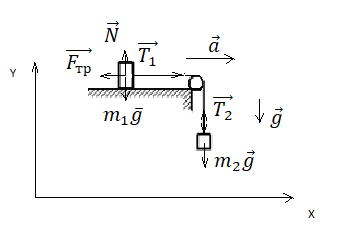
Так как тела связаны, силы натяжения нити на обоих концах равны. Будем обозначать их без индекса. Запишем второй закон Ньютона в векторной форме для первого и второго тела соответственно:
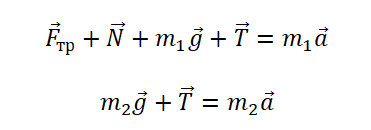
Теперь запишем проекции на ось ОХ и ось ОУ соответственно для бруска:
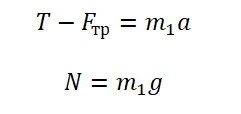
Запишем проекцию на ось ОУ для груза на нити:
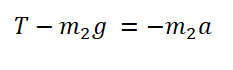
Выразим из этого выражения ускорение и получим:
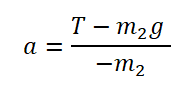
Из проекции на ось ОХ сил, действующих на брусок, тоже выразим ускорение:
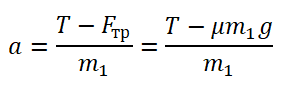
Приравняем правые части уравнений и получим:
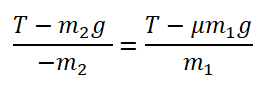
Произведем вычисления:
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22698
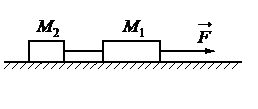Два груза, связанные нерастяжимой и невесомой нитью, движутся по гладкой горизонтальной поверхности под действием постоянной горизонтальной силы F, приложенной к грузу М1 = 2 кг (см. рисунок). Нить обрывается при значении силы натяжения нити 4 Н, при этом модуль силы F равен 12 H. Чему равна масса второго груза М2?
Алгоритм решения
1.Записать исходные данные.
2.Выполнить чертеж, указав все силы, действующие на каждый из грузов.
3.Записать второй закон Ньютона для обоих тел.
4.Записать второй закон Ньютона в проекциях на ось ОХ.
5.Применить третий закон Ньютона.
6.Выразить массу второго груза (найти общее решение).
Решение
Запишем исходные данные:
• Масса первого груза равна: m1 = 2 кг.
• Сила натяжения нити равна: T = 4 Н.
• Модуль силы, которая действует на систему тел: F = 12 Н.
Выполним чертеж:
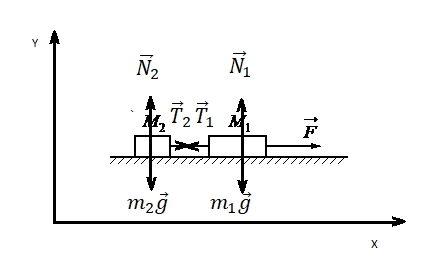
Запишем второй закон Ньютона для 1 и 2 тела соответственно:
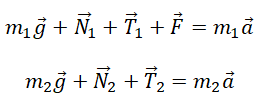
Запишем второй закон Ньютона для 1 и 2 тела в проекции на ось ОХ:
F – T1 = m1a
T2 = m2a
Отсюда масса второго тела равна:
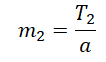
Согласно третьему закону Ньютона, тела действуют друг на друга с равными по модулю, но противоположными по направлению силами. Следовательно, силы натяжения нити равны на обоих концах:
T1 = T2 = T
Поэтому:
T = F – m1a
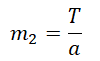
Из первого выражения выразим ускорение и подставим его во второе:
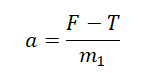
Подставим в формулу и получим:
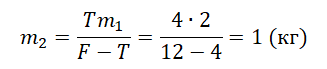
Ответ: 1
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.9k
Условие задачи:
Через неподвижный блок перекинута нить с грузами массой 3 и 5 кг. С каким ускорением будут двигаться грузы?
Задача №2.2.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
(m=3) кг, (M=5) кг, (a-?)
Решение задачи:
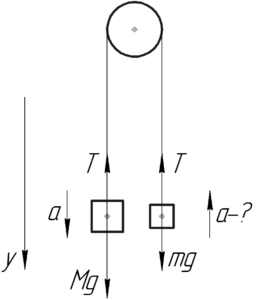Нарисуем схему к задаче и покажем все силы, действующие на каждый груз – силу тяжести и силу натяжения нити. Понятно, что когда грузы отпустят, то груз (M) станет двигаться вниз, поскольку он тяжелее, а груз (m) – вверх. Грузы будут двигаться с одинаковыми ускорениями, так как нить, соединяющая их, нерастяжима.
Запишем второй закон Ньютона для обоих грузов в проекции на вертикальную ось (y):
[left{ begin{gathered}
Mg – T = Ma hfill \
mg – T = – ma hfill \
end{gathered} right.]
Вычтем из первого равенства системы второе, тогда получим следующее:
[Mg – mg = Ma + ma]
[gleft( {M – m} right) = aleft( {M + m} right)]
Выразим искомое ускорение:
[a = frac{{gleft( {M – m} right)}}{{M + m}}]
Считаем ответ:
[a = frac{{10 cdot left( {5 – 3} right)}}{{5 + 3}} = 2,5; м/с^2]
Ответ: 2,5 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.90 На материальную точку массы 1 кг действует две постоянные взаимно перпендикулярные
2.2.2 Три груза массами m1=1 кг, m2=2 кг, m3=3 кг соединены легкими нитями, проходящими
2.2.3 Через неподвижный блок перекинута нить, к концам которой подвешены грузы
ГЛАВА1
КИНЕМАТИКА МАТЕРИАЛЬНОЙ ТОЧКИ И
ПРОСТЕЙШИХ СИСТЕМ
1.1. Теоретический материал
Физическая величина – это количественная характеристика свойства материальных объектов или явлений (процессов). Каждая физическая величина устанавливается однозначным способом ее измерения – экспериментального определения или расчета. Определение физической величины указывает принципиальный способ ее измерения.
Физическое понятие (модель объекта или явления) – это абстракция (филос.), которая отражает только основные, наиболее существенные, свойства материальных объектов или явлений (процессов).
Критерий правильности выбора модели. Если в данной задаче физическая величина, описывающая неосновное свойство, от которого мы абстрагируемся, много меньше другой, характерной для этой задачи, величины той же размерности, то модель выбрана верно.
Заметим, что один и тот же материальный объект или одно и то же явление в различных условиях могут быть рассмотрены в рамках различных моделей, если они удовлетворяют критериям правильности выбора этих моделей.
Тело отсчета – тело, относительно которого рассматривается движение других тел.
Часы – неподвижный относительно тела отсчета прибор для измерения времени, принцип действия которого основан на сравнении длительности исследуемого временного интервала с длительностью выбранного за эталон периодического процесса.
Система отсчета – совокупность системы координат[1], связанной с телом отсчета, и набора синхронизированных часов, размещенных в разных точках координатной системы.
Условие синхронизации часов A и B, расположенных в разных точках системы отсчета (в предположении об изотропности пространства):
(1.1)
Здесь – момент времени излучения из точки A светового сигнала (кванта света) по часам в точке A, – момент времени регистрации этого сигнала в точке B по часам в точке B, – момент времени регистрации в точке A отраженного в точке B сигнала по часам в точке A.
Материальная точка – физическое понятие (модель, абстракция), представляющее тело, размерами (и формой) которого можно пренебречь в условиях данной задачи.
Положение материальной точки относительно данной системы отсчета (в данной системе отсчета) S задается ее координатами или радиус-вектором .
Радиус-вектор материальной точки относительно данной системы отсчета – вектор, начало которого находится в начале координат этой системы, а конец – в месте расположения материальной точки (см. рис. 1.1а):
, (1.2)
где , и – орты декартовой системы координат: , , ; x, y, z – координаты материальной точки.
 |
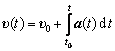Закон движения материальной точки относительно данной системы отсчета – зависимость радиус-вектора или координат материальной точки от времени:
(1.3)
Траектория движения материальной точки – линия, описываемая в пространстве концом радиус-вектора материальной точки.
Уравнение траектории задается совокупностью двух уравнений
(1.4)
которые можно получить, исключая время из закона движения в координатной форме (1.3). Заметим, что сам закон движения в координатной форме представляет собой уравнение траектории, заданное в параметрическом виде.
Перемещение материальной точки – изменение радиус-вектора материальной точки за время Dt с момента времени t (рис. 1а):
. (1.5)
Скорость материальной точки относительно данной системы отсчета – физическая величина, равная производной радиус-вектора материальной точки по времени (производная берется при постоянных ортах системы координат, поскольку они жестко связаны с телом отсчета):
, (1.6)
где , , – проекции скорости на соответствующие оси системы координат. Скорость можно представить в виде суммы составляющих скорости вдоль осей системы координат:
. (1.7)
При этом модуль скорости равен
. (1.8)
В соответствии с определением скорость всегда направлена по касательной к траектории (см. рис. 1.1б).
Зная закон изменения скорости материальной точки , и радиус-вектор в начальный момент времени t0, можно найти закон движения:
. (1.9)
Путь s(t), пройденный материальной точкой вдоль траектории (длина траектории) за время t, равен
, (1.10)
при этом модуль скорости в любой момент времени равен
. (1.11)
Ускорение материальной точки относительно данной системы отсчета – физическая величина, равная производной скорости материальной точки по времени (при постоянных ортах системы координат):
, (1.12)
где ax, ay, az – проекции ускорения на соответствующие оси системы координат. Ускорение можно представить в виде суммы составляющих ускорения вдоль осей системы координат:
. (1.13)
При этом модуль ускорения равен
. (1.14)
Зная закон изменения ускорения материальной точки , а также скорость и радиус-вектор в начальный момент времени t0, можно найти закон изменения скорости и закон движения:
, (1.15)
. (1.16)
Начальные условия для материальной точки – значения радиус-вектора и скорости в начальный момент времени t0 относительно заданной системы отсчета:
(1.17)
Тангенциальное ускорение – составляющая ускорения вдоль направления скорости (см. рис. 1.2):
, , , (1.18)
, (1.19)
где – проекция ускорения на направление скорости .
Движение материальной точки при – ускоренное, при – замедленное, при – равномерное, а при – равнопеременное.
Нормальное ускорение – составляющая ускорения , перпендикулярная направлению скорости (рис. 1.2):
, , , (1.20)
где – проекция ускорения на направление , перпендикулярное скорости и направленное к центру кривизны траектории.
Нормальное ускорение всегда направлено к центру кривизны траектории – центру окружности максимального радиуса (радиуса кривизны траектории), касательной к траектории в данной точке, при этом
, (1.21)
где – радиус кривизны траектории в данной точке, а – угол между скоростями в моменты времени t и t + dt.
Ускорение можно представить в виде суммы нормального и тангенциального ускорений:
. (1.22)
При этом модуль ускорения равен
. (1.23)
В соответствии с (1.21) и (1.22) ускорение всегда отклонено от направления скорости в сторону центра кривизны траектории в данной точке, то есть внутрь траектории (см. рис. 1.2).
В частном случае движения материальной точки по окружности, т.е. движения в плоскости по траектории с постоянным радиусом кривизны – (рис. 1.3), можно ввести угловую скорость и угловое ускорение :
(1.24)
При этом:
(1.25)
Механическая система – совокупность материальных тел.
Система материальных точек – совокупность тел, каждое из которых можно считать материальной точкой. Далее будем считать, что всякую рассматриваемую нами механическую систему можно рассматривать как систему материальных точек.
Абсолютно твердое тело – тело (система материальных точек), расстояния между двумя любыми материальными точками которого не меняются в условиях данной задачи.
Поступательное движение абсолютно твердого тела – движение, при котором прямая, соединяющая любые две материальные точки тела, перемещается параллельно самой себе.
Принцип суперпозиции движений – в случае поступательного движения системы отсчета S¢ относительно системы S (рис. 1.4) радиус-вектор (скорость, ускорение) произвольной материальной точки относительно системы S равен сумме радиус-векторов (скоростей, ускорений) начала отсчета O’ системы S’ и той же материальной точки относительно системы S’:
(1.26)
Здесь и – переносные скорость и ускорение соответственно.
Уравнения кинематической связи – уравнения, связывающие кинематические характеристики различных тел системы:
(1.27)
Существуют два способа нахождения уравнений кинематической связи.
Способ 1. Принцип независимых перемещений. Перемещение какого-либо тела в системе связанных тел складывается из так называемых «независимых» перемещений, каждое из которых обусловлено (вызвано) перемещением соответствующего другого тела системы при покоящихся остальных телах:
. (1.28)
Способ 2. Записать величины постоянных кинематических характеристик элементов связей (нитей, штанг, блоков, поверхностей и т.д.) через координаты тел системы, используя свойства этих элементов (нерастяжимость, неподвижность, недеформированность), и продифференцировать эти величины по времени.
1.2. Основные типы задач и методы их решения
1.2.1. Классификация задач кинематики
Основной задачей кинематики является определение кинематических характеристик тел, движущихся относительно данной системы отсчета.
Большинство задач кинематики можно условно отнести к следующим типам задач или их комбинациям:
1) кинематика материальной точки,
2) принцип суперпозиции движений,
3) уравнения кинематической связи,
4) кинематика простейших механических систем.
Как правило, один из типов задач имеет основное, другие – подчиненное по отношению к условию задачи значение.
1.2.2. Общая схема решения задач кинематики
I. Определиться с моделями материальных объектов и явлений.
1. Нарисовать чертеж, на котором изобразить рассматриваемые тела.
2. Выбрать систему отсчета и изобразить на чертеже ее систему координат (из соображений удобства).
3. Изобразить и обозначить кинематические характеристики тел.
4. Выбрать модели тел и их движения (если это не сделано в условии задачи).
II. Записать полную систему уравнений для искомых величин.
1. Записать в проекциях на оси координат:
а) законы движения,
б) законы изменения скорости,
в) законы изменения ускорения.
2. Записать начальные условия.
3. Записать уравнения кинематических связей.
4. Использовать результаты ранее решенных задач и особые условия задачи (например, заданные соотношения между характеристиками системы).
III. Получить искомый результат в аналитическом и численном видах.
1. Решить систему полученных уравнений.
2. Провести анализ решения (проверить размерность и лишние корни, рассмотреть характерные случаи, установить область применимости).
3. Получить численный результат.
Примечания.
В случае решения задач на кинематику материальной точки в пп. I.3 – II.2 речь идет о кинематических характеристиках материальной точки, а п. II.3 надо опустить.
В случае решения задач на кинематику простейших механических систем в пп. I.3 – II.2 речь идет о кинематических характеристиках тел рассматриваемой системы.
Пункты II.1 – II.3 (в том числе II.2.a – II.2.в) можно выполнять в той или иной последовательности в зависимости от типа задачи.
1.3. Примеры решения задач
Задача 1.1
(Кинематика материальной точки)
Скорость материальной точки зависит от ее положения в декартовой системе координат следующим образом: , где c и b – положительные постоянные величины. В начальный момент времени радиус-вектор материальной точки равен нулю: . Определить:
а) законы движения , изменения скорости и ускорения , тангенциальную и нормальную проекции ускорения;
б) уравнение траектории y(x) материальной точки;
в) радиус кривизны траектории ;
г) угол между скоростью и ускорением .
Решение
Следуем общей схеме решения задач кинематики материальной точки и простейших систем.
I. По условию задачи движение происходит в плоскости XY, образованной координатными осями, направления которых заданы ортами и .
II. Запишем начальные условия и закон изменения скорости тела в проекциях на оси выбранной системы координат:
(1.29)
(1.30)
III. Записанные дифференциальные уравнения относительно координат материальной точки (1.29) с учетом начальных условий (1.29) позволяют найти закон движения материальной точки в проекциях на оси координат и зависимость от времени радиус-вектора :
(1.31)
. (1.32)
Используя найденную зависимость x(t) (1.31), определим закон изменения скорости и закон изменения ускорения :
, (1.33)
. (1.34)
Уравнение траектории находится из закона движения материальной точки путем исключения из (1.31) времени t:
. (1.35)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.7) равен:
. (1.36)
Проекции ускорения и (1.19, 1.23) получим в виде:
(1.37)
Радиус кривизны траектории (1.21) равен:
. (1.38)
Угол между скоростью и ускорением определяется соотношением:
. (1.39)
Заметим, что материальная точка движется по параболической траектории (1.35) с постоянным ускорением, направленным вдоль оси Y (1.34). На рис. 1.5 схематично изображена траектория движения материальной точки и изображены векторы ускорения и начальной скорости.
Нетрудно видеть, что при решения соответствуют начальным условиям задачи. При этом тангенциальное ускорение в указанный момент времени равно нулю, радиус кривизны траектории в данный момент времени , а угол между скоростью и ускорением .
При значения координат точки и модуль скорости, как и следовало ожидать, неограниченно возрастают, нормальное ускорение и угол между скоростью и ускорением стремятся к нулю, а радиус кривизны траектории – к бесконечности.
Задача 1.2
(Кинематика материальной точки)
Находящееся на высоте H над Землей тело бросили горизонтально с начальной скоростью . Найти закон движения тела, уравнение траектории, законы изменения скорости и ускорения, а также нормальную и тангенциальную проекции ускорения и радиус кривизны траектории в произвольный момент времени.
Решение
I. Нарисуем чертеж и изобразим на нем заданную в условии задачи скорость тела в начальный момент времени (t = 0) и предполагаемую траекторию движения тела (рис. 1.6).
Выберем систему отсчета, связанную с Землей. Ось X декартовой системы координат направим горизонтально вдоль поверхности Земли по направлению начальной скорости , а ось Y – вертикально вверх на положение тела в начальный момент времени. Будем считать, что тело является материальной точкой, а движение тела у поверхности Земли происходит с постоянным ускорением свободного падения .
II. В соответствии с выбранной системой отсчета и выбранными моделями тела и его движения запишем начальные условия и закон изменения ускорения тела в проекциях на оси координат:
(1.40)
(1.41)
III. Записанные дифференциальные уравнения относительно проекций скорости материальной точки с учетом начальных значений позволяют найти закон изменения скорости тела и закон его движения в проекциях на оси координат:
(1.42)
(1.43)
Уравнение траектории находится из закона движения тела в координатной форме (1.43) путем исключения времени t:
. (1.44)
Остальные искомые величины определяются в соответствии с формулами, приведенными в п. 1 данной Главы.
Модуль скорости (1.8) равен:
. (1.45)
Модуль ускорения (1.14) имеет вид:
. (1.46)
Проекции ускорения на направление скорости и перпендикулярное ему направление (1.19, 1.23) равны:
, . (1.47)
Радиус кривизны (1.21) определяется соотношением:
. (1.48)
Заметим, что в данной задаче все формулы для нахождения искомых величин справедливы с начального момента времени t0 = 0 до момента падения тела на Землю t0 £ t£ tпад. Этот момент времени легко найти из закона движения (1.43), приняв координату y равной нулю:
. (1.49)
Задача 1.3
(Кинематика материальной точки и принцип
суперпозиции движений)
Лодка пересекает реку с постоянной относительно воды скоростью , перпендикулярной направлению течения реки. Модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, изменяясь от 0 до um. Найти уравнение траектории лодки, время ее движения , а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Решение
I. Выберем декартову систему координат, жестко связанную с берегом реки, и с началом в месте отплытия лодки. Оси системы координат и скорость течения реки изображены на рис. 1.7.
При решении задачи лодку будем считать материальной точкой, а берега реки параллельными.
II. Запишем начальные условия для лодки в соответствии с условиями задачи:
(1.50)
где , – проекции скорости лодки на оси выбранной системы координат.
В соответствии с принципом суперпозиции движений (1.26) в любой момент времени или в проекциях на оси координат:
(1.51)
По условию задачи модуль скорости течения реки, ширина которой d, нарастает от берегов к середине реки по параболическому закону, поэтому можно записать:
, (1.52)
где и – постоянные величины. Для определения величины используем условие задачи:
. (1.53)
Используя начальные условия и соотношение (1.53), получим величину a:
. (1.54)
III. Система уравнений (1.51) с учетом (1.52) – (1.54) преобразуется к виду:
(1.55)
Интегрируя уравнения (1.55) с учетом начальных условий для координат лодки (1.50), находим закон движения:
, (1.56)
. (1.57)
Уравнение траектории получаем, исключая время t из закона движения в координатной форме (1.56) и (1.57):
. (1.58)
Поскольку в момент причаливания , время движения лодки равно:
. (1.59)
Следовательно, для искомого сноса лодки l получим (см. 1.58):
. (1.60)
Задача 1.4
(Принцип суперпозиции движений)
Определить форму траектории капель дождя на боковом стекле трамвая, движущегося горизонтально со скоростью , во время его торможения с ускорением . Капли дождя падают на землю вертикально вниз, и скорость их относительно земли постоянна и равна .
Решение
I. Нарисуем чертеж и изобразим на нем заданные в условии задачи кинематические характеристики капли дождя и трамвая в момент начала торможения трамвая (рис. 1.8).
Выберем систему координат XY, связанную с Землей, так, чтобы ось X была направлена горизонтально вдоль ускорения трамвая, а ось Y – вертикально вниз. Выберем также вторую систему координат X¢Y¢, связанную со стеклом трамвая, так, чтобы ее оси X¢ и Y¢ были сонаправлены с осями X и Y. Время в обеих системах отсчитываем от момента начала торможения трамвая.
Будем считать, что капля дождя является материальной точкой, положение которой в момент начала торможения трамвая совпадает с началом координат системы X¢Y¢.
II. Используя принцип суперпозиции движений (1.26), запишем скорость и ускорение капли дождя относительно стекла трамвая (системы координат X¢Y¢):
, (1.61)
. (1.62)
В соответствии с выбранной системой отсчета запишем начальные условия для капли дождя:
, (1.63)
, (1.64)
III. Записанные дифференциальные уравнения (1.61) и (1.62) с учетом начальных условий (1.63) и (1.64) позволяют найти закон движения капли в проекциях на оси координат:
(1.65)
Уравнение траектории находится из закона движения капли путем исключения из (1.65) времени t:
. (1.66)
Как видим, траектория в системе координат X¢Y¢, связанной со стеклом трамвая, является параболой (см. рис. 1.9) с вершиной в точке с координатами:
, . (1.67)
Задача 1.5
(Уравнения кинематической связи)
Концы твердого стержня MN могут свободно скользить по сторонам прямого угла MON (см. рис. 1.10). Найти уравнение траектории точки P стержня, которая делит его на части длиной а и b.
Решение
I. Выберем и изобразим декартову систему координат, оси которой совпадают со сторонами угла MON (см. рис. 1.10).
В соответствии с условием задачи будем считать стержень абсолютно твердым. Следовательно, его положение в любой момент времени t однозначно задается углом j(t) между осью OX и стержнем MN.
II. Запишем закон движения точки P стержня в координатной форме (см. рис. 1.10):
(1.68)
Искомое уравнение траектории точки P можно получить, исключив время из закона движения (1.68).
III. Преобразуя уравнения (1.68), получаем:
. (1.69)
Следовательно, искомое уравнение траектории принимает вид:
. (1.70)
Уравнение (1.70) является уравнением эллипса с полуосями, совпадающими по направлению с осями выбранной системы координат и равными a и b. В случае, когда a = b, эллипс вырождается в окружность.
Задача 1.6
(Уравнения кинематической связи)
На клине с углом при основании a, расположенном на горизонтальной поверхности, находится система двух тел 1 и 2 (см. рис. 1.11), связанных нерастяжимой нитью, перевешенной через маленький блок, ось которого закреплена в верхней точке клина. Записать уравнение кинематической связи для ускорений клина и двух тел, если тело 2 не отрывается от вертикальной поверхности клина в процессе движения.
Решение
I. Выберем систему отсчета, связанную с горизонтальной поверхностью. Ось X декартовой системы координат направим горизонтально, а ось Y вертикально вверх (см. рис. 1.11).
Будем считать тела 1 и 2 материальными точками, связанными нерастяжимой нитью, а клин – абсолютно твердым телом, которое может двигаться поступательно вдоль оси X. Обозначим координаты первого и второго тел в системе координат XY – (x1, y1) и (x2, y2), соответственно. Линейные размеры блока по условию задачи малы по сравнению с длиной нити, поэтому не будем учитывать их при записи уравнений кинематической связи для координат тел системы.
II. Выразим длину нити l через вертикальные координаты различных точек рассматриваемой системы тел:
, (1.71)
где – координата блока, не изменяющаяся в процессе движения.
Если длину наклонного участка нити выразить через горизонтальные координаты тел системы, то выражение для длины нити принимает вид:
. (1.72)
III. Дифференцируя (1.71) и (1.72) дважды по времени и учитывая, что и , получаем искомые уравнения кинематической связи для ускорений тел рассматриваемой системы:
(1.73)
Задача 1.7
(Уравнения кинематической связи)
Система тел состоит из двух блоков и двух подвешенных к ним тел (см. рис. 1.12). Один из блоков составлен из двух коаксиальных цилиндров с неподвижной относительно потолка осью, имеющих различные радиусы r и R. Первое тело подвешено на нити, намотанной на цилиндр радиуса r, второй – на нити, прикрепленной к оси другого блока. Найти ускорение второго тела, если известно, что ускорение первого тела равно a1. Нити считать нерастяжимыми.
Решение
I. Выберем систему отсчета, жестко связанную с потолком. Направление осей декартовой системы координат, связанной с телом отсчета, показано на рис. 1.12.
Считаем тела 1 и 2 материальными точками, нити – нерастяжимыми. Проскальзывания нитей относительно блоков нет.
II. Пусть за малый интервал времени Dt изменение координаты первого тела равно Dx1 (для определенности будем считать, что оно опускается). Поскольку нить нерастяжима, то угол поворота Dj цилиндра радиусом r связан с величиной Dx1 следующим соотношением:
. (1.74)
При этом второй цилиндр радиусом R повернется на тот же угол Dj, а длина нити, на которой лежит блок с подвешенным к нему телом 2, изменится на величину:
. (1.75)
Изменение координаты центра второго блока, а значит и второго тела, равно:
. (1.76)
III. Решая систему уравнений (1.74) – (1.76), получим уравнение, связывающее изменения координат двух тел:
. (1.77)
Поделив левую и правую части (1.77) на малый интервал времени, получим уравнение кинематической связи для скоростей тел:
. (1.78)
Дифференцируя полученное соотношение по времени, получаем искомую связь между ускорениями тел:
. (1.79)
Задача 1.8
(Кинематика простейших механических систем)
На вал радиуса R, закрепленный на оси, намотана веревка, на конце которой висит груз, опускающийся вниз (см. рис. 1.13). Закон движения груза: x = x0 + bt2, где x0 и b – постоянные положительные величины. Определить угловые скорость w и ускорение b произвольной точки обода вала, модуль ускорения a, его нормальную an и тангенциальную at проекции. Записать закон движения этой точки.
Решение
I. Нарисуем чертеж и изобразим на нем направление скорости движения груза. В соответствии с условием задачи направим ось X декартовой системы координат вертикально вниз (рис. 1.13). Для определения ускорения и закона движения произвольной точки A на ободе вала выберем полярную систему координат с полярной осью Y, в которой угол j однозначно определяет положение рассматриваемой точки A. Поскольку в условии задачи не оговаривается иное, веревку считаем нерастяжимой и что проскальзывания веревки относительно вала нет.
II. Запишем заданный в задаче закон движения груза в декартовой системе координат:
. (1.80)
Поскольку веревка нерастяжима, уравнение кинематической связи имеет вид:
. (1.81)
Для решения задачи записанные уравнения необходимо дополнить определениями (1.24) и выражениями (1.25) для интересующих нас величин, приведенными в п. 1.1.
III. Найдем законы изменения скорости груза и его ускорения в проекциях на оси декартовой системы координат, используя определения (1.6) и (1.12):
, ; (1.82)
, . (1.83)
Точки обода вала совершают неравномерное движение по окружности, причем модуль их скорости (поскольку нить нерастяжима и не проскальзывает по поверхности обода) в каждый момент времени равен модулю скорости груза, поэтому, используя (1.22) для угловой скорости w и углового ускорения b, получаем:
, (1.84)
. (1.85)
Поскольку проекция ускорения груза на ось X равна тангенциальной проекции ускорения точек обода, то:
. (1.86)
Нормальную проекцию ускорения определим, используя (1.22):
. (1.87)
Модуль полного ускорения произвольной точки A на ободе колеса найдем из соотношения (1.20):
. (1.88)
Закон движения произвольной точки A на ободе вала запишем в полярной системе координат:
, (1.89)
где j0 – начальное значение угловой координаты точки A в выбранной полярной системе координат.
Задача 1.9
(На кинематику материальной точки)
Закон движения движущейся в плоскости материальной точки, заданный в полярной системе координат, имеет следующий вид: r = r(t), φ = φ(t). Определить законы изменения проекций скорости и ускорения материальной точки на направления, задаваемые ортами декартовой и полярной систем координат, жестко связанных с телом отсчета. Начало декартовой системы координат совпадает с полюсом полярной системы, а ось X декартовой системы направлена вдоль полярной оси (см. рис. 1.14).
Решение
I. Выберем ось Y декартовой системы координат так, чтобы плоскость XY совпадала с плоскостью, в которой движется материальная точка M (рис. 1.14). Для решения задачи используем две системы координат – декартову систему координат XOY c ортами и , и полярную, орты которой и изображены на рис. 1.14. Заметим, что при движении материальной точки происходит изменение ориентации ортов полярной системы и , в то время как орты декартовой системы координат и не изменяют своего направления.
II, III. Закон движения материальной точки, заданный в полярной системе, запишем в декартовой системе координат XOY:
(1.90)
Дифференцируя закон движения (1.90) по времени, получаем искомые законы изменения проекций скорости материальной точки и ее ускорения в декартовой системе координат:
(1.91)
(1.92)
В формулах (1.92), (1.92) и далее для краткости опустим запись зависимости кинематических величин от времени.
Проекции скорости и ускорения материальной точки в полярной системе координат находим двумя способами.
1 способ. Скорость и ускорение материальной точки в полярной системе координат записываются в виде:
, (1.93)
. (1.94)
Следовательно, проекции скорости и ускорения материальной точки на направления, задаваемые ортами рассматриваемых систем координат, связаны соотношениями:
(1.95)
(1.96)
Сравнивая соотношения (1.90) и (1.95), а также (1.91) и (1.96), получим искомые проекции скорости и ускорения материальной точки в полярной системе координат:
(1.97)
(1.98)
2 способ. Запишем радиус-вектор материальной точки в полярной системе координат:
. (1.99)
Поскольку при движении материальной точки происходит изменение ориентации ортов полярной системы и , найдем скорость их изменения (см. рис. 1.15):
(1.100)
Теперь для нахождения скорости и ускорения точки в той же системе координат необходимо продифференцировать радиус-вектор (1.99) по времени с учетом (1.100):
, (1.101)
. (1.102)
В соответствии с (1.101) и (1.102) искомые проекции скорости и ускорения материальной точки в полярной системе координат равны:
(1.103)
(1.104)
Как видим, оба способа решения дают одинаковый результат.
Задача 1.10
(На кинематику материальной точки)
Движение материальной точки в полярной системе координат задается взаимосвязью полярных координат , при этом полярный угол возрастает линейно во времени . Определить зависимость модуля скорости и модуля ускорения материальной точки от времени.
Решение
I. Решаем задачу в заданной полярной системе координат. Заметим, что материальная точка M движется по замкнутой траектории, периодически, с периодом , возвращаясь в ту же точку пространства (см. рис. 1.16).
II. Определим закон изменения проекций скорости и ускорения материальной точки в полярной системе координат, воспользовавшись формулами (1.103) и (1.104), полученными в предыдущей задаче:
(1.105)
(1.106)
Тогда искомые модули скорости и ускорения материальной точки равны:
, (1.107)
(1.108)
Заметим, что материальная точка в моменты времени (где = 0, 1, 2, …) находится в начале (полюсе) полярной системы координат, имеет нулевую скорость, а ускорение, по модулю равное , направлено противоположно полярной оси.
Задача 1.11
(На кинематику материальной точки)
Планета движется вокруг Солнца в соответствии с законами Кеплера по эллиптической траектории . Параметр эллипса , эксцентриситет и секторную скорость считать заданными. Определить проекции ускорения планеты в зависимости от координат и полярной системы.
Решение
I. При решении задачи будем считать планету и Солнце материальными точками. Согласно первому закону Кеплера все планеты движутся по эллиптическим орбитам, причем Солнце находится в одном из фокусов эллипса O (см. рис. 1.17).
В соответствии с условием задачи введем полярную систему координат в плоскости движения планеты, полюс которой совпадает с Солнцем, а полярная ось совпадает с одной из осей эллипса.
Согласно второму закону Кеплера секторная скорость планеты, равная скорости изменения площади, описываемой радиус-вектором материальной точки, представляющим планету, постоянна при движении планеты вокруг Солнца.
II. Для нахождения проекций ускорения планеты в полярной системе координат воспользуемся формулами (1.104):
(1.109)
Поскольку в уравнения (1.109) входят производные полярных координат по времени, дополним эту систему уравнением траектории планеты и выражением для ее секторной скорости :
, (1.110)
. (1.111)
III. В соответствии с условием задачи секторная скорость постоянна при движении планеты по эллиптической траектории, поэтому ее производная по времени равна нулю:
. (1.112)
Сравнивая (1.112) с выражением (1.109) для проекции ускорения , видим, что . Следовательно, ускорение в любой момент времени имеет только проекцию , которая в соответствии с (1.109) является функцией производных полярных координат по времени.
Продифференцируем обе части уравнения траектории (1.110) по времени:
. (1.113)
Используя уравнение траектории (1.110) и выражение для секторной скорости (1.111), преобразуем (1.113) к виду:
. (1.114)
Продифференцируем теперь обе части уравнения (1.114) по времени
. (1.115)
Опять воспользуемся уравнением траектории (1.110) и выражением для секторной скорости (1.111) для исключения и из (1.115):
. (1.116)
В результате находим:
. (1.117)
Для нахождения искомой проекции ускорения планеты , как функции только координат полярной системы, подставим (1.116) и (см. (1.111)) в выражение (1.109):
. (1.118)
Таким образом, ускорение планеты, движущейся по эллиптической траектории, направлено к Солнцу, не зависит от полярного угла и обратно пропорционально квадрату расстояния до Солнца:
(1.119)
Задача 1.12
(На кинематику материальной точки)
Небольшое тело движется по гладкой внутренней поверхности полого вертикального цилиндра радиуса R. В начальный момент времени скорость тела направлена перпендикулярно оси цилиндра и равна . Определить законы изменения скорости и ускорения материальной точки в цилиндрической системе координат, а также угол между скоростью и ускорением.
Решение
I. Будем считать тело материальной точкой, которая движется по цилиндрической поверхности с постоянной вертикальной составляющей ускорения, равной ускорению свободного падения . Для решения задачи выберем цилиндрическую систему координат, ось Z которой совпадает с осью цилиндра, как показано на рис. 1.18. На том же рисунке изображены орты er, ej и ez цилиндрической системы. Ось, от которой отсчитывается угол системы координат, направим на положение тела в начальный момент времени.
II. В соответствии с условиями задачи и выбранной системой координат запишем начальные значения проекций скорости для рассматриваемого тела:
, , . (1.120)
Воспользуемся формулами (1.103) и (1.104) для проекций скорости и ускорения тела на направления, задаваемые ортами цилиндрической системы:
, , , (1.121)
, , . (1.122)
Кроме того, в соответствии с условиями задачи, запишем:
, , . (1.123)
III. Используя (1.121) – (1.123), получим законы изменения проекций скорости и ускорения:
, , ; (1.124)
, , . (1.125)
Таким образом, искомый закон изменения скорости и ускорения в цилиндрической системе координат имеет следующий вид:
, (1.126)
. (1.127)
Определим также искомый угол a между скоростью и ускорением тела:
. (1.128)
1.4. Задачи для самостоятельного решения
Задача 1
Из пушки, находящейся на самолете, летящем горизонтально со скоростью , выпущен снаряд в направлении движения самолета. Скорость снаряда относительно самолета равна . Пренебрегая сопротивлением воздуха, найти:
1) уравнение траектории снаряда относительно Земли ;
2) уравнение траектории снаряда относительно самолета ;
3) уравнение траектории самолета относительно снаряда .
Ответ: 1) , 2) ,
3) , . Оси X, X‘ и X” декартовой системы координат направлены горизонтально вдоль скорости самолета, а оси Y, Y‘ и Y” – вертикально вверх, при этом начало координат системы XY совпадает с положением самолета в момент выстрела пушки.
Задача 2
Лодка пересекает реку шириной d с постоянной относительно воды скоростью , перпендикулярной скорости течения реки, модуль которой нарастает от берегов к середине реки по линейному закону, меняясь от 0 до u. Найти траекторию лодки, а также снос лодки l вниз по течению от места ее отплытия до места причаливания на противоположном берегу реки.
Ответ: , при y < d/2; , при y > d/2; . Ось X декартовой системы координат XY направлена вдоль берега реки, а ось Y – поперек реки. Начало системы координат, жестко связанной с берегом реки, совпадает с местом отплытия лодки.
Задача 3
По движущемуся вниз эскалатору спускается пассажир со скоростью относительно эскалатора. Скорость эскалатора равна u. Спускаясь по неподвижному эскалатору пассажир проходит N ступеней. Сколько ступеней N‘ пройдет пассажир, спускаясь по движущемуся эскалатору?
Ответ: .
Задача 4
Два трактора, движущиеся со скоростями и , буксируют с помощью тросов автомобиль (см. рис.).
Определить модуль и направление скорости автомобиля в тот момент, когда тросы параллельны векторам и , а угол между ними равен a.
Ответ: ,
, где – угол между векторами и .
Задача 5
Тело А подвешено на нитях, перекинутых через блоки В и С малого диаметра так, что АВ = ВС (см. рис.).
Концы нитей тянут с одинаковыми скоростями . Расстояние между блоками В и С равно L. Найти модуль скорости тела А в тот момент, когда оно находится на расстоянии H от прямой ВС.
Ответ: .
Задача 6
Лодку подтягивают к пристани высотой Н с помощью веревки, наматываемой на вал лебедки. Радиус вала равен R << H. Вал вращается с постоянной угловой скоростью w. Определить зависимость модулей скорости и ускорения лодки от длины веревки L > Н. Движение лодки считается поступательным.
Ответ: , .
Задача 7.
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях (см. рис.).
Ответ: , где , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 8
Определить закон изменения модуля скорости материальной точки, движущейся в плоскости, если ее движение описывается в полярной системе координат следующим законом: , , где и – положительные постоянные величины.
Ответ: , при .
Задача 9
Четыре тела подвешены на нерастяжимых нитях (см. рис.). Найти ускорение тела 4, если известны ускорения остальных трех тел.
Ответ: , где , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 10
Найти уравнение кинематической связи для ускорений тел, подвешенных на нерастяжимых нитях так, как показано на рисунке.
Ответ: ,
где , , , и – проекции ускорений тел на вертикальную ось декартовой системы координат.
Задача 11
Два тела подвешены на нерастяжимых нитях, как показано на рисунке. Определить ускорение тела 2, если известно ускорение тела 1.
Ответ: , где и – проекции ускорений тел на вертикальную ось декартовой системы координат.
[1] Далее в тексте, если это не оговаривается особо, используется декартова система координат.
Решение задач о движении связанных тел
План урока
- Сила натяжения нити
- Примеры решения задач
Цели урока
- Знать алгоритм решения задач о движении связанных тел
- Уметь применять второй и третий законы Ньютона для решения задач на движение связанных тел
Разминка
- Сформулируйте третий закон Ньютона.
- В каких случаях возникает сила упругости?
- Куда направлена сила упругости?
Сила натяжения нити
Решение задач о движении связанных тел осуществляется по уже изученному нами алгоритму.
В данном блоке задач особое внимание следует уделить силам упругости, возникающим в нити при движении связанных тел. Вспомним, что сила упругости, возникающая в нерастяжимой нити, называется сила натяжения нити и обозначается T→.
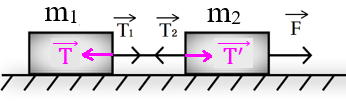
Рис. 1. Силы, возникающие в системе из двух брусков, связанных нитью, в результате действия силы F
Рассмотрим, какие силы возникают в системе из двух брусков, связанных невесомой нитью, если на один из них подействовать с некоторой силой F (рис. 1).
В результате действия силы F брусок 2 приходит в движение, нить, связывающая бруски, начинает действовать на брусок 1 с силой T→1. По третьему закону Ньютона брусок действует на нить с силой T→ такой, что T→=-T→1.
Аналогичные рассуждения применимы ко второму бруску: нить действует на него с силой T→2, брусок действует на нить с силой T’→ такой, что T→’=-T→2.
Таким образом, силы T→ и T’→ действуют на нить, а силы T→1 и T→2 – на связанные бруски.
Если натянутая нить невесома, силы упругости, возникающие в различных частях нити, равны по модулю:
T→=T→’.
Так как T→=-T→1 и T→’=-T→2, справедливо будет записать следующее равенство:
T→=T→1=T→’=T→2.
При решении задач может быть нецелесообразно рисовать силы T→ и T’→, возникающие в нити, за исключением случая, когда нить обладает массой и данные силы не равны друг другу (решение подобной задачи рассмотрено в примере 3).
Примеры решения задач
Пример 1
Два бруска массами m1 = 2 кг и m2 = 6 кг связаны легкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 10 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков. Поверхность и бруски считать гладкими.
Решение
1. После того, как на второй брусок начинает действовать сила F, система начинает двигаться поступательно, поэтому оба тела можно принять за материальные точки.
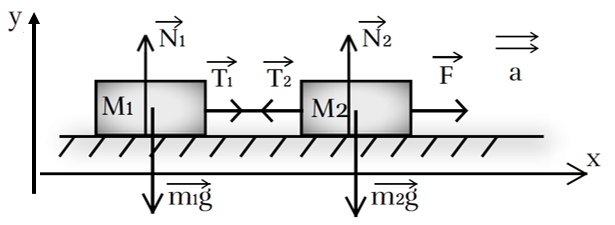
Рис. 2. Иллюстрация к примеру 1
2. В качестве тела отсчета выберем неподвижную плоскость, по которой движутся бруски. Пусть ось ОХ направлена в сторону движения брусков: так как сила F направлена вправо, система будет двигаться в направлении данной силы (рис. 2). Ось OY направлена перпендикулярно оси ОХ.
Изобразим силы, действующие на бруски. Силы упругости, возникающие в нити, изображать не обязательно, так как в данном случае мы не будем применять второй закон Ньютона к нити, связывающей тела.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго бруска:
m1·g→+T→1+N→1=m1·a→;
F→+m2·g→+T→2+N→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси:
OY: N1-m1·g=0;
OX: T1=m1·a;
OY: N2-m2·g=0;
OX: F-T2=m2·a;
5. Как мы уже знаем, при движении связанных невесомой нитью тел силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
T1=T2=T.
6. Обратим внимание, что для решения поставленной задачи достаточно решить систему из уравнений на ось OX.
Решаем полученную систему относительно неизвестного ускорения методом сложения:
T=m1·aF-T=m2·a
Тогда
a=Fm1+m2=102+6=1,25 м/с2.
Ответ: a=1,25 м/с2.
Пример 2
Через неподвижный невесомый блок перекинута легкая нерастяжимая нить. К концам нити прикрепляют грузы массами
m1 = 5 кг и m2 = 10 кг, затем их одновременно отпускают. Найти ускорение системы грузов.
Решение
Рис. 3. Иллюстрация к примеру 2
1. После того, как грузы отпускают, они начинают двигаться поступательно, поэтому оба тела можно принять за материальные точки.
2. В качестве тела отсчета выберем неподвижную плоскость, к которой прикреплен блок. Пусть ось ОY направлена в сторону движения брусков: так как брусок массой m2 тяжелее, система будет двигаться в направлении силы m2·g→ (рис. 3).
Ось OХ направлена перпендикулярно оси ОY.
3. Поскольку нить нерастяжима, то ускорение связанных тел будет одинаково. Запишем второй закон Ньютона в векторной форме для первого и для второго тела:
m1·g→+T→1=m1·a→;
m2·g→+T→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на координатные оси. Учтем, что в выбранной системе отсчета проекции ускорения и сил на ось абсцисс равны нулю, поэтому проекции на данную ось можно не рассматривать.
Так как первое тело движется вверх, проекция ускорения данного тела на ось ординат будет отрицательна.
OY: m1·g-T1=-m1·a;
OY: m2·g-T2=m2·a.
5. Как мы уже знаем, при движении тел, связанных невесомой нитью, силы натяжения нити Т1 и Т2, приложенные к телам, равны по модулю:
T1=T2=T.
6. Решаем полученную систему относительно неизвестного ускорения методом сложения:
m1·g-T=-m1·am2·g-T=m2·a
Тогда
a=m1·g-m2·g-m1-m2=5·10-10·10-5-10≈3,3 м/с2.
Ответ: a=3,3 м/с2.
Пример 3
К одному концу нерастяжимой веревки массой 0,5 кг привязывают груз массой 2 кг. Веревку вместе с грузом поднимают вертикально вверх, прикладывая силу, равную 50 Н. Найти ускорение системы, а также модули сил упругости, действующие на противоположные концы веревки.
Решение
1. Веревка по условию задачи нерастяжима, примем, что груз и веревка движутся поступательно, поэтому оба тела можно принять за материальные точки.
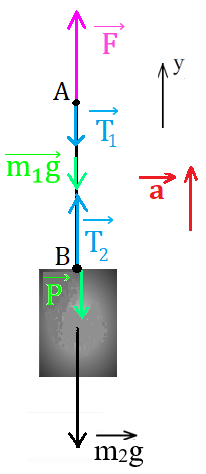
Рис. 4. Иллюстрация к примеру 3: силы, действующие на бруски
2. В качестве тела отсчета выберем поверхность Земли. Ось ОY направим в сторону движения системы – в направлении действия силы F→ (рис. 4). Обозначим массу груза m2, массу веревки m1.
К верхнему концу веревки, к точке А, по условию приложена сила F→, в этой точке возникает сила упругости T→1, действующая на источник силы F→ (например, на руку человека, который тянет веревку).
В месте крепления груза, в точке В, на веревку действует вес груза P→, в результате в этой точке возникает сила упругости T→2, действующая на груз.
3. Запишем второй закон Ньютона в векторной форме для веревки и для груза:
F→+m1·g→+P→=m1·a→;
m2·g→+T→2=m2·a→.
4. Запишем второй закон Ньютона для каждого из тел в проекциях на ось ординат:
OY: F-m1·g-P=m1·a;
OY: T2-m2·g=m2·a.
5. По третьему закону Ньютона силы T→2 и P→ равны по модулю и противоположны по направлению:
P=T2.
6. Решаем полученную систему с учетом соотношения:
F-m1·g-T2=m1·aT2-m2·g=m2·a
Тогда
a=F-g·m1+m2m1+m2=50-10·(0,5+2)0,5+2=10 м/с2.
Найдем Т2:
T2=m2·g+m2·a=40 Н.
Наконец, найдем значение силы Т1: согласно третьему закону Ньютона, данная сила будет равна по модулю и противоположна по направлению силе, с которой веревку тянут вверх:
T1=F=50 Н.
Ответ: a=10 м/с2; T1=50 Н; T2=40 Н.
Упражнение 1
1. Два бруска массами m1 = 1 кг и m2 = 3 кг связаны легкой невесомой нерастяжимой нитью. В некоторый момент времени на брусок массой m2 начинает действовать сила F = 20 Н, в результате чего бруски начинают поступательное движение. Найти ускорение системы брусков, если коэффициент трения между поверхностью и брусками равен 0,4.
2. На нерастяжимой невесомой нити, перекинутой через неподвижный блок, подвешены грузы массами 300 и 500 г. Какова сила натяжения нити во время движения?
3. Тепловоз массой 80 т тянет два вагона массой по 20 т каждый с ускорением 0,2 м/с2. Найти силу тяги тепловоза, если коэффициент трения равен 0,005.
Ответы
Упражнение 1
1. а = 1 м/с2.
2. T = 3.75 Н.
3. F = 30 кН.
