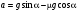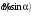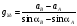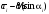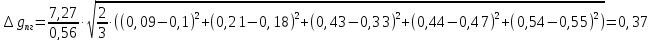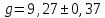Второй закон Ньютона это закон который был выведен в результате проведения опытов Ньютоном.
В результате чего были выведена новая формула второго закона ньютона а = F /m,
Что такое второй закон Ньютона, масса и вес тела

Ньютон сформулировал второй закон динамики, количественно связывающий изменение движения тела с силами, вызывающими это изменение.
Чтобы исследовать зависимость между силой и ускорением количественно, рассмотрим некоторые опыты.
Ускорение от величины силы
I. Рассмотрим, как зависит ускорение одного и того же тела от величины силы, действующей на это тело. Предположим, что к тележке прикреплен динамометр, по показаниям которого измеряют силу.
Измерив длину пройденного тележкой пути за какой-нибудь промежуток времени t, по формуле s = (at2) : 2 определим ускорение a.
Изменяя величину силы, проделаем опыт несколько раз. Результаты измерения покажут, что ускорение прямо пропорционально силе, действующей на тележку
a1 : a2 = F1 : F2
ИЛИ
а ~ F.
Отношение силы, действующей на тело, к ускорению есть величина постоянная, которую обозначим m. Это отношение назовем массой тела.
Зависимость ускорения от массы
II. Установим зависимость ускорения тела от его массы. Для этого будем действовать на тележку какой-нибудь постоянной силой, изменяя массу (помещая различные грузы на тележку).
Ускорения тележки будем определять так же, как и в первом опыте. Опыт покажет, что ускорение тележки обратно пропорционально массе, то есть
(a1/a2) = (m2/m1), или а ~ (1/m)
Обобщая результаты опытов, можно заметить, что ускорение, приобретаемое телом, прямо пропорционально силе, действующей на тело, и обратно пропорционально массе данного тела (второй закон ньютона формулировка).
Этот вывод называется вторым законом Ньютона. Математически этот закон можно записать так (формула второго закона ньютона):
а = F /m
где а — ускорение, m—масса тела, F — результирующая всех сил, приложенных к телу. В частном случае на тело может действовать и одна сила.
Результирующая сила F равна векторной сумме всех сил, приложенных к телу;
F = mа.
Следовательно, сила равна произведению массы на ускорение.
Второй закон динамики можно записать в иной более удобной форме. Учитывая, что ускорение
а = (υ2 — υ1) / (t2 — t1)
подставим это выражение в уравнение второго закона Ньютона. Получим
F = ma = (mυ2 — mυ1) / (t2 — t1) = (∆(mυ))/∆t
Что такое импульс
Импульсом, или количеством движения, называется вектор, равный произведению массы тела на его скорость (тυ).
Тогда основной закон динамики можно сформулировать следующим образом: сила равна изменению импульса в единицу времени (второй закон ньютона в импульсной форме)
F = (∆(mυ))/∆t
Это и есть наиболее общая формулировка второго закона Ньютона. Массу тела Ньютон определил как количество вещества, содержащегося в данной теле. Это определение несовершенно.
Из второго закона Ньютона вытекает следующее определение массы. Из равенства
a1/a2= m2/m1
видно, что чем больше масса тела, тем меньше ускорение получает тело, то есть тем труднее изменить скорость этого тела и наоборот.
Следовательно, чем больше масса тела, тем в большей степени это тело способно сохранять скорость неизменной, то есть больше инертности. Тогда можно сказать, что масса есть мера инертности тела.
Эйнштейн доказал, что масса тела остается постоянной только при определенных условиях. В зависимости от скорости движения тела его масса изменяется по такому закону:
где m — масса тела, движущегося со скоростью υ; m0 — масса этого же тела, находящегося в покое; с = 3 • 108м/с скорость света в вакууме.
Проанализируем данное уравнение:
- Если υ«с, то величиной —, как очень малой, можно пренебречь и m = m0, то есть при скоростях движения, много меньших скорости света, масса тела не зависит от скорости движения;
- Если υ ≈ с, то υ2/с2 ≈ 1, тогда т = m0/0— отсюда вытекает, что m → ∞.
По мере увеличения скорости тела для его дальнейшего ускорения нужно будет прикладывать все увеличивающиеся силы.
Но бесконечно больших сил, которые потребовались бы для сообщения телу скорости, равной скорости света, в природе не существует.
Таким образом, заставить рассматриваемое тело двигаться со скоростью света принципиально невозможно.
Со скоростями, близкими к скорости света, современная физика встречается: так разгоняются, например, элементарные частицы в ускорителях.
Масса тела с ростом скорости
Масса тела с ростом скорости увеличивается, но количество вещества остается неизменным, возрастает инертность. Поэтому массу нельзя путать с количеством вещества.
Покажем связь между силой тяжести, массой тела и ускорением свободного падения. Любое тело, поднятое над Землей и ничем не поддерживаемое, падает снова на Землю.
Это происходит вследствие того, что между телом и Землей существует притяжение (этот вопрос более подробно рассмотрим позже).
Сила, с которой тело притягивается к Земле, называется силой тяжести. Падение тел в безвоздушном пространстве под действием силы тяжести (при υ0 = 0) называется свободным падением.
Отметим, что для тел, покоящихся в поле сил тяготения, сила тяжести равна весу тела Р.
Весом тела называется сила, с которой тело давит на горизонтальную подставку, неподвижную относительно Земли, или действует на подвес.
Если Р— сила тяжести, m — масса, g — ускорение силы тяжести (в данной точке Земли оно для всех тел одинаковой среднее его значение равно 9,8м/с2), то применяя второй закон динамики, получим
P = mg.
Выразим с помощью этой формулы веса двух различных тел. Тогда:
P1 = m1g и Р2 = m2g. Разделив почленно эти два равенства, будем иметь
P1/P2 = m1/m2
Следовательно, веса тел в данной точке земной поверхности прямо пропорциональны их массам.
Задачи на второй закон ньютона
1. Какая сила F действует на автомобиль массой кгm=1000 кг, если он движется с ускорением мсa=1 м/с2.
Дано:
m = 1000 кг
a = 1 м/с2
Найти: F — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
F = 1000 кг • 1 м/с2 = 1000 Н
Ответ: 1000 Н.
2. На мяч действует сила F = 70Н, масса мяча m = 0,2 кг, найти его ускорение a.
Дано:
m = 0,2 кг,
F = 70Н
Найти:
a — ?
Решение:
Запишем второй закон Ньютона :
F = mа.
Следовательно а = F / m.
а = 70Н : 0,2 кг = 350 м/с.
Ответ: а = 350 м/с.
Статья на тему Второй закон Ньютона
СПБНИУ
ИТМО
Отчёт
по лабораторной работе №1
«Изучение
скольжения тележки по наклонной
плоскости.»
Выполнил
студент 1231 группы
Борзенков
Никита Владимирович.
Санкт-Петербург,
15 сентября 2013 года.
Цель
работы:
-
Экспериментальная
проверка равноускоренности движения
тележки по наклонной плоскости. -
Определения
ускорения свободного падения.
Краткая
теория:
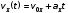
Задание 1.
Измерение ускорения тележки при
движении по рельсу с фиксированным
углом наклона.
Таблица
1.
|
|
|
|
|
|
0,22 |
1 |
155 |
165 |
Приборные
погрешности:
Упражнение
1.
Таблица 2.
|
№ опыта |
Измеренные |
Рассчитанные |
||||
|
x1, |
x2, |
t1, |
t2, |
2( |
( |
|
|
1 |
0,15 |
0,4 |
1,4 |
2,7 |
0,5 |
5,33 |
|
2 |
0,15 |
0,5 |
1,4 |
3,0 |
0,7 |
7,04 |
|
3 |
0,15 |
0,7 |
1,5 |
3,7 |
1,1 |
11,44 |
|
4 |
0,15 |
0,9 |
1,5 |
4,2 |
1,5 |
15,39 |
|
5 |
0,15 |
1,1 |
1,5 |
4,6 |
1,9 |
18,91 |
-
По
измеренным величинам рассчитаем
и
занесём их значения в таблицу.
X: Y:
-
2,72-1,42=5,33. 1)
2(0,4-0,15)=0,5. -
3,02-1,42=7,04. 2)
2(0,5-0,15)=0,7. -
3,72-1,52=11,44. 3)
2(0,7-0,15)=1,1. -
4,22-1,52=15,39. 4)
2(0,9-0,15)=1,5. -
4,62-1,52=18,91. 5)
2(1,1-0,15)= 1,9.
-
Если
тележка движется равноускорено и ее
начальная скорость равна нулю, то из
формулы
следует
то есть 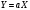
где
величина ускорения тележки. Таким
образом, теоретический график зависимости
от
представляет собой прямую линию,
проходящую через начало координат, а
угловой коэффициент этой прямой равен
ускорению тележки.
-
Нанесём
экспериментальные точки на диаграмму
Y от X
и проведём через начало координат «на
глаз» наилучшую аппроксимирующую
прямую
так,
чтобы она проходила как можно ближе ко
всем экспериментальным точкам. Выберем
на аппроксимирующей прямой точку А,
достаточно удаленную от начала координат.
По её координатам
и
вычислим ускорение как угловой
коэффициент прямой
:
Чем больше расстояние точки
от начала координат, тем меньше погрешность
вычисления углового коэффициента прямой
по формуле
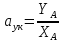
Эта погрешность в дальнейшем не
учитывается.
A (19; 1,85), YA=1,85,
XA=19
-
По
отклонениям
ординат
экспериментальных точек
от соответствующих ординат точек
аппроксимирующей прямой рассчитаю
погрешность ускорения:

где N = 5 – количество
экспериментальных точек.
-
Запишем
доверительный интервал для ускорения:

Упражнение
2.
X1=0,150
м, x2=1,100 м
Приборные
погрешности:
Результаты
измерений представлены в таблицах
3.1-3.5
Таблица 3.1
|
|
|
№ опыта |
t1,с |
t2,с |
|
166 |
156 |
1 |
1,4 |
4,6 |
|
2 |
1,4 |
4,6 |
||
|
3 |
1,5 |
4,7 |
||
|
4 |
1,5 |
4,7 |
||
|
5 |
1,5 |
4,7 |
Таблица 3.2
|
|
|
№ опыта |
t1,с |
t2,с |
|
175 |
155 |
1 |
1,0 |
3,1 |
|
2 |
1,0 |
3,2 |
||
|
3 |
1,0 |
3,1 |
||
|
4 |
0,9 |
3,1 |
||
|
5 |
0,9 |
3,1 |
Таблица 3.3
|
|
|
№ опыта |
t1,с |
t2,с |
|
189 |
155 |
1 |
0,8 |
2,6 |
|
2 |
0,8 |
2,5 |
||
|
3 |
0,8 |
2,6 |
||
|
4 |
0,8 |
2,5 |
||
|
5 |
0,8 |
2,6 |
Таблица 3.4
|
|
|
№ опыта |
t1,с |
t2,с |
|
199 |
154 |
1 |
0,7 |
2,2 |
|
2 |
0,6 |
2,2 |
||
|
3 |
0,7 |
2,2 |
||
|
4 |
0,6 |
2,2 |
||
|
5 |
0,7 |
2,2 |
Таблица 3.5
|
|
|
№ опыта |
t1,с |
t2,с |
|
210 |
154 |
1 |
0,6 |
2,0 |
|
2 |
0,6 |
2,0 |
||
|
3 |
0,6 |
1,9 |
||
|
4 |
0,6 |
2,0 |
||
|
5 |
0,6 |
2,0 |
-
Для каждой
серии измерений в таблицах 3.1 – 3.5
вычислим значение синуса угла наклона
рельса к горизонту по формуле
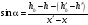
Результаты в таблице 4.
-
0,02
-
0,03
-
0,05
-
-
Таблица 4.
|
Количество |
|
|
|
a, |
|
1 |
0,02 |
1,46±0,066 |
4,66±0,057 |
0,09±0,011 |
|
2 |
0,03 |
0,96±0,05 |
3,12±0,055 |
0,21±0,025 |
|
3 |
0,05 |
0,8±0,05 |
2,56±0,057 |
0,43±0,053 |
|
4 |
0,07 |
0,66±0,057 |
2,2±0,05 |
0,44±0,048 |
|
5 |
0,08 |
0,6±0,05 |
1,98±0,055 |
0,54±0,064 |
-
Для каждой
серии измерений вычислим среднее
значение времени
по формуле
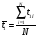
где N – количество
измерений в серии.
Вычислим случайную погрешность по
формуле
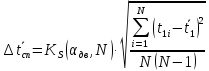
где
– коэффициент Стьюдента для доверительной
вероятности
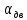
и количества измерений N.
Если результаты отдельных измерений в
серии не отличаются друг от друга, то
случайную погрешность можно положить
равной нулю.
Найдём полную погрешность по формуле,
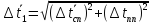
где
– приборная погрешность измерения
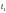
Доверительные интервалы
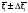
в третий столбец таблицы 4.
-
По каждой
серии измерений с помощью формул
аналогичных формулам из 2 пункта найдём
доверительные интервалы
для времени
и
результаты занесём в четвертый столбец
таблицы 4.
-
Найдём
доверительный интервал для времени
t2:
-
-
-
-
-
=1,98
Вычислим случайную погрешность по
формуле:
Найдём полную погрешность по формуле

-
-
5
-
-
,05
-
Доверительные интервалы
занесём в третий столбец таблицы 4.
-
Для
каждой серии измерений вычислим значение
ускорения и погрешности по формулам
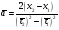
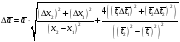
Найденные результаты в виде доверительных
интервалов
занесём в последний столбец таблицы 4.
-
0,011 -
0,025
-
=0,053
-
0,048
-
0,064
-
Пользуясь
результатами из второго и пятого
столбцов таблицы 4 нанесём экспериментальные
точки на диаграмму a
от
.
Покажем погрешность найденных значений
на графике, изобразив доверительные
интервалы для ускорения отрезками,
параллельными оси a.
Проведём аппроксимирующую прямую
.
A
(0,01; 0,03); B (0,087; 0,6)
-
Поскольку
коэффициент трения
и угол
достаточно малы,
в формуле
можно заменить единицей. С учетом этого
теоретическая формула для ускорения
имеет вид

Следовательно, зависимость a
от
является линейной, и угловой коэффициент
этой зависимости равен ускорению
свободного падения
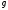
-
Выберем
на аппроксимирующей прямой
достаточно удаленные друг от друга
точки А и B.
По их координатам вычислим ускорение
свободного падения как угловой
коэффициент прямой:

-
По
отклонениям
ординат экспериментальных точек от
соответствующих ординат точек
аппроксимирующей прямой рассчитаем
погрешность:
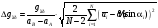
-
Запишем
найденный доверительный интервал для
ускорения свободного падения:
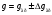
Наше значение
попадает в табличное значение.
Вывод:
С помощью изучения
скольжения тележки по наклонной плоскости
получили табличное значение для ускорения
свободного падения.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задача. Тележку массой = 20,0 кг, на которой лежит груз массой
= 10,0 кг, тянут с силой
, направленной горизонтально (рис. 1). Коэффициент трения между грузом и тележкой
. Пренебрегая трением между тележкой и опорой, найти ускорения тележки
и груза
, а также силу трения между грузом и тележкой в двух случаях: 1)
= 2,00 кгс, 2)
= 6,00 кгс.
Решение. Рассмотрим силы, действующие на оба тела. При этом, поскольку их ускорения направлены по горизонтали, достаточно учитывать лишь силы, действующие горизонтально, так как остальные — направленные по вертикали — заведомо уравновешиваются.
На тележку действуют сила и сила со стороны груза
. Последняя направлена против скорости тележки относительно груза при трении скольжения или против силы
при трении покоя, т. е. в любом случае сила
направлена влево (рис. 1). На груз действует сила трения со стороны тележки
, направленная, согласно третьему закону Ньютона, вправо, причем по модулю
. Направив ось проекций в сторону ускорения, т. е. по горизонтали вправо, запишем в скалярном виде уравнения движения тележки и груза:
Уравнения (1), (2) содержат три неизвестных. Чтобы получить еще одно уравнение, выясним характер силы трения между тележкой и грузом. Если тележка выскальзывает из-под груза, то между ними действует сила трения скольжения, подчиняющаяся закону
Так как в данном случае сила равна по модулю силе тяжести груза, то
Если же тележка и груз двигаются как одно целое, то между ними действует сила трения покоя . Однако в этом случае выполняется равенство
Таким образом, в обоих возможных случаях получим систему трех уравнений.
Итак, необходимо выяснить характер сил трения, действующих между телами.
Рассмотрим подробнее оба возможных варианта:
а) тележка выскальзывает из-под груза. Между ними действует сила трения скольжения, которую найдем по формуле (За):
б) тележка и груз движутся как одно целое, удерживаемые трением покоя. Тогда, обозначив , запишем систему уравнений (1), (2) в виде
Решив эту систему, получим
Формула (5) выражает пропорциональную зависимость между и
. Однако значение
имеет предел, равный силе
, которая уже найдена. Поэтому в действительности два тела будут двигаться как одно целое лишь при таких значениях силы
, при которых значение
, определяемое по (5), не будет превышать ее предельного значения. Проделав расчеты, получим:
1) если = 2,00 кгс = 19,6 Н, то
= 6,5 Н;
2) если = 6,00 кгс = 58,8 Н, то
= 19 Н,
что невозможно, ибо предельное значение равно 9,8 Н. Значит, в этом случае между телами будет действовать трение скольжения.
Теперь легко ответить на все вопросы задачи:
1) = 19,6 Н. Между телами действует сила трения покоя
= 6,5 Н. Из формулы (4) находим
= 0,65 м/с²;
2) = 58,8 Н. Между телами действует сила трения скольжения
=9,8 Н. Из (1) и (2) находим ускорения тел:
= 2,5 м/с²,
= 0,98м/с².
2016-09-08
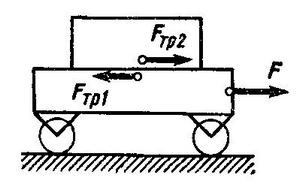
Тележка с водой движется по горизонтальной поверхности с постоянным ускорением. На тележку под углом $alpha$ к вертикали падает луч света, который после отражения распространяется под углом $gamma$ к вертикали (направления ускорения тележки и лучей показаны на рисунке). Найдите ускорение $a$ тележки. Ускорение свободного падения равно $g$.
Решение:
Из закона отражения света вытекает, что нормаль к свободной поверхности воды направлена под углом $phi = frac{ alpha – gamma}{2}$ (см. рисунок).
Следовательно, свободная поверхность воды наклонена под этим углом к горизонтали. Рассмотрим слой воды массой $Delta m$ на свободной поверхности. Запишем для него второй закон Ньютона в проекции на плоскость, касательную к поверхности: $Delta mg sin phi = Delta ma cos phi$. Отсюда $a = g tg phi = g tg frac{ alpha – gamma}{2}$.


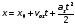

 ,
,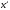 ,
,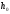 ,
,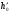 ,
,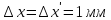
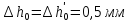
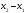 ),
),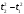 ),
),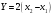
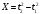
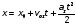
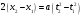


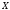
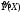 так,
так,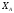
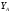
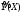 :
: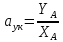
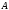
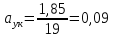
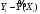 ординат
ординат

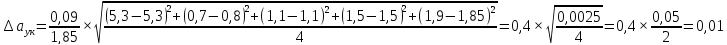

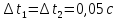
 ,
,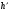 ,мм
,мм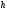 ,
, ,мм
,мм ,
, ,мм
,мм ,
, ,мм
,мм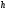 ,
,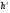 ,мм
,мм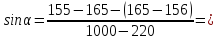 0,02
0,02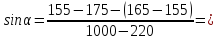 0,03
0,03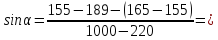 0,05
0,05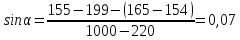
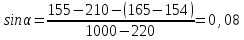
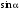
 ,
,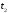 ,
,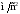
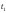
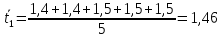
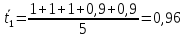

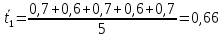
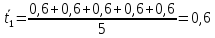
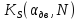
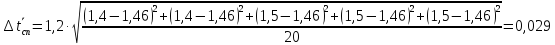
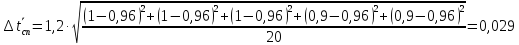
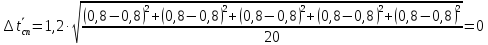
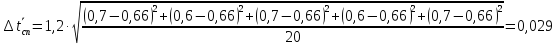
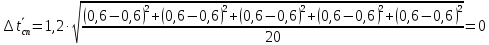
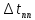
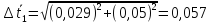

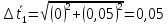

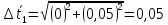
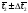
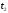 и
и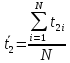
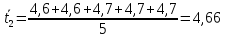
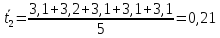
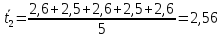
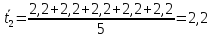
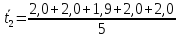 =1,98
=1,98

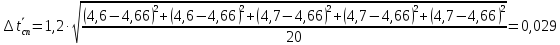
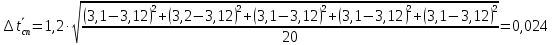
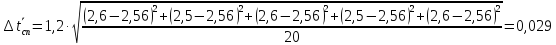
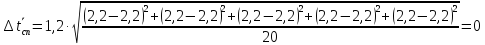
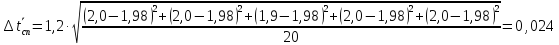
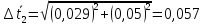
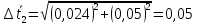 5
5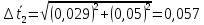
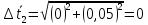 ,05
,05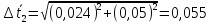
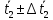
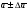
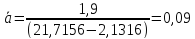
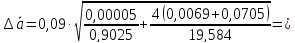

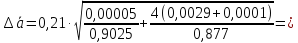 0,025
0,025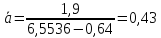
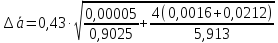 =0,053
=0,053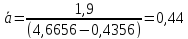
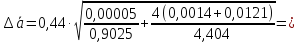 0,048
0,048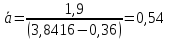
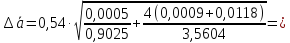 0,064
0,064 .
.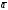
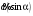 .
.