Пример решения задачи по определению величины и направления скорости и полного ускорения точки колеса, для момента времени, когда угол будет равен заданному значению.
Задача
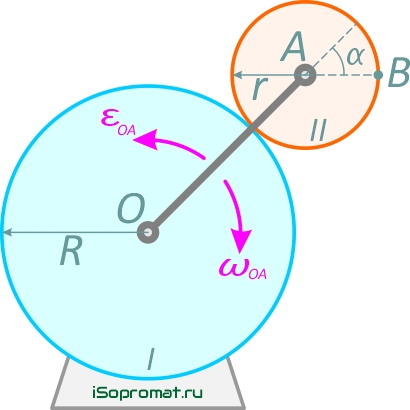
Кривошип ОА, вращаясь вокруг оси, перпендикулярной плоскости чертежа и проходящей через точку О, приводит в движение колесо II, которое катится без скольжения по неподвижному колесу I.
Рис. 2
Найти скорость и ускорение точки В колеса II, для момента времени, когда угол α=45°,
если R=40 см, r=20 см, ωOA=4 с-1, εOA=2 с-2 (рис. 2).
Другие примеры решений >
Помощь с решением задач >
Решение
Теория по теме
Колесо II движется в плоскости чертежа, т.е. совершает плоскопараллельное движение.
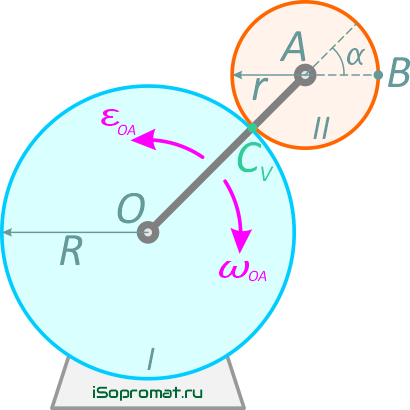
По условию, колесо I неподвижно, значит, точка соприкосновения колес является МЦС для колеса II.
Рис. 2.10
Обозначим ее как CV (эта точка не принадлежит кривошипу ОА). Скорость точки В определяется выражением
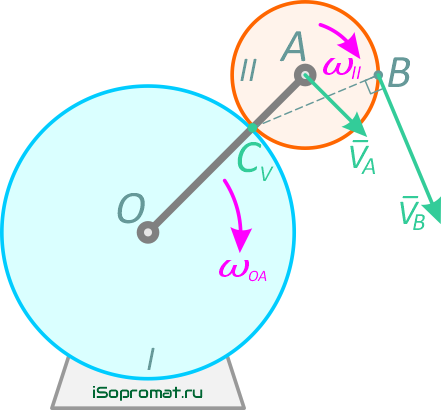
и направлена перпендикулярно отрезку ВСV, в сторону вращения колеса II (рис. 2.11)
Рис. 2.11
Для определения угловой скорости ωII запишем выражение для скорости точки А.
С другой стороны, точка А принадлежит кривошипу ОА. Скорость точки А, принадлежащей кривошипу, определяется выражением
и направлена ⊥ОА в сторону вращения кривошипа ОА. Из этих рассуждений следует:
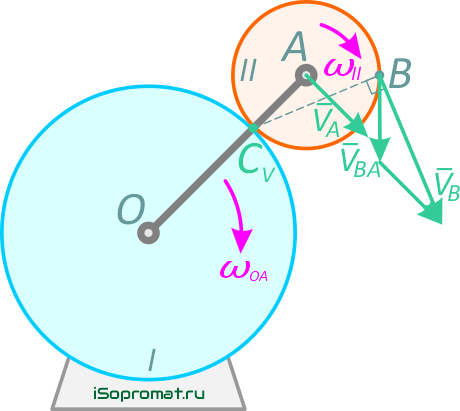
Найдем скорость точки В, используя теорему о скоростях точек плоской фигуры. Для этого примем точку А за полюс.
Тогда
Величина и направление скорости точки А определяются из условий движения кривошипа ОА.
VA=ωOA×OA
и вектор VA⊥ОА и направлен в сторону вращения кривошипа (рис. 2.12).
Рис. 2.12
Скорость VBA — это скорость точки В во вращательном движении вокруг полюса А.
Величина скорости
VBA=ωII×r=12×20=240 см/с
и этот вектор направлен ⊥ отрезку АВ в сторону вращения колеса II.
Чтобы сложить VA и VBA, перенесем вектор VA в конец вектора VBA. Соединяя начало вектора VBA с концом вектора VA, получим вектор VB. Из построения:
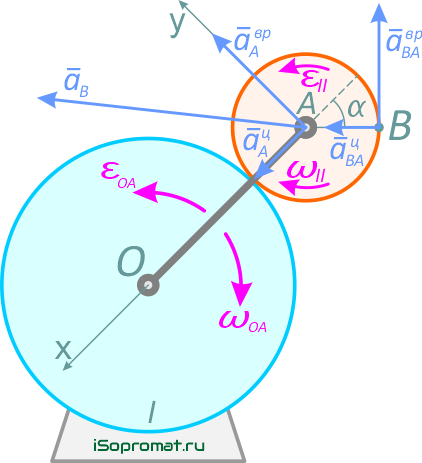
Определим ускорение точки В.
Согласно теореме об ускорении точки плоской фигуры, ускорение точки В можно определить из выражения
где aA — ускорение точки А, принятой за полюс;
aBA — ускорение точки В во вращательном движении, вокруг полюса А.
Рис. 2.13
Точка А – принадлежит колесу II и кривошипу ОА, движение которого известно, тогда
Ускорение aBA (ускорение во вращательном движении) состоит из двух слагаемых:
где
Найдем εII по определению:
Подставляя числовые значения, получим
тогда
Ускорение точки В найдем, спроецировав все векторы уравнения
на выбранные оси координат ОХ и OY.
Углы, которые составляют вектор ускорения aB с осями ОХ и OY, определим через направляющие косинусы.
Скорость и ускорение точки В колеса II, для момента времени, когда угол α=45° найдены.
Другие примеры решения задач >
Рассмотрим
твердое тело, которое вращается
вокруг неподвижной оси. Тогда отдельные
точки этого тела будут описывать
окружности разных радиусов, центры
которых лежат на оси вращения. Пусть
некоторая точка движется по окружности
радиуса R
(рис.6).
Ее положение через промежуток времени
t
зададим
углом .
Элементарные (бесконечно малые) углы
поворота рассматривают как векторы.
Модуль вектора d
равен
углу поворота, а его направление совпадает
с направлением поступательного
движения острия винта, головка которого
вращается в направлении движения
точки по окружности, т. е. подчиняется
правилу
правого, винта (рис.6).
Векторы, направления которых связываются
с направлением вращения, называются
псевдовекторами
или
аксиальными
векторами. Эти
векторы не имеют определенных точек
приложения: они могут откладываться
из любой точки оси вращения.
Угловой
скоростью называется
векторная величина, равная первой
производной угла поворота тела по
времени:
Вектор
«в направлен вдоль оси вращения по
правилу правого винта, т. е. так же, как
и вектор d
(рис. 7). Размерность угловой скорости
dim=T-1,
a .
ее единица — радиан в секунду (рад/с).
Линейная скорость
точки (см. рис. 6)
В векторном виде
формулу для линейной скорости можно
написать как векторное произведение:
При
этом модуль векторного произведения,
по определению, равен
,
а
направление совпадает с
направлением
поступательного движения правого винта
при его вращении от
к R.
Если
=const,
то
вращение равномерное и его можно
характеризовать периодом
вращения Т
—
временем, за которое точка совершает
один полный оборот, т. е. поворачивается
на угол 2.
Так как промежутку времени t=T
соответствует =2,
то =
2/Т,
откуда
Число
полных оборотов, совершаемых телом при
равномерном его движении по окружности,
в единицу времени называется частотой
вращения:
Угловым
ускорением называется
векторная величина, равная первой
производной угловой скорости по
времени:
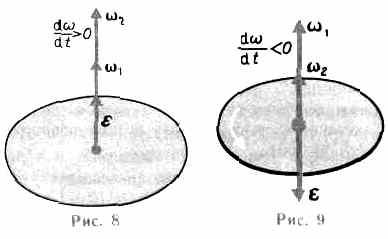
При вращении тела
вокруг неподвижной оси вектор углового
ускорения направлен вдоль оси вращения
в сторону вектора элементарного
приращения угловой скорости. При
ускоренном движении вектор
13
сонаправлен
вектору
(рис.8),
при замедленном.— противонаправлен
ему (рис. 9).
Тангенциальная
составляющая ускорения
Нормальная
составляющая ускорения
Таким
образом, связь между линейными (длина
пути s,
пройденного
точкой по дуге окружности радиуса R,
линейная
скорость v,
тангенциальное
ускорение а,
нормальное ускорение аn)
и угловыми величинами (угол поворота
,
угловая скорость (о, угловое ускорение
)
выражается следующими формулами:
В
случае равнопеременного движения точки
по окружности (=const)
где
0
— начальная угловая скорость.
Контрольные
вопросы
• Что
называется материальной точкой? Почему
в механике вводят такую модель?
• Что
такое система отсчета?
• Что
такое вектор перемещения? Всегда ли
модуль вектора перемещения равен отрезку
пути,
пройденному точкой?
• Какое
движение называется поступательным?
вращательным?
• Дать
определения векторов средней скорости
и среднего ускорения, мгновенной
скорости
и мгновенного
ускорения. Каковы их направления?
• Что
характеризует тангенциальная
составляющая ускорения? нормальная
составляющая
ускорения? Каковы
их модули?
• Возможны
ли движения, при которых отсутствует
нормальное ускорение? тангенциальное
ускорение? Приведите
примеры.
• Что
называется угловой скоростью? угловым
ускорением? Как определяются их
направления?
• Какова
связь между линейными и угловыми
величинами?
Задачи
1.1.
Зависимость
пройденного телом пути от времени
задается уравнением s
= A+Вt+Сt2+Dt3
(С
= 0,1 м/с2,
D
= 0,03 м/с3).
Определить: 1) через какое время после
начала движения ускорение а тела будет
равно 2 м/с2;
2) среднее ускорение <а>
тела за этот промежуток времени. [ 1) 10
с; 2) 1,1 м/с2]
1.2.
Пренебрегая сопротивлением воздуха,
определить угол, под которым тело брошено
к горизонту, если максимальная высота
подъема тела равна 1/4 дальности его
полета. [45°]
1.3.
Колесо
радиуса R
=
0,1 м вращается так, что зависимость
угловой скорости от времени задается
уравнением
= 2At+5Вt4
(A=2
рад/с2
и B=1
рад/с5).
Определить полное ускорение точек обода
колеса через t=1
с после начала вращения и число оборотов,
сделанных колесом за это время. [а =
8,5 м/с2;
N
= 0,48]
14
1.4.
Нормальное ускорение точки, движущейся
по окружности радиуса r=4
м,
задается уравнением аn=А+-Bt+Ct2
(A=1
м/с2,
В=6
м/с3,
С=3
м/с4).
Определить: 1) тангенциальное ускорение
точки; 2) путь, пройденный точкой за время
t1=5
с после начала движения; 3) полное
ускорение для момента времени t2=1
с. [ 1) 6 м/с2;
2) 85 м; 3) 6,32 м/с2]
1.5.
Частота
вращения колеса при равнозамедленном
движении за t=1
мин
уменьшилась от 300 до 180 мин-1.
Определить: 1) угловое ускорение колеса;
2) число полных оборотов, сделанных
колесом за это время. [1)
0,21 рад/с2;
2) 360]
1.6.
Диск
радиусом R=10
см вращается вокруг неподвижной оси
так, что зависимость угла поворота
радиуса диска от времени задается
уравнением =A+Bt+Ct2+Dt3
(B
= l рад/с,
С=1
рад/с2,
D=l
рад/с3).
Определить для точек на ободе колеса к
концу второй секунды после начала
движения: 1) тангенциальное ускорение
а;
2) нормальное ускорение аn;
3) полное ускорение а. [ 1) 0,14 м/с2;
2) 28,9 м/с2;
3) 28,9 м/с2]
Соседние файлы в папке Трофимова
- #
- #
- #
- #
- #
- #
Маховое колесо радиуса начинает вращаться равноускоренно из состояния покоя. Через 10 мин после начала движения оно имеет угловую скорость, равную
. Определить угловое ускорение колеса; скорость и ускорение точки на ободе колеса и число оборотов через 10 мин после начала вращения.
Решение:
1. Колесо вращается равноускоренно, т.е. его угловое ускорение ε постоянно. При этом угловая скорость и угол поворота колеса изменяются по законам:
где , т.к. движение начинается из состояния покоя.
Подставляя и
, находим
причем , где N – число оборотов колеса. Тогда
оборотов.
2. Скорость точки на ободе колеса определяется по формуле и равна
м/с. Скорость направлена по касательной к окружности радиуса R, т.е. перпендикулярно радиусу ОМ.
3. Ускорение точки на ободе колеса складывается из касательного и нормального ускорений: . Значения касательного и нормального ускорений соответственно равны:
. Модуль ускорения точки равен
Векторы скорости и ускорения точки показаны на рисунке 2.2.2.
Подставляя числовые значения, находим:
aτ = 0,628 см/с2, an = 47,37 м/с2, a = 47,4 м/с2.


рис. 2.2.2 рис. 2.2.3 рис. 2.2.4
Рис. 3.2. Циклоида как траектория точки обода катящегося колеса
Циклоиду можно рассматривать как траекторию какой-либо точки обода колеса,
которое катится без проскальзывания по прямой. На рис. 3.2 показана
циклоида, которую «вычерчивает» точка
𝐴,
находившаяся внизу в начальный момент. Точка
𝐴
описывает данную циклоиду независимо от того, катится ли колесо равномерно или
с ускорением, важно только, чтобы оно не проскальзывало.
Проще всего рассмотреть, разумеется, равномерное качение колеса. Такое
качение получается в результате сложения равномерного вращения колеса
вокруг оси и равномерного поступательного движения, линейная скорость которого
𝑣
равна произведению угловой скорости на радиус колеса
𝑟.
Во всех инерциальных системах отсчёта материальная точка имеет одно и то
же ускорение. Поэтому находить его можно в любой такой системе
отсчёта. Ясно, что ускорение точек обода колеса связано только с его
вращением вокруг оси. Поэтому ускорение
𝑎
любой точки обода направлено по радиусу к центру колеса и определяется выражением
𝑎
=
𝑣²
𝑟
.
(1)
Значит, и в высшей точке циклоиды ускорение элемента обода колеса равно
𝑣²/𝑟
и направлено вниз (рис. 3.2).
Теперь рассмотрим движение этой же точки обода как движение по циклоиде.
Скорость в любой точке траектории направлена по касательной к ней;
значит, в высшей точке циклоиды скорость направлена горизонтально.
Ускорение же, как мы выяснили, направлено вертикально вниз, т.е.
перпендикулярно скорости. Поэтому найденное выше ускорение может быть
записано также в виде
𝑎
=
𝑉²
𝑅
,
(2)
где
𝑉
– скорость точки обода в её верхнем положении, а
𝑅
– искомый радиус кривизны циклоиды.
Для нахождения
𝑉
будем рассуждать следующим образом. Скорость любой точки обода катящегося
колеса равна векторной сумме скорости поступательного движения колеса
и линейной скорости вращения вокруг оси. При отсутствии
проскальзывания эти скорости равны по модулю. В верхней точке они и
направлены одинаково. Поэтому
𝑉=2𝑣,
и, сравнивая формулы (1) и (2), находим
𝑅
=
4𝑣
.
(4)
Радиус кривизны циклоиды в верхней точке равен удвоенному диаметру колеса.
Если бы мы рассматривали качение колеса как вращение вокруг
мгновенной оси, совпадающей в каждый момент с нижней неподвижной
точкой колеса (рис. 3.2), то могло бы показаться, что верхняя точка
движется по окружности, радиус которой равен диаметру колеса. Так оно
и было бы, если бы мгновенная ось вращения
𝑂
оставалась неподвижной. На самом деле эта ось перемещается вместе с колесом, и
именно поэтому рассматриваемая точка обода
𝐴
движется в этот момент по окружности, радиус которой даётся формулой (3).
▲
4. Падающий мяч.
Заброшенный в кольцо баскетбольный мяч начинает отвесно падать из корзины без
начальной скорости. В тот же момент из точки, находящейся на расстоянии
𝑙
от кольца, в падающий мяч бросают теннисный мяч (рис. 4.1). С какой
начальной скоростью был брошен теннисный мяч, если мячи столкнулись на расстоянии
ℎ
от кольца?

Рис. 4.1. Падающий мяч
△
В поставленном вопросе подразумевается, что нужно найти вектор
начальной скорости теннисного мяча, т.е. его направление (угол
α)
и модуль
(𝑣₀).
Если решать задачу в исходной (лабораторной) системе отсчёта, то ход
рассуждений может быть следующим. Записываем выражения для
перемещений обоих мячей за время
𝑡
от начала движения до их встречи, затем проецируем их на вертикальное и
горизонтальное направления (рис. 4.2). В результате приходим к
системе уравнений
ℎ
=
𝑔𝑡²
2
,
𝐻
–
ℎ
=
𝑣₀
sin α⋅𝑡
–
𝑔𝑡²
2
,
√
𝑙²-𝐻²
=
𝑣₀
cos α⋅𝑡
.
(1)
Здесь
𝐻
– высота кольца над точкой бросания теннисного мяча, а
√𝑙²-𝐻²
представляет собой расстояние до кольца по горизонтали (рис. 4.2).

Рис. 4.2. Проекции перемещений мячей
В системе трёх уравнений (1) четыре неизвестных величины:
𝑣₀,
α,
𝑡
и
𝐻.
Поэтому может показаться, что задача не имеет единственного решения.
Однако это не так. Действительно, подставляя
ℎ
из первого уравнения во второе, получаем
𝐻
=
𝑣₀
sin α⋅𝑡
.
(2)
Разделив почленно это уравнение на третье уравнение системы (1),
находим выражение для
tg α:
tg α
=
𝐻
√𝑙²-𝐻²
.
(3)
Теперь с помощью рис. 4.2 можно увидеть, что угол
α,
под которым должна быть направлена начальная скорость теннисного мяча, в действительности
соответствует направлению из точки бросания на кольцо. Истинное направление начальной скорости
𝒗₀
показано на рис. 4.3. Итак, бросать теннисный мяч нужно точно в направлении
кольца. Модуль его начальной скорости можно найти, подставляя
𝑡=√2ℎ/𝑔
из первого уравнения системы (1) в уравнение (2).
Учитывая, что
𝐻/sin α=𝑙,
получаем
𝒗₀
=
𝑙
𝑡
=
𝑙
√
2ℎ/𝑔
.
(9)

Рис. 4.3. Истинное направление вектора
𝑣₀
начальной скорости
Но всех этих преобразований можно избежать, если с самого начала перейти
в систему отсчёта, связанную с баскетбольным мячом, т.е. свободно
падающую с ускорением
𝒈
в этой системе отсчёта баскетбольный мяч, естественно,
неподвижен, а теннисный движется равномерно и прямолинейно со скоростью
𝒗₀.
Очевидно, что эта скорость
𝒗₀
должна быть направлена на баскетбольный мяч. Через время
𝑡=𝑙/𝑣₀
мячи столкнутся. В лабораторной системе отсчёта за это время баскетбольный
мяч опустится на расстояние
ℎ
=
𝑔𝑡²
2
=
𝑔
2
⎛
⎜
⎝
𝑙
𝑣₀
⎞²
⎟
⎠
,
(5)
откуда для
𝑣₀
получаем прежнее выражение (4). На примере этой задачи мы видим, что в
некоторых случаях удобным оказывается переход в ускоренно движущуюся
систему отсчёта.
▲
5. В цель с наименьшей начальной скоростью.
Необходимо с поверхности земли попасть камнем в цель, которая расположена на высоте
ℎ
и на расстоянии
𝑠
по горизонтали. При какой наименьшей начальной
скорости камня это возможно? Сопротивлением воздуха пренебречь.
△
На первый взгляд кажется, что начальная скорость камня будет
наименьшей, если верхняя точка его траектории совпадает с мишенью
(рис. 5.1а).

Рис. 5.1. К выбору оптимальной траектории
Может быть, и вам так показалось? Иллюзия эта настолько сильна, что
подобное решение аналогичной задачи можно
встретить в некоторых солидных пособиях по решению физических задач.
Однако, даже не решая задачи, легко убедиться, что это не так.
Действительно, будем мысленно уменьшать высоту, на которой
расположена цель. При этом точка, куда попадает камень, продолжает
согласно предположению оставаться верхней точкой траектории (рис.
5.1б), в том числе и в предельном случае
ℎ=0.
Но совершенно очевидно, что для того чтобы попасть в цель, находящуюся на земле, достаточно
просто добросить камень до цели (рис. 5.1б). Итак, предположение о
том, что цель совпадает с высшей точкой траектории полёта камня,
неверно.
|
vivaka |
|
|
1 |
|
Определить полное ускорение точек на ободе колеса05.06.2014, 17:18. Показов 13651. Ответов 2
колесо вращается с частотой n=250 об/мин. определить полное ускорение точек на ободе колеса r=0.8m |
|
Programming Эксперт 94731 / 64177 / 26122 Регистрация: 12.04.2006 Сообщений: 116,782 |
05.06.2014, 17:18 |
|
Ответы с готовыми решениями:
Во сколько раз нормальное ускорение точки, лежащей на ободе колеса, меньше ее тангенциального ускорения Найти во сколько раз нормальное ускорение точки, лежащей на ободе вращающегося колеса, меньше ее тангенциального ускорения Найти во сколько раз нормальное ускорение точки, лежащей на… Найти для точек на ободе колеса угловую и линейную скорость 2 |
|
Хочу в Исландию 1041 / 840 / 119 Регистрация: 10.11.2010 Сообщений: 1,630 |
|
|
05.06.2014, 18:40 |
2 |
|
Полное ускорение равно векторной сумме тангенциального и нормального ускорений.
0 |
|
4652 / 3404 / 361 Регистрация: 11.11.2010 Сообщений: 6,205 Записей в блоге: 2 |
|
|
05.06.2014, 21:37 |
3 |
|
Решение Так как частота обращения постоянна, то тангенциальное ускорение отбрасывается, т.е. равно 0.
1 |
|
IT_Exp Эксперт 87844 / 49110 / 22898 Регистрация: 17.06.2006 Сообщений: 92,604 |
05.06.2014, 21:37 |
|
3 |
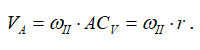
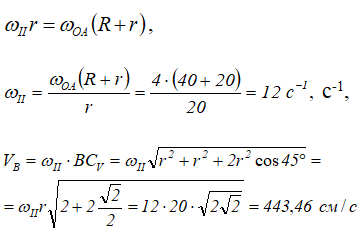
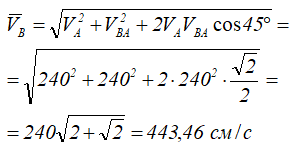
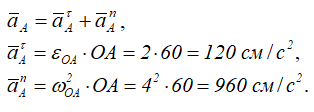
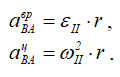
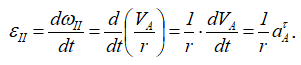
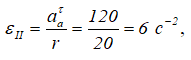
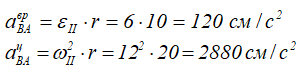
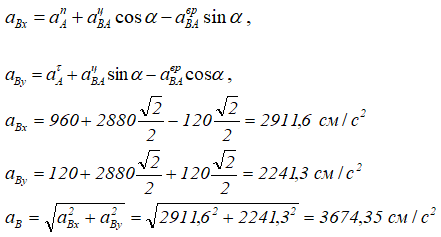
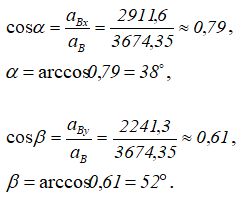
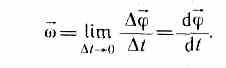



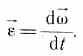

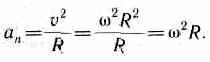


 Определить полное ускорение и линейную скорость точки, находящейся на ободе колеса
Определить полное ускорение и линейную скорость точки, находящейся на ободе колеса