Как найти ускорение в конце второй секунды

Правильно записаны необходимые формулы, проведены вычисления, и получен ответ (верный или неверный), но допущена ошибка в записи краткого условия или переводе единиц в СИ.

Представлено правильное решение только в общем виде, без каких-либо числовых расчётов.

Источник

В конце второй секунды

Определить скорость, а также тангенциальное и нормальное ускорения камня в конце второй секунды
Камень брошен с вышки в горизонтальном направлении со скоростью 20 м/с. Определить скорость, а.

Определите массу и скорость автомобиля в конце 5й секунды
Привет всем. Помогите сделать такую задачу: Под действием силы 2 кН автомобиль движется.

Определить ток в конце последней секунды
При равномерном нарастании плотности тока от нулевого значения в течение 5 с в проводнике.

Определить путь пройденный телом за 5 с , и силу , действующую на тело в конце 5 секунды .
Тело массой 2 гк движется прямолинейно со скоростью , зависимость которой от времени выражается.

Каков будет ток в конце десятой секунды, если в начале опыта был 16 и 2/3 А?
Нужна помощь в решении задачи! «Разность потенциалов на зажимах катушки равномерно падает от 2 В до.

Немецкая армия в конце второй мировой войны
Кажется я слышал в каком-то документальном фильме про вторую мировую войну, что Люфтваффе обладало.

Создать кнопку которая бы включала сразу один привод потом через 2 секунды второй
Для любого человека мало мальски знакомого с делфи я думаю моя задача не вызовет никаких мысленных.

Слияние двух строк по словам в конце в первой и начале второй
нужно зделать програму что плюсует 2 строки , с выключениям одинаковых слов в конце 1-го с началом.

Источник

Перемещение и путь при равноускоренном прямолинейном движении

теория по физике 🧲 кинематика

Геометрический смысл перемещения заключается в том, что перемещение есть площадь фигуры, заключенной между графиком скорости, осью времени и прямыми, проведенными перпендикулярно к оси времени через точки, соответствующие времени начала и конца движения.

При равноускоренном прямолинейном движении перемещение определяется площадью трапеции, основаниями которой служат проекции начальной и конечной скорости тела, а ее боковыми сторонами — ось времени и график скорости соответственно. Поэтому перемещение (путь) можно вычислить по формуле:

Пример №1. По графику определить перемещение тела в момент времени t=3 с.

Перемещение есть площадь фигуры, ограниченной графиком скорости, осью времени и перпендикулярами, проведенными к ней. Поэтому в нашем случае:

Извлекаем из графика необходимые данные:

• Фигура 1. Начальная скорость — 3 м/с. Конечная — 0 м/с. Время — 1,5 с.
• Фигура 2. Начальная скорость — 0 м/с. Конечная — –3 м/с. Время — 1,5 с (3 с – 1,5 с).

Подставляем известные данные в формулу:

Перемещение равно 0, так как тело сначала проделало некоторый путь, а затем вернулось в исходное положение.

Варианты записи формулы перемещения

Конечная скорость движения тела часто неизвестна. Поэтому при решении задач вместо нее обычно подставляют эту формулу:

В итоге получается формула:

Если движение равнозамедленное, в формуле используется знак «–». Если движение равноускоренное, оставляется знак «+».

Если начальная скорость равна 0 (v₀ = 0), эта формула принимает вид:

Если неизвестно время движения, но известно ускорение, начальная и конечная скорости, то перемещение можно вычислить по формуле:

Пример №2. Найти тормозной путь автомобиля, который начал тормозить при скорости 72 км/ч. Торможение до полной остановки заняло 3 секунды. Модуль ускорения при этом составил 2 м/с.

Перемещение при разгоне и торможении тела

Все перечисленные выше формулы работают, если направление вектора ускорения и вектора скорости совпадают ( а ↑↑ v ). Если векторы имеют противоположное направление ( а ↑↓ v ), движение следует описывать в два этапа:

Этап торможения

Время торможения равно разности полного времени движения и времени второго этапа:

Когда тело тормозит, через некоторое время t₁оно останавливается. Поэтому скорость в момент времени t₁ равна 0:

При торможении перемещение s₁ равно:

Этап разгона

Время разгона равно разности полного времени движения и времени первого этапа:

Тело начинает разгоняться сразу после преодоления нулевого значения скорости, которую можно считать начальной. Поэтому скорость в момент времени t₂ равна:

При разгоне перемещение s₂ равно:

При этом модуль перемещения в течение всего времени движения равен:

Полный путь (обозначим его l), пройденный телом за оба этапа, равен:

Пример №3. Мальчик пробежал из состояния покоя некоторое расстояние за 5 секунд с ускорением 1 м/с 2 . Затем он тормозил до полной остановки в течение 2 секунд с другим по модулю ускорением. Найти этот модуль ускорения, если его тормозной путь составил 3 метра.

В данном случае движение нужно разделить на два этапа, так как мальчик сначала разогнался, потом затормозил. Тормозной путь будет соответствовать второму этапу. Через него мы выразим ускорение:

Из первого этапа (разгона) можно выразить конечную скорость, которая послужит для второго этапа начальной скоростью:

Подставляем выраженные величины в формулу:

Перемещение в n-ную секунду прямолинейного равноускоренного движения

Иногда в механике встречаются задачи, когда нужно найти перемещение тела за определенный промежуток времени при условии, что тело начинало движение из состояния покоя. В таком случае перемещение определяется формулой:

За первую секунду тело переместится на расстояние, равное:

За вторую секунду тело переместится на расстояние, равное разности перемещения за 2 секунды и перемещения за 1 секунду:

За третью секунду тело переместится на расстояние, равное разности перемещения за 3 секунды и перемещения за 2 секунды:

Видно, что за каждую секунду тело проходит перемещение, кратное целому нечетному числу:

Из формул перемещений за 1, 2 и 3 секунду можно выявить закономерность: перемещение за n-ную секунду равно половине произведения модуля ускорения на (2n–1), где n — секунда, за которую мы ищем перемещение тела. Математически это записывается так:

Формула перемещения за n-ную секунду

Пример №4. Автомобиль разгоняется с ускорением 3 м/с 2. Найти его перемещение за 6 секунду.

Подставляем известные данные в формулу и получаем:

Таким же способом можно найти перемещение не за 1 секунду, а за некоторый промежуток времени: за 2, 3, 4 секунды и т. д. В этом случае используется формула:

где t — время одного промежутка, а n — порядковый номер этого промежутка.

Пример №5. Ягуар ринулся за добычей с ускорением 2,5 м/с 2 . Найти его перемещение за промежуток времени от 4 до 6 секунд включительно.

Время от 4 до 6 секунд включительно — это 3 секунды: 4-ая, 5-ая и 6-ая. Значит, промежуток времени составляет 3 секунды. До наступления этого промежутка успело пройти еще 3 секунды. Значит, время от 4 до 6 секунд — это второй по счету временной промежуток.

Подставляем известные данные в формулу:

Проекция и график перемещения

Проекция перемещения на ось ОХ. График перемещения — это график зависимости перемещения от времени. Графиком перемещения при равноускоренном движении является ветка параболы. График перемещения при равноускоренном движении, когда вектор скорости направлен в сторону оси ОХ ( v ↑↑OX), а вектора скорости и ускорения сонаправлены ( v ↑↑ a ), принимает следующий вид:

График перемещения при равнозамедленном движении, когда вектор скорости направлен в сторону оси ОХ (v↑↑OX), а вектора скорости и ускорения противоположно ( v ↓↑ a ), принимает следующий вид:

Определение направления знака проекции ускорения по графику его перемещения:

• Если ветви параболического графика смотрят вниз, проекция ускорения тела отрицательна.
• Если ветви параболического графика смотрят вверх, проекция ускорения тела положительна.

Пример №6. Определить ускорение тела по графику его перемещения.

Перемещение тела в момент времени t=0 с соответствует нулю. Значит, ускорение можно выразить из формулы перемещения без начального ускорения. Получим:

Теперь возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 с. Этой точке соответствует перемещение 30 м. Подставляем известные данные в формулу и получаем:

График пути

График пути от времени в случае равноускоренного движения совпадает с графиком проекции перемещения, так как s = l.

В случае с равнозамедленным движением график пути представляет собой линию, поделенную на 2 части:

• 1 часть — до момента, когда скорость тела принимает нулевое значение (v = 0). Эта часть графика является частью параболы от начала координат до ее вершины.
• 2 часть — после момента, при котором скорость тела принимает нулевое значение (v = 0). Эта часть является ветвью такой же, но перевернутой параболы. Ее вершина совпадает с вершиной предыдущей параболы, но ее ветвь направлена вверх.

Такой вид графика (возрастающий) объясняется тем, что путь не может уменьшаться — он либо не меняется (в состоянии покоя), либо растет независимо от того, в каком направлении, с какой скоростью и с каким ускорением движется тело.

Пример №7. По графику пути от времени, соответствующему равноускоренному прямолинейному движению, определить ускорение тела.

При равноускоренном прямолинейном движении графиком пути является ветвь параболы. Поэтому наш график — красный. График пути при равноускоренном прямолинейном движении также совпадает с графиком проекции его ускорения. Поэтому для вычисления ускорения мы можем использовать эту формулу:

Для расчета возьмем любую точку графика. Пусть она будет соответствовать моменту времени t=2 c. Ей соответствует путь, равный 5 м. Значит, перемещение тоже равно 5 м. Подставляем известные данные в формулу:

Тело массой 200 г движется вдоль оси Ох, при этом его координата изменяется во времени в соответствии с формулой х(t) = 10 + 5t – «>– 3t 2 (все величины выражены в СИ).

Установите соответствие между физическими величинами и формулами, выражающими их зависимости от времени в условиях данной задачи.

К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.

Алгоритм решения

Решение

Из условия задачи известна только масса тела: m = 200 г = 0,2 кг.

Так как тело движется вдоль оси Ox, уравнение движения тела при прямолинейном равноускоренном движении имеет

Вид — группа особей, сходных по морфолого-анатомическим, физиолого-экологическим, биохимическим и генетическим признакам, занимающих естественный ареал, способных свободно скрещиваться между собой и давать плодовитое потомство.

x ( t ) = x 0 + v 0 t + a t 2 2 . .

Теперь мы можем выделить кинематические характеристики движения тела:

Перемещение тела определяется формулой:

s = v 0 t + a t 2 2 . .

Начальная координата не учитывается, так как это расстояние было уже пройдено до начала отсчета времени. Поэтому перемещение равно:

x ( t ) = v 0 t + a t 2 2 . . = 5 t − 3 t 2

Кинетическая энергия тела определяется формулой:

Скорость при прямолинейном равноускоренном движении равна:

v = v 0 + a t = 5 − 6 t

Поэтому кинетическая энергия тела равна:

E k = m ( 5 − 6 t ) 2 2 . . = 0 , 2 2 . . ( 5 − 6 t ) 2 = 0 , 1 ( 5 − 6 t ) 2

Следовательно, правильная последовательность цифр в ответе будет: 34.

pазбирался: Алиса Никитина | обсудить разбор | оценить

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.

К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения

1. Определить, какому типу движения соответствует график зависимости координаты тела от времени.
2. Определить величины, которые характеризуют такое движение.
3. Определить характер изменения величин, характеризующих это движение.
4. Установить соответствие между графиками А и Б и величинами, характеризующими движение.

Решение

График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:

Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.

График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.

График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.

Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.

График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».

График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».

pазбирался: Алиса Никитина | обсудить разбор | оценить

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алгоритм решения

1. Охарактеризовать движение тела на различных участках графика.
2. Выделить участки движения, над которыми нужно работать по условию задачи.
3. Записать исходные данные.
4. Записать формулу определения искомой величины.
5. Произвести вычисления.

Решение

Весь график можно поделить на 3 участка:

1. От t₁ = 0 c до t₂ = 10 с. В это время тело двигалось равноускоренно (с положительным ускорением).
2. От t₁ = 10 c до t₂ = 30 с. В это время тело двигалось равномерно (с нулевым ускорением).
3. От t₁ = 30 c до t₂ = 50 с. В это время тело двигалось равнозамедленно (с отрицательным ускорением).

По условию задачи нужно найти путь, пройденный автомобилем в интервале времени от t₁ = 20 c до t₂ = 50 с. Этому времени соответствуют два участка:

1. От t₁ = 20 c до t₂ = 30 с — с равномерным движением.
2. От t₁ = 30 c до t₂ = 50 с — с равнозамедленным движением.

• Для первого участка. Начальный момент времени t₁ = 20 c. Конечный момент времени t₂ = 30 с. Скорость (определяем по графику) — 10 м/с.
• Для второго участка. Начальный момент времени t₁ = 30 c. Конечный момент времени t₂ = 50 с. Скорость определяем по графику. Начальная скорость — 10 м/с, конечная — 0 м/с.

Записываем формулу искомой величины:

s₁ — путь тела, пройденный на первом участке, s₂ — путь тела, пройденный на втором участке.

s₁и s₂ можно выразить через формулы пути для равномерного и равноускоренного движения соответственно:

Теперь рассчитаем пути s₁и s₂, а затем сложим их:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Adblock
detector

Простейшие виды движения твердого тела

• Поступательное
  движение –
  это движение твердого тела, при котором
  всякая прямая линия на теле при движении
  остается параллельной своему начальному
  положению. При поступательном движении
  все точки тела движутся одинаково.

• Вращательное
  движение – это
  движение, при котором все точки тела
  описывают окружности вокруг общей
  неподвижной оси, которая называется
  осью вращения.

Для
описания вращательного тела вокруг
неподвижной оси используют угловые
характеристики:

• Угол
  поворота тела
  .
  Измеряется в радианах. Уравнение
  движения
  

• Угловая
  скорость
  ,
  определяет изменение угла поворота в
  единицу времени. Измеряется рад/с.
  Угловая скорость определяется как
  первая производная от угла поворота
  по времени.

Иногда
для оценки быстроты вращения используют
угловую частоту вращения n,
которая оценивается в оборотах в минуту.
Между угловой скоростью и частотой
вращения существует зависимость:.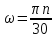

• Угловое
  ускорение
  ,
  определяет изменение угловой скорости
  во времени. Измеряется рад/с².
  Угловое ускорение определяется как
  первая производная от угловой скорости
  по времени или вторая производная от
  угла поворота по времени
  .

Частные
случаи вращательного движения:

• Равномерное
  вращение – угловая скорость постоянна
  .
  

Уравнение
равномерного вращения
.

Кинематические
графики

• Равнопеременное
  вращение –
  угловое ускорение постоянно
  .

Уравнение
равнопеременного вращения
.

Угловое
ускорение при ускоренном движении –
величина положительная, угловая скорость
возрастает.

Угловое
ускорение при замедленном движении –
величина отрицательная, угловая скорость
убывает.

Кинематические
графики

Скорости и ускорения точек вращающегося тела

Тело
вращается вокруг точки О. Определим
параметры движения точки А, расположенной
на расстоянии
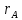от
оси вращения.

Путь
точки А:
;

Линейная
скорость точки А:.

Ускорение
точки А:
;.

Последовательность решения задач расчетно-графической работы

Задание
1.

1. Определить
   вид движения на каждом участке по
   приведенному кинематическому графику.

2. Записать
   законы движения шкива на каждом участке.
   Параметры движения в конце каждого
   участка являются начальными параметрами
   движения на каждом последующем.

3. Определить
   полный угол поворота шкива за время
   вращения. Использовать формулу для
   перехода от угловой частоты вращения
   к угловому ускорению.

4. Определить
   полное число оборотов шкива, используя
   формулу
   .

5. Построить
   графики угловых перемещений и угловых
   ускорений.

6. Определить
   нормальное и касательное ускорения
   точки на ободе шкива в указанные моменты
   времени.

Задание
2.

1. Подставив
   заданные коэффициенты в общее уравнение
   движения, определить вид движения.

2. Определить
   уравнение скорости и ускорения груза.

Примеры
решения задач.

Задача
1.
Дано
уравнение движения точки:
.
Определить скорость точки в конце
третьей секунды движения и среднюю
скорость за первые 3 секунды.

Решение.

1. Уравнение
   скорости
   ;

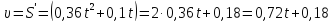2. Скорость
   в конце третьей секунды (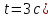

.

1. Средняя
   скорость
   

Задача
2.
Точка
движется по кривой радиуса 10 м согласно
уравнению

.
Определить полное ускорение точки в
конце второй секунды движения и указать
направление касательной и нормальной
составляющих ускорения в точке М и вид
движения точки.

Решение:

1. Касательное
   ускорение определяется как
   .

2. Уравнение
   скорости:
   

3. Касательное
   ускорение
   м/с².

4. Касательное
   ускорение не зависит от времени, оно
   постоянно, следовательно, движение
   равноускоренное.

5. Нормальное
   ускорение:
   .

Скорость
на второй секунде будет равно:
м/с.

Величина
нормального ускорения
м/с².

1. Полное
   ускорение:
   .

Полное
ускорение в конце второй секунды:

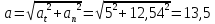м/с².

1. Нормальное
   ускорение направлено перпендикулярно
   скорости к центру дуги.

Касательное
ускорение направлено по касательной
к кривой и совпадает с направлением
скорости, так как касательное ускорение
положительная величина.

Задача
3. По
заданному графику угловой скорости
определить вид движения. Определить
полное число оборотов шкива за время
движения. Построить графики угловых
перемещений и угловых ускорений шкива.

Решение:

1. Из
   графика определяем вид движения:

Участок
1 – скорость возрастает равномерно,
движение равноускоренное;

Участок
2 – скорость постоянна – движение
равномерное;

Участок
3 – скорость убывает равномерно –
движение равноускоренное.

1. Определяем
   угловое ускорение:
   

Участок
1 –

рад/с;
рад/с;рад/с²

Участок
2 –
рад/с;рад/с;рад/с²;

Участок
3 –
рад/с;рад/с.рад/с².

1. Определяем
   угол поворота :
   ;

   ;.

Участок
1 –

рад;

Участок
2 –
рад;

Участок
3 –
рад.

рад.

1. Определяем
   полное число оборотов шкива за время
   движения:

1. Строим
   графики угловых перемещений:

Участок
1 –

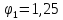
рад;

Участок
2 –
рад;

Участок
3 –
рад.

1. Строим
   графики угловых ускорений.

Участок
1 –

рад/с²

Участок
2 –
рад/с²;

Участок
3 –
рад/с².

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вы находитесь на странице вопроса Вычислить ускорение движения тела в конце 2 й секунды если s(t) = 1 / 6t ^ 3 + 3t ^ 2 – t + 5? из категории Математика.
Уровень сложности вопроса рассчитан на учащихся 10 – 11 классов. На странице
можно узнать правильный ответ, сверить его со своим вариантом и обсудить
возможные версии с другими пользователями сайта посредством обратной связи.
Если ответ вызывает сомнения или покажется вам неполным, для проверки
найдите ответы на аналогичные вопросы по теме в этой же категории, или создайте
новый вопрос, используя ключевые слова: введите вопрос в поисковую строку,
нажав кнопку в верхней части страницы.