В этой статье мы узнаем, как найти ускорение на графике скорости от времени, используя несколько примеров, и решим некоторые задачи.
Ускорение — это разность скоростей, изменяющаяся во времени; следовательно, по графику скорость-время мы можем найти ускорение, измерив наклон графика.
График скорости во времени для положительного ускорения
Давайте посмотрим, как найти ускорение по графику скорость-время. Ниже приводится график зависимости скорости от времени.

По оси x отложено время в секундах, а по оси y отложена скорость объекта в разное время. Наклон графика определяется выражением m=Δy/Δt. Здесь наклон графика скорость-время дает ускорение объекта.
а = м = ΔV/ΔT = v2-v1/t2-t1
Из приведенного выше графика ускорение будет положительным, если V2>V1 то есть, если скорость объекта увеличивается со временем. То же самое будет отрицательным, если V2<V1, то есть если скорость объекта уменьшается со временем. Это тот случай, когда объект замедляется. Так и в том случае, даже когда объект движется в противоположном направлении от направления его движения.
Подробнее о Как найти ускорение с постоянной скоростью: факты и примеры задач.
1 задачи: Рассмотрим объект круглой формы, покоящийся на вершине холма. К объекту прикладывают силу, чтобы сместить его с места. При приложении силы объект ускоряется вниз к подножию холма. Скорость объекта увеличивается до 4 м/с после прохождения расстояния 16 метров. Постройте график для того же, а затем рассчитайте ускорение объекта, учитывая начальную скорость объекта 2 м/с в определенный момент времени.
Решение: Изменение скорости объекта определяется как.
Скорость, равная 4 м/с, наблюдалась после того, как объект прошел расстояние 16 метров. Следовательно, время, затрачиваемое на перемещение 16 м и ускорение тела, равно
2м/с=16м/т
t=16м/2м/с=8с
Следовательно, скорость объекта в момент времени t = 8 секунд была 4 м/с. Теперь мы можем построить график для того же, что и ниже.

Судя по графику, скорость v1=2 м/с при t1=4 сек и скорость v2=4 м/с при t1=8 сек.
Следовательно, ускорение объекта между временными интервалами от 4 до 8 секунд равно
а = v2-v1/t2-t1 = 4-2/8-4 = 2/4 = 1/2 = 0.5 м/с2
Ускорение тела равно 0.5 м/с.2.
График зависимости скорости от времени для нулевого ускорения
Приведенный ниже график показывает, что скорость объекта не меняется со временем и остается постоянной. Это означает, что между этими интервалами времени ускорения объекта не было.

Приведенный выше график показывает, что скорость объекта остается неизменной все время, поэтому мы получаем прямую линию на графике зависимости скорости от времени. Это ясно указывает на то, что в этом случае график зависимости скорости от времени не дает наклона. Поскольку наклон графика отсутствует, ускорение, равное наклону, равно нулю.
Это означает, что перемещение объекта одинаково для разных интервалов времени, следовательно, скорость постоянна.
2 задачи:Скорость объекта, движущегося по плоской поверхности, оказалась равной 0.5 м/с. Через 5 минут другой наблюдатель обнаружил, что скорость равна 0.5 м/с. Тогда каково ускорение объекта на основе наблюдения?
Решение: V1=0.5 м/с; В2=0.5 м/с, временной интервал t=5 минут=300 секунд.
а=в2-v1/t2-t1= 0.5-0.5/300 =0
Поскольку изменений скорости объекта не наблюдалось, ускорение объекта равно нулю.
Подробнее о ускорение.
График зависимости скорости от времени для отрицательного ускорения
Если объект замедляется со временем, то наклон графика скорость-время будет отрицательным. Это показано на приведенном ниже графике зависимости скорости от времени.

Поскольку разница между конечной и начальной рассматриваемой точкой по оси ординат отрицательна, наклон графика ускорения объекта будет отрицательным.
3 задачи: Рассмотрим объект, замедляющийся со временем, как показано на графике ниже.

Вычислите ускорение тела на пути от А до В.
Решение: Скорость объекта в точке А в момент времени t1= 2 секунды v1=10 м/с и в момент времени t2= 5 секунд v2=4м/с. Поэтому ускорение тела равно
а = v2-v1/t2-t1 = 4-10/5-2= -6/3= -2m/s2
Поскольку скорость объекта со временем уменьшается, ускорение объекта отрицательно и равно -2 м/с.2.
Подробнее о График постоянного отрицательного ускорения: что, как, примеры.
График отрицательной скорости для отрицательного ускорения
Когда объект удаляется от точки назначения по отрицательной оси, смещение объекта принимается как отрицательное по отрицательной оси Y. Если положение объекта отклоняется от направления его движения, то считается, что смещение объекта происходит в отрицательном направлении.

Выше приведен график зависимости скорости от времени для отрицательного ускорения. Видно, что скорость со временем уменьшается, наклон графика оказывается отрицательным, а значит, и ускорение отрицательное.
График отрицательной скорости во времени для положительного ускорения
Ниже приведен график зависимости отрицательной скорости от времени в секунду, который дает положительное ускорение.

Поскольку замедляющийся объект однажды начинает ускоряться обратно за счет какого-то внешнего силы, то ускорение, равное наклону График зависимости скорости от времени положителен, потому что скорость объекта продолжает расти со временем.
Подробнее о Отрицательная скорость и нулевое ускорение: как, когда, пример и проблемы.
Часто задаваемые вопросы
Q1. Из приведенного ниже графика вычислите ускорение объекта из точки О в А, из А в В и из В в С; а затем вычислить среднее ускорение объекта от O до C.

Решение: От О до А, v1=0 при t1=0; в2=8 м/с при t2= 4s
Следовательно, ускорение тела из точки О в точку А равно
а = v2-v1/t2-t1=8-0/4-0=8/4=2m/s2
От А до Б, в1=8 м/с при t1=4с; в2=5 м/с при t2= 8s
Следовательно, ускорение тела из точки А в точку В равно
а=в2-v1/t2-t1=5-8/8-4=-3/4=-0.75m/s2
От B до C, v1=5 м/с при t1=8с; в2=5 м/с при t2= 12s
Следовательно, ускорение тела из точки В в С равно
а=в2-v1/t2-t1=5-5/12-8=0/4=0
Среднее ускорение графика от O до C равно
Aсредний= aoa+aab+abc/3
=2-0.75+0/3=1.25/3=0.42m/s2
Следовательно, среднее ускорение тела от О до А равно 0.42 м/с.2.
Почему ускорение является векторной величиной?
Ускорение имеет величину и направление.
Направление ускорения такое же, как и направление скорости после изменения; следовательно, это векторная величина.
- Равноускоренное прямолинейное движение — движение по прямой линии с постоянным ускорением (a=const).
- Ускорение — векторная физическая величина, показывающая изменение скорости тела за 1 с. Обозначается как a.
- Единица измерения ускорения — метр в секунду в квадрате (м/с2).
- Акселерометр — прибор для измерения ускорения.
Формула ускорения
Ускорение тела равно отношению изменения вектора скорости ко времени, в течение которого это изменение произошло:

v — скорость тела в данный момент времени, v0 — скорость тела в начальный момент времени, t — время, в течение которого изменялась скорость
Пример №1. Состав тронулся с места и через 20 секунд достиг скорости 36 км/ч. Найти ускорение его разгона.
Сначала согласуем единицы измерения. Для этого переведем скорость в м/с: умножим километры на 1000 и поделим на 3600 (столько секунд содержится в 1 часе). Получим 10 м/с.
Начальная скорость состава равно 0 м/с, так как изначально он стоял на месте. Имея все данные, можем подставить их в формулу и найти ускорение:

Проекция ускорения
Проекция ускорения на ось ОХ

vx — проекция скорости тела в данный момент времени, v0x — проекция скорости в начальный момент времени, t — время, в течение которого изменялась скорость
Знак проекции ускорения зависит от того, в какую сторону направлен вектор ускорения относительно оси ОХ:
- Если вектор ускорения направлен в сторону оси ОХ, то его проекция положительна.
- Если вектор ускорения направлен в сторону, противоположную направлению оси ОХ, его проекция отрицательная.
При решении задач на тему равноускоренного прямолинейного движения проекции величин можно записывать без нижнего индекса, так как при движении по прямой тело изменяет положение относительно только одной оси (ОХ). Их обязательно нужно записывать, когда движение описывается относительно двух и более осей.
Направление вектора ускорения
Направление вектора ускорения не всегда совпадает с направлением вектора скорости!
Равноускоренным движением называют такое движение, при котором скорость за одинаковые промежутки времени изменяется на одну и ту же величину. При этом направления векторов скорости и ускорения тела совпадают (а↑↑v).
Равнозамедленное движение — частный случай равноускоренного движения, при котором скорость за одинаковые промежутки времени уменьшается на одну и ту же величину. При этом направления векторов скорости и ускорения тела противоположны друг другу (а↑↓v).
Пример №2. Автомобиль сначала разогнался, а затем затормозил. Во время разгона направления векторов его скорости и ускорения совпадают, так как скорость увеличивается. Но при торможении скорость уменьшается, потому что вектор ускорения изменил свое направление в противоположную сторону.

График ускорения
График ускорения — график зависимости проекции ускорения от времени. Проекция ускорения при равноускоренном прямолинейном движении не изменяется (ax=const). Графиком ускорения при равноускоренном прямолинейном движении является прямая линия, параллельная оси времени.

Зависимость положения графика проекции ускорения относительно оси ОХ от направления вектора ускорения:
- Если график лежит выше оси времени, движение равноускоренное (направление вектора ускорения совпадает с направлением оси ОХ). На рисунке выше тело 1 движется равноускорено.
- Если график лежит ниже оси времени, движение равнозамедленное (вектор ускорения направлен противоположно оси ОХ). На рисунке выше тело 2 движется равнозамедлено.
Если график ускорения лежит на оси времени, движение равномерное, так как ускорение равно 0. Скорость в этом случае — величина постоянная.

Чтобы сравнить модули ускорений по графикам, нужно сравнить степень их удаленности от оси времени независимо от того, лежат они выше или ниже нее. Чем дальше от оси находится график, тем больше его модуль. На рисунке график 2 находится дальше от оси времени по сравнению с графиком один. Поэтому модуль ускорения тела 2 больше модуля ускорения тела 1.
Пример №3. По графику проекции ускорения найти участок, на котором тело двигалось равноускорено. Определить ускорение в момент времени t1 = 1 и t2 = 3 с.

В промежуток времени от 0 до 1 секунды график ускорения рос, с 1 до 2 секунд — не менялся, а с 2 до 4 секунд — опускался. Так как при равноускоренном движении ускорение должно оставаться постоянным, ему соответствует второй участок (с 1 по 2 секунду).
Чтобы найти ускорение в момент времени t, нужно мысленно провести перпендикулярную прямую через точку, соответствующую времени t. От точки пересечения с графиком нужно мысленно провести перпендикуляр к оси проекции ускорения. Значение точки, в которой пересечется перпендикуляр с этой осью, покажет ускорение в момент времени t.
В момент времени t1 = 1с ускорение a = 2 м/с2. В момент времени t2 = 3 ускорение a = 0 м/с2.
Задание EF18774

На рисунке показан график зависимости координаты x тела, движущегося вдоль оси Ох, от времени t (парабола). Графики А и Б представляют собой зависимости физических величин, характеризующих движение этого тела, от времени t. Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции графика подберите соответствующую позицию утверждения и запишите в поле цифры в порядке АБ.

Алгоритм решения
- Определить, какому типу движения соответствует график зависимости координаты тела от времени.
- Определить величины, которые характеризуют такое движение.
- Определить характер изменения величин, характеризующих это движение.
- Установить соответствие между графиками А и Б и величинами, характеризующими движение.
Решение
График зависимости координаты тела от времени имеет вид параболы в случае, когда это тело движется равноускоренно. Так как движение тела описывается относительно оси Ох, траекторией является прямая. Равноускоренное прямолинейное движение характеризуется следующими величинами:
- перемещение и путь;
- скорость;
- ускорение.
Перемещение и путь при равноускоренном прямолинейном движении изменяются так же, как координата тела. Поэтому графики их зависимости от времени тоже имеют вид параболы.
График зависимости скорости от времени при равноускоренном прямолинейном движении имеет вид прямой, которая не может быть параллельной оси времени.
График зависимости ускорения от времени при таком движении имеет вид прямой, перпендикулярной оси ускорения и параллельной оси времени, так как ускорение в этом случае — величина постоянная.
Исходя из этого, ответ «3» можно исключить. Остается проверить ответ «1». Кинетическая энергия равна половине произведения массы тела на квадрат его скорости. Графиком квадратичной функции является парабола. Поэтому ответ «1» тоже не подходит.
График А — прямая линия, параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости ускорения от времени (или его модуля). Поэтому первая цифра ответа — «4».
График Б — прямая линия, не параллельная оси времени. Мы установили, что такому графику может соответствовать график зависимости скорости от времени (или ее проекции). Поэтому вторая цифра ответа — «2».
Ответ: 24
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17992
Начальная скорость автомобиля, движущегося прямолинейно и равноускоренно, равна 5 м/с. После прохождения расстояния 40 м его скорость оказалась равной 15 м/c. Чему равно ускорение автомобиля?
Алгоритм решения
- Записать исходные данные.
- Записать формулу, связывающую известные из условия задачи величины.
- Выразить из формулы искомую величину.
- Вычислить искомую величину, подставив в формулу исходные данные.
Решение
Запишем исходные данные:
- Начальная скорость v0 = 5 м/с.
- Конечная скорость v = 15 м/с.
- Пройденный путь s = 40 м.
Формула, которая связывает ускорение тела с пройденным путем:

Так как скорость растет, ускорение положительное, поэтому перед ним в формуле поставим знак «+».
Выразим из формулы ускорение:

Подставим известные данные и вычислим ускорение автомобиля:

Ответ: 2,5
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18202
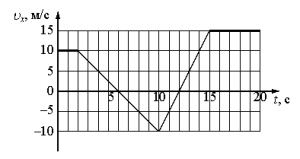
Внимательно прочитайте текст задания и выберите верный ответ из списка. На рисунке приведён график зависимости проекции скорости тела vx от времени.
Какой из указанных ниже графиков совпадает с графиком зависимости от времени проекции ускорения этого тела ax в интервале времени от 6 с до 10 с?

Алгоритм решения
- Охарактеризовать движение тела на участке графика, обозначенном в условии задачи.
- Вычислить ускорение движение тела на этом участке.
- Выбрать график, который соответствует графику зависимости от времени проекции ускорения тела.
Решение
Согласно графику проекции скорости в интервале времени от 6 с до 10 с тело двигалось равнозамедленно. Это значит, что проекция ускорения на ось ОХ отрицательная. Поэтому ее график должен лежать ниже оси времени, и варианты «а» и «в» заведомо неверны.
Чтобы выбрать между вариантами «б» и «г», нужно вычислить ускорение тела. Для этого возьмем координаты начальной и конечной точек рассматриваемого участка:
- t1 = 6 с. Этой точке соответствует скорость v1 = 0 м/с.
- t2 = 10 с. Этой точке соответствует скорость v2 = –10 м/с.
Используем для вычислений следующую формулу:

Подставим в нее известные данные и сделаем вычисления:

Этому значению соответствует график «г».
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18027
На графике приведена зависимость проекции скорости тела от времени при прямолинейном движении по оси х. Определите модуль ускорения тела.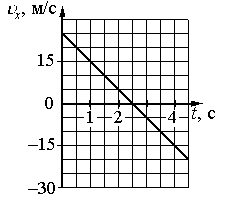
Алгоритм решения
- Записать формулу ускорения.
- Записать формулу для вычисления модуля ускорения.
- Выбрать любые 2 точки графика.
- Определить для этих точек значения времени и проекции скорости (получить исходные данные).
- Подставить данные формулу и вычислить ускорение.
Решение
Записываем формулу ускорения:

По условию задачи нужно найти модуль ускорения, поэтому формула примет следующий вид:

Выбираем любые 2 точки графика. Пусть это будут:
- t1 = 1 с. Этой точке соответствует скорость v1 = 15 м/с.
- t2 = 2 с. Этой точке соответствует скорость v2 = 5 м/с.
Подставляем данные формулу и вычисляем модуль ускорения:

Ответ: 10
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 13.7k
3.2.1. Как правильно понимать условия задачи?
Скорость тела увеличилась в n раз:
Скорость уменьшилась в n раз:
Скорость увеличилась на 2 м/с:
Во сколько раз увеличилась скорость?
Во сколько раз уменьшилась скорость?
Как изменилась скорость?
На сколько увеличилась скорость?
На сколько уменьшилась скорость?
Тело достигло наибольшей высоты:
Тело прошло половину расстояния:
Тело бросают с земли:
(последнее условие часто ускользает из вида — если у тела скорость равна нулю, например у ручки, лежащей на столе, оно может полететь само вверх?), начальная скорость направлена вверх.
Тело бросают вниз: начальная скорость направлена вниз.
Тело бросают вверх: начальная скорость направлена вверх.
В момент падения на землю:
Тело выпадает из аэростата (воздушного шара): начальная скорость равна скорости аэростата (воздушного шара) и направлена в ту же самую сторону.
3.2.2. Как по графику скорости определить ускорение?
Закон изменения скорости имеет вид:
Графиком этого уравнения является прямая линия. Так как — коэффициент перед t, то
является угловым коэффициентом прямой.
Для графика 1:
То, что график 1 «поднимается вверх», означает — проекция ускорения положительна, т. е. вектор направлен в положительном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.
Для графика 2:
То, что график 2 «опускается вниз», означает — проекция ускорения отрицательна, т. е. вектор направлен в отрицательном направлении оси Ox. Пересечение графика с осью — изменение направления движения на противоположное.
Для определения и
выбираем такие точки на графике, в которых можно точно определить значения, как правило, это точки, находящиеся в вершинах клеток.
3.2.3. Как по графику скорости определить пройденный путь и перемещение?
Как сказано в пункте 3.1.6 путь можно как площадь под графиком зависимости скорости от ускорения. Простой случай показан в пункте 3.1.6. Рассмотрим более сложный вариант, когда график скорости пересекает ось времени.
Напомним, что путь может только увеличиваться, поэтому путь, который проехало тело в примере на рисунке 9 равен:
где
и
— площади фигур, закрашенных на рисунке.
Для определения перемещения нужно заметить, что в точках и
тело меняет направление движения. Проезжая путь
тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Проезжая путь
тело движется в обратную сторону, в отрицательном направлении оси Ox так как график лежит под осью времени. Проезжая путь
, тело движется в положительном направлении оси Ox, так как график лежит над осью времени. Таким образом, перемещение равно:
Еще раз обратим внимание:
1) пересечение с осью времени означает поворот в обратную сторону;
2) площадь графика, лежащего под осью времени положительна и входит со знаком «+» в определение пройденного пути, но со знаком «−» в определении перемещения.
3.2.4. Как из графика зависимости ускорения от времени определить зависимость скорости от времени и координаты от времени?
Для того, чтобы определить требуемые зависимости необходимы начальные условия — значения скорости и координаты в момент времени Без начальных условий решить однозначно данную задачу невозможно, поэтому, как правило, в условии задачи они даны.
В данном примере постараемся привести все рассуждения в буквах, для того, чтобы частном примере (при подстановке цифр) не потерять суть действий.
Пусть в момент времени скорость тела равна нулю
и начальная координата
1) От 0 до
Начальные значения скорости и координаты определяем из начальных условий, а ускорение из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
2) От до
Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
3) От до
Начальное значение скорости на этом промежутке должно быть равно конечному значению на предыдущем промежутке, начальное значение координаты равно конечному значению координаты на предыдущем промежутке, а ускорение определяем из графика:
следовательно, движение равноускоренное и закон изменения скорости имеет вид:
К концу данного промежутка времени () скорость (
) и координата (
) будут равны (вместо времени в формулы
и
нужно подставить
):
Для лучшего понимания построим полученные результаты на графике (см. рис.)
На графике скорости:
1) От 0 до прямая линия, «поднимающаяся вверх» (т. к.
);
2) От до
горизонтальная прямая линия (т. к.
);
3) От до
: прямая линия, «опускающаяся вниз» (т. к.
).
На графике координаты:
1) От 0 до : парабола, ветви которой направлены вверх (т. к.
);
2) От до
: прямая линия, поднимающаяся вверх (т. к.
);
3) От до
: парабола, ветви которой направлены вниз (т. к.
).
3.2.5. Как из графика закона движения записать аналитическую формулу закона движения?
Пусть дан график равнопеременного движения.
Закон равнопеременного движения имеет вид:
В этой формуле три неизвестные величины:
и
Для определения достаточно посмотреть на значение функции при
Для определения двух других неизвестных выбираем две точки на графике, значения которых мы можем точно определить — вершины клеток. Получим систему:
При этом считаем, что нам уже известно. Умножим 1-ое уравнение системы на
а 2-ое уравнение на
:
Вычтем из 1-го уравнения 2-ое, после чего получаем:
Полученное из данного выражения значение подставим в любое из уравнений системы (3.67) и решим полученное уравнение относительно
:
3.2.6. Как по известному закону движения определить закон изменения скорости?
Закон равнопеременного движения имеет вид:
Это его стандартный вид для данного типа движения и никак иначе он выглядеть не может, поэтому его стоит запомнить.
В данном законе коэффициент перед t — это значение начальной скорости, коэффициент пред — это ускорение, деленное пополам.
Например, пусть дан закон:
Тогда
И уравнение скорости имеет вид:
Таким образом, для решения подобных задач, необходимо точно помнить вид закона равнопеременного движения и смысл коэффициентов, входящих в это уравнение.
Однако можно пойти и иным путем. Вспомним формулу:
В нашем примере:
3.2.7. Как определить место и время встречи?
Пусть даны законы движения двух тел:
В момент встречи тела оказываются в одной координате, то есть и необходимо решить уравнение:
Перепишем его в виде:
Это квадратное уравнение, общее решение которого приводить не будем, в силу его громоздкости. Квадратное уравнение либо не имеет решений, что означает — тела не встретились; либо имеет одно решение — одна единственная встреча; либо имеет два решения — две встречи тел.
Полученные решения необходимо проверять на физическую реализуемость. Самое главное условие: и
то есть время встречи должно быть положительным.
3.2.8. Как определить путь за -ую секунду?
Пусть тело начинает движение из состояния покоя и за -ую секунду проходит путь Требуется найти, какой путь проходит тело за n-ую секунду.
Для решения этой задачи необходимо воспользоваться формулой (3.25):
Обозначим Тогда
Поделим уравнение на
и получим:
3.2.9. Как движется тело, брошенное вверх с высоты h?
Тело, брошено вверх с высоты h со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время подъема до наивысшей точки полета определяется из условия
:
Для нахождения максимальной высоты H необходимо в необходимо подставить
:
Время всего полета определяется из условия
Получаем уравнение:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Скорость в момент падения:
3.2.10. Как движется тело, брошенное вниз с высоты h?
Тело, брошено вверх с высоты h со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время всего полета определяется из уравнения:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Скорость в момент падения:
3.2.11. Как движется тело брошенное вверх с поверхности земли?
Тело брошено вверх с поверхности земли со скоростью
Уравнение координаты y в произвольный момент времени:
Уравнение проекции скорости в произвольный момент времени:
Время подъема до наивысшей точки полета определяется из условия
Для нахождения максимальной высоты H необходимо в (3.89) необходимо подставить
Время всего полета определяется из условия
Получаем уравнение:
Скорость в момент падения:
Заметьте, что что означает — время подъема равно времени падения на ту же высоту.
Также получили: то есть — с какой скоростью бросили, с такой же скоростью тело упало. Знак «−» в формуле
указывает, что скорость в момент падения направлена вниз, то есть против оси Oy.
3.2.12. Тело побывало на одной высоте дважды…
При бросании тела оно может дважды оказаться на одной высоте — первый раз при движении вверх, второй — при падении вниз.
1) Когда тело оказывается на высоте h?
Для тела, брошенного вверх с поверхности земли справедлив закон движения:
Когда тело окажется на высоте h его координата будет равна Получаем уравнение:
решение которого имеет вид:
2) Известны времена и
когда тело оказалось на высоте h. Когда тело окажется на максимальной высоте?
Время полета с высоты h назад до высоты h равно Как уже было показано, время подъема равно времени падения до той же высоты, поэтому время полета от высоты h до максимальной высоты равно:
Тогда время полета от начала движения до максимальной высоты:
3) Известны времена и
когда тело оказалось на высоте h. Чему равно время полета тела?
Все время полета равно:
4) Известны времена и
когда тело оказалось на высоте h. Чему равна максимальная высота подъема?
3.2.13. Как движется тело, брошенное горизонтально с высоты h?
Тело, брошено горизонтально с высоты h со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета определяется из условия
Для определения дальности полета необходимо в уравнение для координаты x вместо t подставить
Для определения скорости тела в момент падения необходимо в уравнение вместо t подставить
Угол, под которым падает тело на землю:
3.2.14. Как движется тело, брошенное под углом α к горизонту с высоты h?
Тело, брошено под углом α к горизонту с высоты h со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета до наивысшей точки определяется из условия
Скорость в наивысшей точке полета
Максимальная высота H определяется при подстановке в закон изменения координаты y времени
Все время полета находится из условия
получаем уравнение:
Это квадратное уравнение, которое имеет два решения, но в данной задаче тело может оказаться в координате только один раз. Поэтому среди полученных решений нужно одно «убрать». Главный критерий отсева — время полета не может быть отрицательным:
Если подставим в закон изменения координаты x время то получим дальность полета L:
Скорость в момент падения
Угол, который образует вектор скорости с горизонталью в произвольный момент времени:
Угол падения:
3.2.15. Как движется тело, брошенное под углом α к горизонту земли?
Тело, брошено под углом α к горизонту с поверхности земли со скоростью
Проекции начальной скорости на оси:
Проекции ускорения:
Проекции скорости в произвольный момент времени t:
Модуль скорости в произвольный момент времени t:
Координаты тела в произвольный момент времени t:
Время полета до наивысшей точки определяется из условия
Скорость в наивысшей точке полета
Максимальная высота H определяется при подстановке в закон изменения координаты y времени
Все время полета находится из условия
получаем уравнение:
Получаем
Снова получили, что то есть еще раз показали, что время подъема равно времени падения.
Если подставим в закон изменения координаты x время то получим дальность полета L:
Скорость в момент падения
Угол, который образует вектор скорости с горизонталью в произвольный момент времени:
Угол падения:
то есть
3.2.16. Что такое настильная и навесная траектории?
Решим следующую задачу: под каким углом нужно бросить тело с поверхности земли, чтобы тело упало на расстоянии L от точки броска?
Дальность полета определяется формулой:
Отсюда
Из физических соображений ясно, что угол α не может быть больше 90°, поэтому, из серии решений уравнения подходят два корня:
Траектория движения, для которой называется настильной траекторией. Траектория движения, для которой
называется навесной траекторией.
3.2.17. Как пользоваться треугольником скоростей?
Как было сказано в 3.6.1 треугольник скоростей в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.
Тело бросили с вершины башни со скорость так, что дальность полета максимальна. К моменту падения на землю скорость тела равна
Сколько длился полет?
Построим треугольник скоростей (см. рис.). Проведем в ней высоту, которая, очевидно, равна Тогда площадь треугольника скоростей равна:
Здесь мы воспользовались формулой (3.121).
Найдем площадь этого же треугольника по другой формуле:
Так как это площади одного и того же треугольника, то приравняем формулы и
:
Откуда получаем
Как видно из формул для конечной скорости, полученных в предыдущих пунктах, конечная скорость не зависит от угла, под которым бросили тело, а зависит только значения начальной скорости и начальной высоты. Поэтому дальность полета по формуле зависит только от угла между начальной и конечной скоростью β. Тогда дальность полета L будет максимальной, если
примет максимально возможное значение, то есть
Таким образом, если дальность полета максимальна, то треугольник скоростей будет прямоугольным, следовательно, выполняется теорема Пифагора:
Откуда получаем
Свойством треугольника скоростей, который только что был доказан, можно пользоваться при решении других задач: треугольник скоростей является прямоугольным в задаче на максимальную дальность полета.
3.2.18. Как пользоваться треугольником перемещений?
Как было сказано в 3.6.2, треугольник перемещений в каждой задаче будет иметь свой вид. Рассмотрим на конкретном примере.
Тело бросают под углом β к поверхности горы, имеющей угол наклона α. С какой скоростью нужно бросить тело, чтобы оно упало ровно на расстоянии L от точки бросания?
Построим треугольник перемещений — это треугольник ABC (см. рис. 19). Проведем в нем высоту BD. Очевидно, что угол DBC равен α.
Выразим сторону BD из треугольника BCD:
Выразим сторону BD из треугольника ABD:
Приравняем и
:
Откуда находим время полета:
Выразим AD из треугольника ABD:
Выразим сторону DC из треугольника BCD:
Но Получаем
Подставим в это уравнение, полученное выражение для времени полета :
Окончательно получаем
3.2.19. Как решать задачи с помощью закона движения? (по горизонтали)
Как правило, в школе при решении задач на равнопеременное движение применяются формулы
Однако такой подход к решению трудно применить к решению многих задач. Рассмотрим конкретный пример.
Опоздавший пассажир подошёл к последнему вагону поезда в тот момент, когда поезд тронулся, начав движение с постоянным ускорением Единственная открытая дверь в одном из вагонов оказалась от пассажира на расстоянии
Какую наименьшую постоянную скорость он должен развить, чтобы успеть сесть в поезд?
Введем ось Ox, направленную вдоль движения человека и поезда. За нулевое положение примем начальное положение человека («2»). Тогда начальная координата открытой двери («1») L:
Дверь («1»), как и весь поезд, имеют начальную скорость равную нулю. Человек («2») начинает движение со скоростью
Дверь («1»), как и весь поезд, движется с ускорением a. Человек («2») движется с постоянной скоростью:
Закон движения и двери и человека имеет вид:
Подставим условия и
в уравнение для каждого из движущихся тел:
Мы составили уравнение движения для каждого из тел. Теперь воспользуемся уже известным алгоритмом для нахождения места и времени встречи двух тел — нам нужно приравнять и
:
Откуда получаем квадратное уравнение для определения времени встречи:
Это квадратное уравнение. Оба его решения имеют физический смысл — наименьший корень, это первая встреча человека и двери (человек с места может побежать быстро, а поезд не сразу наберет большую скорость, так что человек может обогнать дверь), второй корень — вторая встреча (когда уже поезд разогнался и догнал человека). Но наличие обоих корней означает — человек может бежать и медленнее. Скорость будет минимальна, когда уравнение будет иметь один единственный корень, то есть
Откуда находим минимальную скорость:
В таких задачах важно разобрать в условиях задачи: чему равны начальная координата, начальная скорость и ускорение. После этого составляем уравнение движения и думаем как дальше решать задачу.
3.2.20. Как решать задачи с помощью закона движения? (по вертикали)
Рассмотрим пример.
Свободно падающее тело прошло последние 10 м за 0,5 с. Найти время падения и высоту, с которой упало тело. Сопротивлением воздуха пренебречь.
Для свободного падения тела справедлив закон движения:
В нашем случае:
начальная координата:
начальная скорость:
Подставим условия в закон движения:
Подставляя в уравнение движения нужные значения времени, будем получать координаты тела в эти моменты.
В момент падения координата тела
За с до момента падения, то есть при
координата тела
Уравнения и
составляют систему уравнений, в которой неизвестны H и
Решая эту систему, получим:
Итак, зная вид закона движения (3.30), и используя условия задачи для нахождения и
получаем закон движения для данной конкретной задачи. После чего, подставляя нужные значения времени, получаем соответствующие значения координаты. И решаем задачу!
|
Как найти ускорение через скорость и время? Существует V0 – это начальная скорость, с которой начало двигаться тело, и конечная скорость V, с которой стало двигаться тело к моменту времени t. Так формула нахождения ускорения “a” следующая. а=(V-V0):t; если начальной скорости нет( равна 0), то а=V/t ; ускорение может быть отрицательным, если начальная скорость больше, чем конечная. То есть тело замедляется. система выбрала этот ответ лучшим bezdelnik 5 лет назад Если известны скорости V1 и V2 в некоторые моменты времени t1 и t2, то среднее ускорение аср за этот промежуток времени определяют по формуле аср=(V1-V2)/(t2-t1). Время в скорости необходимо выразить в тех же единицах что и время в промежутке времени. Например, поезд шёл со скоростью V1=120 км/ч и тормозил до скорости V2=60 км/ч или 0,01(6)км/сек в течение t2-t1=10 сек, то а=0,001(6) км/сек или 1,(6) м/сек. Знаете ответ? |
Алгебра и начала математического анализа, 11 класс
Урок №19. Решение задач с помощью производной.
Перечень вопросов, рассматриваемых в теме
- механический смысл первой производной;
- механический смысл второй производных;
- скорость и ускорение.
Глоссарий по теме
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S’(t).
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается f или
или 
Производная от второй производной называется производной третьего порядка и обозначается  или f”’(x). Производную n-го порядка обозначают f(n) (x) или y(n).
или f”’(x). Производную n-го порядка обозначают f(n) (x) или y(n).
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2017.
Теоретический материал для самостоятельного изучения
Давайте вспомним механический смысл производной:
Производная y’(x) функции y=f(x) – это мгновенная скорость изменения этой функции. В частности, если зависимость между пройденным путём S и временем t при прямолинейном неравномерном движении выражается уравнением S=f(t), то для нахождения мгновенной скорости точки в какой-нибудь определённый момент времени t нужно найти производную S’=f’(x) и подставить в неё соответствующее значение t, то есть v(t)=S'(t).
Пример 1. Точка движется прямолинейно по закону  (S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
(S выражается в метрах, t – в секундах). Найти скорость движения через 3 секунды после начала движения.
Решение:
скорость прямолинейного движения равна производной пути по времени, то есть  .
.
Подставив в уравнение скорости t=3 с, получим v(3)=32+4∙3-1= 20 (м/с).
Ответ: 20 м/c.
Пример 2. Маховик, задерживаемый тормозом, поворачивается за t с на угол
 Найдите:
Найдите:
а) угловую скорость вращения маховика в момент t = 6 с;
б) в какой момент времени маховик остановится?
Решение: а) Угловая скорость вращения маховика определяется по формуле ω=φ’. Тогда ω=(4t-0,2t2)=4-0,4t.
Подставляя t = 6 с, получим ω=4-0,4∙6=1,6 (рад/с).
б) В тот момент, когда маховик остановится, его скорость будет равна нулю (ω=0) . Поэтому 4-0,4t=0.. Отсюда t=10 c.
Ответ: угловая скорость маховика равна (рад/с); t=10 c.
Пример 3. Тело массой 6 кг движется прямолинейно по закону S=3t2+2t-5. Найти кинетическую энергию тела  через 3 с после начала движения.
через 3 с после начала движения.
Решение: найдём скорость движения тела в любой момент времени t.
v= S’=(3t2+2t-5)’=6t+2
Вычислим скорость тела в момент времени t=3. v(3)=6∙3+2=20 (м/с)..
Определим кинетическую энергию тела в момент времени t=3.


Ответ: Е=1200 Дж
Производная второго порядка. Производная n-го порядка.
Производная от данной функции называется первой производной или производной первого порядка. Но производная функции также является функцией, и если она дифференцируема, то от неё, в свою очередь, можно найти производную.
Производная от производной называется второй производной или производной второго порядка и обозначается  .
.
Производная от второй производной называется производной третьего порядка и обозначается y”’ или f”'(x) Производную n-го порядка обозначают f(n) (x) или y(n).
Примеры. Найдем производные четвёртого порядка для заданных функций:
1) f(x)= sin 2x
f'(x)=cos 2x∙(2x)’= 2cos 2x
f (x)=-2sin2x∙(2x)’=-4sin 2x
(x)=-2sin2x∙(2x)’=-4sin 2x
f”'(x)= -4 cos 2x∙(2x)= -8 cos 2x
f(4)(x)= 8 sin2x∙(2x)’= 16 sin 2x
2) f(x)=23x
f’(x)=3∙ 23x ∙ln2
f (x)= 9∙ 23x ∙ln22
(x)= 9∙ 23x ∙ln22
f”'(x)= 27∙ 23x ∙ln32
f(4)(x)= 81∙ 23x ∙ln42
Механический смысл второй производной.
Если первая производная функции – это мгновенная скорость изменения любого процесса, заданного функцией, то вторая производная – это скорость изменения скорости, то есть ускорение, то есть 
Итак, первая производная – это скорость изменения процесса, вторая производная – ускорение. (v= S’; a=v’)
Пример 4. Точка движется прямолинейно по закону S(t)= 3t2-3t+8. Найти скорость и ускорение точки в момент t=4 c.
Решение:
найдём скорость точки в любой момент времени t.
v=S’=(3t2-3t+8)’=6t-3.
Вычислим скорость в момент времени t=4 c.
v(4)=6∙4-3=21(м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t-3)’=6 и a(4)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=21(м/с); a= v’= 6 (м/с2).
Пример 5. Тело массой 3 кг движется прямолинейно по закону S(t)=t3-3t2+5. Найти силу, действующую на тело в момент времени t=4 c.
Решение: сила, действующая на тело, находится по формуле F=ma.
Найдём скорость движения точки в любой момент времени t.
v=S’=(t3-3t2+5)’=3t2-6t.
Тогда v(4)=3∙42-6∙4=24 (м/с).
Найдём ускорение: a(t)=v’=(3t2-6t)’=6t-6.
Тогда a(4)= 6∙4-6= 18 (м/с2).
F=ma=3∙18= 54 Н
Ответ: F= 54 Н
Разбор решения заданий тренировочного модуля
№ 1. Тип задания: ввод с клавиатуры пропущенных элементов в тексте
Напишите производную третьего порядка для функции:
f(x)= 3cos4x-5x3+3x2-8
_____________________
Решим данную задачу:
f’’’(x)=( 3cos4x-5x3+3x2-8)’’’=(((3cos4x-5x3+3x2-8)’)’)’=((-12sin4x-15x2+6x)’)’=(-48cos4x-30x)’=192sin4x-30.
Ответ: 192sin4x-30
№ 2. Тип задания: выделение цветом
Точка движется прямолинейно по закону S(t)= 3t2+2t-7. Найти скорость и ускорение точки в момент t=6 c.
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
Решим данную задачу:
Воспользуемся механическим смыслом второй производной:
v= S’(t)=( 3t2+2t-7)’=6t+2.
Вычислим скорость в момент времени t=6 c.
v(6)=6∙6+2=38 (м/с)
Найдём ускорение точки в любой момент времени t.
a= v’= (6t+2)’=6 и a(6)= 6 (м/с2) , то есть ускорение в этом случае является величиной постоянной.
Ответ: v=38(м/с); a= v’= 6 (м/с2).
Верный ответ:
- v=38 м/с; a=6 м/с2
- v=38 м/с; a=5 м/с2
- v=32 м/с; a=6 м/с2
- v=32 м/с; a=5 м/с2
