Ответы Mail.ru
Наука, Техника, Языки
Гуманитарные науки
Естественные науки
Лингвистика
Техника
Вопросы – лидеры.
Дистанционное управление людьми при пситерроре
1 ставка
Значение звучащего"слова"на других языках,которые вы знаете(кроме РУССКОГО)
_иврите ит.ди т.п…Как то так 0DН@КО…!!!
1 ставка
Размеры корпуса шпиндельной бабки (передней бабки) токарно-винторезного станка модели 16к20
1 ставка
Есть ли где спец.залы со всевозможными станками ?
1 ставка
Французский язык упражнение помогите на тему le subjonctif dans le sobordonees circonstancielles
1 ставка
Лидеры категории
Лена-пена
Искусственный Интеллект
М.И.
Искусственный Интеллект
Y.Nine
Искусственный Интеллект
•••
как узнать ускорение, если известно- угол наклона, предложенная сила масса
айдар сапаев
Ученик
(195),
закрыт
10 лет назад
Лучший ответ
Саша Русанов
Высший разум
(209180)
10 лет назад
подъем
a = g(sin(q) +µ*cos(q))
спуск
a = g(sin(q) -µ*cos(q))
при отсутствии дополнительных сил
Остальные ответы
Похожие вопросы
Часто задаваемые вопросы как найти ускорение с учетом угла и коэффициента кинетического трения. В системе ускорения коэффициент трения является одним из основных факторов.
Ускорение в движущейся системе может быть разных форм. Например, в наклонной плоскости мы должны учитывать угол, под которым движется тело. Итак, учитывая все эти атрибуты, мы будем иметь дело с факторами, в основном ответственными за ускорение тела.
Когда наклон имеет тело или любой объект, который находится в постоянном движении, он будет рассчитываться в соответствии с поднятой проблемой. Здесь мы обсудим, как найти ускорение с углом и коэффициентом кинетического трения.
Мы должны знать, как нас ускоряют в движущейся машине. Когда машина движется с определенной скоростью, мы, как правило, возвращаемся на сиденье, когда скорость повышается. Когда в машине применяются тормоза, мы стремимся двигаться вперед, а на поворотах мы склонны двигаться боком. Это способы ускорения.
Ускорению способствуют несколько различных факторов. В одном из них нам нужно сосредоточиться на данных деталях. Здесь мы будем иметь дело с коэффициентом трения и углом, под которым он будет ускоряться.
Подробная информация о коэффициенте трения и его влиянии на ускорение
Коэффициент трения – это, по сути, наименьший фактор, влияющий на ускорение любого объекта, который уже находится в движении. Он основан на силах, действующих на тело, находящееся в постоянном движении.
Во-первых, это сила тяжести, одна из основных причин, по которой тело оказывается на земле без какой-либо левитации. Далее будет нормальная сила, действующая на тело. Эта нормальная сила – это сила, исходящая от окружающей среды. Далее идет сила трения, которая в основном отвечает за то, чтобы тело действительно могло совершать любые движения.
Нормальная сила и сила трения являются одними из основных факторов ускорения. Когда тело движется с определенной скоростью, внезапно набирает скорость и движется с другой скоростью, это называется ускорением.
На самом деле мы должны были знать, как это трение влияет на ускорение и как работает коэффициент трения при ускорении. Когда тело находится в процессе ускорения, в игру вступают несколько аспектов.
На тело в движении действует так много сил. В этой системе ускорения мы должны найти силы, присутствующие и действующие на это тело. Затем нам нужно соответственно рассчитать ускорение.
Сосредоточение внимания на силе трения является одним из факторов, влияющих на движение тела по земле. Например, автомобиль движется из-за трения между шиной автомобиля и дорогой, или в данном случае это может быть любая поверхность.
Как найти ускорение по углу и коэффициенту кинетического трения
Здесь нам нужно рассмотреть столько же примеров, как найти ускорение с учетом угла и коэффициента кинетического трения. Сначала идет угол, затем коэффициент трение. От угла болота зависит, как тело движется по наклонной плоскости.
Теперь рассмотрим случай, когда объект помещен на поверхность, ниже которой он фактически наклонен. Теперь по каким-то причинам объект теряет равновесие и скатывается по наклонной поверхности. Следовательно, необходимо оценить ускорение тела, движущегося в наклонной плоскости.
В этом сценарии сила трения кинетическая, она действует противоположно силе тяжести. Чистая сила также должна быть рассчитана. Нам нужно определить чистую силу, чтобы найти ускорение тела с учетом угла и коэффициента трения.
F = Fg + Fk; F = мг (синус θ) + мкг (cos θ)
Мы знаем, что ускорение – это [сила, деленная на массу, следовательно, a = F / m. Следовательно, из формулы чистой силы мы получаем ускорение как а = g (синус θ) + μ g (cos θ).
Используя эту формулу, мы можем найти ускорение с коэффициентом трения с углом, под которым он движется.
Задача о том, как найти ускорение с учетом угла и коэффициента кинетического трения
1 задачи:
Допустим, автомобиль весом 1200 кг движется по неровной дороге. Значение коэффициента трения равно 0.8. Fnet = 7000N будет расчетной чистой силой, действующей на это движущееся тело. Теперь первое, что нужно оценить, – это ускорение данной конкретной системы.
Решение 1:
Поскольку дана результирующая сила, мы можем найти нормальную силу, используя значение массы и силы тяжести, поскольку сила тяжести и нормальная сила равны друг другу, но действуют в разных направлениях. Сила трения находится с помощью коэффициент величины трения и значения нормальной силы.
м = 1200; Fnet = 7000N; μ = 0.8
Нормальная сила = сила тяжести x масса тела
Fn = 9.8 х 1200; Fn = 11270
Сила трения = μ x нормальная сила; Ff = 0.8x 11270 = 9016 Н
а = ф / м
а = 9016 / 1200
a = 7.51 мс-2
2 задачи:
Как найти ускорение, если задан коэффициент трения и угол наклона.
Итак, в задаче указаны коэффициент трения и угол, под которым он движется. Масса 100 кг движется вниз в наклонной плоскости под углом θ = 45⁰. Коэффициент трения μ = 0.9.
С каким ускорением тело движется вниз?
Решение 2:
Коэффициент силы, действующей на плоскости, равен mgSinθ, а коэффициент, перпендикулярный плоскости, равен mgCosθ. И мы знаем, что f = ma, поэтому a = f / m. исходя из этого, мы можем использовать значение коэффициента трения или нет.
Таким образом, мы получаем формулу как a = μgCosθ
а = 0.9 × 9.8 × 0.52
a = 4.58 мс-2.
Часто задаваемые вопросы
Как найти ускорение с трением и под углом?
Трение – единственная причина, по которой тело перемещается в любом направлении, и когда движение происходит под наклоном, угол будет учитываться.
Формула для определения ускорения с трением, а также угла: a = μgCosθ. Нам нужно знать, что действующие силы будут двух типов: одна будет соответствовать уклону, а другая сила будет перпендикулярна наклону.
Как найти ускорение по чистой силе и массе?
Масса и сила имеют прямое воздействие на тело, независимо от того, находится оно в движении или нет. Таким образом, масса и сила будут основными причинами движения конкретного тела.
Когда тело находится в движении, частью движения будет несколько различных факторов. В одном из таких случаев сила будет иметь большое влияние. Основная сила, действующая на движущееся тело, будет силой тяжести и нормальной силой, которая будет действовать перпендикулярно направлению движения. числовые силы, действующие на эту конкретную систему, должны быть найдены и затем оценены.
Масса имеет прямое воздействие на тело, поскольку это основная причина, по которой тело движется; когда масса тела увеличивается, ускорение уменьшается. Когда масса тела уменьшается, ускорение увеличивается, поэтому действующая сила больше, и телу будет легче двигаться, если только масса будет больше. Таким образом, формула ускорения с чистой силой и массой дается как a = f / m.
Цель этой
работы: с помощью экспериментальной исследовать зависимость
ускорение скольжения бруска по наклонной плоскости от угла наклона.
Для выполнения этой работы мы будем использовать оборудование
из комплекта № 5 в составе: штатив с креплением для наклонной плоскости,
направляющая со шкалой, деревянный брусок с пусковым магнитом, два груза,
массой по 100 г каждый, электронный секундомер с датчиками, линейка и
транспортир.
Прежде чем приступить к работе давайте с вами вспомним, что неравномерное
движение — это такое движение, при котором тело, за любые равные промежутки
времени совершает разные перемещения.
Самым простым видом неравномерного движения является прямолинейное
равноускоренное движение. Так называют движение, при котором за любые
равные промежутки времени скорость тела изменяется на одну и туже величину, а
траекторией движения тела является прямая линия.
Для того,
чтобы описать насколько быстро меняется скорость тела, в физике ввели величину,
которую назвали ускорением тела. Ускорение — это физическая векторная
величина, равная отношению изменения скорости к промежутку времени, в течение
которого это изменение произошло:
Именно ускорение тела нам и предстоит определить в данной
работе. Однако очевидно, что данная формула нам не подходит, так как в ней
фигурирует скорость тела, измерить которую прямыми измерения в классе мы не
можем. А анализ оборудования нам говорит о том, что для определения ускорения
мы с вами должны воспользоваться формулой, для определения перемещения тела при
его равноускоренном движении:
Так как мы будем изучать прямолинейное равноускоренное
движение без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, то мы с вами можем записать, что модуль вектора перемещения
прямо пропорционален квадрату промежутка времени, в течение которого это
перемещение было совершено:
Отсюда, зная пройденный телом путь
и время его движения, мы с вами легко можем определить модуль ускорения, с
которым двигалось тело:
Теперь
приступим к выполнению работы. Итак, для начала давайте соберём
экспериментальную установку. Для этого на штативе закрепим наклонную плоскость.
После этого, используя транспортир, установим направляющую под углом 25° к
поверхности стола.
Далее
установим на направляющей датчики секундомера: первый расположим в точке 0, а
второй — в 40 см. При пуске бруска пусковой магнит мы установим на 0,5 см выше
первого датчика. Грузы закрепим на бруске.
Далее мы
сделаем рисунок нашей установки. Для этого схематически изобразим штатив с
прикреплённой к нему направляющей. На направляющей расположим брусок так, как
это показано на экране. Также на рисунке мы должны будем указать перемещение
тела и направление вектора ускорения.
Запишем формулы, которыми будем пользоваться при выполнении
данной работы. Как мы уже вспоминали, при прямолинейном равноускоренном
движении без начальной скорости при котором направление векторов перемещения и
ускорения совпадают, модуль вектора перемещения (путь) прямо пропорционален
квадрату промежутка времени, в течение которого это перемещение было совершено:
С формулами разобрались, теперь составим таблицу. В первой
колонке мы укажем номера опытов.
Во второй колонке мы запишем значения углов наклона плоскости
к поверхности стола, которые нам даны в условии задания.
Результат измерения пути, пройденного
бруском, с учётом абсолютной погрешности измерения мы запишем в третью колонку
(путь нам дан в условии задания и его значение в ходе опытов меняться не
будет):
Четвёртую колонку мы отведём для записи времени движения
бруска по наклонной плоскости. А в последнюю колонку будем записывать значения
ускорений.
Теперь приступим непосредственно к выполнению работы. Итак,
подключаем электронные датчики к секундомеру, а брусок устанавливаем так, чтобы
пусковой магнит находился на пол сантиметра выше первого датчика. Отпускаем
брусок.
Значение промежутка времени, за которое брусок преодолел
заданный отрезок пути, записываем в таблицу с учётом погрешности измерения:
Теперь установим направляющую под углом 35° и повторим опыт.
Как и в прошлый раз, результат измерения промежутка времени заносим в таблицу:
И, наконец, устанавливаем направляющую под углом 45°:
Прямы измерения мы с вами завершили. Теперь определяем
ускорение бруска для каждого из трёх случаев. Для поочерёдно подставляем в
расчётную формулу значения пути и времени движения бруска. Результаты всех
вычислений заносим в таблицу:
Теперь очень хорошо видно, что с увеличением угла наклона
направляющей, ускорение бруска также увеличивается. Это мы и напишем в выводе.
Динамика и кинематика – это два важных раздела физики, которые изучают законы перемещения объектов в пространстве. Первый рассматривает действующие на тело силы, второй же занимается непосредственно характеристиками динамического процесса, не вникая в причины того, что его вызвало. Знание этих разделов физики необходимо применять для успешного решения задач на движение по наклонной плоскости. Рассмотрим этот вопрос в статье.
Основная формула динамики
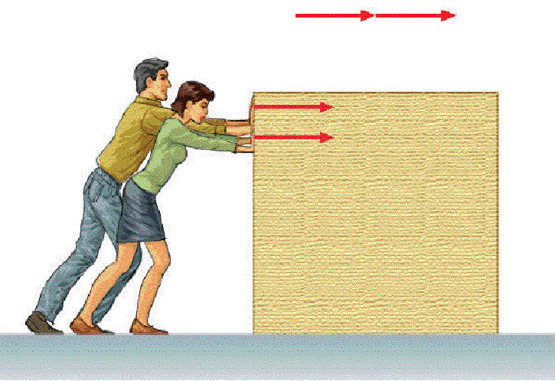
Конечно же, речь идет о втором законе, который постулировал Исаак Ньютон в XVII веке, изучая механическое движение твердых тел. Запишем его в математической форме:
F¯ = m*a¯
Действие внешней силы F¯ вызывает появление линейного ускорения a¯ у тела с массой m. Обе векторные величины (F¯ и a¯) направлены в одну и ту же сторону. Сила в формуле является результатом действия на тело всех сил, которые присутствуют в системе.
В случае движения вращения второй закон Ньютона записывается в виде:
M = I*α
Здесь M и I – моменты силы и инерции, соответственно, α – угловое ускорение.
Формулы кинематики
Решение задач на движение по наклонной плоскости требует знания не только главной формулы динамики, но и соответствующих выражений кинематики. Они связывают в равенства ускорение, скорость и пройденный путь. Для равноускоренного (равнозамедленного) прямолинейного движения применяются следующие формулы:
a = Δv/Δt;
v = v0 ± a*t;
S = v0*t ± a*t2/2
Здесь v0 – значение начальной скорости тела, S – пройденный за время t путь вдоль прямолинейной траектории. Знак “+” следует поставить, если скорость тела увеличивается с течением времени. В противном случае (равнозамедленное движение) следует использовать в формулах знак “-“. Это важный момент.
Если движение осуществляется по круговой траектории (вращение вокруг оси), тогда следует использовать такие формулы:
α = Δω/Δt;
ω = ω0 ± α*t;
θ = ω0*t ± α*t2/2
Здесь α и ω – угловые ускорение и скорость, соответственно, θ – угол поворота вращающегося тела за время t.
Линейные и угловые характеристики друг с другом связаны формулами:
a = α*r;
v = ω*r
Здесь r – радиус вращения.
Движение по наклонной плоскости: силы
Под этим движением понимают перемещение некоторого объекта вдоль плоской поверхности, которая наклонена под определенным углом к горизонту. Примерами может служить соскальзывание бруска по доске или качение цилиндра по металлическому наклоненному листу.
Для определения характеристик рассматриваемого типа движения необходимо в первую очередь найти все силы, которые действуют на тело (брусок, цилиндр). Они могут быть разными. В общем случае это могут быть следующие силы:
- тяжести;
- реакции опоры;
- трения качения и/или скольжения;
- натяжение нити;
- сила внешней тяги.
Первые три из них присутствуют всегда. Существование последних двух зависит от конкретной системы физических тел.
Чтобы решать задачи на перемещение по плоскости наклонной необходимо знать не только модули сил, но и их направления действия. В случае, если тело по плоскости скатывается, сила трения неизвестна. Однако она определяется из соответствующей системы уравнений движения.

Методика решения
Решения задач данного типа начинается с определения сил и их направлений действия. Для этого в первую очередь рассматривают силу тяжести. Ее следует разложить на два составляющих вектора. Один из них должен быть направлен вдоль поверхности наклонной плоскости, а второй должен быть ей перпендикулярен. Первая составляющая силы тяжести, в случае движения тела вниз, обеспечивает его линейное ускорение. Это происходит в любом случае. Вторая равна силе реакции опоры. Все эти показатели могут иметь различные параметры.
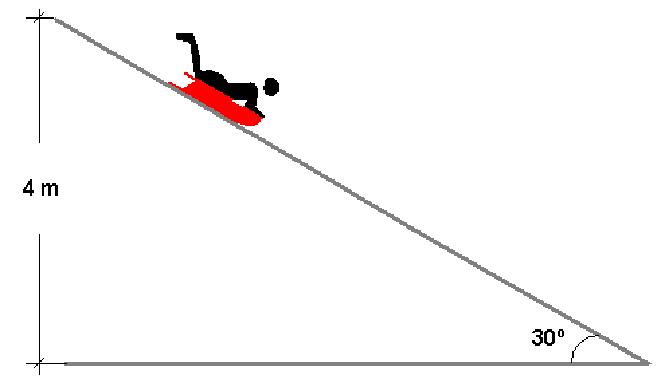
Сила трения при движении по наклонной плоскости всегда направлена против перемещения тела. Если речь идет о скольжении, то вычисления довольно просты. Для этого следует использовать формулу:
Ff = µ*N
Где N – реакция опоры, µ – коэффициент трения, не имеющий размерности.
Если в системе присутствуют только указанные три силы, тогда их результирующая вдоль наклонной плоскости будет равна:
F = m*g*sin(φ) – µ*m*g*cos(φ) = m*g*(sin(φ) – µ*cos(φ)) = m*a
Здесь φ – это угол наклона плоскости к горизонту.
Зная силу F, можно по закону Ньютона определить линейное ускорение a. Последнее, в свою очередь, используется для определения скорости движения по наклонной плоскости через известный промежуток времени и пройденного телом расстояния. Если вникнуть, то можно понять, что все не так уж и сложно.
В случае, когда тело скатывается по наклонной плоскости без проскальзывания, суммарная сила F будет равна:
F = m*g*sin(φ) – Fr = m*a
Где Fr – сила трения качения. Она неизвестна. Когда тело катится, то сила тяжести не создает момента, поскольку приложена к оси вращения. В свою очередь, Fr создает следующий момент:
M = Fr*r = I*α
Учитывая, что мы имеем два уравнения и две неизвестных (α и a связаны друг с другом), можно легко решить эту систему, а значит, и задачу.
Теперь рассмотрим, как использовать описанную методику при решении конкретных задач.
Задача на движение бруска по наклонной плоскости
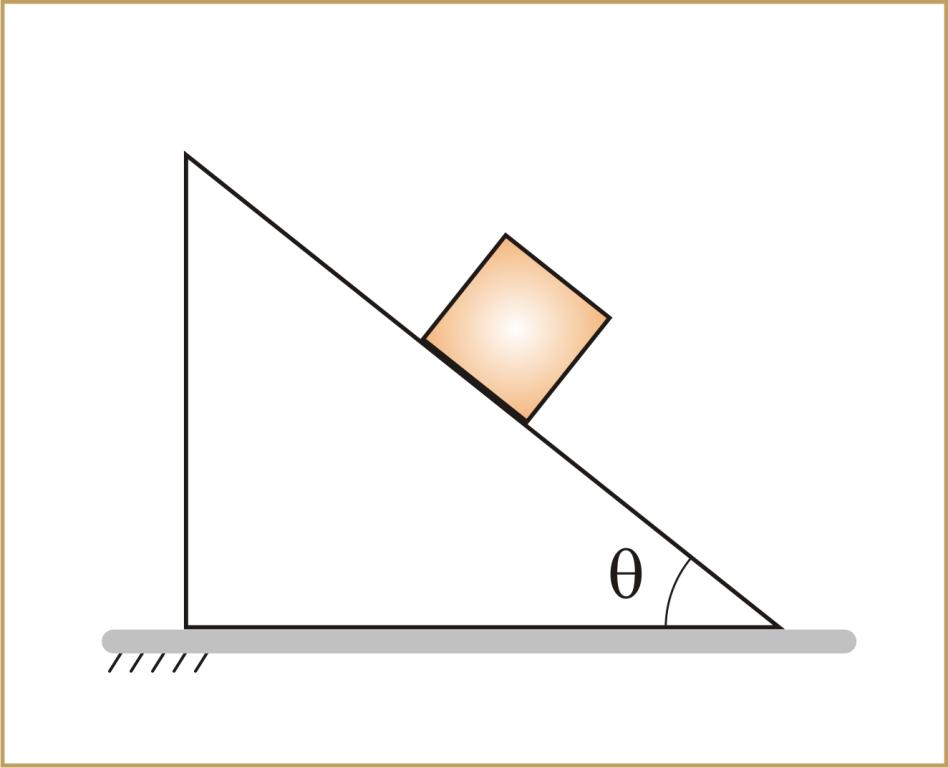
Деревянный брусок находится в верхней части наклонной плоскости. Известно, что она имеет длину 1 метр и располагается под углом 45o. Необходимо вычислить, за какое время брусок опустится по этой плоскости в результате скольжения. Коэффициент трения принять равным 0,4.
Записываем закон Ньютона для данной физической системы и вычисляем значение линейного ускорения:
m*g*(sin(φ) – µ*cos(φ)) = m*a =>
a = g*(sin(φ) – µ*cos(φ)) ≈ 4,162 м/с2
Поскольку нам известно расстояние, которое должен пройти брусок, то можно записать следующую формулу для пути при равноускоренном движении без начальной скорости:
S = a*t2/2
Откуда следует выразить время, и подставить известные значения:
t = √(2*S/a) = √(2*1/4,162) ≈ 0,7 с
Таким образом, время движения по наклонной плоскости бруска составит меньше секунды. Заметим, что полученный результат от массы тела не зависит.
Задача со скатывающимся по плоскости цилиндром
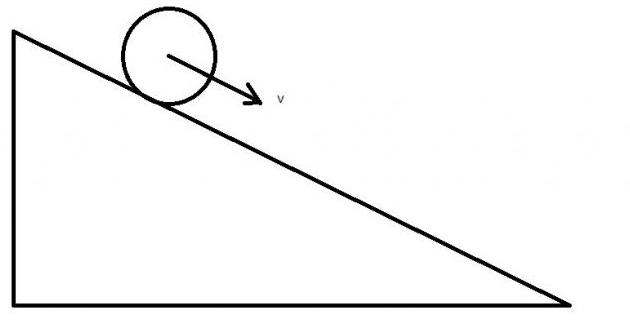
Цилиндр радиусом 20 см и массой 1 кг помещен на наклонную под углом 30o плоскость. Следует вычислить его максимальную линейную скорость, которую он наберет при скатывании с плоскости, если ее длина составляет 1,5 метра.
Запишем соответствующие уравнения:
m*g*sin(φ) – Fr = m*a;
Fr*r = I*α = I*a/r
Момент инерции I цилиндра вычисляется по формуле:
I = 1/2*m*r2
Подставим это значение во вторую формулу, выразим из нее силу трения Fr и заменим полученным выражением ее в первом уравнении, имеем:
Fr*r = 1/2*m*r2*a/r = >
Fr = 1/2*m*a;
m*g*sin(φ) – 1/2*m*a = m*a =>
a = 2/3*g*sin(φ)
Мы получили, что линейное ускорение не зависит от радиуса и массы скатывающегося с плоскости тела.
Зная, что длина плоскости составляет 1,5 метра, найдем время движения тела:
S = a*t2/2 =>
t = √(2*S/a)
Тогда максимальная скорость движения по наклонной плоскости цилиндра будет равна:
v = a*t = a*√(2*S/a) = √(2*S*a) = √(4/3*S*g*sin(φ))
Подставляем все известные из условия задачи величины в конечную формулу, получаем ответ: v ≈ 3,132 м/c.
Постоянное горизонтальное ускорение при заданном угле наклона свободной поверхности Калькулятор
| Search | ||
| Дом | Инженерное дело ↺ | |
| Инженерное дело | Гражданская ↺ | |
| Гражданская | Гидравлика и гидротехнические сооружения ↺ | |
| Гидравлика и гидротехнические сооружения | Жидкости в относительном равновесии ↺ | |
| Жидкости в относительном равновесии | Емкости с жидкостью, подверженные постоянному горизонтальному ускорению ↺ |
|
✖Угол наклона образован наклоном одной линии к другой; измеряется в градусах или радианах.ⓘ Угол наклона [θinclination] |
+10% -10% |
|
✖Постоянное горизонтальное ускорение – это ускорение в одном направлении.ⓘ Постоянное горизонтальное ускорение при заданном угле наклона свободной поверхности [α] |
⎘ копия |
Постоянное горизонтальное ускорение при заданном угле наклона свободной поверхности Решение
ШАГ 0: Сводка предварительного расчета
ШАГ 1. Преобразование входов в базовый блок
Угол наклона: 89.771 степень –> 1.56679952280753 Радиан (Проверьте преобразование здесь)
ШАГ 2: Оцените формулу
ШАГ 3: Преобразуйте результат в единицу вывода
2453.60988738856 метр / Квадрат Второй –> Конверсия не требуется
15 Емкости с жидкостью, подверженные постоянному горизонтальному ускорению Калькуляторы
Постоянное горизонтальное ускорение при заданном угле наклона свободной поверхности формула
Постоянное горизонтальное ускорение = tan(Угол наклона)*[g]
α = tan(θinclination)*[g]
Что такое ускорение?
Ускорение – это скорость изменения скорости. Обычно ускорение означает изменение скорости, но не всегда. Когда объект движется по круговой траектории с постоянной скоростью, он все еще ускоряется, потому что направление его скорости меняется.
