Как найти условное математическое ожидание - Сайт, где вы сможете решить свои вопросы

Важной характеристикой условного распределения вероятностей является условное математическое ожидание.

Условным математическим ожиданием дискретной случайной величины Y при X = x (x – определенное возможное значение X) называют произведение возможных значений Y на их условные вероятности:

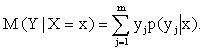(13.1.50)

Для непрерывных величин

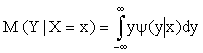где 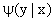— условная плотность случайной величины Y при X = x.

Условное математическое ожидание M (Y | x) есть функция от x:

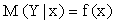которую называют функцией регрессии Y на X.

Аналогично определяются условное математическое ожидание случайной величины X и функция регрессии X на Y: .

ПРИМЕР 13.1.58 Дискретная двумерная случайная величина задана таблицей

Найти условное математическое ожидание составляющей Y при .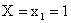

Решение. Найдем 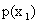, для чего сложим вероятности, помещенные в первом столбце таблицы:

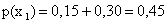Найдем условное распределение вероятностей величины Y при :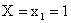

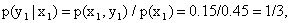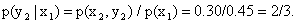
Найдем искомое условное математическое ожидание по формуле (13.1.50):

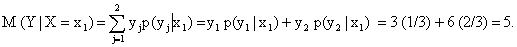
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

Сохранить или поделиться с друзьями

Вы находитесь тут:

На нашем сайте Вы можете получить решение задач и онлайн помощь

Подробнее

Помощь по математике. Решение задач и контрольных работ

Источник

Условное математическое ожидание в теории вероятностей — это среднее значение случайной величины при выполнении некоторого условия (реализации каких-то событий). Часто в качестве условия выступает фиксированное на некотором уровне значение другой случайной величины, которая может быть связана с данной (если эти случайные величины независимы, то условное математическое ожидание совпадает с (безусловным) математическим ожиданием). В этом случае условное математическое ожидание случайной величины при условии, что случайная величина приняла значение обозначается как , соответственно, ее можно рассматривать как функцию от . Эта функция называется функцией регрессии случайной величины на случайную величину и поэтому условное математическое ожидание обозначают как , то есть без указания фиксированного значения .

Условное математическое ожидание – это характеристика условного распределения.

Определения[править | править код]

Будем считать, что дано вероятностное пространство . Пусть — интегрируемая случайная величина, то есть . Пусть также — σ-подалгебра σ-алгебры .

УМО относительно σ-алгебры[править | править код]

Случайная величина называется условным математическим ожиданием относительно σ-алгебры , если

где $mathbf {1} _{A}$ — индикатор события (иными словами, это характеристическая функция множества-события, аргументом которой является случайная величина или элементарный исход).
Условное математическое ожидание обозначается .

Пример. Пусть $Omega ={1,2,3,4},,{mathcal {F}}=2^{Omega },,mathbb {P} (omega )=1/4,,omega =1,ldots ,4.$ Положим . Тогда — σ-алгебра, и . Пусть случайная величина имеет вид

$X(omega )=omega ^{2},;omega =1,ldots ,4$

Тогда

$mathbb {E} [Xmid {mathcal {G}}](omega )=left{{begin{matrix}{frac {5}{2}},&omega =1,2\[5pt]{frac {25}{2}},&omega =3,4.end{matrix}}right.$

УМО относительно семейства событий[править | править код]

Пусть ${mathcal {C}}={C_{alpha }}subset {mathcal {F}}$ — произвольное семейство событий. Тогда условным математическим ожиданием относительно называется

mathbb {E} [Xmid {mathcal {C}}]equiv mathbb {E} [Xmid sigma ({mathcal {C}})]

где — минимальная сигма-алгебра, содержащая .

Пример. Пусть $Omega ={1,2,3,4},,{mathcal {F}}=2^{Omega },,mathbb {P} (omega )=1/4,,omega =1,ldots ,4.$ Пусть также . Тогда . Пусть случайная величина имеет вид

$X(omega )=omega ^{2},;omega =1,ldots ,4$

Тогда

$mathbb {E} [Xmid {mathcal {C}}](omega )=left{{begin{matrix}{frac {14}{3}},&omega =1,2,3\[5pt]16,&omega =4.end{matrix}}right.$

УМО относительно случайной величины[править | править код]

Пусть другая случайная величина. Тогда условным математическим ожиданием относительно называется

mathbb {E} [Xmid Y]equiv mathbb {E} [Xmid sigma (Y)]

где — σ-алгебра, порождённая случайной величиной .

Другое определение УМО относительно :

$mathbb {E} (Xmid Y)=mathbb {E} (Xmid Y=y)mid _{y=Y}$

Такое определение конструктивно описывает алгоритм нахождения УМО:

Пример:
$Xequiv N(a,sigma ^{2})$

$mathbb {E} left[{frac {X}{Y}}mid Yright]=mathbb {E} left[{frac {X}{y}}right]mid _{y=Y}={frac {1}{y}}mathbb {E} [X]mid _{y=Y}={frac {a}{y}}mid _{y=Y}={frac {a}{Y}}$

Условная вероятность[править | править код]

Пусть — произвольное событие, и $mathbf {1} _{B}$ — его индикатор. Тогда условной вероятностью относительно называется

$mathbb {P} (Bmid {mathcal {G}})equiv mathbb {E} [mathbf {1} _{B}mid {mathcal {G}}]$

Замечания[править | править код]

mathbb {E} [X]=mathbb {E} [mathbb {E} [Xmid {mathcal {G}}]]

и в частности справедлива формула полной вероятности:

mathbb {P} (B)=mathbb {E} [mathbb {P} (Bmid {mathcal {G}})]

$mathbb {E} [Xmid {mathcal {G}}]=sum _{i=1}^{infty }mathbb {E} [Xmid C_{i}]mathbf {1} _{C_{i}}$

В частности формула полной вероятности принимает классический вид:

$mathbb {P} (Amid {mathcal {G}})=sum limits _{i=1}^{infty }mathbb {P} (Amid C_{i})mathbf {1} _{C_{i}}$

а следовательно

${displaystyle mathbb {E} [mathbb {P} (Amid {mathcal {G}})]=sum limits _{i=1}^{infty }mathbb {P} (Amid C_{i})mathbb {E} [mathbf {1} _{C_{i}}]=sum limits _{i=1}^{infty }mathbb {P} (Amid C_{i}),mathbb {P} (C_{i})=mathbb {P} (A)}$

Основные свойства[править | править код]

Условное математическое ожидание относительно события {Y=y} по определению равно

mathbb {E} [Xmid {mathcal {G}}]=mathbb {E} [X]

п.н.

В частности, если X,Y независимые случайные величины, то

п.н.

$mathbb {E} [mathbb {E} [Xmid {mathcal {G}}_{2}]mid {mathcal {G}}_{1}]=mathbb {E} [Xmid {mathcal {G}}_{1}]$

mathbb {E} [XYmid {mathcal {G}}]=X,mathbb {E} [Ymid {mathcal {G}}]

«Математическое ожидание убирает условие». Это правило верно для УМО относительно случайной величины (УМО в таком случае будет случайной величиной) и для условной вероятности относительно случайной величины

mathbb {E} [mathbb {E} (Xmid Y)]=mathbb {E} (X)

Дополнительные свойства[править | править код]

Теорема Леви о монотонной сходимости;
Теорема Лебега о мажорируемой сходимости;
Лемма Фату;
Неравенство Йенсена.

УМО для дискретных величин[править | править код]

Пусть — дискретная случайная величина, чьё распределение задаётся функцией вероятности $mathbb {P} (Y=y_{j})equiv p_{Y}(y_{j})=p_{j}>0,;j=1,2,ldots$ . Тогда система событий ${Y=y_{j}}$ является разбиением Omega , и

$mathbb {E} [Xmid Y]=sum limits _{j=1}^{infty }mathbb {E} [Xmid Y=y_{j}]mathbf {1} _{{Y=y_{j}}}$

$mathbb {E} [Xmid Y=y_{j}]=mathbb {E} _{j}[X]$

где $mathbb {E} _{j}$ означает математическое ожидание, взятое относительно условной вероятности $mathbb {P} _{j}(cdot )=mathbb {P} (cdot mid Y=y_{j})$ .

Если случайная величина также дискретна, то

$mathbb {E} [Xmid Y=y_{j}]=sum limits _{i=1}^{infty }x_{i},mathbb {P} (X=x_{i}mid Y=y_{j})=sum limits _{i=1}^{infty }x_{i},p_{Xmid Y}(x_{i}mid y_{j})$

где $p_{Xmid Y}$ — условная функция вероятности случайной величины относительно .

УМО для абсолютно непрерывных случайных величин[править | править код]

Пусть X,Y — случайные величины, такие что вектор $(X,Y)^{top }$ абсолютно непрерывен, и его распределение задаётся плотностью вероятности $f_{{X,Y}}(x,y)$ . Введём условную плотность $f_{Xmid Y}$ , положив по определению

$f_{Xmid Y}(xmid y)={frac {f_{X,Y}(x,y)}{f_{Y}(y)}}$

где $f_{Y}$ — плотность вероятности случайной величины . Тогда

где функция имеет вид

$h(y)=int limits _{-infty }^{infty }x,f_{Xmid Y}(xmid y),dx$

В частности,

$mathbb {E} [Xmid Y=y_{j}]=int limits _{-infty }^{infty }x,f_{Xmid Y}(xmid y_{j}),dx$

УМО в L²[править | править код]

Рассмотрим пространство случайных величин с конечным вторым моментом $L^{2}$ . В нём определены скалярное произведение

$langle X,Yrangle equiv mathbb {E} [XY],;forall X,Yin L^{2}$

и порождённая им норма

$|X|={sqrt {mathbb {E} left[X^{2}right]}},;forall Xin L^{2}$

Множество всех случайных величин $L_{mathcal {G}}^{2}$ с конечным вторым моментом и измеримых относительно , где , является подпространством $L^{2}$ . Тогда оператор $Pi _{L_{mathcal {G}}^{2}}:L^{2}to L^{2}$ , задаваемый равенством

$Pi _{L_{mathcal {G}}^{2}}(X)=mathbb {E} [Xmid {mathcal {G}}]$

является оператором ортогонального проектирования на $L_{mathcal {G}}^{2}$ . В частности:

$|X-mathbb {E} [Xmid {mathcal {G}}]|=inf limits _{Zin L_{mathcal {G}}^{2}}|X-Z|$

Условное математическое ожидание сохраняет скалярное произведение:

$langle X,Zrangle =langle mathbb {E} [Xmid {mathcal {G}}],Zrangle ,;forall Zin L_{mathcal {G}}^{2}$

Условное математическое ожидание идемпотентно:

$Pi _{L_{mathcal {G}}^{2}}^{2}=Pi _{L_{mathcal {G}}^{2}}$

См. также[править | править код]

Условное распределение

Источник

Важной характеристикой
условного распределения вероятностей
является условное математическое
ожидание.

Определение.
Условным математическим ожиданием
дискретной
случайной величины η
при
ξ=х
(х
– определенное возможное значение ξ)
называют произведение возможных значений
η
на
их условные вероятности:

M(η|ξ=х)=
p(y_j|x).

Для непрерывных
величин

M(η|ξ=х)=
ψ(y|x)dy,

где
ψ(y|x)
– условная плотность случайной величины
η
при
ξ=х.

Условное
математическое ожидание M(η|х)
есть функция от х:

M(η|х)=f(x),

которую
называют функцией
регрессии η
на
ξ.

Аналогично
определяются условное математическое
ожидание случайной величины ξ
и
функция
регрессии ξ
на
η:

Пример.
Дискретная двумерная случайная величина
задана таблицей значений.

ξ/η	x₁=1	x₂=3	x₃=4	x₄=8
y₁=3	0,15	0,06	0,25	0,04
y₂=6	0,30	0,10	0,03	0,07

Найти
условное математическое ожидание
составляющей η
при
ξ=х₁=1.

Решение.
Найдем р(х₁),
для чего сложим вероятности, помещенные
в первом столбце таблицы:

р(х₁)=0,15+0,30=0,45.

Найдем
условное распределение вероятностей
величины η
при
ξ=х₁=1:

р(у₁|х₁)=р(х₁,y₁)/p(х₁)=0,15/0,45=1/3;

р(у₂|х₁)=р(х₂,y₂)/p(х₁)=0,30/0,45=2/3.

Найдем искомое
условное математическое ожидание:

M(η|ξ=х₁)=

p(y_j|x₁)=у₁
р(у₁|х₁)+у₂
р(у₂|х₁)=3
(1/3)+6 (2/3)=5.

§29. Ковариация. Коэффициент корреляции

Для описания
системы двух случайных величин кроме
математических ожиданий и дисперсий
составляющих используют и другие
характеристики; к их числу относятся
ковариация (корреляционный момент) и
коэффициент корреляции.

Определение.
Ковариацией
случайных
величин ξ
и
η
называют математическое ожидание
произведения отклонений этих величин:

cov(ξ,η)=М{[ξ–M(ξ)][η–M(η)]}.

Для вычисления
ковариации дискретных величин используют
формулу

cov(ξ,η)=
х_i-М(ξ)]
[y_j–M(η)]р(х_i,y_j),

а для непрерывных
величин – формулу

cov(ξ,η)=
[y–M(η)]f(x,y)dxdy.

Ковариация
служит для характеристики связи между
величинами ξ
и η.
Ковариация
равна нулю, если ξ
и η
независимы;
следовательно, если ковариация не равна
нулю, то ξ
и η
–
зависимые случайные величины.

Отметим,
что
ковариацию можно определить как
математическое ожидание произведения
центрированных случайных величин:

cov(ξ,η)=М[
].

3амечание.
Легко убедиться, что ковариацию можно
записать в виде

cov(ξ,η)=М(ξη)-М(ξ)М(η).

Теорема.
Ковариация
двух независимых случайных величин ξ
и
η
равна нулю.

Доказательство.
Так как ξ
и η
– независимые
случайные величины, то их отклонения
ξ–M(ξ)
и
η–M(η)
также независимы. Пользуясь свойствами
математического ожидания (математическое
ожидание произведения независимых
случайных величин равно произведению
математических ожиданий сомножителей)
и отклонения (математическое ожидание
отклонения равно нулю), получим

cov(ξ,η)=М{[ξ–M(ξ)][η–M(η)]}=M[ξ–M(ξ)]M[η–M(η)]=0.

Из
определения ковариации следует, что
она имеет размерность, равную произведению
размерностей величин ξ
и η.
Другими словами, величина ковариации
зависит от единиц измерения случайных
величин. По этой причине для одних и тех
же двух величин величина ковариации
имеет различные значения в зависимости
от того, в каких единицах были измерены
величины.

Пусть,
например, ξ
и η
были
измерены в сантиметрах и cov(ξ,η)=2
см²;
если измерить ξ
и η
в
миллиметрах, то cov(ξ,η)=200
мм².
Такая особенность ковариации является
недостатком этой числовой характеристики,
поскольку сравнение корреляционных
моментов различных систем случайных
величин становится затруднительным.
Для того чтобы устранить этот недостаток,
вводят новую числовую характеристику
– коэффициент корреляции.

Определение.
Коэффициентом корреляции r(ξ,η)
случайных
величин ξ
и η
называют
отношение ковариации к произведению
средних квадратических отклонений этих
величин:

r(ξ,η)=cov(ξ,η)/(

).

Так
как размерность cov(ξ,η)
равна
произведению размерностей величин ξ
и η,

имеет
размерность величины ξ,

имеет
размерность величины η,
то r(ξ,η)
– безразмерная величина. Таким образом,
величина коэффициента корреляции не
зависит от выбора единиц измерения
случайных величин. Очевидно, коэффициент
корреляции независимых случайных
величин равен нулю (так как cov(ξ,η)=0).

Замечание.
Во многих вопросах теории вероятностей
целесообразно вместо случайной величины
ξ
рассматривать
нормированную случайную величину ξ’,
которую определяют как отношение
отклонения к среднему квадратическому
отклонению:

ξ’=(ξ–M(ξ))/

Нормированная
величина имеет математическое ожидание,
равное нулю, и дисперсию, равную единице.
Действительно, используя свойства
математического ожидания и дисперсии,
имеем:

M(ξ’)=M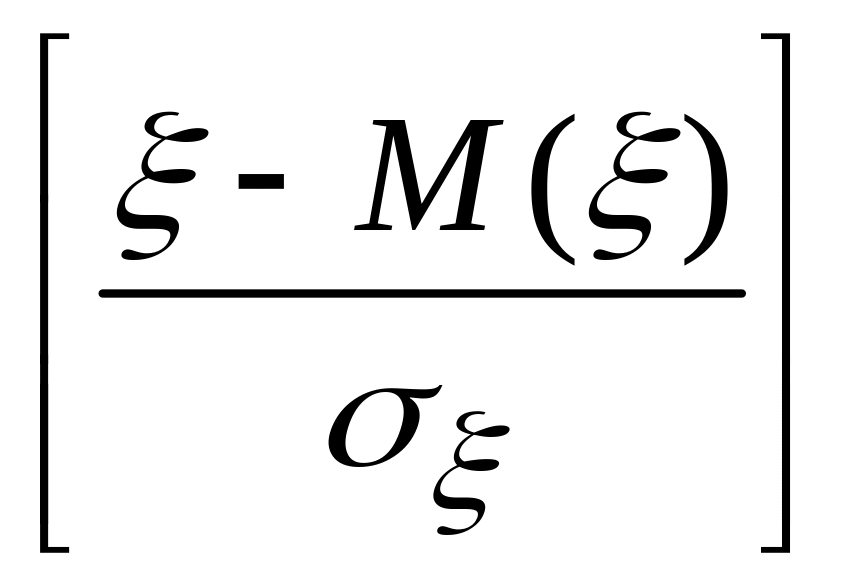
=
М[ξ–M(ξ)]=
0=0;

D(ξ’)=D
=
D[ξ–M(ξ)]=
=1.

Легко
убедиться, что коэффициент корреляции
r(ξ,η)
равен
ковариации нормированных величин ξ’
и
η’:

r(ξ,η)=
=M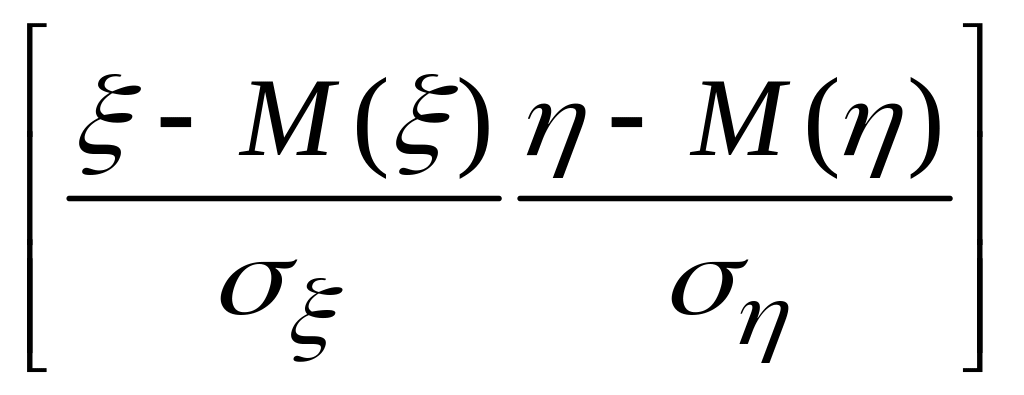
=M(ξ’η’)=cov(ξ‘,η’)

Теорема.
Абсолютная
величина ковариации двух случайных
величин ξ
и
η
не превышает среднего геометрического
их дисперсий:

|cov(ξ,η)|≤

Доказательство.
Введем в рассмотрение случайную величину
θ₁=
ξ–
η
и
найдем ее дисперсию. Выполнив необходимые
преобразования, получим

D(θ₁)=2

-2

cov(ξ,η).

Любая дисперсия
неотрицательна, поэтому

-2

cov(ξ,η)≥0.

Отсюда

cov(ξ,η)≤

Введя
случайную величину θ₂=
ξ+
η
аналогично найдем

cov(ξ,η)≥-

Объединим неравенства

–

≤cov(ξ,η)≤

или

|cov(ξ,η)|≤

Итак,

|cov(ξ,η)|≤
.

Теорема.
Абсолютная
величина коэффициента корреляции не
превышает единицы:

|r(ξ,η)|≤1.

Доказательство:
Разделим обе части двойного неравенства

–

≤cov(ξ,η)≤

.
на произведение положительных чисел

-1≤r(ξ,η)≤1.

Итак,

|r(ξ,η)|≤1.

Определение.
Две
случайные величины ξ
и η
называют
коррелированными,
если их ковариация (или, что то же,
коэффициент корреляции) отлична от
нуля; ξ
и η
называют
некоррелированными
величинами,
если их ковариация равна нулю.

Две
коррелированные величины также и
зависимы. Действительно, допустив
противное, мы должны заключить, что
cov(ξ,η)=0,
противоречит условию, так как для
коррелированных величин
cov(ξ,η)≠0.

Обратное предположение
не всегда имеет место, т.е. если две
величины зависимы, то они могут быть
как коррелированными, так и
некоррелированными. Другими словами,
корреляционный момент двух зависимых
величин может быть не равен нулю, но
может и равняться нулю.

Убедимся на примере,
что две зависимые величины могут быть
некоррелированными.

Пример.
Двумерная случайная величина (ξ,η)
задана
плотностью распределения:

f(x,у)=1/6π
внутри эллипса x²/9+y²/4=1;

f(x,у)=0
вне этого эллипса.

Доказать,
что ξ
и η
– зависимые
некоррелированные величины.

Решение.
Вычислим плотности распределения
составляющих ξ
и η:

f₁(x)=
,
f₂(у)=

внутри заданного эллипса и f₁(x)=0,
f₂(y)=0
вне
его.

Так
как f(x,у)≠f₁(x)f₂(у),
то
ξ
и η
–
зависимые величины.

Для
того чтобы доказать некоррелированность
ξ
и η,
достаточно убедиться в том, что cov(ξ,η)=0.
Найдем корреляционный момент по формуле

cov(ξ,η)=
[y–M(η)]f(x,y)dxdy.

Поскольку
функция f₁(x)
симметрична
относительно оси OY,
то
М(ξ)=0;
аналогично, М(η)=0
в силу симметрии f₂(у)
относительно оси OX.
Следовательно,

cov(ξ,η)=
yf(x,y)dxdy.

Вынося
постоянный множитель f(x,у)
за знак интеграла, получим

cov(ξ,η)=f(x,y)

dy.

Внутренний
интеграл равен нулю (подынтегральная
функция нечетна, пределы интегрирования
симметричны относительно начала
координат), следовательно, cov(ξ,η)=0,
т.е.
зависимые случайные величины ξ
и η
некоррелированы.

Итак, из
коррелированности двух случайных
величин следует их зависимость, но из
зависимости еще не вытекает
коррелированность. Из независимости
двух величин следует их некоррелированность,
но из некоррелированности еще нельзя
заключить о независимости этих величин.

Замечание.
Теперь
мы можем определить дисперсию суммы
двух произвольных случайных величин

D(ξ+η)=D(ξ)+D(η)+2cov(ξ,η).

Справедливость
данного соотношения вытекает
непосредственно из доказательства
соответствующего свойства дисперсии
и определения ковариации.

На практике часто
встречаются двумерные случайные
величины, распределение которых
нормально.

Определение.
Нормальным
законом распределения на плоскости
называют
распределение вероятностей двумерной
случайной величины (ξ,η),
если

f(x,y)=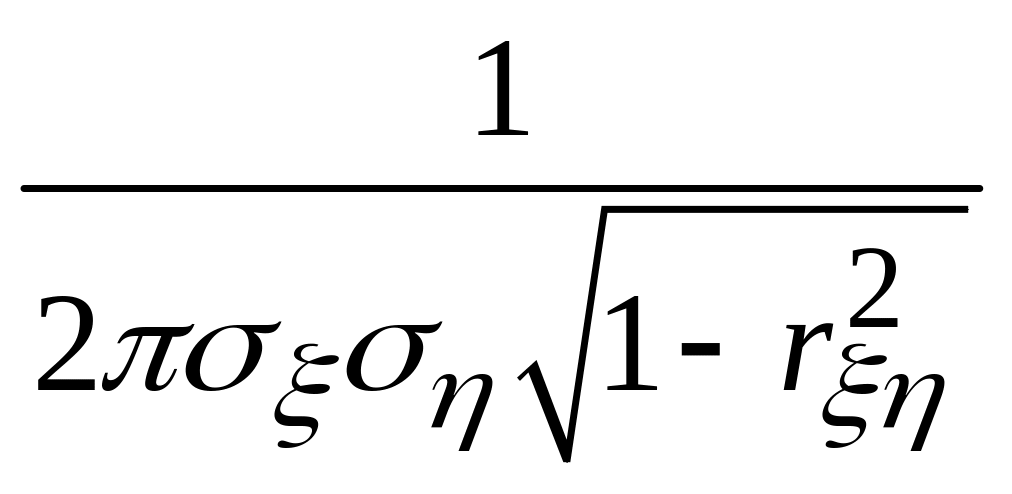
×
.

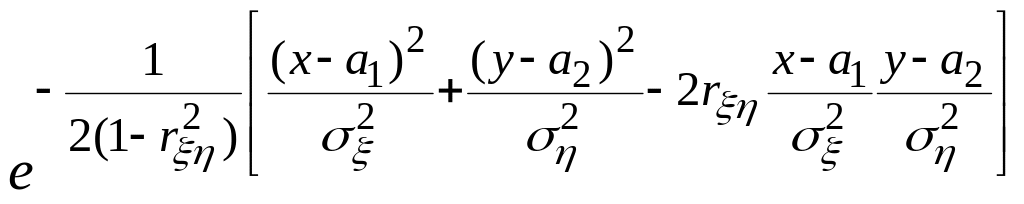
Нормальный
закон на плоскости определяется пятью
параметрами: a₁,a₂,σ₁,σ₂
и r.
Можно доказать, что эти параметры имеют
следующий вероятностный смысл: a₁,a₂–
математические ожидания, σ₁,σ₂
– средние квадратические отклонения, r
– коэффициент корреляции величин ξ
и η.

Убедимся
в том, что если составляющие двумерной
нормально распределенной случайной
величины некоррелированны, то они и
независимы. Действительно, пусть ξ
и η
некоррелированны. Тогда, полагая в

=0,
получим

f(x,y)=
×
=

=

=f₁(x)f₂(у).

Таким образом,
если составляющие нормально распределенной
случайной величины некоррелированны,
то плотность совместного распределения
системы равна произведению плотностей
распределения составляющих, а отсюда
и следует независимость составляющих.
Справедливо и обратное утверждение.

Итак, для нормально
распределенных составляющих двумерной
случайной величины понятия независимости
и некоррелированности равносильны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Одним из наиболее значимых параметров для анализа условного распределения является условное матожидание. Оно позволяет оценить наиболее вероятную область появления случайной величины по усреднённому её значению при некоторых сторонних условиях.

Определение 1

Чтобы задать условное матожидание появления некоторого события необходимо также наличие условия для появления этого события. При рассмотрении двумерной или многомерной случайной величины таким условием может выступать значение, которое принимает вторая случайная величина.

В этом случае принято обозначение:

M(Y/X=x)

Условное матожидание для случайной величины дискретного типа можно вычислить по следующей формуле:

$M(Y/X=x)=sum_{i=1}^n y_icdot p(y_i/x)$

Условное матожидание для случайной величины непрерывного типа определяется согласно следующему выражению:

$M(Y/X=x)=int_{-infty}^{+infty} ycdot f(y/x)dy$

Здесь f(x) —плотность вероятности Y при условии выполнения X=x.

Определение 2

Условное матожидание может быть определено и как функция от x. Такую функцию принято называть «функцией регрессии Y на X». Здесь используется обозначение:

$M(Y/x)=phi (x)$

Похожим же образом устанавливается условное матожидание и для X. В этом случае речь уже идёт о «функции регрессии X на Y». Используется обозначение:

$M(X/y)=psi (y)$

Пример 1

Найти параметр условного матожидания элемента Y двумерной случайной величины, если $X=x_1=1$, а сама величина является дискретной и задаётся следующим образом:

YX $x_1=1$ $x_2=3$ $x_3=4$ $x_4=8$

$y_1=3$ 0,15 0,06 0,25 0,04

$y_2=6$ 0,30 0,10 0,03 0,07

Вычислим значение вероятности событий, происходящих, в случае выполнения исхода $X=x_1$

$p(x_1)=0,15+0,30=0,45$

Далее найдём условные вероятности для событий с исходами $y_1$ и $y_2$. В зависимости от исхода $x_1$ получим следующие значения:

$p(y_1/x_1)=frac {p(x_1,y_1)}{p(x_1)}=frac{0,15}{0,45}=frac{1}{3}$

Теперь можно вычислить и математическое ожидание исхода события y при $X=x_1$:

$ M(Y/X=x_1) =sum_{i=1}^2 y_i cdot p(y_i/x_1) = y_1 cdot p(y_1/x_1)+y_2cdot p(y_2/x_1)= frac{3}{3} + frac{12}{3}= 1+4=5 $

Итак, результат вычислений показывает, что матожидание исхода Y при $X=x_1$: $ M(x)=5$.

Свойства условного матожидания

Условное математическое ожидание обладает набором свойств, соответствующим набору безусловного матожидания. С ним также можно осуществлять математические операции, которые позволяют лучше преобразовывать уравнения, при поиске решений прикладных задач.

Свойство 1

Матожидание взятое от константы, то есть величины постоянной, будет равно самой этой же величине.

$M(C)=C$

Свойство 2

Если берётся матожидание от случайной величины умноженной на постоянную, то данную постоянную можно вынести за обозначение матожидания.

$M(CX)=Cdot M(X)$

Свойство 3

Матожидание от сложения или вычитания двух независимых случайных величин, можно представить как сложение или вычитание самих матожиданий от этих величин, взятых по отдельности.

$M(Xpm Y)=M(X) pm M(Y)$

Свойство 4

Если берётся матожидание от двух случайных величин умноженных друг на друга, то его можно представить как умноженные друг на друга математические ожидания от данных величин взятые по отдельности.

$M(Xcdot Y)=M(X) cdot M(Y)$

Свойство 5

Матожидание от суммы или разности случайной величины и константы, постоянной величины, можно представить в виде суммы или разности самого матожидания от случайной величины и этой же константы.

$M(Xpm С)=M(X) pm С $

Если в системе случайные величины являются независимыми, то условное матожидание совпадает с безусловным.

236

проверенных автора готовы помочь в написании работы любой сложности

Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!

Пример 2

Пусть существует двухэлементная случайная величина непрерывного характера (,). Она задаётся плотностью вероятности:

$f(x,y)=frac{sinx cdot siny}{4}$.

В области $0leq xleqpi$ и $0leq yleqpi$, вне её значение плотности вероятности будет: f(x,y)=0.

Решение

Применим формулы подходящие для отыскания плотностей вероятности двуэлементных случайных величин:

$f_1(x)=int_{-infty}^{+infty} f(x,y)dy$

$f_2(y)=int_{-infty}^{+infty} f(x,y)dx$

С их помощью не трудно установить, что плотности вероятностей будут выражены следующим образом:

$f_1(x)=sin(x/2)$,

$f_2(y)=sin(y/2)$.

Для системы в целом плотность вероятностей совместная получается равной умноженным друг на друга плотностям вероятностей отдельно взятых случайных величин, входящих в систему. Поэтому данные случайные величины могут считать независимыми.

Пример 3

Для посещения казино игрок берёт с собой сумму денег m рублей. Вероятность, что за одну игру он остаётся в выигрыше на 1 рубль, составляет p. Вероятность, что игрок потеряет один рубль в одной игре составляет q=1-p. Если игрок остаётся без денег — проигрывает все свои накопления, то он покидает казино. Если же игрок приобретает сумму N, которая больше изначальной m, то игрок также уходит. Необходимо определить среднее время, в течении которого игра будет продолжаться.

Решение

Для удобства введём случайную величину t(m), значение которой будет соответствовать количеству партий, сыгранных в случае, когда используется первоначальная сумма денег m. При этом конечная сумма, при выигрыше которой игрок уходит из казино, является фиксированной и равной числу N.

Введём новое обозначение, пусть случайная величина $k_0$ получает значение 1 при выигрыше партии и значение 0 при проигрыше. Тогда мы можем записать выражение для математического ожидания количества сыгранных партий, она будет выражена как:

$Mt(m)=M(t(m))k_0=p(1+Mt(m+1))+q(1+Mt(m-1))=1+pMt(k+1)+qMt(k-1)$

Так как выполняется условие

$t(N)=t(0)=0$

То в результате преобразований при $pneq q$, получим следующее решение

$Mt(k)=frac{1}{p-q}left[ N cdot frac{(q/p)^m-1}{(q/p)^N-1} -mright]$

Источник

Помощь по математике. Решение задач и контрольных работ

Определения[править | править код]

УМО относительно σ-алгебры[править | править код]

УМО относительно семейства событий[править | править код]

УМО относительно случайной величины[править | править код]

Условная вероятность[править | править код]

Замечания[править | править код]

Основные свойства[править | править код]

Дополнительные свойства[править | править код]

УМО для дискретных величин[править | править код]

УМО для абсолютно непрерывных случайных величин[править | править код]

УМО в L2[править | править код]

См. также[править | править код]

§29. Ковариация. Коэффициент корреляции

Свойства условного матожидания

Вам также может понравиться

Ты как меня нашел скачать звук

Как найти ординату точки пересечения отрезка

Dying light как найти все чертежи

Добавить комментарий Отменить ответ

УМО в L²[править | править код]