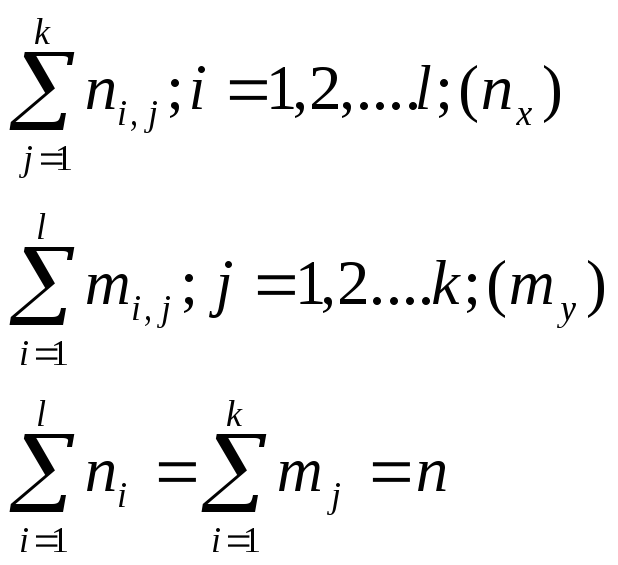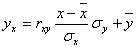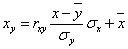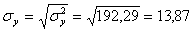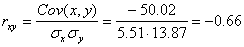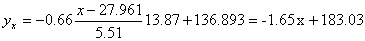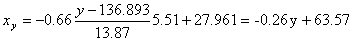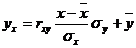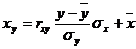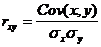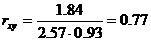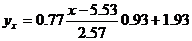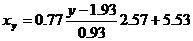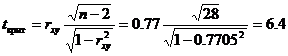Как найти условное среднее значение

Как найти условное среднее значение

При
рассмотрении многомерных случайных
величин рассматривались условные законы
распределения и их числовые характеристики:
математическое ожидание, дисперсия и
различные моменты. Оценками этих величин
служат их выборочные аналоги. Наиболее
важными являются условные математические
ожидания, вычисленные по выборке –
условные
средние.

Условное
среднее
–
среднее арифметическое значений
случайной величины Y,
наблюдавшихся при фиксированном значении
случайной величины X=
x.

Условное
среднее
–
среднее арифметическое значений
случайной величины X,
наблюдавшихся при фиксированном значении
случайной величины Y
=
y.

Напомним определение
уравнения регрессии:

условное
математическое ожидание
является
функциейx.

Эта
функция f
(x)называется
функцией
регрессии Y
на X,
а ее график – линией
регрессии.

Выборочный аналог
этого уравнения,,
называетсявыборочным
уравнением регрессии Y
на X,
функция–выборочной
функцией регрессии Y
на X,
ее график – выборочной
линией регрессии Y
на X.

Аналогично
определяются выборочные характеристики
и для регрессии X
на Y.

§ 6. Корреляционная таблица. Выборочные линии регрессии.

Пусть
в результате эксперимента для системы
(Х,Y)
получена выборка значений
.

Если
значения х
и
y
повторяются, то их группируют

Здесь

и
– наблюдаемые значения X
и
Y,
а
– частота появления пары значений.

Чаще
всего в этом случае данные организуют
в виде корреляционной
таблицы:

X

Y

…

…

…

…

…

….

….

…

…

Группируя данные
по значениям
или
:

по
данным корреляционной таблицы можно
составить законы распределения
составляющих (последняя строка и
последний столбец таблицы) и их средние
по выборки
и.

и
.

Для
наглядности данные таблицы изображают
графически. Каждую пару (xi,yj)изображают
точкой в системе координат (ХОY).
Частоту
,
с которой данная пара встречается в
таблице, изображают соответствующим
числом близко расположенных точек либо
пишут числовозле одной точки. Построенное таким
образом в системе координат изображение
корреляционной таблицы называютполем
корреляции.
Также возможно изображать
данные таблицы кругами, центр которых
находится в точке (xi,yj),
а диаметр (или площадь) пропорционален

.

Точка в системе
координат
(ХОY)
с координатами
называетсяцентром
рассеивания.

Можно
также составить условные законы
распределения, например Y
при Х=или Х приY=.

….

…..

Зная условные
законы распределения, можно найти
условные средние:

и т.п.Построим в
системе координат (ХОY)
точки

и соединим их
отрезками прямых. Полученную ломаную
называют

выборочной линией
регрессии Y
на X.

Если
распределения случайных величин X
и
(или) Y
заданы
интервальным
вариационным
рядом, то удобно перейти к вспомогательным
переменным, значения которых совпадают
с серединами интервалов.

Кроме
того, если варианты(значения
вариационного ряда) являются
равноотстоящими, т.е., образуют
арифметическую прогрессию с разностью
h,
бывает удобно перейти к условным
вариантам:

,

где C
ложный
нуль (новое
начало отсчета),

h –
шаг, т.е.
разность между двумя соседними
первоначальными вариантами (новая
единица
масштаба).

Если в качестве
ложного нуля взята какая-то из вариант

, то условные варианты- целые числа, что
упрощает вычисления

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
  • #
Источник

  • Редакция Кодкампа

17 авг. 2022 г.
читать 1 мин

Вы можете использовать следующий синтаксис для вычисления условного среднего значения в R:

mean(df[df$team == 'A', 'points'])

Это вычисляет среднее значение столбца «баллы» для каждой строки во фрейме данных, где столбец «команда» равен «А».

В следующих примерах показано, как использовать этот синтаксис на практике со следующим фреймом данных:

#create data frame
df <- data.frame(team=c('A', 'A', 'A', 'B', 'B', 'B'),
 points=c(99, 90, 93, 86, 88, 82),
 assists=c(33, 28, 31, 39, 34, 30))

#view data frame
df

 team points assists
1 A 99 33
2 A 90 28
3 A 93 31
4 B 86 39
5 B 88 34
6 B 82 30

Пример 1: Расчет условного среднего для категориальной переменной

В следующем коде показано, как вычислить среднее значение столбца «точки» только для строк во фрейме данных, где столбец «команда» имеет значение «А».

#calculate mean of 'points' column for rows where team equals 'A'
mean(df[df$team == 'A', 'points'])

[1] 94

Среднее значение в столбце «Очки» для строк, где «команда» равно «А», равно 94 .

Мы можем вручную проверить это, рассчитав среднее значение очков только для строк, где «команда» равна «А»:

  • Среднее количество баллов: (99 + 90 + 93) / 3 = 94

Пример 2. Вычисление условного среднего для числовой переменной

В следующем коде показано, как вычислить среднее значение столбца «помощь» только для строк во фрейме данных, где значение столбца «точки» больше или равно 90.

#calculate mean of 'assists' column for rows where 'points' >= 90
mean(df[df$points >= 90 , 'assists'])

[1] 30.66667

Среднее значение в столбце «ассисты» для строк, где «очки» больше или равны 90, составляет 30,66667 .

Мы можем вручную проверить это, рассчитав среднее значение очков только для строк, где «команда» равна «А»:

  • Среднее количество передач: (33 + 28 + 31) / 3 = 30,66667.

Дополнительные ресурсы

В следующих руководствах объясняется, как рассчитать другие средние значения в R:

Как рассчитать усеченное среднее в R
Как рассчитать среднее геометрическое в R
Как рассчитать средневзвешенное значение в R

Источник

Кроме линии регрессии, есть другой способ изучения той же зависимости — УСЛОВНОЕ СРЕДНЕЕ, то есть среднее при выполнении некоторого условия. Это среднее арифметическое значений результативного признака Y ПРИ УСЛОВИИ, что соответствующие значения факторного признака X попадают в заданный интервал.

Вот пример условного среднего: средний вес людей, у которых рост окажется в диапазоне от 160 до 170 см. Мы выбираем людей ростом от 160 до 170 см, измеряем их вес и находим среднее значение веса только по этой группе. Здесь рост — это факторный признак Х, а вес — это результативный признак Y. Мы получили средний «игрек», а условие определяли по «иксу».

На новом листе добавим интервалы группировки по X: нижние и верхние границы, а также среднее значение. Интервалы группировки выбираем точно так же, как описано в первой работе. Ссылка для скачивания пособия по первой работе приводится в конце данного выпуска.

В нашем примере возьмём 10 интервалов по 100 единиц, чтобы охватить диапазон значений от 1000 до 2000.

Для нахождения условного среднего можно использовать функцию

SUMIF

СУММЕСЛИ.

Функция позволяет вычислить сумму при выполнении заданного условия. Формат функции следующий:

SUMIF (range, criteria, [sum_range])

СУММЕСЛИ (диапазон; критерий; [диапазон_суммирования])

range — диапазон — диапазон ячеек;

criteria — критерий — условие;

sum_range — диапазон_суммирования — диапазон ячеек для суммирования. Если диапазон не указан, то суммируются значения из диапазона, указанного в первом аргументе.

Для определения средних значений фактора Х в каждом интервале группировки используем только два первых аргумента функции.

Рассмотрим примеры условных сумм — см. формулы.

Условные суммы

Первая формула вычисляет сумму значений фактора, не превышающих верхнюю границу первого интервала. Сюда попадут все значения из первого интервала, а также все точки, которые окажутся левее этого интервала.

Вторая формула определяет сумму значений фактора, попадающих во второй интервал.

В третьей формуле мы фиксируем номера строк для диапазона исходных данных с помощью символа $. Это позволит нам скопировать формулу и заполнить весь столбец.

Для упрощения расчётов мы определяем разность сумм значений, не превышающих верхние границы интервалов. В этом случае формулы получаются немного короче и понятнее. Мы уже использовали подобный приём в первой работе, когда определяли частоту попадания в интервал. Мы находили относительные частоты как разность соседних значений накопленной частоты.

Функция SUMIF

При вычислении среднего арифметического нужно поделить сумму значений на их количество.

Для определения количества элементов используем функцию

COUNTIF

СЧЕТЕСЛИ.

Формула для расчета условного среднего фактора Х получается довольно громоздкой — см. формулы.

Расчёт условного среднего

Изучите формулы и найдите следующие элементы:

— диапазон ячеек от А2 до А121 на листе 04;

— верхняя граница первого интервала на листе 05;

— верхняя граница второго интервала на листе 05.

Чтобы не запутаться, проведём наши расчёты по частям. Сначала найдём суммы и количества значений Х, не превышающих верхней границы. Затем определим разности соседних ячеек. Затем проведём деление и в результате получим среднее значение Х в каждом интервале группировки.

Вычисление условного среднего значения результативного признака Y немного сложнее. Здесь проверяется условие попадания факторного признака Х в интервал группировки, а сумма считается по столбцу результативного признака Y. Для этого используется третий аргумент функции SUMIF — см. формулу.

Условное среднее Y (X)

Для копирования формулы фиксируем номера строк с помощью знака $.

Вычисление условного среднего

После вычислений наносим линию условного среднего на диаграмму разброса. Для этого нам потребуется ломаная линия с маркерами точек.

Строим диаграмму разброса, как описано выше.

Выбираем второй ряд данных:

Select Data — Select Data Source — Add

Выбрать данные — Выбор источника данных — Добавить.

Добавляем новые данные для графика. В качестве значений x берём условные средние «иксы», а в качестве y — условные средние «игреки». На графике появляются новые точки.

Изменяем тип диаграммы: щёлкаем правой кнопкой по графику и выбираем комбинированный график:

Change Chart Type — Combo

Изменить тип диаграммы — Комбинированная.

Для исходных данных оставляем диаграмму разброса:

Scatter

Точечная.

Для условного среднего выбираем ломаную линию:

Scatter with Straight Lines

Точечная с прямыми отрезками и маркерами.

Для использовани единого масштаба на графиках снимаем выбор пункта:

Secondary Axis

Вспомогательная ось.

Если на графике будет две вертикальных оси, то будет свой масштаб для каждого набора данных. Такие графики будет невозможно сравнивать. Нам нужен общий, единый масштаб.

Комбинация графиков

В процессе настройки графиков можно видеть, как меняется изображение. При выборе данных для графиков мы не указывали названия рядов, поэтому они названы по умолчанию Series1 и Series2. Пока на графике не так много данных, это не доставляет неудобств. В следующей работе всё-таки придётся задать имена для каждого набора данных, чтобы легче было работать с несколькими графиками.

Как и раньше, настраиваем масштаб, заголовки, цвета. График готов.

Условное среднее на диаграмме разброса

Источник

Условные средние. Выборочные уравнения регрессии

Глава 4. Теория линейной корреляции

Функциональная, статистическая и корреляционная зависимости

Во многих задачах требуется установить и оценить зависимость изучаемой случайной величины Y от одной или нескольких других величин. Рассмотрим сначала зависимость Y от одной случайной (или неслучайной) величины X, а затем от нескольких величин.

Две случайные величины могут быть связаны либо функциональной зависимостью, либо зависимостью другого рода, называемой статистической, либо быть независимыми.

Строгая функциональная зависимость реализуется редко, так как обе величины или одна из них подвержены еще действию случайных факторов, причем среди них могут быть и общие для обеих величин. В этом случае возникает статистическая зависимость.

Например, если Y зависит от случайных факторов Z1, Z2, V1, V2, a X зависит от случайных факторов Z1, Z2, U1,то между Y и X имеется статистическая зависимость, так как среди случайных факторов есть общие, а именно: Zlи Z2.

Статистической называют зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, статистическая зависимость проявляется в том, что при изменении одной из величин изменяется среднее значение другой; в этом случае статистическую зависимость называют корреляционной.

Приведем пример случайной величины Y, которая не связана с величиной X функционально, а связана корреляционно. Пусть Y – урожай зерна, X – количество удобрений. С одинаковых по площади участков земли при равных количествах внесенных удобрений снимают различный урожай, то есть Y не является функцией от X. Это объясняется влиянием случайных факторов (осадки, температура воздуха и другие). Вместе с тем, как показывает опыт, среднийурожай является функцией от количества удобрений, то есть Y связан с X корреляционной зависимостью.

Условные средние. Выборочные уравнения регрессии

В качестве оценок условных математических ожиданий принимают условные средние, которые находят по данным наблюдений (по выборке).

Условным средним называют среднее арифметическое наблюдавшихся значений Y, соответствующих X = х. Например, если при х1 = 2 величина Y приняла значения у1 = 5, у2 = 6, у3=10, то условное среднее = (5 + 6+10)/3 = 7.

Аналогично определяется условное среднее .

Условным средним называют среднее арифметическое наблюдавшихся значений X, соответствующих Y = y.

Условное математическое ожидание есть функция от x , которую называют функцией регрессии Y на X. Условное математическое ожидание называют функцией регрессии X на Y.

Отсюда следует, что его оценка, то есть условное среднее ,также функция от х;обозначив эту функцию через f*(х),получим уравнение . Это уравнение называют выборочным уравнением регрессии Y на Х;функцию f*(х)называютвыборочной регрессией Y на X, а ее график – выборочной линией регрессии Y на X.

Аналогично уравнение называют выборочным уравнением регрессии X на Y; функцию j*(у)называют выборочной регрессией X на Y, a ее график – выборочной линией регрессии X на Y.

Дата добавления: 2015-01-12 ; просмотров: 45 | Нарушение авторских прав

Выборочное уравнение регрессии

Две случайные величины могут быть связаны либо функциональной зависимостью, либо статистической зависимостью, либо быть независимыми. Строгая функциональная зависимость реализуется редко, так как обе или одна из двух величин подвержены еще воздействию случайных факторов. Причем среди этих факторов могут быть и общие для обеих величин, т.е. воздействующие на обе случайные величины. В этих случаях возникает статистическая зависимость.

Статистическойназывается зависимость, при которой изменение одной из величин влечет изменение распределения другой. В частности, изменение одной из величин вызывает изменение среднего значения другой. В этом случае статистическая зависимость называется корреляционной.Например, связь между количеством удобрений и урожаем, между вложенными средствами и прибылью.

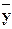
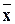
Среднее арифметическое наблюдавшихся значений случайной величины Y , соответствующих значению X=x, называется условным средним xи является точечной оценкой математического ожидания. Аналогично определяется условное среднее y .

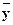
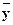
Условное математическое ожидание M ( Y | x )является функцией отx,следовательно, его оценка, т.е. условное среднее x,также функция от x:

x = f*(x).

Это уравнение называется выборочным уравнением регрессии Y на X. Функцию f*(x)называют выборочной регрессией, а ее график – выборочной линией регрессии Y на X . Аналогично уравнение

y = φ * (y),

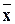
функцию φ * (y) и ее график называют выборочным уравнением регрессии, выборочной регрессией и выборочной линией регрессии X на Y .

Отыскание параметров функций f*(x)и φ * (y), если вид их известен, оценка тесноты связи между величинами X и Y – задачи корреляционного анализа.Задачей регрессионного анализа есть оценка параметров функции регрессии βi и остаточной дисперсии σост 2 .

Остаточная дисперсия – та часть рассеивания Y , которую нельзя объяснить действием X. σост 2 может служить для оценки точности подбора функции регрессии и полноты набора признаков, включенных в анализ. Вид зависимости g(x) выбирают, исходя из характера поля корреляции и природы процесса.

Оценкой коэффициента линейной регрессии β является выборочный коэффициент регрессии Y на X ryx. Значения параметра ryxи параметра b уравнения прямой линии регрессии

Y = ryx x + b

подбираются таким образом, чтобы точки (x1,y1), (x2,y2),…,(xn,yn), построенные по данным наблюдений, на плоскости xOy лежали как можно ближе к прямой линии регрессии. Это равносильно требованию, чтобы сумма квадратов отклонений функции Y(xi) от yi была минимальной. В этом суть МНК.

Выборочное уравнение прямой линии регрессии Y на X может быть записано в таком виде:

x – = rв sy/sx (x – ) ,

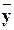
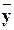
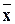
где sx и sy – выборочные средние квадратические отклонения X и Y , а

rв = –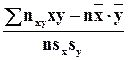

выборочный коэффициент корреляции, вычисленный по сгруппированным данным. Здесь nxy – частота пары вариант (x,y). Аналогично находят выборочное уравнение прямой линии регрессии X на Y :

y – = rв sx/sy (y – )

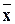
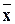
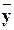
Для того, чтобы установить, соответствует ли найденная по выборке математическая модель зависимости между Y и X статистическим данным, следует оценить значимость коэффициентов регрессии и значимость уравнения регрессии.

Проверить значимость коэффициентов регрессии означает установить, достаточна ли величина оценки для обоснованного вывода о том, что коэффициент регрессии отличен от нуля. Выдвигают гипотезу H0 : коэффициент регрессии равен нулю β =0. Проверку гипотезы H0 осуществляют с помощью распределенной по закону Стьюдента статистики

t = │b / sb│

где b – оценка коэффициента регрессии, а sb – оценка его среднего квадратического отклонения, другими словами стандартная ошибка оценки. Если │t │≥ tкр ( α, k ), нулевую гипотезу о равенстве нулю коэффициента регрессии отвергают, и коэффициент считают значимым. При │t │

b – t(α,k)sb 2 – коэффициент детерминации, n – объем выборки, k – количество факторных признаков.

Корреляционная таблица

Пример 1 . По данной корреляционной таблице построить прямые регрессии с X на Y и с Y на X . Найти соответствующие коэффициенты регрессии и коэффициент корреляции между X и Y .

Читайте также:

  1. A) такие уравнения, которые имеют одни и те же корни.
  2. D. Безусловные местные рефлексы.
  3. IV. Практическое задание №3. Модель множественной регрессии
  4. а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
  5. Алгоритм 2. Расчет параметров уравнения парной линейной регрессии
  6. б) построить уравнение эмпирической линии регрессии и случайные точки выборки
  7. Безусловные рефлексы, их характеристика и классификация
  8. Векторные уравнения электростатики второго порядка
  9. Взаимное расположение двух прямых на плоскости.Рассмотрим две прямые, задаваемы уравнениями и .
  10. Влияние изменения масштаба измерения переменных на коэффициенты регрессии
y/x 15 20 25 30 35 40
100 2 2
120 4 3 10 3
140 2 50 7 10
160 1 4 3
180 1 1

Решение:
Уравнение линейной регрессии с y на x будем искать по формуле

а уравнение регрессии с x на y, использовав формулу:

где x x , y – выборочные средние величин x и y, σx, σy – выборочные среднеквадратические отклонения.
Находим выборочные средние:
x = (15(1 + 1) + 20(2 + 4 + 1) + 25(4 + 50) + 30(3 + 7 + 3) + 35(2 + 10 + 10) + 40(2 + 3))/103 = 27.961
y = (100(2 + 2) + 120(4 + 3 + 10 + 3) + 140(2 + 50 + 7 + 10) + 160(1 + 4 + 3) + 180(1 + 1))/103 = 136.893
Выборочные дисперсии:
σ 2 x = (15 2 (1 + 1) + 20 2 (2 + 4 + 1) + 25 2 (4 + 50) + 30 2 (3 + 7 + 3) + 35 2 (2 + 10 + 10) + 40 2 (2 + 3))/103 – 27.961 2 = 30.31
σ 2 y = (100 2 (2 + 2) + 120 2 (4 + 3 + 10 + 3) + 140 2 (2 + 50 + 7 + 10) + 160 2 (1 + 4 + 3) + 180 2 (1 + 1))/103 – 136.893 2 = 192.29
Откуда получаем среднеквадратические отклонения:
и
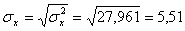
Определим коэффициент корреляции:

где ковариация равна:
Cov(x,y) = (35•100•2 + 40•100•2 + 25•120•4 + 30•120•3 + 35•120•10 + 40•120•3 + 20•140•2 + 25•140•50 + 30•140•7 + 35•140•10 + 15•160•1 + 20•160•4 + 30•160•3 + 15•180•1 + 20•180•1)/103 – 27.961 • 136.893 = -50.02
Запишем уравнение линий регрессии y(x):

и уравнение x(y):

Построим найденные уравнения регрессии на чертеже, из которого сделаем следующие вывод:
1) обе линии проходят через точку с координатами (27.961; 136.893)
2) все точки расположены близко к линиям регрессии.

Пример 2 . По данным корреляционной таблицы найти условные средние y и x . Оценить тесноту линейной связи между признаками x и y и составить уравнения линейной регрессии y по x и x по y . Сделать чертеж, нанеся его на него условные средние и найденные прямые регрессии. Оценить силу связи между признаками с помощью корреляционного отношения.
Корреляционная таблица:

X / Y 2 4 6 8 10
1 5 4 2 0 0
2 0 6 3 3 0
3 0 0 1 2 3
5 0 0 0 0 1

Уравнение линейной регрессии с y на x имеет вид:

Уравнение линейной регрессии с x на y имеет вид:

найдем необходимые числовые характеристики.
Выборочные средние:
x = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 5.53
y = (2(5) + 4(4 + 6) + 6(2 + 3 + 1) + 8(3 + 2) + 10(3 + 1) + )/30 = 1.93
Дисперсии:
σ 2 x = (2 2 (5) + 4 2 (4 + 6) + 6 2 (2 + 3 + 1) + 8 2 (3 + 2) + 10 2 (3 + 1))/30 – 5.53 2 = 6.58
σ 2 y = (1 2 (5 + 4 + 2) + 2 2 (6 + 3 + 3) + 3 2 (1 + 2 + 3) + 5 2 (1))/30 – 1.93 2 = 0.86
Откуда получаем среднеквадратические отклонения:
σx = 2.57 и σy = 0.93
и ковариация:
Cov(x,y) = (2•1•5 + 4•1•4 + 6•1•2 + 4•2•6 + 6•2•3 + 8•2•3 + 6•3•1 + 8•3•2 + 10•3•3 + 10•5•1)/30 – 5.53 • 1.93 = 1.84
Определим коэффициент корреляции:


Запишем уравнения линий регрессии y(x):

и вычисляя, получаем:
yx = 0.28 x + 0.39
Запишем уравнения линий регрессии x(y):

и вычисляя, получаем:
xy = 2.13 y + 1.42
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (5.53; 1.93) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.

По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=30-m-1 = 28 находим tкрит:
tкрит (n-m-1;α/2) = (28;0.025) = 2.048
где m = 1 – количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически – значим.

Пример 3 . Распределение 50 предприятий пищевой промышленности по степени автоматизации производства Х (%) и росту производительности труда Y (%) представлено в таблице. Необходимо:
1. Вычислить групповые средние i и j x y, построить эмпирические линии регрессии.
2. Предполагая, что между переменными Х и Y существует линейная корреляционная зависимость:
а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений;
б) вычислить коэффициент корреляции; на уровне значимости α= 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными Х и Y;
в) используя соответствующее уравнение регрессии, оценить рост производительности труда при степени автоматизации производства 43%.
Скачать решение

Пример . По корреляционной таблице рассчитать ковариацию и коэффициент корреляции, построить прямые регрессии.

Пример 4 . Найти выборочное уравнение прямой Y регрессии Y на X по данной корреляционной таблице.
Решение находим с помощью калькулятора.
Скачать
Пример №4

Пример 5 . С целью анализа взаимного влияния прибыли предприятия и его издержек выборочно были проведены наблюдения за этими показателями в течение ряда месяцев: X – величина месячной прибыли в тыс. руб., Y – месячные издержки в процентах к объему продаж.
Результаты выборки сгруппированы и представлены в виде корреляционной таблицы, где указаны значения признаков X и Y и количество месяцев, за которые наблюдались соответствующие пары значений названных признаков.
Решение.
Пример №5
Пример №6
Пример №7

Пример 6 . Данные наблюдений над двумерной случайной величиной (X, Y) представлены в корреляционной таблице. Методом наименьших квадратов найти выборочное уравнение прямой регрессии Y на X. Построить график уравнения регрессии и показать точки (x;y)б рассчитанные по таблице данных.
Решение.
Скачать решение

Пример 7 . Дана корреляционная таблица для величин X и Y, X- срок службы колеса вагона в годах, а Y – усредненное значение износа по толщине обода колеса в миллиметрах. Определить коэффициент корреляции и уравнения регрессий.

X / Y 0 2 7 12 17 22 27 32 37 42
0 3 6 0 0 0 0 0 0 0 0
1 25 108 44 8 2 0 0 0 0 0
2 30 50 60 21 5 5 0 0 0 0
3 1 11 33 32 13 2 3 1 0 0
4 0 5 5 13 13 7 2 0 0 0
5 0 0 1 2 12 6 3 2 1 0
6 0 1 0 1 0 0 2 1 0 1
7 0 0 1 1 0 0 0 1 0 0

Решение.
Скачать решение

Пример 8 . По заданной корреляционной таблице определить групповые средние количественных признаков X и Y. Построить эмпирические и теоретические линии регрессии. Предполагая, что между переменными X и Y существует линейная зависимость:

  1. Вычислить выборочный коэффициент корреляции и проанализировать степень тесноты и направления связи между переменными.
  2. Определить линии регрессии и построить их графики.

Скачать

[spoiler title=”источники:”]

http://megalektsii.ru/s73693t1.html

http://math.semestr.ru/math/corel.php

[/spoiler]

Источник

Добавить комментарий