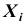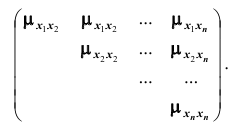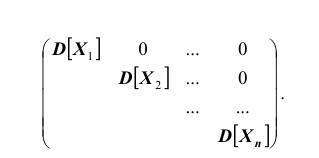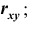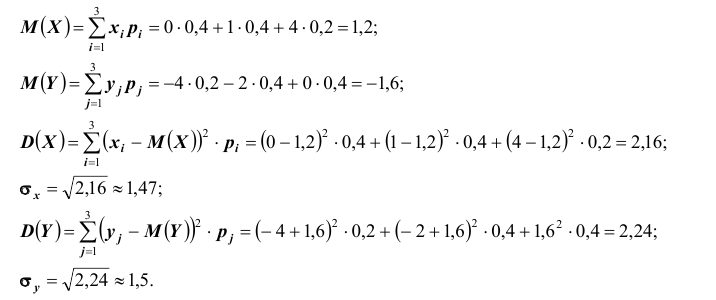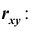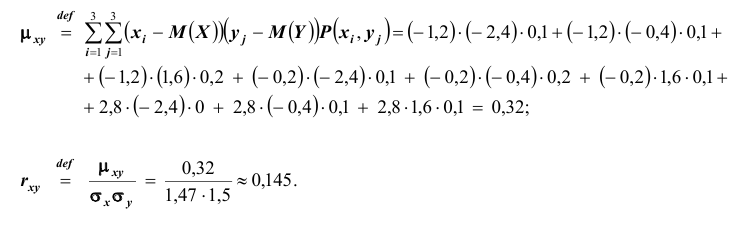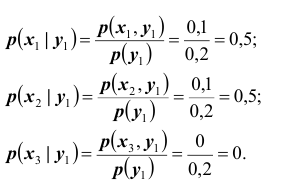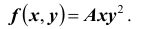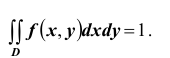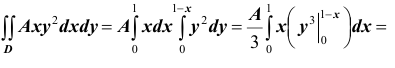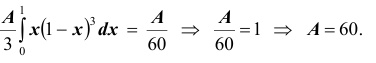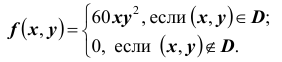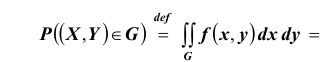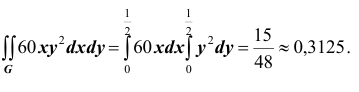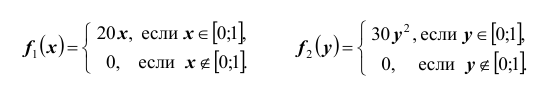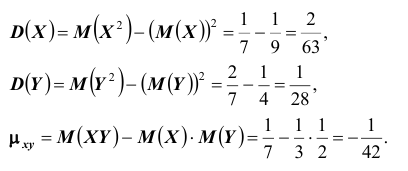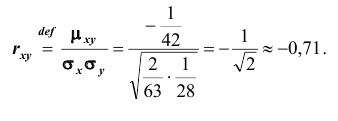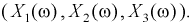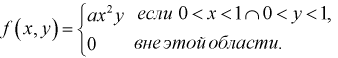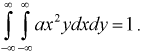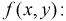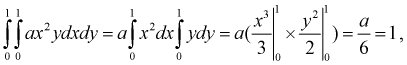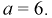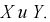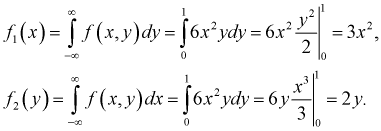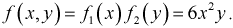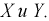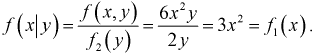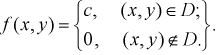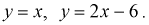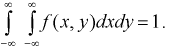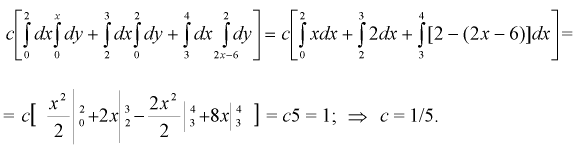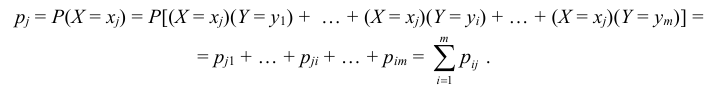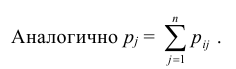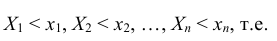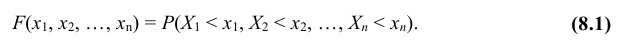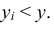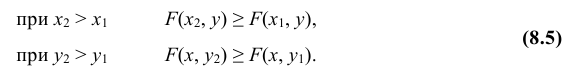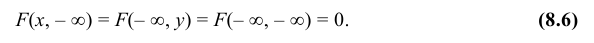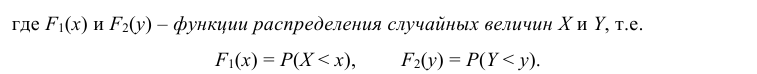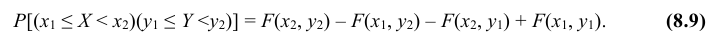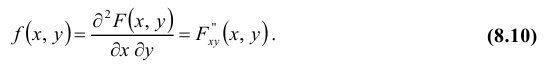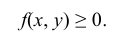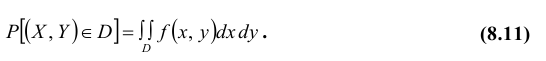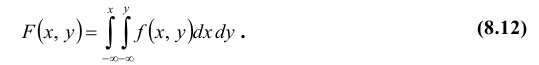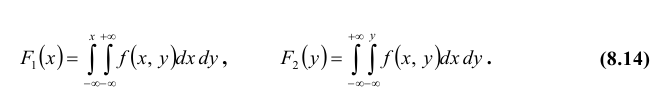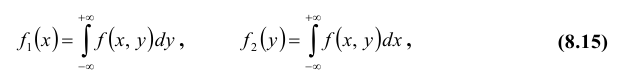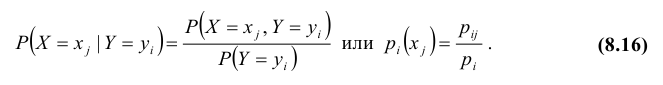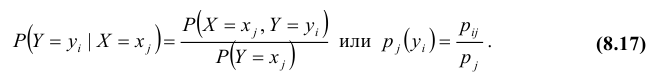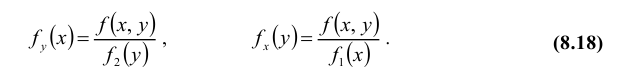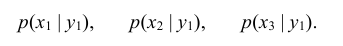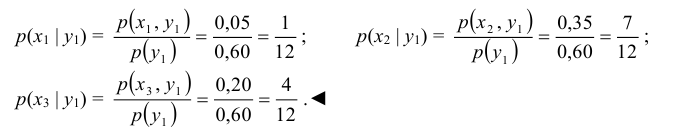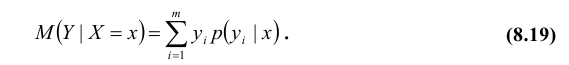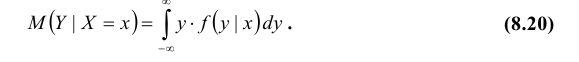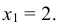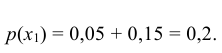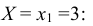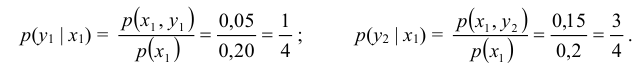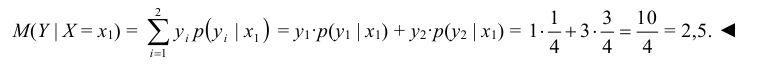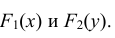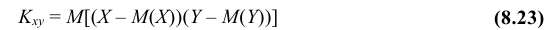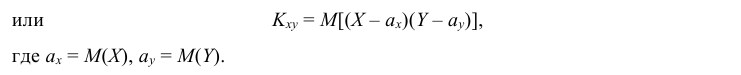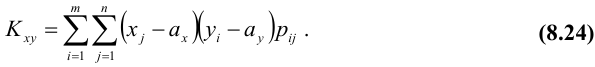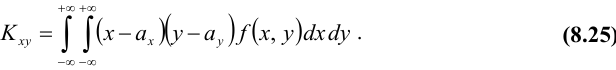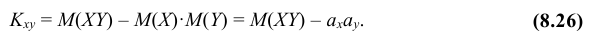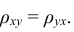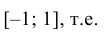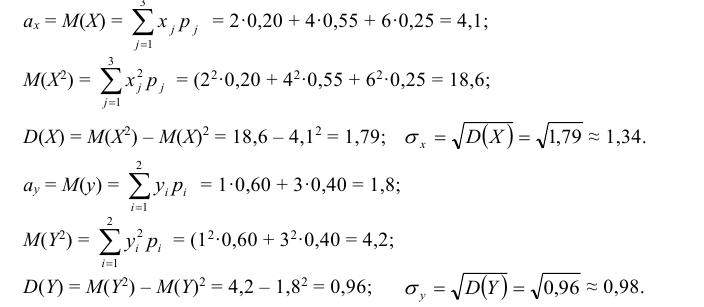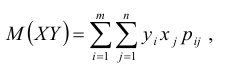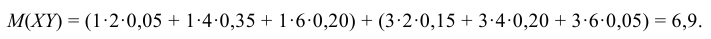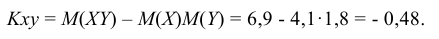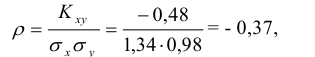Усло́вное распределе́ние в теории вероятностей — это распределение случайной величины при условии, что другая случайная величина принимает определённое значение.
Определения[править | править код]
Будем предполагать, что задано вероятностное пространство 
Дискретные случайные величины[править | править код]
Пусть 





,
где 



Абсолютно непрерывные случайные величины[править | править код]
Пусть 







называется усло́вной пло́тностью вероя́тности случайной величины 

Свойства условных распределений[править | править код]
- Условные функции вероятности и условные плотности вероятности являются функциями вероятности и плотностями вероятности соответственно, то есть они удовлетворяют всем необходимым условиям. В частности,
-
,
,
и
- Справедливы формулы полной вероятности:
-
,
.
или
почти всюду на
.
Условные вероятности[править | править код]
Дискретные случайные величины[править | править код]
Если 

.
Абсолютно непрерывные случайные величины[править | править код]
Если 

.
Замечание. Условная вероятность в левой части равенства не может быть определена классическим способом, так как 
Условные математические ожидания[править | править код]
Дискретные случайные величины[править | править код]
.
.
Абсолютно непрерывные случайные величины[править | править код]
.
.
См. также[править | править код]
- Условное матожидание
77
Внастоящем разделе вводится имеющее существенное значение в теории оценивания понятие условной (апостериорной) ф.п.р.в. и рассматривается правило вычисления параметров условной гауссовской плотности двух векторов, при условии, что один из них зафиксирован. Обсуждается весьма важный при решении задач оценивания пример нахождения параметров условной гауссовской плотности, а также задача регрессии, имеющая тесную связь с байесовскими задачами оценивания, которые рассматриваются в главе 2.
1.4.1.Формулы Байеса. Условные математическое ожидание и матрица ковариаций
Пусть заданы два случайных вектора x и y , для которых будем полагать известной
совместную ф.п.р.в. fx,y (x, y) . Осуществляя интегрирование этой функции по x или y , можем
получить согласно (1.2.5) соответственно ф.п.р.в. fy ( y) и f x (x) , определяющие
статистические свойства для каждого вектора по отдельности. При независимости векторовx и y
fx,y (x, y) = fx (x) fy ( y) .
В более общем случае справедлива формула умножения плотностей вероятности, которая
|
записывается как |
|||
|
fx,y (x, y) = f |
(x / y) fy ( y) = f ( y / x) fx (x). |
(1.4.1) |
|
|
Входящие в эти соотношения плотности |
f (x / y) |
и f ( y / x) определяют статистические |
|
|
свойства векторов x и y при условии, что вектор, |
стоящий справа от черты фиксирован. |
Поэтому эти плотности называются условными плотностями распределения вероятности или просто условными плотностями. При решении задач оценивания условные плотности f (x / y) и f ( y / x) также называют апостериорными плотностями, тем самым
подчеркивается тот факт, что эти плотности соответствуют апостериорной ситуации, т.е. такой, при которой один из векторов, связанный с оцениваемым вектором, фиксируется. В этом
|
случае исходные плотности f x (x) , fy ( y) |
принято называть априорными. Из соотношения |
||||||
|
(1.4.1) следует, что |
|||||||
|
f (x / y) = |
fx,y (x, y) |
= |
fx,y (x, y) |
, |
(1.4.2) |
||
|
∫ |
fx,y (x, y)dx |
fy ( y) |
|||||
а
78
|
f ( y / x) = |
fx,y (x, y) |
= |
fx,y (x, y) |
(1.4.3) |
||
|
∫ |
fx,y (x, y)dy |
fx (x) |
||||
Соотношения (1.4.2), (1.4.3) известны как – формулы Байеса. Они обеспечивают возможность нахождения условных плотностей по известной совместной плотности fx,y (x, y) .
Из них, в частности, следует, что при независимости векторов x и y условные и априорные ф.п.р.в. между собой совпадают.
Согласно (1.4.2) условную плотность формально можно получить в два приема. Сначала в совместной плотности fx,y (x, y) фиксируется значение y , т.е. fx,y (x, y = y* ) . Относительно x
функция fx,y (x, y = y* ) будет пропорциональна условной плотности, т.е.
|
fx,y (x, y = y*) f (x / y = y* ) . Иными словами, условная плотность как функция x |
подобна |
|||
|
совместной ф.п.р.в. при |
фиксированном значении |
y . |
Далее для того, чтобы |
функция |
|
fx,y (x, y = y* ) приобрела |
свойства ф.п.р.в., необходимо, |
обеспечить выполнение |
условия |
|
|
нормировки (1.2.4). Для этого функцию fx,y (x, y = y* ) |
требуется разделить на независящую от |
x величину, представляющую собой интеграл от fx,y (x, y = y* ) по аргументу x . Полученная в результате величина совпадет с fy ( y = y* ) , в силу условия согласованности (1.2.5).
Математическое ожидание
xˆ( y) = ∫x f (x / y)dx
и матрица ковариаций
P x / y = ∫(x − xˆ( y))(x − xˆ( y))T f (x / y)dx ,
соответствующие f (x / y) , называют условным математическим ожиданием и условной матрицей ковариаций. В случае, когда речь идет о скалярной с.в., используют понятие
условной дисперсии.
Условные плотности распределения обладают теми же свойствами, что и обычные плотности. В частности, если рассмотреть плотность для трех векторов fx,y,z (x, y, z) , то,
привлекая условие согласованности (1.2.5), можно записать следующие равенства:
|
f (x / z) = ∫ f (x, y / z)dy; |
(1.4.4) |
|
f (x / z) = ∫ f (x / y, z) f ( y / z)dy. |
(1.4.5) |
Выражения (1.4.4), (1.4.5) удобно использовать в случае необходимости исключения аргументов, стоящих слева и справа от черты в условной плотности [1.7].

79
1.4.2 Правила нахождения параметров условной гауссовской плотности
Получим соотношения, позволяющие находить параметры условной гауссовской плотности распределения. Предположим, что совместная ф.п.р.в. двух гауссовских векторов
|
x и y , размерности n и m имеет вид |
||||||||||||||||||||||||||
|
fx,y (x, y) = N |
(x т , y т )т; (x т , y т )т , P |
, |
(1.4.6) |
|||||||||||||||||||||||
|
где |
||||||||||||||||||||||||||
|
P x |
P xy |
|||||||||||||||||||||||||
|
P = |
P y |
. |
||||||||||||||||||||||||
|
(P xy )т |
||||||||||||||||||||||||||
|
Ясно, что для каждого вектора по отдельности для ф.п.р.в. справедливо представление |
||||||||||||||||||||||||||
|
f x (x) = N (x; x, P x ), |
(1.4.7) |
|||||||||||||||||||||||||
|
fy ( y) = N (y; y, P y ). |
(1.4.8) |
|||||||||||||||||||||||||
|
Найдем параметры условной плотности распределения вероятности |
f (x / y) , |
полагая |
||||||||||||||||||||||||
|
фиксированным значение вектора |
y . |
Предварительно |
запишем |
выражение |
для |
обратной |
||||||||||||||||||||
|
матрицы |
||||||||||||||||||||||||||
|
P−1 |
A |
B |
||||||||||||||||||||||||
|
= |
т |
, |
(1.4.9) |
|||||||||||||||||||||||
|
B |
C |
|||||||||||||||||||||||||
|
В соответствии с правилами обращения блочных матриц можно записать [1.9, с107] |
||||||||||||||||||||||||||
|
x |
− P |
xy |
(P |
y |
−1 |
P |
yx |
−1 |
x |
−1 |
+ (P |
x −1 |
P |
xy |
CP |
yx |
(P |
x |
−1 |
,(1.4.10) |
||||||
|
A = P |
) |
= (P |
) |
) |
) |
|||||||||||||||||||||
B = −AP xy (P y )−1 = −(P x )−1 P xy C ,
|
y |
− P |
yx |
(P |
x |
−1 |
P |
xy |
−1 |
y |
−1 |
+ (P |
y |
−1 |
P |
yx |
AP |
xy |
(P |
y |
−1 |
. |
|
|
C = P |
) |
= (P |
) |
) |
) |
|||||||||||||||||
Используя (1.4.2) с учетом (1.4.6) и (1.4.8) можем записать
|
т |
т |
P |
x |
P |
xy |
|||||||||||||
|
N |
(x т , y т ) ; (x т , y |
т ) |
, |
|||||||||||||||
|
(P xy )т |
P y |
|||||||||||||||||
|
f (x / y) = |
. |
|||||||||||||||||
|
N ( y; y, P y ) |
||||||||||||||||||
|
Это выражение нетрудно преобразовать к виду [1.9] |
||||||||||||||||||
|
1 |
1 |
, |
||||||||||||||||
|
f (x / y) = |
exp − |
J (x, y) |
||||||||||||||||
|
2 |
||||||||||||||||||
|
(2π)n / 2 |
P |
|||||||||||||||||
|
P y |
||||||||||||||||||
(1.4.11)
(1.4.12)
(1.4.13)

|
80 |
||||||
|
в котором |
||||||
|
J (x, y) = [(x − x)T ( y − y)T ] A |
B |
y |
−1 |
x − x |
. |
|
|
T |
C − (P |
) |
||||
|
B |
( y − y) |
Учитывая (1.4.11), (1.4.12), можем записать
|
J (x, y) = [(x − x)т , ( y − y)т ] A |
B |
y |
−1 |
(x − x) |
= |
||||||||||||||||||||||
|
T |
C − |
(P |
) |
||||||||||||||||||||||||
|
B |
( y − y) |
||||||||||||||||||||||||||
|
= (x − x)т A(x − x) + (x − x)т B( y − y) + ( y − y)т B т (x − x) + ( y − y) |
т C − (P y )−1 ( y − |
||||||||||||||||||||||||||
|
= (x − x)т A(x − x) + 2(x − x)т AP xy (P y )−1 ( y − y) + ( y − y)т (P y )−1 P yx AP xy |
(P y )−1 ( y |
||||||||||||||||||||||||||
|
= |
xy |
(P |
y |
−1 |
т |
xy |
(P |
y |
−1 |
||||||||||||||||||
|
(x − x) − P |
) |
( y − y) |
A (x − x) − P |
) |
( y − y) . |
||||||||||||||||||||||
|
Отсюда следует, что |
|||||||||||||||||||||||||||
|
J (x, y) = (x − xˆ)т A(x − xˆ) , |
|||||||||||||||||||||||||||
|
ˆ = |
x |
+ |
P |
xy |
(P |
y −1 |
( y |
− |
y) . |
||||||||||||||||||
|
где x |
) |
Преобразуем теперь первый сомножитель в (1.4.13). Запишем
|
P x |
P xy |
−1 |
xy |
En |
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x |
xy |
y |
yx |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P = |
= P |
− |
P |
(P |
) |
P |
P |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
−1 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(P xy )т |
P y |
0 |
P y |
(P y ) |
P yx |
Em |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Отсюда с очевидностью получаем |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
и таким образом |
P |
= |
P x − P xy (P y )−1 P yx |
P y |
, |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P |
− P xy (P y )−1 P yx |
. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
= |
P x |
(1.4.15) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P y |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
f (x / y) является |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Анализ соотношений (1.4.13)-(1.4.15) показывает, что условная плотность |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
гауссовской, т.е. f (x / y) |
= |
ˆ |
x / y |
), |
а |
ее |
параметры |
определяются |
с помощью |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
N (x; x( y), P |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
следующих соотношений |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
ˆ |
= |
x |
+ |
P |
xy |
(P |
y |
−1 |
( y |
− |
y) , |
(1.4.16) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
x( y) |
) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
P x / y |
= P x |
− P xy (P y )−1 (P xy )т . |
(1.4.17) |
Соотношения (1.4.16), (1.4.17) определяют правило нахождения параметров условной гауссовской плотности для двух совместно гауссовских векторов.
1.4.3 Примеры нахождения параметров условной гауссовской плотности

81
Конкретизируем полученные в предыдущем подразделе выражения для двух примеров. Пример 1.4.1. Пусть задан двумерный центрированный гауссовский случайный вектор
x = (x1 , x2 )т с матрицей ковариаций вида (1.2.14). Требуется найти параметры условной гауссовской плотности для первой его компоненты в предположении, что вторая компонента зафиксирована.
С учетом (1.2.14), (1.2.15), (14.16), (1.4.17) можно записать следующие соотношения для условного математического ожидания и условной дисперсии
|
xˆ = r |
σ1 |
x |
, |
||||||||||||||||||||||
|
1 |
σ |
2 |
2 |
||||||||||||||||||||||
|
σ12усл |
=σ12 (1− r 2 ) , |
||||||||||||||||||||||||
|
т.е. |
|||||||||||||||||||||||||
|
1 |
1 |
σ1 |
2 |
||||||||||||||||||||||
|
exp − |
. |
||||||||||||||||||||||||
|
f (x |
/ x |
2 |
) |
= |
x |
− r |
x |
2 |
|||||||||||||||||
|
2 |
2 |
2 |
|||||||||||||||||||||||
|
1 |
σ |
2π(1 − r |
) |
2(1 − r |
1 |
σ2 |
|||||||||||||||||||
|
1 |
)σ1 |
||||||||||||||||||||||||
|
На Рис. 1.4.1 |
представлены графики условных плотностей приσ1 = σ2 =1 |
при различных |
|||||||||||||||||||||||
|
значениях r и |
x2 =1 . Из графиков следует, |
что при увеличении коэффициента корреляции |
условная дисперсия уменьшается. Это вполне закономерно, поскольку коэффициент корреляции отражает степень статистической зависимости одной величины относительно другой. Чем больше эта зависимость, тем существеннее уменьшается условная дисперсия по
|
σ1 |
||||||||||
|
f (x |
/ x |
x − |
x |
|||||||
|
сравнению с априорной. Нетрудно заметить, что при r →1 , |
2 |
) → δ |
2 |
. |
||||||
|
1 |
1 |
σ2 |
||||||||
f(x1/ x2)
2
1.5
|
1 |
r=0.95 |
||||||||
|
0.5 |
r=0.7 |
||||||||
|
r=0 |
|||||||||
|
0 |
-3 |
-2 |
-1 |
0 |
1 |
2 |
3 |
4 |
|
|
-4 |
x1 |
||||||||
Рис.1.4.1 Графики гауссовской условной плотности распределения при различных значениях нормированного коэффициента корреляции. ♦
82
Пример 1.4.2. Пусть так же, как и в примере 1.3.5, для двух векторов x и v размерности n и m определены математическое ожидание и матрица ковариаций, и, кроме того, известно, что их совместное распределение гауссовское, т.е.
|
x x |
x |
B |
(1.4.18) |
|||
|
fx,v (x, v) = N |
; , P |
. |
||||
|
v v |
BT |
Pv |
||||
|
Пусть вектор y связан с x и v соотношением вида |
||||||
|
y = Hx + v . |
(1.4.19) |
Необходимо найти условную плотность распределения вероятности f (x / y) .
В решении этой задачи удобно выделить два этапа.
Суть первого этапа сводится к нахождению плотности распределения вероятности совместного вектора, включающего x и y . В разделе 1.3.3 (пример 1.3.5) было показано, что
|
x |
x |
P |
x |
P |
x |
H |
т |
+ B |
.(1.4.20) |
|||
|
fx,y (x, y) = N |
; |
, |
||||||||||
|
y Hx + v B т + HP x |
HP x H т + |
HB + B тH т + Pv |
||||||||||
Искомую плотность f (x / y) легко получить на втором этапе, используя приведенное выше
правило нахождения условной гассовской плотности. Применяя это правило, получаем, что
|
f (x / y) |
= |
ˆ |
x / y |
), |
(1.4.21) |
|
N(x; x( y), P |
где условное математическое ожидание и условная матрица ковариаций в соответствии с выражениями (1.4.16), (1.4.17) определяются как
|
xˆ( y) = x + (P x H т + B)(HP x H т + HB + B тH т + Pv )−1( y − Hx − v) , |
(1.4.22) |
|
P x / y = P x − (P x H т + B)(HP x H т + HB + B тH т + Pv )−1 (B т + HP x ) . |
(1.4.23) |
В частном случае, когда векторы x и v независимы и v = 0 , эти выражения упрощаются
|
xˆ( y) = x + K ( y − Hx) , |
(1.4.24) |
|
K = P x H т(HP x H т + Pv )−1 , |
(1.4.25) |
|
P x / y = P x − P x H т(HP x H т + Pv )−1 HP x . |
(1.4.26) |
Для вычисления условной матрицы ковариаций может быть также использовано
|
соотношение |
|||
|
−1 |
−1 |
||
|
P x / y = P x − P x H т(HP x H т + Pv )−1 HP x = |
(P x ) |
+ H т(Pv )−1 H |
, (1.4.27) |
в справедливости которого легко убедиться с помощью леммы об обращении матриц. Принимая во внимание соотношение (1.4.27) и очевидную цепочку равенств [1.9]
83
|
P x H т (HP x H т + Pv )−1 = [(P x )−1 + H т (Pv )−1 H ]−1 [(P x )−1 + H т (Pv )−1 H ]P x H т (HP x H т + Pv )−1 = |
|||||||||
|
= P x / y [H т + H т (Pv )−1 HP x H т ](HP x H т + Pv )−1 = P x / y H т (Pv )−1 , |
|||||||||
|
для матрицы K в (1.4.25) получаем следующее выражение |
|||||||||
|
K = P x / y H т (P v )−1 .♦ |
(1.4.28) |
||||||||
|
По аналогии с результатом, полученным в примере для |
f (x / y) , можно показать, что (см. |
||||||||
|
задачу 1.4.2) |
), |
||||||||
|
f ( y / x) |
= |
ˆ |
y / x |
(1.4.29) |
|||||
|
N (y; y(x), P |
|||||||||
|
где |
|||||||||
|
yˆ(x) = Hx + v + B т(P x )−1(x − x) , |
(1.4.30) |
||||||||
|
P y / x = Pv − B т (P x )−1 B . |
(1.4.31) |
||||||||
|
Нетрудно заметить, что |
vˆ(x) = v + Bт (P x )−1(x − x) |
и |
P y / x = P v / x |
представляют собой |
|||||
|
условное математическое ожидание и матрицу ковариаций вектора |
v |
при фиксированном |
|||||||
|
значения вектора x . Это |
вполне объяснимо, |
поскольку |
y = Hx + v , |
и при фиксации x |
|||||
|
математическое ожидание и матрица ковариаций случайного вектора |
y |
будут определяться |
|||||||
|
условным математическим ожиданием и условной матрицей ковариаций вектора v . |
|||||||||
|
Наиболее важные выражения, связанные с задачей нахождения |
параметров условной |
гауссовской плотности широко и часто используемые при решении задач оценивания, сведены в таблицу 1.4.1.
Таблица 1.4.1.
Нахождение параметров условной гауссовской плотности
|
Условия |
Задача |
Решение |
||||||||||||||||||||||||||||||||||||
|
Найти |
) |
|||||||||||||||||||||||||||||||||||||
|
Задана ф.п.р.в. |
условную |
f (x / y) |
= |
N |
ˆ |
x / |
y |
|||||||||||||||||||||||||||||||
|
x ; |
x , |
P |
x |
P |
xy |
ф.п.р.в. |
(x; x( y), P |
|||||||||||||||||||||||||||||||
|
f |
x, y |
(x, y) = N |
f (x / y) |
ˆ |
= |
+ |
xy y |
−1 |
− |
|||||||||||||||||||||||||||||
|
P y |
x |
P |
(P |
) |
( y |
y) |
||||||||||||||||||||||||||||||||
|
y |
y |
(P xy )т |
для |
x( y) |
x |
|||||||||||||||||||||||||||||||||
|
P |
x / y |
= P |
− P |
xy |
(P |
y |
) |
−1 |
(P |
xy |
) |
т |
||||||||||||||||||||||||||
|
вектора |
x |
|||||||||||||||||||||||||||||||||||||
|
Найти |
f (x / y) |
= |
ˆ |
x / y |
||||||||||||||||||||||||||||||||||
|
условную |
N (x; x( y), P ), |
|||||||||||||||||||||||||||||||||||||
|
Задана ф.п.р.в. |
xˆ( y) = x + K ( y |
− Hx) , |
||||||||||||||||||||||||||||||||||||
|
ф.п.р.в. |
||||||||||||||||||||||||||||||||||||||
|
K = P x H т(HP x H |
т + Pv )−1 , |
|||||||||||||||||||||||||||||||||||||
|
x x |
x |
f (x / y) |
||||||||||||||||||||||||||||||||||||
|
fx,v (x,v) = N |
; |
, P |
0 |
P x / y = P x − P x H т (HP x H т + Pv )−1 HP x , |
||||||||||||||||||||||||||||||||||
|
v 0 |
0 |
Pv |
||||||||||||||||||||||||||||||||||||
|
−1 |
||||||||||||||||||||||||||||||||||||||
|
и вектор |
−1 |
+ H т |
||||||||||||||||||||||||||||||||||||
|
y = Hx + v |
P x / y = (P x ) |
(Pv )−1 H , |
||||||||||||||||||||||||||||||||||||
|
K = P x / y H т (Pv )−1 . |

84
Найти
условную ф.п.р.в. f ( y / x)
f ( y / x) = N(x; yˆ(x), P y / x ),
yˆ(x) = Hx + v + (B т + HP x )(P x )−1(x − x) ,
P y / x = Pv − B т (P x )−1 B .
|
|
Макеты страниц
Пользуясь понятием условной вероятности, можно определить условные функции распределения случайных величин относительно тех или иных событий. События, относительно которых определяется условная функция распределения, обычно заключаются в том, что некоторые случайные величины удовлетворяют определенным неравенствам, или в том, что случайная точка, соответствующая этим случайным величинам, попадает в определенную область.
Условной функцией распределения случайной величины X относительно события В называется условная вероятность неравенства 



Выражая здесь вероятности неравенств через функции распределения по формулам (7.5) и (14.2), получим:

Можно также выразить вероятности в формуле (16.1) через соответствующие плотности вероятности по формулам (8.5) и (15.3). Тогда получим выражение условной функции распределения через плотности вероятности случайных величин 

Наибольший практический интерес представляет условная функция распределения случайной величины X относительно равенства 




На основании общего определения плотности вероятности условными плотностями вероятности называются производные соответствующих условных функций распределения. В частности, условной плотностью вероятности случайной величины X относительно 


Эта формула дает выражение условной плотности вероятности случайной величины X относительно К через плотности вероятности случайных величин 


Формулы (16.5) и (16.6) можно переписать в виде:

Таким образом, двумерная плртность вероятности случайных величин 
Случайные величины 





Подставляя это выражение в формулу (15.6) и выполняя дифференцирование, получим:

Таким образом, двумерная плотность вероятности двух независимых случайных величин 
Легко убедиться в том, что равенство (16.9) является не только необходимым, но и достаточным условием независимости двух случайных величин. Для этого достаточно подставить выражение (16.9) в формулу (15.5) и выполнить интегрирование. Тогда, принимая во внимание (8.6), получим (16.8), что и свидетельствует о независимости случайных величин 
Подставляя выражение (16.8) в формулу (16.2), получим:

Таким образом, все условные функции распределения случайной величины X относительно неравенств вида 



Легко понять, что любое из равенств (16.11) является необходимым и достаточным условием независимости величин 
Считая событием В в определении условной функции распределения выполнение неравенства 


достаточно взять в формуле (16.15) бесконечно малую область В, содержащую точку 


Дифференцируя эту формулу по одному разу по 

Совершенно так же, как выше было дано определение зависимости и независимости двух скалярных случайных величин, можно дать определение зависимости и независимости двух случайных векторов. Для двух независимых случайных векторов совместная функция распределения равна произведению их функций распределения, а совместная плотность вероятности равна произведению их плотностей вероятности.
Случайные величины 


Если событие В в определении условной функции распределения заключается в попадании случайной точки с координатами 



если точка 

Пример 1. Случайный вектор с составляющими 

Найти плотности вероятности случайных величин 
Подставляя выражение (16.20) в формулу (15.8), находим плотность вероятности случайной величины X:

Аналогично найдем плотность вероятности случайной величины У:

Подставляя полученные выражения в формулы (16.5) и (16.6), найдем условные плотности вероятности случайных величин X и Y:

Очевидно, что случайные величины 
Пример 2. Принимаемый радиосигнал состоит из двух случайных импульсов 


пропускает, если 




В данном случае полезный сигнал 


Аналогично условная вероятность того, что детектор не пропустит сигнал при наличии полезного сигнала, равна:

Полная вероятность ошибки детектора на основании (5.2) равна:

Пример 3. В условиях предыдущего примера определить функцию 
Если 





где интегрирование распространяется на полосу заключенную между двумя кривыми 



где 







Рис. 12.
к кривой С теорему о среднем, получим с точностью до малых второго порядка относительно а:

где 




Так как вероятность ошибки 


Функция 





Очевидно, что в области наивероятнейших значений сигнала 




Отношение условных плотностей вероятности в левой части уравнения (16.33) часто называют отношением Правдоподобия. В случае нормального условного закона распределения сигнала 


в качестве функции 

Рекомендуем читателю в качестве упражнения самостоятельно решить примеры 2 и 3 для случая, когда принимаемый сигнал состоит из 



Оглавление
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА 1. ВЕРОЯТНОСТЬ СОБЫТИЯ И ЕЕ СВОЙСТВА
- § 1. Случайные явления. Предмет теории вероятностей
- § 2. Экспериментальные основы теории вероятностей. Частота и вероятность события
- § 3. Теорема сложения частот. Принцип сложения вероятностей
- § 4. Условные частоты и условные вероятности. Зависимые и независимые события
- § 5. Формула полной вероятности. Формула Бейеса
- § 6. Повторение опытов
- ГЛАВА 2. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
- § 7. Функция распределения
- § 8. Плотность вероятности
- § 9. Применение импульсных функций и обобщение понятия плотности вероятности
- § 10. Моменты случайной величины. Математическое ожидание, дисперсия и среднее квадратическое отклонение
- § 11. Нормальный закон распределения
- § 12. Закон распределения Пуассона
- § 13. Приближенное аналитическое представление законов распределения
- ГЛАВА 3. ВЕКТОРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
- § 14. Функция распределения случайного вектора
- § 15. Плотность вероятности случайного вектора
- § 16. Условные функции распределения и плотности вероятности
- § 17. Моменты двумерного случайного вектора. Корреляционный момент и коэффициент корреляции
- § 18. Моменты многомерного случайного вектора. Корреляционная матрица случайного вектора
- § 19. Математическое ожидание комплексной случайной величины. Свойства математических ожиданий
- § 20. Дисперсии и корреляционные моменты комплексных случайных величин. Свойства дисперсий и корреляционных моментов
- § 21. Приведение случайного вектора к случайному вектору с некоррелированными составляющими
- § 22. Двумерный нормальный закон распределения
- § 23. Многомерный нормальный закон распределения
- § 24. Квадратическое приближение случайной величины
- ГЛАВА 4. ХАРАКТЕРИСТИЧЕСКИЕ ФУНКЦИИ СЛУЧАЙНЫХ ВЕЛИЧИН
- § 25. Характеристическая функция скалярной случайной величины
- § 26. Выражение плотности вероятности через характеристическую функцию
- § 27. Связь между характеристической функцией и моментами случайной величины
- § 28. Характеристическая функция случайного вектора
- § 29. Связь между характеристической функцией и моментами случайного вектора
- ГЛАВА 5. ФУНКЦИИ СЛУЧАЙНЫХ АРГУМЕНТОВ
- § 30. Определение моментов функций случайных аргументов
- § 31. Применение линеаризации функций для приближенного определения моментов нелинейных функций случайных аргументов
- § 32. Закон распределения функции случайного аргумента
- § 33. Другой метод определения закона распределения функции случайного аргумента
- § 34. Закон распределения суммы случайных величин
- § 35. Применение характеристических функций для определения законов распределения функций случайных величин
- ГЛАВА 6. ЗАКОН БОЛЬШИХ ЧИСЕЛ
- § 36. Неравенство Чебышева
- § 37. Теоремы Маркова и Чебышева. Виды вероятностной сходимости
- § 38. Теоремы Пуассона и Бернулли
- § 39. Теоремы Ляпунова и Лапласа
- § 40. Доказательство теоремы Ляпунова
- ГЛАВА 7. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ИНФОРМАЦИИ
- § 41. О возможности измерения неопределенности результатов наблюдений случайных явлений
- § 42. Энтропия прерывной случайной величины
- § 43. Энтропия непрерывной случайной величины
- § 44. Информация и ее измерение
- § 45. Энтропия равномерного и нормального распределений
- § 46. Единственность определения энтропии прерывной случайной величины
- § 47. Энтропия неограниченных случайных последовательностей
- ГЛАВА 8. СЛУЧАЙНЫЕ ФУНКЦИИ
- § 48. Определение случайной функции. Законы распределения случайных функций
- § 49. Математическое ожидание и корреляционная функция случайной функции. Взаимная корреляционная функция двух случайных функций
- § 50. Моменты случайных функций
- § 51. Свойства корреляционных функций
- § 52. Сложение случайных функций
- § 53. Дифференцирование случайной функции
- § 54. Интегрирование случайной функции
- § 55. Предельная теорема для среднего значения случайной функции. Общая эргодическая теорема
- ГЛАВА 9. КАНОНИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ СЛУЧАЙНЫХ ФУНКЦИЙ
- § 56. Два вида канонических представлений случайных функций
- § 57. Общие формулы для координатных функций
- § 58. Каноническое разложение случайной функции в дискретном ряде точек
- § 59. Практический способ построения канонического разложения случайной функции в дискретном ряде точек
- § 60. Каноническое разложение случайной функции в данной области изменения аргумента
- § 61. Практический способ построения канонического разложения случайной функции в данной области изменения аргумента
- § 62. Общая форма канонического разложения случайной функции
- § 63. Построение канонического разложения случайной функции по каноническому разложению ее корреляционной функции
- § 64. Некоторые способы построения канонического разложения корреляционной функции
- § 65. Способ получения приближенного канонического разложения случайной функции
- § 66. Разложение случайной функции в ряд
- § 67. Интегральные канонические представления случайных функций
- ГЛАВА 10. ВЕКТОРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
- § 68. Приведение векторной случайной функции к скалярной
- § 69. Математическое ожидание и корреляционная функция векторной случайной функции
- § 70. Канонические разложения векторных случайных функций
- § 71. Интегральные канонические представления векторных случайных функций
- ГЛАВА 11. СТАЦИОНАРНЫЕ СЛУЧАЙНЫЕ ФУНКЦИИ
- § 72. Определение стационарной случайной функции
- § 73. Стационарная векторная случайная функция
- § 74. Эргодическое свойство стационарных случайных функций
- § 75. Стационарные случайные функции, эргодические по отношению к корреляционным функциям
- § 76. Каноническое разложение стационарной случайной функции
- § 77. Интегральное каноническое представление стационарной случайной функции. Спектральная плотность стационарной случайной функции
- § 78. Каноническое разложение стационарной векторной случайной функции
- § 79. Интегральное каноническое представление стационарной векторной случайной функции
- § 80. Случайные функции, приводимые к стационарным
- ГЛАВА 12. ХАРАКТЕРИСТИКИ ДИНАМИЧЕСКИХ СИСТЕМ
- § 81. Преобразование функций динамическими системами. Понятие оператора
- § 82. Оператор динамической системы как общая ее характеристика
- § 83. Весовые функции одномерных линейных систем
- § 84. Одномерные линейные системы, описываемые дифференциальными уравнениями
- § 85. Весовые функции многомерных линейных систем
- § 86. Другие характеристики линейных систем
- § 87. Стационарные линейные системы
- ГЛАВА 13. ИССЛЕДОВАНИЕ ТОЧНОСТИ ЛИНЕЙНЫХ СИСТЕМ
- § 88. Линейное преобразование случайной функции
- § 89. Линейное преобразование векторной случайной функции
- § 90. Общие методы исследования точности линейных систем
- § 91. Методы вычисления установившихся систематических ошибок стационарных линейных систем
- § 92. Исследование точности одномерных стационарных линейных систем с одним стационарным случайным возмущением
- § 93. Исследование точности одномерных стационарных линейных систем с одним нестационарным случайным возмущением
- § 94. Исследование точности одномерных линейных систем, близких к стационарным
- § 95. Исследование точности многомерных стационарных линейных систем
- § 96. Исследование точности многомерных линейных систем, близких к стационарным
- § 97. Один тип интегральных канонических представлений входных случайных возмущений
- § 98. Преобразование случайной функции случайным линейным интегральным оператором
- ГЛАВА 14. ИССЛЕДОВАНИЕ ТОЧНОСТИ НЕЛИНЕЙНЫХ СИСТЕМ
- § 99. Методы исследования точности нелинейных систем
- § 100. Общие принципы метода линеаризации операторов
- § 101. Непосредственная линеаризация уравнений Нелинейных систем
- § 102. Линеаризация уравнений нелинейных систем при помощи канонических разложений
- § 103. Метод статистической линеаризации
- § 104. Применение метода статистической линеаризации для исследования точности стационарных систем
- § 105. Применение метода статистической линеаризации для исследования точности нестационарных систем
- § 106. Преобразования случайных функций, приводимые к линейным
- § 107. Нелинейные интегральные преобразования случайных функций
- § 108. Применение метода канонических разложений для исследования нелинейных преобразований случайных функций
- ГЛАВА 15. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК СЛУЧАЙНЫХ ВЕЛИЧИН И СЛУЧАЙНЫХ ФУНКЦИЙ ПО РЕЗУЛЬТАТАМ ОПЫТОВ
- § 109. О характере задач определения вероятностных характеристик по результатам опытов
- § 110. Определение вероятностей событий, функций распределения и плотностей вероятности
- § 111. Определение математических ожиданий и дисперсий случайных величин
- § 112. Определение корреляционных моментов случайных величин
- § 113. Оценка точности экспериментального определения вероятностных характеристик
- § 114. Определение математических ожиданий и корреляционных функций эргодических стационарных случайных функций
- § 115. Определение математического ожидания случайной функции сглаживанием ее реализаций
- § 116. Основные понятия теории оценок
- § 117. Применение метода максимума правдоподобия для нахождения оценки математического ожидания случайной функции
- ГЛАВА 16. ЗАДАЧИ ТЕОРИИ ОПТИМАЛЬНЫХ СИСТЕМ
- § 118. Задачи определения оптимальных систем
- § 119. Критерии оптимума
- § 120. Общее условие минимума средней квадратической ошибки
- § 121. Общие условия экстремума данной функции математического ожидания и дисперсии ошибки
- § 122. Уравнения, определяющие оптимальный линейный оператор
- § 123. Уравнения, определяющие оптимальное неоднородное линейное преобразование
- § 124. Общий анализ уравнений, определяющих оптимальный линейный оператор
- § 125. Уравнения, определяющие весовые функции оптимальных линейных систем
- § 126. Уравнение, определяющее оптимальный нелинейный интегральный оператор
- ГЛАВА 17. МЕТОДЫ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ ЛИНЕЙНЫХ СИСТЕМ
- § 127. Определение оптимальной одномерной линейной системы в случае белого шума на входе
- § 128. Общая формула для определения весовой функции оптимальной одномерной линейной системы
- § 129. Формулы, определяющие оптимальную линейную систему в случае бесконечного интервала наблюдения и стационарной случайной функции на входе
- § 130. Определение оптимальной линейной системы в случае, когда входное возмущение связано с белым шумом линейным дифференциальным уравнением
- § 131. Другие варианты метода определения оптимальной линейной системы в случае, когда входное возмущение связано с белым шумом линейным дифференциальным уравнением
- § 132. Случай, когда входное возмущение представляет собой стационарную случайную функцию с дробно-рациональной спектральной плотностью
- § 133. Определение оптимального линейного оператора методом интегральных канонических представлений в общем случае
- § 134. Определение оптимальной одномерной линейной системы методом канонических разложений
- § 135. Определение оптимального линейного оператора методом канонических разложений в общем случае
- § 136. Определение оптимального линейного оператора в особых случаях
- § 137. Единственность решения и оценка приближения к оптимальному линейному оператору для критерия минимума средней квадратической ошибки
- ГЛАВА 18. МЕТОДЫ ОПРЕДЕЛЕНИЯ ОПТИМАЛЬНЫХ НЕЛИНЕЙНЫХ СИСТЕМ
- § 138. Определение оптимального оператора в классе приводимых к линейным
- § 139. Определение оптимального нелинейного интегрального оператора
- § 140. Определение оптимального оператора по критерию минимума средней квадратической ошибки в классе всех возможных операторов
- § 141. Определение оптимального оператора по критерию минимума среднего риска при произвольной функции потерь
- § 142. Определение оптимального оператора по критерию минимума среднего риска в особых случаях
- § 143. Случай нормально распределенных сигнала и помехи
- § 144. Общий метод определения оптимального оператора по критерию минимума среднего риска
- § 145. Случай, когда функция потерь является функционалом, а сигнал и помеха распределены нормально
- ДОПОЛНЕНИЕ
- 1. Некоторые сведения из теории линейных преобразований
- II. Некоторые сведения из теории линейных интегральных уравнений с симметричным ядром
- III. Нахождение минимума функции или функционала методом наискорейшего спуска
- ПРИЛОЖЕНИЕ. ТАБЛИЦЫ ФОРМУЛ И ТАБЛИЦЫ ФУНКЦИЙ
Содержание:
Многомерные случайные величины:
До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости – дискретная одномерная величина; расстояние от орудия до места падения снаряда – непрерывная одномерная случайная величина. Однако, при изучении случайных явлений в зависимости от их сложности иногда приходится использовать две, три и более случайных величин. Например, точка попадания снаряда определяется не одной, а двумя случайными величинами – абсциссой и ординатой. При различных измерениях очень часто имеем дело с двумя или тремя случайными величинами. Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин X ,Y , . . . , W обозначать (X ,Y , . . . , W) Такая система называется также многомерной случайной величиной. При изучении системы случайных величин недостаточно изучить отдельно случайные величины, составляющие систему, а необходимо учитывать связи или зависимости между этими величинами.
При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин
В дальнейшем, при изучении системы случайных величин ограничимся подробным рассмотрением системы двух случайных величин.
Закон распределения вероятностей системы случайных величин
Законом распределения вероятностей системы случайных величин называется соответствие, устанавливающее связь между областями возможных значений данной системы случайных величин и вероятностями появления системы в этих областях.
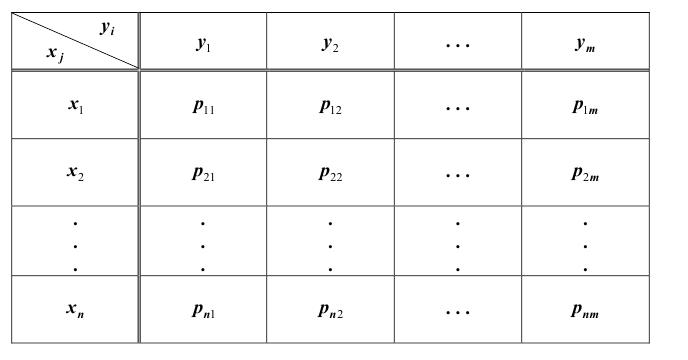
Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы двух дискретных случайных величин. Пусть
Одномерную случайную величину иногда называют скалярной случайной величиной.
X и Y – дискретные случайные величины, возможные значения которых 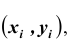
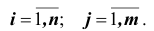
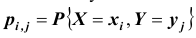
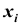
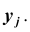
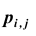
Такая таблица называется таблицей распределения вероятностей системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события 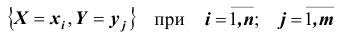
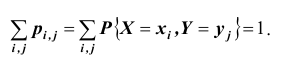
Функцией распределения вероятностей системы двух случайных величин называется функция 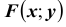
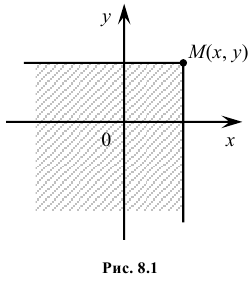
Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки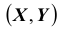
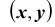
5. Функция распределения является неубывающей функцией по каждому из своих аргументов, то есть:
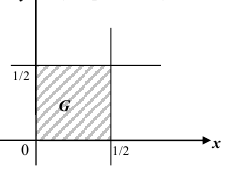
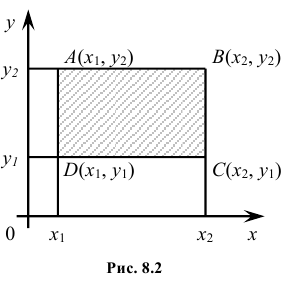
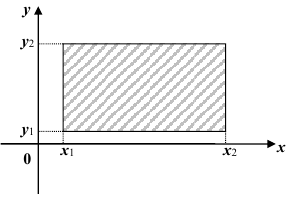
6. Вероятность попадания случайной точки (X,Y ) в произвольный прямоугольник со сторонами, параллельными координатным осям (см. рис.) вычисляется по формуле:
Плотность распределения вероятностей системы двух случайных величин
Предположим, что функция распределения F(x, y) всюду непрерывна и дважды дифференцируема21 (за исключением, быть может, конечного числа кривых). Тогда, смешанная частная производная функции F(x, y)
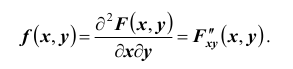
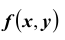
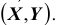
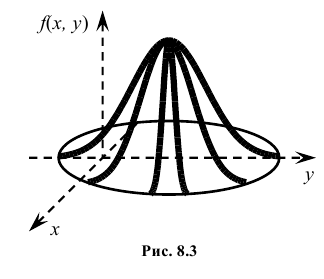
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
Зная плотность распределения 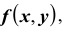
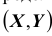
Используя последнюю формулу, выразим интегральную функцию F(x, y) распределения вероятностей системы двух непрерывных случайных величин через плотность распределения f (x, y):
Рассмотрим некоторые свойства плотности распределения системы двух непрерывных случайных величин:
Предполагается, что интегральная функция распределения вероятностей имеет непрерывную
смешанную частную производную второго порядка
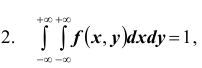
Пример №1
Пусть плотность распределения системы двух случайных величин (X,Y ) задана выражением:
Найти параметр А. Определить функцию распределения F(x, y) и вероятность попадания случайной точки (X,Y ) в прямоугольник D с вершинами:
Решение. Использовав свойство 2 плотности распределения, найдём постоянную величину А:
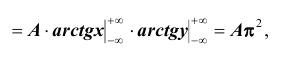
Определим теперь интегральную функцию распределения:
Таким образом, нетрудно теперь найти вероятность попадания случайной точки (X,Y ) в заданный прямоугольник D:
Условные законы распределения
Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:
Перейдём теперь к решению обратной задачи: по известным законам распределения отдельных случайных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними. Таким образом, если случайные величины X ,Y взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определённое значение, называется условным законом распределения.
Для дискретных случайных величин условным распределением составляющей
X при условии, что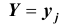
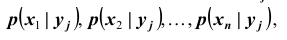
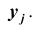
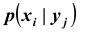
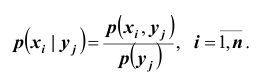
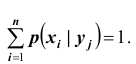
Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается F(x | y); условная плотность распределения обозначается
Плотностью распределения для случайной величины X при условии, что случайная величина Y приняла определённое значение (условной плотностью распределения), назовём величину
Аналогично, плотностью распределения для случайной величины Y при условии, что случайная величина X приняла определённое значение, назовём величину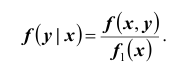
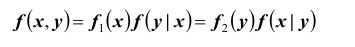
Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,
Числовые характеристики условных законов распределения
Для описания условных законов распределения можно использовать различные характеристики подобно тому, как для одномерных распределений. Наиболее важной характеристикой является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины X при Y = y ( y – определённое возможное значение случайной величины Y )
Мы записали условные законы распределения случайной величины X при условии, что другая случайная величина Y приняла определённое значение.
называется сумма произведений возможных значений X на их условные вероятности:
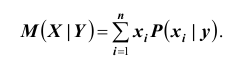
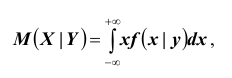
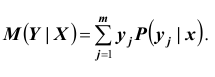
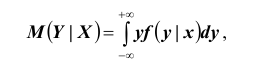
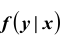
Числовые характеристики системы двух случайных величин
Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых случайных величин равны их безусловным распределениям. Укажем необходимые и достаточные условия независимости случайных величин.
ТЕОРЕМА 1: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения
системы (X ,Y ) была равна произведению функций распределения составляющих:
ТЕОРЕМА 2: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность вероятности
системы (X ,Y ) была равна произведению плотностей вероятностей составляющих:
Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, к которым относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом 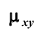
Для вычисления корреляционного момента дискретных величин используют формулу: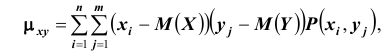
Корреляционный момент служит для характеристики связи между величинами X и Y .
ТЕОРЕМА 3: Корреляционный момент двух независимых случайных величин X и Y равен нулю.
Замечание: из теоремы 3 следует, что если корреляционный момент двух случайных величин X и Y не равен нулю, то X и Y – зависимые случайные величины.
Коэффициентом корреляции 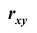
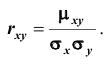
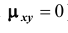
Коррелированность и зависимость случайных величин
Две случайные величины X и Y называются коррелированными, если их корреляционный момент (или коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Обратное утверждение не всегда имеет место, то есть если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равным нулю, но может и равняться нулю.
Заметим, что для нормально распределённых составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.
Если 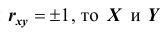
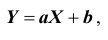
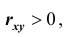
X и Y , то есть с возрастанием одной случайной величины другая случайная величина также возрастает.
Если 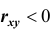
Функция и плотность распределения системы случайных величин
На практике очень часто приходится рассматривать системы более чем двух случайных величин. Функция распределения системы нескольких (более двух) случайных величин вводится как обобщение функции распределения системы двух случайных величин. Так, функцией распределения системы n случайных величин 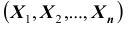
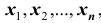
совместного выполнения n неравенств 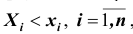
Эта функция является неубывающей функцией каждой переменной при фиксированных значениях других переменных. Если хотя бы одна из переменных стремится к 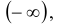
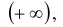
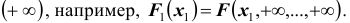
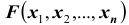
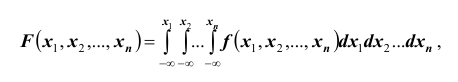
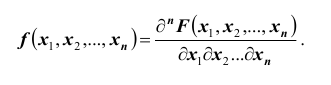
Вероятность попадания случайной точки с координатами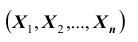
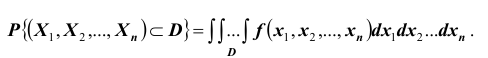
Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам. Например,
Числовые характеристики произвольного числа случайных величин
Основными числовыми характеристиками, с помощью которых может быть охарактеризована система n случайных величин 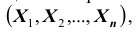
- 1) математические ожидания случайных величин, входящих в систему
которые в совокупности определяют математическое ожидание n –мерного случайного вектора;
- 2) дисперсии
случайных величин, входящих в систему;
- 3) корреляционные моменты каждой пары из n случайных величин
характеризующие попарно корреляцию всех случайных величин, входящих в систему.
Зная корреляционные моменты, можно найти коэффициенты корреляции 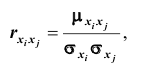
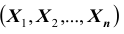
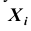
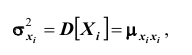
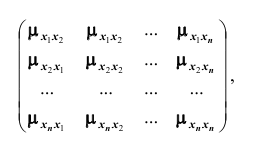
Из определения корреляционного момента следует, что 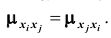
Если случайные величины системы некоррелированы, имеем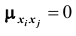
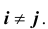
Такая матрица, как вам известно, называется диагональной. Вместо
корреляционной матрицы часто используют нормированную корреляционную матрицу. Матрица, элементами которой являются коэффициенты корреляции, называется нормированной корреляционной матрицей. Все элементы главной диагонали нормированной корреляционной матрицы равны единице. Нормированная корреляционная матрица имеет вид:
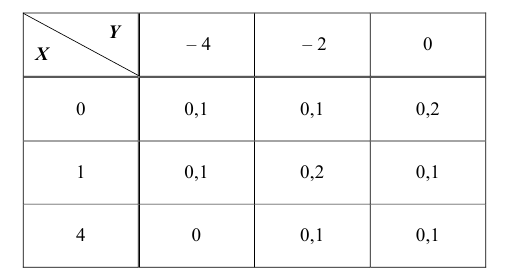
Задача 1.
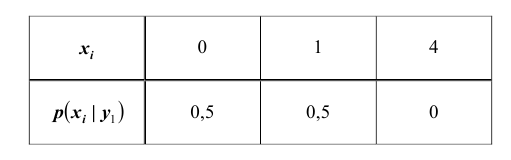
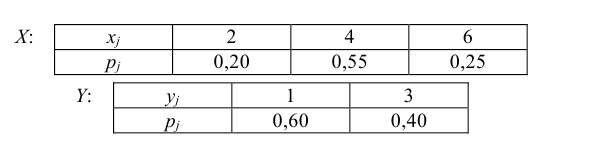
Закон распределения двумерной дискретной случайной величины (X ,Y ) задан таблицей
Найти:
– собственные законы распределения случайных величин X и Y ;
– математические ожидания M(X) M(Y );
– дисперсии D(X), D(Y );
– корреляционный момент 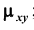
– коэффициент корреляции
– закон распределения случайной величины X при условии, что случайная
величина Y принимает своё наименьшее значение.
Решение. Складывая вероятности по строкам, получим закон распределения случайной величины X в виде ряда распределения
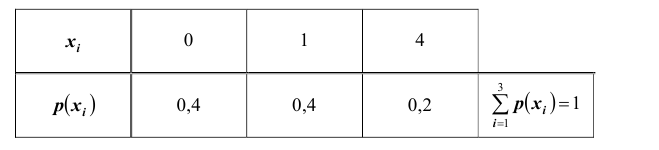
Складывая вероятности по столбцам, получим закон распределения случайной величины Y в виде ряда распределения
Найдём математические ожидания и дисперсии составляющих:
Найдём корреляционный момент 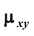
Найдём закон распределения случайной величины X при условии, что случайная величина Y принимает своё наименьшее значение, то есть при условии, что 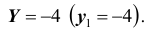
определяется совокупностью условных вероятностей 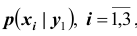
Следовательно, искомый закон распределения имеет вид:
Задача 2.
Вне области 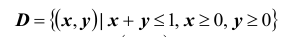
плотность распределения
Найти:
Решение. Для нахождения параметра А воспользуемся формулой
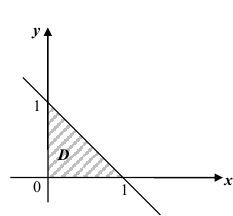
Получим
Найдём теперь вероятность 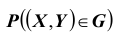
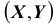
Далее, найдём одномерные плотности распределения:
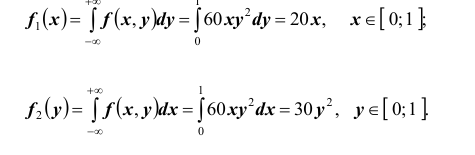
Найдём математические ожидания и дисперсии составляющих
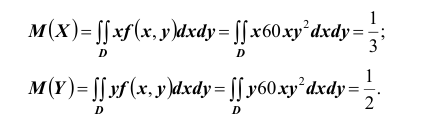
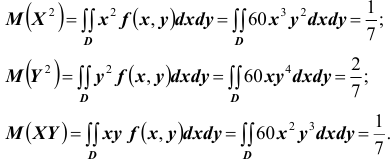
Так как 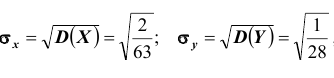
Что такое многомерные случайные величины
Ранее мы рассматривали случайные величины, возможные значения которой определялись одним числом. Такие величины называют одномерными. Однако часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин, которую называют многомерной случайной величиной или случайным вектором.
Понятие многомерной случайной величины
Многомерная случайная величина, случайный вектор, система случайных величин – это все различные интерпретации одного и того же математического объекта. В зависимости от удобства изложения мы будем пользоваться той или иной интерпретацией.
Так же, как и в случае одномерных случайных величин, случайные величины входящие в систему, могут быть как дискретными, так и непрерывными. Например, успеваемость студентов вуза, которая характеризуется системой n случайных величин 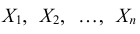
Геометрически двумерную (X, Y) и трехмерную (X, Y, Z) случайные величины можно изобразить случайной точкой плоскости Oxy или трехмерного пространства Oxyz. При этом случайные величины X, Y или X, Y, Z являются составляющими этих векторов. В случае n-мерного пространства (n > 3) также говорят о случайной точке этого пространства, хотя геометрическая интерпретация в этом случае теряет свою наглядность.
Пример №2
Пусть вероятностный эксперимент состоит в рождении ребенка. Тогда каждому элементарному событию 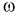
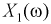
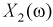
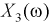
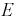
Пример №3
Пусть эксперимент состоит в измерении коэффициента усиления транзистора 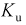
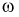
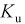
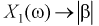
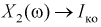
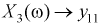
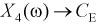
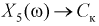
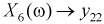
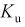
При изучении многомерных случайных величин удобно пользоваться следующей геометрической интерпретацией. Например (рис. 3.1), систему двух случайных величин 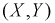
Пример №4
Пусть двумерная случайная величина 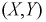
Найти коэффициент 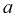
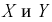
Решение.
Для определения коэффициента 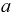
Учтем область определения
откуда
1-й способ проверки независимости
Найдем плотности распределений отдельных составляющих 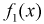
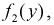
Подставим эти выражения в условие (3.13):
Значит случайные величины 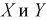
2-й способ проверки независимости
Найдем условную плотность распределения:
Видим, что выполняется условие (3.12), значит случайные величины 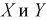
3-й способ проверки независимости
Все предыдущие вычисления можно не делать, а сослаться на следствие к доказанной выше теореме. Видим, что двумерная плотность 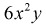
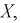
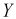
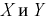
Пример №5
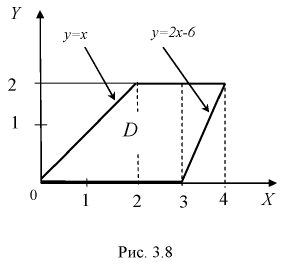
Двумерная случайная величина равномерно распределена внутри области 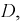
Найти константу
Решение.
Запишем уравнения прямых (см. рис. 3.7):
Используем условие нормировки
Этот интеграл вычислим в виде суммы трех интегралов, разбивая область 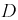
Закон распределения вероятностей двумерной дискретной случайной величины
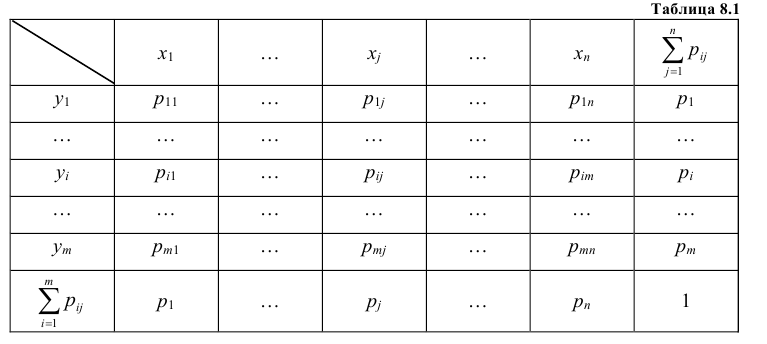
Так же как и для одномерной случайной величины наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном множестве возможных значений многомерной случайной величины такой закон может быть задан в виде таблицы (матрицы), содержащей все возможные сочетания значений каждой из одномерных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X, Y), то ее двумерное распределение можно представить в виде таблицы распределения (табл. 8.1), в каждой клетке (i, j) которой располагаются вероятности произведения событий
Так как события 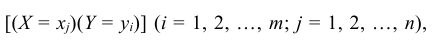
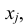
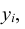
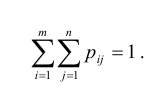
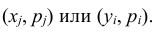
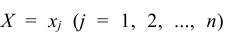
Таким образом, чтобы по таблице распределения (табл. 8.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности pij из соответствующего этому значению строки (столбца) данной таблицы.
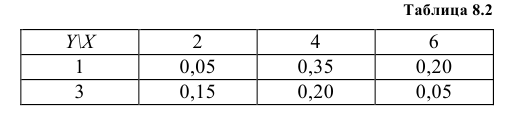
Пример №6
Закон распределения дискретной двумерной случайной величины (X, Y) задан в табл. 8.2. Найти законы распределения одномерных случайных величин X и Y.
Решение:
Случайная величина Х может принять значения: Х = 2 с вероятностью 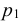
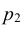
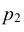
Аналогично закон распределения Y
Функция распределения многомерной случайной величины
При изучении одномерных случайных величин уже говорилось, что самой универсальной характеристикой случайной величины является функция распределения. Она существует для всех случайных величин: как дискретных, так и непрерывных. Точно также функция распределения полностью характеризует и многомерную случайную величину.
Определение: Функцией распределения n-мерной случайной величины 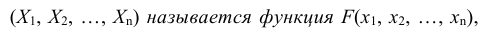
совместного выполнения n неравенств
В случае двумерной случайной величины XY функция распределения определяется неравенством
Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна с л е в а по каждому аргументу. В случае двумерной дискретной случайной величины ее функция распределения определяется по формуле: 
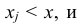
Отметим свойства функции распределения двумерной случайной величины.
1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей, т.е.
2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е.
3. Если хотя бы один из аргументов обращается в – ∞, то функция распределения равна нулю, т.е.
4. Если один из аргументов обращается в + ∞, то функция распределения становится равной функции распределения случайной величины, соответствующей другому аргументу, т.е.
5. Если оба аргумента равны + ∞, то функция распределения равна единице:
Геометрически функция распределения есть некоторая поверхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y). Зная функцию распределения F(x, y) можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 8.2). Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной 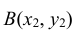
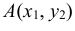
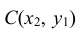
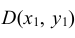
Плотность вероятности двумерной случайной величины
Для непрерывной двумерной случайной величины, так же как и для одномерной, существует понятие плотности вероятности.
Определение: Плотностью вероятности (или совместной плотностью) непрерывной двумерной случайной величины XY называется вторая смешанная частная производная ее функции распределения, т.е.
Геометрически плотность вероятности двумерной случайной величины XY представляет собой поверхность распределения в пространстве Oxyz.
Отметим свойства плотности вероятности двумерной случайной величины.
1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.
2. Вероятность попадания непрерывной случайной величины XY в область D равна
3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле:
4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице: 
Так как в соответствии с (8.7) 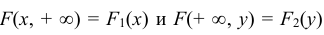
Дифференцируя функции распределения 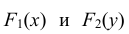
т.е. несобственный интеграл в бесконечных пределах от совместной плотности двумерной случайной величины по аргументу x дает плотность вероятности 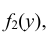
Условные законы распределения двумерной случайной величины
Итак, мы выяснили, как по известному закону распределения системы двух случайных величин определить законы распределения одномерных величин, входящих в систему.
Естественно возникает вопрос: нельзя ли по законам распределения одномерных величин, входящих в систему, найти закон распределения системы в целом? Оказывается, в общем случае этого сделать нельзя. Для того, чтобы полностью описать систему случайных величин, недостаточно знать распределение каждой из ее составляющих. Нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.
Определение: Условным законом распределения одной из одномерных составляющих двумерной случайной величины XY называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в определенный интервал).
Для дискретных случайных величин условные вероятности находятся по формулам:
В случае непрерывных случайных величин необходимо определить плотность вероятности условных распределений. Заменяя в формулах для дискретных величин вероятности событий «элементами вероятностей», получим:
т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равно отношению ее совместной плотности к плотности вероятности другой составляющей.
Пример №7
По данным примера 8.1 найти условный закон распределения составляющей Х при условии, сто составляющая Y приняла значение y1 =1.
Решение:
Искомый закон определяется следующей совокупностью условных вероятностей
Воспользовавшись формулой (8.16) и учитывая, что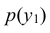
Важной характеристикой условного распределения вероятностей является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины Y при Х = х (х – определенное возможное значение Х) называют произведение возможных значений Y на их условные вероятности:
Для непрерывных величин
Аналогично определяется условное математическое ожидание случайной величины Х.
Пример №8
Найти условное математическое ожидание составляющей Y при условии, что составляющая Х примет значение
Решение:
Найдем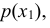
Найдем условное распределение вероятностей величины Y при при
Найдем условное математическое ожидание по формуле (8.19):
Условное математическое ожидание случайной величины Y при Х = х, т.е. Mx(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по Х. Аналогично My(X) называется функцией регрессии или регрессией X по Y. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) Y по Х и Х по Y.
Зависимые и независимые случайные величины
Ранее мы назвали две случайные величины независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Теперь можно дать общее определение независимости случайных величин, основанное на независимости событий X < x и Y < y, т.е. функций распределения
Определение: Случайные величины X и Y называются независимыми, если их совместная функция распределения F(x, y) представляется в виде произведения функций 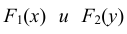
При невыполнении этого равенства случайные величины называются зависимыми. Дифференцируя дважды равенство (8.19) по аргументам x и y, получим
т.е. для независимых непрерывных случайных величин их совместная плотность равна произведению плотностей вероятностей этих случайных величин.
Другими словами, независимость двух случайных величин, что условные вероятности каждой из них совпадают с соответствующими безусловными плотностями вероятностей.
Числовые характеристики двумерной случайной величины
Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используются и другие характеристики, к числу которых относятся ковариация и коэффициент корреляции.
Определение: Ковариацией (или корреляционным моментом) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.
Из определения следует, что Kxy = Kyx.
Для дискретных случайных величин
Для непрерывных случайных величин
Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ax, ay).
Отметим свойства ковариации:
1. Ковариация двух независимых случайных величин равна нулю.
2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е.
3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е.
Не трудно заметить, что ковариация имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. Такая особенность затрудняет сравнение ковариаций различных систем случайных величин. Для устранения этого недостатка вводится безразмерная характеристика – коэффициент корреляции.
Определение: Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отношений этих величин, т.е.
Из определения следует, что
Отметим свойства коэффициента корреляции.
1. Коэффициент корреляции принимает значения на отрезке
2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. ρ = 0.
3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.
Пример №9
Определить ковариацию и корреляционный момент случайных величин Х и Y.
Решение:
В примере были получены следующие распределения одномерных случайных величин
Найдем математические ожидания и средние квадратические отклонения этих случайных величин:
Для нахождения математического ожидания M(XY) произведения случайных величин Х и Y можно составить закон распределения произведения двух дискретных случайных величин, а затем по нему найти M(XY). Однако M(XY) можно найти непосредственно по табл. 8.2 распределения двумерной случайной величины (X, Y) по формуле:
где двойная сумма означает суммирование по всем mn клеткам таблицы (m – число строк, n – число столбцов):
Вычисляем ковариацию по формуле (8.26):
Вычисляем коэффициент корреляции по формуле (8.28):
т.е. между случайными величинами Х и Y существует отрицательная линейная зависимость.
- Случайные события – определение и вычисление
- Системы случайных величин
- Вероятность и риск
- Определения вероятности событий
- Генеральная и выборочная совокупности
- Интервальные оценки параметров распределения
- Алгебра событий – определение и вычисление
- Свойства вероятности










![mathbb {E} [Xmid Y=y_{0}]=sum limits _{x}x,p_{Xmid Y}(xmid y_{0})](https://wikimedia.org/api/rest_v1/media/math/render/svg/74c4220c543f70627e7d1d32dee19b41a6a576ea)
=mathbb {E} [Xmid Y=Y(omega )],;omega in Omega](https://wikimedia.org/api/rest_v1/media/math/render/svg/59fb555bcf1a7dc8732e413ac36d2a2a0b41bcfe)
![mathbb {E} [Xmid Y=y_{0}]=int limits _{mathbb {R} ^{m}}x,f_{Xmid Y}(xmid y_{0}),dx](https://wikimedia.org/api/rest_v1/media/math/render/svg/64cb04e311d4acd9780cd8450b769bd92efa2385)

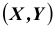
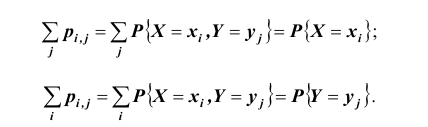
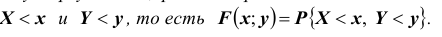

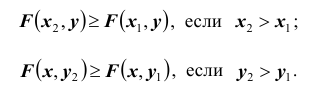
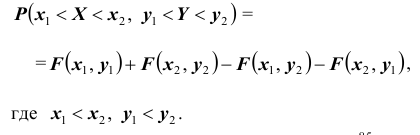
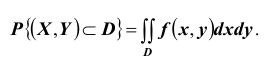
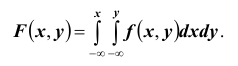
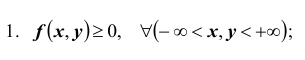
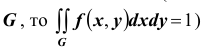
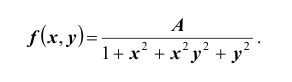
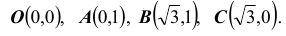
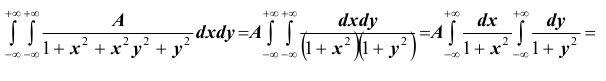
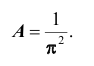
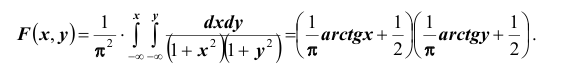
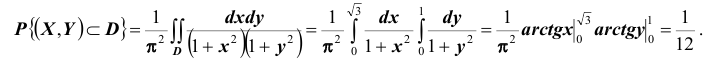
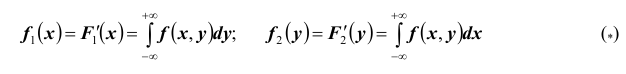
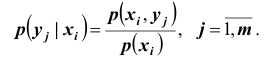
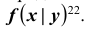
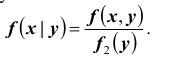
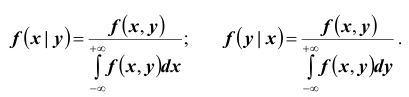
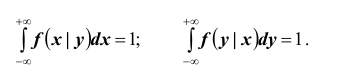
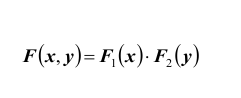
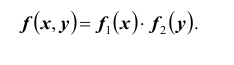
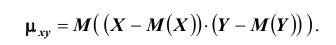
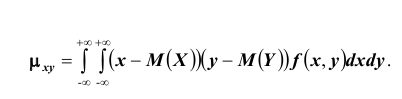
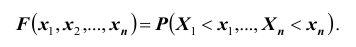
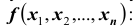
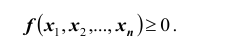
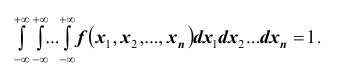
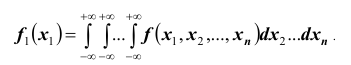
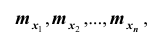 которые в совокупности определяют математическое ожидание n –мерного случайного вектора;
которые в совокупности определяют математическое ожидание n –мерного случайного вектора;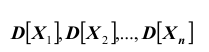 случайных величин, входящих в систему;
случайных величин, входящих в систему;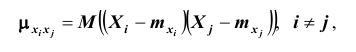 характеризующие попарно корреляцию всех случайных величин, входящих в систему.
характеризующие попарно корреляцию всех случайных величин, входящих в систему.