
Условная вероятность – это фундаментальная тема в вероятностном исчислении, которая позволяет нам оценить вероятность события, учитывая сведение о другом событии.
На практике, вычисление условной вероятности возникает почти каждый день во время разного рода исследований, анализа и принятия решений. Именно поэтому ее понимание является ключевым для успешного решания многих проблем, связанных с вероятностью.
В своем развитии, теория условной вероятности, играет важную роль понимании процессов в науке, технике и даже в обыденной жизни. Таким образом, изучение принципов нахождения условной вероятности необходим не только для специалистов в статистике, но и для тех, кто носит изысканно-логический мышление.
В данной статье мы углубимся в вопрос о том, как найти условную вероятность двух событий и рассмотрим фундаментальные принципы, используемые для ее нахождения, а также покажем, как применить их в реальных задачах.
Основные понятия теории вероятностей

Элементарное событие
Элементарным событием называется любое возможное конкретное значение переменной при проведении эксперимента. Например, в случае одного подбрасывания игральной кости, выпадение двух, трех, четырёх и т.д. до шести очков считается элементарным событием.
Эксперимент и пространство элементарных событий

Эксперимент в теории вероятностей – это сам процесс, который инициирует случайную ситуацию. Когда мы говорим о круге случайных событий, указываем на результаты этого эксперимента. Например, подбрасывание игральной кости или рулетку в казино. При этом пространство элементарных событий условительно объединяет все возможные результаты эксперимента, что позволяет анализировать систему возможных обстоятельств и будущие расчёты.
Случайное событие

Случайным событием называют набор элементарных событий. Если при одном рассмотрении мы не ограничиваемся значением конечного набора элементарных событий, имея определенное число возможных результатов эксперимента, мы называем его общее пространство элементарных событий. Это структура позволяет упростить применение и анализ вероятностных процессов.
Ирина, обучающая профессиональные занимающиеся азартными играми, указывает на то, что вероятность каждого результата случайных событий и процессов, в отличие от количества результатов, зависит от конкретных условий проведения экспериментов. Основы теории вероятностей безусловно помогут тебе понять эту красочную и наполненную азартом науку по-полной.
Автоматизация расчётов условной вероятности
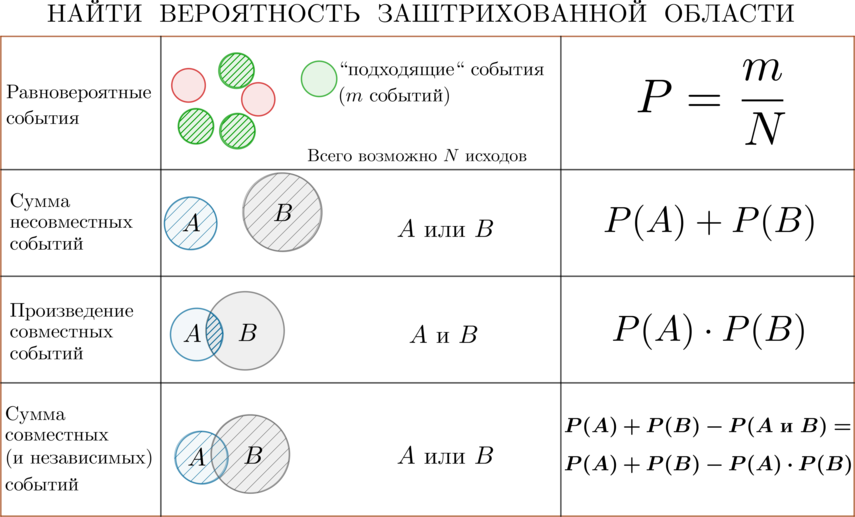
1. Введение в автоматизированные расчёты условной вероятности
В процессе выполнения экономических анализов, научных исследований или принятия решений в управленческой практике, часто возникает необходимость рассчитать условную вероятность различных событий. Это требуют не только математические знания для вычисления параметров вероятностных распределений, но и способность эффективно использовать информационные технологии для быстрого получения точных результатов.
Автоматизация расчётов условной вероятности является ключевым шансом повысить качество данных и эффективность принятия решений. Некоторые сильные стороны автоматизированного вычисления очевидно проявляются при работе с большими объемами данных и множеством событий, когда отдельная расчётная процедура будет занимать несколько недель или месяцев.
2. Методы и инструменты для автоматизированных расчётов условной вероятности
Большинство программных пакетов для статистического анализа и массштабного моделирования позволяют автоматизировать расчёты условной вероятности, предлагая разные инструменты и технологии для эффективной работы с данными и выполнения математических операций.
Одним из самых популярных и универсальных инструментов для автоматизированных расчётов условной вероятности является пакет программ Microsoft Excel. Имея удобные функциональные возможности, такие как циклы, макросы и формулы для статистического анализа, Excel упрощает процесс вычисления условной вероятности, а также предоставляет возможность построения данных графически.
Программное обеспечение для научного вычисления, такое как Python с библиотекой Pandas и даже специальные инструменты R для статистического анализа, позволяет использовать сложные методы процессуальной математики в автоматизации вычислений условной вероятности, например, через обработку бинарных и стохастических графов, оптимизацию по параметрам и другие методы анализа.
3. Преимущества и ограничения автоматизированных расчётов
Автоматизация расчетов условной вероятности предоставляет несколько ключевых преимуществ, в том числе:
- Увеличение скорости выполнения расчетов – автоматические программы способны быстро обрабатывать большие объемы данных и производить вычисления намного быстрее, чем человеческий анализ.
- Уменьшение вероятности ошибок – программные инструменты значительно снижают вероятность ошибочной деятельности, которая может привести к значительным недостаткам в экономическом анализе или принятии управленческих решений.
- Улучшение качества результатов анализа и принятие информированных решений – прозрачность и точность расчетов условной вероятности значительно повышают качество данных, а также способствуют принятию информированных и балансированных решений на стратегическом и оперативном уровнях управления.
Однако, автоматизированный анализ условной вероятности также может иметь свои ограничения, например, проблемы с адекватностью и качеством данных, а также необходимость подготовки обученных специалистов, способных работать с автоматизированными процессами.
Автоматизация расчетов условной вероятности является мощным инструментом, способным повысить качество исследований, эффективно разрешать задачи, связанные с анализом вероятностных свойств данных и принимать информированные управленческие решения. Умение эффективно использовать автоматизированные программные решения для анализа условной вероятности является решающим фактором не только удержания конкурентоспособности на современном рынке, но и возможности успешно отвечать на сложные вызовы бизнеса и науки.
Применение условных вероятностей в статистике
В классификации, условные вероятности используются для оценки вероятности принадлежности объектов к различным классам, основанной на определённых свойствах объектов. Это часто достигается с использованием таких методов, как правило Байеса, которое основывается на теоретических представлениях условных вероятностей и принципов принятия решений в соответствии с теми вероятностями.
Условным вероятностям также придаётся существенное значение в прогностике, где они используются для оценки вероятности возникновения некоторых событий в будущем на основе имеющихся данных. К примеру, в медицинской прогностике управление объективной вероятностью наступления различных неблагоприятных результатов заболевания позволяет оптимизировать выбор мер предосторожности и лечения.
В контексте идентификации статистических моделей, условные вероятности позволяют оценить степень согласованности пригодность некоторого набора параметров модели для объяснения имеющихся данных. Методы оценки условных вероятностей, как правило, используются при разработке эконометрических моделей и анализе временных рядов для получения максимально полной информации о структурах экономических явлений.
В общем, применение условных вероятностей в статистике различно и охватывает множество формальных и прикладных задач. Понимание принципов использования условных вероятностей позволяет статистику быть более эффективным в деле моделирования и интерпретации сложных и неравномерно распределённых процессов для получения надежных прогнозов и рекомендаций.
Практические задачи условной вероятности
В этом разделе мы рассмотрим несколько практических задач, встречающихся в повседневной жизни и научных отраслях, и научимся их решать с использованием условной вероятности.
Задача 1: Выявление аномалий в данных с серией измерений
Представим, что вы имеете дело с многомерными данными и выполняете предварительный анализ для выявления аномалий. Как вы можете использовать условную вероятность для обнаружения данных, не соответствующих общей модели?
| Метрика 1 | Метрика 2 |
|---|---|
| 0.34 | 0.12 |
| 0.23 | 0.09 |
| -0.13 | 0.56 |
| 0.17 | 0.78 |
Сначала вы можете перевести эти данные в стандартизованные значения по каждой метрике, используя формулу:
(значение – среднее значение) / стандартное отклонение
После этого вы можете определить условную вероятность того, что данные отображают аномалию. Вы считаете условную вероятность по контрольным точкам, зная, что примерно 99.7% данных в нормальной равномерной выборке попадают в интервалы от -3 стандартных отклонений до 3 стандартных отклонений.
| Станд. отч. | Условная вероятность |
|---|---|
| -3 | 0.00135 |
| -2 | 0.01587 |
| -1 | 0.10413 |
| 1 | 0.5 |
| 2 | 0.8413 |
| 3 | 0.98865 |
Если условная вероятность меньше определенной нормы, например 0.001, вы задействуете сигнал о том, что данные являются аномалиями.
Задача 2: Медицинские прототипы

Медицинский исследователь получает две панели данных: одна об переходе пациентов к постоянному лечению после предъявления показаний к вмешательству, а другая – о событиях, которые более вероятно переходят в лечение.
| Событие 1 | Событие 2 | Процент перехода к лечению |
|---|---|---|
| зимний сезон | другие сезоны | 40% |
| болезнь X | другие болезни | 55% |
| возраст > 60 лет | возраст < 60 лет | 60% |
Используя условную вероятность и данные выше, вы можете относительно подробно ответить на следующие вопросы:
- Какова вероятность перехода к лечению во время зимнего сезона, если пациент болеет болезнью X и старше 60 лет?
- Какова вероятность того, что пациент будет направлен на лечение после административного заключения, если у пациента болезнь X и он старше 60 лет?
Для вопросов о условной вероятности вы можете перекрыть вероятности событий, которые указаны на таблицах, и умножайте их на заводимый процент.
Задача 3: Прогнозирование прибыли в бизнес-проекте

Предполагаем, что предположительная прибыль от определённого события рассчитывается из данных нескольких различных источников с различной крайньостью.
| Источник | Вероятность | Прибыль | Условная вероятность |
|---|---|---|---|
| источник 1 | 10% | 1000 | 0.01 |
| источник 2 | 50% | 500 | 0.5 |
| источник 3 | 90% | 200 | 0.9 |
Используя формулы условной вероятности и данные, предоставленные выше, вы можете предсказать примерную вовлечённую прибыль в бизнес-проект.
Результат: Если все источники несут прибыль, общая прибыль составит: (0.01*1000) + (0.5*500) + (0.9*200) = $250 + $250 + $180 = $680
Стать известным в мире условной вероятности

Чтобы стать известным в мире условной вероятности, необходимо проявить себя в научных работах, стать автором важных открытий и развивать эту область математики. Вот несколько шагов, которые он может предпринять в этом направлении.
Научные исследования

Все начинается с проведения обширных научных исследований и анализа на тему условной вероятности. Для того, чтобы стать авторитетом в этой области, необходимо тщательно изучить почти все существующие теории и принципы в рамках данной области знаний. Помимо этого, сам научно-исследовательский процесс затрагивает структурирование собранных данных и их системное анализирование.
Публикация работ

Так, как технологии и людское знание постоянно развиваются и изменяются, всегда представляется возможность внести свой вклад. Поэтому важно проводить собственные эксперименты и совершенствовать существующие методы. Результаты полученных исследований тогда должны быть усиленно изложены на конференциях, опубликованы в специальных журналах и журналах научных исследований, участвуете в различных конкурсах, чтобы собрать максимальное количество свидетельств вашей значимой работы в данной области.
Важно содержать актуальность полученных данных и нововведений. Поэтому язык, в который переводится работа и с которым читатель на протяжении всей работы будет работать, должен быть описан максимально точно и легко понятен для представителей данной сферы научных исследований, ознакомившихся с вашими результатами. Известность вездесуща и, следуя по стопам известных авторитетов в области условной вероятности, можно развивать и свои интеллектуальные способности.
Вопрос-ответ:
Что такое условная вероятность и как ее отличить от генеральной вероятности?
Условная вероятность представляет собой вероятность того, что определенное событие произойдет при условии, что другое событие уже произошло. В отличие от генеральной (абсолютной) вероятности, она зависит от дополнительной информации о другом событии. Например, если известно, что человек прокатился на велосипеде, условная вероятность того, что он получил травму, будет зависеть от того, что произошло до или во время езды (например, столкновение с машиной).
Как измерить условную вероятность определенного события?
Условная вероятность может быть измерена с помощью математического выражения P(B|A), которое заключается в отношении вероятности совместного появления событий A и B к вероятности того, что произойдет событие A. Вот пять шагов, с которых полезно начать: составление совместной таблицы вероятностей для событий A и B, вычисление условной вероятности того, что будет событие B при условии, что уже произошло событие A (P(B|A)), тестирование вычислений с помощью исходных данных и проверки на достоверность (например, убедившись, что условная вероятность меньше или равна единице, и не больше 1).
Существуют ли какие-то практические прикладные методы определения условной вероятности?
Если вы хотите определить условную вероятность того, что произойдет какое-то событие, при условии, что уже произошло другое событие (например, выяснить вероятность получения прибыли от бизнеса при условии, что в нем традиционно осуществляется онлайн-маркетинг), вы можете это сделать с помощью трех методов: математического моделирования, экспериментального исследования или получения статистических данных. Для математического моделирования может быть использован подход теории вероятностей и теории вероятностей и математической статистики. Для экспериментального исследования можно провести случайную или контролируемую экспериментальную серию бутылок, чтобы выразить вероятность того, что выпадет определенное количество монет. Получение статистических данных может быть достигнуто путём анализа данных официальных статистических источников. Исходя из выбранного метода, достоверность и точность данных должны быть подтверждены с помощью строгих эмпирических методов проверки.