Как найти условные координаты

Вопрос 10. Условная система координат и локальная система высот

.. Условная система координат, по существу, является местной системой координат, ось абсцисс которой совпадает с направлением стороны хода, а начало координат — с точкой А. Иногда в прямоугольной системе координат удобно ось абсцисс (X) не совмещать с меридианом, а дать ей другое, более выгодное направление. Такая система называется условной. В строительстве часто за ось абсцисс принимается направление одной из главных осей строящегося объекта.

Ориентирование линий на местности определяется относительно исходного направления по ходу часовой стрелки до направления, совпадающего с линиями на местности. За исходные направления в геодезии приняты следующие:

-географический(местный)меридиан мнимый – это линии, проходящие по земной поверхности, соединяющие соответственно С и Ю полюса.

Различают высоты абсолютные, условные и относительные(превышения). Счёт абсолютных высот ведётся от среднего уровня моря или океана. В Респ. Бел. За начало отсчёта абсолютных принята уровенная поверхность, совпадающая со средним уровнем Балтийского моря.(Балтийская система координат)

Началом счётаусловныхвысот может являться любая условно принятая уровневая поверхность. Разность высот двух точек наз. относительной высотой или превышением h.

Превышение может быть как положит. Так и отрицат.

11. Исходные геодезические сети.Государственная геодезическая сеть является основой для развития детальных геодезических сетей, выполнения топографических съемок, производства инженерно-геодезических работ. Она должна отвечать требованиям решения научных задач геодезии

Съёмочные сети предназначены для выноса на местность запроектированного объекта, установки тех оборудования и для составления тапограф плана крупного масштаба на терр строительства. Самым распростр видом съемочных и опорных сетей явл стр сетка(в виде квадратов) и теодолитные ходы. Теодолитные ходы- это постр на местности в виде ломанных замкнутых и разомкнутых линий, где вершины поворотов явл точками съёмочного и опорного обоснования. Разомкнутый теод ход должен опираться на пункты с известн корд. В теод ходе на местности измер углы поворота(левые и правые), длины линий между точками. Сети сгущения могут создаваться как самостоятельные геодезические сети, так и в дополнение к государственной геодезической сети. Их делят на плановые, состоящие из полигонометрии 4-го класса и триангуляции, трилатерации и полигонометрии 1-го и 2-го разрядов, и высотные, создаваемые техническим нивелированием

Замкнутый теодолитный ход начинается с одной точки с известными координатами и заканчивается на той же точке. Висячий теод ход начинается с одной точки с известными координатами и заканчивается произвольно.

Висячие ходы бесконтрольны и поэтому допускаются только в исключительных случаях для определения координат 2-3 точек в труднодоступных местах.

12. Географическая и километровая рамка топографической карты. Зарамочное оформление.

Для удобства пользования топографической картой на листе карт наносят координатную сетку,которая представляет собой систему линий, параллельных координатным осям. Для карт масштабов 1:50000 и крупнее километровая( координатная сетка наносится через 1 км. На картах масшатаба 1:100000 – через км, а на картах более мелких 10 км

Внутренняя рамка образована отрезками параллелей. На каждом листе топографической карты с внешней стороны рамки помещаются различные сведения, необходимые для работы с картой. Под номенклатурой даются номер и год издания карты. Под нижней(южной) стороной рамки слева приводятся данные о магнитном склонении, сближении меридианов и поправке направления, а на чертеже показана взаимосвязь этих угловых величин; посередине помещаются линейный и численный масштабы карты, правее масштаба находится шкала заложений, предназначенная для определения крутизны скатов, справа указывается когда и каким методом создана карта. Данные о времени создания карты позволяют судить о соответствии карты местности на данный момент(период). Между внутренней и внешней линиями рамки листа карты даются оцифровка вертикальных и горизонтальных линий координатной(километровой) сетки и подписи географических координат(широты и долготы) углов рамки. Стороны рамки разбиты на минутные деления(по широте и долготе), а каждое минутное деление точками разбито на шесть частей по десять секунд каждая. Кроме того, у выходов железных и шоссейных дорог дано название ближайшего города, поселка или станции, куда ведет данная дорога, с указанием расстояния в километрах от рамки до этого населенного пункта(станции). Внутри рамок подписываются также собственные названия населенных пунктов, которые только частично изображены на данном листе, а большая часть их расположена на соседнем листе. На топографических картах и планах изображаются опознаваемые на местности объекты ситуации и рельефа с подробностью, зависящей главным образом от масштаба карты или плана. Для изображения ситуации служат контурные, внемасштабные и пояснительные условные знаки установленного образца

Источник

Вопрос 10. Условная система координат и локальная система высот.

Ориентирование линий на местности определяется относительно исходного направления по ходу часовой стрелки до направления, совпадающего с линиями на местности. За исходные направления в геодезии приняты следующие:

-географический(местный)меридиан мнимый – это линии проход. по земной пос-ти соед. соотв. С и Ю полюса.

Различ. высоты абсолютные, условные и относительные(превышения). Счёт абсолютных высот ведётся от среднего уровня моря или океана. В Респ. Бел. За начало отсчёта абсолютных принята уровенная поверхность, совпадающая со средним уровнем Балтийского моря.(Балтийская система координат)

Началом счёта условных высот может являться любая условно принятая уровневая поверхность. Разность высот двух точек наз. относит. высотой или превышением h.

Превышение может быть как положит. Так и отрицат.

11. Исходные геодезические сети.

Государственная геодезическая сеть (ГГС) представляет совокупность пунктов с известными координатами и высотами, равномерно расположенных на всей территории страны. ГГС создается для распространения на территории республики единой системы координат и высот, которые определяются для геодезических пунктов (ГП), закрепленных на местности. ГП состоит из знака и центра (рис.13). Знак представляет собой устройство или сооружение, обозначающее положение ГП на местности и необходимое для взаимной видимости между смежными пунктами. Центр является носителем координат и высот (X,Y,H), определяемых с погрешностью до 1 мм.

Рис.13.Схемы геодезических пунктов

ГГС делится на плановую и высотную. Плановая ГГС создается астрономическими или геодезическими методами. Высотная ГГС создается методами геометрического нивелирования, т.е. горизонтальным лучом визирования.

С целью увеличения числа плановых и высотных пунктов на единицу площади строятся сети сгущения, на основе которых создается съемочное обоснование. На примере учебного комплексного задания 1 можно предположить: пунктом ГГС является пункт триангуляции «Грабово»; сети сгущения — пункты полигонометрии 511, 512, 513; съемочного обоснования – пункты 1,2,3,В1. Пункты высотной сети закрепляется на местности реперами.

Репером называется знак предназначенный для долговременного и надежного закрепления на местности высоты точки. Реперы по конструкции различают грунтовые и стенные.

В зависимости от точности геометрическое нивелирование делится на четыре класса и техническое. Для технического нивелирования предельно допустимая погрешность определяется по формуле

где L — число километров.

В отдельных случаях, когда неизвестна длина нивелирного хода

f _hдоп.=10ммn,

где n — число нивелирных станций.

13. Прямая геодезическая задачи

Рис.11. Прямая и обратная геодезические задачи

где X и Y — приращения координат, т.е. проекции горизонтального проложения на соответствующие оси координат.

Контроль вычислений координат выполняют по формуле

ПГЗ – заключ. в том, что по известным прямоугольным координатам одной

точки X , Y , горизонт. Проложению d и её направлению (румбу r или дирекционному углу альфа линии А-В) требуется определить координаты другой точки X , Y .

Знаки приращения координат зависят от направлений румбов (т.е. от cosr и sinr)

Источник

3 Вопрос. Системы координат, применяемые в геодезии

Положение точек поверхности земли определяется координатами.

Координаты — величины, определяющие положение точки на поверхности, в пространстве, на плоскости.

Системы координат — составляют исходные плоскости, линии, точки.

Все системы координат, применяемые в геодезии, можно разделить на две группы:

1. Географическая система координат (обще название), которая объединяет астрономическую и геодезическую системы координат. Будем рассматривать геодезическую систему координат.

2.Пространственная полярная система координат.

1. Зональная система плоских прямоугольных координат.

2. Плоская условная система прямоугольных координат.

3. Система плоских полярных координат.

А) зональная система плоских прямоугольных координат В соответствии с принятой равноугольной поперечно-цилиндрической проекцией Гаусса, в геодезии принята зональная система плоских прямоугольных координат.

Положение точек земной поверхности определяется прямоугольными координатами Х и У. Оси координат в геодезии развернуты на 90 градусов по сравнению с декартовой системой координат.

Счет абсцисс ведется от экватора к северу со знаком плюс. К югу — со знаком минус. Для территории нашей страны абсциссы положительны, поэтому знак перед значением абсциссы не ставится (опускается).

Ординаты к востоку от осевого меридиана положительны, а к западу отрицательны.

Для того, чтобы все значения ординат были со знаком плюс, счет их ведется от условного меридиана, вынесенного на запад на 500 км, т.е. осевому меридиану придается значение 500 000 м. при этом впереди значения ординаты пишут номер зоны.

Исправленнуютаким образом ординату называют приведенной или условной, а координаты называют условными или действительными.

Связь между условными координатами и их

Х’, У’ — действительные значения координат

Х, У — условные значения координат.

Хм = 5 650 450, где 5 650 км, 450 м

Ум = 3 250 550, где 3 — номер зоны, 250 км, 550 м.

Это полные условные прямоугольные координаты точки.

Полные действительные координаты:

Точка М расположена в третьей зоне в 249 км 550 м к западу от осевого меридиана (250 550 — 500 000) и к северу от экватора на удалении 5 650 км 450 м.

Для измерения прямых координат на карты наносится координатная сетка. Координаты, в которых указываются только десятки и единицы километров и метров, называются сокращенными.

Хм= 05450 Ум =50550

Они применяются при работе в пределах границ карты, плана. Система применяется при составлении планов, карт.

Элементсистемы:

— начало координатной системы (полюс)

Возможные варианты элементов системы координат: Полярная ось — любое ориентирное направление (А, Ам, а, сторона теодолитного хода и т.д.)

Начало координат: — точка стояния

— точка теодолитного хода

Координаты, определяющие положение точки:

— горизонтальный угол между полярной осью и направлением на определяемую точку

— горизонтальное расстояние от полюса до определяемой точки (d).

— при теодолитной съемке

— при выполнении разбивочных работ (вынос точки в натуру).

-начало — произвольная точка

-ось абсцисс (произвольно)

— ось ординат (перпендикулярна к оси абсцисс)

1. Осями координат горизонтальная плоскость делится на 4 четверти.

2. В геодезии принята правая система прямоугольных координат (в отличие от принятой в математике левой декартовой системы)

3.Нумерация четвертей ведется по ходу стрелки часов, начиная с северо-восточной четверти, что позволяет использовать в геодезических вычислениях формулы тригонометрии без каких-либо изменений. Ось абсцисс 1 четверти ориентирована на север (0градусов).

4. Координаты точек равны кратчайшим расстояниям от начала координат до проекции этих точек на оси Х и У.

5. Разность между проекциями двух точек на оси Х и У принято называть приращением координат и обозначать (х, у) (разность между координатами двух точек)

6. Приращения координат имеют знаки (+), значение которых определяется координатными осями четвертей.

7. Если известны координаты одной точки, то координаты другой можно найти

Хв =Ха + ()

Yв = Yа + ()

8. 8. Система плоских координат имеет широкое применение в инженерной геодезии.

Источник

Условная
система прямоугольных координат

Такую
систему удобно использовать на небольших
территориях административных районов,
строительных площадках, землеотводных
участках. Ось абсцисс (Х) совмещаются
с меридианом точки местности, так чтобы
он совпадал (или был параллелен) основным
магистралям, осям сооружений, линиям
застройки и т.д. начало координат
означают таким образом, чтобы все точки
объекта, участка местности, имели только
положительные координаты

10. Исходные геодезические сети. Сети съёмочного обоснования в виде теодолитного хода

Для
производства инженерно-геодезических
работ в строительстве, для выполнения
топографических съемок и для решения
научных задач необходимо иметь на
местности исходные точки с известными
координатами и высотами. Геодезическая
сеть (геодезическое обоснование) –
это система закрепленных точек земной
поверхности, положение которых определено
в принятой для них системе геодезических
координат
Х, У, Н с
большой точностью. Геодезические сети
делятся на государственные и рабочие
(сети сгущения), которые в свою очередь
делятся на плановы6е и высотные (рис
5.1).

12.
Прямая
геодезическая задача
(ПГЗ) – Это
вычисление координат Х₂
и У₂
второй конечной точки, если
известны координаты Х₁
и У₁

,
первой
(начальной), дирекционный угол α и длина
(горизонтальное проложение) d
линии соединяющей эти точки

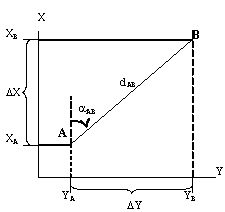
П
рямая

Дано:
X_A,
Y_A,
_AB,
d_AВ

Определить:
X_B,
Y_B

Решение:

X_B=X_A+d_AB^.
cos
_AB=X_A+X,

Y_B=Y_A+d_AB^.
sin
_AB=Y_A+Y,

где
X
и Y
– приращения координат, т.е. проекции
горизонтального проложения на
соответствующие оси координат. Контроль
вычислений координат выполняют по
формуле

13.
Обратная
геодезическая задача (ОГЗ)
– это величина дирекционного угла

(румба) и горизонтального проложения
d
по заданным прямоугольным координатам
точек 1 и 2

Дано:
X_A,
Y_A,
X_B,
Y_B.

Определить:
_AB,
d_AB.

Решение:

_AB
–
r
= arctg
(Y/X),

Контроль:
d ^.
cos

+ X_A
= X_B,

d
^.
sin

+ Y_B
= Y_B.

14. Устройство теодолита.

Основным
угломерным прибором на местности
является теодолит
– оптико-механический прибор, с помощью
которого
измеряют горизонтальные и вертикальные
углы, расстояния и магнитные азимуты.

Основные
узлы и принадлежности технического
теодолита

1)
горизонтальный круг, состоящий из лимба
– оцифрованной по ходу часовой стрелки
круговой полосы с градусными делениями;

2)
алидада – часть, расположенная соосно
с лимбом и несущая элементы отсчетного
устройства;

3)
цилиндрический уровень – предназначен
для приведения плоскости лимба
горизонтального круга в положение
перпендикулярное относительно отвесной
линии (горизонтальное положение);

4)
зрительная труба – состоит из объектива,
окуляра, сетки нитей и фокусирующего
устройства с кремальерой;

5)
вертикальный круг – устроен аналогично
горизонтальному и предназначен для
измерения углов наклона;

6)
подъемные винты – служат для приведения
пузырька цилиндрического уровня на
середину;

7)
становой (закрепительный) винт –
закрепляет теодолит на штативе и
позволяет подвесить нитяной отвес.

Основные
геометрические оси теодолита:

1.
ОО₁
– ось вращения прибора (вертикальная
ось теодолита),

2.
UU₁
– ось цилиндрического уровня (касасельная
к внутренней поверхности ампулы в
нульпункте),

3.
WW₁
– визирная ось зрительной трубы (прямая,
соединяющая оптический центр объектива
и крест сетки нитей),

4.VV₁
– ось вращения зрительной трубы.

Геометрические
требования, предъявляемые к осям:
1)UU₁

OO₁,
2)WW₁

VV₁,
3)VV₁
ОО₁.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

Общие сведения о системах координат

Система координат — это комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки. В общем и целом систему координат можно определить как опорную систему для определения положения точек в пространстве или на плоскостях и поверхностях относительно выбранных осей, плоскостей или поверхностей.

Систему координат широко применяют во многих отраслях науки:

В математике координаты – это совокупность чисел, сопоставленных точками многообразия в некоторой карте определённого атласа.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты выбираются как (приближённо) сферическая система координат — широта, долгота и высота над известным общим уровнем (например, океана).

В астрономии небесные координаты — упорядоченная пара угловых величин (например, прямое восхождение и склонение), с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой сферическую систему координат (без радиальной координаты) с соответствующим образом выбранной фундаментальной плоскостью и началом отсчёта. В зависимости от выбора фундаментальной плоскости система небесных координат называется горизонтальной (плоскость горизонта), экваториальной (плоскость экватора), эклиптической (плоскость эклиптики) или галактической (галактическая плоскость).

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

Что такое координатная сетка?

Одним из элементов географической карты является сетка координатных линий. Существуют два вида координатной сетки: картографическая, образуемая линиями меридианов и параллелей, и сетка прямоугольных координат, образуемая линиями, параллельными осям координат OX и OY.

На топографических картах меридианы и параллели являются границами листа карты; в углах карты подписываются их долгота и широта. Внутри листа вычерчивается сетка прямоугольных координат в виде квадратов, называемая иногда километровой сеткой, так как на картах масштаба 1:10 000 и мельче линии сетки проводятся через целое число километров.
Вертикальные линии сетки параллельны осевому меридиану зоны (оси OX) и имеют уравнение Y = Const; значение координаты Y подписывается у каждой линии. Горизонтальные линии сетки параллельны оси OY и имеют уравнение X = Const; значение координаты X подписывается у каждой линии.

Классификация систем координат

Назначение систем координат

1.    Общеземные (мировые ) WGS 84, ПЗ 9011, ITRS
Общеземными принято называть такие системы координат, которые получены под условием совмещения их начала с центром масс Земли. Они устанавливаются в отношении территории, покрывающей весь земной эллипсоид. И используется для решения общеземных задач. Наиболее удобными являются географические координаты (широта и долгота) отсчитываемые от поверхности экватора и начального меридиана в виде дуг, которым соответствуют центральные углы.

2. Государственные (СК-95, СК-63, ГСК-2011)
Эта система координат ограничивается территорией одного государства и используется, для осуществления геодезических и картографических работ внутри этого государства. В РФ в качестве координатной поверхности в этой системе используется поверхность эллипсоида Красовского.

3. Местные (МСК-50, МСК-50.2, Московская)
Под местной системой координат понимается условная система координат, устанавливаемая в отношении ограниченной территории, не превышающей территорию субъекта Российской Федерации, начало отсчета координат и ориентировка осей координат которой смещены по отношению к началу отсчета координат и ориентировке осей координат единой государственной системы координат, используемой при осуществлении геодезических и картографических работ. Местные системы координат устанавливаются для проведения геодезических и топографических работ при инженерных изысканиях, строительстве и эксплуатации зданий и сооружений, межевании земель, ведении кадастров и осуществлении иных специальных работ. Обязательным требованием при установлении местных систем координат является обеспечение возможности перехода от местной системы координат к государственной системе координат, который осуществляется с использованием параметров перехода (ключей). Каждая местная система координат может создаваться с одной или несколькими трех или шести градусными зонами. Параметры местных систем координат и ключи перехода к государственной системе координат (формулы и правила, по которым координаты точек в одной системе можно получить в другой системы) устанавливает Росреестр по согласованию с Минобороны РФ.

Определение положения точек в различных СК

Положение точек непосредственно на физической поверхности Земли или в околоземном пространстве, а также на поверхности земного эллипсоида могут определяться в различных как прямолинейных, так и криволинейных системах координат. Однако в теории и практике производства топографо-геодезических работ наибольшее распространение получили следующие СК:

Пространственные прямоугольные декартовы СК – Х, У, Z;
Отличительной особенностью использования в геодезии системы пространственных полярных геодезических координат является то, что ее основная плоскость выбирается на поверхности и представляет собой плоскость геодезического горизонта (или параллельная плоскости горизонта). За полярную ось принимается линия пересечения плоскости горизонта с плоскостью геодезического меридиана данной точки О (полюса системы) с положительным направлением на северный полюс Земли. Положение точки Q в этой СК определяется тремя величинами (координатами): S – длина прямой OQ; А – геодезический азимут (двугранный угол между плоскостью геодезического меридиана начальной точки О и нормальной плоскостью точки О, содержащей точку Q); Zг – зенитное расстояние (угол между нормалью точки О и линией OQ).

Различные виды систем полярных координат как пространственных, так и на поверхностях (сферы, эллипсоида, плоскости);

Пространственные прямоугольные топоцентрические координаты – Xт, Ут, Zт;
Системы плоских прямоугольных декартовых координат – х, у и H (геодезической высоты)

Название Местных Систем Координат по регионам

МСК-01 Республика Адыгея
МСК-02 Республика Башкортостан
МСК-03 Республика Бурятия
МСК-04 Республика Алтай
МСК-05 Республика Дагестан
МСК-06 Республика Ингушетия
МСК-07 Кабардино-Балкарская Республика
МСК-08 Республика Калмыкия
МСК-09 Республика Карачаево-Черкесия
МСК-10 Республика Карелия
МСК-11 Республика Коми
МСК-12 Республика Марий Эл
МСК-13 Республика Мордовия
МСК-14 Республика Саха (Якутия)
МСК-15 Северная Осетия — Алания
МСК-16 Республика Татарстан
МСК-18 Удмуртская Республика
МСК-20 Чеченская Республика
МСК-21 Чувашская Республика
МСК-22 Алтайский край
МСК-23 Краснодарский край
МСК-24 Красноярский край
МСК-25 Приморский край
МСК-26 Ставропольский край
МСК-27 Хабаровский край
МСК-28 Амурская область
МСК-29 Архангельская область
МСК-30 Астраханская область
МСК-31 Белгородская область
МСК-32 Брянская область
МСК-33 Владимирская область
МСК-34 Волгоградская область
МСК-35 Вологодская область
МСК-36 Воронежская область
МСК-37 Ивановская область
МСК-38 Иркутская область
МСК-39 Калининградская область
МСК-40 Калужская область
МСК-41 Камчатский край
МСК-42 Кемеровская область
МСК-43 Кировская область
МСК-44 Костромская область
МСК-45 Курганская область
МСК-46 Курская область
МСК-47 Ленинградская область
МСК-1964 город Санкт-Петербург
МСК-48 Липецкая область
МСК-49 Магаданская область
МСК-50 Московская область
МГГТ Москва
МСК-51 Мурманская область
МСК-52 Нижегородская область
МСК-53 Новгородская область
МСК-54 Новосибирская область
МСК-55 Омская область
МСК-56 Оренбургская область
МСК-57 Орловская область
МСК-58 Пензенская область
МСК-59 Пермский край
МСК-60 Псковская область
МСК-61 Ростовская область
МСК-62 Рязанская область
МСК-63 Самарская область
МСК-64 Саратовская область
МСК-65 Сахалинская область
МСК-66 Свердловская область
МСК-67 Смоленская область
МСК-68 Тамбовская область
МСК-69 Тверская область
МСК-70 Томская область
МСК-71 Тульская область
МСК-72 Тюменская область
МСК-73 Ульяновская область
МСК-74 Челябинская область
МСК-75 Забайкальский край
МСК-76 Ярославская область
МСК-83 Ненецкий автономный округ
МСК-86 Ханты-Мансийский автономный округ — Югра
МСК-87 Чукотский автономный округ

Обновлено: 19.05.2023

Как отмечалось выше, наиболее рациональна в практическом отношении плоская прямоугольная система координат. Однако применить её на поверхности эллипсоида проблематично. Известно, что поверхность сфероида нельзя изобразить на плоскости без искажений, то есть невозможно соблюсти полного подобия геометрических построений на плоскости и поверхности эллипсоида. Поэтому найти такой закон изображения поверхности эллипсоида на плоскости проекции, искажения на которой были бы минимальны, является задачей первостепенной важности.

Файлы: 1 файл

К-р по геодезии №1№2.doc

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

Высшего профессионального образования

«Магнитогорский государственный технический университет

Кафедра геологии и геодезии

Контрольная работа №1

Выполнил: студент Казиканов Н. Г.

Преподаватель: Колесатова О. С.

Магнитогорск 2011 г.

1. Зональная и условная система плоских прямоугольных координат.

Зональная прямоугольная система координат

Как отмечалось выше, наиболее рациональна в практическом отношении плоская прямоугольная система координат. Однако применить её на поверхности эллипсоида проблематично. Известно, что поверхность сфероида нельзя изобразить на плоскости без искажений, то есть невозможно соблюсти полного подобия геометрических построений на плоскости и поверхности эллипсоида. Поэтому найти такой закон изображения поверхности эллипсоида на плоскости проекции, искажения на которой были бы минимальны, является задачей первостепенной важности.

В настоящее время в картографии законов изображения поверхности эллипсоида на плоскости множество, что зависит от целевого назначения проекций. В геодезии желателен такой закон изображения, который обеспечивал всю территорию страны единой системой плоскихпрямоугольных координат, что приводит к единообразию математической обработки результатов измерений и единой системе создания топографических карт. При этом искажения на плоскости проекции должны быть минимальными или искажались бы не все элементы геодезических построений, а только некоторые из них, например, длины сторон, и чтобы в пределах определённой зоны масштаб изображения можно было считать постоянным. Такими свойствами обладают конформные проекции:

а) угловые искажения отсутствуют;

б) масштаб в данной точке одинаков по всем направлениям;

в) в пределах небольших участков масштаб можно считать практически постоянным;

г) изображение небольших участков подобно натуре.

Перечисленными свойствами обладает принятая в странах СНГ система плоских прямоугольных координат в проекции Гаусса-Крюгера. Гаусс предложил и обосновал эту проекцию, а Крюгер дал рабочие формулы для вычислений в этой проекции.

Система координат Гаусса-Крюгера определяется следующими условиями:

а) изображение на плоскости равноугольное;

б) осевой меридиан и экватор изображаются на плоскости проекции прямыми линиями, принимаемыми за оси абсцисс и ординат с началом координат в точке их пересечения;

в) масштаб вдоль осевого меридиана постоянен и принят равным единице.

В своей проекции, которая называется равноугольной поперечно-цилиндрической, Гаусс предложил поверхность эллипсоида делить меридианами на зоны шириной 6о по долготе (рис.5).

Здесь возникает новое понятие меридиана – осевой, объяснение которому будет дано ниже.

Графически проекция Гаусса может быть объяснена следующим образом (рис.6).

В цилиндр соответствующего диаметра помещается сфероид таким образом, чтобы средний (осевой) меридиан зоны касался поверхности цилиндра, а крайние меридианы развертывались на поверхность цилиндра с минимальным искажением.

Если прокатить сфероид (шар- для лучшего понимания геометрии проекции) по цилиндру, поворачивая его на 6о и выделяя полученную зону на поверхности цилиндра, то после разрезания последнего вдоль полюсов и развёртки его на плоскость получим общую картину изображения эллипсоида в проекции Гаусса-Крюгера

Как видим, в каждой зоне имеются две взаимно перпендикулярные прямые линии, отвечающие условию системы плоских прямоугольных координат. В каждой зоне осевой меридиан принимается за ось абсцисс, а экватор (общий для всех зон) за ось ординат с положительным направлением соответственно на север и восток. Линии, параллельные осевому меридиану и экватору, образуют координатную сетку. Таким образом, получена система плоских прямоугольных координат, жёстко привязанная к поверхности эллипсоида, – начало координат для каждой зоны имеет: широту В = 0, долготу LO,N = N x 6o – 3o. Здесь N – номер зоны, Всего зон 60 и счёт их ведётся к востоку от Гринвича

Из анализа рис.6 видно, что наличие 60 зон приводит к тому, что разные точки (а, в, с, d) в разных зонах могут иметь одинаковые координаты. Чтобы избежать возникающей неопределённости и отрицательных значений ординат, немецкий учёный Баумгард предложил к величине ординаты прибавлять 500 км и к полученному результату приписывать номер зоны. Например, действительные координаты точки D в четвёртой зоне (см. рис.7) равны:

Х = 6 311 524 м, У = – 182 365 м.

По предложению Баумгарда эти координаты будут записаны:

Х = 6 311 524 м, У = 317 635 м.

Как показали исследования, шестиградусные координатные зоны вполне удовлетворяют по точности мелкомасштабные съёмки. В проекции Гаусса-Крюгера искажения длин линий возрастают по мере удаления от осевого меридиана и достигают максимальных значений на краю зоны.

Величина искажения может быть рассчитана по формуле

где Уср= , R – средний радиус кривизны, Х1 У1 и Х2 У2 – координаты концов отрезка S.

Искажения в длинах линий на краю зоны достигают в относительном выражении величин . Такие искажения недопустимы при крупномасштабных съёмках – при съёмке в масштабе 1:5000 и крупнее.

Решение этой проблемы было предложено Баумгардом, путём применения трёхградусных координатных зон с долготой осевых меридианов

где n – номер трёхградусной зоны.

В трёхградусной зоне максимальные искажения изображений в 4 раза меньше максимальных искажений шестиградусных зон.

В некоторых случаях для участков, расположенных на краях зон, целесообразно применять частные системы координат, принимая за осевой меридиан, линию в середине участка. Действительно, как показал анализ влияния кривизны Земли на измерения длин линий (см. рис.2), в пределах 20 км поверхность эллипсоида можно принимать за плоскость.

При длине d = 10 км и R = 6371 км d = 1 см, что в относительном выражении будет равно .

Эта величина соответствует максимальной точности при измерении расстояний на земной поверхности. Отсюда следует, что в практическом отношении, особенно, на краях зоны целесообразно использовать частные плоские прямоугольные системы координат.

2. Ориентирование линий. Азимуты, румбы, дирекционные углы.

Ориентировать линию – значит определить ее направление относительно меридиана.

Вообразим в данной точке земной поверхности отвесную линию; плоскость, проходящая через эту отвесную линию и ось вращения Земли, называется плоскостью географического или истинного меридиана в данной точке.

Направление истинного меридиана определяется на данной точке при помощи астрономических наблюдений, а направление магнитного меридиана – при помощи магнитной стрелки, которая устанавливается под действием земного магнетизма в направлении магнитного меридиана.

Конец стрелки, обращенный северному полюсу Земли, называют северным, а другой конец – южным. Магнитный меридиан в данной точке земной поверхности, как правило, не совпадает с истинным: угол между ними называется склонением магнитной стрелки.

Склонение называют восточным или западным, смотря по тому, отклоняется ли северный конец магнитной стрелки к востоку или к западу от географического меридиана.

Для ориентирования линий служат углы ориентирования, называемыеазимутами, дирекционными углами и румбами.

Азимутом называется горизонтальный угол, отсчитываемый от северного направления меридиана по ходу часовой стрелки до направления данной линии;азимуты могут иметь значения от 0 до 360°. Азимут называется истинным, если он отсчитывается от истинного меридиана, и магнитным, если он отсчитывается от магнитного меридиана.

Если линия СЮ есть истинный меридиан, то и азимуты этих линий будут истинными азимутами. Если же СЮ – магнитный меридиан, то эти углы – магнитные азимуты.

Так как меридианы в разных точках Земли не параллельны между собой, тоазимут одной и той же линии в разных ее точках различен. Так, для линии М1М2азимут в точке М1 равен А1, в точке М2—А2; азимут А2 отличается от азимутаА1 на величину угла γ между меридианами этих точек. Этот угол γ называется сближением меридианов. Его легко представить, если провести мысленно через одну из двух данных точек направление, параллельное меридиану другой точки. На угол γ представлен как угол между меридианом С2Ю2 точки М2 и направлением С1

Если точки М1 и М2 близки, то можно принять γ=0, и тогда А2=А1, а меридианы в соответствующих точках можно рассматривать как параллельные.

Азимут данного направления называется прямым, а противоположного – обратным.

Для линии M1M2 А1 и А2—прямые азимуты этой линии в разных ее точках, А2 – обратный азимут той же линии в точке М2.

т. е. прямой и обратный азимуты одной и той же линии в разных ее точках отличаются между собой на 180°+ γ; прямой и обратный азимуты данной линии в одной и той же точке различаются на 180°.

Дирекционные углы применяются в геодезии для ориентирования линий относительно осевого меридиана, или линии, ему параллельной. дирекционный угол отсчитывается от северного направления осевого меридиана или линии, ему параллельной, по ходу часовой стрелки до направления данной линии в пределах 0 – 360°.

т. е. разность между истинным азимутом и дирекционным углом какой-нибудь линии в данной на ней точке равна сближению истинного меридиана в этой точке с осевым меридианом зоны.

Но обыкновенно сближение меридианов для точек, расположенных к западу от осевого меридиана, выражают числом отрицательным. В отличие от азимута Адирекционный угол а одной и той же линии в разных ее точках остается постоянным.

На небольших участках, когда по малости величиной γ можно пренебречь и меридианы в различных точках рассматривать как параллельные между собой, то один из них, с которым совмещают ось абсцисс произвольной системы прямоугольных координат, принимается за осевой меридиан. В таких случаях направления линий определяются дирекционными углами.

Иногда на практике удобнее определять направление линий острыми углами. В этих

случаях пользуются румбами. Румбом, называется острый горизонтальный угол отсчитываемый от ближайшего направления меридиана (северного или южного) до данной линии. Румбы могут иметь значения только в пределах между 0 и 90°. Чтобы определить румбом направление данной линии относительно меридиана, необходимо, кроме числового значения румба, указать название той четверти, в которой проходит линия.

В зависимости от того, отсчитываются ли румбы от магнитного или истинного меридиана, их называют магнитными или истинными.

Для линий юго-восточного направления азимут и румб в сумме составляют 180°. Если линия проходит в юго-западной четверти, то ее азимут больше румба на 180°,

и, наконец, для линий северо-западного направления а зимут и румб составляют в сумме 360°. Эти соотношения позволяют переводить азимуты в румбы и обратно. Прямой и обратный румбы в одной и той же точке данной линии равны, но имеют названия противоположных четвертей. Прямой и обратный румбы одной и той же линии в разных ее точках имеют названия противоположных четвертей и отличаются на величину сближения меридианов в этих точках. Осевые прямой и обратный румбы одной и той же линии в разных ее точках имеют названия противоположных четвертей, но равны по величине.

Вычисление исходных дирекционных углов линий;

решение прямой геодезической задачи.

Правый угол при т. В (между сторонами АВ и ВС) β1=189º 59,2´;

Правый угол при т. С (между сторонами ВС и СD) β2=159º 28,0´;

Найти: дирекционные углы линии ВС и СD, если известны дирекционный угол αАВ линии АВ и измеренные по правому ходу углы β1 и β2.

Дирекционный угол вычисляется по правилу: дирекционный угол последующей стороны равен дирекционному углу предыдущей стороны плюс 180º и минус горизонтальный угол, справа по ходу лежащий

Системы координат в геодезии. Достоинства и недостатки. Геодезические пространственные координаты. Определение сближения меридианов и масштаба изображения в проекции Гаусса-Крюгера. Связь геодезических пространственных общеземных и референцных координат.

Рубрика	Геология, гидрология и геодезия
Вид	курсовая работа
Язык	русский
Дата добавления	05.04.2016
Размер файла	617,1 K

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное

учреждение высшего образования

«СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

Кафедра физической геодезии и дистанционного зондирования

СИСТЕМЫ КООРДИНАТ И ПРЕОБРАЗОВАНИЯ МЕЖДУ НИМИ

Новосибирск 2016 г.

Содержание

1. Системы координат в геодезии. Достоинства и недостатки

1.1 Геодезические пространственные координаты

1.2 Пространственные прямоугольных координаты

1.3 Плоские прямоугольные координаты Гаусса – Крюгера

2. Рабочие формулы

2.1Соотношения между геодезическими пространственными и пространственными прямоугольными координатами

2.2 Определение плоских прямоугольных координат Гаусса – Крюгера по геодезическим координатам

2.3 Определение сближения меридианов и масштаба изображения в проекции Гаусса – Крюгера

2.4 Связь прямоугольных пространственных общеземных и референцных координат

2.5 Связь геодезических пространственных общеземных и референцных координат

3. Технологические схемы преобразования

4. Ввод местной системы координат (СКМ) плоских прямоугольных координат Гаусса – Крюгера

Список используемой литературы

1. Системы координат в геодезии. Достоинства и недостатки

1.1 Геодезические пространственные координаты

Положение любой точки пространства задаются: геодезической широтой (В), геодезической долготой (L) и геодезической высотой (Н). (Рис.1.)

Рисунок 1- Система геодезических пространственных координат

Геодезической широтой (В) – это острый угол, образованный нормалью Kn к поверхности эллипсоида вращения и плоскостью его экватора. Нормалью к поверхности в заданной точке является перпендикуляр к касательной плоскости в точке . Она изменяется от 0? на экваторе до 90? на полюсах. Для соответствующих полушарий различают северные и южные широты.

Геодезическая параллель – это координатная линия равных широт. Представляет собой линию пересечения поверхности эллипсоида вращения и плоскости, перпендикулярной оси его вращения. Практически все геодезические параллели – это окружности разного радиуса (R). Параллель максимального радиуса, называемая экватором будет получена, если секущая плоскость будет проходить через центр эллипсоида.

Геодезическая долгота (L) – это двугранный угол, образованный плоскостями геодезических меридианов начального (Гринвича) и точки К (меридиан РG). Она может изменяться от 0? до 360? и отсчитываться от Гринвичского меридиана на восток или изменяться от 0? до 180?. При этом необходимо указать, к западу или к востоку от Гринвича находится точка К.

Геодезическим меридианом называется часть линии пересечения поверхности эллипсоида вращения и плоскости, содержащей ось вращения и заключенная между полюсами. Геодезические меридианы являются половинами эллипсов и имеют одинаковый размер.

Геодезическая высота (Н) – это отрезок нормали К к поверхности эллипсоида вращения, заключенный между этой поверхностью и точкой К (Н = К). Она обычно положительна, но есть особые случаи, когда она может быть отрицательной (например, в шахтах, карьерах и т. п.). Её не следует путать с нормальной и ортометрической высотами, которые отсчитываются от начальных уровенной (геоид) или почти уровенной (квазигеоид) поверхностей соответственно. Бывают различия между ними, которые могут достигать десятков метров. На нашей территории РФ в каталогах координат пунктов и реперов хранятся нормальные высоты.

Достоинства данной системы координат:

1. Координаты (B), (L), (H) определяет положение любой точки пространства.

2. Едина для всей поверхности Земли, и это позволяет объединять в общей координатной системе материалы съемочных, картографических и геодезических работ.

3. В этой системе координатными линиями являются геодезические меридианы и параллели, которые относятся к поверхности эллипсоида вращения. Они являются основными линиями любой картографической проекции. Используются для составления карт и объединения съемочных картографических материалов в единое целое.

4. Положение нормали к поверхности принятого эллипсоида определяют геодезические широта и долгота. Это используется при определении составляющих уклонений отвесных линий и проведении множества других исследований поверхности Земли.

5. Геодезические широта и долгота точек К и одинаковы, а высоты разные (= 0). Использование данной системы позволяет общую сложную задачу по определению координат разделить на две подзадачи и тем самым уменьшая размерность вектора совместно вычисляемых координат точек. На объекте создаются плановыегеодезические сети для определения B, L (х, у) а по результатам нивелирования вычисляется третья координата т.е. (высота).

6. Поправки в измеренные величины (редукции) за переход с физической поверхности Земли на поверхность эллипсоида вращения незначительны.

· Позволяет использовать приближенные (грубые) значения аргументов для их вычисления.

· Не учитывает такие поправки при выполнении работ невысокой точности.

Недостатки данной системы координат:

1. Решение прямых и обратных геодезических задач выполняется по очень сложным, большим формулам.

2. Применение геодезических пространственных координат будет невыгодным или даже практически невозможным при использовании спутниковых технологий создания геодезических сетей поправки в результаты измерений за редукцию на поверхность эллипсоида вращения станут большими, соизмеримыми с самими измерениями.

1.2 Пространственные прямоугольные координаты

геодезия координата меридиана масштаб

В этой системе координаты положения точек в пространстве задаются тремя координатами X,Y,Z.(рис.2.)

Рисунок 2- Система пространственных прямоугольных координат

Достоинства данной системы:

1. Можно определить положение любой точки пространства.

2. Для применения этой системы не нужно иметь поверхность относимости (поверхность эллипсоида вращения).

3. Отсутствует необходимость в редуцировании результатов полевых измерений на поверхность относимости. Практически незаменима при математической обработке результатов спутниковых измерений.

Недостатки данной системы:

1. Нельзя уменьшить размерность задач по определению координат точек (размерность вектора координат). Необходимо сразу выполнять данное количество измерений, которое позволит нам вычислить главные три координаты определяемых точек.

2. Неудобно использовать в топографии, и при проектировании и строительстве инженерных сооружений.

3. Система плоских прямоугольных координат Гаусса – Крюгера является основной системой для решения практических задач геодезии, топографии, землеустройства. Такой переход осуществляется в два этапа:

· необходимо вычислить пространственные геодезические координаты по пространственным прямоугольным координатам;

· необходимо вычислить плоские прямоугольные координаты по геодезическим.

1.3 Система плоских прямоугольных координат Гаусса – Крюгера

Применение систем пространственных прямоугольных или пространственных геодезических координат становится неудобным и обременительным при производстве топографо-геодезичеких работ. Таких как производство топографических и кадастровых съемок, геодезическое обеспечение проектирования, строительства и эксплуатации инженерных сооружений и других. Наибольшее применение находит система плоских прямоугольных координат.(рис.3.)

Ввод такой системы координат сопряжен с отображением поверхности модели Земли на плоскости по какому-либо математическому закону. Закон, связывающий геодезические координаты на поверхности эллипсоида вращения и плоские прямоугольные координаты, называется проекцией. В математической картографии есть огромное количество геодезических проекций и соответствующих им систем плоских прямоугольных координат. При изображении поверхности модели Земли на плоскости в любой проекции неизбежно деление ее на отдельные участки, которые принято называть зонами.

На территории России используется проекция Гаусса-Крюгера. В этой проекцией поверхность эллипсоида вращения делится на зоны геодезическими меридианами. В нашей стране установлены размеры зон в шесть и три градуса по долготе. Первые считаются основными, поэтому математическая обработка результатов измерений и оформление материалов топосъемок выполняются в шестиградусных зонах. Трехградусные зоны используются при производстве крупномасштабного картографирования (масштабов 1:5000 и крупнее) и вводе систем региональных плоских прямоугольных координат. Меридианы, проходящие посредине зон, называются осевыми.

Рисунок 3- Система плоских прямоугольных координат Гаусса – Крюгера

1. Отсутствие искажений вследствие равноугольности проекции.

2. Зоны в проекции Гаусса-Крюгера совершенно одинаковые и поэтому вид применяемых формул для связи систем координат и редуцирования измеренных величин на плоскость не будут зависеть от номера зоны.

3. Пара действительных координат абсцисса х и ордината у однозначно определяет положение любой точки внутри одной зоны.

4. Применение системы плоских прямоугольных координат позволяет значительно упростить решение многих задач геодезии, топографии, землепользования. Поэтому в массовых работах она является основной.

Недостатков у проекции Гаусса-Крюгера, по мнению специалистов, два. Во-первых, в данной системе координат возникают трудности при математической обработке результатов полевых измерений на объектах, вытянутых вдоль параллели и занимающих значительную площадь (объектах, расположенных в нескольких зонах). Во-вторых, действительные плоские прямоугольные координаты не дают представление о том, где на поверхности земли находится точка. Она может располагаться в любой из 60 шестиградусных зон. Для того чтобы по значениям координат можно было судить о местоположении точки на Земле в каталогах координат пунктов принято помещать так называемые условные координаты Гаусса-Крюгера x’, y’. При этом действительные и условные координаты связаны соотношениями

Действительные и условные абсциссы равны. Для получения условной ординаты надо к действительной прибавить номер зоны умноженный на 10 6 и 500000. Перенос начала координат к востоку на 500 километров необходим для исключения отрицательных координат.

2. Рабочие формулы

2.1 Соотношения между геодезическими пространственными и пространственными прямоугольными координатами

Формулу для вычисления геодезической долготы

Формулу для вычисления расстояния :

Формулу для вычисления начального значения широты

Итерационный процесс по определению геодезической широты (i=1,2,3- номер итерации)

Определение геодезической высоты

2.2 Определение плоских прямоугольных координат Гаусса – Крюгера по геодезическим координатам

Вычисление долготы осевого меридиана зоны с номером n и получение разности долгот l

Определение действительных плоских прямоугольных координат Гаусса -Крюгера х, у

Определение условных плоских прямоугольных координат Гаусса – Крюгера

2.3 Определение сближения меридианов и масштаба изображения в проекции Гаусса – Крюгера

2.4 Связь прямоугольных пространственных общеземных и референцных координат

Формулы преобразования координат из общеземной системы в референцную

Параметры эллипсоида-, , , Дm, x, y, z

Формулы для обратного преобразования

2.5 Связь геодезических пространственных общеземных и референцных координат

Геодезические пространственные общеземные координаты находятся по формулам

Поправки ,, находятся по следующим формулам

Формулы обратного перехода от геодезических пространственных общеземных координат к геодезическим пространственным референцным координатам

3. Технологические схемы преобразования координат из одной системы в другую. Привести рабочие формулы, необходимые для этих преобразований. Сделать выбор оптимальной технологической схемы

1)*В качестве исходных данных заданы прямоугольные пространственные координаты точки в системе координат ПЗ-90.02.

*В результате решения задач необходимо получить прямоугольные пространственные, геодезические пространственные и плоские прямоугольные координаты Гаусса – Крюгера в системах ПЗ-90.02, СК-42, СК-95. Приведем одну из возможных технологических схем преобразования координат.(рис.4.)

Рисунок 4- Технологическая схема преобразования координат

На первом и втором этапах технологии необходимо выполнить переход от пространственных прямоугольных координат точки в системе ПЗ-90.02, заданных в качестве исходных данных, к пространственным прямоугольным координатам в системах СК-42 и СК-95. На этих этапах вычислений необходимо использовать формулы (28)-(30), приведенные в разделе 2.4. Числовые значения семи параметров преобразования координат для систем СК-42 и СК-95 приведены в тексте задания на выполнение курсовой работы.

Третий, четвертый и пятый этапы технологической схемы посвящены решению одной, с теоретической точки зрения, задачи – вычислению геодезических пространственных координат по пространственным прямоугольным координатам. Формулы (1)-(10) для ее решения приведены в разделе 2.1 данного пособия. При этом в зависимости от системы координат (вертикальные столбцы технологической схемы) необходимо использовать параметры разных эллипсоидов вращения. В СК-42 и СК-95 должны применяться параметры эллипсоида Красовского, а в системе ПЗ-90.02 – параметры общеземного эллипсоида ПЗ-90.

На заключительных этапах (шестой, седьмой и восьмой этапы) должен выполняться переход от геодезических широт и долгот точки к ее плоским прямоугольным координатам Гаусса – Крюгера. Формулы для решения таких задач приведены в разделе 2.2 под номерами (11)-(21). Такая задача должна решаться три раза с различными значениями параметров эллипсоидов и геодезических координат точки.

2) Рассмотрим еще одну возможную схему преобразования координат (рис.2.)

* В качестве исходных данных заданы прямоугольные пространственные координаты точки в системе координат ПЗ-90.02.

* В результате решения задач необходимо получить прямоугольные пространственные, геодезические пространственные и плоские прямоугольные координаты Гаусса – Крюгера в системах ПЗ-90.02, СК-42, СК-95 (рис.5.)

Рисунок 5- Технологическая схема преобразования координат

На первом и втором этапах технологии необходимо выполнить переход от пространственных прямоугольных координат точки в системе ПЗ-90.02, заданных в качестве исходных данных, к пространственным прямоугольным координатам в системах СК-42 и СК-95. На этих этапах вычислений необходимо использовать формулы (28)-(30), приведенные в разделе 2.4. Числовые значения семи параметров преобразования координат для систем СК-42 и СК-95 приведены в тексте задания на выполнение курсовой работы (см. прил. 1).

На третьем этапе мы выполняем вычисление геодезических пространственных координат по пространственным прямоугольным координатам. Формулы (1)-(10) для ее решения приведены в разделе 2.1 данного пособия. (см.прил. 3)

На четвертом и пятым этапе мы находим пространственные координаты для СК-42 и СК-95 через пространственные координаты ПЗ-90.02. Для этого мы используем формулы (31-51), приведенные в разделе 2.5. В данном случае параметры эллипсоида берутся как средние значения между параметрами эллипсоид Красовского и параметрами ПЗ-90.02 (см.прил. 5-6)

На заключительных этапах (шестом, седьмом и восьмом этапы) должен выполняться переход от геодезических широт и долгот точки к ее плоским прямоугольным координатам Гаусса – Крюгера. Формулы для решения таких задач приведены в разделе 2.2 под номерами (11)-(21). Такая задача должна решаться три раза с различными значениями параметров эллипсоидов и геодезических координат точки. (см.прил. 7)

Первая технологическая схема будит более уместна для использования, так как по этой схеме полученные координаты будут точнее, чем при использовании второй схеме

4. Ввод местной системы координат (СКМ) плоских прямоугольных координат Гаусса-Крюгера

Вторая причина вызвана желанием геодезистов уменьшить величины поправок за переход на плоскость в проекции Гаусса – Крюгера с тем, чтобы их можно было не учитывать при работе на своем объекте (населенном пункте, строительной площадке, карьере и т. п.), занимающем небольшую площадь. Максимальная площадь объекта не может превышать территорию субъекта РФ.

• Для учеников 1-11 классов и дошкольников
• Бесплатные сертификаты учителям и участникам

ООО Учебный центр

Реферат по дисциплине:

Исполнитель: Яцентюк Ольга Александровна

Москва 2018 год.

1.Системв координат применяемые в топографии

2.Определение географических координат

3.Определение прямоугольных координат

Система координат необходима для определения расстояний и направлений на земле. Географическая система координат, использующая широту и долготу, хороша для определения положений объектов, расположенных на сферической поверхности Земли или промежуточном глобусе ( reference globe ). Поскольку чаще всего мы будем иметь дело с двухмерными картами, спроецированными с этого глобуса, нам потребуется одна или несколько систем координат, соответствующих различным проекциям. Такие системы координат на плоскости называются картографическими (геодезическими) прямоугольными системами координат,они позволяют нам точно указывать положение объектов на плоских картах.

Декартова система координат. Классическая система прямоугольных координат. Каждая точка определяется парой величин — координатой Х (абсциссой) и координатой Y (ординатой).

1. Системы координат, применяемые в топографии

Координатами называются угловые и линейные величины (числа), определяющие положение точки на какой-либо поверхности или в пространстве.Существует много различных систем координат, которые находят широкое применение в различных областях науки и техники.

В топографии применяют такие системы координат, которые позволяют наиболее просто и однозначно определять положение точек земной поверхности как по результатам непосредственных измерений на местности, так и с помощью карт. К числу таких систем относятся географические, плоские прямоугольные, полярные и биполярные координаты.

В системе географических координат положение любой точки земной поверхности относительно начала координат определяется в угловой мере. За начало у нас и в большинстве других государств принята точка пересечения начального (Гринвичского) меридиана с экватором. Являясь, таким образом, единой для всей нашей планеты, система географических координат удобна для решения задач по определению взаимного положения объектов, расположенных на значительных расстояниях друг от друга. Поэтому в военном деле эту систему используют главным образом для ведения расчетов, связанных с применением боевых средств дальнего действия, например баллистических ракет, авиации и др.

Система плоских прямоугольных координат является зональной; она установлена для каждой шестиградусной зоны, на которые делится поверхность Земли при изображении ее на картах в проекции Гаусса, и предназначена для указания положения изображений точек земной поверхности на плоскости (карте) в этой проекции.

Началом координат в зоне является точка пересечения осевого меридиана с экватором, относительно которой и определяется в линейной мере положение всех остальных точек зоны. Начало координат зоны и ее координатные оси занимают строго определенное положение на земной поверхности. Поэтому система плоских прямоугольных координат каждой зоны связана как с системами координат всех остальных зон, так и с системой географических координат.

Применение линейных величин для определения положения точек делает систему плоских прямоугольных координат весьма удобной для ведения расчетов как при работе на местности, так и на карте. Поэтому в войсках эта система находит наиболее широкое применение. Прямоугольными координатами указывают положение точек местности, своих боевых порядков и целей, с их помощью определяют взаимное положение объектов в пределах одной координатной зоны или на смежных участках двух зон.

Системы полярных и биполярных координат являются местными системами. В войсковой практике они применяются для определения положения одних тачек относительно других на сравнительно небольших участках местности, например при целеуказании, засечке ориентиров и целей, составлении схем местности и др. Эти системы могут быть связаны с системами прямоугольных и географических координат.

Система плоских полярных координат состоит из точки О — начало координат, или полюса, и начального направления ОР, называемого полярной осью. Положение точки М на местности или на карте в этой системе определяется двумя координатами: углом положения Q, который измеряется по ходу часовой стрелки от полярной оси до направления на определяемую точку М (от 0 до 360°), и расстоянием OM=D.

В зависимости от решаемой задачи за полюс принимают наблюдательный пункт, огневую позицию, исходный пункт движения и т. п., а за полярную ось – географический (истинный) меридиан, магнитный меридиан (направление магнитной стрелки компаса) или же направление на какой-либо ориентир.

Система плоских биполярных (двухполюсных) координат состоит из двух полюсов А и В и общей оси АВ, называемой базисом или базой засечки. Положение любой точки М относительно двух данных на карте (местности) точек А и В определяется координатами, которые измеряются на карте или на местности.

Этими координатами могут служить либо два угла положения, определяющих направления с точек А и В на искомую точку М, либо расстояния D1=AМ и D2=BM до нее. Углы положения при этом, как показано на рис. 17, измеряются в точках А и В или от направления базиса (т. е. ÐА=ВАМ и ÐB=ABM) или от других каких-либо направлений, проходящих через точки Л и В и принимаемых за начальные. Например, на рис. 17 место точки М определено углами положения Q1 н Q2, измеренными от направлений магнитных меридианов.

Указанные выше системы координат определяют плановое положение точек на поверхности земного эллипсоида. Чтобы определить положение точки на физической поверхности Земли, дополнительно к плановому положению указывают ее высоту (отметку) над уровнем моря. В СССР счет высот ведется от среднего уровня Балтийского моря, от нульпункта Кронштадтского водомерного поста. Высоты точек земной поверхности над уровнем моря называются абсолютными, а их превышения над какой-либо другой точкой — относительными.

2. Определение географических координат

Различают географические координаты, полученные из наблюдений небесных светил, называемые астрономическими, и из геодезических измерений земной поверхности, называемые геодезическими.

Астрономические координаты определяют положение точек местности на поверхности геоида (рис. 1 и 2), на которую эти точки проектируются отвесными линиями с физической поверхности Земли.

Геодезические координаты указывают положение точек на поверхности земного эллипсоида, куда они проектируются нормалями к этой поверхности.

При создании топографических карт применяются преимущественно геодезические координаты. Поэтому, говоря о географических координатах, в дальнейшем будем иметь в виду лишь геодезические координаты.

Географическими координатами какой-либо точки, например М (рис. 18), являются ее широта В и долгота L.

Широта точки — угол, составленный плоскостью экватора и нормалью к поверхности земного эллипсоида, проходящей через данную точку. Счет широт ведется по дуге меридиана в обе стороны от экватора, от 0 до 90°. Широты точек северного полушария называются северными, а южного — южными.

Долгота точки — двугранный угол между плоскостью начального (Гринвичского) меридиана и плоскостью меридиана данной точки. Счет долгот ведется по дуге экватора или параллели в обе стороны от начального меридиана, от 0 до 180°. Долготы точек, расположенных к востоку от Гринвича до 180°, называются восточными, а к западу — западными.

По топографическим картам масштабов 1:25000 — 1:200000 географические координаты определяют с помощью шкал, имеющихся на рамке каждого листа (рис. 19). Цена деления шкал на картах масштабов 1:25000 — 1:100000 равна 10″, а на карте масштаба 1 : 200000 — Г. Для определения географических координат по склеенной карте внутри рамки каждого листа проставлены короткие черточки, показывающие выходы меридианов и параллелей внутрь листа с интервалом через V.

На картах масштабов 1:500000 (рис. 20) и 1:1000000 кроме шкал на рамках имеются и сами линии меридианов и параллелей, образующие сетку географических координат (географическую сетку).

Оцифровка шкал и линий сетки географических координат показана на рис. 19 и 20.

Чтобы определить широту какой-либо точки, например точки М, по карте масштабов 1 : 25 000 — 1 : 200 000 (рис. 19), надо приложить линейку к этой точке так, чтобы она проходила через одноименные деления (или их доли) на шкалах западной и восточной сторон рамки, и по одной из этих шкал сделать отсчет. Аналогично, пользуясь шкалами северной и южной сторон рамки определяют и долготу точки.

При определении географических координат по карте масштаба 1:500000 или 1:1000000 вместо шкал на рамке карты линейку прикладывают к одноименным делениям (или их долям), находящимся на меридианах (параллелях), ближайших к определяемой точке (рис. 20).

3. Определение прямоугольных координат.

Особенности системы плоских прямоугольных координат, применяемой в топографии. За оси координат (рис. 21) в этой системе приняты изображение осевого меридиана координатной зоны — ось абсцисс Х и изображение экватора — ось ординат Y.

Оси координат делят зону на четверти, счет которых ведется по ходу часовой стрелки от положительного направления оси X. За положительное направление осей принимают: для оси абсцисс — направление на север, для оси ординат — на восток.

Положение какой-либо точки, например М, указывается ее расстоянием от осей координат: абсциссой х и ординатой у.

Чтобы не иметь дела с отрицательными ординатами, условились значение ординаты у осевого меридиана каждой зоны принимать равным 500 км. Этим самым ось Х как бы переносят к западу от осевого меридиана на 500 км.

Так как в каждой зоне числовые значения ординат повторяются, то для того чтобы по координатам точки можно было определить, к какой зоне она относится, к значению ординаты слева приписывается номер зоны.

Прямоугольная координатная сетка на топографических картах. На всех листах карт (кроме карты масштаба 1:1000000) имеется сетка квадратов (рис. 19), которую называют прямоугольной координатной сеткой.

Линии сетки (рис. 22) проведены параллельно осям координат через 2 см на картах масштабов 1 : 50 000 — 1 : 500 000 и через 4 см на карте масштаба 1 : 25 000, что соответствует целому числу километров на местности. Поэтому прямоугольную координатную сетку называют также километровой, а ее линии — километровыми.

Координатная сетка используется для определения прямоугольных координат точек, отыскания на карте местоположения различных объектов при докладах, постановке задач, составлении донесений, для быстрой глазомерной оценки расстояний, площадей, определения направлений и ориентирования карты.

Километровые линии , ближайшие к углам рамки листа карты, подписываются полным числом километров, остальные — сокращенно, последними двумя цифрами. Таким образом, подпись 5588 (рис. 19) у крайней снизу горизонтальной линии означает, что эта линия проходит в 5588 км к северу от экватора. Подпись 6394 у крайней слева вертикальной километровой линии означает, что она находится в шестой зоне и проходит в 394 км от начала счета ординат, т. е. на 106 км западнее осевого меридиана зоны.

В том случае, когда приходится пользоваться картой в сложенном виде, определить числовое значение километровых линий можно по подписям, расположенным внутри листа у пересечений горизонтальных линий с вертикальными (рис. 19).

Дополнительная сетка на стыке координатных зон. Так как вертикальные километровые линии параллельны осевому меридиану своей зоны, а осевые меридианы соседних зон между собой не параллельны, то при смыкании сеток двух зон линии одной из них расположатся под углом к линиям другой. Вследствие этого при работе на стыке зон могут возникнуть затруднения с использованием координатных сеток, так как они будут относиться к разным осям координат.

Чтобы устранить это неудобство, в каждой зоне на всех листах карт, расположенных в пределах 2° к востоку и западу от границы зоны, обозначена координатная сетка смежной зоны. Чтобы не затемнять такие листы карты, эта сетка показана на карте лишь ее выходами за рамку листа (рис. 23). Ее оцифровка представляет собой продолжение нумерации километровых .линий смежной зоны.

Километровой сеткой смежной зоны пользуются тогда, когда работа ведется с листами карт на стыке двух зон и требуется пользоваться на всех этих листах единой системой координат. Эту сетку проводят карандашом на листах карт одной из этих зон, соединяя по линейке противоположные концы одноименных километровых (вертикальных и горизонтальных) линий сетки соседней зоны.

Использование километровой сетки для определения прямоугольных координат точек и нанесения на карту точек по их координатам. Чтобы указать приближенное местоположение какого-либо пункта на карте, достаточно назвать квадрат сетки, в котором он расположен. Для этого сначала читают (называют) оцифровку горизонтальной километровой линии, образующей южную сторону квадрата, а затем вертикальной линии, образующей его западную сторону, т. е. сначала абсциссу, а затем ординату юго-западного угла квадрата.

Для более точного указания положения какой-либо точки определяют ее координаты. Для этого к координатам южной и западной линий квадрата, в котором она находится, добавляют расстояния до определяемой точки от этих линий, записывая отдельно абсциссу х и ординату у точки.

Определяя, например, координаты точки Л (рис. 24), сначала записывают абсциссу нижней километровой линии квадрата, в котором находится эта точка (т. е. 78). Затем измеряют по масштабу (расстояние (по перпендикуляру) от точки А до этой километровой линии, т. е. отрезок т, и полученную величину (1,225км) добавляют к абсциссе линии. Так получается абсцисса х точки А.

Для получения ординаты у точки записывают ординату левой (вертикальной) стороны того же квадрата (т. е. 14) и затем добавляют к ней расстояние, измеренное по перпендикуляру от определяемой точки до этой линии, т. е. отрезок п (в нашем примере 1,365 км).

Таким образом, координаты точки Л будут

x =79225 м; у =15 365 м.

Так как в данном случае при определении координат точки цифровое обозначение километровых линий было записано не полностью а, лишь последними двумя цифрами (78 и 14), то такие координаты называют сокращенными координатами точки Л.

Если же оцифровку километровых линий записывать полностью, то получим полные координаты. Для точки Л:

x=6179225 м; у=8315365 м.

Если сокращенные подписи километровых линий на данном участке карты не повторяются, а потому положение объектов на нем определяется однозначно, то пользуются сокращенными координатами. В противном случае применяются полные координаты.

При определении координат точек по карте и нанесении точек на карту по координатам измерения выполняют циркулем или линейкой с миллиметровыми делениями. Для этой цели могут применяться также специальные координатомеры, которые несколько упрощают работу, заменяя циркуль и масштабную линейку.

Координатомеры (отдельно для карты масштаба 1:25000 и карты масштаба 1:50000) имеются, например, на артиллерийском целлулоидном круге АК-3 (рис. 27). Каждый из них представляет по площади квадрат километровой сетки на карте соответствующего масштаба, разбитый на более мелкие квадраты со сторонами по 200 м в масштабе карты. Наименьшее деление на координатомере, изготовленном в масштабе 1: 25 000, соответствует 20 м, в масштабе 1 : 50 000 — 50 м.

Точность измерения (отсчета) прямоугольных координат на карте по поперечному масштабу примерно равна ±0,2 мм, по миллиметровой линейке и координатомеру ±0,5 мм.

Координатная сетка на карте представляет собой сетку квадратов, образованных линиями, параллельными координатным осям зоны. Линии сетки проведены через целое число километров. Поэтому координатную сетку называют также километровой сеткой, а ее линии километровыми.

На карте 1:25000 линии, образующие координатную сетку, проведены через 4 см, то есть через 1 км на местности, а на картах 1:50000-1:200000 через 2 см (1,2 и 4 км на местности соответственно). На карте 1:500000 наносятся лишь выходы линий координатной сетки на внутренней рамке каждого листа через 2 см (10 км на местности). При необходимости по этим выходам координатные линии могут быть нанесены на карту.

На топографических картах значения абсцисс и ординат координатных линий подписывают у выходов линий за внутренней рамкой листа и девяти местах на каждом листе карты. Полные значения абсцисс и ординат в километрах подписываются около ближайших к углам рамки карты координатных линий и около ближайшего к северо-западному углу пересечения координатных линий. Остальные координатные линии подписываются сокращенно двумя цифрами (десятки и единицы километров). Подписи около горизонтальных линий координатной сетки соответствуют расстояниям от оси ординат в километрах.

Подписи около вертикальных линий обозначают номер зоны (одна или две первые цифры) и расстояние в километрах (всегда три цифры) от начала координат, условно перенесенного к западу от осевого меридиана зоны на 500 км. Например, подпись 6740 означает: 6 – номер зоны, 740 – расстояние от условного начала координат в километрах.

Цель работы: Изучить способы преобразования координат в различных системах: референцной и общеземной; геодезической, прямоугольной плоской и пространственной. Положение точек на поверхности земного эллипсоида, на поверхности Земли и в пространстве может быть определено с помощью следующих систем координат. В геодезии наибольшее распространение получили следующие системы: система прямоугольных пространственных координат (X,Y,Z). система геодезических пространственных координат (B,L,H). система геоцентрических широт и геодезических долгот (Ф,L). система плоских прямоугольных координат Гаусса-Крюгера (x,y).

Вложенные файлы: 1 файл

Kursova_rabota_VG_shevchenko (1).docx

Сибирская Государственная Геодезическая Академия

Кафедра высшей геодезии

На тему: Системы координат и преобразования между ними.

Ст. гр. ПГ-31 Афонин К. Ф.

Цель работы: Изучить способы преобразования координат в различных системах: референцной и общеземной; геодезической, прямоугольной плоской и пространственной.

1) Задание на выполнение курсовой работы.

2) Прямоугольные пространственные координаты точки в системе координат ПЗ-90.02.

3) Параметры эллипсоидов Красовского и ПЗ-90:

а=6378245м, е 2 =0.00669342162,

а=6378136.3м, е 2 =0.00669436619.

4) Элементы ориентирования системы координат СК-42 относительно системы ПЗ-90.02:

x=23.93м, y=-141.03м, z=-79.98м,

5) Элементы ориентирования системы координат СК-95 относительно системы ПЗ-90.02:

Положение точек на поверхности земного эллипсоида, на поверхности Земли и в пространстве может быть определено с помощью следующих систем координат. В геодезии наибольшее распространение получили следующие системы:

1. система прямоугольных пространственных координат (X,Y,Z).
2. система геодезических пространственных координат (B,L,H).
3. система геоцентрических широт и геодезических долгот (Ф,L).
4. система плоских прямоугольных координат Гаусса-Крюгера (x,y).

1.1. Система прямоугольных пространственных координат (X,Y,Z).

За начало координат принимается центр эллипсоида О (рис.1.1.). Ось OZ располагается но полярной оси эллипсоида РОР₁, ось ОХ — в плоскости экватора в меридиане РЕР₁, который принимается за начальный; ось OY — в плоскости экватора, но в меридиане РКР_1: плоскость которого составляет с плоскостью начального меридиана угол в 90°.

Таким образом, положение точки М поверхности эллипсоида определяется координатами: X=M_IM_II, Y=OM_II, Z=MM_I.

Пространственные координаты X, У, Z до последнего времени имели небольшое применение как в теоретических выводах, так и в практических вычислениях. Это объясняется тем, что как сами измерения, так и вычисления производились на поверхности Земли и заключались в вычислении координат ее точек, расстояний между этими точками.

1. Позволяет однозначно определять положение точки в пространстве.
2. Для вычисления координат не нужно редуцировать результаты измерений на поверхности эллипсоида. Эту систему удобно применять при математической обработки результатов спутниковых измерений.

1. Нельзя разорвать тройку координат.
2. Нельзя уменьшить размерность вектора координат, как в системе геодезических и пространственных координат.
3. Нет формул прямого перехода к плоским прямоугольным координатам.

1.2.Система геодезических пространственных координат (B,L,H).

Геодезической широтой точки М называется острый угол В, образованный нормалью Мп к поверхности эллипсоида в данной точке и плоскостью экватора ERE₁ .

Геодезическая широта обозначается буквой В. Широты отсчитываются от экватора к северу и югу и называются, соответственно, северными и южными широтами. Пределы измерения от 0 0 до 90 0 .

Геодезическая долгота L точки М – двугранный угол РМР₁Е, образованный плоскостью начального меридиана РЕР₁ и плоскостью меридиана данной точки.

Долгота измеряется от 0 0 до 360 0 или от 0 0 до 180 0 на восток и запад от гринвичского меридиана.

В качестве начального меридиана для счета долгот в настоящее время повсеместно принят меридиан, проходящий через Гринвичскую обсерваторию.

Геодезическая высота Н – отрезок нормали к поверхности эллипсоида вращения, заключенный между этой поверхностью и данной точки.

Иначе говоря, предварительно редуцируя результаты измерений на поверхность референц- эллипсоида, мы приводим их к нулевой высоте (Н — 0). Этим существенно упрощается решение геодезических задач: от вычисления трех координат (B, L, H), определяющих положение точки в пространстве, переходят к вычислению двух (B, L). Это целесообразно для точек земной поверхности, для которых Н всегда мало, а следовательно малы и редукции. При значительных высотах Н указанное редуцирование измеренных величин становится нецелесообразным, чем и вызывается необходимость перехода в этом случае к системе пространственных прямоугольных координат.

1. Едина для всей поверхности эллипсоида и, таким образом, объединяет в общей для всей земной поверхности координатной системе геодезические, съемочные и картографические материалы.
2. Геодезическая широта и долгота определяют положение нормали к эллипсоиду, проходящей через данную точку.
3. ) Координатные линии в этой системе (параллели и меридианы) являются основными линиями любой картографической проекции.

1. Сложность решения всех геодезических задач.
2. Из-за необходимости редуцирования результатов на поверхность эллипсоида накладно использовать для обработки результатов спутниковых наблюдений.

1.3. Система геоцентрических широт и геодезических долгот (Ф,L).

Одной из координат в этой системе является геодезическая долгота L, которая определяет меридианный эллипс, проходящий через точку М. Положение точки М на этом эллипсе в рассматриваемой системе координат определяется геоцентрической широтой Ф. Геоцентрическая широта определяется как угол между радиусом-вектором р точки М и плоскостью экватора или, что все равно, большой полуосью меридианного эллипса. На рис.1.3. ОМ — радиус-вектор р меридианного эллипса, проведенного через точку М; угол МОЕ₁ — геоцентрическая широта Ф точки М.

Эта система координат в высшей геодезии применяется редко; чаще в астрономии, теории фигуры Земли и математической картографии.

1. Позволяет однозначно определить положение точки в пространстве.
2. В этой системе координат иногда формулы сфероидической геодезии записываются короче, выглядят проще, чем формулы геодезической.
3. Эта система имеет вспомогательные значения.

1.4. Система плоских прямоугольных координат Гаусса-Крюгера (x,y).

Практически необходимо иметь координаты пунктов геодезической сети в прямоугольной плоской системе прямолинейных координат для того, чтобы можно было легко использовать геодезические данные при выполнении различного рода проектных работ, при землеустройстве и т. д. Это вызывает необходимость введения проекции поверхности эллипсоида на плоскость, т. е. изображения частей земной поверхности на плоскости по определенному закону.

В настоящее время в России принята проекция Гаусса — Крюгера или система прямоугольных плоских прямолинейных координат в конформной проекции Гаусса, в которой производят вычисления всех пунктов опорной геодезической сети.

Читайте также:

  

• И кант о нравственном воспитании реферат

  

• Режимы работы электрических сетей реферат

  

• Реферат развитие ипотечного кредитования в россии

  

• Педагог как субъект педагогического процесса реферат

  

• Реферат на тему безногие земноводные