Пусть у функции
аргументы являются не независимыми
переменными, а связаны между собой
соотношениями
:
Эти соотношения
называются условиями связи. Пусть
координаты точки
удовлетворяют этим уравнениям.
Говорят, что функция
имеет в точке
условный (относительный) минимум(максимум) при условиях связи
если существует такая окрестность
точки
,
что для любой точки
из этой окрестности, координаты которой
удовлетворяют заданным условиям связи,
выполняется неравенство
.
Иначе говоря,
условный(относительный) максимум(минимум) – это наибольшее (наименьшее)
значение функции в точке
по отношению не ко всем точкам из
некоторой окрестности точки
,
а только к тем из них, которые связаны
между собой условиями связи.
Задачу отыскания
условного экстремума функции можно
решить двумя способами.
1. Метод исключения.
Если уравнения связи можно разрешить
относительно части переменных. Найденные
выражения подставляются в исследуемую
функцию, тем самым задача нахождения
условного экстремума сводится к
исследованию на экстремум функции одной
переменной. Рассмотренный выше пример,
когда мы исследовали заданную функцию
на границе области, по сути своей, был
на нахождение условного экстремума
функции. И решали мы его именно методом
исключения.
2. Метод Лагранжа.
Этот метод обычно используется, когда
уравнения связи неразрешимы относительно
переменных. В таком случае задача
нахождения условного экстремума сводится
к исследованию на обычный экстремум
функции Лагранжа:
.
Коэффициенты
называются множителями Лагранжа.
Необходимое
условие экстремума выражается системой
уравнений:
Решая эту систему,
находим точки
,
подозрительные на экстремум. Их может
быть несколько.
Достаточным условием
экстремума в каждой из исследуемых
точек
является положительная (минимум) или
отрицательная (максимум) определенность
второго дифференциала
функции Лагранжа в этой точке.
Рассмотрим два метода
решения задачи об условном экстремуме
функции на примерах.
Пример
20. Методом исключения части переменных
найти экстремум функции
(1)
при
условиях связи
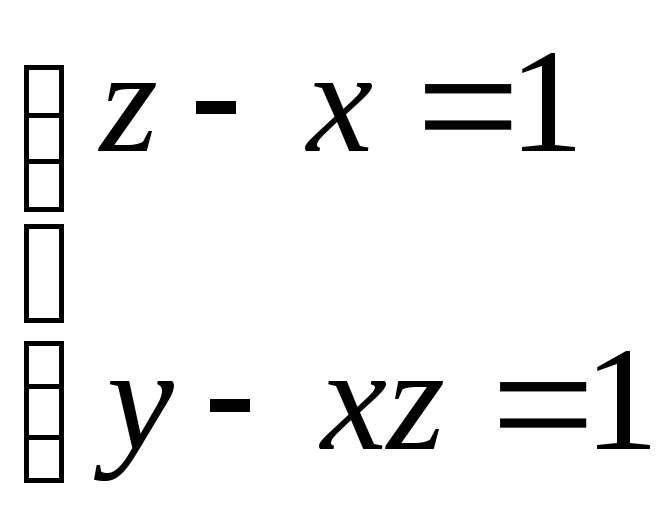(2)
Решение.Решая
систему уравнений (2) относительно
,
находим
(3)
Подставляя выражения
(3) в равенство (1), приходим к функции
одной переменной
:
,
для
которой рассмотрим задачу о безусловном
экстремуме. Так как
при
,
то функция
имеет единственную точку возможного
экстремума. Поскольку вторая производная
в этой точке
,
то в точке
функция
имеет минимум. Подставляя
в (3), находим соответствующие значения
и
:
,
.
Итак, функция (1) при условиях связи (2)
имеет в точке
минимум, причём
Пример
21. Методом Лагранжа найти экстремум
функции (1) при условиях связи (2).
Решение. Составим
функцию Лагранжа
и
рассмотрим систему уравнений:
Она имеет единственное
решение:
,
т.е.
–
единственная точка возможного экстремума
функции (1) при условиях связи (2). Отметим,
что в окрестности точки
система (2) определяет единственную
пару неявных функций
.
Хотя в данном случае их легко найти в
явном виде, нам эти явные выражения не
понадобятся. Предполагая, что в систему
(2) подставлено её решение
,
и дифференцируя полученные тождества,
приходим к равенствам:
(4)
Теперь вычислим второй
дифференциал функции Лагранжа:
и подставим
и выражение (4) для
;
получаем
Отсюда следует, что
функция (1) при условиях связи (2) имеет
в точке
условный минимум.
Пример
22. Найти наименьшее значение для
суммы
четырех положительных чисел при условии,
что их произведение сохраняет постоянную
величину, т.е.
.
Решение. Составим
функцию Лагранжа
и
рассмотрим систему уравнений:
Из первых четырех
равенств следует, что
,
поэтому,
учитывая условие связи, получаем, что
.
.
Подставим найденное
значение
в выражение для функции Лагранжа и
найдем ее второй дифференциал в точке
:
.
Продифференцируем
условие связи в той же точке:
,
.
Выразив из последнего,
например,
и подставив в выражение для второго
дифференциала функции Лагранжа, получим,
что
Очевидно, что выражение,
стоящее справа, положительно при любых
значениях дифференциалов переменных,
следовательно, в данной точке функция
Лагранжа будет достигать минимума.
Тогда и заданная функция
в точке с координатами
>0
будет достигать требуемого, а именно:
своего наименьшего значения
при
заданном условии
.
53
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 27 сентября 2021 года; проверки требуют 2 правки.
Усло́вный экстре́мум — максимальное или минимальное значение, которое функция, определённая на множестве 
и принимающая вещественные значения, достигает в предположении, что значения некоторых других функций с той же областью определения подчинены определённым ограничительным условиям (если такие дополнительные условия отсутствуют, то говорят о безусловном экстремуме)[1].
В частности, множество может быть подмножеством арифметического векторного пространства 
а упомянутые ограничительные условия, в свою очередь, могут быть заданы в виде равенств или неравенств. Ниже рассматриваются классическая задача на условный экстремум, в которой все условия заданы в виде равенств, а также задача Лагранжа — одна из классических задач вариационного исчисления[1].
Постановка классической задачи на условный экстремум[править | править код]
Пусть 
— открытое множество, и на нём заданы функции 
Пусть 
Уравнения
называют уравнениями связей (терминология заимствована из механики).
Пусть на определена также функция 
Точка 
называется точкой условного экстремума данной функции относительно уравнений связей 
если она является точкой обычного (безусловного) экстремума функции 
на множестве 
(модификация определения экстремума сводится к тому, что в нём вместо окрестностей в , то есть 
, рассматриваются окрестности в , то есть 
)[2].
Метод множителей Лагранжа для решения задачи условного экстремума[править | править код]
Теорема[править | править код]
Предположим, что все фигурирующие в постановке классической задачи на условный экстремум функции непрерывно дифференцируемы, и пусть 
— точка условного экстремума функции при выполнении уравнений связей 
Тогда в этой точке градиенты 
являются линейно зависимыми, т. e. 
но 
[3].
Числа 
называются множителями Лагранжа и определены с точностью до умножения на произвольную ненулевую константу. Наибольший интерес представляет случай, когда 
(тогда, умножив все 
на подходящую ненулевую константу, можно сделать множитель 
равным 
и, таким образом, вообще исключить его из рассмотрения). В такой ситуации вместо только что сформулированной теоремы пользуются следующим следствием из неё[4].
Следствие[править | править код]
Если — точка условного экстремума функции относительно уравнений связей и в ней градиенты 
линейно независимы, то 
такие, что в данной точке 
В координатном виде это векторное равенство эквивалентно выполнению равенств
где 
[3].
Равенствам 
можно дать следующую интерпретацию. Предположим, что для чисел 
данные равенства выполняются, и объединим их в столбец 
Составим функцию Лагранжа:
где — уже произвольные числа. Тогда при 
точка является стационарной точкой функции Лагранжа, а равенства могут быть записаны в виде
эти соотношения и являются условиями стационарности точки 
Добавляя к ним уравнения связей получаем 
уравнений относительно неизвестных 
[5][6].
Пример. Найдём стороны прямоугольника максимальной площади, вписанного в окружность 
Здесь 
Составив функцию Лагранжа
и записав условия её стационарности в точке условного экстремума
находим: 
и 
(прямоугольник максимальной площади оказался квадратом)[6].
Достаточное условие условного экстремума[править | править код]
Если равенства при выполнены и при этом (дополнительно предполагается, что в точке все фигурирующие в постановке классической задачи на условный экстремум функции двукратно непрерывно дифференцируемы) 
представляет собой отрицательно (положительно) определённую квадратичную форму переменных 
то является точкой строгого условного максимума функции (строгого условного минимума для положительно определенной формы). Если же рассматриваемая квадратичная форма не является знакоопределённой, тогда условного экстремума нет[7].
Задача Лагранжа[править | править код]
Данная задача относится к вариационному исчислению и является одним из возможных обобщений классической задачи на условный экстремум. В задаче Лагранжа требуется найти непрерывно дифференцируемую функцию 
заданную на отрезке ![{displaystyle [t_{0},t_{1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ffe2ab6560fe2acf9a63ad878ad482164b79012d)
и доставляющую экстремум (максимум или минимум) функционалу
(точкой обозначена операция дифференцирования по 
) при фиксированных граничных условиях 
и выполнении уравнений связей
где 
[8][9].
В данной задаче также применим метод множителей Лагранжа. Предполагая уравнения связей независимыми, вводят в рассмотрение 
неизвестных функций 
и сводят исходную задачу к задаче безусловной оптимизации, заменяя подынтегральную функцию функцией
в качестве аналога равенств (т. e. в роли необходимых условий экстремума) теперь выступают уравнения Эйлера — Лагранжа, имеющие в рассматриваемом случае вид
где 
Из этих 
обыкновенных дифференциальных уравнений, дополненных уравнениями связей, находят (с учётом имеющихся граничных условий) неизвестных функций 
[10].
См. также[править | править код]
- Метод множителей Лагранжа
- Экстремум
Примечания[править | править код]
- ↑ 1 2 Вапнярский И. Б. . Условный экстремум // Математическая энциклопедия. Т. 5 / Гл. ред. И. М. Виноградов. — М.: Советская энциклопедия, 1985. Архивная копия от 17 ноября 2020 на Wayback Machine — 1248 стб. — Стб. 565—566.
- ↑ Кудрявцев, т. 2, 1981, с. 92—93.
- ↑ 1 2 Кудрявцев, т. 2, 1981, с. 96.
- ↑ Алексеев, Тихомиров, Фомин, 1979, с. 48.
- ↑ Кудрявцев, т. 2, 1981, с. 96—97.
- ↑ 1 2 Корн и Корн, 1978, с. 336.
- ↑ Кудрявцев, т. 2, 1981, с. 110.
- ↑ Алексеев, Тихомиров, Фомин, 1979, с. 40—41, 80—81.
- ↑ Корн и Корн, 1978, с. 346—349.
- ↑ Корн и Корн, 1978, с. 348—349.
Литература[править | править код]
- Алексеев В. М., Тихомиров В. М., Фомин С. В. . Оптимальное управление. — М.: Наука, 1979. — 432 с.
- Корн Г., Корн Т. . Справочник по математике для научных работников и инженеров. 4-е изд. — М.: Наука, 1978. — 832 с.
- Кудрявцев Л. Д. . Курс математического анализа. Т. 2. — М.: Высшая школа, 1981. — 584 с.
Условный экстремум
4 раздела
от теории до практики
2 примера
Примеры решения задач
видео
Примеры решения задач
-
Понятие условного экстремума.
Начать изучение
-
Прямой метод отыскания точек условного экстремума.
Начать изучение
-
Метод множителей Лагранжа.
Начать изучение
-
Несколько замечаний о методе множителей Лагранжа.
Начать изучение
Понятие условного экстремума.
Пусть на открытом множестве (G subset boldsymbol{R}^{n}) заданы функции (f_{0}(x)), (f_{1}(x), ldots, f_{m}(x)), причем (m < n), и пусть (E) — множество точек множества (G), удовлетворяющих системе уравнений
$$
f_{1}(x) = 0, ldots, f_{m}(x) = 0.label{ref1}
$$
Уравнения eqref{ref1} будем называть уравнениями связей (или просто связями).
Определение 1.
Точка (x^{0} = (x_{1}^{0}, ldots, x_{n}^{0}) in G) называется точкой условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in G cap S_{delta}(x^{0})) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Определение 2.
Точка (x^{0} in G) называется точкой строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, если найдется такая окрестность (S_{delta}(x^{0})), что для всех (x in dot{S}_{delta}(x^{0}) cap G) выполнено неравенство (f_{0}(x) geq f_{0}(x^{0})).
Аналогично определяются точки условного максимума. Точки условного максимума и минимума называются точками условного экстремума.
Прямой метод отыскания точек условного экстремума.
Предположим, что из системы уравнений eqref{ref1} можно выразить какие-либо (m) переменных (x_{i}) через остальные переменные. Тогда, подставив вместо соответствующих переменных (x_{i}) их выражения через остальные (n-m) переменных в функцию (f_{0}(x)), получим функцию (F) от (n-m) переменных.
Задача о нахождении точек экстремума функции (f_{0}(x)) при наличии связей eqref{ref1} сведется к задаче нахождения обычного (безусловного) экстремума функции (F), зависящей от (n-m) переменных.
Пример 1.
Найти точки условного экстремума функции (z = 1-x^{2}-y^{2}), если (x+y = 1).
Решение.
(vartriangle) Уравнение связи (x+y = 1) легко разрешается относительно переменной (y), а именно (y = 1-x). Подставив это выражение для (y) в функцию (z = 1-x^{2}-y^{2}), получаем, что (z = 1-x^{2}-(1-x)^{2} = 2x-2x^{2}). Функция (2x-2x^{2}) имеет максимум при (x = frac{1}{2}). Точка ((frac{1}{2}, frac{1}{2})) является точкой условного максимума функции (z(x, y)) при наличии связи (x+y = 1), причем (z_{max} = displaystylefrac{1}{2}). (blacktriangle)
Замечание 1.
Прямой метод нахождения условного экстремума редко бывает эффективным ввиду трудности разрешения уравнений связей относительно какой-либо группы переменных.
Метод множителей Лагранжа.
Определение 3.
Рассмотрим функцию (n+m) переменных
$$
L(x, lambda) = f_{0}(x)+lambda_{1}f_{1}(x)+ldots+lambda_{m}f_{m}(x),nonumber
$$
где (x in G), а (lambda = (lambda_{1}, ldots, lambda_{m}) in boldsymbol{R}^{m}). Числа (lambda_{1}, ldots, lambda_{m}) называются множителями Лагранжа, а функция (L(x, lambda)) называется функцией Лагранжа.
Будем говорить, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, если
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{1}} (x^{0}, lambda^{0}) = 0, ldots, frac{partial L}{partial x_{n}} (x^{0}, lambda^{0}) = 0\
&\
& displaystylefrac{partial L}{partial lambda_{1}} (x^{0}, lambda^{0}) = f_{1}(x^{0}) = 0, ldots, frac{partial L}{partial lambda_{m}} (x^{0}, lambda^{0}) = f_{m}(x^{0}) = 0.
end{array}label{ref2}
$$
Теорема 1.
(Теорема Лагранжа).
Пусть (x^{0}) — точка условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{0, m}), непрерывно дифференцируемы в окрестности точки (x^{0}), причем в точке (x^{0}) ранг матрицы Якоби
$$
A = begin{pmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{1}}{partial x_{n}}(x)\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x)&ldots&displaystylefrac{partial f_{m}}{partial x_{n}}(x)end{pmatrix}label{ref3}
$$
равен (m).
Тогда найдутся такие множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}), что ((x^0, lambda^0)) будет стационарной точкой функции Лагранжа.
Доказательство.
(circ) Так как (m < n), а ранг матрицы Якоби в точке (x^{0}) равен (m), то хотя бы один из миноров этой матрицы порядка (m) отличен от нуля.
Без ограничения общности можно считать, что
$$
begin{vmatrix}displaystylefrac{partial f_{1}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{1}}{partial x_{m}}(x^{0})\………&…..&…….\displaystylefrac{partial f_{m}}{partial x_{1}}(x^{0})&ldots&displaystylefrac{partial f_{m}}{partial x_{m}}(x^{0})end{vmatrix} neq 0,label{ref4}
$$
так как выполнения условия eqref{ref4} всегда можно добиться, перенумеровывая переменные и уравнения связей в нужном порядке.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)). Тогда существует окрестность (K'(x^{0}) = K’_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) такая, что
$$
f_{0}(x)-f_{0}(x^{0}) geq 0 mbox{при всех} x in E cap K’ (x^{0}).label{ref5}
$$
В силу непрерывности частных производных и выполнения условия eqref{ref4} можно применить теорему о неявных функциях. В силу этой теоремы найдется такая окрестность
$$
K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}) subset K'(x^{0}),nonumber
$$
в которой система уравнений связей eqref{ref1} определяет переменные (x_{1}, ldots, x_{m}) как неявные функции переменных (x_{m+1}, ldots, x_{m}). Это означает, что найдется единственный набор непрерывно дифференцируемых в окрестности (K’_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) функций (varphi_{i}(x_{m+1}, ldots, x_{n})), (i = overline{1, m}), таких, что
$$
varphi_{i}(x_{m+1}^{0}, ldots, x_{m}^{0}) = x_{i}^{0}, i = overline{1, m};label{ref6}
$$
$$
f_{i}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n}) equiv 0,label{ref7}
$$
$$
(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n})) in K_{1}(x_{1}^{0}, ldots, x_{m}^{0})nonumber
$$
при ((x_{m+1}, ldots, x_{n}) in K_{2}(x_{1}^{0}, ldots, x_{m}^{0})), (i = overline{1, m}).
Другими словами, множество (E cap K(x^{0})) можно задать следующим образом:
$$
begin{array}{cc}
& E cap K(x^{0}) = {x: x = (x_{1}, ldots, x_{n}), (x_{m+1}, ldots, x_{n}) in K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0}),\
& \
& x_{i} = varphi_{i}(x_{m+1}, ldots, x_{n}), i = overline{1, m}}.
end{array}label{ref8}
$$
Так как (K(x^{0}) subset K'(x^{0})), то из неравенства eqref{ref5} следует, что функция (f_{0}(x)) принимает на множестве (E cap K(x^{0})) наименьшее значение в точке (x^{0}). Если взять представление множества (E cap K(x^{0})) в виде eqref{ref8}, то сложная функция
$$
F(x_{m+1}, ldots, x_{n}) = f_{0}(varphi_{1}(x_{m+1}, ldots, x_{n}), ldots, varphi_{m}(x_{m+1}, ldots, x_{n}), x_{m+1}, ldots, x_{n})label{ref9}
$$
определена в окрестности (K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})) и принимает в этой окрестности наименьшее значение в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Следовательно, в силу необходимых условий экстремума должно выполняться равенство (dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = 0). Воспользовавшись инвариантностью формы первого дифференциала и равенством eqref{ref9}, получаем, что
$$
sum_{k=1}^{n} frac{partial f_{0}(x^{0})}{partial x_{k}} dx_{k} = 0.label{ref10}
$$
В равенстве eqref{ref10} (dx_{m+1}, ldots, dx_{n}) есть дифференциалы независимых переменных, a (dx_{1}, ldots, dx_{n}) — дифференциалы функций (varphi_{i}, ldots, varphi_{m}), зависящих от (x_{m+1}, ldots, x_{n}). Для краткости будем говорить о независимых и зависимых дифференциалах.
Найдем связи между зависимыми и независимыми дифференциалами. Дифференцируя тождества eqref{ref7} в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})) и пользуясь инвариантностью формы первого дифференциала, получаем
$$
sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} dx_{k} = 0, i = overline{1, m}.label{ref11}
$$
Умножая равенства eqref{ref11} на множители (lambda_{i}) и складывая полученные равенства с равенством eqref{ref10}, находим
$$
0 = sum_{k=1}^{n} left(frac{partial f_{0}}{partial x_{k}}+sum_{i=1}^{m} frac{partial f_{i}}{partial x_{k}} lambda_{i}right)_{x = x^{0}} dx_{k} = sum_{k=1}^{n} frac{partial L(x^{0}, lambda)}{partial x_{k}} dx_{k},label{ref12}
$$
где (L(x^{0}, lambda)) есть функция Лагранжа.
Подберем множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}) так, чтобы коэффициенты при зависимых дифференциалах в равенстве eqref{ref12} обратились в нуль, то есть
$$
frac{partial L(x^{0}, lambda)}{partial x_{k}} = frac{partial f_{0}(x^{0})}{partial x_{k}}+sum_{i=1}^{m} lambda_{i}^{0} frac{partial f_{i}(x^0)}{partial x_{k}} = 0, k = overline{1, m}.label{ref13}
$$
Система уравнений eqref{ref13} единственным образом определяет множители (lambda_{1}^{0}, ldots, lambda_{m}^{0}), так как ее определитель eqref{ref4} отличен от нуля.
При выполнении условий eqref{ref13} уравнение eqref{ref12} примет вид
$$
sum_{k=m+1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} dx_{k} = 0.label{ref14}
$$
Так как дифференциалы независимых переменных (dx_{m+1}, ldots, dx_{n}), могут принимать любые значения, то из eqref{ref14} следует, что
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = m+1, ldots, n.label{ref15}
$$
Объединяя равенства eqref{ref13} и eqref{ref15}, получаем
$$
frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} = 0, k = overline{1, n}.nonumber
$$
Так как точка (x^{0} in E) и, следовательно, удовлетворяет уравнениям связей, то
$$
frac{partial L(x^{0}, lambda^{0})}{partial lambda_{j}} = f_{i}(x^{0}) = 0, j = overline{1, m}.nonumber
$$
Таким образом, ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)). (bullet)
Второй дифференциал функции Лагранжа, вычисленный при фиксированных (lambda_{1}^{0}, ldots, lambda_{m}^{0}) по переменным ((x_{1}, ldots, x_{n})) в точке ((x_{1}^{0}, ldots, x_{n}^{0})), будем обозначать через (d_{xx}^{2}L(x^{0}, lambda^{0})).
Таким образом,
$$
d_{xx}^{2}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}.label{ref16}
$$
Иногда вместо (d_{xx}^{2}L(x^{0}, lambda^{0})) будем писать (d^{2}L(x^{0}, lambda^{0})).
Обозначим через (E_{T}) следующее линейное многообразие в (boldsymbol{R}^{n}):
$$
E_{T} = left{xi = (xi_{1}, ldots, xi_{n}) in boldsymbol{R}^{n}: sum_{k=1}^{n} frac{partial f_{i}(x^{0})}{partial x_{k}} xi_{k} = 0, i = overline{1, m}right}.label{ref17}
$$
Равенства eqref{ref11} означают, что (dx = (dx_{1}, ldots, dx_{n}) in E_{T}).
Теорема 2.
Пусть (x^{0}) есть точка условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}, и пусть функции (f_{i}(x)), (i = overline{1, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0}), причем в точке (x^{0}) ранг функциональной матрицы eqref{ref3} равен (m).
Тогда найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, a (d^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}).
Доказательство.
(circ) Так как выполнены все условия теоремы 1, то найдутся множители Лагранжа (lambda_{1}^{0}, ldots, lambda_{m}^{0}) такие, что ((x^{0}, lambda^{0})) будет стационарной точкой функции Лагранжа, то есть выполняются условия eqref{ref2}. Повторяя рассуждения теоремы 1, рассмотрим сложную функцию eqref{ref9}, имеющую безусловный экстремум в точке ((x_{m+1}^{0}, ldots, x_{n}^{0})). Так как эта функция имеет непрерывные частные производные второго порядка, то, в силу теоремы о необходимом условии минимума должно быть выполнено условие (d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) geq 0).
Воспользовавшись правилом нахождения второго дифференциала сложной функции и формулой eqref{ref9}, находим, что
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{0}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{0}}{partial x_{k}}(x^{0}) d^{2}x_{k} geq 0.label{ref18}
$$
Дифференцируя два раза в точке (x_{m+1}^{0}, ldots, x_{n}^{0}) тождества eqref{ref7}, получаем равенства
$$
sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} f_{i}(x^{0})}{partial x_{k} partial x_{j}} dx_{k} dx_{j}+sum_{k=1}^{n} frac{partial^{2} f_{i}}{partial x_{k}}(x^{0}) d^{2}x_{k} = 0.label{ref19}
$$
Если умножить каждое из равенств eqref{ref19} на соответствующий множитель Лагранжа (lambda_{i}^{0}) и сложить с неравенством eqref{ref18}, то получаем неравенство
$$
d_{xx}^{2}L(x^{0}, lambda^{0})+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} geq 0.label{ref20}
$$
Последняя сумма в неравенстве eqref{ref20} равна нулю, так как ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа и в ней выполняются условия eqref{ref2}. Таким образом, (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при ((dx_{1}, ldots, dx_{n}) in E_{T}). (bullet)
Теорема 3.
(Достаточные условия условного экстремума).
Пусть функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка в окрестности точки (x^{0} in boldsymbol{R}^{n}), причем в точке (x^{0}) ранг функциональной матрицы (3) равен (m), и пусть ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа (L(x, lambda)).
Тогда если (d_{xx}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) является точкой условного строгого минимума функции (f_{0}(x)) при наличии связей eqref{ref1}. Если (d_{xx}L(x^{0}, lambda^{0})) есть отрицательно определенная квадратичная форма при (dx in E_{T}), то (x^{0}) — точка условного строгого максимума. Если (d_{xx}L(x^{0}, lambda^{0})) есть неопределенная квадратичная форма при (dx in E_{T}), то (x^{0}) не есть точна условного экстремума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Доказательство.
(circ) Пусть
$$
E = {x: f_{i}(x) = 0, i = overline{1, m}}.label{ref21}
$$
По условию теоремы функции (f_{i}(x)), (i = overline{0, m}), имеют непрерывные частные производные второго порядка, а ранг функциональной матрицы eqref{ref3} равен (m). Повторяя рассуждения теоремы 1, можем без ограничения общности считать, что выполнено условие eqref{ref4} и что найдется такая окрестность (K(x^{0}) = K_{1}(x_{1}^{0}, ldots, x_{m}^{0}) times K_{2}(x_{m+1}^{0}, ldots, x_{n}^{0})), что множество (E cap K(x^{0})) можно задать формулой eqref{ref8}. На (E cap K(x^{0})) функция (f_{0}(x)) становится функцией (n-m) переменных (F(x_{m+1}^{0}, ldots, x_{n}^{0})), определенной формулой eqref{ref9} и имеющей непрерывные частные производные второго порядка.
По условию теоремы ((x^{0}, lambda^{0})) есть стационарная точка функции Лагранжа, то есть
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x_{k}} (x^{0}, lambda^{0}) = 0, k = overline{1, n};\
&\
& displaystylefrac{partial L}{partial lambda_{i}} (x^{0}, lambda^{0}) = f_{i}(x^{0}) = 0, i = overline{1, m}.
end{array}label{ref22}
$$
Из формул eqref{ref22} следует, что (x^{0} in E) и что
$$
d_{x}L(x^{0}, lambda^{0}) = sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = 0.label{ref23}
$$
Рассмотрим функцию (L(x, lambda^{0})) на множестве (E cap K(x^{0})). Очевидно, что
$$
L(x, lambda^{0}) = f_{0}(x) = F(x_{m+1}, ldots, x_{n}) mbox{при} x in E cap K(x^{0}).label{ref24}
$$
В силу инвариантности формы первого дифференциала из формулы eqref{ref24} следует, что
$$
dF(x_{m+1}^{0}, ldots, x_{n}^{0}) = d_{x}L(x^{0}, lambda^{0}) = 0.label{ref25}
$$
Находя второй дифференциал от обеих частей равенства eqref{ref24} и используя равенства eqref{ref22}, получаем
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) = sum_{k=1}^{n} sum_{j=1}^{n} frac{partial^{2} L(x^{0}, lambda^{0})}{partial x_{j} partial x_{k}} dx_{j} dx_{k}+sum_{k=1}^{n} frac{partial L(x^{0}, lambda^{0})}{partial x_{k}} d^{2}x_{k} = d_{xx}^{2}L(x^{0}, lambda^{0}).label{ref26}
$$
Пусть (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Так как множество (E cap K(x^{0})) можно задать в форме eqref{ref8}, то, выбирая (dx_{m+1}, ldots, dx_{n}) произвольным образом, получим, что дифференциалы (dx_{1},…, dx_{m}) зависят от ((dx_{m+1}, ldots, dx_{n})). Дифференцируя тождества eqref{ref7} в точке (x^{0}), получаем соотношения eqref{ref11}, которые означают, что (dx in E_{T}).
Из формулы eqref{ref26} тогда следует, что
$$
d^{2}F(x_{m+1}^{0}, ldots, x_{n}^{0}) > 0 mbox{при} dx_{m+1}^{2}+ldots+dx_{n}^{2} > 0.label{ref27}
$$
Из eqref{ref25} и eqref{ref27} получаем, что ((x_{m+1}^{0}, ldots, x_{n}^{0})) есть точка строгого минимума функции (F(x_{m+1}, ldots, x_{n})), то есть (x^{0}) есть точка строгого минимума функции (f_{0}(x)) на множестве (E cap K(x^{0})). Таким образом, (x^{0}) есть точка строгого условного минимума функции (f_{0}(x)) при наличии связей eqref{ref1}.
Аналогично рассматривается случай, когда (d_{xx}^{2}L(x^{0}, lambda^{0}) < 0), (dx in E_{T}), (dx neq 0). Если же (d_{xx}^{2}L(x^{0}, lambda^{0})) при (dx in E_{T}) есть неопределенная квадратичная форма, то не выполняется условие (d_{xx}^{2}L(x^{0}, lambda^{0}) geq 0) при (dx in E_{T}), являющееся, в силу теоремы 2, необходимым условием минимума. Поэтому (x^{0}) не есть точка условного минимума функции (f_{0}(x)) при связях eqref{ref1}. Аналогично доказывается, что (x^{0}) не может быть точкой условного минимума функции (-f_{0}(x)), а следовательно, и точкой условного максимума функции (f_{0}(x)) при связях eqref{ref1}. (bullet)
Замечание.
Если окажется, что (d_{xx}^{2}L(x^{0}, lambda^{0})) есть положительно определенная квадратичная форма на всем пространстве (boldsymbol{R}^{n}), то (d_{xx}^{2}L(x^{0}, lambda^{0}) > 0) при (dx in E_{T}), (dx neq 0). Поэтому в этом случае в квадратичной форме (d_{xx}^{2}L(x^{0}, lambda^{0})) не нужно исключать зависимые дифференциалы.
Пример 1.
Найти экстремумы функции (x-2y+2z = u) и на сфере (x^{2}+y^{2}+z^{2} = 1).
Решение.
(vartriangle) Строим функцию Лагранжа
$$
L(x, y, z, lambda) = x-2y+2z+lambda(x^{2}+y^{2}+x^{2}-1)nonumber
$$
Стационарные точки функции Лагранжа находим, решая систему уравнений
$$
frac{partial L}{partial x} = 1+2lambda x = 0,quad frac{partial L}{partial y} = -2+2lambda y = 0,quad frac{partial L}{partial z} = 2+2lambda z = 0,nonumber
$$
$$
frac{partial L}{partial lambda} = x^{2}+y^{2}+z^{2}-1 = 0.nonumber
$$
Исключая из этой системы (x, y, z), получаем (displaystyleleft(frac{1}{2lambda}right)^{2}+left(frac{1}{lambda}right)^{2}+left(frac{1}{lambda}right)^{2}-1 = 0), откуда (lambda_{1} = displaystylefrac{3}{2}), (lambda_{2} = -displaystylefrac{3}{2}).
У функции Лагранжа есть две стационарные точки,
$$
M_{1} = left(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)quad mbox{и}quad M_{2} = left(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right).nonumber
$$
Так как (d^{2}L(M_{1}) = 3(dx^{2}+dy^{2}+dz^{2}) > 0), a (d^{2}L(M_{2}) = -3(dx^{2}+dy^{2}+dz^{2}) < 0) при (dx^{2}+dy^{2}+dz^{2} > 0), тo (displaystyleleft(-frac{1}{3}, frac{2}{3}, -frac{2}{3}, frac{3}{2}right)) — точка условного минимума, a (displaystyleleft(frac{1}{3}, -frac{2}{3}, frac{2}{3}, -frac{3}{2}right)) — точка условного максимума функции (u = x-2y+2x) при наличии ограничения (x^{2}+y^{2}+z^{2}-1 = 0), Причем (u_{min} = -3), (u_{max} = 3). (blacktriangle)
Пример 2.
Найти условные экстремумы функции (f_{0}(x, y) = e^{axy}), (a neq 0), при наличии ограничения (f_{i}(x, y) = x^{3}+y^{3}+x+y-4 = 0).
Решение.
(vartriangle) Построим функцию Лагранжа:
$$
L(x, y) = e^{axy}+lambda(x^{3}+y^{3}+x+y-4).nonumber
$$
Стационарные точки функции Лагранжа определяются из системы уравнений
$$
begin{array}{cc}
& displaystylefrac{partial L}{partial x} = aye^{axy}+lambda(3x^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial y} = axe^{axy}+lambda(3y^{2}+1) = 0,\
&\
& displaystylefrac{partial L}{partial lambda} = x^{3}+y^{3}+x+y-4 = 0.
end{array}label{ref28}
$$
Умножая первое уравнение на (x), а второе на (y) и вычитая, получаем
$$
lambda(3x^{3}-3y^{3}+x-y) = lambda(x-y)(3x^{2}+3xy+3y^{2}+1) = 0.label{ref29}
$$
Если (lambda = 0), то из первых двух уравнений eqref{ref28} получаем (x = y = 0). Но (x = y = 0) не удовлетворяет уравнению связи. Итак, (lambda neq 0), поэтому из eqref{ref29} следует, что (x = y) (второй сомножитель всегда положителен: (3(x^{2}+xy+y^{2})+1 > 0)). Подставляя (x = y) в уравнение связи, получаем (x^{3}+x = 2), (x = y = 1). Первое из уравнений eqref{ref28} дает при (x = y = 1) значение (lambda = -displaystylefrac{a}{4} e^{a}).
Итак, ((1, 1, -displaystylefrac{a}{4} e^{a})) есть единственная стационарная точка функции Лагранжа.
Так как
$$
d(e^{axy}) = a(x dy+y dx) e^{axy},nonumber
$$
$$
d^{2}(e^{axy}) = a^{2}(x dy+y dx)^{2} e^{axy}+2a dx dy e^{axy},nonumber
$$
$$
d^{2}(x^{3}+y^{3}+x+y-4) = 6x dx^{2}+6y dy^{2},nonumber
$$
то для второго дифференциала функции Лагранжа при (lambda_{0} = -displaystylefrac{a}{4} e^{a}) и (x = y = 1) получается следующее выражение:
$$
d^{2}L(1, 1, lambda_{0}) = ae^{a}left[a(dx+dy)^{2}+2 dx dy-frac{3}{2}(dx^{2}+dy^{2})right].label{ref30}
$$
Дифференцируя уравнение связи при (x = y = 1), получаем, что (dy+dx = 0). Подставляя (dy = -dx) в уравнение eqref{ref30}, получаем равенство
$$
d^{2}L(1, 1, lambda_{0}) = -5ae^{a}dx^{2}.label{ref31}
$$
Поэтому при (a < 0) в точке (1,1) будет условный минимум, а при (a > 0) — условный максимум функции (f_{0}(x, y)) при наличии связи (x^{3}+y^{3}+x+y = 4), причем экстремальное значение функции равно (e^{a}). (blacktriangle)
Замечание.
Уравнение связи (x^{3}+y^{3}+x+y = 4) было бы затруднительно разрешить относительно одной из переменных. Метод Лагранжа для примера 2 более эффективен, чем прямой метод исключения зависимых переменных.
Несколько замечаний о методе множителей Лагранжа.
Задачи об отыскании экстремумов функций (как числовых, так и функций более общей природы) при наличии ограничений являются весьма распространенными. Теория экстремальных задач интенсивно развивается и находит широкий круг приложений. Здесь были рассмотрены ограничения типа равенств, задаваемые достаточно гладкими функциями (гладкие связи). Метод множителей Лагранжа имеет глубокие обобщения и на более общий случай, когда ограничения задаются системой равенств и неравенств при помощи недифференцируемых в обычном смысле функций.
В конкретных прикладных вопросах множители Лагранжа имеют содержательную интерпретацию. Так, в механике множители Лагранжа задают реакции связей, а в математической экономике — цены на продукты производства. Широко развиты приближенные методы решения экстремальных задач, использующие современную вычислительную технику.
Условный экстремум. Метод множителей Лагранжа. Первая часть.
Для начала рассмотрим случай функции двух переменных. Условным экстремумом функции $z=f(x,y)$ в точке $M_0(x_0;y_0)$ называется экстремум этой функции, достигнутый при условии, что переменные $x$ и $y$ в окрестности данной точки удовлетворяют уравнению связи $varphi (x,y)=0$.
Название «условный» экстремум связано с тем, что на переменные наложено дополнительное условие $varphi(x,y)=0$. Если из уравнения связи можно выразить одну переменную через другую, то задача определения условного экстремума сводится к задаче на обычный экстремум функции одной переменной. Например, если из уравнения связи следует $y=psi(x)$, то подставив $y=psi(x)$ в $z=f(x,y)$, получим функцию одной переменной $z=fleft(x,psi(x)right)$. В общем случае, однако, такой метод малопригоден, поэтому требуется введение нового алгоритма.
Метод множителей Лагранжа для функций двух переменных.
Метод множителей Лагранжа состоит в том, что для отыскания условного экстремума составляют функцию Лагранжа: $F(x,y)=f(x,y)+lambdavarphi(x,y)$ (параметр $lambda$ называют множителем Лагранжа). Необходимые условия экстремума задаются системой уравнений, из которой определяются стационарные точки:
$$
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.
$$
Достаточным условием, из которого можно выяснить характер экстремума, служит знак $d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2$. Если в стационарной точке $d^2F > 0$, то функция $z=f(x,y)$ имеет в данной точке условный минимум, если же $d^2F < 0$, то условный максимум.
Есть и другой способ для определения характера экстремума. Из уравнения связи получаем: $varphi_{x}^{‘}dx+varphi_{y}^{‘}dy=0$, $dy=-frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dx$, поэтому в любой стационарной точке имеем:
$$d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=F_{xx}^{”}dx^2+2F_{xy}^{”}dxleft( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)+F_{yy}^{”}left( -frac{varphi_{x}^{‘}}{varphi_{y}^{‘}}dxright)^2=\
=-frac{dx^2}{left(varphi_{y}^{‘} right)^2}cdotleft( -(varphi_{y}^{‘})^2 F_{xx}^{”}+2varphi_{x}^{‘}varphi_{y}^{‘}F_{xy}^{”}-(varphi_{x}^{‘})^2 F_{yy}^{”} right)$$
Второй сомножитель (расположенный в скобке) можно представить в такой форме:
$$
H=left| begin{array} {ccc}
0 & varphi_{x}^{‘} & varphi_{y}^{‘}\
varphi_{x}^{‘} & normred{F_{xx}^{”}} & normred{F_{xy}^{”}} \
varphi_{y}^{‘} & normred{F_{xy}^{”}} & normred{F_{yy}^{”}} end{array} right|
$$
Красным цветом выделены элементы определителя $left| begin{array} {cc} F_{xx}^{”} & F_{xy}^{”} \ F_{xy}^{”} & F_{yy}^{”} end{array} right|$, который является гессианом функции Лагранжа. Если $H > 0$, то $d^2F < 0$, что указывает на условный максимум. Аналогично, при $H < 0$ имеем $d^2F > 0$, т.е. имеем условный минимум функции $z=f(x,y)$.
Примечание относительно формы записи определителя $H$. показатьскрыть
Алгоритм исследования функции двух переменных на условный экстремум
- Составить функцию Лагранжа $F(x,y)=f(x,y)+lambdavarphi(x,y)$
- Решить систему $
left { begin{aligned}
& frac{partial F}{partial x}=0;\
& frac{partial F}{partial y}=0;\
& varphi (x,y)=0.
end{aligned} right.$ - Определить характер экстремума в каждой из найденных в предыдущем пункте стационарных точек. Для этого применить любой из указанных способов:
- Составить определитель $H$ и выяснить его знак
- С учетом уравнения связи вычислить знак $d^2F$
Метод множителей Лагранжа для функций n переменных
Допустим, мы имеем функцию $n$ переменных $z=f(x_1,x_2,ldots,x_n)$ и $m$ уравнений связи ($n > m$):
$$varphi_1(x_1,x_2,ldots,x_n)=0; ; varphi_2(x_1,x_2,ldots,x_n)=0,ldots,varphi_m(x_1,x_2,ldots,x_n)=0.$$
Обозначив множители Лагранжа как $lambda_1,lambda_2,ldots,lambda_m$, составим функцию Лагранжа:
$$F(x_1,x_2,ldots,x_n,lambda_1,lambda_2,ldots,lambda_m)=f+lambda_1varphi_1+lambda_2varphi_2+ldots+lambda_mvarphi_m$$
Необходимые условия наличия условного экстремума задаются системой уравнений, из которой находятся координаты стационарных точек и значения множителей Лагранжа:
$$left{begin{aligned}
& frac{partial F}{partial x_i}=0; (i=overline{1,n})\
& varphi_j=0; (j=overline{1,m})
end{aligned} right.$$
Выяснить, условный минимум или условный максимум имеет функция в найденной точке, можно, как и ранее, посредством знака $d^2F$. Если в найденной точке $d^2F > 0$, то функция имеет условный минимум, если же $d^2F < 0$, – то условный максимум. Можно пойти иным путем, рассмотрев следующую матрицу:
Определитель матрицы
$$left| begin{array} {ccccc} frac{partial^2F}{partial x_{1}^{2}} & frac{partial^2F}{partial x_{1}partial x_{2}} & frac{partial^2F}{partial x_{1}partial x_{3}} &ldots & frac{partial^2F}{partial x_{1}partial x_{n}}\
frac{partial^2F}{partial x_{2}partial x_1} & frac{partial^2F}{partial x_{2}^{2}} & frac{partial^2F}{partial x_{2}partial x_{3}} &ldots & frac{partial^2F}{partial x_{2}partial x_{n}}\
frac{partial^2F}{partial x_{3} partial x_{1}} & frac{partial^2F}{partial x_{3}partial x_{2}} & frac{partial^2F}{partial x_{3}^{2}} &ldots & frac{partial^2F}{partial x_{3}partial x_{n}}\
ldots & ldots & ldots &ldots & ldots\
frac{partial^2F}{partial x_{n}partial x_{1}} & frac{partial^2F}{partial x_{n}partial x_{2}} & frac{partial^2F}{partial x_{n}partial x_{3}} &ldots & frac{partial^2F}{partial x_{n}^{2}}\
end{array} right|,$$
выделенной в матрице $L$ красным цветом, есть гессиан функции Лагранжа. Используем следующее правило:
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ матрицы $L$ совпадают с знаком $(-1)^m$, то исследуемая стационарная точка является точкой условного минимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
- Если знаки угловых миноров $H_{2m+1},; H_{2m+2},ldots,H_{m+n}$ чередуются, причём знак минора $H_{2m+1}$ совпадает с знаком числа $(-1)^{m+1}$, то исследуемая стационарная точка является точкой условного максимума функции $z=f(x_1,x_2,x_3,ldots,x_n)$.
Пример №1
Найти условный экстремум функции $z(x,y)=x+3y$ при условии $x^2+y^2=10$.
Решение
Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости $z=x+3y$ для точек ее пересечения с цилиндром $x^2+y^2=10$.
Выразить одну переменную через другую из уравнения связи и подставить ее в функцию $z(x,y)=x+3y$ несколько затруднительно, поэтому будем использовать метод Лагранжа.
Обозначив $varphi(x,y)=x^2+y^2-10$, составим функцию Лагранжа:
$$
F(x,y)=z(x,y)+lambda varphi(x,y)=x+3y+lambda(x^2+y^2-10);\
frac{partial F}{partial x}=1+2lambda x; frac{partial F}{partial y}=3+2lambda y.
$$
Запишем систему уравнений для определения стационарных точек функции Лагранжа:
$$
left { begin{aligned}
& 1+2lambda x=0;\
& 3+2lambda y=0;\
& x^2+y^2-10=0.
end{aligned} right.
$$
Если предположить $lambda=0$, то первое уравнение станет таким: $1=0$. Полученное противоречие говорит о том, что $lambdaneq 0$. При условии $lambdaneq 0$ из первого и второго уравнений имеем: $x=-frac{1}{2lambda}$, $y=-frac{3}{2lambda}$. Подставляя полученные значения в третье уравнение, получим:
$$
left( -frac{1}{2lambda} right)^2+left( -frac{3}{2lambda} right)^2-10=0;\
frac{1}{4lambda^2}+frac{9}{4lambda^2}=10; lambda^2=frac{1}{4}; left[ begin{aligned} & lambda_1=-frac{1}{2};\ & lambda_2=frac{1}{2}. end{aligned} right.\
begin{aligned}
& lambda_1=-frac{1}{2}; ; x_1=-frac{1}{2lambda_1}=1; ; y_1=-frac{3}{2lambda_1}=3;\
& lambda_2=frac{1}{2}; ; x_2=-frac{1}{2lambda_2}=-1; ; y_2=-frac{3}{2lambda_2}=-3.end{aligned}
$$
Итак, система имеет два решения: $x_1=1;; y_1=3;; lambda_1=-frac{1}{2}$ и $x_2=-1;; y_2=-3;; lambda_2=frac{1}{2}$. Выясним характер экстремума в каждой стационарной точке: $M_1(1;3)$ и $M_2(-1;-3)$. Для этого вычислим определитель $H$ в каждой из точек.
$$
varphi_{x}^{‘}=2x;; varphi_{y}^{‘}=2y;; F_{xx}^{”}=2lambda;; F_{xy}^{”}=0;; F_{yy}^{”}=2lambda.\
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 2x & 2y\ 2x & 2lambda & 0 \ 2y & 0 & 2lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|
$$
В точке $M_1(1;3)$ получим:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & 1 & 3\ 1 & -1/2 & 0 \ 3 & 0 & -1/2 end{array} right|=40 > 0.$$
Следовательно, в точке $M_1(1;3)$ функция $z(x,y)=x+3y$ имеет условный максимум, $z_{max}=z(1;3)=10$.
Аналогично, в точке $M_2(-1;-3)$ найдем:
$$H=8cdotleft| begin{array} {ccc} 0 & x & y\ x & lambda & 0 \ y & 0 & lambda end{array} right|=
8cdotleft| begin{array} {ccc} 0 & -1 & -3\ -1 & 1/2 & 0 \ -3 & 0 & 1/2 end{array} right|=-40$$
Так как $H < 0$, то в точке $M_2(-1;-3)$ имеем условный минимум функции $z(x,y)=x+3y$, а именно: $z_{min}=z(-1;-3)=-10$.
Отмечу, что вместо вычисления значения определителя $H$ в каждой точке, гораздо удобнее раскрыть его в общем виде. Дабы не загромождать текст подробностями, этот способ скрою под примечание.
Запись определителя $H$ в общем виде. показатьскрыть
Вопрос о характере экстремума в стационарных точках $M_1(1;3)$ и $M_2(-1;-3)$ можно решить и без использования определителя $H$. Найдем знак $d^2F$ в каждой стационарной точке:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=2lambda left( dx^2+dy^2right)
$$
Отмечу, что запись $dx^2$ означает именно $dx$, возведённый в вторую степень, т.е. $left( dx right)^2$. Отсюда имеем: $dx^2+dy^2>0$, посему при $lambda_1=-frac{1}{2}$ получим $d^2F < 0$. Следовательно, функция имеет в точке $M_1(1;3)$ условный максимум. Аналогично, в точке $M_2(-1;-3)$ получим условный минимум функции $z(x,y)=x+3y$. Отметим, что для определения знака $d^2F$ не пришлось учитывать связь между $dx$ и $dy$, ибо знак $d^2F$ очевиден без дополнительных преобразований. В следующем примере для определения знака $d^2F$ уже будет необходимо учесть связь между $dx$ и $dy$.
Ответ: в точке $(-1;-3)$ функция имеет условный минимум, $z_{min}=-10$. В точке $(1;3)$ функция имеет условный максимум, $z_{max}=10$.
Пример №2
Найти условный экстремум функции $z(x,y)=3y^3+4x^2-xy$ при условии $x+y=0$.
Решение
Первый способ (метод множителей Лагранжа)
Обозначив $varphi(x,y)=x+y$ составим функцию Лагранжа:
$$F(x,y)=z(x,y)+lambda varphi(x,y)=3y^3+4x^2-xy+lambda(x+y).$$
$$
frac{partial F}{partial x}=8x-y+lambda; ; frac{partial F}{partial y}=9y^2-x+lambda.\
left { begin{aligned} & 8x-y+lambda=0;\ & 9y^2-x+lambda=0; \ & x+y=0. end{aligned} right.
$$
Решив систему, получим: $x_1=0$, $y_1=0$, $lambda_1=0$ и $x_2=frac{10}{9}$, $y_2=-frac{10}{9}$, $lambda_2=-10$. Имеем две стационарные точки: $M_1(0;0)$ и $M_2 left(frac{10}{9};-frac{10}{9} right)$. Выясним характер экстремума в каждой стационарной точке с использованием определителя $H$.
$$
H=left| begin{array} {ccc} 0 & varphi_{x}^{‘} & varphi_{y}^{‘}\ varphi_{x}^{‘} & F_{xx}^{”} & F_{xy}^{”} \ varphi_{y}^{‘} & F_{xy}^{”} & F_{yy}^{”} end{array} right|=
left| begin{array} {ccc} 0 & 1 & 1\ 1 & 8 & -1 \ 1 & -1 & 18y end{array} right|=-10-18y
$$
В точке $M_1(0;0)$ $H=-10-18cdot 0=-10 < 0$, поэтому $M_1(0;0)$ есть точка условного минимума функции $z(x,y)=3y^3+4x^2-xy$, $z_{min}=0$. В точке $M_2left(frac{10}{9};-frac{10}{9}right)$ $H=10 > 0$, посему в данной точке функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Исследуем характер экстремума в каждой из точек иным методом, основываясь на знаке $d^2F$:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=8dx^2-2dxdy+18ydy^2
$$
Из уравнения связи $x+y=0$ имеем: $d(x+y)=0$, $dx+dy=0$, $dy=-dx$.
$$
d^2 F=8dx^2-2dxdy+18ydy^2=8dx^2-2dx(-dx)+18y(-dx)^2=(10+18y)dx^2
$$
Так как $ d^2F Bigr|_{M_1}=10 dx^2 > 0$, то $M_1(0;0)$ является точкой условного минимума функции $z(x,y)=3y^3+4x^2-xy$. Аналогично, $d^2F Bigr|_{M_2}=-10 dx^2 < 0$, т.е. $M_2left(frac{10}{9}; -frac{10}{9} right)$ – точка условного максимума.
Второй способ
Из уравнения связи $x+y=0$ получим: $y=-x$. Подставив $y=-x$ в функцию $z(x,y)=3y^3+4x^2-xy$, получим некоторую функцию переменной $x$. Обозначим эту функцию как $u(x)$:
$$
u(x)=z(x,-x)=3cdot(-x)^3+4x^2-xcdot(-x)=-3x^3+5x^2.
$$
Таким образом задачу о нахождении условного экстремума функции двух переменных мы свели к задаче определения экстремума функции одной переменной.
$$
u_{x}^{‘}=-9x^2+10x;\
-9x^2+10x=0; ; xcdot(-9x+10)=0;\
x_1=0; ; y_1=-x_1=0;\
x_2=frac{10}{9}; ; y_2=-x_2=-frac{10}{9}.
$$
Получили точки $M_1(0;0)$ и $M_2left(frac{10}{9}; -frac{10}{9}right)$. Дальнейшее исследование известно из курса дифференциального исчисления функций одной переменой. Исследуя знак $u_{xx}^{”}$ в каждой стационарной точке или проверяя смену знака $u_{x}^{‘}$ в найденных точках, получим те же выводы, что и при решении первым способом. Например, проверим знак $u_{xx}^{”}$:
$$u_{xx}^{”}=-18x+10;\
u_{xx}^{”}(M_1)=10;;u_{xx}^{”}(M_2)=-10.$$
Так как $u_{xx}^{”}(M_1)>0$, то $M_1$ – точка минимума функции $u(x)$, при этом $u_{min}=u(0)=0$. Так как $u_{xx}^{”}(M_2)<0$, то $M_2$ – точка максимума функции $u(x)$, причём $u_{max}=uleft(frac{10}{9}right)=frac{500}{243}$.
Значения функции $u(x)$ при заданном условии связи совпадают с значениями функции $z(x,y)$, т.е. найденные экстремумы функции $u(x)$ и есть искомые условные экстремумы функции $z(x,y)$.
Ответ: в точке $(0;0)$ функция имеет условный минимум, $z_{min}=0$. В точке $left(frac{10}{9}; -frac{10}{9} right)$ функция имеет условный максимум, $z_{max}=frac{500}{243}$.
Рассмотрим еще один пример, в котором характер экстремума выясним посредством определения знака $d^2F$.
Пример №3
Найти наибольшее и наименьшее значения функции $z=5xy-4$, если переменные $x$ и $y$ положительны и удовлетворяют уравнению связи $frac{x^2}{8}+frac{y^2}{2}-1=0$.
Решение
Составим функцию Лагранжа: $F=5xy-4+lambda left( frac{x^2}{8}+frac{y^2}{2}-1 right)$. Найдем стационарные точки функции Лагранжа:
$$
F_{x}^{‘}=5y+frac{lambda x}{4}; ; F_{y}^{‘}=5x+lambda y.\
left { begin{aligned}
& 5y+frac{lambda x}{4}=0;\
& 5x+lambda y=0;\
& frac{x^2}{8}+frac{y^2}{2}-1=0;\
& x > 0; ; y > 0.
end{aligned} right.
$$
Все дальнейшие преобразования осуществляются с учетом $x > 0; ; y > 0$ (это оговорено в условии задачи). Из второго уравнения выразим $lambda=-frac{5x}{y}$ и подставим найденное значение в первое уравнение: $5y-frac{5x}{y}cdot frac{x}{4}=0$, $4y^2-x^2=0$, $x=2y$. Подставляя $x=2y$ в третье уравнение, получим: $frac{4y^2}{8}+frac{y^2}{2}-1=0$, $y^2=1$, $y=1$.
Так как $y=1$, то $x=2$, $lambda=-10$. Характер экстремума в точке $(2;1)$ определим, исходя из знака $d^2F$.
$$
F_{xx}^{”}=frac{lambda}{4}; ; F_{xy}^{”}=5; ; F_{yy}^{”}=lambda.
$$
Так как $frac{x^2}{8}+frac{y^2}{2}-1=0$, то:
$$
dleft( frac{x^2}{8}+frac{y^2}{2}-1right)=0; ; dleft( frac{x^2}{8} right)+dleft( frac{y^2}{2} right)=0; ; frac{x}{4}dx+ydy=0; ; dy=-frac{xdx}{4y}.
$$
В принципе, здесь можно сразу подставить координаты стационарной точки $x=2$, $y=1$ и параметра $lambda=-10$, получив при этом:
$$
F_{xx}^{”}=frac{-5}{2}; ; F_{xy}^{”}=-10; ; dy=-frac{dx}{2}.\
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=-frac{5}{2}dx^2+10dxcdot left(-frac{dx}{2} right)-10cdot left(-frac{dx}{2} right)^2=\
=-frac{5}{2}dx^2-5dx^2-frac{5}{2}dx^2=-10dx^2.
$$
Однако в других задачах на условный экстремум стационарных точек может быть несколько. В таких случаях лучше $d^2F$ представить в общем виде, а потом подставлять в полученное выражение координаты каждой из найденных стационарных точек:
$$
d^2 F=F_{xx}^{”}dx^2+2F_{xy}^{”}dxdy+F_{yy}^{”}dy^2=frac{lambda}{4}dx^2+10cdot dxcdot frac{-xdx}{4y} +lambdacdot left(-frac{xdx}{4y} right)^2=\
=frac{lambda}{4}dx^2-frac{5x}{2y}dx^2+lambda cdot frac{x^2dx^2}{16y^2}=left( frac{lambda}{4}-frac{5x}{2y}+frac{lambda cdot x^2}{16y^2} right)cdot dx^2
$$
Подставляя $x=2$, $y=1$, $lambda=-10$, получим:
$$
d^2 F=left( frac{-10}{4}-frac{10}{2}-frac{10 cdot 4}{16} right)cdot dx^2=-10dx^2.
$$
Так как $d^2F=-10cdot dx^2 < 0$, то точка $(2;1)$ есть точкой условного максимума функции $z=5xy-4$, причём $z_{max}=10-4=6$.
Ответ: в точке $(2;1)$ функция имеет условный максимум, $z_{max}=6$.
В следующей части рассмотрим применение метода Лагранжа для функций большего количества переменных.
