Сергей Евгеньевич Грамотинский
Эксперт по предмету «Математика»
Задать вопрос автору статьи
Определение 1
Условным законом распределения одной из составляющих двумерной случайной величины $(X,Y)$ называется её закон распределения, вычисленный при условии, что другая составляющая принимает определенное значение или попадает в определенный интеграл.
Введем теперь по отдельности определения условного закона распределения для составляющей $X$ и для составляющей $Y$.
Условные законы распределения составляющих дискретной двумерной случайной величины
Пусть $(X,Y)$ – дискретная двумерная случайная величина.
Определение 2
Условным распределением составляющей $X$ при $Y=y$ называется совокупность условных вероятностей $pleft(x_1,yright), pleft(x_2,yright),..,pleft(x_n,yright)$ при условии, что событие $Y=y$ уже произошло.
Если известен закон распределения двумерной случайной величины $(X,Y)$, то условная составляющая $X$ представляется в виде
Определение 3
Условным распределением составляющей $Y$ при $X=x$ называется совокупность условных вероятностей $pleft(x,y_1right), pleft(x,y_2right),..,pleft(x,y_mright)$ при условии, что событие $X=x$ уже произошло.
Если известен закон распределения двумерной случайной величины $(X,Y)$, то условная составляющая $X$ представляется в виде
Условные законы распределения составляющих непрерывной двумерной случайной величины
Пусть $(X,Y)$ – непрерывная двумерная случайная величина.
Напомним, что для непрерывной случайной величины существует понятие плотности распределения случайной величины.
Определение 4
Условной плотностью $varphi (x/y)$ распределения составляющей $X$ при $Y=y$ называется отношение плотности $varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $varphi (y)$ при условии, что составляющая $Y$ приняла конкретное значение или попала в заданный интервал. То есть
[varphi (x/y)=frac{varphi (x,y)}{varphi (y)}]
«Условные законы распределения составляющих системы» 👇
Определение 5
Условной плотностью $varphi (y/x)$ распределения составляющей $Y$ при $X=x$ называется отношение плотности $varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $varphi (x)$ при условии, что составляющая $X$ приняла конкретное значение или попала в заданный интервал. То есть
[varphi (y/x)=frac{varphi (x,y)}{varphi (x)}]
Приведем еще две формулы для вычисления условных плотностей распределения. Если известна плотность совместного распределения, то условные плотности по составляющей $X$ и по составляющей $Y$ можно найти по формулам:
Введем несколько свойств для функций условной плотности распределения.
Свойство 1: Функции условной плотности распределения неотрицательны на всей области определения, то есть:
Свойство 2: Выполняются следующие равенства:
Условное математическое ожидание
Введем формулы для вычисления условных математических ожиданий для различных случаев.
- Условное математическое ожидание дискретной случайной величины $Y$ при $X=x$:
- Условное математическое ожидание дискретной случайной величины $X$ при $Y=y$:
- Условное математическое ожидание непрерывной случайной величины $Y$ при $X=x$:
- Условное математическое ожидание непрерывной случайной величины $X$ при $Y=y$:
Определение 7
Условное математическое ожидание $M(X/Y)$ называется функцией регрессии $Y$ на $X$.
Пример задачи на условное распределение
Пример 1
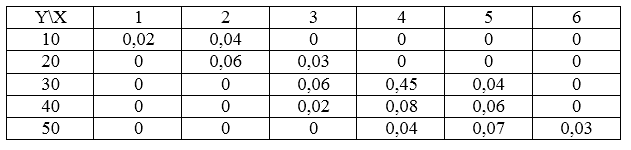
Распределение случайной величины задано таблицей.
Рисунок 1.
Найти для этой двумерной случайной величины условное распределение по составляющей $X$, если $Y=10$.
Решение.
Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:
[pleft(x_i/yright)=frac{pleft(x_i,yright)}{p(y)}]
Для начала необходимо найти ряд распределения случайной величины $Y$.
С помощью простейших вычислений, получим:
Рисунок 2.
Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:
[pleft(x_i/yright)=frac{pleft(x_i,yright)}{p(y)}]
- Y=10
[pleft(x_1/Y=10right)=frac{0,02}{0,06}=frac{1}{3}] [pleft(x_2/Y=10right)=frac{0,04}{0,06}=frac{2}{3}] [pleft(x_3/Y=10right)=frac{0}{0,06}=0] [pleft(x_4/Y=10right)=frac{0}{0,06}=0] [pleft(x_5/Y=10right)=frac{0}{0,06}=0] [pleft(x_6/Y=10right)=frac{0}{0,06}=0]
Получаем следующий ряд условного распределения по составляющей $X$:
Рисунок 3.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Обратимся
теперь к зависимым величинам. Вероятностная
зависимость между случайными величинами
часто встречается на практике. Если
случайные величины X
и Y
находятся в вероятностной зависимости,
это не означает, что с изменением величины
X
величина Y
изменяется вполне определенным образом;
это лишь означает, что с изменением
величины X
величина Y
имеет тенденцию также изменяться
(например, возрастать или убывать с
ростом X).
Эта тенденция соблюдается лишь в общих
чертах, и в каком-то отдельном случае
от неё возможны отступления. Примеры
случайных величин, находящихся в
вероятностной зависимости: рост и
возраст ребенка; затраты и прибыль при
производстве определенной продукции;
затраты на рекламу и объем продаваемой
продукции.
Для
того, чтобы полностью описать систему,
недостаточно знать распределение каждой
из составляющих; нужно ещё знать
зависимость между величинами, входящими
в систему. Эта зависимость характеризуется
с помощью условных
законов распределения.
Условным
законом распределения одной из случайных
величин,
входящих в систему (X,Y),
называется её закон распределения,
найденный при условии, что другая
случайная величина приняла определённое
значение (или попала в какой-то интервал).
Пусть
(X,Y)
– дискретная двумерная случайная
величина и
В
соответствии с определением условных
вероятностей событий*),
условная вероятность того, что случайная
величина Х примет значение
при условии
,
определяется равенством
(34)
Совокупность
вероятностей (34), то есть
,
представляет собой условный закон
распределения случайной величины Х при
условии.
Сумма условных вероятностей
Аналогично
определяются условная вероятность и
условный закон распределения случайной
величины Y
при условии
:
.
(35)
Пример
8. Пусть закон
распределения двумерного случайного
вектора (X,Y)
задан таблицей 2 (стр. 8). Найти условный
закон распределения случайной величины
Х при Y
=0,1.
Решение.
С учетом
формулы (34) имеем:
(значение
взято из безусловного закона распределения
случайной величиныY,
приведенного в таблице 4 на стр. 9).
*)
Пусть А и
В – случайные события. Тогда вероятность
их совместного появления равна
,
где– условная вероятность события В при
условии, что событие А произошло;– условная вероятность события А при
условии, что событие В произошло. Тогда,
.
Таким
образом, условный закон распределения
случайной величины Х при Y
=0,1 таков:
Таблица 5
-
Х
5
6
7
0,4
0,6
0
Сравнивая
найденный условный закон распределения
случайной величины Х с безусловным
законом её распределения (таблица 3 на
стр. 8), видим, что они различны.
Следовательно, случайные величины X
и Y
находятся в
вероятностной зависимости.
Пусть
теперь (X,Y)
– непрерывная двумерная случайная
величина с плотностью
;
и
–
плотности распределения соответственно
случайной величины Х и случайной величиныY.
Условной
плотностью распределения составляющей
X
при условии Y=y
называют отношение плотности совместного
распределения к плотности распределения
составляющей Y:

Аналогично
определяется условная плотность
распределения составляющей Y
при условии X=x:

Из
(36) и (37) получим:
.
(38)
Таким
образом, плотность распределения системы
двух непрерывных случайных величин
равна произведению плотности одной
составляющей на условную плотность
другой составляющей.
Как
и любая плотность распределения, условные
плотности обладают следующими свойствами:
(39)
Пример
9. Непрерывный
вектор (X,Y)
равномерно распределен в круге с
радиусом 1, то есть
Найти
условные плотности распределения
компонент этого вектора.
Решение
Условную
плотность составляющей Х при
найдём по формуле (36):
Так
как
при
,
топри
.
Аналогично находим:
;
при
Итак,
искомые условные плотности распределения
составляющих системы (X,Y)
имеют вид:
Для
независимых случайных величин условная
плотность распределения совпадает с
безусловной плотностью распределения.
Действительно,
(40)
Аналогично
(41)
Степень
зависимости между случайными величинами
обычно оценивают с помощью числовых
характеристик зависимости.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Известно, что если события A и B зависимы, то условная вероятность события B отличается от его безусловной вероятности. В этом случае
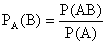
Аналогичное положение имеет место и для случайных величин. Для того, чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.
Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющих таковы: 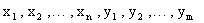
Допустим, что в результате испытания величина Y приняла значение 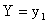
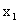
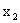
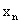
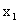
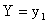
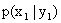
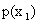
В общем случае условные вероятности составляющей будем обозначать так:
(i=1, 2, …, n; j=1, 2, …, m).
Условным распределением составляющей X при называют совокупность условных вероятностей 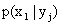
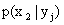
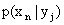
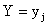
Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (13.1.43), вычислить условные законы распределения составляющих. Например, условный закон распределения X в предположении, что событие 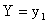
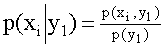
В общем случае условные законы распределения составляющей X определяются соотношением
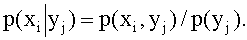
Аналогично находят условные законы распределения составляющей Y:
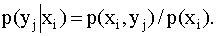
Замечание. Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном 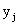
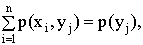
то 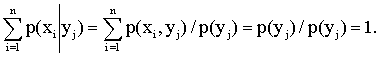
Аналогично доказывается, что при фиксированном
Это свойство условных распределений используют для контроля вычислений.
ПРИМЕР 13.1.56 Дискретная двумерная случайная величина задана таблицей
Найти условный закон распределения составляющей X при условии, что составляющая Y приняла значение 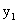
Решение. Искомый закон определяется совокупностью следующих условных вероятностей: 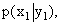
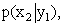
Воспользовавшись формулой (13.1.44) и приняв во внимание, что 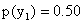
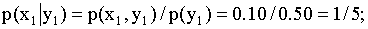
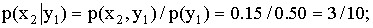
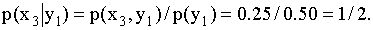
Сложив для контроля найденные условные вероятности, убедимся, что их сумма равна единице, как и должно быть, в соответствии с замечанием, помещенным выше: 1/5+3/10+1/2=1.
Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >
Содержание:
- Примеры с решением
Мы знаем, что если дан случайный вектор 



В общем случае нам нужно знать зависимость между величинами, входящими в систему. Эта зависимость может быть определена из знания так называемых условных законов распределения, т.е. закона распределения одной случайной величины при условии, что другая случайная величина приняла определенное значение.
Если случайные величины 
Если известен закон распределения 
По этой ссылке вы найдёте полный курс лекций по теории вероятности:
Нетрудно проверить, что любая из формул 7.34-37 определяет закон распределения, т.е. сумма вероятностей равна 1.
Для непрерывных случайных величин вероятность отдельного значения равна 0, поэтому мы не можем сразу применить указанные формулы. Поэтому рассмотрим точку 

Вероятность попадания системы
в эту полосу можно найти, используя теорему умножения вероятностей
Если устремить 


Определение. Функция
называется условным распределением 


Возможно вам будут полезны данные страницы:
Для абсолютно непрерывных случайных величин условные плотности определяют аналогичным образом
- Заметим, что полученные функции можно рассматривать как функции плотности некоторой случайной величины, иными словами, они обладают свойствами неотрицательности и нормирован-ности. Действительно, из (7.40) сразу следует, что
С другой стороны
Если случайные величины 
Пример с решением
Пример 7.1.
Пусть двумерная случайная величина имеет функцию плотности 

Решение:
Найдем плотности компонент
Отсюда
Поскольку
то величины 
Зная как находятся условные законы распределения, можно поставить задачу о нахождении условных математических ожиданий.
Определение. Условным математическим ожиданием случайной величины 


Аналогично определяется условное математическое ожидание 
Заметим, что, вообще говоря, условное математическое ожидание, определенное формулой (7.41), не является числом, а выражается в виде некоторой функции, зависящей от 

Сформулируем полученное соотношение в виде теоремы.
Теорема 7.3. Выполняются следующие соотношения
Если не прибегать к излишней строгости, соотношения (7.43) и (7.44) можно выразить словами: «Математическое ожидание от условного математического ожидания дает математическое ожидание исходной величины».
Пример 7.2.
В условиях примера 7.1 найти условное математическое ожидание случайной величины
Решение:
Подставляя найденное выражение для условной плотности 
В данном случае условное математическое ожидание 


Проверим выполнение (7.43) в данном частном случае. Имеем
С другой стороны
что совпадает с предыдущим результатом.
Лекции:
- Неравенство Чебышева
- Неравенство Маркова
- Закон больших чисел
- Центральная предельная теорема
- Полином Жегалкина
- Случайный вектор распределения
- Системы случайных величин
- Условное нормальное распределение
- Нормальное распределение на плоскости
- Многомерный нормальный закон
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
–
определить одномерные законы распределения случайных величин X и Y;
– найти
условные плотности распределения вероятностей величин;
–
вычислить математические ожидания mx и my;
–
вычислить дисперсии σx и σy;
–
вычислить ковариацию μxy;
–
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |







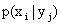
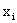
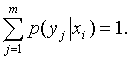
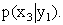



 в эту полосу можно найти, используя теорему умножения вероятностей
в эту полосу можно найти, используя теорему умножения вероятностей






















