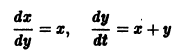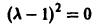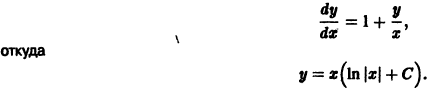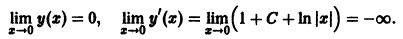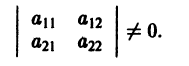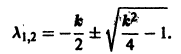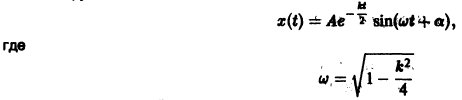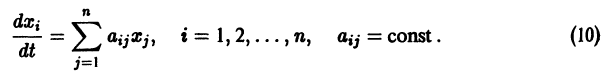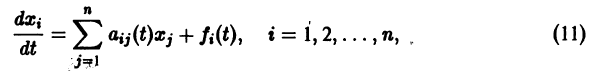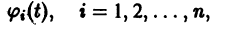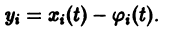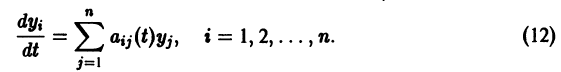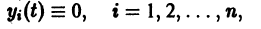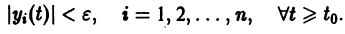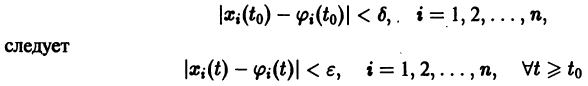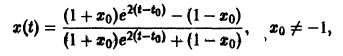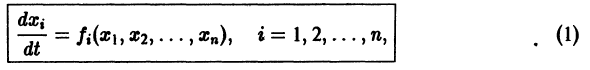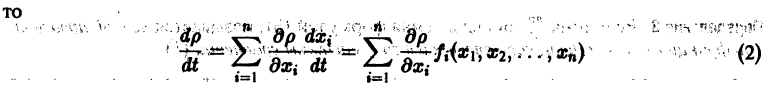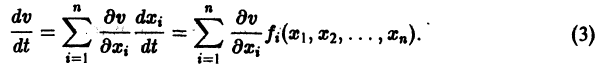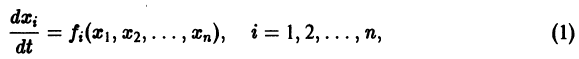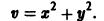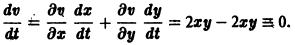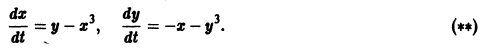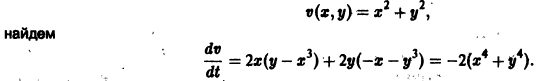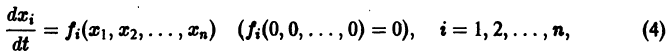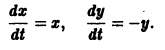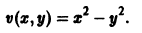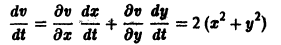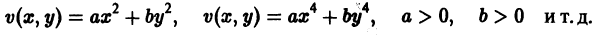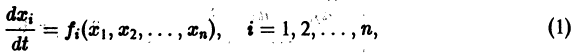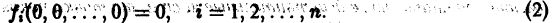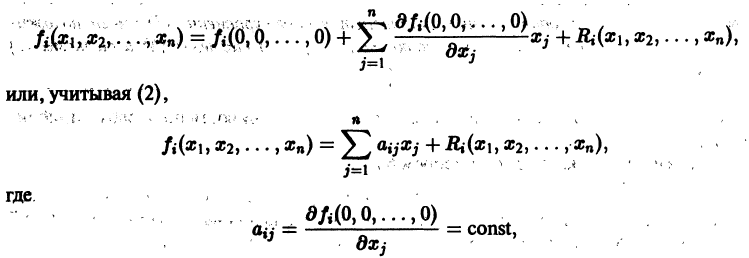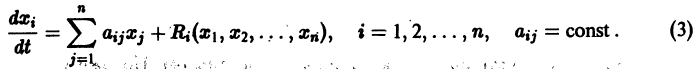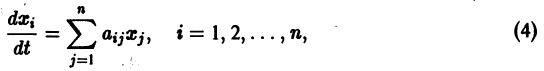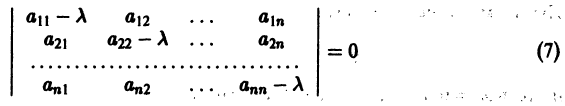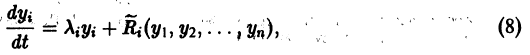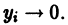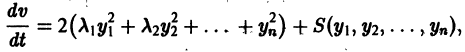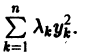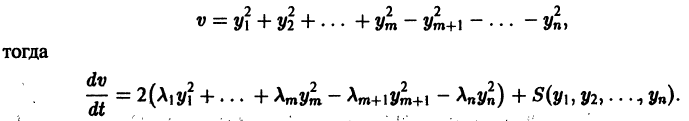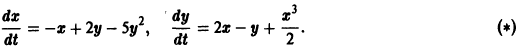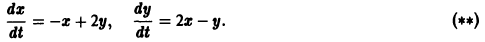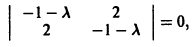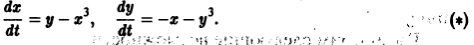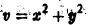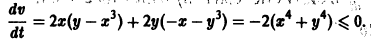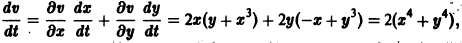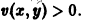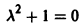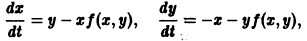Простейшие типы точек покоя
Пусть имеем систему двух линейных однородных дифференциальных уравнений с постоянными коэффициентами причем
(1)
Причём
Точка , в которой правые части уравнений системы (1) обращаются в ноль, называется точкой покоя системы (1).
Для исследования точки покоя системы (1) надо составить характеристическое уравнение
(2)
и найти его корни и
.
Возможны следующие случаи.
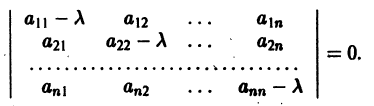
1. Корни характеристического уравнения (2) вещественные и разные:
а) . Точка покоя асимптотически устойчива (устойчивый узел, рис. 32);
б) . Точка покоя неустойчива (неустойчивый узел, рис. 33);
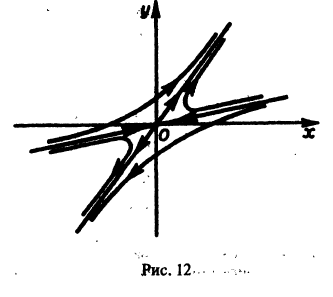
в) . Точка покоя неустойчива (седло, рис. 34).
2. Корни характеристического уравнения (2) комплексные:
а) . Точка покоя асимптотически устойчива (устойчивый фокус, рис.35);
б) . Точка покоя неустойчива (неустойчивый фокус, рис.36);
в) . Точка покоя устойчива (центр, рис. 37).
3. Корни кратные:
а) . Точка покоя асимптотически устойчива (устойчивый узел, рис.38, 39);
б) . Точка покоя неустойчива (неустойчивый узел, рис.40, 41).
Пример 1. Определить характер точки покоя (0,0) системы
Решение. Составляем характеристическое уравнение
или
Его корни вещественные, разные, положительные. Следовательно, точка покоя
— неустойчивый узел.
Связь между типами точек покоя и значениями корней характеристического уравнения (2) можно представить наглядно. Для этого введем обозначения
. Тогда характеристическое уравнение запишется в виде
.
Рассмотрим плоскость с прямоугольными декартовыми координатами и
и отметим на ней области, соответствующие различным типам покоя (рис. 42). Из приведенной выше классификации следует, что условиями устойчивости точки покоя являются
. Они выполняются при
и
, т. е. для точек, которые находятся в первой четверти.
Если и
комплексные, то точка покоя будет типа фокуса. Этому условию удовлетворяют точки, которые лежат между ветвями параболы
и не принадлежат оси
.
Точки полуоси , для которых
, соответствуют точкам покоя типа центра.
Точки, расположенные вне параболы , соответствуют точкам покоя типа узла.
Область плоскости , где
, содержит точки покоя типа седла.
Исключая особые случаи (прохождение через начало координат), замечаем, что седло может перейти в узел устойчивый или неустойчивый (рис.42). Устойчивый узел может перейти либо в седло, либо в устойчивый фокус. Случай равных корней соответствует границе между узлами и фокусами, т.е. параболе
.
Пример 2. Исследовать уравнение упругих колебаний с учетом трения и сопротивления среды (при )
(3)
Решение. Переходим от уравнения (3) к эквивалентной ему системе уравнений
(4)
Для определения характера точки покоя системы (4) составляем характеристическое уравнение
или
отсюда
(5)
Рассмотрим следующие случаи:
а) (сопротивление среды отсутствует). Из (5) получаем
. Точка покоя устойчива — центр (все движения являются периодическими);
б) . Корни
и
комплексно-сопряженные, причем
. Точка покоя — устойчивый фокус (колебания затухают);
в) (случай “отрицательного трения”),
. Корни
и
— комплексно-сопряженные, причем
. Точка покоя — неустойчивый фокус;
г) (сопротивление среды велико
). Корни
и
— действительные и отрицательные. Точка покоя — устойчивый узел (все движения затухающие и неколеблющиеся);
д) (случай большого “отрицательного трения”). Корни
и
действительные и положительные. Точка покоя — неустойчивый узел.
Пусть имеем систему линейных однородных дифференциальных уравнений с постоянными коэффициентами
(6)
Для нее имеют место аналогичные типы расположения интегральных кривых около начала координат (обобщенное седло, обобщенный узел и т.д.).
Теорема. Если все корни характеристического уравнения для системы (6) имеют отрицательную вещественную часть, то точка покоя системы (6)
, асимптотически устойчива. Если хотя бы один корень характеристического уравнения имеет положительную вещественную часть, то точка покоя неустойчива.
Пример 3. Будет ли устойчива точка покоя системы
Решение. Составляем характеристическое уравнение
или
Корни этого уравнения имеют отрицательные вещественные части. Следовательно, точка покоя данной системы асимптотически устойчива.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
Рассмотрим систему

Если точка
удовлетворяет условиям
,
то
есть решение
рассматриваемой системы, при этом точку
называют точкой покоя этой системы.
Будем рассматривать
однородную систему двух линейных
уравнений с постоянными коэффициентами

Точка
,
очевидно, точка покоя этой системы.
Составим характеристический определитель
системы
Его корни
определяют вид решений и устойчивость
точки покоя. Если корниимеют отрицательные вещественные части,
то точка покоя устойчива асимптотически.
Если корни чисто
мнимые, т.е.
,
то точка покоя устойчива, но не
асимптотически.
Если хотя бы один
корень имеет положительную вещественную
часть
,
то точка покоя неустойчива. Если один
корень нулевой, а другой отрицательный,
то точка покоя устойчива, но не
асимптотически. Если два нулевых корня,
то точка может быть как устойчивой не
асимптотически, так и неустойчивой.
Наиболее наглядно
устойчивость и неустойчивость точки
покоя проявляется при рассмотрении
фазовых траекторий системы (2.2).
Фазовая траектория
системы (2.2) есть кривая на плоскости
,
задаваемая функциямиесть решение системы (2.2). На этой кривой
обычно стрелками указывают движение
точки при возрастании.
В зависимости от корней характеристического
уравнения различают следующие точки
покоя:
-
если корни
вещественные отрицательные, то точку
покоя называют устойчивым узлом (рис.
2.2). -
если корни
вещественные положительные, точку
покоя называют неустойчивым узлом
(рис. 2.3). -
Если корни
вещественные разного знака, то точку
покоя называют седлом (рис. 2.4). -
Если корни
комплексные, то при положительных
вещественных частях точка покоя есть
неустойчивый фокус, при отрицательных
– устойчивый фокус (рис. 2.5 и 2.6
соответственно). -
Если корни чисто
мнимые, то точка покоя называется
центром (устойчива не асимптотически)
(рис. 2.7).
Фазовые траектории
вблизи различных точке покоя показаны
на рис. 2.2 – 2.7. следует отметить, что для
асимптотически устойчивой точки покоя
все фазовые траектории при
стремятся к началу координат. В случае
неасимптотической устойчивости (центр)
фазовые траектории для всехнаходятся в ограниченной окрестности
начала координат. Для неустойчивой
точки покоя существуют траектории,
начинающиеся сколь угодно близко к
началу и со временем неограниченно
удаляющиеся.
2.3. Решение задач
1.
Решение.
Корни
,
т.е.
Ответ: Точка покоя
– неустойчивый фокус (рис. 2.5).
Рис. 2.2
Рис. 2.3
Рис. 2.4.
2.
Решение.
Корни
.
Ответ. Точка покоя
– центр (рис. 2.7).
3.
Решение.
Корни – комплексные,
.
Ответ. Точка покоя
– устойчивый фокус (рис. 2.6).
4.
Решение.
Корни
– корни вещественные положительные.
Ответ. Точка покоя
– неустойчивый узел (рис. 2.3).
2.4. Исследование
на устойчивость по первому приближению.
Пусть исследуется
на устойчивость точка покоя
системы

(т.е. предполагается
).
Пусть
– дважды непрерывно дифференцируемы
в окрестности точки.
Для системы (4.1) составим уравнения
первого приближения в окрестности
начала координат.

где
.
(Здесь учтено, что).
Исследование на
устойчивость точки покоя (4.2) вместо
исследования на устойчивость точки
покоя (4.1) называется исследованием на
устойчивость по первому приближению.
Справедливы
следующие теоремы:
-
Если все корни
характеристического уравнения системы
(4.2)
имеют отрицательную вещественную часть
,
то точка покоясистемы (4.1) асимптотически устойчива.
-
Если хотя бы один
корень характеристического уравнения
системы (4.2) имеет вещественную
положительную часть, то точка покоя
системы (4.1) неустойчива.
Замечание.
Если среди корней характеристического
уравнения (4.2) есть корни с отрицательной
вещественной частью и нулевые или чисто
мнимые, то исследование на устойчивость
системы (4.2) не дает ответа на вопрос об
устойчивости точки покоя
системы (4.1).
Указанные выше
теоремы I
и II
дают возможность решать задачу об
устойчивости точки покоя системы (4.1)
на основе исследования более простой
системы (4.2).
Решение примеров.
Исследовать на устойчивость точку покоя
.
6.
Теоремы I
и II
применимы.
Здесь
,
ее дифференциал в точкеравен
,
ее дифференциал.
Уравнения первого
приближения:
Один корень
положительный, следовательно, точка
покоя неустойчива.
7.
Теоремы I
и II
применимы, т.к.
дважды (и более) непрерывно дифференцируемы.
Уравнения первого
приближения
Все корни
отрицательные. Точка покоя асимптотически
устойчива.
-
Функции Ляпунова
и теорема Ляпунова об устойчивости.
Будем рассматривать
систему (4.1) из предыдущего параграфа в
окрестности точки покоя
.
Сформулируем теорему Ляпунова об
устойчивости.
Если существует
непрерывно дифференцируемая функция
такая, что
1)
в окрестности начала координат, за
исключение точки,
где;
2)

то точка покоя системы (4.1) устойчива.
Если
обращается в нуль лишь при
,
то точка покоя асимптотически устойчива.
Функция
при этом называется функцией Ляпунова,
аназывается производной от функции
Ляпунова по времени, вычисленной в силу
системы (4.1) и обозначается:

Теорема Ляпунова
дает метод установления устойчивости
точки покоя системы путем подбора
соответствующей функции
.
Решение примеров.
Установить
устойчивость точки покоя
.
8.
Рассмотрим функцию

в окрестности
начала
за исключением самого начала. Поэтому
все условия теоремы Ляпунова выполнены.
Точка покоя системы асимптотически
устойчива. Заметим, что установить
устойчивость по первому приближению в
данном случае невозможно, так как один
из корней характеристического уравнения
равен нулю.
9.
Рассмотрим
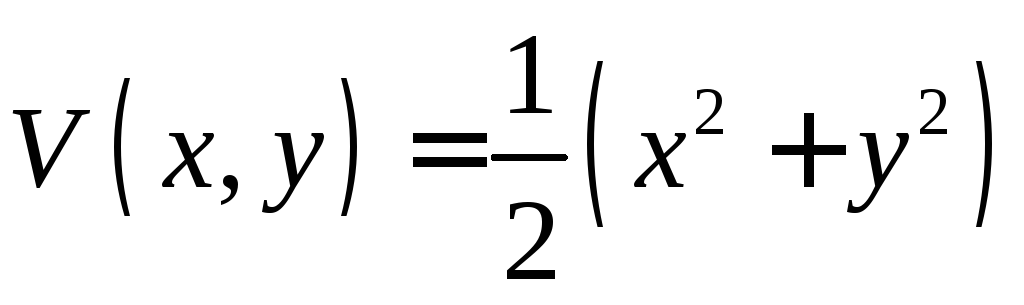

Как и в предыдущем
случае устанавливаем, что в силу теоремы
Ляпунова точка покоя устойчива
асимптотически:
всюду, за исключением
начала координат.
Уравнения первого
приближения
Имеют характеристическое
уравнение вида
Все корни чисто
мнимые, поэтому теоремы об устойчивости
по первому приближению не дают ответа
на вопрос об устойчивости.
Рассмотрим вопрос о зависимости решения задачи Коши от начальных данных. Пусть дана задача Коши
Если функция f(t, х) непрерывна по совокупности аргументов и имеет ограниченную производную 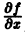
Справедлива следующая теорема о непрерывной зависимости решения от начальных условий.
Теорема:
Если правая часть f(t, х) дифференциального уравнения
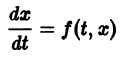
непрерывна по совокупности переменных и имеет ограниченную частную производную 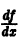
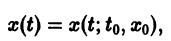
удовлетворяющее начальному условию 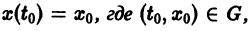
Иными словами, пусть через точку 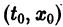
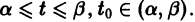
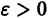
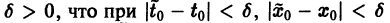
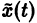
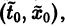
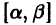
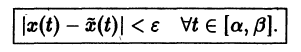
Аналогичная теорема справедлива и для системы дифференциальных уравнений
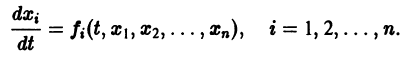
При выполнении условий теоремы (1) решение задачи Коши существует, единственно и непрерывно зависит от начальных данных. В этом случае говорят, что задача Коши поставлена корректно. Существенным является то обстоятельство, что отрезок [а, b] изменения t конечен. Однако во многих задачах нас интересует зависимость решения от начальных данных в бесконечном промежутке 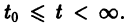
Остановимся вкратце на понятии о продолжаемости решения. Пусть имеем систему дифференциальных уравнений
где t — независимая переменная (время); 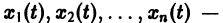
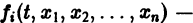
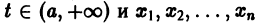
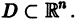
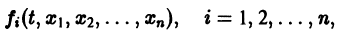
в их области определения непрерывны по совокупности аргументов и имеют ограниченные частные производные по 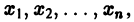
для каждой системы значений
существует единственное решение
системы (3), определенное в некотором интервале 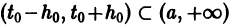
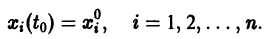
Введем следующее понятие. Пусть
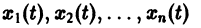
— решение задачи Коши (3)-(4), определенное на некотором интервале I = (t1,t2). Это решение может бьггь продолжено, вообще говоря, на больший интервал времени. Решение
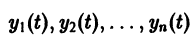
называется продолжением решения 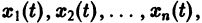
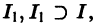
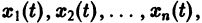
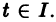
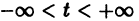
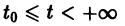
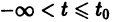
Для дальнейших рассмотрений важен вопрос о существовании решения хi(t), 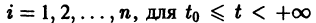
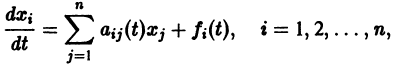
где 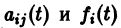
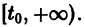
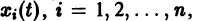
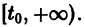
Не все системы обладают таким свойством. Например, для скалярного уравнения
функция
непрерывна и имеет производные всех порядков по х. Нетрудно проверить, что функция
является решением задачи
Однако это решение существует только в интервале 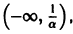
Уравнение (5) есть уравнение сверхбыстрого размножения, когда прирост пропорционален числу всевозможных пар. Его решение показывает, что при таком законе прироста населения количество населения становится бесконечным за конечное время (в то время как обычный закон прироста — экспоненциальный).
Задача:
Показать, что решения уравнения
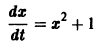
нельзя продолжить неограниченно ни вправо, ни влево.
Устойчивость по Ляпунову. Основные понятия и определения
Рассмотрим дифференциальное уравнение первого порядка
где функция f(t,x) определена и непрерывна для 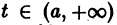
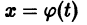
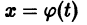
есть решение уравнения (1), удовлетворяющее начальному условию
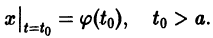
Пусть, далее, функция
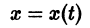
есть решение того же уравнения, удовлетворяющее другому начальному условию
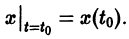
Предполагается, что решения 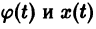
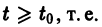
Определение:
Решение 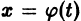
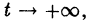
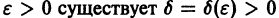
следует неравенство
для всех 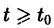
Это значит, что решения, близкие по начальным значениям к решению 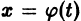
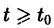
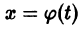
уравнения (1) устойчиво, если, какой бы узкой ни была е-полоска, содержащая кривую 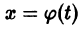
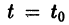
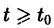
Если при сколь угодно малом 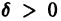
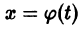
Определение:
Решение 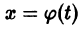
1) решение 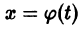
2) существует 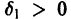
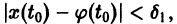
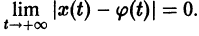
Это означает, что все решения х = x(t), близкие по начальным условиям к асимптотически устойчивому решению 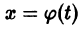
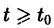
Вот простая физическая модель. Пусть шарик лежит на дне полусферической лунки (находится в положении равновесия). Если малым возмущением вывести шарик из этого положения, то он будет колебаться около него. При отсутствии трения положение равновесия будет устойчивым, при наличии трения колебания шарика будут уменьшаться с возрастанием времени, т. е. положение равновесия будет асимптотически устойчивым.
Пример:
Исследовать на устойчивость тривиальное решение
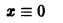
уравнения

Решение 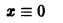
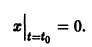
Решение уравнения (*), удовлетворяющее начальному условию
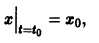
имеет вид
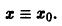
Легко видеть (рис. 2), что, какова бы ни была 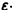
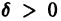
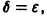
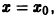
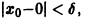
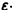
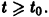
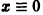
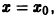
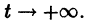
Пример:
Исследовать на устойчивость тривиальное решение 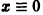
Решение уравнения (**), удовлетворяющее начальному условию
имеет вид
Возьмем любое 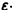
Поскольку 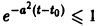
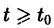
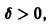
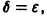
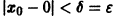
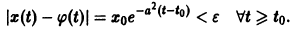
Согласно определению (1) это означает, что решение 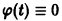
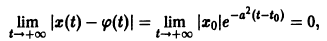
поэтому решение 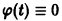
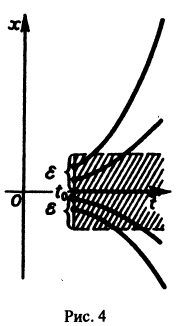
Пример:
Показать, что решение
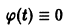
уравнения
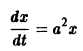
неустойчиво.
В самом деле, при сколь угодно малом 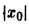
этого уравнения не удовлетворяет условию
при достаточно больших t > to. Более того, при любых 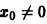
(рис.4).
Рассмотрим теперь систему дифференциальных уравнений
где функции fi определены для 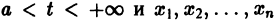
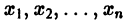
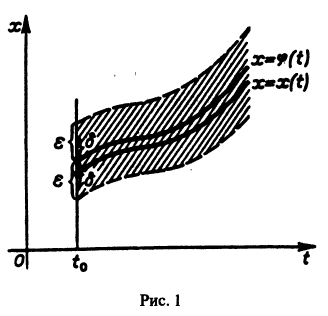
Определение:
Решение
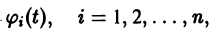
системы (4) называется устойчивым по Ляпунову при 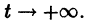
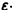
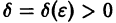
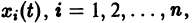
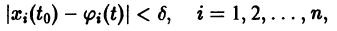
выполняются неравенства
для всех 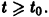
Если при сколь угодно малом 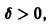
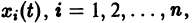
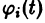
Определение:
Решение
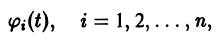
системы (4) называется асимптотически устойчивым, если:
1) решение это устойчиво;
2) существует 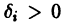
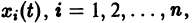
удовлетворяет условию
Пример:
Исходя из определения устойчивости по Ляпунову, показать, что решение системы
удовлетворяющее начальным условиям
устойчиво.
Решение системы (*), удовлетворяющее начальным условиям (**), есть
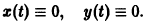
Решение этой системы, удовлетворяющее условиям 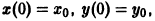
Возьмем произвольное 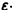
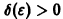
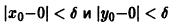
для всех 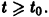
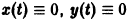
то при 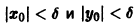
для всех 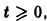
Из устойчивости нетривиального решения дифференциального уравнения не следует ограниченности этого решения. Рассмотрим, например, уравнение
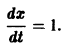
Решением этого уравнения, удовлетворяющим условию х(0) = 0, является функция
Решение, удовлетворяющее начальному условию 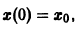
Геометрически очевидно (рис.5), что для всякого 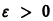
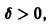
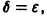
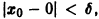
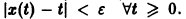
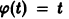
Из ограниченности решений дифференциального уравнения не следует устойчивости решений.
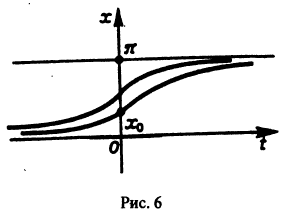
Рассмотрим уравнение

Оно имеет очевидные решения
Интегрируя уравнение (6), находим
Все решения (7) и (8) ограничены на 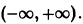
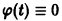
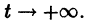
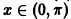
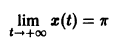
(рис. 6).
Таким образом, ограниченность и устойчивость решений являются понятиями, независимыми друг от друга.
Замечание:
Исследуемое на устойчивость решение
системы (4) всегда можно преобразовать в тривиальное решение
другой системы заменой
В самом деле, пусть имеем (для простоты) одно дифференциальное уравнение
и пусть требуется исследовать на устойчивость какое-либо решение 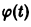
(величину 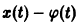
и подстановка в (*) приводит к равенству
Но 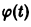
и из (**) имеем
Обозначив здесь правую часть через F(t, у), получим
Это уравнение имеет решение 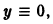
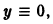
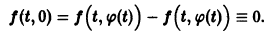
Таким образом, вопрос об устойчивости решения 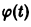
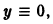
Устойчивость автономных систем. Простейшие типы точек покоя
Нормальная система дифференциальных уравнений называется автономной, если ее правые части fi не зависят явно от t, т. е. если она имеет вид
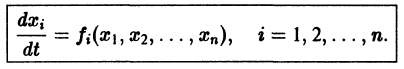
Это значит, что закон изменения неизвестных функций, описываемый автономной системой, не меняется со временем, как это бывает с физическими законами. Пусть имеем автономную систему
и пусть (а1, a2, …, аn) — такая совокупность чисел, что
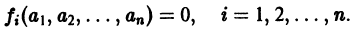
Тогда система функций
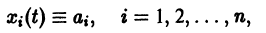
будет решением системы (1). Точку 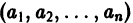
есть точка покоя этой системы. Обозначим через S(R) шар
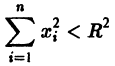
и будем считать, что для рассматриваемой системы в шаре S(R) выполнены условия теоремы существования и единственности решения задачи Коши.
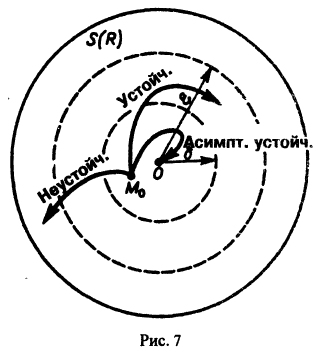
Определение:
Будем говорить, что точка покоя
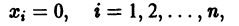
системы (1) устойчива, если для любого 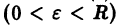
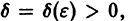
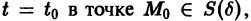
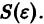
1) она устойчива;
2) существует такое 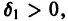
Поясним это определение примерами.
Пример:
Рассмотрим систему
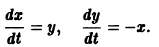
Траектории здесь — концентрические окружности
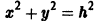
с центром в начале координат — единственной точкой покоя системы. Если взять 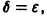
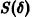
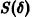
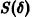
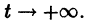
Пример:
Пусть дана система
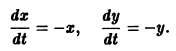
Ее решения:
Отсюда имеем
поэтому траекториями являются лучи, входящие в начало координат (рис.8). Можно снова выбрать 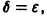
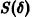
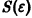
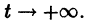
Пример:
Возьмем, наконец, систему
Здесь также
и траекториями являются лучи, исходящие из начала координат, но в отличие от примера 2 движение по лучам происходит в направлении от центра. Точка покоя неустойчива.
Простейшие типы точек покоя
Исследуем расположение траекторий в окрестности точки покоя х = 0, у = 0 системы двух линейных однородных уравнений с постоянными коэффициентами:
Решение будем искать в виде
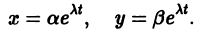
Для определения 
Величины 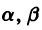
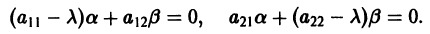
Возможны следующие случаи.
А. Корни 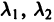
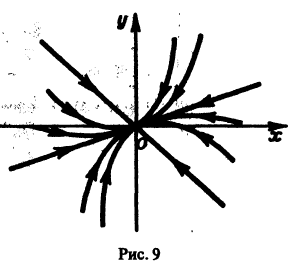
- Пусть
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
все точки каждой траектории, находившиеся в начальный момент
в произвольной
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, а при
стремятся к этому началу. Такая точка покоя называется устойчивым узлом
При С2 = 0 из (4) получаем
и траекториями являются два луча, входящие в начало координат с угловым коэффициентом
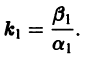
Аналогично, при С1 = 0 получаем еще два луча, входящие в начало координат с угловым коэффициентом
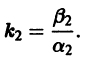
Пусть теперь 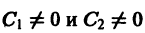
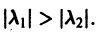
т. е. все траектории (исключая лучи 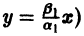
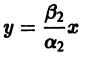
(рис. 9).
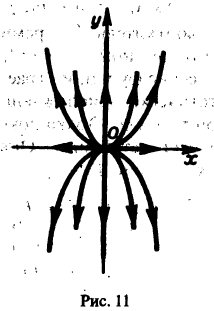
2. Если 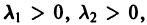
Пример:
Рассмотрим систему
Для нее точка О(0,0) — точка покоя. Характеристическое уравнение
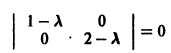
имеет корни 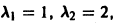
Оно имеет решения

так что траекториями системы будут лучи падающие с координатными полуосями, семейство парабол, касающихся оси Oх в начале координат (рис. 11)
3. Пусть теперь 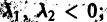
При С2 = 0 получаем решение
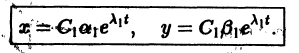
С возрастанием t точка этой траектории движется по лучу
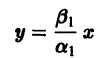
в направлении от начала 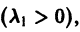
Отсюда видно, что при возрастании t точка движется по лучу
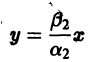
в направлении к началу координат 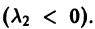
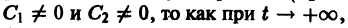
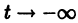
Пример:
Исследуем характер точки покоя О(0,0) системы
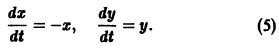
Характеристическое уравнение системы
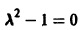
имеет корни 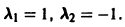
интегрируя которое получаем
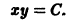
Уравнение (6) имеет также решения
Таким образом, интегральные кривые этого уравнения (траектории системы (5)) — равнобочные гиперболы и лучи, совпадающие с координатными полуосями.
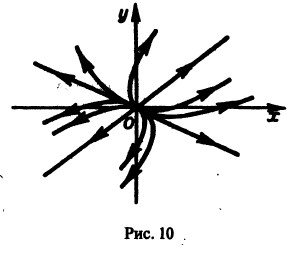
Б. Корни 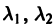
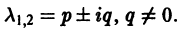
где C1 и C2 — произвольные постоянные, а 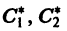
- Пусть
в этом случае множитель
стремится к нулю при
а вторые множители в (7) — ограниченные периодические функции. Траектории — спирали, асимптотически приближающиеся к началу координат при
Точка покоя х = 0, у = 0 асимптотически устойчива. Она называется устойчивым фокусом (рис. 13).,
- Если
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
- Если же
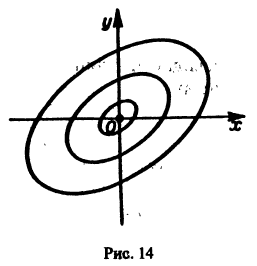
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
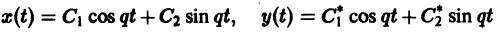
не стремится к нулю при
Пример. Рассмотрим систему уравнений
Характеристическое уравнение системы
имеет комплексные корни
Перейдем от системы к одному уравнению
и введем полярные координаты 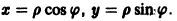
Следовательно,
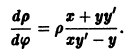
Используя уравнение (9), находим, что
Эти интегральные кривые являются логарифмическими спиралями, навивающимися на начало координат, которое достигается в пределе при 
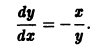
Интегральные кривые этого уравнения — окружности с центром в начале координат, которое при а = 0 является точкой покоя системы (8) типа центра.
В. Корни 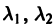
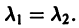
(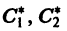
- Если
то из-за наличия множителя
решения х(t), y(t) стремятся к нулю при
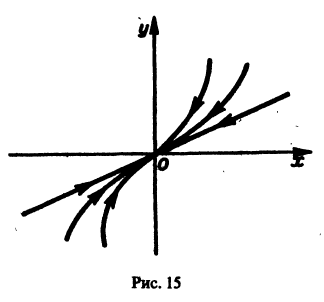
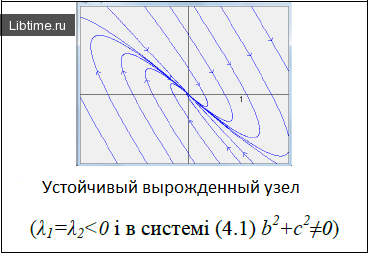
Точка покоя х = 0, у = 0 асимптотически устойчива. Ее называют устойчивым вырожденным узлам (рис. 15). Он отличается от узла в случае А. 1 (там одна из траекторий имела касательную, отличную от всех остальных). Возможен также дикритический узел (см. рис. 8).
- При
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
Пример:
Для системы уравнений
характеристическое уравнение
имеет кратные корни 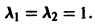
В этом случае
Поэтому все интегральные кривые проходят через начало координат, и все они имеют там ось Оу общей касательной.
Мы перебрали и исчерпали все возможности, поскольку случай 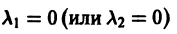
Пример:
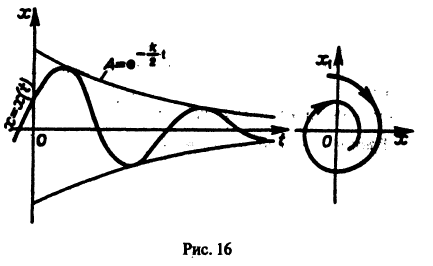
Исследовать уравнение малых колебаний маятника с учетом трения.
Уравнение малых колебаний маятника в этом случае имеет вид
где x — угол малого отклонения маятника от вертикали, к — коэффициент трения. Заменим уравнение (*) эквивалентной системой
Характеристическое уравнение для системы (**)
имеет корни
Если 0 < к < 2, то эти корни будут комплексными с отрицательной действительной частью, так что нижнее положение равновесия маятника х = х1 = 0 будет устойчивом фокусом. Решением уравнения (*) является функция
— частота колебаний, а величины А, а определяются из начальных условий.
График решения и фазовая кривая при 0 < к < 2 имеют вид, изображенный на рис. 16. При 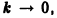
Сформулируем результаты, касающиеся устойчивости решений системы п линейных однородных дифференциальных уравнений первого порядка с постоянными коэффициентами
Рассмотрим для системы (10) характеристическое уравнение
Справедливы следующие предложения:
1) если все корни характеристического уравнения имеют отрицательную действительную часть, то все решения системы (10) асимптотически устойчивы. Действительно, в этом случае все слагаемые общего решения содержат множители 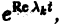
2) если хотя бы один корень 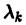
3) если характеристическое уравнение имеет простые корни с нулевой действительной частью (т. е. чисто мнимые или равные нулю корни), а остальные корни, если они есть, имеют отрицательную действительную часть, та все решения устойчивы, но асимптотической устойчивости нет.
Эти результаты относятся и к одному линейному дифференциальному уравнению с постоянными коэффициентами.
Следует обратить внимание на то, что для линейной системы все решения либо устойчивы, либо неустойчивы одновременна
Теорема:
Решения Системы линейных дифференциальных уравнений
либо все одновременно устойчивы, либо неустойчивы.
Преобразуем произвольное частное решение
системы (11) в тривиальное с помощью замены
Система (11) преобразуется при этом в линейную однородную систему относительно yi(t):
Следовательно, все частные решения системы (11) в смысле устойчивости ведут себя одинаково, а именно как тривиальное решение однородной системы (12).
В самом деле, пусть тривиальное решение
системы (12) устойчиво. Это значит, что для любого 
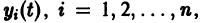
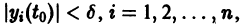
Замечая, что 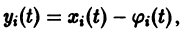
для всякого решения 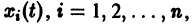
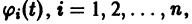
Это предложение не имеет места для нелинейных систем, некоторые решения которых могут быть устойчивыми, а другие — неустойчивыми.
Пример:
Рассмотрим нелинейное уравнение
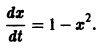
Оно имеет очевидные решения
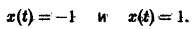
Решение x(t) = -1 неустойчиво, а решение x(t) = 1 является асимптотически устойчивым. В самом деле, при 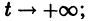
стремятся к +1. Это означает, согласно определению, что решение x(t) = 1 асимптотически устойчиво.
Замечание:
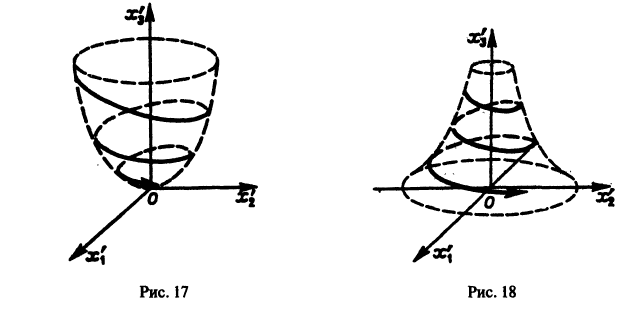
Как и в случае n = 2, можно исследовать расположение траекторий в окрестности точки покоя О(0,0,0) системы (10). Для n = 3 возможны так называемые узлофокусы (рис. 17), седлофокусы (рис. 18) и т. д.
Метод функций Ляпунова
Метод функций Ляпунова состоит в исследовании устойчивости точки покоя системы дифференциальных уравнений с помощью подходящим образом выбранной функции 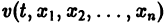
Ограничимся рассмотрением автономных систем
для которых Xi = 0, i = 1, 2,…, n, есть точка покоя.
Идея метода состоит в следующем. Предположим, что на устойчивость исследуется точка покоя 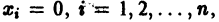
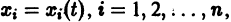
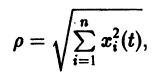
(производная вдоль траектории): Правая часть в (2) есть известная функция от х1, х2,…, хn, и можно исследовать ее знак. Если окажется, что 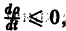
Определение:
Функция v(x1, х2, … xn), определенная в некоторой окрестности начала координат, называется знакоопределенной (знакоположительной или знакоотрицательной), если в области G
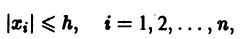
где h — достаточно малое положительное число, она может принимать значения только одного определенного знака и обращается в нуль лишь при

Так, в случае n = 3 функции
будут знакоположительными, причем здесь величина h > 0 может быть взята сколь угодно большой.
Определение:
Функция 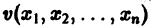

Например, функция
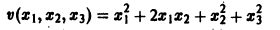
будет знакопостоянной (положительной). В самом деле, функцию v(x1, x2, x3) можно представить так:
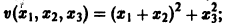
отсюда видно, что она неотрицательна всюду, но обращается в нуль и при 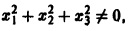
Пусть 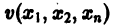
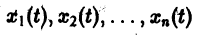
являются некоторыми функциями времени, удовлетворяющими системе дифференциальных уравнений (1). Тогда для полной производной функции v повремени имеем
Определение:
Величина 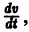
Определение:
Функций 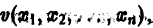
1) 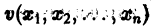
2) 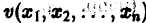
3) полная производная 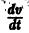
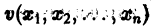
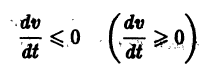
всюду в 
Теорема:
Теорема Ляпунова об устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 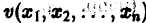
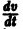
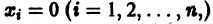
Приведем идею доказательства. Пусть для определенности 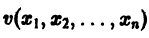
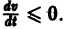
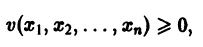
причем v = 0 лишь при 
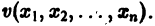
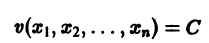
функции v являются, Как можно показать, замкнутыми поверхностями, внутри которых находится начало координат. Чтобы картина стала нагляднее, остановимся на случае n = 2. Так как 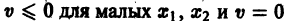
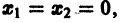
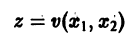
в общих чертах напоминает параболоид, вогнутый Вверх (рис. 19).
Линии уровня 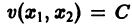
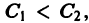
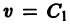
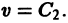
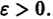
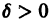
Рассмотрим траекторию системы (1), выходящую в начальный момент времени t = to из какой-нибудь точки 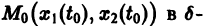
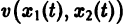
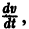
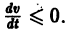
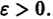
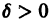
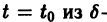
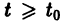
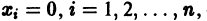
Теорема:
Теорема Ляпунова об асимптотической устойчивости. Если для системы дифференциальных уравнений
существует дифференцируемая знакоопределенная функция 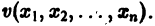
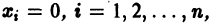
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Выберем в качестве функции v(x, y) функцию
Эта функция знакоположительная. В силу системы (*) найдем
Из теоремы 3 следует, что точка покоя О(0,0) системы (*) устойчива (центр). Асимптотической устойчивости нет, так как траектория системы (*) — окружности.
Пример 2. Исследовать на устойчивость точку покоя О(0,0) системы
Беря опять
Таким образом, 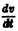
Теорема:
О неустойчивости. Пусть для системы дифференциальных уравнений
существует дифференцируемая в окрестности начала координат функция 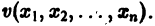
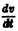
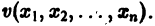
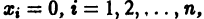
Пример:
Исследовать на устойчивость точку покоя О(0,0) системы
Возьмем функцию
Для нее функция
знакоположительная. Так как сколь угодно близко к началу координат найдутся точки, в которых v > 0 (например, 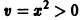
Метод функций Ляпунова оказывается универсальным и эффективным для широкого круга проблем теории устойчивости. Недостаток же метода в том, что достаточно общего конструктивного способа построения функций Ляпунова пока нет. В простейших случаях функцию Ляпунова можно искать в виде
Устойчивость по первому (линейному) приближению
Пусть имеем систему дифференциальных уравнений
и пусть 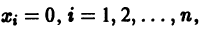
Будем предполагать, что функции 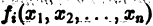
а слагаемые Ri содержат члены не ниже второго порядка малости относительно 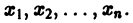
Так как понятие устойчивости точки покоя O(0,0,…, 0) связано с малой окрестностью начала координа’т в- фазовом пространстве, то естественно ожидать, что поведение решения (1) будет определяться главными линейными членами разложения функций fi по х. Поэтому наряду с системой (3) рассмотрим систему
называемую системой уравнений первого (линейного) приближения для системы (3).
Вообще говоря, строгой связи между системами (3) и (4) нет. Рассмотрим, например, уравнение
Здесь f(x) = 0; линеаризированное уравнение для уравнения (5) имеет вид
Решение 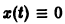
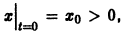
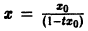
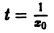
Теорема:
Если все корни характеристического уравнения
имеют отрицательные действительные части, то точка покоя 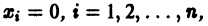
При выполнении условий теоремы возможно исследование на устойчивость по первому приближению.
Теорема:
Если хотя бы один корень характеристического уравнения (7) имеет положительную действительную часть, то точка покоя Xi= 0 системы (4) и системы (3) неустойчива.
В этом случае также возможно исследование на устойчивость по первому приближению.
Наметим идею доказательства теорем 6 и 7.
Пусть для простоты корни 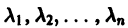
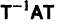
где 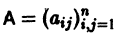
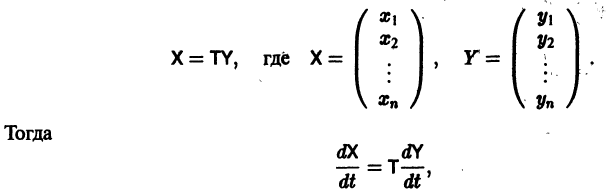
и система (4) преобразуется к виду
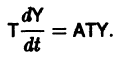
Отсюда получаем
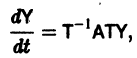
или, в силу выбора матрицы Т,
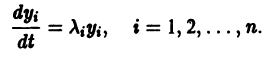
Система (3) при том же преобразовании перейдет в систему
причем в 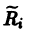
Рассмотрим следующие возможности:
1. Все корни 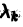
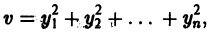
тогда производная 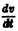
где 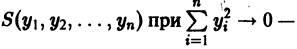
Таким образом, в достаточно малой окрестности 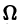
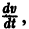
2. Некоторые из корней 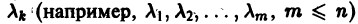
Отсюда видно, что сколь угодно близко к началу координат найдутся точки (например, такие, у которых 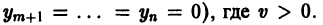
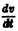
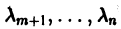
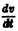
В критическом случае, когда все действительные части корней характеристического уравнения неположительны, причем действительная часть хотя бы одного корня равна нулю, на устойчивость тривиального решения системы (3) начинают влиять нелинейные члены Ri и исследование на устойчивость по первому приближению становится невозможным.
Пример:
Исследовать на устойчивость по первому приближению точку покоя х = 0, у = 0 системы
Система первого приближения имеет вид
Нелинейные члены удовлетворяют нужным условиям: их порядок не меньше 2. Составляем характеристическое уравнение для системы (**):
Корни характеристического уравнения 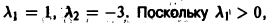
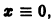
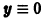
Пример:
Исследуем на устойчивость точку покоя О(0, 0) системы
Точка покоя х = 0, у = 0 системы (*) асимптотически устойчива, так как для этой системы функция Ляпунова
удовлетворяет условиям теоремы Ляпунова об асимптотической устойчивости. В частности,
В то же время точка покоя х = 0, у = 0 системы
неустойчива.
В самом деле, для функции 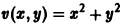
т.е. 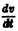
В силу теоремы 5 заключаем о неустойчивости точки покоя О(0,0) системы (**).
Для системы (*) и (**) система первого приближения одна и та же:
Характеристическое уравнение
для системы (***) имеет чисто мнимые корни — критический случай (действительные части корней характеристического уравнения равны нулю). Для системы первого приближения (***) начало координат является устойчивой точкой покоя — центром. Системы (*) и (**) получаются малым возмущением правых частей (***) в окрестности начала координат. Однако эти малые возмущения приводят к тому, что для системы (*) точка покоя О(0,0) становится асимптотически устойчивой, а для системы (**) неустойчивой.
Этот пример показывает, что в критическом случае нелинейные члены могут влиять на устойчивость точки покоя.
Задача. Исследовать на устойчивость точку покоя О(0,0) системы
где функция f(х,у) разлагается в сходящийся отеленной ряд и f(0,0) = 0.
Решение заданий и задач по предметам:
- Математика
- Высшая математика
- Математический анализ
- Линейная алгебра
Дополнительные лекции по высшей математике:
- Тождественные преобразования алгебраических выражений
- Функции и графики
- Преобразования графиков функций
- Квадратная функция и её графики
- Алгебраические неравенства
- Неравенства
- Неравенства с переменными
- Прогрессии в математике
- Арифметическая прогрессия
- Геометрическая прогрессия
- Показатели в математике
- Логарифмы в математике
- Исследование уравнений
- Уравнения высших степеней
- Уравнения высших степеней с одним неизвестным
- Комплексные числа
- Непрерывная дробь (цепная дробь)
- Алгебраические уравнения
- Неопределенные уравнения
- Соединения
- Бином Ньютона
- Число е
- Непрерывные дроби
- Функция
- Исследование функций
- Предел
- Интеграл
- Двойной интеграл
- Тройной интеграл
- Интегрирование
- Неопределённый интеграл
- Определенный интеграл
- Криволинейные интегралы
- Поверхностные интегралы
- Несобственные интегралы
- Кратные интегралы
- Интегралы, зависящие от параметра
- Квадратный трехчлен
- Производная
- Применение производной к исследованию функций
- Приложения производной
- Дифференциал функции
- Дифференцирование в математике
- Формулы и правила дифференцирования
- Дифференциальное исчисление
- Дифференциальные уравнения
- Дифференциальные уравнения первого порядка
- Дифференциальные уравнения высших порядков
- Дифференциальные уравнения в частных производных
- Тригонометрические функции
- Тригонометрические уравнения и неравенства
- Показательная функция
- Показательные уравнения
- Обобщенная степень
- Взаимно обратные функции
- Логарифмическая функция
- Уравнения и неравенства
- Положительные и отрицательные числа
- Алгебраические выражения
- Иррациональные алгебраические выражения
- Преобразование алгебраических выражений
- Преобразование дробных алгебраических выражений
- Разложение многочленов на множители
- Многочлены от одного переменного
- Алгебраические дроби
- Пропорции
- Уравнения
- Системы уравнений
- Системы уравнений высших степеней
- Системы алгебраических уравнений
- Системы линейных уравнений
- Системы дифференциальных уравнений
- Арифметический квадратный корень
- Квадратные и кубические корни
- Извлечение квадратного корня
- Рациональные числа
- Иррациональные числа
- Арифметический корень
- Квадратные уравнения
- Иррациональные уравнения
- Последовательность
- Ряды сходящиеся и расходящиеся
- Тригонометрические функции произвольного угла
- Тригонометрические формулы
- Обратные тригонометрические функции
- Теорема Безу
- Математическая индукция
- Показатель степени
- Показательные функции и логарифмы
- Множество
- Множество действительных чисел
- Числовые множества
- Преобразование рациональных выражений
- Преобразование иррациональных выражений
- Геометрия
- Действительные числа
- Степени и корни
- Степень с рациональным показателем
- Тригонометрические функции угла
- Тригонометрические функции числового аргумента
- Тригонометрические выражения и их преобразования
- Преобразование тригонометрических выражений
- Комбинаторика
- Вычислительная математика
- Прямая линия на плоскости и ее уравнения
- Прямая и плоскость
- Линии и уравнения
- Прямая линия
- Уравнения прямой и плоскости в пространстве
- Кривые второго порядка
- Кривые и поверхности второго порядка
- Числовые ряды
- Степенные ряды
- Ряды Фурье
- Преобразование Фурье
- Функциональные ряды
- Функции многих переменных
- Метод координат
- Гармонический анализ
- Вещественные числа
- Предел последовательности
- Аналитическая геометрия
- Аналитическая геометрия на плоскости
- Аналитическая геометрия в пространстве
- Функции одной переменной
- Высшая алгебра
- Векторная алгебра
- Векторный анализ
- Векторы
- Скалярное произведение векторов
- Векторное произведение векторов
- Смешанное произведение векторов
- Операции над векторами
- Непрерывность функций
- Предел и непрерывность функций нескольких переменных
- Предел и непрерывность функции одной переменной
- Производные и дифференциалы функции одной переменной
- Частные производные и дифференцируемость функций нескольких переменных
- Дифференциальное исчисление функции одной переменной
- Матрицы
- Линейные и евклидовы пространства
- Линейные отображения
- Дифференциальные теоремы о среднем
- Функции комплексного переменного
- Преобразование Лапласа
- Теории поля
- Операционное исчисление
- Системы координат
- Рациональная функция
- Интегральное исчисление
- Интегральное исчисление функций одной переменной
- Дифференциальное исчисление функций нескольких переменных
- Отношение в математике
- Математическая логика
- Графы в математике
- Линейные пространства
- Первообразная и неопределенный интеграл
- Линейная функция
- Выпуклые множества точек
- Система координат
- Главная
- Моделирование
- Точки равновесия для динамических систем
08 Декабрь 2011 24877
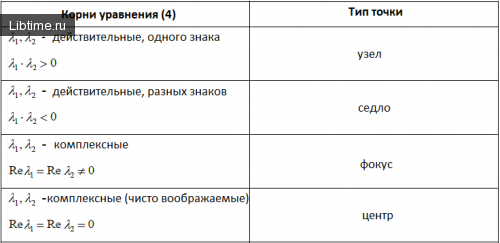
Пусть имеем линейную однородную систему дифференциальных уравнений с постоянными коэффициентами: 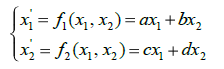

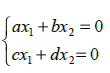
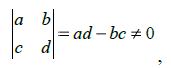
(4) где:
– след матрици,
– детерминант. Классификация точек равновесия в случае, когда Δ ≠ 0, представленная в таблице:
Классификация точек равновесия
Характер устойчивости положений равновесия
Собственные значения матрицы системы (1) однозначно определяют характер стойкости положений равновесия:
- Устойчивый узел – если действительные части всех корней уравнения (4) отрицательны, то точка равновесия системы (1)асимптотически устойчива.
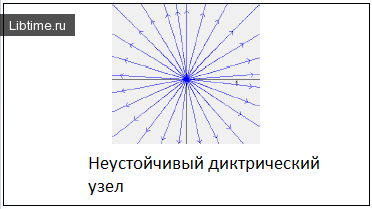
- Седло, неустойчивый узел, неустойчивый фокус – если действительная часть хотя бы одного корня уравнения (4) положительна, то точка равновесия системы (1)неустойчивая.
- Центр – если уравнение (4) имеет чисто воображаемые корни, то точка равновесия системы (1) устойчива, но не асимптотически
Ниже изображены фазовые портреты динамических систем для каждого типа точек равновесия. Направление стрелок на фазовой кривой указывает направление движения фазовой точки при возрастании t. 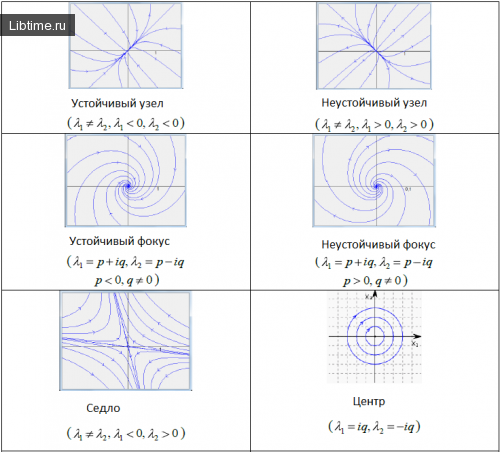

Рейтинг: 4,4/5 – 7
голосов




















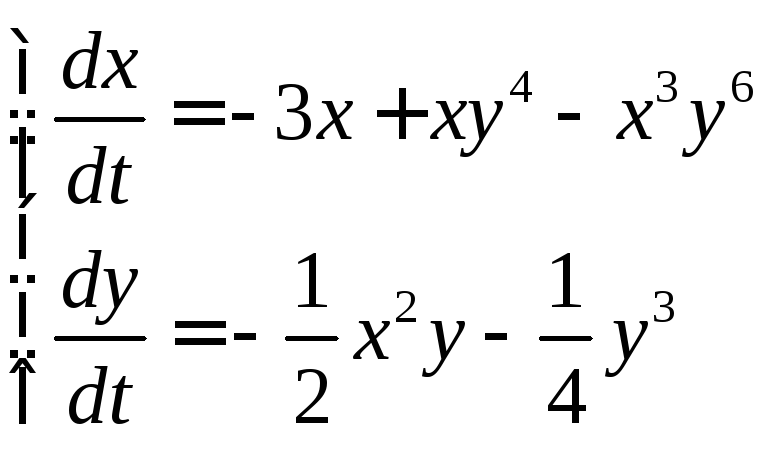





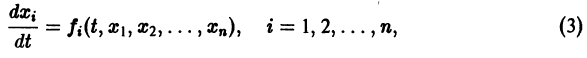
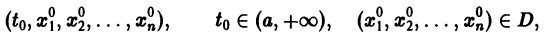
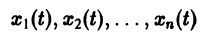
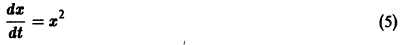
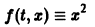
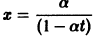
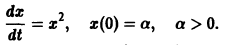
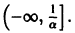




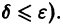
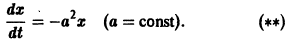
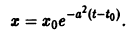
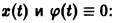
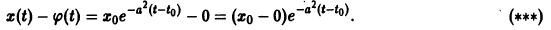
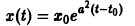
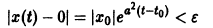
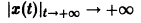
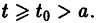
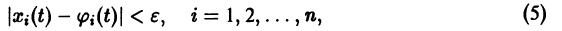
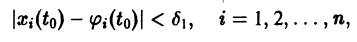
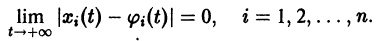


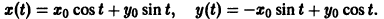
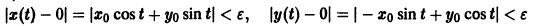
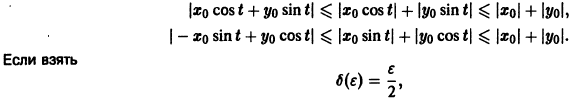
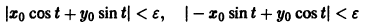
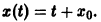

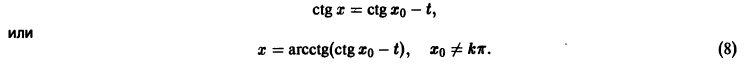
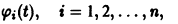
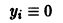
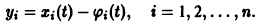

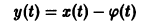
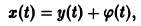

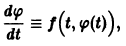
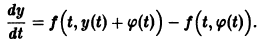

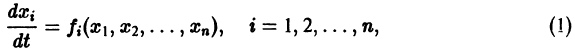
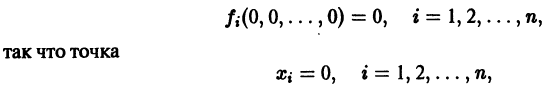
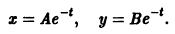
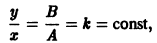
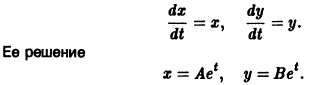
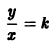
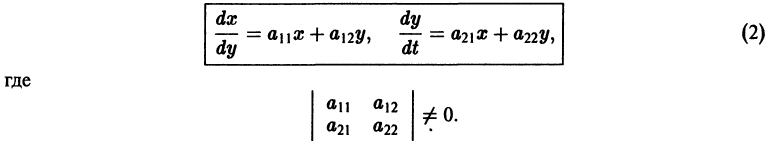
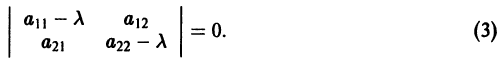
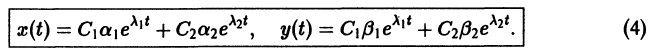
 Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей
Точка покоя (0,0) в этом случае асимптотически устойчива, так как из-за наличия множителей 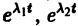 все точки каждой траектории, находившиеся в начальный момент
все точки каждой траектории, находившиеся в начальный момент 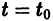 в произвольной
в произвольной  окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой,
окрестности начала координат, при достаточно большом t переходят в точки, лежащие в сколь угодно малой, 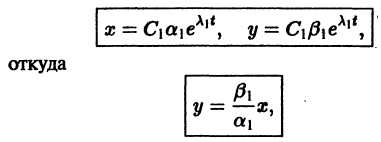
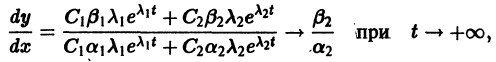
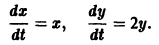
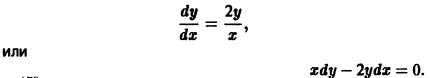
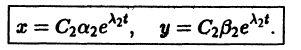
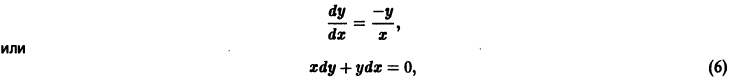
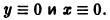
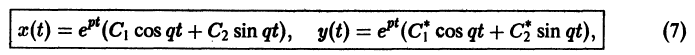
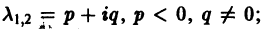 в этом случае множитель
в этом случае множитель 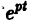 стремится к нулю при
стремится к нулю при 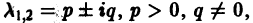 то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.
то этот случай переходит в предыдущий при замене t на -t. Траектории не отличаются от траекторий предыдущего случая, но движение по ним при возрастании t происходит в противоположном направлении. Точка покоя неустойчива — неустойчивый фокус.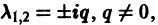 то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение
то решения системы (2) — периодические функции. Траекториями являются замкнутые кривые, содержащие внутри себя точку покоя, называемую в этом случае центром (рис. 14). Центр является устойчивой точкой покоя, однако асимптотической устойчивости нет, так как решение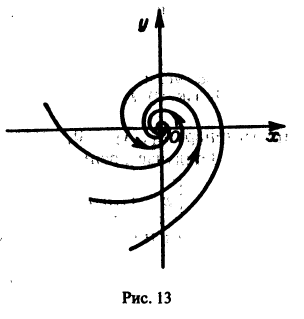
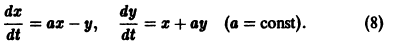
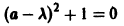
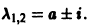

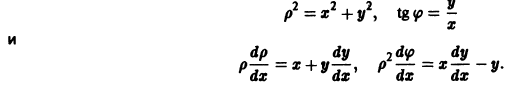

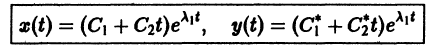
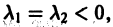 то из-за наличия множителя
то из-за наличия множителя 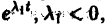 решения х(t), y(t) стремятся к нулю при
решения х(t), y(t) стремятся к нулю при 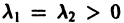 замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.
замена t на -t приводит к предыдущему случаю, но движение по траекториям происходит в противоположном направлении. Точка покоя в этом случае называется неустойчивым вырожденным узлом.