1. Внутренняя энергия газа
Из курса физики основной школы вы знаете, что сумму кинетической энергии хаотического движения частиц и потенциальной энергии их взаимодействия называют внутренней энергией.
Внутренняя энергия U данной массы одноатомного идеального газа равна произведению средней кинетической энергии 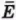 одной молекулы на число молекул N:
одной молекулы на число молекул N:
U = 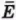 N.
N.
? 1. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой

Итак, внутренняя энергия идеального газа определяется только его абсолютной температурой и числом молекул в нем.
? 2. Объем одного моля газа при температуре 20 ºС и нормальном атмосферном давлении составляет 24 л.
а) Чему равна внутренняя энергия этого газа, если он одноатомный и его можно считать идеальным?
б) На какую высоту можно было бы забросить мяч массой 365 г, если бы можно было сообщить ему такую кинетическую энергию и пренебречь сопротивлением воздуха?
Выполнив это задание, вы сможете представить, как велика внутренняя энергия тела. Объясняется это тем, что скорость хаотического движения молекул в десятки и сотни раз превышает скорости движения окружающих нас тел. А кинетическая энергия пропорциональна квадрату скорости. Поэтому при увеличении скорости в 10 раз кинетическая энергия увеличивается в 100 раз, а при увеличении скорости в 100 раз кинетическая энергия увеличивается в 10 000 раз.
Внутреннюю энергию идеального одноатомного газа можно выразить также через его давление p и объем V.
? 3. Объясните, почему внутренняя энергия U данной массы одноатомного идеального газа выражается формулой
U = (3/2)pV. (2)
Подсказка. Воспользуйтесь формулой (1) и уравнением состояния идеального газа.
? 4. Из формулы (1) следует, что внутренняя энергия одного моля газа зависит только от его абсолютной температуры и количества вещества (числа молекул). А из формулы (2) следует, что она зависит от давления и объема, но зато не зависит от количества вещества. Объясните, почему тут нет противоречия.
? 5. Ширина класса 5 м, длина 10 м, а высота – 4 м. Температура воздуха 20 ºС, давление равно нормальному атмосферному давлению.
а) Чему была бы равна внутренняя энергия газа, заполняющего класс, если бы он был одноатомным? (Воздух состоит в основном из двухатомных молекул. Как показывает расчет, выходящий за рамки нашего курса, внутренняя энергия двухатомного газа при тех же макроскопических параметрах в 5/3 раза больше, чем внутренняя энергия одноатомного газа.)
б) На какую высоту можно было бы поднять автомобиль массой 1 т, затратив такую энергию?
в) Есть ли в условии лишние данные?
Результаты выполнения этого задания раскроют, какая огромная энергия «окружает» каждого из нас! А ведь мы ее практически не замечаем, считая воздух «пустотой».
Большую внутреннюю энергию имеют, конечно, и другие тела. Например, внутренняя энергия литра кипятка больше внутренней энергии того же литра воды при комнатной температуре на величину, равную работе, которую надо совершить для того, чтобы поднять легковой автомобиль на двенадцать этажей!
При изучении тепловых явлений мы учитываем только кинетическую энергию хаотического движения молекул и потенциальную энергию их взаимодействия. А ведь есть еще и во много раз большая энергия взаимодействия частиц в атомных ядрах. Вы знаете о ней из курса физики основной школы. К ядерной физике мы вернемся в 11-м классе.
Соотношение между различными видами энергии, которыми обладает данное тело, схематически представлено на рисунке 42.1. Мы видим, что непосредственно наблюдаемая механическая энергия составляет лишь очень малую долю всей энергии тела. Соблюсти масштаб на этом рисунке невозможно, потому что тепловая внутренняя энергия в тысячи раз больше механической, а ядерная – в миллионы раз больше тепловой.

Два способа изменения внутренней энергии
Из курса физики основной школы вы знаете, что внутреннюю энергию тела можно изменить двумя способами:
- совершая работу над телом – например, сжимая газ (рис. 42.2, а);
- посредством теплопередачи, то есть без совершения работы, – например, при контакте с более горячим телом (рис. 42.2, б). (Теплопередачу называют иногда также теплообменом.)

Напомним, что меру изменения внутренней энергии при теплопередаче называют количеством теплоты и обозначают Q. Количество теплоты измеряют в джоулях.
Как мы знаем, внутренняя энергия данной массы идеального газа определяется только его температурой и числом молекул. Поэтому при постоянном числе молекул изменить внутреннюю энергию идеального газа можно только изменив его температуру.
Например, при сжатии газа в теплоизолированном сосуде газ нагревается вследствие того, что над ним производят работу. Нагревание газа может быть при атом весьма заметным.
Поставим опыт
Поместим кусочек сухой ваты в толстостенный прозрачный цилиндр и быстро (резким толчком) вдвинем в цилиндр поршень (рис. 42.3).

Воздух в цилиндре нагреется так сильно, что вата воспламенится.
Нагревание газа при сжатии используют в дизельных двигателях: при сжатии горючая смесь в цилиндре нагревается настолько, что воспламеняется без искры.
Газовый процесс, который происходит в теплоизолированном сосуде, то есть без теплопередачи, называют адиабатным. Адиабатным можно считать также процесс, когда тепло- передачей можно пренебречь: например, если процесс происходит за время, в течение которого не успевает произойти теплообмен с окружающей средой.
При адиабатном расширении газ охлаждается. По этой причине, например, образуются облака. Поднимающийся влажный воздух попадает в более разреженные слои атмосферы, расширяется и вследствие этого охлаждается. Как мы увидим далее, при охлаждении ниже определенной температуры (точки росы) содержащийся в воздухе водяной пар конденсируется: образуются капельки тумана, из которого и состоят облака.
Увеличить или уменьшить температуру газа можно, конечно, и посредством теплопередачи. Например, сосуд с газом можно поместить над огнем, в кипящую воду или в морозильную камеру.
? 6. Изменяется ли, н если да, то как внутренняя энергия данной массы идеального газа:
а) при изотермическом расширении? сжатии?
б) при изобарном расширении? сжатии?
в) при изохорном охлаждении? нагревании?
г) при адиабатном сжатии? расширении?
2. Первый закон термодинамики
Итак, внутренняя энергия газа U может изменяться как вследствие того, что ему сообщают количество теплоты Q, так и потому, что внешние силы совершают работу A над газом.
Согласно закону сохранения энергии
изменение внутренней энергии газа ∆U равно сумме количества теплоты Q, переданного газу, и работы A, совершенной над газом:
∆U = Q + A. (3)
Закон сохранения энергии применительно к тепловым явлениям называют первым законом термодинамики. (Термодинамикой называют раздел физики, изучающий общие законы тепловых явлений.)
Как Q, так и A могут быть положительными, отрицательными или равными нулю. Если газ сжимают, то A > 0, а если он расширяется, то A < 0. Если объем газа не изменяется, то A = 0. Если газу передают некоторое количество теплоты, то Q > 0, а если газ отдает некоторое количество теплоты, то Q < 0.
В практических расчетах и при решении многих задач часто используют другую формулировку первого закона термодинамики. Дело в том, что при рассмотрении тепловых двигателей главный интерес представляет работа, совершенная самим газом (то есть силой давления, действующей со стороны газа на поршень; при расширении газа работа газа положительна).
Обозначим работу газа Aг. Она связана с работой A, совершенной внешними силами над газом, соотношением
Aг = –A.
При сжатии газа A > 0, Aг < 0; а при расширении газа A < 0, Aг > 0.
Используя понятие работы газа, первый закон термодинамики формулируют так:
количество теплоты, переданное газу, равно сумме изменения внутренней энергии газа и работы, совершенной газом:
Q = ∆U + Aг. (4)
Чтобы использовать соотношения (3) и (4) на практике, надо уметь находить выражения для изменения внутренней энергии газа и работы газа (или работы внешних сил).
Как найти изменение внутренней энергии газа?
Для одноатомного идеального газа внутренняя энергия выражается формулой (1), поэтому для изменения ∆U внутренней энергии получаем:
∆U = (3/2)νR∆T. (5)
Здесь ∆T = T2 – T1, ∆U = U2 – U1, а индексами 1 и 2 обозначены соответственно начальное и конечное состояния газа.
? 7. Начальная температура пяти молей гелия 100 ºС. Газ нагрели на 50 ºС.
а) Насколько увеличилась внутренняя энергия газа?
б) Есть ли в условии лишние данные?
Изменение внутренней энергии одноатомного идеального газа можно найти и с помощью формулы (2):
∆U = (3/2)∆(pV). (6)
Здесь ∆(pV) – изменение произведения давления на объем. Например, при переходе газа из состояния 1 в состояние 2
∆(pV) = p2V2 – p1V1. (7)
? 8. Чему равно изменение внутренней энергии одного моля одноатомного идеального газа:
а) при изобарном расширении, если давление газа равно p0, а объем газа увеличился от V0 до 3V0?
б) при изохорном охлаждении, если объем газа равен V0, а давление газа уменьшилось от p0 до 0,5p0?
в) в процессе, в котором начальные давление и объем газа равны p0 и V0, а конечные равны 2p0 и 3V0?
Есть ли в условии лишние данные?
Важным достоинством формулы (6) является то, что в нее не входят ни количество вещества в газе, ни его масса. Поэтому, например, если давление и объем газа остались неизменными, то не изменилась и внутренняя энергия газа, хотя при этом могла измениться его масса. Рассмотрим пример, в котором речь идет о воздухе, который состоит в основном из двух- атомных молекул. Их средняя кинетическая энергия при заданной температуре больше, чем у одноатомных молекул (двухатомные молекулы обладают еще кинетической энергией вращательного движения). Однако для выполнения следующего задания то, что воздух состоит из двухатомных молекул, несущественно.
? 9. До включения отопления температура воздуха в комнате объемом 60 м3 была равна 15 ºС. После включения отопления воздух нагрелся до 20 ºС. Давление воздуха постоянно и равно 105 Па.
а) На сколько процентов увеличилась средняя кинетическая энергия молекул в воздухе?
б) Как изменилась внутренняя энергия воздуха в комнате?
в) На сколько процентов изменилась концентрация молекул воздуха?
г) Насколько изменилась масса воздуха в комнате?
Как найти совершенную газом работу?
Рассмотрим сначала изобарное расширение газа в цилиндре под поршнем (рис. 42.4). Газ давит на поршень с силой F = pS, где p – давление газа, S – площадь поршня.

Если поршень переместился на ∆x, то совершенная газом работа Aг = F * ∆x = pS * ∆x. Так как S * ∆x = ∆V, получаем, что при изобарном расшинерии работа газа выражается формулой
Aг = p * ∆V. (8)
? 10. Используя рисунок 42.5, объясните, почему работа газа численно равна площади фигуры под графиком зависимости p(V).

Это свойство графика зависимости p(V) сохраняется и тогда, когда давление газа изменяется.
Пусть, например, график зависимости p(V) имеет вид, изображенный на рисунке 42.6. Процесс расширения газа мысленно разобьем на большое число этапов, в каждом из которых объем газа изменяется настолько мало, что его давление можно считать практически постоянным. Поскольку для каждого этапа работа газа численно равна площади под соответствующим участком графика, то и вся работа, совершенная газом при расширении, равна площади под всем графиком p(V).

? 11. Один моль идеального газа можно перевести из состояния 1 в состояние 2 многими способами. Рассмотрим процессы, которым соответствуют графики а и б (рис. 42.7).
а) В каком случае совершенная газом работа больше? Во сколько раз больше?
б) В каком случае изменение внутренней энергии газа больше? Во сколько раз больше?
в) В каком случае переданное газу количество теплоты больше? Во сколько раз больше?

На примере этого задания вы могли заметить, что изменение ∆U внутренней энергии данной массы идеального газа определяется только начальным и конечным состоянием газа.
Обусловлено это тем, что каждому состоянию данной массы газа (с определенными значениями p, V и T) соответствует одно определенное значение внутренней энергии, которое можно найти либо по формуле (1), либо по формуле (2).
А вот работа, совершенная газом при переходе из начального состояния в конечное, зависит от характера процесса, которым газ был переведен из начального состояния в конечное.
Действительно, работа газа численно равна площади под графиком зависимости p(V). А эта площадь зависит от того, какой вид имела функция p(V).
Если газ не расширяется, а сжимается (рис. 42.8), то внешние силы производят работу над газом. В таком случае говорят также, что газ производит отрицательную работу. Она численно равна взятой со знаком минус площади S под графиком зависимости p(V).

На том, что работа газа зависит от вида зависимости p(V), а не только от начального и конечного состояния, основан принцип действия тепловых двигателей (в следующем параграфе мы рассмотрим их подробнее).
В тепловых двигателях газ расширяется при высокой температуре. При атом давление газа велико, поэтому он совершает большую работу. А сжимают газ при более низкой температуре, когда давление газа меньше. Поэтому для того, чтобы вернуть газ в начальное состояние, внешние силы должны совершить меньшую работу.
Рассмотрим пример.
? 12. Газ совершает циклический процесс: переходит из состояния 1 в состояние 2 (рис. 42.9), а потом возвращается в состояние 1. При этом объем газа не должен быть меньше начального и больше конечного.

а) Какую максимально возможную работу может совершить газ при переходе 1–2, если давление газа не должно превышать 3p0?
б) Какую минимально возможную работу должны совершить внешние силы при переходе 2–1, если давление газа не должно быть меньше p0?
в) Насколько в этом случае работа газа при циклическом процессе больше работы внешних сил?
Применение первого закона термодинамики к изопроцессам и адиабатному процессу
? 13. Используя первый закон термодинамики, а также выражения для внутренней энергии и работы газа, объясните, почему:
а) при изохорном процессе Aг = 0, Q = ∆U, то есть сообщенное газу количество теплоты (напомним, что оно может быть как положительным, так и отрицательным) равно изменению внутренней энергии газа;
б) при изотермическом процессе ∆U = 0, Q = Aг, то есть сообщенное газу количество теплоты равно работе газа;
в) при изобарном процессе Aг ≠ 0, ∆U ≠ 0;
г) при адиабатном процессе Q = 0, Aг = –∆U, то есть при расширении газ совершает работу за счет уменьшения внутренней энергии, а при сжатии газа его внутренняя энергия увеличивается за счет работы внешних сил.
Подсказка. Если давление не изменяется, то ∆(pV) = p∆V.

Дополнительные вопросы и задания
14. На рисунках 42.10, а, б, в изображены графики трех процессов с данной массой одноатомного идеального газа. Чему равно изменение внутренней энергии газа для каждого из этих процессов при переходе 1–2?

15. При изобарном расширении данной массы одноатомного идеального газа его температура возросла от 0 ºС до 100 ºС. При этом газу было передано количество теплоты, равное 5 кДж.
а) Насколько изменилась внутренняя энергия газа?
б) Чему равно количество вещества в сосуде с газом?
Решение задач – занятие, которое любит далеко не каждый. Здесь мы стараемся сделать так, чтобы оно занимало у вас поменьше времени без ущерба для качества самого решения. Тема этой статьи — задачи на внутреннюю энергию.
Подписывайтесь на наш телеграм и читайте полезные материалы для студентов каждый день!
Решение задач: внутренняя энергия
Прежде чем приступать к задачам на внутреннюю энергию тела, посмотрите общую памятку по решению физических задач. И пусть под рукой на всякий случай всегда будут основные физические формулы.
Задача №1. Изменение внутренней энергии
Условие
Воздушный шар объёмом 500 м3 наполнен гелием под давлением 105 Па. В результате нагрева температура газа в аэростате поднялась от 10 °С до 25 °С. Как увеличилась внутренняя энергия газа?
Решение
Для решения будем использовать формулу внутренней энергии идеального газа:
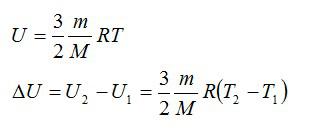
Массу гелия выразим из уравнения Клапейрона-Менделеева:
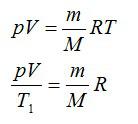
Тогда можно записать:
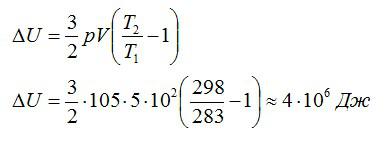
Ответ: 4 МДж.
Задача №2. Внутренняя энергия и работа
Условие
Азот массой 200 г расширяется изотермически при температуре 280 К, причем объём газа увеличивается в 2 раза. Найти:
- Изменение ∆U внутренней энергии газа.
- Совершенную при расширении газа работу А.
- Количество теплоты Q, полученное газом.
Решение
Так как процесс изотермический, то изменение внутренней энергии равно нулю, а работа равна количеству теплоты, полученному газом:
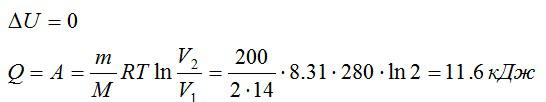
Ответ: 0; 11,6 кДж; 11,6 кДж.
Задача №3. Изменение внутренней энергии при изобарном и изохорном процессе
Условие
Кислород занимает объём V1= 3 л при давлении p1= 820 кПа. В результате изохорного нагревания и изобарного расширения газ переведён в состояние с объёмом V2= 4,5 л и давлением p2= 600 кПа. Найти количество теплоты, полученное газом; изменение внутренней энергии газа.
Решение
Теплота, подведенная к газу, идет на совершение работы и изменение внутренней энергии:
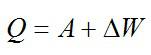
В изохорном и изобарном процессе соответственно:
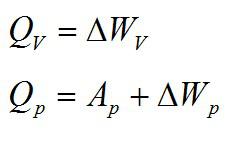
Изохорное нагревание:
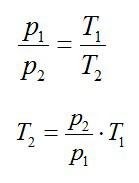
Изменение внутренней энергии при изохорном процессе:
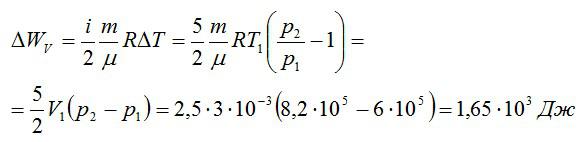
Изменение внутренней энергии при изобарном процессе:
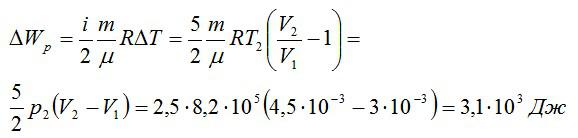
Общее изменение внутренней энергии:
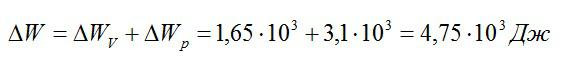
Ответ: 4,75 кДж.
Задача №4. Изменение внутренней энергии двухатомного газа
Условие
Кислород массой 2 кг занимает объём 6 м3 и находится под давлением 1 атм. Газ был нагрет сначала при постоянном давлении до объёма 13 м3, а затем при постоянном объёме – до давления 23 атм. Найти изменение внутренней энергии газа.
Решение
Изменение внутренней энергии находим по формуле:
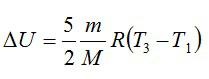
Эту форму можно преобразовать, используя уравнение Клапейрона-Менделеева:
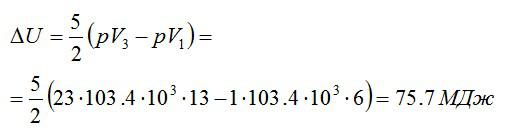
Ответ: 75,7 МДж.
Задача №5. Внутренняя энергия смеси газов
Условие
В закрытом сосуде находится масса m1 = 20 г азота и масса m2 = 32 г кислорода. Определить изменение ΔU внутренней энергии смеси газов при охлаждении ее на ΔТ = 28 К.
Решение
Определим количество молей азота и кислорода, а затем общее количество вещества в смеси соответственно:
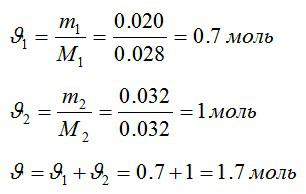
Изменение внутренней энергии:
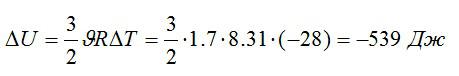
Знак «минус» означает, что внутренняя энергия уменьшается.
Ответ: -539 Дж.
Вопросы на тему «Внутренняя энергия тела»
Вопрос 1. Что такое внутренняя энергия?
Ответ. Для начала, внутренняя энергия чего? Бутылки с пивом, воздуха в шарике, тазика с водой? Все макроскопические тела обладают энергией, заключенной внутри них: атомы твердого тела колеблются в кристаллической решетке около положений равновесия, молекулы газа находятся в постоянном хаотическом движении и т.д.
По определению:
Внутренняя энергия вещества – это энергия, которая складывается из кинетической энергии всех атомов и молекул, и потенциальной энергии их взаимодействия друг с другом.
Для идеального газа с числом степеней свободы i внутренняя энергия вычисляется по формуле:
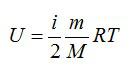
Вопрос 2. От чего зависит внутренняя энергия идеального газа?
Ответ. Эта величина не зависит от объёма и определяется только температурой.
Вопрос 3. Как изменяется внутренняя энергия тела?
Ответ. Если тело совершает работу, его внутренняя энергия уменьшается. Например, газ передвигает поршень. Если же работа совершается над телом, то внутренняя энергия увеличивается.
Вопрос 4. Что такое функция состояния?
Ответ. Функция состояния – это один из параметров, которым можно описать термодинамическую систему. Функция состояния не зависит от того, как система пришла в то или иное состояние, а определяется несколькими переменными состояния.
Внутренняя энергия – это функция состояния термодинамической системы. В общем случае она зависит от температуры и объёма.
Вопрос 5. Можно ли изменить внутреннюю энергию тела, не совершая над ним работы?
Ответ. Да, еще один способ изменения внутренней энергии – теплопередача. В процессе теплопередачи внутренняя энергия тел изменяется.
Нужна помощь в решении задач по любой теме и других студенческих заданий? Профессиональный студенческий сервис поспособствует в выполнении работы вне зависимости от ее сложности.
Внутренняя
энергия и способы ее изменения
U
– внутренняя энергия – это
энергия движения и взаимодействия
частиц, из которых состоит тело.
Внутренняя энергия зависит от температуры
тела, его агрегатного состояния
(газообразное, жидкое, твердое), от
химических, атомных
и ядерных
реакций.
Она не зависит ни от механического
движения тела, ни от положения этого
тела относительно других тел.
U=Ек+Еп
Т.к.
у идеального газа отсутствуют силы
притяжения молекул, то Еп=0, следовательно
U=Ек=3/2*КТ
– для одноатомного газа; U=Ек=5/2*КТ
– для 2х-атомного; U=Ек=7/2*КТ
– для 3х-атомного.
Внутреннюю
энергию идеального газа можно выразить
через термодинамические параметры:
U=3/2*PV
Внутреннюю
энергию газа можно изменить двумя
способами:
1.
Путем теплообмена.
2.
Путем совершения работы.
Работа
газа в изопроцессах.
А=P*ΔV=[Дж]
1.Изотермический.
Т=const
, m=const
Уравнение
изопроцесса: P*V=const
Формула
работы в изопроцессе: A=![]()
а)
изотермическое расширение: V1<V2
![]()
б)изотермическое
сжатие: V1>V2
![]()
2.Изобарический.P=const,
m=const
Уравнение
изопроцесса:![]()
Формула
работы в изопроцессе: A=P*∆V
При
изобарическом расширении: V2
>V1,
∆V=(V2-V1)>0,
A>0
При
изобарическом сжатии:
V2
<V1,
∆V<0,
A<0
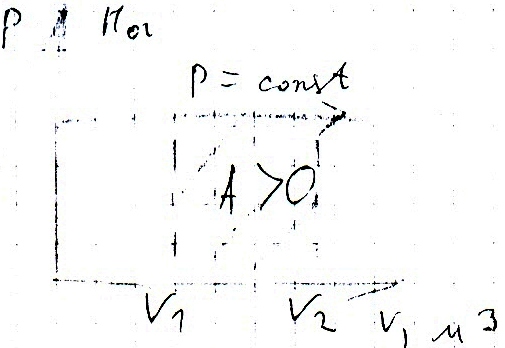
3.Изохорический.V=const,
m=const
Уравнение
изопроцесса: ![]()
Формула
работы в изопроцессе:A=p*∆V=0
– газ работу не совершает
23.
-
Первый
закон термодинамики.Первый
закон термодинамики (закон сохранения
энергии для тепловых процессов)
определяет количественное соотношение
между изменением внутренней энергии
системы дельта U, количеством теплоты
Q, подведенным к ней, и суммарной работой
внешних сил A, действующих на систему.Первый
закон термодинамики – количество
теплоты, подведенное к системе, идет
на изменение ее внутренней энергии и
на совершение системой работы над
внешними телами:Q=∆U+A.Применение
первого закона термодинамики к
изопроцессам.При
изохорном процессе
объем газа остается постоянным, поэтому
газ не совершает работу. Изменение
внутренней энергии газа происходит
благодаря теплообмену с окружающими
телами:Q=∆U.При
изотермическом
процессе количество теплоты, переданное
газу от нагревателя, полностью
расходуется на совершение работы:Q=A
При
изобарном процессе кол- во газа
подведенное к нему количество теплоты
расходуется как на увеличение его
внутренней энергии и на совершение
работы газом:Q=∆U+A
Адиабатный
процесс – термодинамический процесс в
теплоизолированной системе. Q=A.Второй
закон термодинамики (необратимость
процессов в природе).Формулировка: Все
процессы в природе необратимы, т.е
самопроизвольно протекают только в
одном направлении.Обратимым называется
процесс, который отвечает следующим
условиям:
1. его
можно провести в двух противоположных
направлениях;
2. в
каждом из этих случаев система и
окружающие ее тела проходят через одни
и те же промежуточные состояния;
3. после
проведения прямого и обратного процессов
система и окружающие ее тела возвращаются
к исходному состоянию.
Необратимым-это
процессы самопроизвольно протекающие
только в одном направлении.
При
изобарном
процессе кол- во газа подведенное к
нему количество теплоты расходуется
как на
24.
Принцип действия теплового двигателя.
КПД теплового двигателя. Цикл Карно.
ДВС–
это машина в которой внутренняя энергия
топлива превращается в механическую
работу.
–ДВС +ДВС
1.Низкий
КПД 1.Топливо содержит гораздо больше
энергии, чем лучшие
2.Сильный
шум электрические аккумуляторы.
3.Токсичные
выбросы
4.Меньший
ресурс
4-х
тактный ДВС
Такты
работы:
1.Впуск(поршень
движется вниз и открывается впускной
клапан)
2.Сжатие(поршень
поднимается вверх, сжимает горючую
смесь, значит давление увеличивается
=> температура увеличивается)
3.Рабочий
цикл(при проскакивании искры смесь
воспламеняется, давление ещё больше
увеличивается и внутренняя энергия
газа превращается в механическую
работу;газы давят на поршень и он
движется вниз)
4.Выпуск(поршень
движется вверх, открывается выпускной
клапан, переработанные газы выбрасываются
в атмосферу(холодильник)).
Любой
тепловой двигатель имеет 3 неотъемлемые
части:
1.Нагреватель
2.Рабочее
тело
3.Газ
или пар
4.Холодильник(атмосфера).
КПД
теплового двигателя.
Отношение
работы к энергии, которое получило
рабочее тело от нагревателя, называют
коэффициентом полезного действия
(КПД):
![]()
Паровая или газовая турбина, двигатель
внутреннего сгорания, реактивный
двигатель работают на базе ископаемого
топлива. В процессе работы многочисленных
тепловых машин возникают тепловые
потери, которые в конечном счете приводят
к повышению внутренней энергии атмосферы,
т. е. к повышению ее температуры. Это
может привести к таянию ледников и
катастрофическому повышению уровня
Мирового океана, а вместе с тем к
глобальному изменению природных
условий. При работе тепловых установок
и двигателей в атмосферу выбрасываются
вредные для человека, животных и растений
оксиды азота, углерода и серы. С вредными
последствиями работы тепловых машин
можно бороться путем повышения КПД, их
регулировки и создания новых двигателей,
не выбрасывающих вредные вещества с
отработанными газами.
Цикл
Карно.
–
это замкнутый
цикл который
состоит из 2-х изотерм и 2-х адиобат.
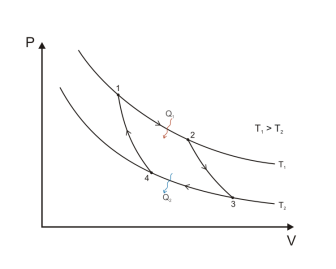
Если
двигатель будет работать, то получается
максимальное КПД
КПД=Smax
=![]()
T1-
это температура нагревания
T2-
это температура холодильника
Smax=![]()
Q1-
это тепло, которое получает рабочее
тело от нагревателя
Q2-
это тепло, которое отдает рабочее тело
холодильнику.
КПД≠100%,
т.к. 100% можно было бы получить тогда,
когда температура холодильника равнялась
0К.
1→2
Изотермическое расширение. Т=const,
m=const,
V1<V2,∆U=0,
U=const,
A>0,
Q
подводим.
2→3
Адиаботическое расширение. Q=0,
V2<V3,
газ отдает часть энергии => ∆U↓
и T1↓
до Т2
3→4
Изотермическое сжатие.Т2=const,
∆U=0,
A<0,
Q
отводится.
4→1
Адиабатическое сжатие. Q=0,
U↑,
T↑
до Т1
25.Адиабат.
называют процесс,
Протекающий,
без теплообмена
с
окружающей средой. Q = 0,
следовательно,
газ при расширении
совершает
работу за счет уменьше-
-ния
его внутренней энергии,
следовательно,
газ охлаждается
,
![]()
Кривая,
изображающая
адиабатный
процесс, называется адиабатой.
Есл
воздух насыщен паром,то измен P,V,T
Происход
медленно а в сухом за счёт
Водяного
пара внутри Vвыделят
тепло.
При
насыщенной t,
Растёт
медленнее чем в сухом.
В
атмосфере при подъёме воздуха
Происходит
его расшир.
Адиаб.процесс
применяют при работе
Холод.и
мороз.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.05.2015430.93 Кб221.pdf
- #
- #
Числом степеней свободы механической системы называют количество независимых величин, с помощью которых может быть задано положение системы.
Внутренняя энергия идеального газа представляет собой сумму только кинетической энергии всех молекул, а потенциальной энергией взаимодействия можно пренебречь:
U=∑Ek0=NEk0=mNAM·ikT2=i2·mMRT=i2νRT=i2pV
i — степень свободы. i = 3 для одноатомного (или идеального) газа, i = 5 для двухатомного газа, i = 6 для трехатомного газа и больше.
Изменение внутренней энергии идеального газа в изопроцессах
| Основная формула |
ΔU=32·mMRT=32νRT=32νR(T2−T1) |
| Изотермический процесс |
ΔU=0 Температура при изотермическом процессе — величина постоянная. Так как внутренняя энергия идеального газа постоянной массы в замкнутой системе зависит только от изменения температуры, то она тоже остается постоянной. |
| Изобарное расширение |
ΔU=32νR(T2−T1)=32(pV2−pV1)=32pΔV |
| Изохорное увеличение давления |
ΔU=32νR(T2−T1)=32(p2V−p1V)=32VΔp |
| Произвольный процесс |
ΔU=32νR(T2−T1)=32(p2V2−p1V1) |
Пример №1. На рисунке показан график циклического процесса, проведенного с идеальным газом. На каком из участков внутренняя энергия газа уменьшалась?

Внутренняя энергия газа меняется только при изменении температуры. Так как она прямо пропорциональная температуре, то уменьшается она тогда, когда уменьшается и температура. Температура падает на участке 3.
Работа идеального газа
Если газ, находящийся под поршнем, нагреть, то, расширяясь, он поднимет поршень, т.е. совершит механическую работу.

Механическая работа вычисляется по формуле:
A=Fscosα
Перемещение равно разности высот поршня в конечном и начальном положении:
s=h2−h1
Также известно, что сила равна произведению давления на площадь, на которое это давление оказывается. Учтем, что направление силы и перемещения совпадают. Поэтому косинус будет равен единице. Отсюда работа идеального газа равна произведению давления на площадь поршня:
Работа идеального газа
F=pS
p — давление газа, S — площадь поршня
Работа, необходимая для поднятия поршня — полезная работа. Она всегда меньше затраченной работы, которая определяется изменением внутренней энергии идеального газа при изобарном расширении:
A‘=p(V2−V1)=pΔV>0
Внимание! Знак работы определяется только знаком косинуса угла между направлением силы, действующей на поршень, и перемещением этого поршня.
Работа идеального газа при изобарном сжатии:
A‘=p(V2−V1)=pΔV<0
Работа идеального газа при нагревании газа:
A‘=νRΔT=νR(T2−T1)=mMνRΔT
Внимание! В изохорном процессе работа, совершаемая газом, равна нулю, так как работа газа определяется изменением его объема. Если изменения нет, работы тоже нет.
Геометрический смысл работы в термодинамике
В термодинамике для нахождения работы можно вычислить площадь фигуры под графиком в осях (p, V).
Примеры графических задач
| Изобарное расширение:
A‘=p(V2−V1) A‘>0 |
 |
| Изобарное сжатие:
A‘=p(V2−V1) A‘<0 |
 |
| Изохорное охлаждение:
V=const A‘=0 |
 |
|
Изохорное охлаждение и изобарное сжатие: 1–2: A‘=0 2–3: A‘=pΔV<0 |
 |
| Замкнутый цикл:
1–2: A‘>0 2–3: A‘=0 3–4: A‘<0 4–1: A‘=0 A‘=(p1−p3)(V2−V1) |
 |
| Произвольный процесс:
A‘=p1+p22(V2−V1) |
 |
Пример №2. На pV-диаграмме показаны два процесса, проведенные с одним и тем же количеством газообразного неона. Определите отношение работ A2 к A1 в этих процессах.

Неон — идеальный газ. Поэтому мы можем применять формулы, применяемые для нахождения работы идеального газа. Работа равна площади фигуры под графиком. С учетом того, что в обоих случаях изобарное расширение, получим:
A2=p(V2−V1)=4p(5V−3V)=4p2V=8pV
A1=p(V2−V1)=p(5V−V)=4pV
Видно, что работа, совершенная во втором процессе, вдвое больше работы, совершенной газом в первом процессе.
Задание EF17505
 Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Идеальный одноатомный газ переходит из состояния 1 в состояние 2 (см. диаграмму). Масса газа не меняется. Как изменяются при этом следующие три величины: давление газа, его объём и внутренняя энергия?
Для каждой величины подберите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Алгоритм решения
- Определить по графику, как меняется давление.
- Определить, как меняется объем.
- Определить, отчего зависит внутренняя энергия газа, и как она меняется в данном процессе.
Решение
На графике идеальный одноатомный газ изотермически сжимают, так как температура остается неизменной, а давление увеличивается. При этом объем должен уменьшаться. Но внутренняя энергия идеального газа определяется его температурой. Так как температура постоянна, внутренняя энергия не изменяется.
Ответ: 123
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17758
Один моль аргона, находящийся в цилиндре при температуре T1=600 K и давлении p1=4⋅105 Па, расширяется и одновременно охлаждается так, что его температура при расширении обратно пропорциональна объёму. Конечное давление газа p2=105 Па. Какое количество теплоты газ отдал при расширении, если при этом он совершил работу A=2493 Дж?
Алгоритм решения
1.Записать исходные данные.
2.Записать уравнение состояния идеального газа.
3.Записать формулу для расчета внутренней энергии газа.
4.Используя первое начало термодинамики, выполнить общее решение задачи.
5.Подставив известные данные, вычислить неизвестную величину.
Решение
Запишем исходные данные:
• Начальная температура газа: T1 = 600 К.
• Начальное давление: p1 = 4∙105 Па.
• Конечное давление: p2 = 105 Па.
• Работа, совершенная газом: A = 2493 Дж.
Аргон является одноатомным газом. Поэтому для него можно использовать уравнение состояния идеального газа:
pV=νRT
Внутренняя энергия одноатомного идеального газа пропорциональна температуре:
U=32νRT
Внутренняя энергия аргона до расширения и после него:
U1=32νRT1
U2=32νRT2
Согласно условию задачи, температура при расширении обратно пропорциональна объёму. Следовательно:
T=constV
T1V1=T2V2
Выразим конечную температуру:
T2=T1V1V2
Составим уравнение состояния газа для состояний аргона 1 и 2:
p1V1=νRT1
p2V2=νRT2
Отсюда:
νR=p1V1T1=p2V2T2
Отсюда отношение объема аргона в состоянии 1 к объему газа в состоянии 2 равно:
V1V2=p2T1p1T2
Подставим это отношение в формулу для конечной температуры:
T2=T1V1V2=p2T12p1T2
Отсюда:
T2=T1√p2p1
Отсюда внутренняя энергия газа в состоянии 2 равна:
U2=32νRT1√p2p1
Уменьшение внутренней энергии аргона составило (изначально она была выше):
ΔU=U1−U2=32νRT1−32νRT1√p2p1=32νRT1(1−√p2p1)
В соответствии с первым началом термодинамики уменьшение внутренней энергии равно сумме совершённой работы и количества теплоты, отданного газом:
ΔU=Q+A
Следовательно, газ отдал следующее количество теплоты:
Q=ΔU−A=32νRT1(1−√p2p1)−A

pазбирался: Алиса Никитина | обсудить разбор
Задание EF17966
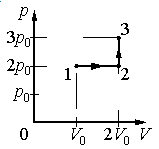 Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Идеальный газ переводят из состояния 1 в состояние 3 так, как показано на графике зависимости давления газа от объёма. Работа, совершённая при этом газом, равна
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 15k
Наука о тепловых явлениях называется термодинамика. Термодинамика исходит из наиболее общих закономерностей тепловых процессов и свойств макроскопических систем.
При изучении основ термодинамики необходимо помнить следующие определения. Физическая система, состоящая из большого числа частиц — атомов или молекул, которые совершают тепловое движение и, взаимодействуя между собой, обмениваются энергиями, называется термодинамической системой.
Состояние термодинамической системы определяется макроскопическими параметрами, например удельным объемом, давлением, температурой.
Термодинамика рассматривает изолированные системы тел, находящиеся в состоянии термодинамического равновесия. Это означает, что в таких системах прекратились все наблюдаемые макроскопические процессы. Важным свойством термодинамически равновесной системы является выравнивание температуры всех ее частей.
Термодинамика рассматривает только равновесные состояния, т.е. состояния, в которых параметры термодинамической системы не меняются со временем.
Если термодинамическая система была подвержена внешнему воздействию, то в конечном итоге она перейдет в другое равновесное состояние. Такой переход называется термодинамическим процессом.
Термодинамическим процессом называется переход системы из начального состояния в конечное через последовательность промежуточных состояний.
Процессы бывают обратимыми и необратимыми.
Обратимым называется такой процесс, при котором возможен обратный переход системы из конечного состояния в начальное через те же промежуточные состояния, чтобы в окружающих телах не произошло никаких изменений. Обратимый процесс является физической абстракцией. Примером процесса, приближающегося к обратимому, является колебание тяжелого маятника на длинном подвесе. В этом случае кинетическая энергия практически полностью превращается в потенциальную, и наоборот. Колебания происходят долго без заметного уменьшения амплитуды ввиду малости сопротивления среды и сил трения.
Любой процесс, сопровождаемый трением или теплопередачей от нагретого тела к холодному, является необратимым. Примером необратимого процесса является расширение газа, даже идеального, в пустоту. Расширяясь, газ не преодолевает сопротивления среды, не совершает работы, но, для того чтобы вновь собрать все молекулы газа в прежний объем, т. е. привести газ в начальное состояние, необходимо затратить работу. Таким образом, все реальные процессы являются необратимыми.
Изменение внутренней энергии газа в процессе теплообмена и совершаемой работы.
Одним из важнейших понятий термодинамики является внутренняя энергия тела. Все макроскопические тела обладают энергией, заключенной внутри самих тел. С точки зрения молекулярно-кинетической теории внутренняя энергия вещества складывается из кинетической энергии всех атомов и молекул и потенциальной энергии их взаимодействия друг с другом.
Внутренняя энергия – это сумма энергий молекулярных взаимодействий и энергии теплового движения молекул.
В частности, внутренняя энергия идеального газа равна сумме кинетических энергий всех частиц газа, находящихся в непрерывном и беспорядочном тепловом движении. Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема (закон Джоуля).
Молекулярно-кинетическая теория приводит к следующему выражению для внутренней энергии одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение:
Поскольку потенциальная энергия взаимодействия молекул зависит от расстояния между ними, в общем случае внутренняя энергия ![]()
U тела зависит наряду с температурой T также и от объема V: U = U(T, V).
Таким образом, внутренняя энергия системы зависит только от её состояния и является однозначной функцией состояния, внутренняя энергия U тела однозначно определяется макроскопическими параметрами, характеризующими состояние тела. Она не зависит от того, каким путем было реализовано данное состояние.
Внутреннюю энергию тела можно изменить разными способами:
- Совершение механической работы.
- Теплообмен.
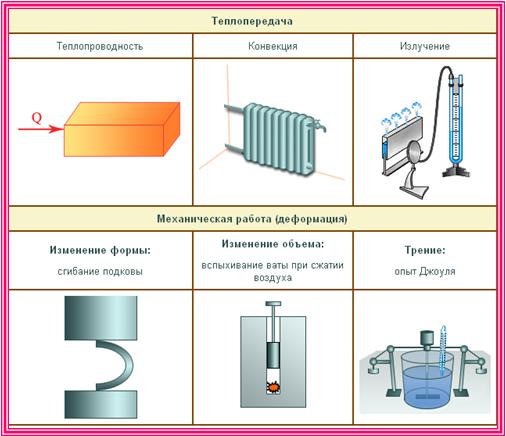
Внутренняя энергия тела может изменяться, если действующие на него внешние силы совершают работу (положительную или отрицательную).
Например, газ подвергается сжатию в цилиндре под поршнем площадью S. Поршень, сжимая газ, движется с некоторой скоростью v. Молекулы газа, беспорядочно двигаясь, ударяются о поршень. После упругого удара молекулы о поршень скорость молекулы возрастает, а значит возрастает и её кинетическая энергия, что приводит к увеличению внутренней энергии газа.
При сжатии газа его внутренняя энергия увеличивается за счет совершения поршнем механической работы. При расширении газа его внутренняя энергия уменьшается, превращаясь в механическую энергию поршня.
При сжатии газа внешние силы совершают над газом некоторую положительную работу A’.
В то же время силы давления, действующие со стороны газа на поршень, совершают работу
A = –A’.
Если объем газа изменился на малую величину ΔV, то газ совершает работу pSΔx = pΔV, где p – давление газа, S – площадь поршня, Δx – его перемещение.
При расширении работа, совершаемая газом, положительна, при сжатии – отрицательна.
В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:
![]()
или в пределе при ΔVi → 0: 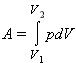
Работа численно равна площади под графиком процесса на диаграмме (p, V):
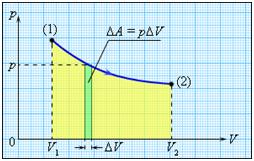
Величина работы зависит от того, каким путем совершался переход из начального состояния в конечное. На рис. 2 изображены три различных процесса, переводящих газ из состояния (1) в состояние (2). Во всех трех случаях газ совершает различную работу.
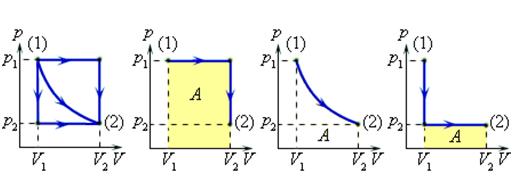
Рисунок 2.
Три различных пути перехода из состояния (1) в состояние (2).
Во всех трех случаях газ совершает разную работу, равную площади под графиком процесса.
Процессы, изображенные на рис. 2, можно провести и в обратном направлении; тогда работа A просто изменит знак на противоположный.
Процессы которые можно проводить в обоих направлениях, называются обратимыми.
В отличие от газа, жидкости и твердые тела мало изменяют свой объем, так что во многих случаях работой, совершаемой при расширении или сжатии, можно пренебречь. Однако, внутренняя энергия жидких и твердых тел также может изменяться в результате совершения работы. При механической обработке деталей (например, при сверлении) они нагреваются. Это означает, что изменяется их внутренняя энергия.
Внутренняя энергия тела может изменяться не только в результате совершаемой работы, но и вследствие теплообмена.
При тепловом контакте тел внутренняя энергия одного из них может увеличиваться, а внутренняя энергия другого – уменьшаться. В этом случае говорят о тепловом потоке от одного тела к другому. Передача энергии от одного тела другому в форме тепла может происходить только при наличии разности температур между ними.
Приведем в соприкосновение два тела с разными температурами. Пусть температура первого тела выше, чем второго. В результате обмена энергиями температура первого тела уменьшается, а второго — увеличивается. В рассматриваемом примере кинетическая энергия хаотического движения молекул первого тела переходит в кинетическую энергию хаотического движения молекул второго тела.
Тепловой поток всегда направлен от горячего тела к холодному.
Процесс передачи внутренней энергии без совершения механической работы называется теплообменом.
Мерой энергии, получаемой или отдаваемой телом в процессе теплообмена, служит физическая величина, называемая количеством теплоты.
Количеством теплоты Q, полученной телом, называют изменение внутренней энергии тела в результате теплообмена.
Количество теплоты Q является энергетической величиной. В СИ количество теплоты измеряется в единицах механической работы – джоулях (Дж).
До введения СИ количество теплоты выражали в калориях.
Калория – это количество теплоты, необходимое для нагревания 1 г дистиллированной воды на 1°С, от 19,5°С до 20,5°С.
Единица, в 1000 раз большая калории, называется килокалорией (1 ккал = 1000 кал). Соотношение между единицами: 1 кал =4,19 Дж.
Если в результате теплообмена телу передается некоторое количество теплоты, то внутренняя энергия тела и его температура изменяются.
Чтобы нагреть тело массой m от температуры t1 до температуры t2 ему необходимо сообщить количество теплоты
Q = cm(t2 – t1)
Количество теплоты Q, необходимое для нагревания 1 кг вещества на 1 К называют удельной теплоемкостью вещества c.
c = Q / (mΔT).
Во многих случаях удобно использовать молярную теплоемкость C:
C = M · c, где M – молярная масса вещества.
При передаче тепла от одного тела к другому всегда выполняется уравнение теплового баланса, по которому количество теплоты Q1, отданное первым телом, равно количеству теплоты Q2, полученному вторым телом.
Q1 = Q2
Теплота и работа являются не видом энергии, а формой ее передачи, они существуют лишь в процессе передачи энергии.
В реальных условиях оба способа передачи энергии системе в форме работы и форме теплоты обычно сопутствуют друг другу.
Первое начало термодинамики.
На рисунке изображены энергетические потоки между термодинамической системой и окружающими телами. в результате теплообмена и совершаемой работы:
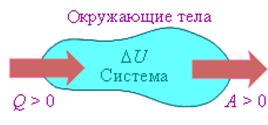
Величина Q > 0, если тепловой поток нправлен в сторону термодинамической системы. Величина A > 0, если система совершает положительную работу над окружающими телами.
Если система обменивается теплом с окружающими телами и совершает работу (положительную или отрицательную), то изменяется состояние системы, то есть изменяются ее макроскопические параметры (температура, давление, объем).
Процессы теплообмена и совершения работы сопровождаются изменением ΔU внутренней энергии системы.
Первый закон термодинамики является обобщением закона сохранения и превращения энергии для термодинамической системы. Он формулируется следующим образом:
Изменение ΔU внутренней энергии неизолированной термодинамической системы равно разности между количеством теплоты Q, переданной системе, и работой A, совершенной системой над внешними телами.
ΔU = Q – A.
Соотношение, выражающее первый закон термодинамики, часто записывают в другой форме:
Q = ΔU + A.
Количество теплоты, полученное системой, идет на изменение ее внутренней энергии и совершение работы над внешними телами.
Первый закон термодинамики является обобщением опытных фактов. Согласно этому закону, энергия не может быть создана или уничтожена; она передается от одной системы к другой и превращается из одной формы в другую. Если между телами, составляющими замкнутую систему, действуют силы трения, то часть механической энергии превращается во внутреннюю энергию тел (нагревание).
При любых физических взаимодействиях энергия не возникает и не исчезает. Она лишь превращается из одной формы в другую. Этот экспериментально установленный факт выражает фундаментальный закон природы – закон сохранения и превращения энергии.
Задачи для самостоятельного решения ( Дмитриева В.Ф. Задачи по физике)
№ 2, стр. 148
Определите p – давление насыщенного водяного пара при температуре Т=290 К, если пло ность насыщенного водяного пара при этой температуре ρ=2,56·10-2 кг/м3 (ответ р=3,43 Па)
№ 12, стр. 149
Определите m – массу стоградусного водяного пара, необходимого для нагревания m1=10 кг воды от t1=100С до t2=600С. (ответ m=0,086 кг)
№ 1, стр. 156
Поверхностное натяжение керосина α=2,4·10-2 Н/м. Какую работу А совершат силы поверхностного натяжения при уменьшении поверхностного слоя керосина на 25 см2? (ответ А=60 мкДж)
№ 7, стр. 156
В одной и той же капиллярной трубке вода поднимается на 50 мм, а спирт на 19 мм. Определите поверхностное натяжение спирта αс. Поверхностное натяжение воды αв=0,072 Н/м (ответ αс=22·10-3 Н/м)
№ 8, стр. 163
Определите Q – теплоту, необходимую для плавления свинца массой m=10 кг, находящегос при температуре плавления. Удельная теплота плавления свинца λ=25 кДж/кг. (ответ Q=250 кДж)
