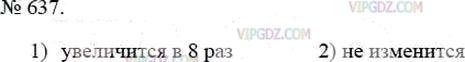Как найти увеличенный объем прямоугольного параллелепипеда

Как изменится объем прямоугольного параллелепипеда, если:
1) каждое измерение увеличить в 2 раза;
2) длину уменьшить в 3 раза, высоту − в 5 раз, а ширину увеличить в 15 раз?

Математика

5 класс

Урок №32

Объём прямоугольного параллелепипеда. Единицы объёма

Перечень рассматриваемых вопросов:

– куб;

– параллелепипед;

– элементы параллелепипеда;

– объём прямоугольного параллелепипеда, куба.

Тезаурус

Прямоугольный параллелепипед – это шестигранник, у которого все грани являются прямоугольниками.

Высота, длина и ширина – это измерения прямоугольного параллелепипеда.

Единичный куб – куб, ребро которого равно линейной единице.

Обязательная литература

1. Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017. – 272 с.

Дополнительная литература

1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О.Ф. Зарапина. – М.: Просвещение, 2009. – 142 с.

2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95 с.

Теоретический материал для самостоятельного изучения

Как вы думаете, что больше занимает места– 1 кг ваты или 1 кг гвоздей? Чтобы ответить на этот вопрос, нужно знать величину, которая называется объём. В данной задаче ответ очевиден, так как мы можем представить предметы визуально. Но не всегда ответ может быть таким простым. Чаще всего нужно произвести определённые вычисления.

Сегодня мы рассмотрим объём прямоугольного параллелепипеда и научимся его находить.

Объём можно измерить. Его измеряют в кубических миллиметрах, кубических сантиметрах, кубических метрах, литрах и т. д.

Найдём соотношение между единицами измерения объёма.

Так как 1 см = 10 дм, то 1 см³ = 1 000 мм³.

1 дм³ = 1000 см³ = 1 л

1 м³ = 1000 дм³

1 км³ = 1000000000 м³

В древности в разных частях планеты люди по-разному измеряли объём. Например, в Древней Греции использовали глиняные мерные сосуды для зерна или жидкостей. Причём это были амфоры разного размера. Поэтому значение единицы объёма менялось от 2 до 26 литров.

На Руси основной мерой жидкостей считалось ведро, в котором 10 кружек или 12 литров. Также для подсчётов объём ведра делили пополам, то есть на два полуведра, которые, в свою очередь, тоже можно было поделить пополам. Для торговли с иностранцами использовали меру объёма, называемую бочка, которая равнялась 40 вёдрам.

Дадим определение единичного куба – это куб, ребро которого равно линейной единице. Его тоже принимают за единицу объёма.

Если прямоугольный параллелепипед можно разрезать на К единичных кубов, то говорят, что его объём V равен К кубическим единицам.

Например, на рисунке объём параллелепипеда равен 24 кубическим единицам.

V = 24 куб. единиц

Введём формулу объёма прямоугольного параллелепипеда.

Объём прямоугольного параллелепипеда равен произведению трёх его измерений, то есть произведению длины а, ширины bи высоты c, или произведению площади основания S на высоту c.

V = а · b · c = S · с

Так как куб является прямоугольным параллелепипедом, у которого все измерения равны, то его объём равен третьей степени длины его ребра а.

V = а³

Решим задачу.

Мальчик купил аквариум в форме прямоугольного параллелепипеда, который имеет площадь дна, равную 1400 см³, и высоту 6 дм. Какой объём воды он налил в аквариум, если уровень жидкости не доходил до края 5 см? Выразите ответ в кубических сантиметрах.

Чтобы решить эту задачу переведём единицы измерения длины в сантиметры.

6 дм = 60 см

Получается, что высота аквариума равна 60 см. Но по условию задачи требуется определить объём налитой жидкости, а её высота соответствует разности между высотой аквариума и уровнем жидкости, не доходящей до края:

с = 60 см – 5 см = 55 см

Получается, что высота жидкости в сосуде соответствует 55 см.

Теперь можно определить объём воды, которая налита в аквариум.

Для этого используем следующую формулу:

V = S · с = 1400 см² · 55 см = 77000 см³

Ответ: мальчик налил в аквариум 77000 см³ воды.

Разбор решения заданий тренировочного модуля

№ 1. Чему равен объём куба, если длина его ребра равна 3 см?

Решение: для нахождения объёма куба нужно воспользоваться формулой.

V = а³ = (3 см)³ = 27 см³

Ответ: 27 см³.

№2. Как изменится объём прямоугольного параллелепипеда, если его длину увеличить в три раза. Подчеркните правильный ответ.

Решение: чтобы ответить на вопрос, нужно воспользоваться формулой для вычисления объёма прямоугольного параллелепипеда.

V = а · b · c, где а – длина прямоугольного параллелепипеда.

Если длина возрастет в три раза, то объём, соответственно, увеличится в три раза, так как, длина – это один из трёх множителей, входящих в формулу объёма прямоугольного параллелепипеда:

V = 3 · а · b · c

Ответ: объём увеличится в три раза.

ГДЗ и решебники
вип уровня