Как найти увеличивающий путь – Сайт, где вы сможете решить свои вопросы

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 29 апреля 2022 года; проверки требуют 3 правки.

У этого термина существуют и другие значения, см. Алгоритм Форда.

Алгоритм Форда — Фалкерсона решает задачу нахождения максимального потока в транспортной сети.

Идея алгоритма заключается в следующем. Изначально величине потока присваивается значение 0: $f(u,v)=0$ для всех $u,vin V$ . Затем величина потока итеративно увеличивается посредством поиска увеличивающего пути (путь от источника $s$ к стоку $t$ , вдоль которого можно послать больший поток). Процесс повторяется, пока можно найти увеличивающий путь.

Алгоритм[править | править код]

Неформальное описание[править | править код]

Обнуляем все потоки. Остаточная сеть изначально совпадает с исходной сетью.
В остаточной сети находим любой путь из источника в сток. Если такого пути нет, останавливаемся.
Пускаем через найденный путь (он называется увеличивающим путём или увеличивающей цепью) максимально возможный поток:
1. На найденном пути в остаточной сети ищем ребро с минимальной пропускной способностью $c_{min }$ .
2. Для каждого ребра на найденном пути увеличиваем поток на $c_{min }$ , а в противоположном ему — уменьшаем на $c_{min }$ .
3. Модифицируем остаточную сеть. Для всех рёбер на найденном пути, а также для противоположных (антипараллельных) им рёбер, вычисляем новую пропускную способность. Если она стала ненулевой, добавляем ребро к остаточной сети, а если обнулилась, стираем его.
Возвращаемся на шаг 2.

Важно, что алгоритм не конкретизирует, какой именно путь мы ищем на шаге 2 или как мы это делаем. По этой причине алгоритм гарантированно сходится только для целых пропускных способностей, но даже для них при больших значениях пропускных способностей он может работать очень долго. Если пропускные способности вещественны, алгоритм может работать бесконечно долго, не сходясь к оптимальному решению (см. пример ниже).

Если искать не любой путь, а кратчайший, получится алгоритм Эдмондса — Карпа или алгоритм Диница. Эти алгоритмы сходятся для любых вещественных весов за время $O(|V||E|^{2})$ и $O(|V|^{2}|E|)$ соответственно.

Формальное описание[править | править код]

Дан граф $G(V,E)$ с пропускной способностью $c(u,v)$ и потоком $f(u,v)=0$ для рёбер из ${displaystyle u}$ в ${displaystyle v}$ . Необходимо найти максимальный поток из источника $s$ в сток $t$ . На каждом шаге алгоритма действуют те же условия, что и для всех потоков:

Остаточная сеть $G_{f}(V,E_{f})$ — сеть с пропускной способностью ${displaystyle c_{f}(u,v)=c(u,v)-f(u,v)+f(v,u)}$ и без потока.

Вход Граф $G$ с пропускной способностью $c$ , источник $s$ и сток $t$
Выход Максимальный поток $f$ из $s$ в $t$

${displaystyle f(u,v):=0}$ для всех рёбер $(u,v)$
Пока есть путь $p$ из $s$ в $t$ в $G_f$ , такой что ${displaystyle c_{f}(u,v)>0}$ для всех рёбер $(u,v)in p$ :
1. Найти ${displaystyle c_{f}(p)=min{c_{f}(u,v);|;(u,v)in p}}$
2. Для каждого ребра $(u,v)in p$
  1. ${displaystyle f(u,v):=f(u,v)+c_{f}(p)}$
  2. ${displaystyle f(v,u):=f(v,u)-c_{f}(p)}$
  3. ${displaystyle c_{f}(u,v)=c(u,v)-f(u,v)}$
  4. ${displaystyle c_{f}(v,u)=f(u,v)}$

Путь может быть найден, например, поиском в ширину (алгоритм Эдмондса — Карпа) или поиском в глубину в $G_{f}(V,E_{f})$ .

Сложность[править | править код]

На каждом шаге алгоритм добавляет поток увеличивающего пути к уже имеющемуся потоку. Если пропускные способности всех рёбер — целые числа, легко доказать по индукции, что и потоки через все рёбра всегда будут целыми. Следовательно, на каждом шаге алгоритм увеличивает поток по крайней мере на единицу, следовательно, он сойдётся не более чем за ${displaystyle O(|f|)}$ шагов, где f — максимальный поток в графе. Можно выполнить каждый шаг за время ${displaystyle O(|E|)}$ , где ${displaystyle |E|}$ — число рёбер в графе, тогда общее время работы алгоритма ограничено ${displaystyle O(|E|max |f|)}$ .

Если величина пропускной способности хотя бы одного из рёбер — иррациональное число, то алгоритм может работать бесконечно, даже не обязательно сходясь к правильному решению. Пример дан ниже.

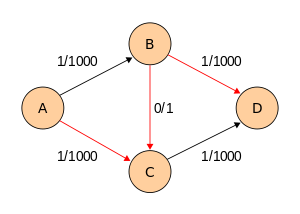
Пример несходящегося алгоритма[править | править код]

Рассмотрим приведённую справа сеть, с источником $s$ , стоком $t$ , пропускными способностями рёбер ${displaystyle e_{1}=1}$ , ${displaystyle e_{2}=r=({sqrt {5}}-1)/2}$ , ${displaystyle e_{3}=1}$ и пропускной способностью всех остальных рёбер, равной целому числу $Mgeq 2$ . Константа $r$ выбрана так, что ${displaystyle r^{2}=1-r}$ . Мы используем пути из остаточного графа, приведённые в таблице, причём ${displaystyle p_{1}={s,v_{4},v_{3},v_{2},v_{1},t}}$ , ${displaystyle p_{2}={s,v_{2},v_{3},v_{4},t}}$ и ${displaystyle p_{3}={s,v_{1},v_{2},v_{3},t}}$ .

Шаг	Найденный путь	Добавленный поток	Остаточные пропускные способности
$e_{1}$	$e_{2}$	$e_{3}$
0			$r^{0}=1$	$r$	$1$
1	${s,v_{2},v_{3},t}$	$1$	$r^{0}$	$r^{1}$	${displaystyle 0}$
2	$p_{1}$	$r^{1}$	$r^{2}$	${displaystyle 0}$	$r^{1}$
3	$p_{2}$	$r^{1}$	$r^{2}$	$r^{1}$	${displaystyle 0}$
4	$p_{1}$	$r^{2}$	${displaystyle 0}$	$r^{3}$	$r^{2}$
5	$p_{3}$	$r^{2}$	$r^{2}$	$r^{3}$	${displaystyle 0}$

Заметим, что после шага 1, как и после шага 5, остаточные способности рёбер $e_{1}$ , $e_{2}$ и $e_{3}$ имеют форму $r^{n}$ , $r^{{n+1}}$ и ${displaystyle 0}$ , соответственно, для какого-то натурального $n$ . Это значит, что мы можем использовать увеличивающие пути $p_{1}$ , $p_{2}$ , $p_{1}$ и $p_{3}$ бесконечно много раз, и остаточные пропускные способности этих рёбер всегда будут в той же форме. Полный поток после шага 5 равен $1+2(r^{1}+r^{2})$ . За бесконечное время полный поток сойдётся к $textstyle 1+2sum _{{i=1}}^{infty }r^{i}=3+2r$ , тогда как максимальный поток равен $2M+1$ . Таким образом, алгоритм не только работает бесконечно долго, но даже и не сходится к оптимальному решению.^[1]

Пример[править | править код]

Следующий пример показывает первые шаги алгоритма Форда — Фалкерсона в транспортной сети с четырьмя узлами, источником A и стоком D. Этот пример показывает худший случай. При использовании поиска в ширину алгоритму потребуется всего лишь 2 шага.

Путь	Пропускная способность	Результат
	Начальная транспортная сеть
$A,B,C,D$	${displaystyle min(c_{f}(A,B),c_{f}(B,C),c_{f}(C,D))=}$ ${displaystyle min(c(A,B)-f(A,B),c(B,C)-f(B,C),c(C,D)-f(C,D))=}$ $min(1000-0,1-0,1000-0)=1$
$A,C,B,D$	$min(c_{f}(A,C),c_{f}(C,B),c_{f}(B,D))=$ $min(c(A,C)-f(A,C),c(C,B)-f(C,B),c(B,D)-f(B,D))=$ $min(1000-0,0-(-1),1000-0)=1$
	После 1998 шагов …
	Конечная сеть

См. также[править | править код]

Теорема Форда — Фалкерсона

Ссылки[править | править код]

Пример решения задачи на YouTube
Визуализатор алгоритма
Реализация поиска максимального потока методом Форда-Фалкерсона на Java
На Викискладе есть медиафайлы по теме Алгоритм Форда — Фалкерсона

Литература[править | править код]

Томас Х. Кормен и др. Алгоритмы: построение и анализ = INTRODUCTION TO ALGORITHMS. — 2-е изд. — М.: «Вильямс», 2006. — С. 1296. — ISBN 0-07-013151-1.

Примечания[править | править код]

↑ Zwick, Uri. The smallest networks on which the Ford-Fulkerson maximum flow procedure may fail to terminate (англ.) // Theoretical Computer Science (англ.) (рус. : journal. — 1995. — 21 August (vol. 148, no. 1). — P. 165—170. — doi:10.1016/0304-3975(95)00022-O.

Источник

Алгоритм Форда-Фалкерсона

Время на прочтение
3 мин

Количество просмотров 40K

Привет, Хабр!
В свободное от учебы время пишу статьи, которых мне не хватало несколько лет назад.

При решении задачи о максимальном потоке я столкнулся с тем, что во всех мне известных источниках было дано формальное описание самих алгоритмов, что очень сильно затрудняло понимание изложенного материала. И в этой статье я попробую на базовом уровне разобрать Алгоритм Форда-Фалкерсона на конкретном примере, чтобы после прочтения данной статьи, вы хотя бы понимали основную суть самого алгоритма.

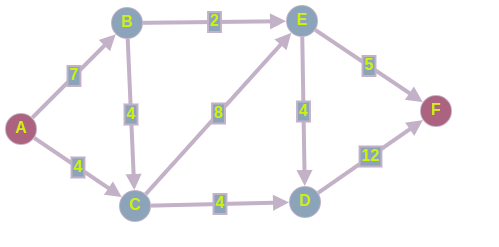
Постановка задачи

Имеется следующий ориентированный граф, в котором вес ребра обозначает пропускную способность между вершинами. Нужно найти максимальный поток, который можно пропустить из истокав сток.

Исходный граф

Как работает сам алгоритм?

Следует понимать остаточную сеть как тот же граф, который имеется на входе, но в этом случае мы будем производить над ним некоторые операции:

Отправлять определенное количество потока из текущей вершины в соседние.
Возвращать определенное количество потока из соседних вершин в текущую.

В начальный момент времени поток, который мы хотим провести через нашу сеть, должен быть равен нулю. Остаточная сеть совпадает с исходной сетью.
Находим любой путь из истока в сток в остаточной сети. Если путь не находим, утверждается, что поток является максимальным.
Пускаем через найденный путь поток равный минимальному весу ребра, которое входит в множество рёбер найденного пути.
Из веса рёбер на этом пути высчитываем размер потока, который мы пустили.
А к весу обратных рёбер (будем считать, что они существуют в остаточной сети и равны 0) прибавляем размер потока. Другими словами, на предыдущем шаге мы отправили некоторое количество потока из текущей вершины в следующую, а теперь при желании можем вернуть это же количество потока обратно в текущую.
Возвращаемся обратно к нахождению пути в остаточной сети после модификации.

Разбор конкретного примера

Разобьем одну итерацию проведения потока по выбранному пути на маленькие шаги, чтобы визуально стало понятно, как меняется остаточная сеть после проталкивания очередного потока.

Допустим наш алгоритм нашел следующий путь из вершинывнашей остаточной сети, которая на момент начала, совпадает с исходным графом.

Начальная остаточная сеть

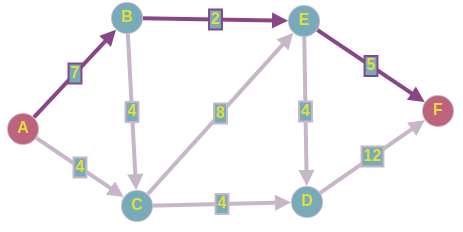
Сколько потока можем провести по этому пути???
– Больше2 ед.мы никак не сможем пустить, пропускаем наш поток по этим рёбрам из истока в сток.
Получаем следующее:

Остаточная сеть после 1-ой итерации

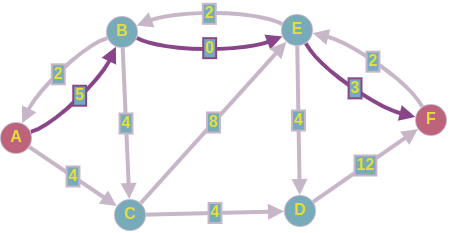
Рёбра с нулевым весом можно удалять. Таким образом, на первой итерации мы смогли увеличить максимальный поток на 2 ед.

Теперь дело за малым, остается всего лишь итерироваться до тех пор, пока существует путь из в .

Допустим, на 2-ой итерации мы нашли такой путь в нашей остаточной сети:

Остаточная сеть после 1-ой итерации

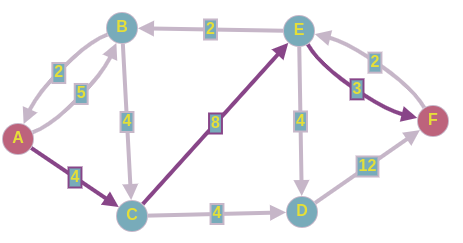
Пропускаем 3 ед. потока по этому пути, и перестраиваем остаточную сеть.
Получаем следующее:

Остаточная сеть после 2-ой итерации

На 3-ей итерации нашли такой путь в нашей модифицированной остаточной сети:

Остаточная сеть после 2-ой итеации

Пускаем 1 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:

Остаточная сеть после 3-ей итерации

На 4-ой итерации находим следующий путь в остаточной сети:

Остаточная сеть после 3-ей итерации

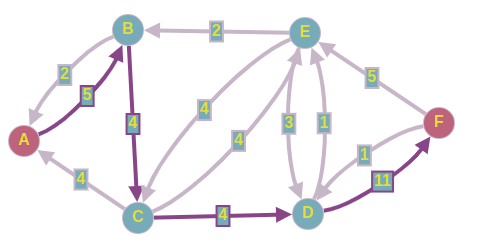
Пускаем 4 ед. потока по этому пути и перестраиваем нашу остаточную сеть.
Получим следующую картину:

Итоговая остаточная сеть

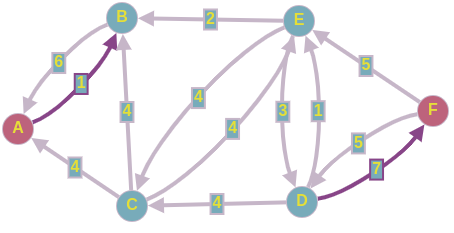
На этом этапе наш алгоритм прекратит выполнение из-за того, что пути из истока в сток не существует. И ответом к поставленной задаче будет служить сумма потоков всех найденных увеличивающихся путей.
Ответ: 10 ед.

Спасибо большое за внимание, надеюсь, был полезен!
Буду рад любым отзывам или поправкам для повышения доступности изложения материала!

Источники

Паша и Алгосы
Инструмент для работы с графами

Источник

Задача
о максимальном потоке.

Сеть
– это ориентированный взвешанный граф
G = (v,e) с положительными весами ребер
с(е), в котором есть ровно одна вершина
– источник (S) и ровно одна
вершина – сток (T).

Вершины
не равные S и Т называются внунтренними,

Вес
ре6ра с(e) – пропускная
способность ребра.

Потоком
называется функция f, которая переводит
множество ребер в множество действительных
чисел.

Функция
f удовлетворяет:

Для любого
ребра e € E: 0<=f(e)<=c(e)
Для всех
v€ V,v<>S,v=T:div+
(v) =div_(v),
где

div+
– суммарный поток по всем ребрам е,
таким что е=(u,v)
div+(v)
=,e=(u,v)
– величина входящего потока
div_
– величина исходящего потока
div_(v)
=,

Свойство
потока: div_(S)=div+(T)

Величина
div_(S)=div+(T)
называется величиной потока в сети.

Задача
о максимальном потоке.

Найти
поток, величина которого не меньше
величины любого другого потока (найти
поток с максимальной величиной)

Остаточная
сеть.

Пусть
дана сеть G и в ней запущен поток f,
остаточная сеть – это взвешенный
ориентированный граф с множеством
вершин V и множеством дуг, определяющих:

если в
сети G есть ребро (u,v)
и величина потока по этому ребру меньше
с(е), то в остаточной сети есть ребро
e=(u,v) с весом
с(е)-f(e) –прямые ребра
если в Gесть ребро е=(u,v)
и поток через это ребро >0, то в остаточной
сети есть реброe’=(u,v)
с весомf(e)
–встречные ребра

Аугментальный
(увеличивающий) путь.

Если
в остаточной сети существует ориентированный
путь из S в T, то в исходной сети можно
увеличить поток вдоль этого пути. При
этом проход по прямым ребрам – увеличение
потока в данном ребре исходной сети, а
по встречному ребру – уменьшение потока.

Алгоритм
Форда-Фалкерсона

Запустить
0-й поток f(e)=0
Построить
остаточную сеть
Найти в
остаточной сети ориентированный путь
из S в T
Если путь
найден, то увеличить поток вдоль этого
пути и перейти к шагу 2. Иначе конец
алгоритма. Текущий поток является
максимальным.

21. Задача о максимальном потоке минимальной стоимости (МаПМиС). Алгоритм решения.

Пусть существует сеть и каждому ребру
приписана стоимость S(e).
Стоимость потока через ребро равна
S(e)*f(e).
Стоимость потока в сети – суммарная
стоимость потока через все ребра

Задача о МаПМиС заключается в поиске
такого max потока, стоимость которого не
превышает стоимость любого другого max
потока. (в дальнейшем рассматриваются
только maxпотоки)

При
построении остаточной сети будем
отмечать не только пропускные способности
ребер, но и их стоимость. Для прямых
ребер стоимость равна стоимости исходного
ребра. Для встречных: стоимость
противоположна стоимости исходного
ребра.

Алгоритм:

Построить
максимальный поток
Построить
остаточную сеть со стоимостями
Найти в
остаточной сети ориентированный цикл
с отрицательной стоимостью
Если цикл
найден, то увеличивается вдоль него
поток. Иначе конец. Текущий поток –
МаПМиС

Определение
транспортной сети.

22. Метод ветвей и границ. Решение задачи «о рюкзаке» методом ветвей и границ.

Пусть
Q– задача минимизации

S– множество допустимых решений

φ(S)
– качество решения

Задача:
найти S* такое, чтоφ(S*)
– минимальное.

Метод:

Разбиваем
Sна подмножества.
Для всех подмножеств строится оценка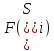такое, что.
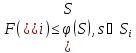Если найдено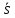такое, что,
то все решения из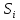рассматривать не нужно.

Задача
«о рюкзаке»

Дано:

nпредметов

Веса:

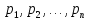
Стоимости:

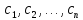
Рюкзак
вместимостью V

Ограничение:
.

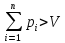Найти:

Множество
предметов M: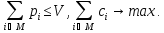

Задача
является NP-полной.

1
способ:

Рассчитать
ценность предметов
Упорядочить
предметы по уменьшению ценности.
Ветвление
(бинарное):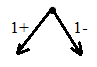

S₁– 1-ый предмет берем

S₂– 1-ый предмет не берем

Оценка:

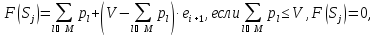иначе.

где
M– множество предметов,
которые уже взяли;

i+1 – номер очередного,
еще не рассмотренного, предмета.

Выбираем
вершину с максимальной оценкой, изменяем
значение iи переходим к
п.3

Пример:

4
предмета, V=5

Вершины графа пронумерованы сверху
вниз слева направо

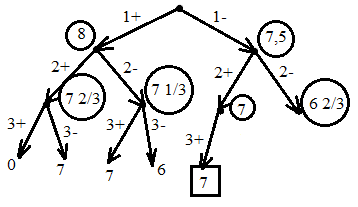
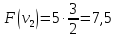
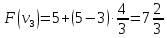
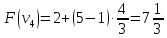
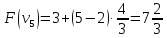
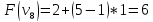
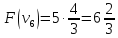
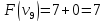
Ответ:
набор {2;3}.

2
способ:

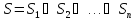
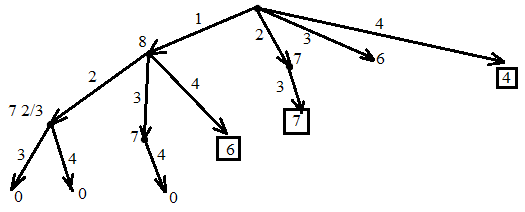
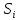– попадают все случаи, когда минимальный
набор предметов, сложенных в рюкзак,
равенi. Наj-ом
шаге ветвление аналогично, но рассматриваем
не минимальный номер, аj-ый
по величине.

Вершины
графа пронумерованы сверху вниз слева
направо

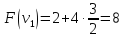
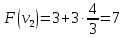
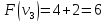
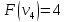
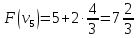
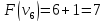
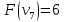
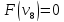
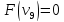
Ответ:
{2,3}

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сайт переезжает. Большинство статей уже перенесено на новую версию.
Скоро добавим автоматические переходы, но пока обновленную версию этой статьи можно найти там.

Паросочетания

Задача. Пусть есть (n) мальчиков и (m) девочек. Про каждого мальчика и про каждую девочку известно, с кем они не против танцевать. Нужно составить как можно больше пар, в которых партнёры хотят танцевать друг с другом.

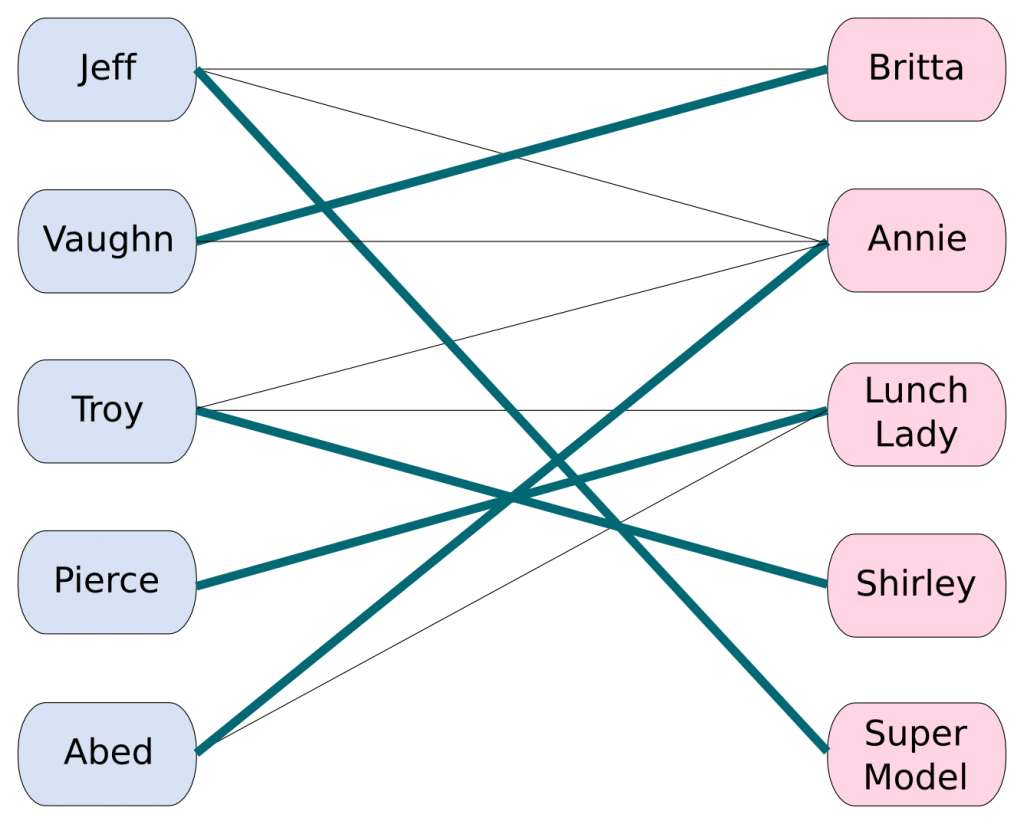
Формализуем эту задачу, представив мальчиков и девочек как вершины в двудольном графе, рёбрами которого будет отношение «могут танцевать вместе».

Паросочетанием (M) называется набор попарно несмежных рёбер графа (иными словами, любой вершине графа должно быть инцидентно не более одного ребра из (M)).

Все вершины, у которых есть смежное ребро из паросочетания (т.е. которые имеют степень ровно один в подграфе, образованном (M)), назовём насыщенными этим паросочетанием.

Мощностью паросочетания назовём количество рёбер в нём. Наибольшим (максимальным) паросочетанием назовём паросочетание, мощность которого максимальна среди всех возможных паросочетаний в данном графе, а совершенным — где все вершины левой доли им насыщенны.

Паросочетания можно искать в любых графах, однако этот алгоритм неприятно кодить, и он работает за (O(n^3)), так что сегодня мы сфокусируемся только на двудольных графах. Будем в дальнейшем обозначать левую долю графа как (L), а правую долю как (R).

Цепью длины (k) назовём некоторый простой путь (т.е. не содержащий повторяющихся вершин или рёбер), содержащий ровно (k) рёбер.

Чередующейся цепью относительно некоторого паросочетания назовём простой путь длины (k) в которой рёбра поочередно принадлежат/не принадлежат паросочетанию.

Увеличивающей цепью относительно некоторого паросочетания назовём чередующуюся цепь, у которой начальная и конечная вершины не принадлежат паросочетанию.

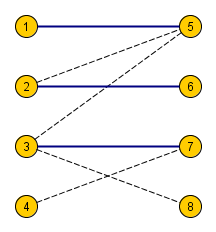
Здесь красными помечены вершины паросочетания, а в графе есть увеличивающая цепь: (1 to 8 to 4 to 6 to 3 to 7).

Зачем нужны увеличивающие цепи? Оказывается, можно с их помощью увеличивать паросочетание на единицу (отсюда и название). Можно взять такой путь и провести чередование — убрать из паросочетания все рёбра, принадлежащие цепи, и, наоборот, добавить все остальные. Всего в увеличивающей цепи нечетное число рёбер, а первое и последнее были не в паросочетании. Значит, мощность паросочетания увеличилась ровно на единицу.

В примере добавятся синие рёбра ((1, 8)), ((3, 7)) и ((4, 6)), а удалятся красные ((3, 6)) и ((4, 8)). С ребром ((2, 5)) ничего не случится — оно не в увеличивающей цепи. Таким образом, размер паросочетания увеличится на единицу.

Алгоритм Куна в этом и заключается — будем искать увеличивающую цепь, пока ищется, и проводить чередование в ней. Увеличивающие цепи удобны тем, что их легко искать: можно просто запустить поиск пути из произвольной свободной вершины из левой доли в какую-нибудь свободную вершину правой доли в том же графе, но в котором из правой доли можно идти только по рёбрам паросочетания (то есть у вершин правой доли будет либо одно ребро, либо ноль). Это можно делать как угодно (для упражнения автор рекомендует явно строить такой граф, искать путь и явно проводить чередования), однако устоялась эффективная реализация в виде dfs на 20 строчек кода, приведённая ниже.

const int maxn;

vector<int> g[maxn]; // будем хранить только рёбра из левой доли в правую
int mt[maxn]; // с какой вершиной сматчена вершина правой доли (-1, если ни с какой)
bool used[maxn]; // вспомогательный массив для поиска пути dfs-ом

// dfs возвращает, можно ли найти путь из вершины v
// в какую-нибудь вершину правой доли
// если можно, то ещё и проводит чередование
bool dfs(int v) {
    if (used[v])
        return false;
    used[v] = true;
    for (int u : g[v]) {
        // если вершина свободна, то можно сразу с ней соединиться
        // если она занята, то с ней можно соединиться только тогда,
        // когда из её текущей пары можно найти какую-нибудь другую вершину
        if (mt[u] == -1 || dfs(mt[u])) {
            mt[u] = v;
            return true;
        }
    }
    return false;
}


// где-то в main:

memset(mt, -1, sizeof mt);
for (int i = 0; i < n; i++) {
    memset(used, 0, sizeof mt);
    if (dfs(i))
        cnt++;
}

Корректность

Для доказательства алгоритма нам будет достаточно ещё доказать, что если увеличивающие цепи уже не ищутся, то паросочетание в принципе нельзя увеличить.

Теорема (Бержа). Паросочетание без увеличивающих цепей является максимальным.

Доказательство проведём от противного: пусть есть два паросочетания вершин (|A| leq |B|), и для (A) нет увеличивающих путей, и покажем, как найти этот путь и увеличить (A) на единицу.

Раскрасим ребра из паросочетания, соответствующего (A) в красный цвет, (B) — в синий, а ребра из обоих паросочетаний — в пурпурный. Рассмотрим граф из только красных и синих ребер. Любая компонента связности в нём представляет собой либо путь, либо цикл, состоящий из чередующихся красных и синих ребер. В любом цикле будет равное число красных и синих рёбер, а так как всего синих рёбер больше, то должен существовать путь, начинающийся и оканчивающийся синим ребром — он и будет увеличивающей цепью для (A), а значит (A) не оптимальное, и мы получили противоречие.

Скорость работы

Такой алгоритм ровно (n) раз ищет увеличивающий путь, каждый раз просматривая не более (m) рёбер, а значит работает за (O(nm)).

Что примечательно, его можно не бояться запускать на ограничениях и побольше ((n, m approx 10^4)), потому что для него есть мощные неасимптотические оптимизации:

Eго можно жадно инициализировать (просто заранее пройтись по вершинам левой доли и сматчить их со свободной вершиной правой, если она есть).
Можно не заполнять нулями на каждой итерации массив used, а использовать следующий трюк: хранить в нём вместо булева флага версию последнего изменения, а конкретно – номер итерации, на которой это значение стало true. Если этот номер меньше текущего номера итерации, то мы можем воспринимать это значение как false. В каком-то смысле это позволяет эмулировать очищение массива за константу.
Очень часто граф приходит из какой-то другой задачи, природа которой накладывает ограничения на его вид. Например, в задачах на решетках (когда есть двумерный массив, и соседние клетки связаны друг с другом) граф двудольный, но степень каждой вершины маленькая, и граф имеет очень специфичную структуру, и на нём алгоритм Куна работает быстрее, чем ожидается из формулы (n times m). Контрпримеры в таких задачах на самом деле почти всегда можно сгенерировать, но авторы редко так заморачиваются.

Вообще говоря, увлекаться ускорением алгоритма Куна не стоит — существует более асимптотически быстрый алгоритм. Задача нахождения максимального паросочетания — частный случай задачи о максимальном потоке, и если применить алгоритм Диница к двудольным графам с единичной пропускной способностью, то выясняется, что работать он будет за (O(m sqrt n)).

Покрытие путями DAG-а

Сводить задачи к поиску максимального паросочетания обычно не очень трудно, но в некоторых случаях самому додуматься сложно. Разберём одну такую известную задачу. Дан ориентированный ациклический граф (G) (англ. directed acyclic graph). Требуется покрыть его наименьшим числом путей, то есть найти наименьшее множество простых путей, где каждая вершина принадлежит ровно одному пути.

Построим соответствующие изначальному графу (G) два двудольных графа (H) и (overline{H}) следующим образом:

В каждой доле графа (H) будет по (n) вершин. Обозначим их через (a_i) и (b_i) соответственно.
Для каждого ребра ((i, j)) исходного графа (G) проведём соответствующее ребро ((a_i, b_j)) в графе (H).
Теперь из графа (H) сделаем граф (overline{H}), добавив обратное ребро ((b_i, a_i)) для каждого (i).

Если мы рассмотрим любой путь (v_1, v_2, ldots, v_k) в исходном графе (G), то в графе (overline{H}) ему будет соответствовать путь (a_{v_1}, b_{v_2}, a_{v_2}, b_{v_3}, ldots, a_{v_{k-1}}, b_{v_k}). Обратное тоже верно: любой путь, начинающийся в левой доле (overline{H}) и заканчивающийся в правой будет соответствовать какому-то пути в (G).

Итак, есть взаимно однозначное соответствие между путями в (G) и путями (overline{H}), идущими из левой доли в правую. Заметим, что любой такой путь в (overline{H}) — это паросочетание в (H) (напомним, это (overline{H}) без обратных рёбер). Получается, любому пути из (G) можно поставить в соответствие паросочетание в (H), и наоборот. Более того, непересекающимся путям в (G) соответствуют непересекающиеся паросочетания в (H).

Заметим, что если есть (p) непересекающихся путей, покрывающих все (n) вершин графа, то они вместе содержат (r = n – p) рёбер. Отсюда получаем, что чтобы минимизировать число путей (p), мы должны максимизировать число рёбер (r) в них.

Мы теперь можем свести задачу к нахождению максимального паросочетания в двудольном графе (H). После нахождения этого паросочетания мы должны преобразовать его в набор путей в (G). Это делается тривиальным алгоритмом: возьмем (a_1), посмотрим, с какой (b_k) она соединена, посмотрим на (a_k) и так далее. Некоторые вершины могут остаться ненасыщенными — в таком случае в ответ надо добавить пути нулевой длины из каждой из этих вершин.

Лемма Холла

Лемма Холла (или: теорема о свадьбах) — очень удобный критерий в задачах, где нужно проверить, что паросочетание существует, но при этом не требуется строить его явно.

Лемма Холла. Полное паросочетание существует тогда и только тогда, когда любая группа вершин левой доли соединена с не меньшим количеством вершин правой доли.

Доказательство. В одну сторону понятно — если совершенное паросочетание есть, то для любого подмножества вершин левой доли можно взять вершины правой, соединенные с ним паросочетанием.

В другую сложнее — нужно воспользоваться индукцией. Будем доказывать, что если паросочетание не полное, то можно в таком графе найти увеличивающую цепь, и с её помощью увеличить паросочетание на единицу.

База индукции: одна вершина из (L), которая по условию соединена с хотя бы одной вершиной из (R).

Индукционный переход: пусть после (k < n) шагов построено паросочетание (M). Докажем, что в (M) можно добавить вершину (v) из (L), не насыщенную паросочетанием.

Рассмотрим множество вершин (H) — все вершины, достижимые из (x), если можно ходить из правой доли в левую только по рёбрам паросочетания, а из левой в правую — по любым (мы такой граф по сути строим, когда ищем увеличивающую цепь в алгоритме Куна)

Тогда в (H) найдется вершина (y) из (R), не насыщенная паросочетанием. Иначе, если такой вершины нет, то получается, что если рассмотреть вершины (H_L) (вершины левой доли, насыщенные паросочетанием), то для них не будет выполнено условие, что (|H_L| leq |N(H_L)|) (здесь (N(X)) — множество вершин, соединенным паросочетанием с (X)).

Тогда должен существовать путь из (x) в (y), и он будет увеличивающим для паросочетания (M), потому что из (R) в (L) мы всегда шли только по ребрам паросочетания. Проведя чередование вдоль этого пути, получим большее паросочетание, следовательно предположение индукции верно.

Минимальное вершинное покрытие

Задача. Дан граф. Назовем вершинным покрытием такое множество вершин, что каждое ребро графа инцидентно хотя бы одной вершине из множества. Необходимо найти вершинное покрытие наименьшего размера.

Следует заметить, что в общем случае это очень сложная задача, но для двудольных графов она имеет достаточно простое решение.

Теорема. (mid V_{min} mid le mid M mid), где (V_{min}) — минимальное вершинное покрытие, а (M) — максимальное паросочетание.

Доказательство. (mid V_{min} mid ge mid M mid), поскольку (M) — множество независимых ребер. Теперь приведем алгоритм, который строит вершинное покрытие размера (mid M mid). Очевидно, оно будет минимальным.

Алгоритм. Мысленно ориентируем ребра графа: ребра из (M) проведем из правой доли в левую, остальные — из левой в правую, после чего запустим обход в глубину из всех вершин левой доли, не включенных в (M).

Заметим, что граф разбился на несколько множеств: (L^+, L^-, R^+, R^-), где “плюсовые” множества — это множества посещенных в процессе обхода вершин. В графе такого вида не бывает ребер (L^+ rightarrow R^-), (L^- leftarrow R^+) по очевидным соображениям. Ребер (L^+ leftarrow R^-) не бывает, потому что в противном случае паросочетание (M) не максимальное — его можно дополнить ребрами такого типа.

[
L^- cup R^+ = V_{min}
]

Понятно, что данное множество покроет все ребра. Осталось выяснить, почему (L^- cup R^+). Это верно потому, что (L^- cup R^+) покрывает все ребра (M) ровно один раз (ведь ребра (L^- rightarrow R^+) не принадлежат (M)), а также потому, что в нем нет вершин, не принадлежащих (M) (для (L^-) это справедливо по определению, для (R^+) можно провести доказательство от противного с использованием чередующихся цепей).

Упражнение. Подумайте, как это можно применить к решению задачи о нахождении максимального независимого множества.

Для ноулайферов: матроиды

С весьма большой вероятностью матроиды вам никогда не пригодятся в школьных олимпиадах, однако, если вам совсем нечего делать, можете про них почитать.

Математика вообще занимается тем, что обобщает всякие объекты и старается формулировать все теоремы максимально абстрактно. Так, концепцию хороших подмножеств (паросочетаний) обобщает понятие матроида. Практическое применение — жадный алгоритм Радо-Эдмондса, который нужен для обоснования большого числа жадников, где нужно набрать какое-то подмножество минимального / максимального веса. Сам алгоритм максимально простой: давайте отсортируем эти объекты по весу и будем добавлять их в таком порядке в наше хорошее множество, если оно после добавления остается хорошим.

Применимо к паросочетаниям: пусть у вершин левой доли есть вес, и нам нужно набрать максимальное паросочетание минимального веса. Тогда выясняется, что можно просто отсортировать вершины левой доли по весу и пытаться в таком порядке добавлять их в паросочетание стандартным алгоритмом Куна.

Источник

Мем
fd_al

Алгоритм Форда-Фалкерсона

Метод предназначен для распределенной системы динамического управления потоками информации в сетях связи, позволяет найти кратчайшие пути от всех узлов сети к одному общему входящему узлу.

Был придуман в 1954 году двумя учёными – Фордом Л.Р. и Фалкерсоном Д.Р.
Это достаточно простой, но действенный алгоритм – позволяющий определять максимальную пропускную способность потока в направленном графе.

Алгоритм работает следующим образом:

Начинаем с нулевого потока и выбираем увеличивающий путь, который будет увеличивать поток сети.
Если увеличивающий путь существует, увеличиваем поток по нему и переходим к шагу 1.
Если увеличивающих путей больше нет, мы находим максимальный поток в сети.
Увеличивающий путь – это путь от источника к стоку, который может быть увеличен путем увеличения потока через минимальное ребро на этом пути.

Процесс поиска увеличивающего пути может быть реализован различными способами, например, с помощью поиска в ширину или глубину. Однако, в общем случае, итерационный алгоритм нахождения увеличивающего пути может занять время, пропорциональное числу ребер в графе, что может привести к экспоненциальной сложности алгоритма в худшем случае.

Задача:

Задание мы возьмём с предыдущего раза, когда делали алгоритм Дейкстры.

Изображение задания

Решим её с помощью Алгоритма Форда-Фалкерсона

Задача найти максимальный поток! Не оптимальный путь, а максимум, который можно пропустить через него.

Для начала создадим матрицу расстояний для нашего графа.

Пояснение кода:

Функция max_flow использует алгоритм Форда-Фалкерсона для
нахождения максимального потока в сети, заданной в виде графа.
Алгоритм заключается в последовательном поиске увеличивающих
путей из источника в сток и увеличении потока на этих путях до тех пор,
пока не будет достигнут максимальный поток.

Входные параметры функции:

‘graph’: матрица смежности, представляющая сеть в виде графа.
Каждый элемент матрицы graph[i][j] соответствует пропускной способности
ребра между вершинами i и j. Если ребра между вершинами нет,
то значение равно 0.

‘source’: вершина-источник.

‘sink’: вершина-сток.


    def bfs(graph, source, sink, parent):

        visited = [False] * len(graph)
        queue = [source]
        visited[source] = True

        while queue:
            u = queue.pop(0)

            for idx, val in enumerate(graph[u]):
                if not visited[idx] and val > 0:
                    queue.append(idx)
                    visited[idx] = True
                    parent[idx] = u

                    if idx == sink:
                        return True

        return False

    parent = [-1] * len(graph)
    max_flow = 0

Внутри функции определена вспомогательная функция bfs,
которая реализует поиск пути в графе с помощью
алгоритма обхода в ширину (BFS).
Эта функция используется для поиска увеличивающих путей
в алгоритме Форда-Фалкерсона.

Функция bfs работает следующим образом:

Создается список visited, в котором будут храниться флаги посещения вершин.
Изначально он заполняется значениями False.
Создается очередь queue с начальным элементом source.
Вершина source помечается как посещенная (visited[source] = True).
Пока очередь не пуста:
Извлекается первый элемент u из очереди.
Для каждого смежного элемента v с вершиной u,
для которого еще не был выполнен поиск и его пропускная способность больше 0,
выполняются следующие действия:
Добавляется вершина v в конец очереди queue.
В visited отмечается, что вершина v посещена (visited[v] = True).
В словаре parent для вершины v устанавливается значение u.
Если v равно sink, то возвращается True, так как был найден путь из source в sink.
Если путь из source в sink не был найден, возвращается False.
После определения функции bfs основная функция max_flow начинает работу.

        while bfs(graph, source, sink, parent):
        path_flow = float("Inf")
        s = sink

        while s != source:
            path_flow = min(path_flow, graph[parent[s]][s])
            s = parent[s]

        max_flow += path_flow
        v = sink

        while v != source:
            u = parent[v]
            graph[u][v] -= path_flow
            graph[v][u] += path_flow
            v = parent[v]

    return max_flow

Внутри цикла while происходит последовательный поиск
увеличивающих путей и увеличение потока на этих путях.
Поиск увеличивающих путей реализован с помощью функции bfs.
Если найден путь из источника в сток, то определяется
максимальный поток, который может пройти по этому пути.
Далее этот поток увеличивается на найденном пути,
а пропускные способности ребер на этом пути уменьшаются соответственно.
Этот процесс продолжается до тех пор,
пока не будет достигнут максимальный поток.

На выходе функция max_flow возвращает значение максимального потока в сети.

Источник

Алгоритм[править | править код]

Неформальное описание[править | править код]

Формальное описание[править | править код]

Сложность[править | править код]

Пример несходящегося алгоритма[править | править код]

Пример[править | править код]

См. также[править | править код]

Ссылки[править | править код]

Литература[править | править код]

Примечания[править | править код]

Алгоритм Форда-Фалкерсона

Постановка задачи

Как работает сам алгоритм?

Разбор конкретного примера

Источники

21. Задача о максимальном потоке минимальной стоимости (МаПМиС). Алгоритм решения.

22. Метод ветвей и границ. Решение задачи «о рюкзаке» методом ветвей и границ.

Паросочетания

Корректность

Скорость работы

Покрытие путями DAG-а

Лемма Холла

Минимальное вершинное покрытие

Для ноулайферов: матроиды

Алгоритм Форда-Фалкерсона

Алгоритм работает следующим образом:

Задача:

Пояснение кода:

Вам также может понравиться

Как исправить ход часов

Как найти стекло крафт

Мне нужны деньги как найти деньги

Добавить комментарий Отменить ответ