Главная
→
Примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
→
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
Методы и примеры решения задач ТОЭ
→
РЕШЕНИЕ ЗАДАЧ ТОЭ — МЕТОДЫ, АЛГОРИТМЫ, ПРИМЕРЫ РЕШЕНИЯ
→
1 Методы расчета электрических цепей при постоянных токах и напряжениях
1.4 Метод узловых потенциалов. Метод узлового напряжения (метод двух узлов)
В методе узловых потенциалов за вспомогательные расчетные величины принимают потенциалы узлов схемы. При этом потенциалом одного из узлов задаются, обычно считая его равным нулю (заземляют). Этот узел называют опорным узлом. Затем для каждого узла схемы, кроме опорного узла, составляют систему уравнений методом узловых потенциалов. По найденным потенциалам узлов находят токи ветвей по обобщенному закону Ома (закону Ома для ветви с ЭДС).
Отметим, что метод узловых потенциалов без предварительного преобразования схемы не применим к схемам с взаимной индукцией.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), не имеющих общего узла нужно применять особые способы составления системы уравнений метода узловых потенциалов.
Для схем, содержащих несколько ветвей только с идеальными источниками ЭДС (без пассивных элементов), имеющих общий узел, этот общий узел принимают за опорный узел (заземляют). Тогда потенциалы узлов, соединенных этими идеальными источниками ЭДС без пассивных элементов с опорным узлом, равны ЭДС этих идеальных источников (+E, если идеальный источник ЭДС направлен от опорного узла и –E в противном случае).
Метод двух узлов является частным случаем метода узловых потенциалов. Он применяется для определения токов в ветвях схемы с двумя узлами и произвольным числом параллельных активных и пассивных ветвей.
Решение задач методом узловых потенциалов и методом двух узлов
Задача 1.4.1 Рассчитать цепь рис. 1.4.1 методом узловых, потенциалов.
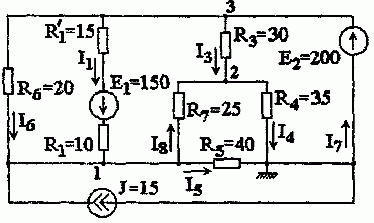
Рис. 1.4.1
Решение. В рассматриваемой схеме четыре узла. Заземлим узел 4 (опорный узел)
φ 4 =0.
Тогда
φ 3 = φ 4 + E 2 =200 B.
Необходимо найти потенциалы узлов 1 и 2. Составим систему уравнений по методу узловых потенциалов для узлов 1 и 2.
Рассматривая узел 1, получим
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 − φ 3 ⋅ g 13 =J+ E 1 R 1 + R ′ 1
или
φ 1 ⋅ g 11 − φ 2 ⋅ g 12 =J+ E 1 R 1 + R ′ 1 + E 1 ⋅ g 13 .
В правой части этого уравнения оба слагаемых учтены со знаком плюс, так как J и E1 направлены к узлу 1.
Рассматривая узел 2 (правая часть уравнения равна нулю, так как в ветвях, подсоединенных к узлу 2, нет источников энергии), получим
Индивидуалка Лиза (25 лет) т.8 929 529-57-81 Москва, метро Полянка. газификатор – вся актуальная информация на нашем сайте.
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 − φ 3 ⋅ g 23 =0
или
− φ 1 ⋅ g 21 + φ 2 ⋅ g 22 = E 2 ⋅ g 23 .
Найдем собственную проводимость первого узла
g 11 = 1 R 6 + 1 R 1 + R ′ 1 + 1 R ИТ + 1 R 2 + 1 R 5 = 1 20 + 1 25 + 1 25 + 1 40 =0,155 См.
Проводимость ветви с идеальным источником тока равна нулю, так как внутреннее сопротивление идеального источника тока RИТ равно бесконечности.
Собственная проводимость узла 2
g 22 = 1 R 2 + 1 R 3 + 1 R 4 = 1 25 + 1 30 + 1 35 =0,102 См.
Взаимные проводимости между узлами
g 13 = 1 R 6 + 1 R 1 + R ′ 1 = 1 20 + 1 25 =0,09 См; g 21 = g 12 = 1 R 2 = 1 25 =0,04 См; g 23 = 1 R 3 = 1 30 =0,033 См.
Подставив в уравнения известные величины, получим
{ φ 1 ⋅0,155− φ 2 ⋅0,04=39 − φ 1 ⋅0,04+ φ 2 ⋅0,102=6,6
Для решения этой системы используем метод определителей. Главный определитель системы
Δ=| 0,155 −0,04 −0,04 0,102 |=0,01421.
Частные определители
Δ 1 =| 39 −0,04 6,6 0,102 |=4,242; Δ 2 =| 0,155 39 −0,04 6,6 |=2,583.
Находим потенциалы узлов
φ 1 = Δ 1 Δ = 4,242 0,01421 =298,6 В; φ 2 = Δ 2 Δ = 2,583 0,01421 =181,8 В.
Определяем токи в ветвях (положительные направления токов в ветвях с ЭДС выбираем по направлению ЭДС, в остальных ветвях произвольно)
I 1 = φ 3 − φ 1 + E 1 R 1 + R ′ 1 = 200−298,6+150 10+15 =2,056 А.
В числителе этого выражения от потенциала узла 3, из которого вытекает ток I1, вычитается потенциал узла 1, к которому ток подтекает. Если ЭДС ветви совпадает (не совпадает) с выбранным направлением тока, то она учитывается со знаком плюс (минус). В знаменателе выражения учитываются сопротивления ветви.
Аналогично определяем другие токи (направления токов указаны на схеме рис. 1.4.1)
I 1 = φ 3 − φ 1 R 6 = 200−298,6 20 =−4,93 А; I 2 = φ 1 − φ 2 R 2 = 298,6−181,8 25 =4,67 А; I 3 = φ 3 − φ 2 R 3 = 200−181,8 30 =0,607 А; I 4 = φ 2 − φ 4 R 4 = 181,8−0 35 =5,194 А.
Для определения тока в ветви с идеальной ЭДС зададимся направлением тока I7. По первому закону Кирхгофа для узла 3 составим уравнение
− I 7 + I 3 + I 1 + I 6 =0.
Откуда
I 7 = I 3 + I 1 + I 6 =0,607+2,056−4,98=−2,317 A.
Задача 1.4.2 Определить токи в схеме рис. 1.4.2 методом узлового напряжения.
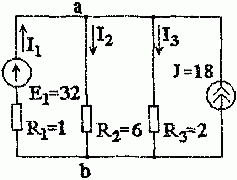
Рис. 1.4.2
Решение
1 Находим напряжение между двумя узлами по методу двух узлов
U ab = φ a − φ b = E 1 ⋅ g 1 +J g 1 + g 2 + g 3 = 32⋅ 1 1 +18 1 1 + 1 6 + 1 2 =30 B.
При составлении этого уравнения по методу двух узлов в числителе необходимо брать произведение ЭДС на проводимость своей ветви со знаком плюс, если ЭДС направлена к узлу a, и минус — если направлена от узла a к узлу b.
Аналогичное правило определяет и знаки токов источников тока.
2 Находим токи по закону Ома (по закону Ома для ветви с ЭДС)
I 1 = E 1 + φ b − φ a R 1 = E 1 − U ab R 1 = 32−30 1 =2 А; I 2 = U ab R 2 = 30 6 =5 А; I 3 = U ab R 3 = 30 2 =15 А.
Правильность решения проверим по первому закону Кирхгофа
I 1 − I 2 + I 3 +J=0; 2−5−15+18=0.
Метод узловых потенциалов в статье ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА. Основные положения и соотношения. Упражнения и задачи
 опорный узел,
опорный узел,
метод двух узлов,
метод узловых напряжений,
метод узловых потенциалов,
собственная проводимость,
взаимная проводимость
Содержание:
Метод узловых напряжений:
Метод узловых напряжений (узловых потенциалов) является наиболее общим. Он базируется на первом законе Кирхгофа (ЗТК) и законе Ома. В отличие от методов, рассмотренных в лекции 4, метод позволяет уменьшить число уравнений, описывающих схему, до величины, равной количеству рёбер (ветвей) дерева (2.1)
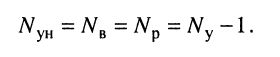
Идея метода состоит в следующем:
- Выбирается базисный узел — один из узлов цепи, относительно которого рассчитываются напряжения во всех узлах; базисный узел помечается цифрой 0.
- Потенциал базисного узла принимается равным нулю.
- Рассчитываются напряжения во всех узлах относительно базисного.
- По закону Ома находятся токи и напряжения в соответствующих ветвях.
Напряжения в узлах цепи, отсчитанные относительно базисного, называют узловыми напряжениями.
Определение:
Метод анализа колебаний в электрических цепях, в котором неизвестными, подлежащими определению, являются узловые напряжения, называется методом узловых напряжений.
В дальнейшем будем полагать, что цепь имеет 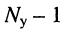
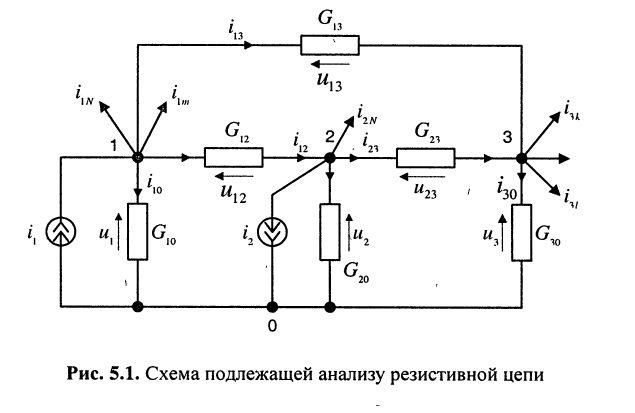
Предварительно покажем, что при известных узловых напряжениях можно найти напряжения на всех элементах цепи, а потому и все токи. Действительно, напряжение на любой ветви определяется по второму закону Кирхгофа (ЗНК) как разность соответствующих узловых напряжений, а токи в элементах найдутся по закону Ома. Для контура, включающего элементы 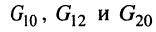 (рис. 5.1), по ЗНК имеем:
(рис. 5.1), по ЗНК имеем:
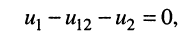
откуда
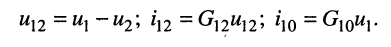
Аналогично можно записать
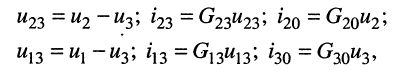
что и требовалось показать.
Составление узловых уравнений
При составлении уравнений для, схемы рис. 5.1 будем полагать, что задающие токи 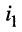 и
и 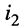 источников тока (их на схеме два) известны.
источников тока (их на схеме два) известны.
Тогда согласно первому закону Кирхгофа для узлов 1 и 2 в предположении, что в общем случае они связаны со всеми другими узлами, получим:
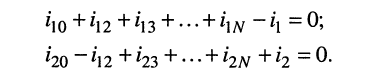
Выразим токи в уравнениях через узловые напряжения, как показано в разд. 5.1:
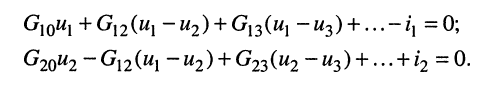
Раскрыв скобки и приведя подобные члены, получаем узловые уравнения:
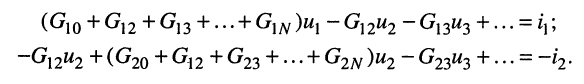
Полученный результат позволяет сделать следующие выводы:
 – ый и
– ый и 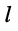 -ый узлы; все эти слагаемые входят в уравнение с отрицательным знаком.
-ый узлы; все эти слагаемые входят в уравнение с отрицательным знаком.
Аналогично записываются узловые уравнения для всех других узлов цепи, в результате чего образуется система узловых уравнений вида:
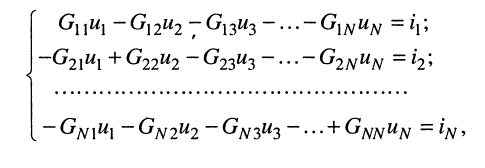
где:
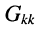 — собственная проводимость
— собственная проводимость  -го узла цепи, являющаяся арифметической суммой проводимостей всех элементов, подключённых одним из зажимов к
-го узла цепи, являющаяся арифметической суммой проводимостей всех элементов, подключённых одним из зажимов к  -му узлу;
-му узлу;
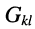 — взаимная проводимость
— взаимная проводимость  -го и
-го и 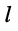 -го узлов цепи, являющаяся проводимостью элемента, включённого между
-го узлов цепи, являющаяся проводимостью элемента, включённого между  -ым и
-ым и 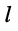 -ым узлами;
-ым узлами;
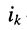 — задающий ток
— задающий ток  -го узла цепи, являющийся алгебраической суммой задающих токов источников тока, подключённых одним из зажимов к
-го узла цепи, являющийся алгебраической суммой задающих токов источников тока, подключённых одним из зажимов к  -му узлу цепи; слагаемые этой суммы входят в правые части уравнений со знаком “+”, если направление отсчёта задающего тока источника ориентировано в сторону к-го узла, и со знаком
-му узлу цепи; слагаемые этой суммы входят в правые части уравнений со знаком “+”, если направление отсчёта задающего тока источника ориентировано в сторону к-го узла, и со знаком  в противном случае.
в противном случае.
Систему узловых уравнений принято записывать в канонической форме, а именно:
- токи, как свободные члены, записываются в правых частях уравнений;
- неизвестные напряжения записываются в левых частях уравнений с последовательно возрастающими индексами;
- уравнения располагаются в соответствии с порядковыми номерами узлов. Такая запись применена в (5.2).
Система (5.2) является линейной неоднородной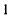 системой независимых уравнений, поэтому позволяет найти искомые узловые напряжения. Методы решения таких систем широко известны (Крамера, Гаусса, Гаусса—Жордана).
системой независимых уравнений, поэтому позволяет найти искомые узловые напряжения. Методы решения таких систем широко известны (Крамера, Гаусса, Гаусса—Жордана).
Метод узловых напряжений даёт существенное сокращение необходимого числа уравнений по сравнению с методом токов элементов. Выигрыш оказывается тем значительнее, чем больше независимых контуров имеет цепь.
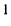 Система называется неоднородной, если хотя бы один из свободных членов (в данном случае это
Система называется неоднородной, если хотя бы один из свободных членов (в данном случае это 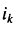 ) не равен нулю.
) не равен нулю.
Особенности составления узловых уравнений
Метод узловых напряжений можно применять и в тех случаях, когда в анализируемой цепи имеются источники напряжения. При этом:
- напряжение между любой парой узлов, к которым подключён источник напряжения, известно;
- в качестве базисного желательно выбирать узел, к которому одним из своих зажимов подключён источник напряжения — тогда узловое напряжение, отсчитываемое между базисным узлом и вторым зажимом источника, равно ЭДС источника или отличается от него знаком; кроме того, базисным может быть выбран узел, к которому подключено наибольшее число элементов, если этот выбор не противоречит первой рекомендаций;
- уменьшается число независимых узловых напряжений, а потому понижается и порядок системы, т. е. число входящих в систему независимых уравнений;
- если цепь содержит
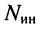 источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
источников напряжения, имеющих один общий зажим, то число узловых уравнений, которое можно составить для такой цепи, равно
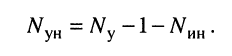
Пример 5.1.
Записать систему узловых уравнений для удлинителя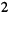 (рис. 5.2), рассмотренного в лекции 4.
(рис. 5.2), рассмотренного в лекции 4.
Решение. Удлинитель содержит четыре узла и один источник тока, поэтому согласно (5.3) достаточно составить всего два узловых уравнения
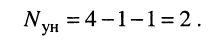
Положим узел 0 базисным, поскольку к нему одним из своих зажимов подключён источник напряжения. Узловое напряжение узла 1 известно и равно. ЭДС источника напряжения 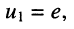 поэтому остаётся записать уравнения для узлов 2 и 3 по правилам, рассмотренным в разд. 5.1. Предварительно запишем собственные и взаимные проводимости узлов.
поэтому остаётся записать уравнения для узлов 2 и 3 по правилам, рассмотренным в разд. 5.1. Предварительно запишем собственные и взаимные проводимости узлов.
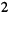 Такое обращение справедливо,-поскольку удлинители применяются для построения магазина затуханий, или аттенюатора.
Такое обращение справедливо,-поскольку удлинители применяются для построения магазина затуханий, или аттенюатора.
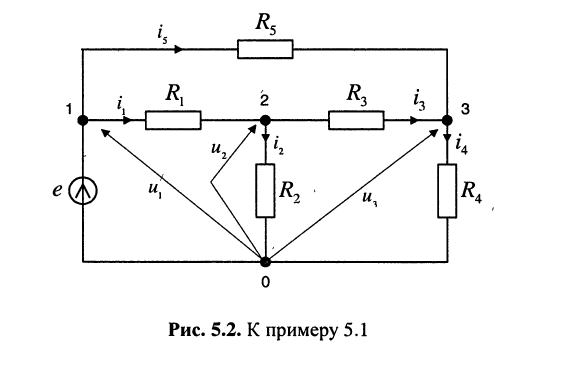
Собственная проводимость второго узла
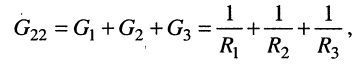
взаимные проводимости второго узла
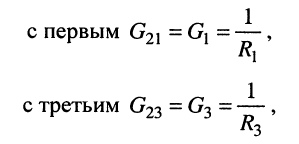
собственная проводимость третьего узла
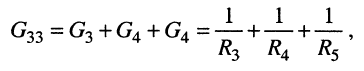
взаимные проводимости третьего узла
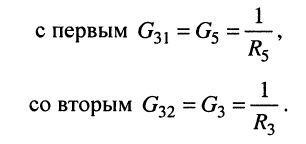
Теперь получим систему узловых уравнений, записав узловые уравнения для второго и третьего узлов:
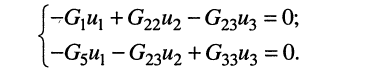
Поскольку 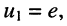 запишем эту систему уравнений в каноническом виде
запишем эту систему уравнений в каноническом виде
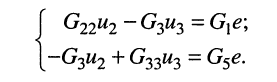
Эта система уравнений и является окончательным результатом решения задачи, поставленной в примере.
Если содержащиеся в цепи источники напряжения не имеют общего зажима, то задачу анализа следует решать или методом узловых напряжений в сочетании с принципом наложения или путём эквивалентных преобразований перейти к другой модели цепи.
При составлении узловых уравнений для цепей, содержащих многополюсники (например, транзисторы, операционные усилители
и т. д), следует прежде всего заменить эти многополюсники их схемами замещения.
Метод узлового напряжения
Расчет сложных разветвленных электрических цепей с несколькими источниками и двумя узлам, можно осуществить методом узлового напряжения. Напряжение межи узлами и называется узловым. UAB R3 узловое напряжение цепи (рис. 4.9) Для различных ветвей (рис. 4.9) узловое напряжение UAB можно опредо лить следующим образом.
1. Поскольку для первой ветви источник работает в режиме генератор:
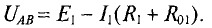
Величина тока определяется как
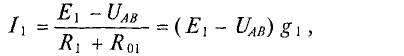
где 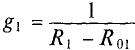 — проводимость
— проводимость
2.Для второй ветви источник работает в режиме потребителя следовательно
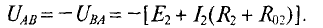
Тогда ток
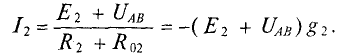
3.Для третьей ветви
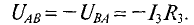
(Потенциал точки В для третьей ветви больше, чем потенций точки А, так как ток направлен из точки с большим потенциалом в точку с меньшим потенциалом)
Величину тока 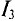 можно определить по закону Ома
можно определить по закону Ома
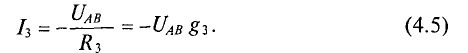
По первому закону Кирхгофа для узловой точки А (или В):

Подставив в уравнение (4.6) значения токов из уравнений (4.3), .4) и (4.5) для рассматриваемой цепи, можно записать
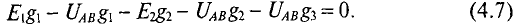
Решив это уравнение относительно узлового напряжения UAB, можно определить его значение
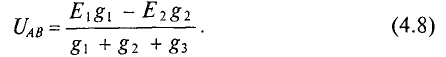
Следовательно, величина узлового напряжения определяется отношением алгебраической суммы произведений ЭДС и проводимости ветвей с источниками к сумме проводимостей всех ветвей:

Для определения знака алгебраической суммы направление токов во всех ветвях выбирают одинаковым, т.е. от одного узла другому (рис. 4.9). Тогда ЭДС источника, работающего в режиме генератора, берется со знаком «плюс», а источника, работающего в режиме потребителя, со знаком «минус». Таким образом, для определения токов в сложной цепи с двумя узлами вычисляется сначала узловое напряжение по выражению 4.9), а затем значения токов по формулам (4.3), (4.4), (4.5). Узловое напряжение UAB может получиться положительным или отрицательным, как и ток в любой ветви.
Знак «минус» в вычисленном значении тока указывает, что реальное направление тока в данной ветви противоположно словно выбранному.
Пример 4.7
В ветвях схемы (рис. 4.10) требуется определить токи, если: 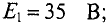
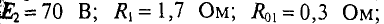
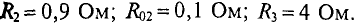
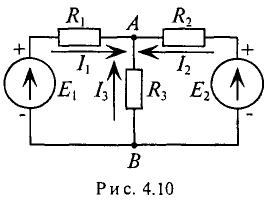
Решение
Узловое напряжение 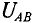
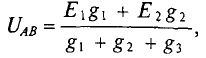
где 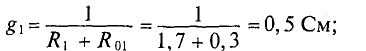
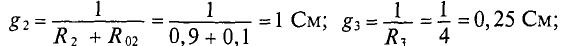
тогда 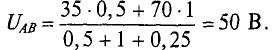
Токи в ветвях будут соответственно равны
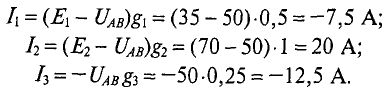
Как видно из полученных результатов, направление токов 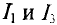 противоположно выбранному. Следовательно, источник £ работает в режиме потребителя.
противоположно выбранному. Следовательно, источник £ работает в режиме потребителя.
Пример 4.8
Два генератора (рис. 4.11), ЭДС и внутреннее сопротивление которых одинаковы: 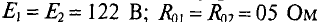 , питают потребитель (нагрузку) с сопротивлением R= 5,85 Ом.
, питают потребитель (нагрузку) с сопротивлением R= 5,85 Ом.
Как изменится ток второго генератора: 1) при увеличении его ЭДС (£2) на 1 %; ” 2) при увеличении узлового напряжения (UAB) на 1 %.
Решение
Определяется узловое напряжение UAB цепи (рис. 4.11)
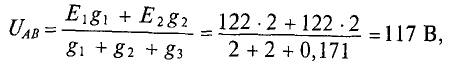
где
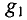 =
=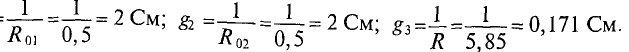
Тогда ток второго генератора
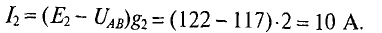
При увеличении Е2 на 1 %, его величина станет равной
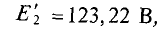
тогда
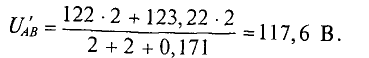
При этом 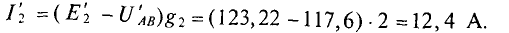
Следовательно, увеличение ЭДС генератора Е2 на 1 % приводит увеличению тока этого генератора на 24 %.
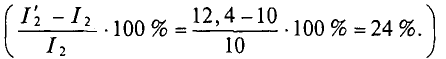
2. При увеличении узлового напряжения на 1% его величины станет равной
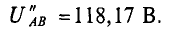
При этом 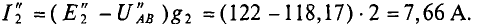 Таким образом, ток второго генератора при увеличении узлового напряжения на 1 % уменьшится на 23,4 %.
Таким образом, ток второго генератора при увеличении узлового напряжения на 1 % уменьшится на 23,4 %.
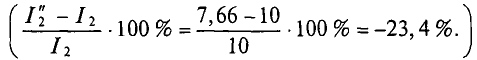
Знак «минус» означает уменьшение, а не увеличение тока 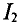 .
.
Определение метода узловых напряжений
Метод узловых напряжений заключается в том, что на основании первого закона Кирхгофа определяются потенциалы в узлах электрической цепи относительно некоторого базисного узла. Эти разности потенциалов называются узловыми напряжениями, причем положительное направление их указывается стрелкой от рассматриваемого узла к базисному.
Напряжение на какой-либо ветви равно, очевидно, разности узловых напряжений концов данной ветви; произведение же этого напряжения на комплексную проводимость данной ветви равно току в этой ветви. Таким образом, зная узловые напряжения в электрической цепи, можно найти токи в ветвях.
Если принять потенциал базисного узла равным нулю, то напряжения между остальными узлами и базисным узлом будут равны также потенциалам этих узлов. Поэтому данный метод называется также методом узловых потенциалов.
На рис. 7-7 в виде примера изображена электрическая схема с двумя источниками тока, имеющая три узла: 1, 2 и 3. Выберем в данной схеме в качестве базиса узел 3 и
обозначим узловые напряжения точек 1 и 2 через 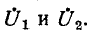 Согласно принятым на рис. 7-7 обозначениям комплексные проводимости ветвей равны соответственно:
Согласно принятым на рис. 7-7 обозначениям комплексные проводимости ветвей равны соответственно:
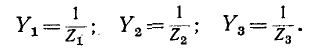
Для заданной электрической цепи с тремя узлами могут быть записаны два уравнения по первому закону Кирхгофа, а именно: для узла 1
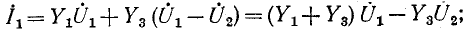
для узла 2
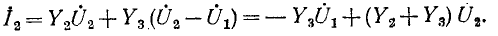
Величина 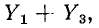 представляющая собой сумму комплексных проводимостей ветвей, сходящихся в узле 1, называется собственной проводимостью узла 1 величина
представляющая собой сумму комплексных проводимостей ветвей, сходящихся в узле 1, называется собственной проводимостью узла 1 величина 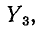 равная комплексной проводимости ветви между узлами 1 и 2, входящая в уравнения со знаком минус, называется об-, щей проводимостью между узлами 1 и 2.
равная комплексной проводимости ветви между узлами 1 и 2, входящая в уравнения со знаком минус, называется об-, щей проводимостью между узлами 1 и 2.
Если заданы токи источников тока и комплексные проводимости ветвей, то узловые напряжения находятся совместным решением уравнений.
В общем случае если электрическая схема содержит q узлов, то на основании первого закона Кирхгофа получается система из q — 1 уравнений (узел q принят за базисный):
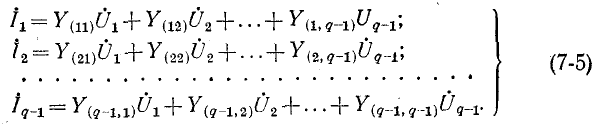
Здесь ток источника тока, подходящий к узлу, берется со знаком плюс, а отходящий от узла — со знаком минус;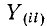 — собственная проводимость всех ветвей, сходящихся в данном узле
— собственная проводимость всех ветвей, сходящихся в данном узле 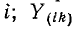 — общая проводимость между узламп
— общая проводимость между узламп 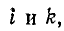 входящая со знаком минус при выбранном направлении всех узловых напряжений к базису, независимо от того, является ли данная электрическая цепь планарной или непланарной.
входящая со знаком минус при выбранном направлении всех узловых напряжений к базису, независимо от того, является ли данная электрическая цепь планарной или непланарной.
Решив систему уравнений (7-5) при помощи определителей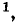 получим формулу для
получим формулу для 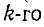 узлового напряжения относительно базиса:
узлового напряжения относительно базиса:
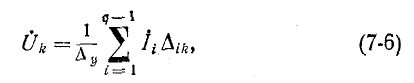
где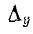 — определитель системы
— определитель системы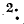
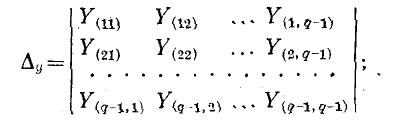
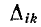 — алгебраическое дополнение элемента
— алгебраическое дополнение элемента 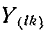 данного определителя.
данного определителя.
Первый индекс i алгебраического дополнения, обозначающий номер строки, вычеркиваемой в определителе системы, соответствует номеру узла, заданный ток источника тока которого умножается на данное алгебраическое дополнение. Второй индекс 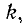 обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру узла, для которого вычисляется узловое напряжение.
обозначающий номер столбца, вычеркиваемого в определителе системы, соответствует номеру узла, для которого вычисляется узловое напряжение.
Уравнения (7-5), выражающие первый закон Кирхгофа, записаны в предположении, что в качестве источников электрической энергии служат источники тока. При наличии в электрической схеме источников э. д. с. последние должны быть заменены эквивалентными источниками тока.
Если в схеме имеются ветви, содержащие только э. д, с. (проводимости таких ветвей бесконечно велики), то эти ветви следует рассматривать как источники неизвестных токов, которые затем исключаются при сложении соответствующих уравнений. Дополнительными связями между неизвестными узловыми напряжениями будут являться известные напряжения между узлами, равные заданным э. д. с.
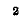 Определитель снабжен индексом у, так как его элементами являются комплексные проводимости.
Определитель снабжен индексом у, так как его элементами являются комплексные проводимости.
При наличии только одной ветви с э. д. с. и бесконечной проводимостью целесообразно принять за базисный узел один из узлов, к которому примыкает данная ветвь; тогда напряжение другого узла становится известным и число неизвестных сокращается на одно.
Метод узловых напряжений имеет преимущество перед методом контурных токов в том случае, когда число уравнений, записанных по первому закону Кирхгофа, меньше числа уравнений, записанных по второму закону Кирхгофа. Если заданная электрическая схема имеет q узлов и р ветвей, то в соответствии со сказанным выше, метод узловых напряжений представляет преимущество при q — 1 < р — q + 1. или, что то же, при 2 (q — 1) < р.
Здесь имеется в виду общий случай, когда число уравнений не сокращается за счет известных контурных токов
или узловых напряжении.
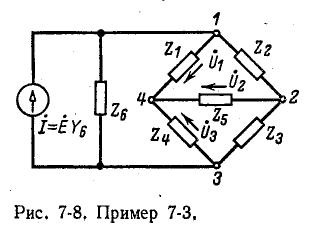
Пример 7-3.
Пользуясь методом узловых напряжений определить ток в диагонали мостовой схемы (см. рис. 7-6).
В результате замены заданного источника э. д. с. .эквивалентным источником тока получается схема (рис. 7-8), содержащая четыре узла. Для этой схемы по первому закону Кирхгофа записывают 4—1 = 3 уравнения (по числу независимых узлов). Если выбрать в данной схеме в качестве базиса узел 4 и направить узловые напряжения к базису, то уравнения примут вид:
для узла 1
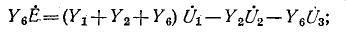
для узла 2
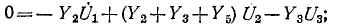
для узла 3
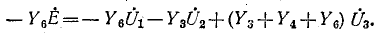
Решение полученной системы уравнений относительно 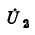 даст
даст
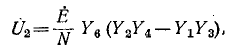
где
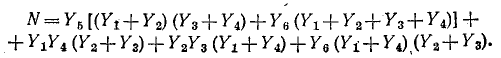
Умножив найденное узловое напряжение 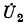 на проводимость
на проводимость 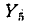 диагональной ветви мостовой схемы и изменив знак в соответствии с выбранным ранее направлением тока
диагональной ветви мостовой схемы и изменив знак в соответствии с выбранным ранее направлением тока 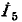 (см. рис. 7,-3), найдем искомый ток:
(см. рис. 7,-3), найдем искомый ток:
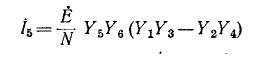
- Метод узловых потенциалов
- Принцип и метод наложения
- Входные и взаимные проводимости
- Преобразование треугольника сопротивлений в эквивалентную звезду
- Электрическая цепь
- Электрический ток
- Электрические цепи постоянного тока
- Методы анализа сложных электрических цепей
Ме́тод узловы́х потенциа́лов — формальный метод расчета электрических цепей путём записи системы линейных алгебраических уравнений, в которой неизвестными являются потенциалы в узлах цепи. В результате применения метода определяются потенциалы во всех узлах цепи, а также, при необходимости, силу тока во всех рёбрах (ветвях).
Введение[править | править код]
Часто необходимым этапом при решении самых разных задач электротехники и электроники является расчет электрической цепи. Под этим термином понимается процесс получения полной информации о напряжениях во всех узлах и о токах во всех рёбрах заданной электрической цепи. Для расчета линейной цепи достаточно записать необходимое число уравнений, которые базируются на правилах Кирхгофа и законе Ома, а затем решить полученную систему уравнений.
Однако на практике записать систему уравнений просто из вида принципиальной электрической схемы удается только для очень простых схем. Если в схеме более десятка элементов или она содержит много взаимосвязанных контуров (участки типа мостов), то для записи, определяющей схему системы уравнений, уже требуются специальные методики. К таким методикам относятся метод узловых потенциалов и метод контурных токов.
Метод узловых потенциалов не привносит ничего нового к правилам Кирхгофа и закону Ома. Данный метод лишь формализует их использование настолько, чтобы их можно было применить к любой, сколь угодно сложной цепи и пригоден для расчёта посредством вычислений на компьютерах. Иными словами, метод даёт ответ на вопрос «как использовать законы для расчета данной цепи?».
Теоретические основы[править | править код]
Если в цепи, состоящей из У узлов и Р рёбер, известны все характеристики звеньев (полные сопротивления R, величины источников ЭДС E и тока J), то возможно вычислить токи Ii во всех рёбрах и потенциалы φi во всех узлах. Поскольку электрический потенциал определён с точностью до произвольного постоянного слагаемого, то потенциал в одном из узлов (назовём его базовым узлом) можно принять равным нулю, а потенциалы в остальных узлах определять относительно базового узла. Таким образом, при расчёте цепи имеем У+Р-1 неизвестных переменных: У-1 узловых потенциалов и Р токов в рёбрах.
Не все из указанных переменных независимы. Например, исходя из закона Ома для участка цепи, токи в звеньях полностью определяются потенциалами в узлах:
С другой стороны, токи в рёбрах однозначно определяют распределение потенциала в узлах относительно базового узла:
Таким образом, минимальное число независимых переменных в уравнениях цепи равно либо числу звеньев, либо числу узлов минус 1, в зависимости от того, какое из этих чисел меньше.
При расчёте цепей чаще всего используются уравнения, записываемые, исходя из правил Кирхгофа. Система состоит из У-1 уравнений по 1-му правилу Кирхгофа (для всех узлов, кроме базового) и К уравнений по 2-му правилу Кирхгофа для каждого независимого контура. Независимыми переменными в уравнениях составленных по правилам Кирхгофа являются токи звеньев. Поскольку согласно формуле Эйлера для плоского графа число узлов, рёбер и независимых контуров связаны соотношением
или
то число уравнений составленных по правилам Кирхгофа равно числу переменных, и система разрешима. Однако число уравнений в системе Кирхгофа избыточно. Одним из методов сокращения числа уравнений является метод узловых потенциалов. Переменными в системе уравнений являются У-1 узловых потенциалов. Уравнения записываются для всех узлов, кроме базового. Уравнения для контуров в системе отсутствуют.
Уравнение для потенциала в узлах[править | править код]

Рис. 1. Фрагмент цепи: узел с примыкающими звеньями
Рассмотрим фрагмент цепи, состоящий из узла и примыкающих к нему звеньев (рис. 1). Согласно 1-му правилу Кирхгофа сумма токов в узле равна нулю:
Ток в звене определим, исходя из закона Ома для участка цепи:
откуда:
Обозначив проводимости рёбер через
получим окончательное уравнение для узла:
Последнее уравнение получено, исходя из предположения, что все источники тока и ЭДС направлены в сторону рассматриваемого узла. Если какой-либо источник направлен в противоположную сторону, его ЭДС или ток необходимо взять с обратным знаком.
Записав последнее уравнение для каждого узла цепи, кроме базового, получим систему уравнений для узловых потенциалов.
Практическое применение[править | править код]
Составление системы уравнений[править | править код]
Перед началом расчёта выбирается один из узлов (базовый узел), потенциал которого считается равным 0. Затем узлы нумеруются, после чего составляется система уравнений.
Уравнения составляются для каждого узла, кроме базового. Слева от знака равенства записывается:
- потенциал рассматриваемого узла, умноженный на сумму проводимостей рёбер, примыкающих к нему (проводимости рёбер, содержащих источники тока, считаются нулевыми и не принимаются в расчёт);
- минус потенциалы узлов, примыкающих к данному, умноженные на проводимости рёбер, соединяющих их с данным узлом. Если узел соединён с данным узлом ребром, содержащим источник тока, этот узел не принимается в расчёт.
Справа от знака равенства записывается:
- сумма всех источников токов, примыкающих к данному узлу;
- сумма произведений всех ЭДС, примыкающих к данному узлу, на проводимость соответствующего звена.
Если источник направлен в сторону рассматриваемого узла, то он записывается со знаком «+», в противном случае — со знаком «−». Не стоит забывать, что проводимость звена с последовательно подключенным идеальным источником тока равна 0.

Рис. 2. Пример электрической схемы
Пример системы уравнений[править | править код]
На схеме (рис. 2) четыре узла. Потенциал в узле 0 принят равным нулю (φ0 = 0). Записываем уравнения для узлов 1, 2 и 3:

где проводимости рёбер равны:
Формальный подход[править | править код]
В матричном виде система уравнений для метода узловых потенциалов выглядит следующим образом[1]:
,
где

- 0, если ребро j не присоединено к узлу i;
- 1, если ребро выходит из узла;
- −1, если ребро входит в узел.
Термины «входит» и «выходит» означает, что для каждого ребра задаётся направление, которое обычно ассоциируется с направлением тока в этом ребре;





Пример системы уравнений[править | править код]
Для схемы рис. 2 матрицы имеют вид:


Перемножаем матрицы в соответствии с матричным уравнением:




Раскрывая матричную запись, получаем следующую систему уравнений:

Ограничения[править | править код]
Метод узловых потенциалов применяется к эквивалентной схеме, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем. Если изначально дана реальная схема, то для неё необходимо составить эквивалентную схему и дальнейший расчет производить с ней. Таким образом, схема, к которой применяется метод узловых потенциалов, не содержит никаких реальных[уточнить] элементов (транзисторов, диодов, ламп, гальванических элементов, пассивных элементов с паразитными параметрами и т. д.).
Примечания[править | править код]
- ↑
Нейман Л. Р., Демирчян К. С. Теоретические основы электротехники: в 2-х т. Учебник для вузов. Том I. — 3-е изд., перераб. и доп. — Л.: Энергоиздат. Ленингр. отд-ние, 1981. — 536 с., ил.
См. также[править | править код]
- Эквивалентная схема
- Источник ЭДС
- Источник тока

При изучении основ электротехники приходится сталкиваться с необходимостью расчета тех или иных параметров различных схем. И самое простое, что приходится делать – это расчет токов ветвей в цепях постоянного тока.
Существует несколько наиболее применяемых методов расчетов для таких цепей: с помощью законов Кирхгофа, методом контурных токов, узловых потенциалов, методом эквивалентного генератора, эквивалентного источника тока, методом наложения. Для расчета более сложных цепей, например, в нелинейных схемах, могут применяться метод аппроксимации, графические методы и другие.
В данном разделе рассмотрим один из методов определения токов в цепи постоянного тока – метод узловых потенциалов.
Важно отличать метод узловых напряжений (потенциалов) от метода узлового напряжения (метод двух узлов).
Метод узловых потенциалов примеры решения задач
Для того, чтобы лучше разобраться в этом вопросе, рассмотрим конкретный пример схемы, показанной на рис.1.

![]()
![]()
![]()
![]()
![]()
Для начала обозначают направления токов в ветвях. Направление можно выбирать любым. Если в результате вычислений какой-то из токов получится с отрицательным значением, значит, его направление в действительности будет направлено в противоположную сторону относительно ранее обозначенного. Если в ветви имеется источник, то для удобства лучше обозначить направление тока в этой ветви совпадающим с направлением источника в этой ветви, хотя и не обязательно. Далее один из узлов схемы заземляем. Заземленный узел будет называться опорным, или базисным. Такой метод заземления на общее токораспределение в схеме влияния не оказывает.
Какой именно узел заземлять, значения не имеет. Заземлим, например, узел 4 φ4 = 0.
Каждый из этих узлов будет обладать своим значением потенциала относительно узла 4. Именно значения этих потенциалов для дальнейшего определения токов и находят. Соответственно, для удобства этим потенциалам присваивают номера в соответствии с номером узла, т.е. φ1, φ2, φ3. Далее составляется система уравнений для оставшихся узлов 1, 2, 3.
В общем виде система имеет вид:

Использованные в этой системе уравнений буквенно-цифровые обозначения
имеют следующий смысл:
![]() – сумма проводимостей ветвей, сходящихся в узле 1. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 1. В данном случае

![]() – сумма проводимостей ветвей, сходящихся в узле 2. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 2. В данном случае

![]() – сумма проводимостей ветвей, сходящихся в узле 3. В данном случае
– сумма проводимостей ветвей, сходящихся в узле 3. В данном случае

![]() – сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 2, взятая со знаком «минус». Для этого единица и взята с отрицательным знаком:

![]() – сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:
– сумма проводимостей ветвей, соединяющих узлы 1 и 3, взятая со знаком «минус». Для этого единица и в этом случае взята с отрицательным знаком:

Аналогично находятся и остальные проводимости:

J11 – узловой ток узла 1, в котором участвуют ветви, подходящие именно к этому узлу, и содержащие в своем составе ЭДС. При этом, если ЭДС ветви, входящий в узел, направлена к рассматриваемому узлу (в данном случае к узлу 1), то такой узловой ток записывается с плюсом, если от узла, то с минусом. В данном случае

Аналогично

В результате всех ранее приведенных вычисленных значений исходная система уравнений примет вид:

Решать данную систему можно всеми доступными методами, мы же для упрощения решим ее в пакете Mathcad:

В результате получены следующие значения потенциалов в узлах цепи:
![]()
Токи в ветвях находятся в соответствии с законом Ома. Поясним это простыми словами.
В ветви с сопротивлением и источником, учитывая ранее обозначенное направление тока в рассматриваемой ветви, необходимо из потенциала узла, находящегося у начала стрелки направления тока, вычесть потенциал узла, находящегося у конца стрелки направления тока, а затем прибавить значение ЭДС в этой ветви. Далее все это разделить на сопротивление, имеющееся в ветви. Если бы ток и ЭДС в рассматриваемой ветви не совпадали по направлению, тогда значение ЭДС вычиталось. В ветви без ЭДС действует то же самое правило, только ЭДС в числителе, разумеется, отсутствует. В нашем примере получим, что


Значение тока первой ветви, как видно из расчета, получилось отрицательным. Значит, в действительности, этот ток направлен в противоположную сторону относительно его обозначенного направления на рис.1.
Правильность расчетов можно проверить, например, составлением баланса мощностей либо, к примеру, моделированием, схемы. Выполним моделирование в программе Multisim.

Как видим, результаты моделирования совпадают с расчетными значениями. Незначительная разница в тысячных долях из-за округлений промежуточных вычислений.
(узловых
потенциалов)
Ещё один метод расчёта цепей – метод
узловых напряжений (метод узловых
потенциалов). В качестве неизвестных
промежуточных величин принимаются
напряжения (или потенциалы) в узлах
схемы.
Рассмотрим схему на рисунке 1.23.

В схеме три узла (не показалось ли вам,
что их четыре?) – обозначенных числами
1, 2, 3. Потенциал каждого узла: φ1,
φ2, φ3. Напряжения между ними:
U12=φ1
– φ2 (напряжение U12 направлено
от узла 1 к узлу 2)
U13 = φ1
– φ3
U23 = φ2
– φ3
В схеме играют роль не сами потенциалы,
а их разность – напряжение. Примем
потенциал одного узла, например 3, равным
нулю – φ3=0. Так часто делается в
электронике – называется «общий провод».
Таким образом, между величиной напряжения
и потенциала нет никакой разницы:
U13= φ1 = U1
U23= φ2 = U2
U3 = φ3 = 0
При расчёте схемы за неизвестные примем
напряже-ния (или потенциалы, что
безразлично) узлов. Число уравнений
такое же, как по первому закону Кирхгофа,
в данном случае – два, так как узлов –
три. Понятно, что если известны два
потенциала, то легко найти и третий.
Искомыми напряжениями будут U1 и
U2.
Для составления уравнений введём новые
понятия.
Собственная проводимость узла
Gii
– сумма про-водимостей всех ветвей,
подключённых к этому узлу. При этом
нужно учитывать проводимости источников
энергии.
Источник ЭДС – R = 0, G = ∞;
Источник тока – R = ∞, G = 0; (G = 1/R)
В данной схеме:
G11 = G1
+ G2 + G3
G22 = G3
+ G4
(проводимость ветви с источником тока
равна нулю)
Общая проводимость двух узлов
Gik
– сумма проводимостей всех ветвей
между двумя узлами.
G12 = G21
= G3
Узел с потенциалом, равным нулю, не
учитывается, поэтому получилась только
одна величина общей проводимости.
Узловой ток Jii
– алгебраическая сумма токов
источников, действующих в ветвях,
подключённых к данному узлу i.
При этом необходимо учитывать знак.
Если ток, вызываемый источником, подтекает
к узлу, то он считается со знаком «плюс»,
а если вытекает из узла – то «минус».
Ток в ветви с источником тока считается
равным Ji. Ток, вызываемый источником
ЭДС равен: Jэкв = E/R = EG.
В данной схеме:
J11 = E2G2
– E1G1
= E2/R2
– E1/R1
J22 = J (источники ЭДС
в ветвях узла 2 отсутствуют)
Составляем систему уравнений.
Коэффициенты при собственных проводимостях
Gii
положительны, при общих проводимостях
Gik –
отрицательны.

Решаем систему уравнений относительно
напряжений.
Теперь определяем токи в ветвях, учитывая
направление узловых напряжений и
источников ЭДС: если направление
источника ЭДС и узлового напряжения
совпадают с направлением тока в ветви,
то оно берётся со знаком «плюс», если
противоположны – со знаком «минус».
I1
= (E1+U1)/R1=
(E1+U1)G1
I2
= (E2 -U1)/R2
= (E2-U1)G2
I3
= (U1-U2)/R3=
(U1
-U2)G3
I4 = U2/R4
= U2G4
I5 = J
– это очевидно
Порядок расчёта методом узловых
напряжений
1) Выбираем направления токов в ветвях;
2)
Выбираем узел, потенциал которого будем
считать нулевым;
3) Для остальных узлов определяем
собственные и
общие проводимости;
4) Определяем узловые токи;
5) Составляем и решаем уравнения;
6) Находим токи в ветвях.
Методы контурных токов и узловых
потенциалов являются основными методами
расчёта сложных цепей. Оба этих метода
получены из законов Кирхгофа и достоинством
их является меньшее число уравнений: в
методе контурных токов их число такое
же, как по второму закону Кирхгофа, а в
методе узловых напряже-ний – такое же,
как по 1-му закону. Исходя из числа
уравнений, и выбирают обычно метод
расчёта.
Если количество уравнений одинаково,
то всё же проще использовать метод
контурных токов. Во-первых, так значительно
легче определить токи после решения
уравнений, во-вторых, – обычно в условии
заданы сопротивления резисторов, а не
их проводимости, что влечёт дополнительные
вычисления при решении методом узловых
напряжений.
Метод
двух узлов
Метод двух узлов является частным
случаем метода узловых напряжений. Как
очевидно из названия, он используется
в схемах, имеющих только два узла –
тогда этот метод будет оптимальным. В
этом случае составляется только одно
уравнение. Для примера рассмотрим схему
на рисунке 1.24.

Считаем нулевым потенциал узла 0. В
данном случае никаких общих проводимостей
нет, есть только собственная проводимость
и узловой ток узла 1.
G11
= G1 +
G2 +
G3 +
G4
J11
= – E1G1
+ J + E2G4
Уравнение: U1G11
= J11
![]()
Затем определяем токи в ветвях. Подсчитайте
для сравнения: сколько уравнений будет
в системе при расчёте схемы методом
контурных токов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #












