Как найти узлы интерполяции – Сайт, где вы сможете решить свои вопросы

Материал из MachineLearning.

Перейти к: навигация, поиск

Содержание

1 Полином в каноническом виде
2 Способ вычисления полинома в точке
3 Анализ метода
- 3.1 Сложность вычислений
- 3.2 Погрешность интерполяции
- 3.3 Выбор узлов интерполяции
4 Вычислительный эксперимент
- 4.1 Пример: Интерполяция синуса
5 Рекомендации программисту
- 5.1 Предварительные настойки
- 5.2 Использование программы
6 Вывод
7 Прикреплённые файлы
8 Литература
9 Смотри также
10 Ссылки

Интерполяция — приближение одной функции другой функцией.

С самого начала хотелось бы заметить, что мы занимаемся интерполяцией функций, а не узлов. Разумеется, интерполяция будет проводиться в конечном числе точек, но выбирать их мы будем сами.

В настоящем исследовании будет изучена проблема интерполяции функции одной переменной полиномом каноническим полиномом, будет рассмотрен вопрос точности приближения, и как, варьируя узлы, через которые пройдёт полином, достигнуть максимальной точности интерполяции.

Полином в каноническом виде

Известно, что любая непрерывная на отрезке [a,b] функция f(x) может быть хорошо приближена некоторым полиномом P_n(x).
Справедлива следующая Теорема (Вейерштрасса): Для любого $eps$ >0 существует полином P_n(x) степени $n=n(eps)$ , такой, что $max_{x in [a,b]}|f(x)-P_n(x)|<eps$

В качестве аппроксимирующей функции выберем полином степени n в каноническом виде:

$f(x)=P_n(x)=c_0+c_1x+c_2x^2+ ldots + c_nx^n$

Коэффициенты полинома $c_i$ определим из условий Лагранжа $P_n(x_i)=y_i$ , $i=1, ldots, n$ , что с учётом предыдущего выражения даёт систему линейных алгебраических уравнений с n+1 неизвестными:

$begin{matrix} c_0 + c_1x_0 + c_2x_0^2 + ldots + c_nx_0^n = y_0 \ c_0 + c_1x_1 + c_2x_1^2 + ldots + c_nx_1^n = y_1 \ ldots ldots ldots ldots ldots \ c_0 + c_1x_n + c_2x_n^2 + ldots + c_nx_n^n = y_n end{matrix}$

Обозначим систему таких уравнений символом (*) и перепишем её следующим образом:

$sum_{p=0}^n c_i^p = y_i, quad i=1, ldots, n$

или в матричной форме: $mathbf{Ac}=mathbf{y},$ где $mathbf{c}$ – вектор-столбец, содержащий неизвестные коэффициенты $c_i$ , $mathbf{y}$ – вектор-столбец, составленный из табличных значений функции $y_i$ , а матрица $mathbf{A}$ имеет вид:

$mathbf{A} = begin{pmatrix} 1 & x_0 & x_0^2 & ldots & x_0^n \ 1 & x_1 & x_1^2 & ldots & x_1^n \ ldots & ldots & ldots & ldots & ldots \ 1 & x_n & x_n^2 & ldots & x_n^n \ end{pmatrix}$

Система линейных алгебраических уравнений (*) относительно неизвестных $c_i$ иметь единственное решение, если определитель матрицы $mathbf{A}$ отличен от нуля.

Определитель матрицы $mathbf{A}$ называют определителем Вандермонда, его можно вычислить по следующей формуле:

$mathbf{detA} = prod_{i,j=0 \ i neq j }^n (x_i - x_j) neq 0$

Число узлов интерполяционного полинома должно быть на единицу больше его степени. Это понятно из интуитивных соображений: через 2 точки можно провести единственную прямую, через 3 – единственную параболу и т.д. Но полином может получиться и меньшей степени. Т.е. если 3 точки лежат на одной прямой, то через них пройдёт единственный полином первой степени (но это ничему не противоречит: просто коэффициент при старшей степени равен нулю).

При достаточной простоте реализации метода он имеет существенный недостаток: число обусловленности матрицы быстро растёт с увеличением числа узлов интерполяции, что можно показать на следующем графике

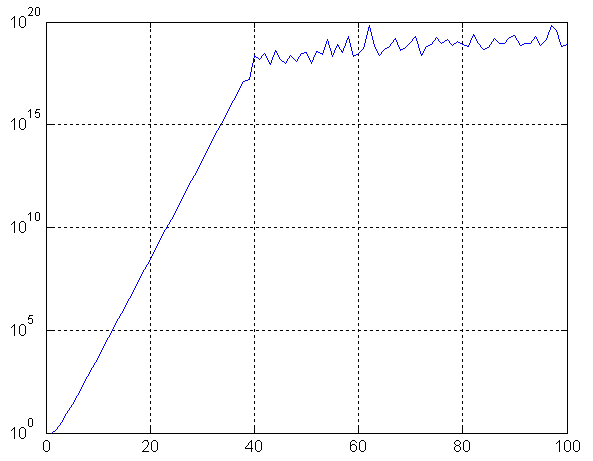
Зависимость числа обусловленности матрицы от количества узлов интерполяции

Из-за плохой обусловленности матрицы рекомендуется применять другие методы интерполяции (например, интерполяция полиномами Лагранжа). При этом важно понимать, что при теоретическом применении различных методов они приводят к одинаковому результату, т.е. мы получим один и тот же полином.

Однако при практической реализации мы получим полиномы различной точности аппроксимации из-за погрешности вычислений аппаратуры.

Способ вычисления полинома в точке

Чтобы изобразить графически аппроксимирующий полином, необходимо вычислить его значение в ряде точек. Это можно сделать следующими способами.

Первый способ. Можно посчитать значение a₁x и сложить с a₀. Далее найти a₂x², сложить с полученным результатом, и так далее. Таким образом, на j-ом шаге вычисляется значение a_jx^j и складывается с уже вычисленной суммой $a_0 + a_1x + ldots + a_{j-1}x^{j-1}$ .

Вычисление значения a_jx^j требует j операций умножения. Т.е. для подсчёта многочлена в заданной точке требуется (1 + 2 + … + n) = n(n+1)/2 операций умножения и n операций сложения. Всего операций в данном случае: Op₁ = n(n+1)/2 + n.

Второй способ. Полином можно также легко вычислить с помощью так называемой схемы Горнера: $P_n(x) = (ldots ((a_nx + a_{n-1})x + a_{n-2})x + ldots)x + a_0$

Для вычисления значения во внутренних скобках a_nx + a_n-1 требуется одна операция умножения и одна операция сложения. Для вычисления значения в следующих скобках (a_nx + a_n-1)x + a_n-2 требуется опять одна операция умножения и одна операция сложения, т.к. a_nx + a_n-1 уже вычислено, и т.д.

Тогда в этом способе вычисление P_n(x) потребует n операций умножения и n операций сложения, т.е. сложность вычислений Op₂ = n+n = 2n.
Ясно, что Op₂ << Op₁.

Анализ метода

Сложность вычислений

Оценка сложности интерполирования функции складывается из количества операций для решения системы линейных алгебраических уравнений (СЛАУ) и нахождения значения полинома в точке.

Сложность решения СЛАУ, например, методом Гаусса для матрицы размера nxn: 2n³/3, т.е. O(n³).

Для нахождения полинома в заданной точке требуется n умножений и n сложений. В результате сложность метода: O(n³).

Погрешность интерполяции

Предположим, что на отрезке интерполирования [a,b] функция f(x) n раз непрерывно-дифференцируема. Погрешность интерполяции складывается из погрешности самого метода и ошибок округления.

Ошибка приближения функции f(x) интерполяционным полиномом n-ой степени P_n(x) в точке x определяется разностью: R_n(x) = f(x) – P_n(x).

Погрешность R_n(x) определяется следующим соотношением:

$R_n(x) = frac{f^{n+1}(xi)}{(n+1)!}omega_n(x)$

Здесь $f^{n+1}(xi)$ – производная (n+1)-го порядка функции f(x) в некоторой точке $xi in [a,b],$ а функция $omega_n(x)$ определяется как

$omega_n(x)=(x-x_0)(x-x_1)ldots (x-x_n).$

Если максимальное значение производной fⁿ⁺¹(x) равно $M_{n+1} = sup_{x in [x_0, x_n]} left| f^{n+1}(x) right| ,$ то для погрешности интерполяции следует оценка: $left| R_n(x) right| = frac{M_{n+1}}{(n+1)!}omega_n(x).$

При реализации данного метода на ЭВМ ошибкой интерполяции E_n(x) будем считать максимальное уклонение полинома от исходной функции на выбранном промежутке: $E_n(x) = max_{x in [a, b]} left| f(x) - P_n(x) right| .$

Выбор узлов интерполяции

Ясно, что от выбора узлов интерполируемой функции напрямую зависит, насколько точно многочлен будет являться её приближением.

Введём следующее определение: полиномом Чебышева называется многочлен вида

T_k(x) = cos(k arccos x), |x|≤1.

Известно (см. ссылки литературы), что если узлы интерполяции x₀, x₁,…,x_n являются корнями полинома Чебышева степени n+1, то величина $max_{x in [a,b]} left| omega_{n+1}(x) right|$ принимает наименьшее возможное значение по сравнению с любым другим выбором набора узлов интерполяции.

Очевидно, что в случае k = 1 функция T₁(x), действительно, является полиномом первой степени, поскольку T₁(x) = cos(arccos x) = x.

В случае k = 2 T₂(x) тоже полином второй степени. Это нетрудно проверить. Воспользуемся известным тригонометрическим тождеством: cos2θ = 2cos²θ – 1, положив θ = arccos x.

Тогда получим следующее соотношение: T₂(x) = 2x² – 1.

С помощью тригонометрического тождества cos(k + 1)θ = 2cosθcoskθ – cos(k – 1) легко показать, что для полиномов Чебышева справедливо реккурентное соотношение:

T_k+1(x) = 2xT_k(x) – T_k-1(x)

При помощи данного соотношения можно получить формулы для полиномов Чебышева любой степени.

Корни полинома Чебышева легко находятя из уравнения: T_k(x) = cos(k arccos x) = 0. Получаем, что уравнение имеет k различных корней, расположенных на отрезке [-1,1]: $x_m = cos frac{2m+1}{2k}pi, , m = 0,1, cdots, k-1,$ которые и следует выбирать в качестве узлов интерполирования.

Нетрудно видеть, что корни на [-1,1] расположены симметрично и неравномерно – чем ближе к краям отрезка, тем корни расположены плотнее. Максимальное значение модуля полинома Чебышева равно 1 и достигается в точках $cos frac{m}{k}pi.$

Если положить $omega_k(x) = frac1{2^{k-1}}T_k(x),$ то для того, чтобы коэффициент при старшей степени полинома ω_k(x) был равен 1, $max_{x in [-1,1]}omega_k(x) = frac1{2^{k-1}}.$

Известно, что для любого полинома p_k(x) степени k с коэффициентом, равным единице при старшей производной верно неравенство $max_{x in [-1,1]}p_k(x) geq frac1{2^{k-1}},$ т.е. полиномы Чебышева являются полиномами, наименее уклоняющимися от нуля.

Вычислительный эксперимент

Для реализации поставленной задачи была написана программа на языке С++, которая по заданной функции приближает её каноническим полиномом. Разумеется, необходимо указать узлы, через которые полином пройдёт, и значения функции в этих узлах.

Далее строится СЛАУ, которая решается методом Гаусса. На выходе получаем коэффициенты для полинома и ошибку аппроксимации.

Как было показано выше, и в чём мы убедимся в дальнейшем, от выбора узлов зависит точность, с которой полином будет приближать функцию.

Пример: Интерполяция синуса

Попробуем интерполировать функцию y = sin(x) на отрезке [1, 8.5]. Выберем узлы интерполяции: {1.1, 2, 4.7, 7.5, 8.5}

Полученный в результате интерполяции полином отображён на рисунке (синим цветом показан график y = sin(x), красным – интерполяционного полинома)

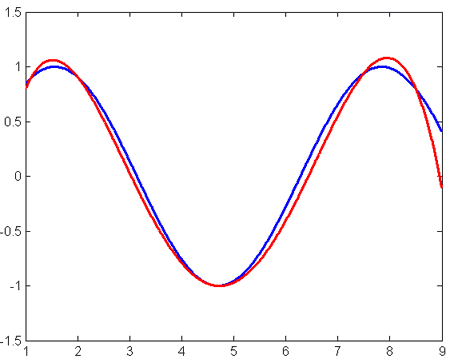
Изображение:Report1-fig2.gif

Ошибка интерполяции в этом случае: 0.1534

Давайте посмотрим, что произойдёт, если выбрать равномерно стоящие узлы {2, 3.5 5, 6.5, 8} для той же функции на том же отрезке.

На отрезке [3, 6] приближение, бесспорно, стало лучше. Однако разброс на краях очень большой. Ошибка интерполяции: 2.3466.

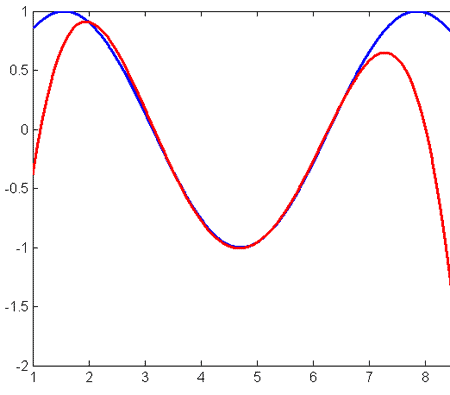
Изображение:Report1-fig3.gif

Наконец, выберем узлы интерполяции в соответствии с Чебышевским алгоритмом. Получим их по следующей формуле (просто сделаем замену переменной):
$x_m = frac{a+b}{2} + frac{b-a}{2}cos frac{pi(2m-1)}{2n}, , m=1,2, cdots, n.$
$y_m = y(x_m)$

В нашем случае [a,b] – отрезок [1, 8.5], y = cosx, n+1 – количество узлов.

Остаётся открытым вопрос, какое количество узлов выбрать.

При значении n меньше 3 ошибка аппроксимации получается более 10.6626.
При n = 4: приближение лучше (ошибка равна 1.0111),
при n = 5: ошибка аппроксимации 0.2797

График функций при n = 4 выглядит следующим образом:

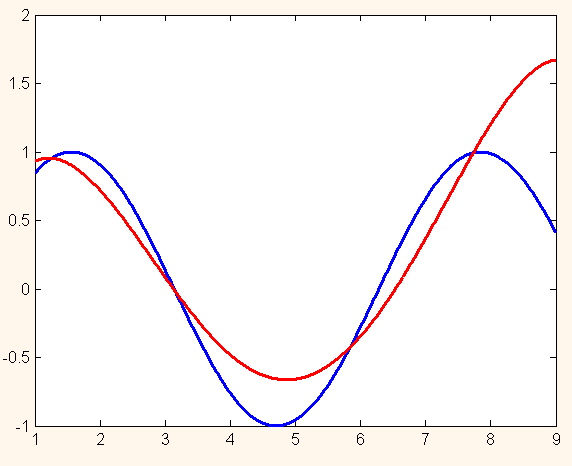
Изображение:Report1-fig4-4pts.gif

Продолжим исследования.

n = 6: ошибка аппроксимации 1.0233.

При n = 7 ошибка аппроксимации принимает наименьшее из полученных ранее значений (для данного промежутка): 0.0181. График синуса (обозначен синим цветом) и аппроксимационного полинома (обозначен красным цветом) представлены на следующем графике:

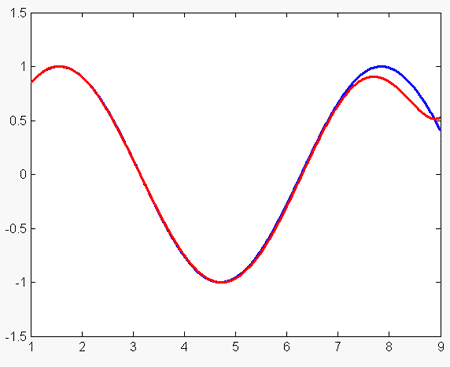
Изображение:Report1-fig4-7pts.gif

Что интересно, если при этом же количестве узлов выбирать их на отрезке [1, 8], то ошибка аппроксимации становится ещё меньше : 0.0124. График в этом случае выглядит так:

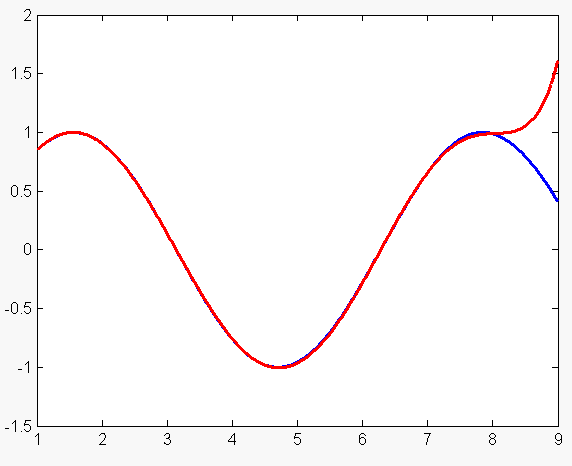
Изображение:Report1-fig4-7-2pts.gif

При выборе большего количества узлов ситуация ухудшается: мы стараемся слишком точно приблизить исходную функцию:

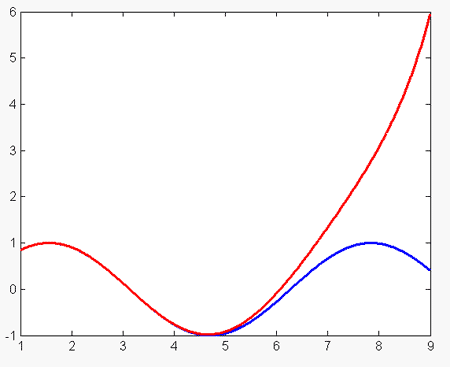
Изображение:Report1-fig4-8pts.gif

Ошибка аппроксимации будет только расти с увеличением числа узлов.

Как видим, наилучшее приближение получается при выборе узлов по методу Чебышева. Однако рекомендаций, какое количество узлов является оптимальным, нет – это определяется только экспериментальным путём.

Вывод

Был исследован и программно реализован метод интерполяции функции каноническим полиномом. В ходе исследований установлено, что ошибка интерполяции получается как из-за ошибок компьютерных вычислений, так и из-за ошибок метода.

Также замечено, что от выбора узлов интерполяции напрямую зависит качество интерполяции. Минимальная ошибка интерполяции достигается при выборе «чебышевских» узлов.

Прикреплённые файлы

Программная реализация на языке С++ (исходный текст) [2.55Кб]

Литература

Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. Численные методы. Изд-во “Лаборатория базовых знаний”. Москва. 2003.
И.С. Березин, Н.П. Жидков. Методы вычислений. Изд. ФизМатЛит. Москва. 1962.
Дж. Форсайт, М.Мальком, К. Моулер. Машинные методы математических вычислений. Изд-во “Мир”. Москва. 1980.

Смотри также

Проблема выбора узлов для интерполяции
Ошибки вычислений
Метод наименьших квадратов
Интерполяционный многочлен Лагранжа
Практикум ММП ВМК, 4й курс, осень 2008

Ссылки

Собрание библиотек Boost

Источник

Алгоритм построения интерполяционного многочлена Ньютона

Для
построения интерполяционного многочлена
Ньютона необходимо вычислить ряд
разделенных разностей, входящих в
интерполяционную формулу Ньютона
(4.2.5). Но на самом деле, наряду с этими
разделенными разностями, придется
вычислить и другие разности, которые
непосредственно в формулу (4.2.5) не входят,
но через которые вычисляются и другие
разности нужные нам. Поместим все
разделенные разности, необходимые для
построения многочлена Ньютона в таблицу.
Приведем такую таблицу для случая
(табл. 4.1).

Таблица 4.1

Интерполяционный
многочлен Ньютона в этом случае примет
вид

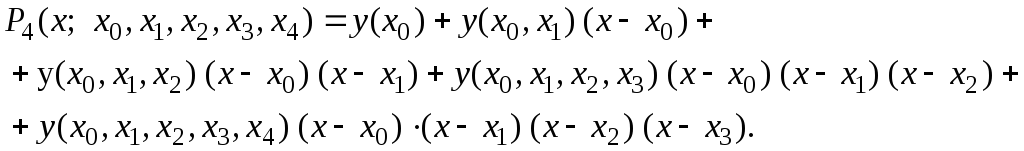
Для
построения интерполяционного многочлена
Ньютона нам понадобятся только
подчеркнутые в табл.4.1 разности, но
вычислять необходимо все. Вести вычисления
следует слева направо. Вначале вычисляются
все разности первого порядка, затем –
второго, и так далее.

Пример

Требуется
построить для функции

интерполяционный многочлен Ньютона
третьего порядка с узлами
.

Требуемый
интерполяционный многочлен Ньютона
имеет вид

Пользуясь
определением, вычислим значения
разделенных разностей и поместим их в
табл. 4.2

Таблица
4.2

Осталось составить
интерполяционный многочлен

Построенный
интерполяционный многочлен в рассмотренном
примере совпал с исходной функцией
.
Это не случайно и непосредственно
следует из единственности интерполяционного
многочлена.

4.3. Кратные узлы интерполяции. Интерполяционный многочлен Эрмита Кратные узлы интерполяции. Формулировка задачи интерполяции с кратными узлами

Иногда
оказываются известными значения функции
в заданных точках и значения ее
производных. Эту дополнительную
информацию можно использовать при
построении интерполяционного многочлена.
В результате чего получается
интерполяционный многочлен Эрмита.

Пусть
заданы табличные значения функции
и ее производных в заданных точках,
причем известными считаются значения

_(4.3.1)

_{…………………………….}

Здесь
,.
Введем величину

.
(4.3.2)

Будем
искать алгебраический многочлен n-й
степени
такой, что

_(4.3.3)

_{………………………………………….…………………………..}

Точки
называютсяузлами
интерполяции,
а искомый многочлен

интерполяционным
многочленом Эрмита.

Если
,
то узелназываетсяпростым,
или однократным,
а если
,
то узелназываетсякратным,
причем величина
называетсякратностью
узла
.

Условия
(4.3.3) называются условиями
интерполяции с кратными узлами.

В
дальнейшем будем использовать для
многочлена Эрмита, наряду с введенным
кратким обозначением, развернутое
обозначение. В нем указываются узлы
интерполяции в качестве параметров,
причем количество повторений узла в
обозначении многочлена Эрмита совпадает
с его кратностью:

.
(4.3.4)

Теорема.
Может
существовать только один многочлен
Эрмита.

Доказательство.
Доказательство
будем вести от противного. Пусть
существуют два разных алгебраических
многочлена n-й
степени
и,
удовлетворяющие условиям интерполяции
(4.3.3). Тогда их разностьбудет представлять собой алгебраический
многочлен степени не вышеn,
не равный тождественно нулю, причем для
него будут выполнены условия

_(4.3.5)

_{………………………………………….…..}

Таким
образом, многочлен
имеетm
корней суммарной кратности
.
Полученное противоречие доказывает
наше утверждение.

Соседние файлы в папке ВМ_УЧЕБНИК

Источник

Мы уже говорили, что сетки могут быть равномерными и неравномерными. Возникает естественный вопрос: существует ли оптимальное распределение узлов на отрезке при интерполяции полиномами? То есть существует ли распределение узлов, при котором погрешность интерполяции полиномами минимальна при фиксированном n?

Отметим, что во многих задачах вычислительной математики введение неравномерной сетки позволяет уменьшить погрешность или сделать ее минимальной. Таким образом в вычислительной математике существует общий прием – введение неравномерной сетки.

Рассмотрим применение этого приема при интерполяции полиномами. Рассмотрим оценку погрешности:

Первые два сомножителя не зависят от .

От зависит третий сомножитель , полином степени . То есть нужно решить задачу:

Если в качестве рассмотреть отрезок , то мы получим задачу, которая решается с помощью полиномов Чебышева. Оптимальным распределением узлов интерполяции на отрезке [-1, 1] являются нули полинома Чебышева .

Полиномы Чебышева определяются следующим образом:

, .

Запишем полиномы Чебышева степени 0 и степени 1: , . Полиномы более высокой степени вычисляются по рекуррентной формуле:

Найдем нули полинома Чебышева степени n:.

, ,

, .

Запишем формулу для нулей полинома Чебышева степени n таким образом, чтобы вычислялись в порядке возрастания:

, .

Точки являются оптимальными узлами сетки размерности n при интерполяции полиномами на отрезке [-1, 1]. Из формулы для нулей полинома Чебышева вытекает, что для любого i, то есть на отрезке [-1, 1] имеет n вещественных корней.

Если интерполирование производится на отрезке [a, b], то линейной заменой переменных

переводим отрезок [a, b] в отрезок [-1, 1].

Отметим два свойства полиномов Чебышева:

1) старший коэффициент равен;

2) – это ортогональные полиномы на отрезке [-1, 1] с весом , т.е.

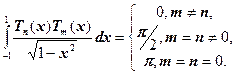
Теорема Чебышева

Из всех полиномов n-й степени со старшим коэффициентом, равным единице, для полинома выполнено неравенство:

то есть полиномы – это полиномы, наименее уклоняющиеся от нуля в равномерной норме на отрезке [-1, 1].

Сформируем два важных утверждения, связанных с оптимальным выбором узлов интерполяции.

Первое утверждение – это оценка погрешности для оптимального распределения узлов. Второе утверждение – это теорема о сходимости интерполяционных полиномов при оптимальном распределении узлов.

Теорема (оценка погрешности)

Если в качестве узлов интерполяции на отрезке [-1, 1] выбраны нули полинома Чебышева степени n + 1, то для интерполяционного полинома , построенного по соответствующей интерполяционной таблице, справедлива оценка погрешности:

Если же интерполяция проводится на отрезке [a, b] и в качестве узлов интерполяции выбраны точки, соответствующие нулям полинома Чебышева на отрезке [-1, 1], то справедлива оценка:

Теорема (о сходимости)

Если функция является непрерывно дифференцируемой на отрезке [–1, 1], то интерполяционный полином , совпадающий с в нулях полинома Чебышева степени n + 1, сходится к при для любой точки x из отрезка [-1, 1].

Практический вывод. Если интерполяция может выполняться с произвольным выбором узлов на отрезке [-1, 1], то целесообразно в качестве узлов выбрать нули полинома Чебышева.

Геометрический смысл. Для отрезка [a, b] точки, соответствующие нулям полинома Чебышева на отрезке[-1, 1], получаются построением на отрезке [a, b] полукруга,

делением этого полукруга на n равных дуг и проецированием середин каждой из дуг на данный отрезок (рис. 5.4). Нули полинома Чебышева сгущаются к концам отрезка.

Кратко остановимся на главных моментах темы интерполяции полиномами.

Если в интерполяционной таблице все различны ( при ), то существует единственный интерполяционный полином, степень которого на единицу меньше, чем размерность интерполяционной таблицы.

Известны разные формы записи одного и того же интерполяционного полинома (форма Лагранжа, форма Ньютона, форма Стирлинга).

Рис. 5.4. Нули полинома Чебышева

Существует оптимальное распределение узлов интерполяции на отрезке [-1,1], а именно нули полинома Чебышева, использование которых для непрерывно дифференцируемых функций обеспечивает сходимость интерполяционных полиномов.

С ростом степени интерполяционного полинома требуется существование у производных все более высокого порядка.

При неоптимальном распределении узлов интерполяции на отрезке [a, b] возможно увеличение погрешности с ростом степени интерполяционного полинома и возникновение осцилляции на концах отрезка.

Объем арифметических действий, необходимых для построения полинома Лагранжа – , полинома Ньютона – . Объем памяти – .

Источник

Макеты страниц

Как мы видели, отклонение от определяется величиной Если о первой величине мы можем иногда сказать, в каких пределах она заключена, то вторую мы можем в некоторых случаях менять по нашему желанию, изменяя точки х. Поставим следующую задачу: как нужно выбрать узлы для того, чтобы была наименьшей. Для ответа на этот вопрос нам придется использовать многочлены Чебышева.

Многочлен Чебышева определяется так:

При

Далее, из тождества

полагяя получим:

Таким образом, действительно являются многочленами, причем коэффициент при старшей степени х равен Из рекуррентной формулы последовательно находим:

как многочлен степени имеет ровно корней. Из следует

Давая значения получим различных корней, причем все они оказываются заключенными между Заметим также, что на отрезке равен 1

и достигается в точках Если в качестве отрезка интерполирования взять и в качестве узлов интерполирования — корни многочлена Чебышева то Покажем, что какой бы многочлен степени со старшим коэффициентом 1 мы ни взяли, Действительно, если бы это было не так, то разность представляла бы собой многочлен степени принимающий в точках попеременно то положительные, то отрицательные значения. Следовательно, он должен иметь по крайней мере корней, что невозможно.

Таким образом, если ограничиться рассмотрением отрезка то будет иметь наименьшее возможное значение при условии, что в качестве узлов интерполирования взяты корни многочлена Чебышева, и в этом случае, наша оценка примет вид

Если интерполирование производится на произвольном отрезке то линейной заменой переменного

его можно перевести в При этом корни многочлена перейдут в

Оценка для этого случая будет такова:

Полученные нами результаты дают наилучшую оценку в целом по всему отрезку Мы воспользовались тем свойством многочленов что для них имеет меньшее значение среди всех многочленов степени с коэффициентом при старшей степени, равным единице. Благодаря этому свойству многочлены получили название многочленов, наименее

отклоняющихся от нуля. Можно поставить и другую задачу: при фиксированных узлах интерполирования изучить, для каких промежутков изменения остаточный член будет принимать большие значения и для каких меньшие. Для решения этой задачи нам нужно изучить поведение функции при фиксированных Многочлен обращается в нуль в точках меняет знак, переходя через каждое из этих значений, и где-то в промежутках между ними принимает попеременно то максимальное, то минимальное значение (рис. 19).

Рис. 19.

Абсолютные значения этих экстремумов будут равны друг другу только в том случае, если являются корнями многочлена

В остальных случаях они будут различны. При интерполировании вблизи больших по абсолютной величине экстремумов можно ожидать большей погрешности, там же, где эти экстремумы будут принимать меньшие значения, следует ожидать меньшей погрешности. Исследование общего случая при произвольном распределении узлов интерполяции довольно затруднительно. Поэтому мы ограничимся случаем равноотстоящих узлов, т. е. будем предполагать, что

Опять введем при помощи соотношения Тогда

и нам следует изучить поведение функции

при различных значениях Прежде всего заметим, что эта функция будет четной или нечетной относительно точки в зависимости от четности Действительно, если произвести замену то получим:

Правая часть этого равенства будет четной функцией если нечетно, и будет нечетной функцией если четно. Далее, заметим, что

Таким образом, если разбить отрезок на части [0, 1], [1, 2], то значение функции в отрезке будет получаться из соответствующего значения функции в предыдущем отрезке путем умножения его на Последний множитель всегда отрицателен при изменении от до Поэтому знаки значений функции будут чередоваться при переходе от одного интервала к следующему. Абсолютная величина этого множителя будет меньше 1 на отрезке Таким образом, экстремальные значения будут убывать по абсолютной величине до середины отрезка и затем в силу симметрии снова возрастать.

Рис. 20.

Вне пределов отрезка функция быстро возрастает по абсолютной величине. Итак, графики функции будут следующих двух типов (рис. 20). Какие же выводы можно сделать о точности интерполирования из приведенного нами анализа? Во-первых, оценка остаточного члена формулы Лагранжа будет особенно велика для значений х, лежащих вне отрезка Поэтому следует

ожидать, что если мы производим вычисления по интерполяционной формуле для значений х, лежащих вне отрезка или, как принято говорить, производим экстраполирование, то погрешности будут очень велики. Во-вторых, при интерполировании для значений х, лежащих не близко к узлам интерполирования, точность будет больше для средних отрезков и меньше для крайних.

Источник

Интерполя́ция алгебраи́ческими многочле́нами функции $f(x)$ действительного аргумента на отрезке $[a,b]$ — нахождение коэффициентов многочлена $P_n(x)$ степени меньшей или равной $n$ , принимающего при значениях аргумента $x_0, x_1, ldots, x_n$ значения $f(x_{i})$ , множество $x_0, x_1, ldots, x_n$ называют узлами интерполяции:

${displaystyle P_{n}(x_{i})=f(x_{i}),quad i=0, 1, ..., n.}$

Система линейных алгебраических уравнений, определяющих коэффициенты $a_{i}$ такого многочлена, имеет вид:

${displaystyle P_{n}(x_{i})=a_{0}+a_{1}x_{i}+a_{2}x_{i}^{2}+ldots +a_{n}x_{i}^{n}=f(x_{i}),quad i=0, 1, ldots , n.}$

Её определителем является определитель Вандермонда.

${displaystyle triangle ={begin{vmatrix}1&x_{0}&x_{0}^{2}&...&x_{0}^{n}\1&x_{1}&x_{1}^{2}&...&x_{1}^{n}\.......\1&x_{n}&x_{n}^{2}&...&x_{n}^{n}end{vmatrix}}=prod _{i,j=0 atop i>j}^{n}(x_{i}-x_{j}).}$

Он отличен от нуля при всяких попарно различных значениях $x_{i}$ , и интерполирование функции $f(x)$ по её значениям в узлах $x_{i}$ с помощью многочлена $P_n(x)$ всегда возможно и единственно.

Применение[править | править код]

Полученную интерполяционную формулу ${displaystyle f(x)approx P_{n}(x)}$ часто используют для приближённого вычисления значений функции $f$ при значениях аргумента $x$ , отличных от узлов интерполирования. При этом различают интерполирование в узком смысле, когда ${displaystyle xin left[a,bright]}$ , и экстраполирование, когда ${displaystyle xnot in left[a,bright]}$ .

Задача интерполяции в пространстве[править | править код]

Пусть в пространстве заданы $n$ точек ${displaystyle P_{1}, P_{2}, dots , P_{n}}$ , которые в некоторой системе координат имеют радиус-векторы ${displaystyle mathbf {r} _{1}, mathbf {r} _{2}, dots , mathbf {r} _{n}.}$

Задача интерполяции состоит в построении кривой, проходящей через указанные точки
в указанном порядке.

Решение задачи[править | править код]

Через фиксированный упорядоченный набор точек можно провести бесконечное число кривых, поэтому задача интерполяции произвольной функцией не имеет единственного решения. Для единственности решения необходимо наложить определённые ограничения на вид функции.

Будем строить кривые в виде ${mathbf {r}}(t)$ , где параметр $t$ изменяется на некотором отрезке $[a, b]$ :

${displaystyle aleq tleq b}$ .

Введем на отрезке ${displaystyle [a,b]}$ сетку ${displaystyle {t_{i}}}$ из $n$ точек:
${displaystyle a=t_{1}<t_{2}<t_{3}<dots <t_{n}=b}$ и потребуем, чтобы при значении параметра
${displaystyle t=t_{i}}$ кривая проходила через точку $P_{i}$ , так что ${displaystyle mathbf {r} (t_{i})=mathbf {r} _{i}.}$

Введение параметризации и сетки может быть выполнено различными способами. Обычно выбирают либо равномерную сетку, полагая
${displaystyle a=0}$ , ${displaystyle b=n-1}$ , ${displaystyle t_{i}=i-1}$ , либо, что более предпочтительно, соединяют точки отрезками и в качестве разности значений параметра ${displaystyle t_{i+1}-t_{i}}$ берут длину отрезка ${displaystyle mathbf {r} _{i+1}-mathbf {r} _{i}}$ .

Одним из распространенных способов интерполяции является использование кривой в виде многочлена от $t$ степени $n-1$ , то есть в виде функции:

${displaystyle mathbf {r} (t)=mathbf {p} ^{(n-1)}(t)=sum _{k=1}^{n}mathbf {a} _{k}t^{n-k}.}$

Многочлен имеет $n$ коэффициентов ${displaystyle mathbf {a} _{k}}$ , которые можно найти из условий:

${displaystyle mathbf {r} (t_{i})=mathbf {r} _{i}.}$

Эти условия приводят к системе линейных уравнений для коэффициентов ${displaystyle mathbf {a} _{k}}$ :

${displaystyle {begin{pmatrix}1&t_{1}&t_{1}^{2}&ldots &t_{1}^{n-1}\1&t_{2}&t_{2}^{2}&ldots &t_{2}^{n-1}\vdots &vdots &vdots &&vdots \1&t_{n}&t_{n}^{2}&ldots &t_{n}^{n-1}end{pmatrix}}{begin{pmatrix}mathbf {a} _{n}\mathbf {a} _{n-1}\vdots \mathbf {a} _{1}end{pmatrix}}={begin{pmatrix}mathbf {r} _{1}\mathbf {r} _{2}\vdots \mathbf {r} _{n}end{pmatrix}}}$

Обратим внимание, что для отыскания коэффициентов, например, в трёхмерном пространстве нужно решить три системы уравнений: для $x$ , $y$ и $z$ координат. Все они имеют одну матрицу коэффициентов, обращая которую по значениям радиус-векторов ${mathbf {r}}_{i}$ точек вычисляются векторы ${displaystyle mathbf {a} _{k}}$ коэффициентов многочлена. Определитель матрицы

${displaystyle W(t_{1},t_{2},ldots ,t_{n})={begin{vmatrix}1&t_{1}&t_{1}^{2}&ldots &t_{1}^{n-1}\1&t_{2}&t_{2}^{2}&ldots &t_{2}^{n-1}\vdots &vdots &vdots &&vdots \1&t_{n}&t_{n}^{2}&ldots &t_{n}^{n-1}end{vmatrix}}=prod _{i,j,i>j}(t_{i}-t_{j})}$

называется определителем Вандермонда. Если узлы сетки не совпадают, он отличен от нуля и система уравнений имеет единственное решение.

Кроме прямого обращения матрицы, имеются несколько других способов вычисления
интерполяционного многочлена. В силу единственности многочлена речь идет о различных формах его записи.

Преимущества[править | править код]

Для заданного набора точек и сетки параметра кривая строится однозначно.
Кривая является интерполяционной, то есть проходит через все заданные точки.
Кривая имеет непрерывные производные любого порядка.

Недостатки[править | править код]

Пример[править | править код]

Интерполяция на последовательности сеток. Пример осцилляций Рунге.

Классическим примером (Рунге), показывающим возникновение осцилляций у интерполяционного многочлена, служит интерполяция на равномерной сетке значений функции
${displaystyle f(x)={frac {1}{1+x^{2}}}.}$

Введем на отрезке ${displaystyle [-5,5]}$ равномерную сетку ${displaystyle x_{i}=-5+(i-1)h}$ ,
${displaystyle h=10/(n-1)}$ , ${displaystyle 1leq ileq n}$ и рассмотрим поведение многочлена
${displaystyle y(x)=sum _{i=1}^{n}a_{i}x^{n-i},}$ который в точках $x_{i}$ принимает значения ${displaystyle y_{i}=1/(1+x_{i}^{2})}$ .

На рисунке представлены графики самой функции (штрих-пунктирная линия) и трех интерполяционных кривых при ${displaystyle n=3,5,9}$ :

интерполяция на сетке ${displaystyle x_{1}=-5,x_{2}=0,x_{3}=5}$ — квадратичная парабола;
интерполяция на сетке ${displaystyle x_{1}=-5,x_{2}=-2.5,x_{3}=0,x_{4}=2.5,x_{5}=5}$ — многочлен четвёртой степени;
интерполяция на сетке ${displaystyle x_{1}=-5,x_{2}=-3.75,x_{3}=-2.5,x_{4}=-1.25,x_{5}=0,x_{6}=1.25,x_{7}=2.5,x_{8}=3.75,x_{9}=5}$ — многочлен восьмой степени.

Значения интерполяционного многочлена даже для гладких функций в промежуточных точках, не совпадающих с узлами интерполяции, могут сильно уклоняться от значений самой функции, такое поведение многочлена называют осцилляциями.

См. также[править | править код]

Интерполяционный многочлен Лагранжа
Интерполяционный многочлен Ньютона
Вейвлет

Источник

Материал из MachineLearning.

Содержание

Полином в каноническом виде

Способ вычисления полинома в точке

Анализ метода

Сложность вычислений

Погрешность интерполяции

Выбор узлов интерполяции

Вычислительный эксперимент

Пример: Интерполяция синуса

Рекомендации программисту

Предварительные настойки

Использование программы

Вывод

Прикреплённые файлы

Литература

Смотри также

Ссылки

Алгоритм построения интерполяционного многочлена Ньютона

4.3. Кратные узлы интерполяции. Интерполяционный многочлен Эрмита Кратные узлы интерполяции. Формулировка задачи интерполяции с кратными узлами

Применение[править | править код]

Задача интерполяции в пространстве[править | править код]

Решение задачи[править | править код]

Преимущества[править | править код]

Недостатки[править | править код]

Пример[править | править код]

См. также[править | править код]

Вам также может понравиться

Метро театральная как найти

Цвет диванов румянцево как найти

Как найти оборот населения

Добавить комментарий Отменить ответ