Как найти в какой четверти альфа

Если посмотреть на числовую окружность, то можно заметить, что оси абсцисс и ординат разбивают ее на четыре части. Эти части называют четвертями и нумеруют в том порядке как их проходят, двигаясь в положительном направлении (против часовой стрелки).

(()(frac{π}{2})(;π))- вторая четверть		((0;)(frac{π}{2})()) – первая четверть
((π;)(frac{3π}{2})()) – третья четверть	(()(frac{3π}{2})(;2π)) – четвертая четверть

Почему так важно определять какой четверти принадлежит угол?

Дело в том, что каждая четверть уникальна в плане знаков тригонометрических функций.

Например, для любого угла из второй четверти – синус положителен, а косинус, тангенс
и котангенс отрицательны. А для любого угла из первой четверти – все четыре функции будут положительны.

Теперь давайте рассмотрим пример задачи, которую не решить без использования знаний про четверти.

Пример (ЕГЭ):

Найдите (sin⁡a), если (cos⁡a=-0,6) и (π<a<)(frac{3π}{2})		Нам известен косинус, а найти нужно синус того же угла. Какая тригонометрическая формула связывает синус и косинус того же угла?  Основное тригонометрическое тождество. Запишем его.
(sin^2⁡a+cos^2⁡a=1)		Подставим известное, и проведем вычисления.
(sin^2⁡a+(-0,6)^2=1) (sin^2⁡a+0,36=1) (sin^2⁡a=0,64)
(sin⁡a=0,8)   или   (sin⁡a=-0,8)		У нас два ответа, и оба нам подходят. Но у угла не может быть два синуса! Один лишний! А какой? Вот тут нам и поможет знание о четвертях: обратите внимание, что у нас в условии есть двойное неравенство  (π<a<) (frac{3π}{2}), то есть угол (a) такой, что больше (π), но меньше (frac{3π}{2}). Значит он лежит в третьей четверти. А в третьей четверти синус отрицателен. Поэтому верный ответ: (-0,8).

Ответ: (sin⁡a=-0,8).

Про непостоянство четвертей:

Важно понимать, что, например, первой четверти принадлежат не только углы от (0) до (frac{π}{2}), но и углы от (2π) до (frac{5π}{2}), и от (4π) до (frac{9π}{2}), и от (6π) до (frac{13π}{2}) и так далее. Ведь как только мы заканчиваем полный оборот – кончается четвертая четверть и опять начинается первая.

Кроме того, нужно помнить, что углы могут откладываться в отрицательную сторону (по часовой стрелке), и тогда мы попадем в первую четверть только в конце круга. Ведь сначала мы пройдем четвертую четверть, потом в третью и т.д.

((-π;-)(frac{3π}{2})())- вторая четверть		((-)(frac{3π}{2})(;-2π)) – первая четверть
((-)(frac{π}{2})(;-π)) – третья четверть	((0;-)(frac{π}{2})()) – четвертая четверть

Ну и, конечно, мы можем в отрицательную сторону делать обороты, так же как и в положительную.

Смотрите также:
Числовая окружность (шпаргалка)
Тригонометрическая таблица с кругом
Как обозначать точки на числовой окружности

Тригонометрия — это раздел математики, в котором изучаются тригонометрические функции, их свойства, взаимосвязи и применение.

Слово «тригонометрия» образовано от греческих слов «trigonom» (треугольник) и «metreo» (измерять).

Возникновение и развитие тригонометрии связаны с практическими потребностями в измерении и вычислении сначала элементов треугольников на местности, а позднее — в строительстве, мореплавании и астрономии. Современная тригонометрия широко применяется в разных областях математики, в частности в геометрии, других науках, в технике. Например, тригонометрические функции используются при решении задач оптики, задач кинематического анализа и синтеза механизмов, гармонического анализа и других.

Cинус, косинус, тангенс, котангенс острого угла прямоугольного треугольника

Нет понятий «просто синус» или «просто косинус», не имеют смысла записи типа «sin» и «cos» сами по себе, они сами по себе никакой величины не обозначают (точно так же, как и, например, значок квадратного корня сам по себе). Те, кто этого не понимает, часто делает грубую ошибку типа: sin x /cos x = in /co

Есть понятие синуса, косинуса, тангенса, котангенса как тригонометрических функций угла. Здесь угол — аргумент функции. Он может обозначаться «х», «а», «альфа», «бета», «гамма», «фи», «дельта» или ещё какой-нибудь буквой. Суть от этого не меняется.

Для того, чтобы более наглядно представить приведенные ниже определения, начертите прямоугольный треугольник. Это треугольник, один из углов которого — прямой (т.е. один из углов равен 90 градусов). Стороны, прилежащие к прямому углу (перпендикулярные друг другу стороны) — это катеты данного прямоугольного треугольника. Противолежащая прямому углу сторона — это гипотенуза.

Теперь выберите любой из двух других (острых) углов треугольника и обозначьте его, например, альфа. Один из катетов будет примыкать к вершине этого угла (и, собственно, образовывать этот угол вместе с гипотенузой). Это — прилежащий катет. Другой катет не примыкает к вершине этого угла, он находится как бы напротив данной вершины. Это — противолежащий катет.

Кстати, почему-то не все представляют, что такое угол треугольника при данной вершине. У треугольника (обозначим его ABC) есть три вершины: А, В и С. Когда говорят об угле А треугольника, то подразумевают угол, образованный сторонами ВА и АС. Это и есть угол при вершине А.

Итак,

Синусом острого угла называется отношение противолежащего этому углу катета к гипотенузе.

Косинусом острого угла называется отношение прилежащего к этому углу катета к гипотенузе.

Тангенсом острого угла называется отношение противолежащего этому углу катета к прилежащему катету.

Котангенсом острого угла называется отношение прилежащего этому углу катета к противолежащему катету.

Секансом острого угла называется отношение гипотенузы к прилежащему к этому углу катету. Обозначается: sec x.

Косекансом острого угла называется отношение гипотенузы к противолежащему этому углу катету. Обозначается: cosec x.

Как найти углы в прямоугольном треугольнике, если известны стороны?

Дан треугольник АВС, угол С — прямой.

Стороны АВ, АС и ВС известны.

Т.к. угол С — прямой, он равен 90 градусам.

Другие углы можно найти, например, так:

если известен катет и гипотенуза

sinA = BC / AB,

sinB = AC / AB,

если известны два катета

tg A = BC / AC

tg B = AC / BC

Предположим, получили, что sin A = ½. По таблице смотрим, что такому значению sin x соответствует величина угла 30 градусов.

Или, к примеру, получили, что tg B = 1. Значит, угол В равен 45 градусов.

Или, к примеру, мы получили, что sin B = 0,259. По таблице Брадиса или с помощью калькулятора находим, что угол В равен 15 градусов.

sin 15° = 0,259

arcsin0,259 = 15°

Как найти углы в прямоугольном треугольнике, если известен один угол?

Поскольку треугольник прямоугольный, то один из его углов равен 90 градусов. Величина второго угла известна (по условию задачи, обозначим её альфа). В сумме углы треугольника составляют 180 градусов. Значит, третий угол равен 180—90—альфа.

Еединичная окружность (единичный круг)

Единичный круг — это круг с центром в начале координат и радиусом, равным единице (R = 1).

Единичная окружность — это окружность единичного круга (т.е. окружность с центром в начале координат и с радиусом, равным единице).

Единичный радиус-вектор — это вектор, начало которого совпадает с началом координат, а его длина равна единице.

Углы отсчитывают от начального положения подвижного радиуса-вектора (совпадает с положением Ох).

Координатные четверти отсчитываются так:

                        y

                       |

                       |

(II четверть)   |   (I четверть)

                       |

________________________ x

                       |0

                       |

(III четверть)  |   (IV четверть)

                       |

                       |

Угол первой четверти — от 0 до 90 градусов (от 0 до пи/2).

Угол второй четверти — от 90 до 180 градусов (от пи/2 до пи).

Угол третьей четверти — от 180 до 270 градусов (от пи до 2пи/3).

Угол четвертой четверти — от 270 до 360 градусов (от 2пи/3 до 2пи).

Например:

• углы первой четверти: 30 градусов, 85 градусов, пи/4;
• углы второй четверти: 120 градусов, 178 градусов;
• углы третьей четверти: 205 градусов, 260 градусов;
• углы четвертой четверти: 272 градуса, 305 градусов.

Тригонометрические функции

К тригонометрическим функциям относятся функции:

y = sin x;

y = cos x;

y = tg x;

y = ctg x;

y = sec x;

y = cosec x.

Синусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его длине.

Косинусом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его длине.

Тангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Оу к его проекции на ось Ох.

Котангенсом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение проекции этого вектора на ось Ох к его проекции на ось Оу.

Секансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Ох.

Косекансом угла, образованного осью Ох и произвольным радиусом-вектором ОА, называется отношение длины этого вектора к его проекции на ось Оу.

Тригонометрические функции связаны между собой, и этим можно воспользоваться для нахождения синуса угла по его косинусу или котангенсу или косинуса угла по его синусу или тангенсу.

Как найти синус угла, если известен косинус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

sin²a = 1 − cos²a

|sin a| = КОРЕНЬ(1 − cos²a)

sin a = ± КОРЕНЬ(1 − cos²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти косинус угла, если известен синус?

Нужно воспользоваться основным тригонометрическим тождеством:

sin²a + cos²a = 1

cos²a = 1 − sin²a

|cos a| = КОРЕНЬ(1 − sin²a)

cos a = ± КОРЕНЬ(1 − sin²a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, косинус положительный в I и IV четвертях)

Как найти синус угла, если известен котангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + ctg² a = 1/sin² a

sin² a = 1 / (1 + ctg² a)

|sin a| = 1/ КОРЕНЬ(1 + ctg² a)

sin a = ±1/ КОРЕНЬ(1 + ctg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (синус положительный в I и II четвертях, котангенс положительный в I и III четвертях)

Как найти косинус угла, если известен тангенс?

Нужно воспользоваться тригонометрическим тождеством

1 + tg² a = 1/cos² a

cos² a = 1 / (1 + tg² a)

|cos a| = 1/ КОРЕНЬ(1 + tg² a)

cos a = ±1/ КОРЕНЬ(1 + tg² a)

знак перед корнем нужно выбрать в соответствии с четвертью данного угла (косинус положительный в I и IV четвертях, тангенс положительный в I и III четвертях)

Тригонометрическое тождество

Тригонометрическим тождеством называется равенство, в которое входят тригонометрические функции и которое удовлетворяется произвольным допустимым значением угла — аргумента тригонометрических функций, но не удовлетворяется, если каждую в отдельности тригонометрическую функцию заменить произвольной величиной.

Основные тригонометрические тождества:

sin²a + cos²a = 1

tg a = sin a / cos a

ctg a = cos a / sin a

sec a = 1 / cos a

cosec a = 1 / sin a

Arcsin, arcos, arctg, arcctg (обратные тригонометрические функции)

• arcsin — читается: арксинус;
• arcos — читается: арккосинус;
• arctg — читается: арктангенс;
• arcctg — читается: арккотангенс.

arcsin, arcos, arctg, arcctg — это обратные тригонометрические функции.

Обратной тригонометрической функцией y = arcsin x называют угол у, взятый на отрезке от –пи/2 до +пи/2, синус которого равен х:

y = arcsin x sin y = x

Обратной тригонометрической функцией y = arccos x называют угол у, взятый на отрезке от –пи до +пи, косинус которого равен х:

y = arccos x cos y = x

Обратной тригонометрической функцией y = arctg x называют угол у, взятый на промежутке от –пи/2 до +пи/2 (исключая концы), тангенс которого равен х:

y = arctg x tg y = x

Обратной тригонометрической функцией y = arcctg x называют угол у, взятый на промежутке от 0 до пи (исключая концы), котангенс которого равен х:

y = arctg x tg y = x

Например,

sin 30° = 0,5

arcsin0,5 = 30°

Синусоида и косинусоида

График функции y = sin x называется синусоидой.

График функции y = cos x называется косинусоидой.

Источники информации:

• Справочник по элементарной математике. Геометрия, тригонометрия, векторная алгебра. Под редакцией П.Ф. Фильчакова. —К.: Наукова думка, 1967. — 442 с.
• В.Д. Гетманцев, О.Ф. Саушкiн. Математика: Тригонометрiя: Посiбник для слухачiв пiдотовчих вiддiлень, вступникiв до вищих навчальних закладiв, студентiв педагогiчних iнститутiв (на укр.). —К.: Либiдь, 1994. — 144 с.
• docme.ru — зачем нужна тригонометрия?
• ru.wikipedia.org — Википедия — тригонометрия;
• ru.wikihow.com — как изучать тригонометрию?

        В прошлом уроке мы с вами успешно освоили (или повторили — кому как) ключевые понятия всей тригонометрии. Это тригонометрический круг, угол на круге, синус и косинус этого угла, а также освоили знаки тригонометрических функций по четвертям. Освоили подробно. На пальцах, можно сказать.

        Но этого пока мало. Для успешного практического применения всех этих простых понятий нам необходим ещё один полезный навык. А именно — правильная работа с углами в тригонометрии. Без этого умения в тригонометрии — никак. Даже в самых примитивных примерах. Почему? Да потому, что угол — ключевая действующая фигура во всей тригонометрии! Нет, не тригонометрические функции, не синус с косинусом, не тангенс с котангенсом а именно сам угол. Нет угла — нету и тригонометрических функций, да…

        Как правильно работать с углами на круге? Для этого нам надо железно усвоить два пункта.

        1) Как отсчитываются углы на круге?

        2) В чём они считаются (измеряются)?

        Ответ на первый вопрос — и есть тема сегодняшнего урока. С первым вопросом мы детально разберёмся прямо здесь и сейчас. Ответ на второй вопрос здесь не дам. Ибо достаточно развёрнутый он. Как и сам второй вопрос очень скользкий, да.) Вдаваться в подробности пока не буду. Это — тема следующего отдельного урока.

        Приступим?

Как отсчитываются углы на круге? Положительные и отрицательные углы.

        У прочитавших название параграфа, возможно, уже волосы встали дыбом. Как так?! Отрицательные углы? Разве такое вообще возможно?

        К отрицательным числам мы с вами уже попривыкли. На числовой оси их изображать умеем: справа от нуля положительные, слева от нуля отрицательные. Да и на градусник за окном поглядываем периодически. Особенно зимой, в мороз.) И денежки на телефоне в “минус” (т.е. долг) иногда уходят. Это всё знакомо.

        А что же с углами? Оказывается, отрицательные углы в математике тоже бывают! Всё зависит от того, как отсчитывать этот самый угол… нет, не на числовой прямой, а на числовой окружности! То бишь, на круге. Круг — вот он, аналог числовой прямой в тригонометрии!

        Итак, как же отсчитываются углы на круге? Ничего не поделать, придётся нам для начала этот самый круг нарисовать.

        Я нарисую вот такую красивую картинку:

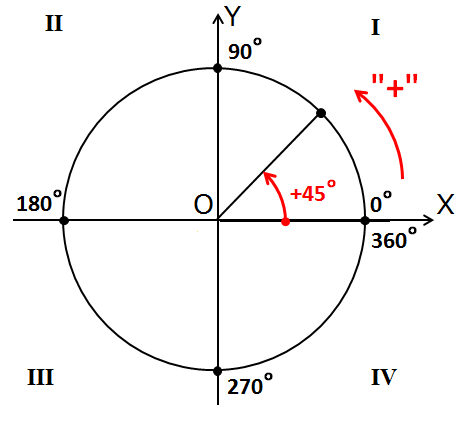
        Она очень похожа на картинки из прошлого урока. Есть оси, есть окружность, есть угол. Но есть и новая информация.

        Во-первых, я добавил номера четвертей (или квадрантов). Напоминаю, что четверти всегда нумеруются против часовой стрелки.

        Также я добавил циферки 0°, 90°, 180°, 270° и 360° на осях. Вот это уже поинтереснее.) Что это за циферки? Правильно! Это значения углов, отсчитанные от нашей неподвижной стороны, которые попадают на координатные оси. Вспоминаем, что неподвижная сторона угла у нас всегда крепко-накрепко привязана к положительной полуоси ОХ. И любой угол в тригонометрии отсчитывается именно от этой полуоси. Это базовое начало отсчёта углов надо держать в голове железно. А оси — они же под прямым углом пересекаются, верно? Вот и прибавляем по 90° в каждой четверти.

        И ещё добавлена красная стрелочка. С плюсом. Красная — это специально, чтобы в глаза бросалась. И в память хорошенько врезалась. Ибо это надо запомнить надёжно.) Что же означает эта стрелочка?

        Так вот оказывается, если наш угол мы будем крутить по стрелочке с плюсом (против часовой стрелки, по ходу нумерации четвертей), то угол будет считаться положительным! В качестве примера на рисунке показан угол +45°. Кстати, обратите внимание, что осевые углы 0°, 90°, 180°, 270° и 360° также отмотаны именно в плюс! По красной стрелочке.

        А теперь посмотрим на другую картинку:

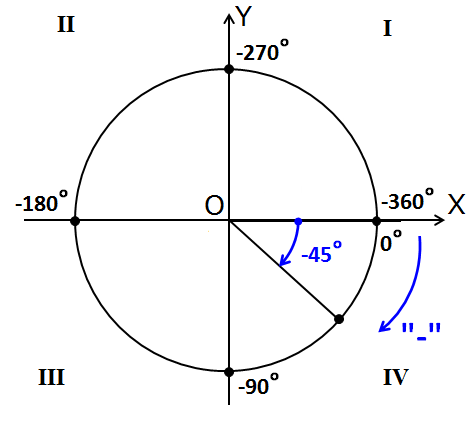
        Здесь почти всё то же самое. Только углы на осях пронумерованы в обратную сторону. По часовой стрелке. И имеют знак “минус”.) Ещё нарисована синяя стрелочка. Также с минусом. Эта стрелочка — направление отрицательного отсчёта углов на круге. Она нам показывает, что, если мы будем откладывать наш угол по ходу часовой стрелки, то угол будет считаться отрицательным. Для примера я показал угол -45°.

        Кстати, прошу заметить, что нумерация четвертей никогда не меняется! Неважно, в плюс или в минус мы мотаем углы. Всегда строго против часовой стрелки.)

        Запоминаем:

        1. Начало отсчёта углов — от положительной полуоси ОХ. По часам — “минус”, против часов — “плюс”.

        2. Нумерация четвертей всегда против часовой стрелки вне зависимости от направления исчисления углов.

        Кстати говоря, подписывать углы на осях 0°, 90°, 180°, 270°, 360°, каждый раз рисуя круг — вовсе не обязаловка. Это чисто для понимания сути сделано. Но эти циферки обязательно должны присутствовать в вашей голове при решении любой задачи по тригонометрии. Почему? Да потому, что эти элементарные знания дают ответы на очень многие другие вопросы во всей тригонометрии! Самый главный вопрос — в какую четверть попадает интересующий нас угол? Хотите верьте, хотите нет, но правильный ответ на этот вопрос решает львиную долю всех остальных проблем с тригонометрией. Этим важным занятием (распределением углов по четвертям) мы займёмся в этом же уроке, но чуть позже.

        Величины углов, лежащих на осях координат (0°, 90°, 180°, 270° и 360°), надо запомнить! Запомнить накрепко, до автоматизма. Причём как в плюс, так и в минус.

        А вот с этого момента начинаются первые сюрпризы. И вместе с ними и каверзные вопросы в мой адрес, да…) А что будет, если отрицательный угол на круге совпадёт с положительным? Выходит, что одну и ту же точку на круге можно обозначить как положительным углом, так и отрицательным???

        Совершенно верно! Так и есть.) Например, положительный угол +270° занимает на круге то же самое положение, что и отрицательный угол -90°. Или, например, положительный угол +45° на круге займёт то же самое положение, что и отрицательный угол -315°.

        Смотрим на очередной рисунок и всё видим:

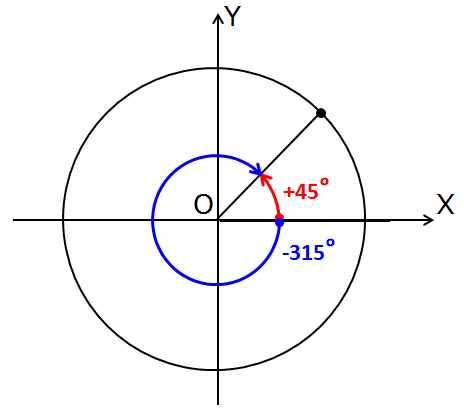
        Точно так же положительный угол +150° попадёт туда же, куда и отрицательный угол -210°, положительный угол +230° — туда же, куда и отрицательный угол -130°. И так далее…

        И что теперь делать? Как именно считать углы, если можно и так и сяк? Как правильно?

        Ответ: по-всякому правильно! Ни одно из двух направлений отсчёта углов математика не запрещает. А выбор конкретного направления зависит исключительно от задания. Если в задании ничего не сказано прямым текстом про знак угла (типа “определите наибольший отрицательный угол” и т.п.), то работаем с наиболее удобными нам углами.

        Конечно, например, в таких крутых темах, как тригонометрические уравнения и неравенства направление исчисления углов может колоссально влиять на ответ. И в соответствующих темах мы эти подводные камни рассмотрим.

        Запоминаем:

        Любую точку на круге можно обозначить как положительным, так и отрицательным углом. Любым! Каким хотим.

        А теперь призадумаемся вот над чем. Мы выяснили, что угол 45° в точности совпадает с углом -315°? Как же я узнал про эти самые 315°? Не догадываетесь? Да! Через полный оборот.) В 360°. У нас есть угол 45°. Сколько не хватает до полного оборота? Отнимаем 45° от 360° — вот и получаем 315°. Мотаем в отрицательную сторону — и получаем угол -315°. Всё равно непонятно? Тогда смотрим на картинку выше ещё раз.

        И так надо поступать всегда при переводе положительных углов в отрицательные (и наоборот) — рисуем круг, отмечаем примерно заданный угол, считаем, сколько градусов не хватает до полного оборота, и мотаем получившуюся разность в противоположную сторону. И всё.)

        Чем ещё интересны углы, занимающие на круге одно и то же положение, как вы думаете? А тем, что у таких углов совершенно одинаковые синус, косинус, тангенс и котангенс! Всегда!

        Например:

        sin45° = sin(-315°)

        cos120° = cos(-240°)

        tg249° = tg(-111°)

        ctg333° = ctg(-27°)

        И так далее и тому подобное. В общем, вы поняли… Кстати, прошу заметить, что углы в этих парочках различны. Зато тригонометрические функции у них — одинаковы! Идея ясна?

        А вот это уже крайне важно! Зачем? Да всё за тем же!) Для упрощения выражений. Ибо упрощение выражений — ключевая процедура успешного решения любых заданий по математике. И по тригонометрии в том числе.

        Итак, с общим правилом отсчёта углов на круге разобрались. Ну а коли мы тут заикнулись про полные обороты, про четверти, то пора бы уже покрутить и порисовать эти самые углы. Порисуем?)

        Начнём пока с положительных углов. Они попроще в рисовании будут.

Рисуем углы в пределах одного оборота (между 0° и 360°).

        Нарисуем, например, угол 60°. Тут всё просто, никаких заморочек. Рисуем координатные оси, круг. Можно прямо от руки, безо всякого циркуля и линейки. Рисуем схематично: у нас не черчение с вами. Никаких ГОСТов соблюдать не надо, не накажут.)

        Можно (для себя) отметить значения углов на осях и указать стрелочку в направлении против часов. Ведь мы же в плюс откладывать собираемся?) Можно этого и не делать, но в голове держать всяко надо.

        И теперь проводим вторую (подвижную) сторону угла. В какой четверти? В первой, разумеется! Ибо 60 градусов — это строго между 0° и 90°. Вот и рисуем в первой четверти. Под углом примерно 60 градусов к неподвижной стороне. Как отсчитать примерно 60 градусов без транспортира? Легко! 60° — это две трети от прямого угла! Делим мысленно первую чертвертинку круга на три части, забираем себе две трети. И рисуем… Сколько у нас там по факту получится (если приложить транспортир и померить) — 55 градусов или же 64 — неважно! Важно, что всё равно где-то около 60°.

        Получаем картинку:

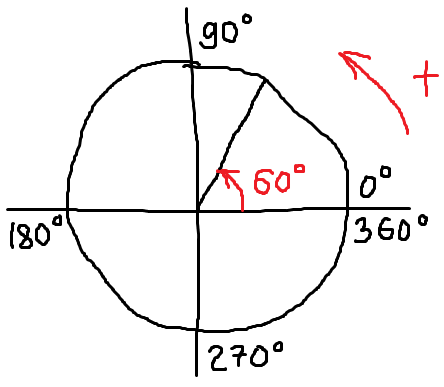
        Вот и всё. И инструментов не понадобилось. Развиваем глазомер! В задачах по геометрии пригодится.) Этот неказистый рисунок бывает незаменим, когда надо нацарапать круг и угол на скорую руку, не особо задумываясь о красоте. Но при этом нацарапать правильно, без ошибок, со всей необходимой информацией. Например, как вспомогательное средство при решении тригонометрических уравнений и неравенств.

        Нарисуем теперь угол, например, 265°. Прикидываем, где он может располагаться? Ну, ясное дело, что не в первой четверти и даже не во второй: они на 90 и на 180 градусов оканчиваются. Можно сообразить, что 265° – это 180° плюс ещё 85°. То есть, к отрицательной полуоси ОХ (там, где 180°) надо добавить примерно 85°. Или, что ещё проще, догадаться, что 265° не дотягивает до отрицательной полуоси OY (там, где 270°) каких-то несчастных 5°. Одним словом, в третьей четверти будет этот угол. Очень близко к отрицательной полуоси OY, к 270 градусам, но всё-таки в третьей!

        Рисуем:

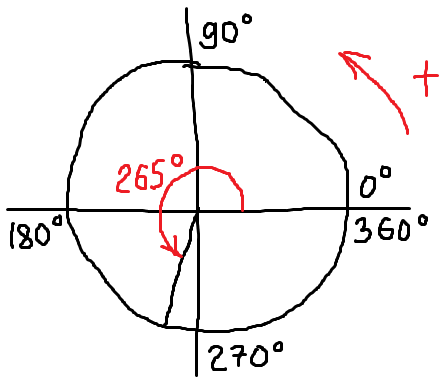
        Повторюсь, абсолютная точность здесь не требуется. Пускай в реальности этот угол получился, скажем 263 градуса. Но на самый главный вопрос (какая четверть?) мы ответили безошибочно. Почему этот вопрос самый главный? Да потому, что любая работа с углом в тригонометрии (неважно, будем мы рисовать этот угол или не будем) начинается с ответа именно на этот вопрос! Всегда. Если этот вопрос проигнорировать или пробовать на него ответить мысленно, то ошибки почти неизбежны, да… Оно вам надо?

        Запоминаем:

        Любая работа с углом (в том числе и рисование этого самого угла на круге) всегда начинается с определения четверти, в которую попадает этот угол.

        Теперь, я надеюсь, вы уже безошибочно изобразите углы, например, 182°, 88°, 280°. В правильных четвертях. В третьей, первой и четвёртой, если что…)

        Четвёртая четверть заканчивается углом 360°. Это один полный оборот. Ясен перец, что этот угол занимает на круге то же самое положение, что и 0° (т.е. начало отсчёта). Но углы на этом не заканчиваются, да…

Что делать с углами, большими 360°?

        “А такие разве бывают?” — спросите вы. Бывают, ещё как! Бывает, например, угол 444°. А бывает, скажем, угол 1000°. Всякие углы бывают.) Просто визуально такие экзотические углы воспринимаются чуть сложнее, чем привычные нам углы в пределах одного оборота. Но рисовать и просчитывать такие углы тоже надо уметь, да.

        Для правильного рисования таких углов на круге необходимо всё то же самое — выяснить, в какую четверть попадает интересующий нас угол. Здесь умение безошибочно определять четверть куда более важно, чем для углов от 0° до 360°! Сама процедура определения четверти усложняется всего одним шагом. Каким, скоро увидите.

        Итак, например, нам надо выяснить, в какую четверть попадает угол 444°. Начинаем крутить. Куда? В плюс, разумеется! Угол-то нам дали положительный! +444°. Крутим, крутим… Крутанули на один оборот — дошли до 360°.

        Ну и крутим себе дальше!

        Сколько там осталось до 444°? Считаем оставшийся хвостик:

        444°-360° = 84°.

        Итак, 444° – это один полный оборот (360°) плюс ещё 84°. Очевидно, это первая четверть. Итак, угол 444° попадает в первую четверть. Полдела сделано.

        Осталось теперь изобразить этот угол. Как? Очень просто! Делаем один полный оборот по красной (плюсовой) стрелке и добавляем ещё 84°.

        Вот так:

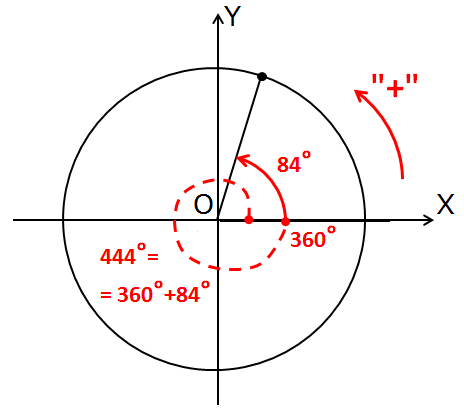
        Здесь я уж не стал загромождать рисунок — подписывать четверти, рисовать углы на осях. Это всё добро уже давно в голове быть должно.)

        Зато я “улиткой” или спиралькой показал, как именно складывается угол 444° из углов 360° и 84°. Пунктирная красная линия — это один полный оборот. К которому дополнительно прикручиваются 84° (сплошная линия). Кстати, обратите внимание, что, если этот самый полный оборот отбросить, то это никак не повлияет на положение нашего угла!

        А вот это важно! Положение угла 444° полностью совпадает с положением угла 84°. Никаких чудес нет, так уж получается.)

        А можно ли отбросить не один полный оборот, а два или больше?

        А почему — нет? Если угол здоровенный, то не просто можно, а даже нужно! Угол-то не изменится! Точнее, сам-то угол по величине, конечно же, изменится. А вот его положение на круге — никак нет!) На то они и полные обороты, что сколько экземпляров ни добавляй, сколько ни убавляй, всё равно будешь в одну и ту же точку попадать. Приятно, правда?

        Запоминаем:

        Если к углу прибавить (отнять) любое целое число полных оборотов, положение исходного угла на круге НЕ изменится!

        Например:

        В какую четверть попадает угол 1000°?

        Никаких проблем! Считаем, сколько полных оборотов сидит в тысяче градусов. Один оборот — это 360°, ещё один — уже 720°, третий – 1080°… Стоп! Перебор! Значит, в угле 1000° сидит два полных оборота. Выбрасываем их из 1000° и считаем остаток:

        1000° – 2·360° = 280°

        Значит, положение угла 1000° на круге то же самое, что и у угла 280°. С которым работать уже гораздо приятнее.) И куда же попадает этот угол? В четвёртую четверть он попадает: 270° (отрицательная полуось OY) плюс ещё десяточка.

        Рисуем:

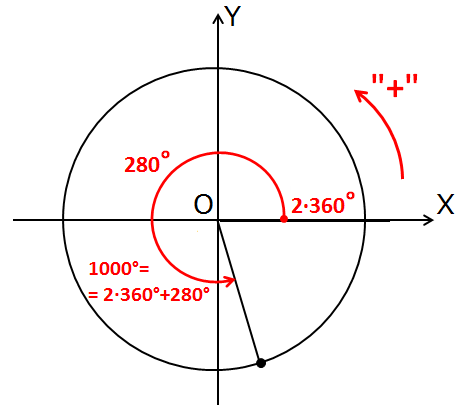
        Здесь я уже не рисовал пунктирной спиралькой два полных оборота: уж больно длинная она получается. Просто нарисовал оставшийся хвостик от нуля, отбросив все лишние обороты. Как будто бы их и не было вовсе.)

        И ещё раз. По-хорошему, углы 444° и 84°, а также 1000° и 280° — разные. Но для синуса, косинуса, тангенса и котангенса эти углы — одинаковые!

        Как вы видите, для того чтобы работать с углами, большими 360°, надо определить, сколько полных оборотов сидит в заданном большом угле. Это и есть тот самый дополнительный шаг, который обязательно надо предварительно проделывать при работе с такими углами. Ничего сложного, правда?

        Отбрасывание полных оборотов, конечно, занятие приятное.) Но на практике при работе с совсем уж кошмарными углами случаются и затруднения.

        Например:

        В какую четверть попадает угол 31240° ?

        И что же, будем много-много раз прибавлять по 360 градусов? Можно, если не горит особо. Но мы же не только складывать можем.) Ещё и делить умеем!

        Вот и поделим наш большущий угол на 360 градусов!

        Этим действием мы как раз и узнаем, сколько полных оборотов запрятано в наших 31240 градусах. Можно уголком поделить, можно (шепну на ушко :)) на калькуляторе.)

        Получим 31240:360 = 86,777777….

        То, что число получилось дробным — не страшно. Нас же только целые обороты интересуют! Стало быть, до конца делить и не надо.)

        Итак, в нашем лохматом угле сидит аж 86 полных оборотов. Ужас…

        В градусах это будет 86·360° = 30960°

        Вот так. Именно столько градусов можно безболезненно выкинуть из заданного угла 31240°. Останется:

        31240° – 30960° = 280°

        Всё! Положение угла 31240° полностью идентифицировано! Там же, где и 280°. Т.е. четвёртая четверть.) Кажется, мы уже изображали этот угол ранее? Когда угол 1000° рисовали?) Там мы тоже на 280 градусов вышли. Совпадение.)

        Итак, мораль сей басни такова:

        Если нам задан страшный здоровенный угол, то:

        1. Определяем, сколько полных оборотов сидит в этом угле. Для этого делим исходный угол на 360 и отбрасываем дробную часть.

        2. Считаем, сколько градусов в полученном количестве оборотов. Для этого умножаем число оборотов на 360.

        3. Отнимаем эти обороты от исходного угла и работаем с привычным углом в пределах от 0° до 360°.

Как работать с отрицательными углами?

        Не вопрос! Точно так же, как и с положительными, только с одним единственным отличием. Каким? Да! Крутить углы надо в обратную сторону, в минус! По ходу часовой стрелки.)

        Нарисуем, например, угол -200°. Сначала всё как обычно для положительных углов — оси, круг. Ещё синюю стрелочку с минусом изобразим да углы на осях по-другому подпишем. Их, естественно, также придётся отсчитывать в отрицательном направлении. Это будут всё те же самые углы, шагающие через 90°, но отсчитанные в обратную сторону, в минус: 0°, -90°, -180°, -270°, -360°.

        Картинка станет вот такой:

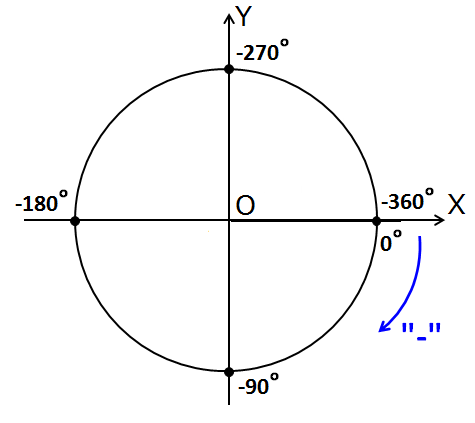
        При работе с отрицательными углами часто возникает чувство лёгкого недоумения. Как так?! Получается, что одна и та же ось — это одновременно, скажем, и +90° и -270°? Неее, что-то тут нечисто…

        Да всё чисто и прозрачно! Мы ведь же уже в курсе, что любую точку на круге можно обозвать как положительным углом, так и отрицательным! Совершенно любую. В том числе и на какой-то из координатных осей. В нашем случае нам нужно отрицательное исчисление углов. Вот и отщёлкиваем в минус все углы.)

        Теперь нарисовать правильно угол -200° никакого труда не составляет. Это -180° и минус ещё 20°. Начинаем мотать от нуля в минус: четвёртую четверть пролетаем, третью тоже мимо, доходим до -180°. Куда мотать оставшуюся двадцатку? Да всё туда же! По часам.) Итого угол -200° попадает во вторую четверть.

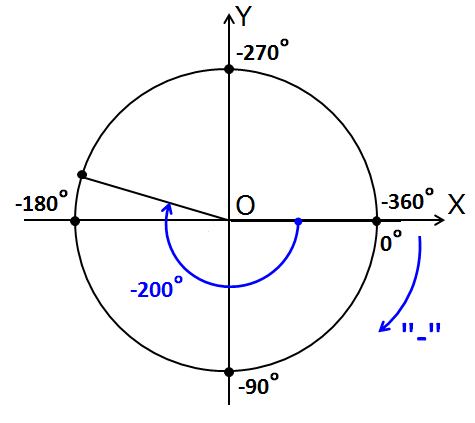
        Теперь вы понимаете, насколько важно железно помнить углы на осях координат?

        Углы на осях координат (0°, 90°, 180°, 270°, 360°) надо помнить именно для того, чтобы безошибочно определять четверть, куда попадает угол!

        А если угол большой, с несколькими полными оборотами? Ничего страшного! Какая разница, куда эти самые полные обороты крутить — в плюс или в минус? Точка-то на круге не изменит своего положения!

        Например:

        В какую четверть попадает угол -2000°?

        Всё то же самое! Для начала считаем, сколько полных оборотов сидит в этом злом угле. Чтобы не косячить в знаках, оставим минус пока в покое и просто поделим 2000 на 360. Получим 5 с хвостиком. Хвостик нас пока не волнует, его чуть позже сосчитаем, когда рисовать угол будем. Считаем пять полных оборотов в градусах:

        5·360° = 1800°

        Воот. Именно столько лишних градусов можно смело выкинуть из нашего угла без ущерба для здоровья.

        Считаем оставшийся хвостик:

        2000° — 1800° = 200°

        А вот теперь можно и про минус вспомнить.) Куда будем мотать хвостик 200°? В минус, конечно же! Нам же отрицательный угол задан.)

        -2000° = -1800° – 200°

        Вот и рисуем угол -200°, только уже без лишних оборотов. Только что его рисовали, но, так уж и быть, накалякаю ещё разок. От руки.

        Ясен перец, что и заданный угол -2000°, так же как и -200°, попадает во вторую четверть.

        Итак, мотаем себе на кру… пардон… на ус:

        Если задан очень большой отрицательный угол, то первая часть работы с ним (поиск числа полных оборотов и их отбрасывание) та же самая, что и при работе с положительным углом. Знак “минус” на данном этапе решения не играет никакой роли. Учитывается знак лишь в самом конце, при работе с углом, оставшимся после удаления полных оборотов. 

        Как видите, рисовать отрицательные углы на круге ничуть не сложнее, чем положительные.

        Всё то же самое, только в другую сторону! По часам!

        А вот теперь — самое интересное! Мы рассмотрели положительные углы, отрицательные углы, большие углы, маленькие — полный ассортимент. Также мы выяснили, что любую точку на круге можно обозвать положительным и отрицательным углом, отбрасывали полные обороты… Нету никаких мыслей? Должно отложиться…

        Да! Какую точку на круге ни возьми, ей будет соответствовать бесконечное множество углов! Больших и не очень, положительных и отрицательных — всяких! И разница между этими углами будет составлять целое число полных оборотов. Всегда! Так уж тригонометрический круг устроен, да…) Именно поэтому обратная задача — найти угол по известным синусу/косинусу/тангенсу/котангенсу — решается неоднозначно. И куда сложнее. В отличие от прямой задачи — по заданному углу найти весь набор его тригонометрических функций. И в более серьёзных темах тригонометрии (арки, тригонометрические уравнения и неравенства) мы с этой фишкой будем сталкиваться постоянно. Привыкаем.)

        Итак, будем считать, что самые-самые азы работы с углами на круге мы с вами освоили. Можно и на вопросы поотвечать. Самостоятельно.)

        1. В какую четверть попадает угол -345°?

        2. В какую четверть попадает угол 666°?

        3. В какую четверть попадает угол 5555°?

        4. В какую четверть попадает угол -3700°?

        Всё хорошо? Поехали дальше.

        5. Какой знак имеет cos999°?

        6. Какой знак имеет ctg999°?

        И это получилось? Прекрасно! Есть проблемы? Тогда вам сюда.

        Ответы:

        1. 1

        2. 4

        3. 2

        4. 3

        5. “+”

        6. “-“

        В этот раз ответы выданы по порядку в нарушение традиций. Ибо четвертей всего четыре, а знаков так и вовсе два. Особо не разбежишься…)

        В следующем уроке мы с вами поговорим про радианы, про загадочное число “пи”, научимся легко и просто переводить радианы в градусы и обратно. И с удивлением обнаружим, что даже этих простых знаний и навыков нам будет уже вполне достаточно для успешного решения многих нетривиальных задачек по тригонометрии!

Знаки тригонометрических функций

5 ноября 2011

• Знаки триг. функций

Знак тригонометрической функции зависит исключительно от координатной четверти, в которой располагается числовой аргумент. В прошлый раз мы учились переводить аргументы из радианной меры в градусную (см. урок «Радианная и градусная мера угла»), а затем определять эту самую координатную четверть. Теперь займемся, собственно, определением знака синуса, косинуса и тангенса.

Синус угла α — это ордината (координата

y

) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Косинус угла α — это абсцисса (координата

x

) точки на тригонометрической окружности, которая возникает при повороте радиуса на угол α.

Тангенс угла α — это отношение синуса к косинусу. Или, что то же самое, отношение координаты

y

к координате

x

.

Обозначение: sin α =

y

; cos α =

x

; tg α =

y

:

x

.

Все эти определения знакомы вам из курса алгебры старших классов. Однако нас интересуют не сами определения, а следствия, которые возникают на тригонометрической окружности. Взгляните:

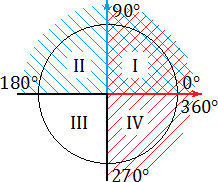
Синим цветом обозначено положительное направление оси

OY

(ось ординат), красным — положительное направление оси

OX

(ось абсцисс). На этом «радаре» знаки тригонометрических функций становятся очевидными. В частности:

1. sin α > 0, если угол α лежит в

   I

   или

   II

   координатной четверти. Это происходит из-за того, что по определению синус — это ордината (координата

   y

   ). А координата

   y

   будет положительной именно в

   I

   и

   II

   координатных четвертях;

2. cos α > 0, если угол α лежит в

   I

   или

   IV

   координатной четверти. Потому что только там координата

   x

   (она же — абсцисса) будет больше нуля;

3. tg α > 0, если угол α лежит в

   I

   или

   III

   координатной четверти. Это следует из определения: ведь tg α =

   y

   :

   x

   , поэтому он положителен лишь там, где знаки

   x

   и

   y

   совпадают. Это происходит в

   I

   координатной четверти (здесь

   x

   > 0,

   y

   > 0) и

   III

   координатной четверти (

   x

   < 0,

   y

   < 0).

Для наглядности отметим знаки каждой тригонометрической функции — синуса, косинуса и тангенса — на отдельных «радарах». Получим следующую картинку:

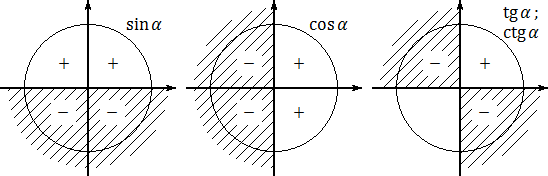
Заметьте: в своих рассуждениях я ни разу не говорил о четвертой тригонометрической функции — котангенсе. Дело в том, что знаки котангенса совпадают со знаками тангенса — никаких специальных правил там нет.

Теперь предлагаю рассмотреть примеры, похожие на задачи B11 из пробного ЕГЭ по математике, который проходил 27 сентября 2011. Ведь лучший способ понять теорию — это практика. Желательно — много практики. Разумеется, условия задач были немного изменены.

Задача. Определите знаки тригонометрических функций и выражений (значения самих функций считать не надо):

1. sin (3π/4);
2. cos (7π/6);
3. tg (5π/3);
4. sin (3π/4) · cos (5π/6);
5. cos (2π/3) · tg (π/4);
6. sin (5π/6) · cos (7π/4);
7. tg (3π/4) · cos (5π/3);
8. ctg (4π/3) · tg (π/6).

План действий такой: сначала переводим все углы из радианной меры в градусную (π → 180°), а затем смотрим в какой координатной четверти лежит полученное число. Зная четверти, мы легко найдем знаки — по только что описанным правилам. Имеем:

1. sin (3π/4) = sin (3 · 180°/4) = sin 135°. Поскольку 135° ∈ [90°; 180°], это угол из

   II

   координатной четверти. Но синус во

   II

   четверти положителен, поэтому sin (3π/4) > 0;

2. cos (7π/6) = cos (7 · 180°/6) = cos 210°. Т.к. 210° ∈ [180°; 270°], это угол из

   III

   координатной четверти, в которой все косинусы отрицательны. Следовательно, cos (7π/6) < 0;

3. tg (5π/3) = tg (5 · 180°/3) = tg 300°. Поскольку 300° ∈ [270°; 360°], мы находимся в

   IV

   четверти, где тангенс принимает отрицательные значения. Поэтому tg (5π/3) < 0;

4. sin (3π/4) · cos (5π/6) = sin (3 · 180°/4) · cos (5 · 180°/6) = sin 135° · cos 150°. Разберемся с синусом: т.к. 135° ∈ [90°; 180°], это

   II

   четверть, в которой синусы положительны, т.е. sin (3π/4) > 0. Теперь работаем с косинусом: 150° ∈ [90°; 180°] — снова

   II

   четверть, косинусы там отрицательны. Поэтому cos (5π/6) < 0. Наконец, следуя правилу «плюс на минус дает знак минус», получаем: sin (3π/4) · cos (5π/6) < 0;

5. cos (2π/3) · tg (π/4) = cos (2 · 180°/3) · tg (180°/4) = cos 120° · tg 45°. Смотрим на косинус: 120° ∈ [90°; 180°] — это

   II

   координатная четверть, поэтому cos (2π/3) < 0. Смотрим на тангенс: 45° ∈ [0°; 90°] — это

   I

   четверть (самый обычный угол в тригонометрии). Тангенс там положителен, поэтому tg (π/4) > 0. Опять получили произведение, в котором множители разных знаков. Поскольку «минус на плюс дает минус», имеем: cos (2π/3) · tg (π/4) < 0;

6. sin (5π/6) · cos (7π/4) = sin (5 · 180°/6) · cos (7 · 180°/4) = sin 150° · cos 315°. Работаем с синусом: поскольку 150° ∈ [90°; 180°], речь идет о

   II

   координатной четверти, где синусы положительны. Следовательно, sin (5π/6) > 0. Аналогично, 315° ∈ [270°; 360°] — это

   IV

   координатная четверть, косинусы там положительны. Поэтому cos (7π/4) > 0. Получили произведение двух положительных чисел — такое выражение всегда положительно. Заключаем: sin (5π/6) · cos (7π/4) > 0;

7. tg (3π/4) · cos (5π/3) = tg (3 · 180°/4) · cos (5 · 180°/3) = tg 135° · cos 300°. Но угол 135° ∈ [90°; 180°] — это

   II

   четверть, т.е. tg (3π/4) < 0. Аналогично, угол 300° ∈ [270°; 360°] — это

   IV

   четверть, т.е. cos (5π/3) > 0. Поскольку «минус на плюс дает знак минус», имеем: tg (3π/4) · cos (5π/3) < 0;

8. ctg (4π/3) · tg (π/6) = ctg (4 · 180°/3) · tg (180°/6) = ctg 240° · tg 30°. Смотрим на аргумент котангенса: 240° ∈ [180°; 270°] — это

   III

   координатная четверть, поэтому ctg (4π/3) > 0. Аналогично, для тангенса имеем: 30° ∈ [0; 90°] — это

   I

   координатная четверть, т.е. самый простой угол. Поэтому tg (π/6) > 0. Снова получили два положительных выражения — их произведение тоже будет положительным. Поэтому ctg (4π/3) · tg (π/6) > 0.

В заключение рассмотрим несколько более сложных задач. Помимо выяснения знака тригонометрической функции, здесь придется немного посчитать — именно так, как это делается в настоящих задачах B11. В принципе, это почти настоящие задачи, которые действительно встречается в ЕГЭ по математике.

Задача. Найдите sin α, если sin² α = 0,64 и α ∈ [π/2; π].

Поскольку sin² α = 0,64, имеем: sin α = ±0,8. Осталось решить: плюс или минус? По условию, угол α ∈ [π/2; π] — это

II

координатная четверть, где все синусы положительны. Следовательно, sin α = 0,8 — неопределенность со знаками устранена.

Задача. Найдите cos α, если cos² α = 0,04 и α ∈ [π; 3π/2].

Действуем аналогично, т.е. извлекаем квадратный корень: cos² α = 0,04 ⇒ cos α = ±0,2. По условию, угол α ∈ [π; 3π/2], т.е. речь идет о

III

координатной четверти. Там все косинусы отрицательны, поэтому cos α = −0,2.

Задача. Найдите sin α, если sin² α = 0,25 и α ∈ [3π/2; 2π].

Имеем: sin² α = 0,25 ⇒ sin α = ±0,5. Снова смотрим на угол: α ∈ [3π/2; 2π] — это

IV

координатная четверть, в которой, как известно, синус будет отрицательным. Таким образом, заключаем: sin α = −0,5.

Задача. Найдите tg α, если tg² α = 9 и α ∈ [0; π/2].

Все то же самое, только для тангенса. Извлекаем квадратный корень: tg² α = 9 ⇒ tg α = ±3. Но по условию угол α ∈ [0; π/2] — это

I

координатная четверть. Все тригонометрические функции, в т.ч. тангенс, там положительны, поэтому tg α = 3. Все!

Смотрите также:

1. Радианная мера угла
2. Тест к уроку «Знаки тригонометрических функций» (1 вариант)
3. Тест к параграфу «Что такое логарифм» (легкий)
4. Сводный тест по задачам B12 (1 вариант)
5. Изюм и виноград (смеси и сплавы)
6. Задача B4: транзит нефти

Построение тригонометрической окружности

А теперь сделай вот что: возьми-ка в руки циркуль и нарисуй любую (самую любую, но лучше достаточно немаленькую) окружность.

Получилось?

Ну да ладно, задачка не самая сложная. Так, ты не потерял ту точку, в которой у тебя был центр (куда ты прикладывал острую ножку циркуля)? Я вот у себя потерял, растяпа! Ну ладно, найду!

А что пока делать тебе?

А вот что: проведи через эту точку две линии, которые пересекаются «прямым крестиком», то есть под прямым углом. И пусть их точка пересечения – это центр (который ты не потерял!) окружности.

Нарисовал? У меня получилось что-то вроде вот этого.

Правда я чуть-чуть поторопился и сразу «обозвал» эти прямые ( displaystyle x) и ( displaystyle y) и точку пересечения через ( displaystyle O).

А что такое в таком случае ( displaystyle R)?

Это радиус нашей окружности.

Как называлась наша тема? Единичная окружность.

Тогда будем считать ( но не будем так рисовать!), что ( displaystyle R=1 ).

А рисовать мы так не будем, потому что на такой крошечной картинке ты ничего не разберешь! Ты же понимаешь, что когда инженеры проектируют самолеты, скажем, они не рисуют его в натуральную величину?

Так и мы не будем рисовать единичную окружность в самом деле единичной. Это нам нужно исключительно для удобства.

Теперь отмечаем: ( displaystyle OR=1). Что же мы с тобой на самом деле сделали? А вот что:

Мы поместили нашу окружность в систему координат ( displaystyle mathbf{X0Y}), сделав центр окружности началом координат!

Это позволит изучать свойства такой окружности уже не с геометрической, а с математической точки зрения. Этот подход был придуман хитрым математиком и философом Рене Декартом еще в 17 веке!

Перегнать фигуру в цифры, каково, а?

Но допустим, мы поместили нашу окружность в координаты. В скольких точках она пересекается с осями системы координат?

В четырех. Вот они:

Эти точки ( displaystyle left( A; B; C; D right)) имеют координаты:

( displaystyle Aleft( 1,0 right)); ( displaystyle Bleft( 0,1 right)); ( displaystyle Cleft( -1;0 right)); ( displaystyle Dleft( 0;-1 right)).

Теперь вспомни, как называются области, на которые этот «координатный крестик» делит всю плоскость?

Они называются координатные четверти.

Тогда посмотри на рисунок. Наша окружность тоже оказалась разрезанной на 4 равные дольки. Давай пронумеруем каждую из этих долек против часовой стрелки:

Ты уже можешь догадаться, как называются эти самые дольки:

1 четверть, 2 четверть, 3 четверть, 4 четверть

(Прямо как четверти в школе!)

Углы на тригонометрической окружности

Теперь давай сделаем еще вот что. Снова посмотрим на предыдущую картинку.

Чему на ней равен ( displaystyle angle AOB)?

Он равен ( displaystyle 90{}^circ ).

Также, как и ( displaystyle angle BOC), как и угол ( displaystyle angle COD), и угол ( displaystyle angle DOA).

Она равна ( displaystyle 360{}^circ ).

Вместе же эти 4 угла составляют всю окружность целиком!

Градусная мера окружности равна ( displaystyle 360{}^circ )!

Однако, ты нередко можешь увидеть и вот такую картинку:

где вместо привычных нам градусов появляются некие буковки «пи» ( displaystyle pi ) с цифрами.

В чем же тут дело, кто прав и кто виноват?

Ну так вот, кто прав, кто виноват, решать, увы, не нам. Но чтобы «воз не был поныне там», нам нужно уделить этому моменту пару минут времени.

В самом деле, есть два способа измерять углы:

• Через градусы
• Через радианы

Как измерять углы через градусы мы все знаем. Это нам привычно. Однако в некоторых случаях их измеряют по-другому (как в градуснике есть несколько шкал: цельсий, кельвин, фаренгейт и т. д.), а именно: через радианы.

Для того, чтобы перейти от одной формы записи к другой, используется вот такое основное соотношение:

По пропорции ты легко получишь, что для того, чтобы пересчитать угол из градусов в радианы, нужно применить вот такую незамысловатую формулу:

( displaystyle P~рад.=frac{alpha {}^circ cdot pi }{180})

И наоборот: от радиан к градусам:

( displaystyle alpha {}^circ =frac{P~рад.cdot 180}{pi })

Ты должен уметь ориентироваться и в той, и в другой форме записи.

Потренируйся на следующих примерах:

• Перевести угол в ( displaystyle 30) градусов в радианы;
• Перевести угол ( displaystyle frac{pi }{4}) радиан в градусы;
•  Перевести угол в ( displaystyle 60) градусов в радианы; 
•  Перевести угол в ( displaystyle frac{pi }{2}) радиан в градусы; 
•  Перевести угол в ( displaystyle 120) градусов в радианы; 
•  Перевести угол в ( displaystyle frac{3pi }{4}) радиан в градусы; 
• Перевести угол в ( displaystyle 150) градусов в радианы.

Я сделаю только первые два, а остальные реши сам!

• ( P~рад.=frac{30cdot pi }{180}=frac{pi }{6}), тогда угол в ( displaystyle 30) градусов равен углу в ( displaystyle frac{pi }{6}) радиан;
• ( alpha {}^circ =frac{frac{pi }{4}cdot 180}{pi }=frac{45pi }{pi }=45{}^circ ), тогда угол в ( displaystyle frac{pi }{4}) радиан равен углу в ( displaystyle 45) градусов.

Все очень просто, не так ли? Остальные значения ты можешь найти в следующей таблице:

( displaystyle 0{}^circ )	( displaystyle 30{}^circ )	( displaystyle 45{}^circ )	( displaystyle 60{}^circ )	( displaystyle 90{}^circ )	( displaystyle 120{}^circ )	( displaystyle 135{}^circ )	( displaystyle 150{}^circ )	( displaystyle 180{}^circ )
( displaystyle 0)	( displaystyle frac{pi }{6})	( displaystyle frac{pi }{4})	( displaystyle frac{pi }{3})	( displaystyle frac{pi }{2})	( displaystyle frac{2pi }{3})	( displaystyle frac{3pi }{4})	( displaystyle frac{5pi }{6})	( displaystyle pi )

( displaystyle 210{}^circ )	( displaystyle 225{}^circ )	( displaystyle 240{}^circ )	( displaystyle 270{}^circ )	( displaystyle 300{}^circ )	( displaystyle 315{}^circ )	( displaystyle 330{}^circ )	( displaystyle 360{}^circ )
( displaystyle frac{7pi }{6})	( displaystyle frac{5pi }{4})	( displaystyle frac{4pi }{3})	( displaystyle frac{3pi }{2})	( displaystyle frac{5pi }{3})	( displaystyle frac{7pi }{4})	( displaystyle frac{11pi }{6})	( displaystyle 2pi )

Так что впредь не удивляйся, когда ты увидишь вместо привычных градусов углы в радианах. Теперь ты знаешь, что это такое, и с чем его едят!

Синус, косинус, тангенс и котангенс на тригонометрической окружности

Но мы с тобой и так слишком увлеклись. Ты давно уже, наверное, заждался обещанных синусов и косинусов на тригонометрической окружности. Не смею более отвлекаться!

Давай сделаем вот что: совместим два знакомых нам объекта: тригонометрическую окружность (пока в том виде, в котором она у нас есть) и прямоугольный треугольник.

Что нам нужно, чтобы наш треугольник «целиком влез» в окружность?

Его гипотенуза должна быть не более единицы. Пусть же она у нас в точности будет равна единице.

Совместим мы их вот так:

Я нарисовал прямоугольный треугольник с центром в начале координат и гипотенузой равной ( 1). Это так потому, что окружность-то у меня единичная!

Тогда по определению синуса и косинуса:

• ( sin alpha =frac{AB}{OB}=frac{AB}{1}=AB)
• ( cos alpha =frac{OA}{OB}=frac{OA}{1}=OA)

А что же такое отрезки ( OA) и ( OB)? Чему равны их длины?

Смотри, сейчас будет самое главное: мы взяли угол ( alpha ) и провели луч, соединяющий этот угол с точкой на окружности.

Обозначим эту точку через ( B). Пусть ( B) имеет координаты ( Bleft( x,y right)).

Тогда длина отрезка ( OA) равна ( x), а длина отрезка ( AB)–равна ( y).

Но мы с тобой помним, что ( sin alpha =AB), ( cos alpha =OA), тогда:

• ( y=sin alpha )
• ( x=cos alpha )

Ух ты! Это надо еще раз обдумать, что же мы такое получили.

Давай проговорим еще раз: мы выбрали некоторый угол ( alpha ) и хотим найти его синус и косинус.

Что мы делаем?

• Проводим единичную окружность с центром, совпадающим с вершиной угла;
• Ищем точку пересечения нашего угла с окружностью;
•  Её «иксовая» координата – это косинус нашего угла; 
• Её «игрековая» координата – это синус нашего угла.

Вот и все! Теперь синус и косинус искать стало намного проще! Допустим, мы хотим найти синус, косинус ( 30) градусов.

Отмечаем ( 30) градусов на окружности и «достраиваем» этот угол до треугольника (как показано на рисунке выше).

Как найти ( x) и ( y)?

Да очень просто: в прямоугольном треугольнике катет, лежащий против угла в ( 30) градусов равен половине гипотенузы (это известный факт из геометрии 7 класса).

Так как гипотенуза равна ( 1), то противолежащий ей катет равен ( 0,5), откуда:

Наши катеты в треугольничке равны ( x) и ( y), которые в свою очередь совпадают с ( cos alpha ) и ( sin alpha ). Гипотенуза в треугольнике равна ( 1).

Тогда:

В частности, если:

( si{{n}^{2}}30{}^circ +co{{s}^{2}}30{}^circ =1) и ( sin 30{}^circ =0,5), то

Определение знака синуса, косинуса, тангенса и котангенса

Вообще, этот вопрос заслуживает особого внимания, но здесь все просто: у угла ( displaystyle 30) градусов и синус и косинус положительны (смотри рисунок), тогда берем знак «плюс».

C ( displaystyle 45) градусами все еще проще: так если один из углов прямоугольного треугольника равен ( displaystyle 45) градусам, то и другой тоже равен ( displaystyle 45) градусам, а значит такой треугольник равнобедренный.

Значит, его катеты равны. А значит равны его синус и косинус.

Теперь найди сам по новому определению (через икс и игрек!) синус и косинус углов в ( displaystyle 0) градусов и ( displaystyle 90) градусов. Здесь уже никакие треугольники нарисовать не получится! Уж слишком они будут плоские!

У тебя должно было получиться:

Теперь все полученные числа можно свести в таблицу:

Здесь приведены значения синуса, косинуса, тангенса и котангенса углов I четверти.

Для удобства углы приведены как в градусах, так и в радианах (но ты-то теперь знаешь связь между ними!). Обрати внимание на 2 прочерка в таблице: а именно у котангенса нуля и тангенса ( displaystyle 90) градусов. Это неспроста!

В частности:

Теперь давай обобщим понятие синус и косинус на совсем произвольный угол. Я рассмотрю здесь два случая:

• Угол лежит в пределах от ( displaystyle 0) до ( displaystyle 360) градусов;
• Угол больше ( displaystyle 360) градусов.

Честно говоря, я скривил немного душой, говоря про «совсем все» углы. Они бывают также и отрицательными! Но этот случай мы с тобой рассмотрим чуть позже. Вначале остановимся на первом случае.

Если угол лежит в 1 четверти – то тут все понятно, мы этот случай уже рассмотрели и даже таблицы нарисовали.

Теперь же пусть наш угол больше ( displaystyle 90) градусов и не больше чем ( displaystyle 360).

Это значит, что он расположен либо во 2, либо в 3 или же в 4 четверти.

Как мы поступаем? Да точно так же!

Давай рассмотрим вместо вот такого случая…

…вот такой:

То есть рассмотрим угол ( displaystyle alpha ), лежащий во второй четверти. Что мы можем сказать про него?

У точки ( displaystyle {{M}_{1}}), которая является точкой пересечения луча и окружности по-прежнему имеет 2 координаты (ничего сверхъестественного, правда?). Это координаты ( displaystyle {{x}_{1}}) и ( displaystyle {{y}_{1}}).

Причем первая координата отрицательная, а вторая – положительная! Это значит, что у углов второй четверти косинус отрицателен, а синус – положителен!

Удивительно, правда? До этого мы еще ни разу не сталкивались с отрицательным косинусом.

Да и в принципе этого не могло быть, когда мы рассматривали тригонометрические функции как отношения сторон треугольника.

Кстати, подумай, у каких углов косинус равен ( displaystyle -1)? А у каких ( displaystyle -1) равен синус?

Аналогично можно рассмотреть углы во всех остальных четвертях. Я лишь напомню, что угол отсчитывается против часовой стрелки! (так, как это показано на последнем рисунке!).

Конечно, можно и отсчитывать в другую сторону, но вот подход к таким углам будет уже несколько другой.

Исходя из приведенных выше рассуждений, можно расставить знаки у синуса, косинуса, тангенса (как синус деленный на косинус) и котангенса (как косинус деленный на синус) для всех четырех четвертей.

Но еще раз повторюсь, нет смысла запоминать этот рисунок. Все, что тебе нужно знать:

Синус – это игрек. Косинус – это икс. Тангенс – это синус деленный на косинус. Котангенс – это косинус деленный на синус.

Углы больше 360 градусов

А как быть с углами, большими чем ( displaystyle 360) градусов?

Возьму я, скажем, угол в ( displaystyle 30) градусов (( displaystyle frac{pi }{6}) радиан) и пойду от него против часовой стрелки…

На рисунке я нарисовал спираль, но ты-то понимаешь, что на самом деле у нас нет никакой спирали: у нас есть только окружность.

Так куда же мы попадем, если стартуем от определенного угла и пройдем полностью весь круг (( displaystyle 360) градусов или ( displaystyle 2pi ) радиан)?

Куда мы придем? А придем мы в тот же самый угол!

Это же, конечно, справедливо и для любого другого угла:

Взяв произвольный угол ( displaystyle alpha ) и пройдя полностью всю окружность, мы вернемся в тот же самый угол ( displaystyle alpha ).

Что же нам это даст? А вот что: если ( displaystyle sin alpha =y,~cos alpha =x), то

( displaystyle sin left( alpha +2pi k right)=y), ( displaystyle cos left( alpha +2pi k right)=x), откуда окончательно получим:

( displaystyle sin left( alpha +2pi k right)=sinalpha )

( displaystyle cos left( alpha +2pi k right)=cosalpha )

Для любого целого ( displaystyle k). Это значит, что синус и косинус являются периодическими функциями с периодом ( displaystyle 2pi ).

Таким образом, нет никакой проблемы в том, чтобы найти знак теперь уже произвольного угла: нам достаточно отбросить все «целые круги», которые умещаются в нашем угле и выяснить, в какой четверти лежит оставшийся угол.

Например, найти знак:

• ( displaystyle text{sin}1000{}^circ ),
• ( displaystyle text{cos} 605{}^circ ),
• ( displaystyle text{cos}frac{16pi }{7}),
• ( displaystyle text{sin}frac{19pi }{4}).

Проверяем:

Отрицательные углы

Отрицательные углы в тригонометрии откладываются на тригонометрическом круге вниз от начала, по направлению движения часовой стрелки:

Давай вспомним, как мы до этого откладывали углы на тригонометрической окружности.

Мы шли от положительного направления оси ( displaystyle Ox) против часовой стрелки:

Тогда на нашем рисунке построен угол, равный ( displaystyle 180+45=225{}^circ ). Аналогичным образом мы строили все углы.

Однако ничего нам не запрещает идти от положительного направления оси ( displaystyle Ox) по часовой стрелке.

Мы будем тоже получать различные углы, но они будут уже отрицательными:

А следующей картинке изображено два угла, равные по абсолютной величине (если не знаешь, что это такое, читай здесь про «Модуль числа»), но противоположные по знаку:

В целом правило можно сформулировать вот так:

• Идем против часовой стрелки – получаем положительные углы
• Идем по часовой стрелке – получаем отрицательные углы

Схематично правило изображено вот на этом рисунке:

Ты мог бы задать мне вполне резонный вопрос: ну углы нам нужны для того, чтобы измерять у них значения синуса, косинуса, тангенса и котангенса.

Так есть ли разница, когда у нас угол положительный, а когда – отрицательный? Я отвечу тебе: как правило есть.

Однако ты всегда можешь свести вычисление тригонометрической функции от отрицательного угла к вычислению функции в угле положительном.

Посмотри на следующую картинку:

Я построил два угла, они равны по абсолютному значению, но имеют противоположный знак. Отметим для каждого из углов его синус и косинус на осях.

Что мы с тобой видим? А вот что:

Синусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) противоположны по знаку!

Тогда если ( displaystyle text{sin} text{ }!!alpha!!text{ }=text{y}), 

то ( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{y})

( displaystyle sin left( -text{ }!!alpha!!text{ } right)=-text{sin} text{ }!!alpha!!text{ }).

Косинусы у углов ( displaystyle alpha ) и ( displaystyle -alpha ) совпадают!

Кстати, вспомни-ка, как называется функция ( displaystyle f(x)), у которой для любого допустимого ( displaystyle x) выполняется:( displaystyle f(-x)=-f(x))?

Такая функция называется нечетной.

А если же для любого допустимого ( displaystyle x) выполняется: ( displaystyle f(-x)=f(x))? То в таком случае функция называется четной.

Таким образом, мы с тобой только что показали, что:

Синус, тангенс и котангенс – нечетные функции, а косинус – четная.

Таким образом, как ты понимаешь, нет никакой разницы, ищем ли мы синус от положительного угла или отрицательного: справиться с минусом очень просто. Так что нам не нужны таблицы отдельно для отрицательных углов.

С другой стороны, согласись, было бы очень удобно зная только тригонометрические функции углов первой четверти, уметь вычислять аналогичные функции и для остальных четвертей.

Можно ли это сделать? Конечно, можно!

У тебя есть по крайней мере 2 пути: первый – строить треугольник и применять теорему Пифагора (так мы с тобой и отыскали значения тригонометрических функций для основных углов первой четверти)

Второй – запомнив значения функций для углов в первой четверти и некое несложное правило, уметь вычислять тригонометрические функции для всех остальных четвертей.

Второй способ избавит тебя от долгой возни с треугольниками и с Пифагором, поэтому мне он видится более перспективным:

Итак, данный способ (или правило) называется формулами приведения.

Формулы приведения

Грубо говоря, эти формулы помогут тебе не запоминать вот такую таблицу (она между прочим содержит 98 чисел!):

…если ты помнишь вот эту (всего на 20 чисел):

То есть ты сможешь не забивать себе голову совершенно ненужными 78 числами! Пусть, например, нам нужно вычислить ( displaystyle text{sin} 855{}^circ ). Ясно, что в маленькой таблице такого нет. Что же нам делать? А вот что:

Во-первых, нам понадобятся следующие знания:

Синус и косинус имеют период ( displaystyle 2pi ) (( displaystyle 360) градусов)

То есть

( displaystyle sinleft( 2pi k+x right)=sin x)
( displaystyle cosleft( 2pi k+x right)=cos x)

Тангенс (котангенс) имеют период ( displaystyle pi ) (( displaystyle 180) градусов)

( displaystyle tgleft( pi k+x right)=tg x)

( displaystyle ctgleft( pi k+x right)=ctg x)
( displaystyle k) – любое целое число

Синус и тангенс – функции нечетные, а косинус – четная:

Непосредственно правило приведения выглядит вот так:

Если мы вычисляем значение тригонометрической функции от отрицательного угла – делаем его положительным при помощи группы формул о четности.

Иначе ищем, в какой четверти лежит наш угол ( displaystyle alpha ): это будет 2, 3 или 4 четверть. Смотрим, какой знак имеет искомая функция в четверти. Запомнили этот знак!!!

Представляем угол ( displaystyle alpha )в одной из следующих форм:

• ( displaystyle alpha =90+beta ) (если во второй четверти)
• ( displaystyle alpha =180-beta ) (если во второй четверти)
• ( displaystyle alpha =180+beta ) (если в третьей четверти)
• ( displaystyle alpha =270-beta ) (если в третьей четверти)
• ( displaystyle alpha =270+beta ) (если в четвертой четверти)
• ( displaystyle alpha =360-beta ) (если в четвертой четверти)

( displaystyle 135{}^circ =180{}^circ -45{}^circ )
( displaystyle 135{}^circ =90{}^circ +45{}^circ )
( displaystyle 315{}^circ =270{}^circ+45{}^circ )
( displaystyle 240{}^circ =180{}^circ +60{}^circ )
( displaystyle 240{}^circ =270{}^circ -30{}^circ )…

В принципе не важно, в какой из двух альтернативных форм для каждой четверти ты представишь угол. На конечном результате это не скажется.

Ставим перед получившимся выражением знак, который мы запомнили.