Производная положительна только тогда, когда функция возрастает. То есть, нам необходимо найти точки, в которых функция растет. Смотрим на график нашей функции: функция растет на промежутках: от (x=-7) до (x=0) и от (x = 6) до (x=12).
Так как по условию нам нужны только ЦЕЛЫЕ точки, в которых производная положительна, то это будут: (x=—6); (x=-5), (x=-4), (x=-3), (x=-2), (x=-1), (x=7), (x=8), (x=9), (x=10), (x=11). Всего точек получилось (11). Я отметил их зеленым цветом.
Обратите внимание, что точки (x=-7), (x=0), (x=6), (x=12) мы не считаем, так как в этих точках у нас будут минимумы и максимумы функции, а в них производная равна нулю, то есть не положительна.
Ответ: (11.)
Пример 2
На рисунке 6 изображен график функции, определенной на промежутке ((-10;12)). Найдите количество точек, в которых производная функции равна нулю.
Производная функции. Геометрический смысл производной
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?

Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:

На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Определение.
Производная – это скорость изменения функции.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.

Нарисован график некоторой функции . Возьмем на нем точку А с абсциссой
. Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной.
Производная функции в точке
равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси ОХ.
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике.
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
.
Величина k в этом уравнении называется угловым коэффициентом прямой. Она равна тангенсу угла наклона прямой к оси X.
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
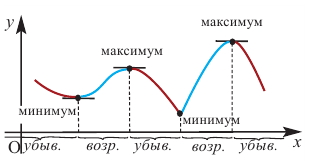
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.

В точке A функция возрастает. Касательная к графику, проведенная в точке A, образует острый угол
с положительным направлением оси X. Значит, в точке A производная положительна.
В точке B наша функция убывает. Касательная в этой точке образует тупой угол с положительным направлением оси X. Поскольку тангенс тупого угла отрицателен, в точке B производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках C (точка максимума) и D (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка С — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке С с «плюса» на «минус».
В точке D — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция
возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задач ЕГЭ. Другое — на первом курсе, при более серьезном изучении функций и производных.
1. Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая точка перегиба:

В точке E касательная к графику горизонтальна, и производная равна нулю. Однако до точки E функция возрастала — и после точки E продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
2. Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.

А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется таблица производных. В ней вы найдете производные всех элементарных функций и правила взятия производных, то есть дифференцирования.
Геометрический смысл производной, задачи
Покажем, что такое геометрический смысл производной, на примере нескольких задач из Банка заданий ФИПИ.
Задача 1. На рисунке изображен график функции ). Найдите количество решений уравнения
)=0 на отрезке [-2,5; 9,5].

Решение:
Производная функции равна нулю в точках максимума и минимума функции
Таких точек на графике 5.
Ответ: 5.
Задача 2. На рисунке изображен график функции y= ) — производной функции
). Сколько точек максимума имеет функция
) на отрезке
? В ответе запишите это число.

Решение:
Обратите внимание, что на этом рисунке изображен не график функции, а график ее производной.
В вариантах ЕГЭ по математике таких задач много. Пользуясь графиком производной, надо ответить на вопрос о поведении функции.
В точке максимума функции производная равна нулю и меняет знак с «плюса» на «минус». Такая точка на отрезке на графике одна.
Ответ: 1.
Задача 3. На рисунке изображены график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке

Решение:
Вспомним определение.
Производная функции в точке равна тангенсу угла наклона касательной, проведенной к графику функции в этой точке (то есть угловому коэффициенту касательной).
Это геометрический смысл производной.
В точке функция y = f(x) убывает. Касательная, проведенная к ее графику в этой точке, образует тупой угол
с положительным направлением оси Х. Найдем тангенс острого угла
смежного с углом
Ответ: -0,5.
Задача 4. На рисунке изображен график производной функции определенной на отрезке
В какой точке отрезка
принимает наименьшее значение?

Решение:
На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».
На рисунке есть такая точка, и это x = 1,5.
Слева от этой точки, на отрезке [1; 1,5] производная отрицательна, и функция убывает. Справа от этой точки, на интервале [1,5; 5), производная положительна, и функция возрастает.
Значит, – точка минимума функции
Поэтому и свое наименьшее значение функция принимает в точке 1,5.
Ответ: 1,5.
Задача 5. На рисунке изображен график — производной функции
В какой точке отрезка
функция
принимает наименьшее значение?

Решение:
На рисунке изображен график производной. Если функция возрастает — ее производная положительна. Если функция убывает — ее производная отрицательна. В точке минимума производная равна нулю и меняет знак с «минуса» на «плюс».
На рисунке есть такая точка, и это x = 3.
Слева от этой точки производная отрицательна, и функция убывает. Справа от точки x = 3 производная положительна, и функция возрастает.
Значит, – точка минимума функции
Кстати, вид графика функции определить нетрудно. Это квадратичная парабола с ветвями вверх.
Ответ: 3.
Задача 6. На рисунке изображен график производной непрерывной функции
В какой точке отрезка
функция
принимает наибольшее значение?

Решение:
На отрезке расположена точка
в которой производная равна нулю и меняет знак с «+» на «-».
Это значит, что — точка максимума функции
на отрезке
и наибольшее значение функция
принимает именно в этой точке.
Ответ: – 2,5.
Задача 7. На рисунке изображен график производной функции определенной на интервале (-3;7). В какой точке отрезка [-2; 4] функция
принимает наименьшее значение?

Решение:
Точка минимума функции f(x) — это x = 0. В этой точке производная равна 0 и меняет знак с «минуса» на «плюс».
Слева от точки 0 производная отрицательна, функция убывает. Справа от этой точки производная положительна, функция возрастает.
Наименьшее значение на отрезке достигается при x = 0.
Ответ: 0.
Задача 8. На рисунке изображены график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке

Решение:
Производная функции в точке
равна тангенсу угла наклона касательной, проведенной к графику функции
в этой точке.
– касательная к
В точке производная отрицательная,
т.к. функция
— убывает в этой точке.
— угол, который образует касательная с положительным направлением оси Х.
Угол — тупой, а смежный с ним угол
— острый.
Ответ: -0,375.
Задача 9. На рисунке изображен график непрерывной функции f(x) и касательные CD и MN, проведенные к ее графику в точках А и В. Найдите отношение значений производной функции f(x) в точках А и В.

Решение:
Найдём значения производных в точках А и В с помощью графика.
где
— угол наклона касательной к графику функции в точке с абсциссой
Для точки А:
Для точки В:
Отношение производных:
Ответ: 0,15.
Условия касания
Пусть прямая касается графика функции
в точке
Тогда для точки
выполняются условия касания:
Первое уравнение показывает, что значения функций и
в точке
равны друг другу. Это верно, поскольку эта точка лежит и на одном, и на другом графике.
Второе условие показывает, что производная функции в точке
равна угловому коэффициенту касательной, то есть k.
Задача 10. Прямая касается графика функции
причем абсцисса точки касания положительна. Найдите b.
Решение:
Запишем условие касания:
Начнем со второго уравнения:
Т.к. то
Найдем подставив
в первое уравнение:
отсюда
Ответ: -7.
Условия касания встречаются нам не только в заданиях 1 части ЕГЭ по математике, но и в задачах с параметрами. Более того, это один из приемов решения уравнений и неравенств с параметрами.
Физический смысл производной
Мы узнали, что такое геометрический смысл производной. Научились находить производную с помощью графика функции и решать задачи ЕГЭ. Производная помогает нам исследовать функции, находить их точки максимума и минимума, строить графики функций.
И оказывается, что с производной вы познакомились намного раньше — в школьном курсе физики. Вы уже пользовались этим математическим понятием, но не называли его словом «производная».
Вспомним тему «Кинематика» в физике. Это раздел физики, описывающий механическое движение. Величины, которыми описывается движение какого-либо тела, — это скорость v, время t, координата х, если тело движется вдоль прямой. Или координаты x и y, если оно движется по плоскости.
Вспомним формулу для равномерного прямолинейного движения: где x — координата.
Пусть 3 материальных точки — например, три автомобиля — одновременно выезжают с постоянными скоростями из точки А и едут по прямолинейному шоссе. На графике показано, как меняется их координата x с течением времени. У какого из автомобилей скорость больше?

Очевидно, у третьего. Считая, что x = vt, для первого автомобиля найдем = 20 км/ч. Возможно, это машина, которая поливает или чистит дорогу, и поэтому так медленно едет. Для второго автомобиля
= 40 км/ч, для третьего
= 75 км/ч.
Но если пройденный путь, то есть изменение координаты тела, мы разделим на время, то найдем тангенс угла наклона для каждой из этих прямых. Так и есть.
Скорость тела — это производная от его координаты по времени.
А теперь пусть тело, например, автомобиль, движется вдоль оси x, причем его скорость не является постоянной. Зависимость его координаты от времени x(t) показана на графике.

Возьмем на графике точку, соответствующую моменту времени и проведем в этой точке касательную к графику функции.
Тангенс угла наклона этой касательной численно равен мгновенной скорости тела в момент
Мы получили, что мгновенная скорость — это производная от координаты по времени.
Это физический смысл производной.
Но не только скорость в физике является производной от другой физической величины, координаты.
Ускорение — это производная от скорости по времени. Сила тока — производная от заряда по времени.
Изучая курс физики в школе и в вузе, вы увидите множество уравнений, связывающих одни физические величины с производными других физических величин. Такие уравнения называются дифференциальными. А само действие взятия производной называется дифференцированием.
Вот задача из вариантов ЕГЭ по математике, где используется физический смысл производной.
Задача 11. Материальная точка M начинает движение из точки A и движется по прямой на протяжении 12 секунд. График показывает, как менялось расстояние от точки A до точки M со временем. На оси абсцисс откладывается время t в секундах, на оси ординат — расстояние s.
Определите, сколько раз за время движения скорость точки M обращалась в ноль (начало и конец движения не учитывайте).

Решение:
Производная — это скорость изменения функции. Мгновенная скорость движущегося тела (материальной точки) является производной от его координаты по времени. Это физический смысл производной.
Найдем на графике s(t) точки, в которых производная функции s(t) равна нулю. Таких точек 6. Это точки максимума и минимума функции s(t).
Ответ: 6.
Изучая высшую математику в вузе, вы узнаете еще одно определение производной.
Производной функции f(x) в точке называется предел отношения приращения функции к приращению аргумента при приращении аргумента, стремящемся к нулю.
Это определение есть в вашем школьном учебнике алгебры. Но намного важнее не механически его запомнить, а понять его смысл. Первые шаги к этому мы сделали, определив производную как скорость изменения функции. Мы также узнали, что такое геометрический смысл производной и физический смысл производной.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Производная функции. Геометрический смысл производной» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
08.05.2023
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
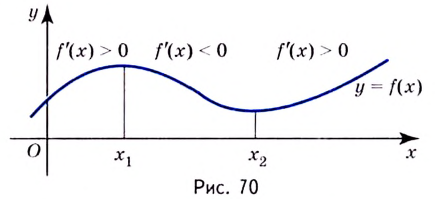
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
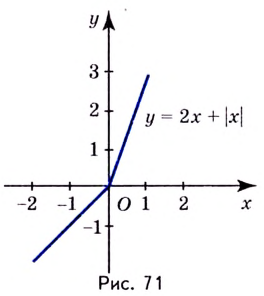
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция 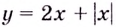
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 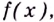 нужно решить неравенства
нужно решить неравенства 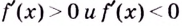 или найти все критические точки функции,разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
или найти все критические точки функции,разбить ими область определения функции на промежутки, а потом исследовать, на каких из них функция возрастает, а на каких — убывает.
Пример:
Найдите промежутки возрастания и убывания функции 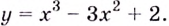
Решение:
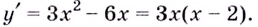
Уравнение 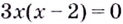 имеет корни
имеет корни 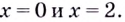 Это — критические точки. Область определения данной функции — множество
Это — критические точки. Область определения данной функции — множество 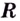 — они разбивают на три промежутка:
— они разбивают на три промежутка: 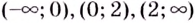 (рис. 72). Производная функции на этих промежутках имеет соответственно такие знаки:
(рис. 72). Производная функции на этих промежутках имеет соответственно такие знаки: 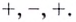 Следовательно, данная функция на промежутках
Следовательно, данная функция на промежутках 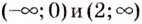 возрастает, а на
возрастает, а на 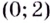 убывает.
убывает.
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 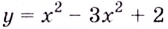 в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках
в точках 0 и 2 непрерывна, то можно утверждать, что она возрастает на промежутках 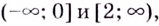 на
на 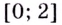 — убывает.
— убывает.
Пример:
Найдите промежутки убывания функции 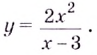
Решение:
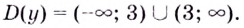
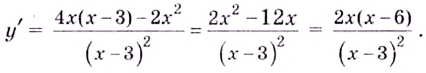
Критические точки: 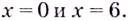 Они всю область определения функции разбивают на интервалы:
Они всю область определения функции разбивают на интервалы: 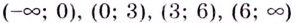 (рис. 73). Производная
(рис. 73). Производная 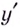 на этих промежутках имеет соответственно такие знаки:
на этих промежутках имеет соответственно такие знаки: 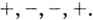 Следовательно, функция убывает на промежутках
Следовательно, функция убывает на промежутках 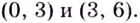 Поскольку в точках
Поскольку в точках 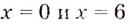 данная функция непрерывна, то ответ можно записать и так:
данная функция непрерывна, то ответ можно записать и так: 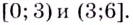
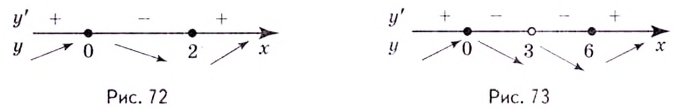
Пример:
Найдите критические точки функции 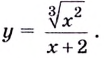
Решение:
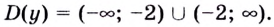 Найдем произвольную функции:
Найдем произвольную функции: 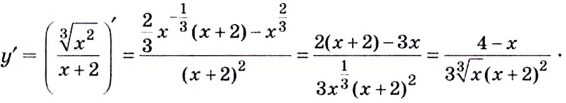
Найдём точки, в которых производная равна нулю или не существует: 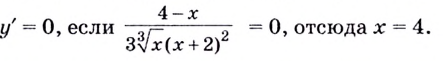
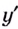 — не существует, если знаменатель равен нулю, отсюда
— не существует, если знаменатель равен нулю, отсюда 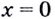 и
и 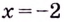 Точка
Точка  не входит в область определения функции. Следовательно, функция имеет две критические точки:
не входит в область определения функции. Следовательно, функция имеет две критические точки: 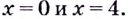
Ответ. 0 и 4.
Пример:
Докажите, что функция 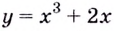 возрастает на
возрастает на 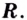
Решение:
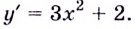 При любом значении
При любом значении 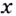 выражение
выражение 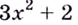 имеет положительное значение. Следовательно, данная функция возрастает на всей области определения, т.е. на множестве
имеет положительное значение. Следовательно, данная функция возрастает на всей области определения, т.е. на множестве 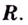
Пример:
Установите, на каком промежутке функция 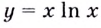 возрастает, а на каком убывает.
возрастает, а на каком убывает.
Решение:
Способ 1. 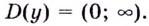 Найдём производную функции:
Найдём производную функции:
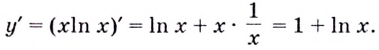
Найдём критические точки функции:
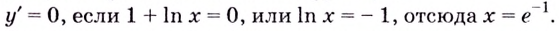
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
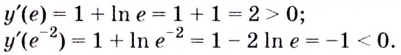
Следовательно, функция 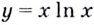 возрастает на промежутке
возрастает на промежутке 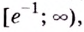 а убывает на
а убывает на 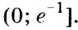
Способ 2. Решим неравенство 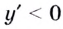 и
и 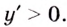
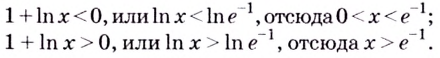
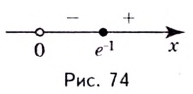
Ответ. Возрастает, если 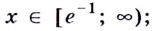 убывает если
убывает если 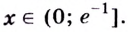
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 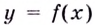 является дифференцируемой,
является дифференцируемой, 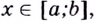 её производная
её производная 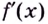 — функция, которая также дифференцируема. Тогда можно найти производную
— функция, которая также дифференцируема. Тогда можно найти производную 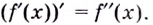 Это производная второго порядка, или вторая производная функции
Это производная второго порядка, или вторая производная функции 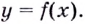
Например, найти производную 2-го порядка функции 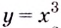
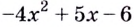 означает найти производную этой функции
означает найти производную этой функции 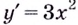
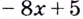 и полученную функцию продифференцировать:
и полученную функцию продифференцировать: 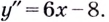
Кривая 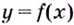 называется выпуклой на интервале
называется выпуклой на интервале 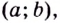 если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1).
если все её точки, кроме точки касания, лежат ниже произвольной её касательной на этом интервале (на рис. 86 — 1).
Кривая 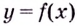 называется вогнутой на интервале
называется вогнутой на интервале 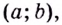 если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2).
если все её точки, кроме точки касания, лежат выше произвольной её касательной на этом интервале (на рис. 86 — 2).
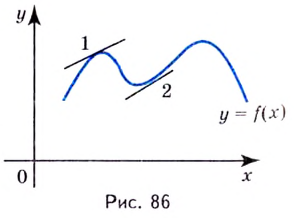
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 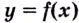 отрицательна
отрицательна 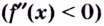 на интервале
на интервале 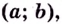 то кривая
то кривая 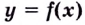 выпуклая на данном интервале; если вторая производная функции
выпуклая на данном интервале; если вторая производная функции 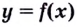 положительная
положительная 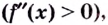 то кривая вогнутая на
то кривая вогнутая на 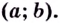
Из теоремы следует, что точками перегиба кривой 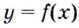 могут быть только точки, в которых вторая производная
могут быть только точки, в которых вторая производная 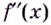 равна нулю или не существует. Такие точки называют критическими точками второго рода.
равна нулю или не существует. Такие точки называют критическими точками второго рода.
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 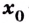 — критическая точка второго рода функции
— критическая точка второго рода функции 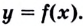 Если при переходе через точку
Если при переходе через точку 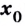 производная
производная 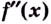 меняет знак, то точка
меняет знак, то точка 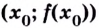 является точкой перегиба кривой
является точкой перегиба кривой 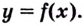
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
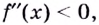 то кривая выпуклая; если
то кривая выпуклая; если 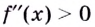 — кривая вогнутая;
— кривая вогнутая; - если производная
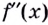 меняет знак при переходе через точку
меняет знак при переходе через точку 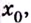 то точка
то точка 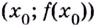 является точкой перегиба кривой
является точкой перегиба кривой 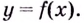
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой 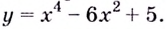
Решение:
1) Область определения функции: 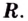
2) Найдём вторую производную: 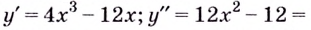
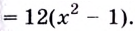 Критические точки второго рода:
Критические точки второго рода: 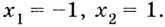 Других критических точек нет.
Других критических точек нет.
3) Разбиваем область определения на интервалы 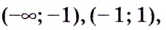
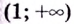 и определяем знак второй производной на каждом из них.
и определяем знак второй производной на каждом из них.
Если 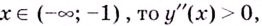 поэтому кривая вогнутая.
поэтому кривая вогнутая.
Если 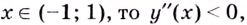 поэтому кривая выпуклая.
поэтому кривая выпуклая.
Если 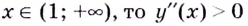 — кривая вогнутая.
— кривая вогнутая.
Следовательно, точки 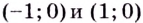 — точки перегиба кривой. Рассмотрим ещё один компонент в исследовании функций, благодаря которому упрощается построение некоторых графиков. Это асимптоты. В предыдущих параграфах рассматривались горизонтальные и вертикальные асимптоты. Повторим, расширим и обобщим это понятие. Асимптоты бывают вертикальные, наклонные и горизонтальные (рис. 87).
— точки перегиба кривой. Рассмотрим ещё один компонент в исследовании функций, благодаря которому упрощается построение некоторых графиков. Это асимптоты. В предыдущих параграфах рассматривались горизонтальные и вертикальные асимптоты. Повторим, расширим и обобщим это понятие. Асимптоты бывают вертикальные, наклонные и горизонтальные (рис. 87).
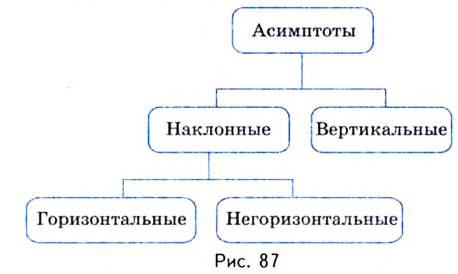
Напомним, что прямая 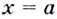 будет вертикальной асимптотой кривой
будет вертикальной асимптотой кривой 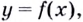 если при
если при 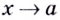 (справа или слева) значение функции
(справа или слева) значение функции 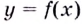 стремится к бесконечности, т.е. выполняется одно из условий:
стремится к бесконечности, т.е. выполняется одно из условий: 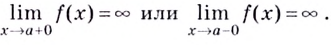
Уравнение наклонной асимптоты: 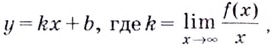
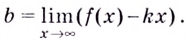
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 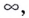 то кривая наклонной асимптоты не имеет.
то кривая наклонной асимптоты не имеет.
Если 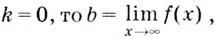 поэтому
поэтому 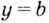 — уравнение горизонтальной асимптоты.
— уравнение горизонтальной асимптоты.
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 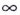 следует понимать и
следует понимать и 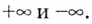 При этом указанные пределы могут быть разными при
При этом указанные пределы могут быть разными при 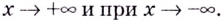
Пример №2
Найдите асимптоты кривых:
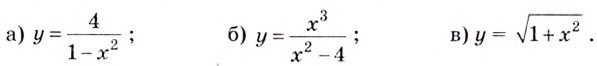
Решение:
а) 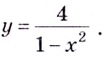 Найдём вертикальные асимптоты. Поскольку функция не определена в точках
Найдём вертикальные асимптоты. Поскольку функция не определена в точках 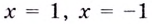 и
и 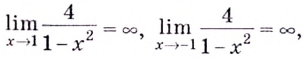 то прямые
то прямые 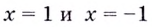 — вертикальные асимптоты.
— вертикальные асимптоты.
Найдём наклонную асимптоту: 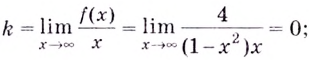
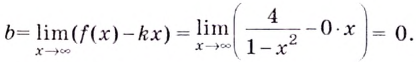 Кривая имеет горизонтальную асимптоту, её уравнение:
Кривая имеет горизонтальную асимптоту, её уравнение: 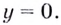
Следовательно, заданная кривая имеет три асимптоты: 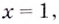
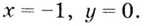
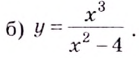 Найдем вертикальные асимптоты.
Найдем вертикальные асимптоты.
Поскольку функция не определена в точках 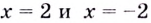 и
и 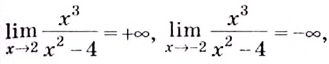 то прямые
то прямые 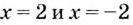 — вергикальные асимптоты.
— вергикальные асимптоты.
Для наклонной асимптоты 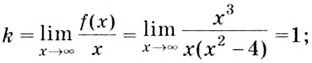
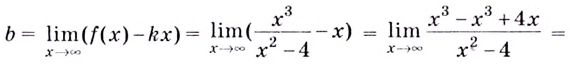
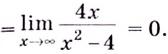
Значит прямая 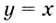 — наклонная асимптота. Горизонтальной асимптоты нет.
— наклонная асимптота. Горизонтальной асимптоты нет.
Итак, асимптоты кривой: 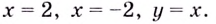
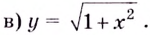 Будем искать наклонные асимптоты:
Будем искать наклонные асимптоты:
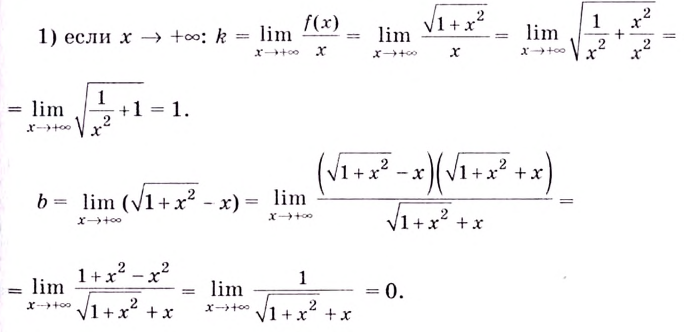
Следовательно, 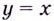 — наклонная асимптота, если
— наклонная асимптота, если 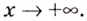
2) если 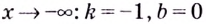 (проверьте самостоятельно), отсюда
(проверьте самостоятельно), отсюда  — наклонная асимптота, если
— наклонная асимптота, если 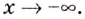
Следовательно, заданная кривая имеет две асимптоты: 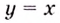
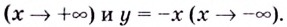
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
возрастающая функция
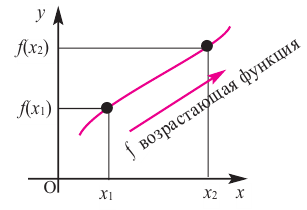
Если для любых 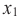 и
и 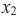 из некоторого промежутка области определения при
из некоторого промежутка области определения при 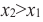 выполняется условие
выполняется условие 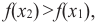 то на этом промежутке функция возрастающая.
то на этом промежутке функция возрастающая.
убывающая
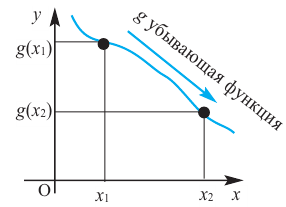
Если для любых 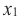 и
и 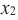 из некоторого промежутка области определения при
из некоторого промежутка области определения при 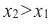 выполняется условие
выполняется условие 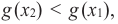 на этом промежутке функция убывающая.
на этом промежутке функция убывающая.
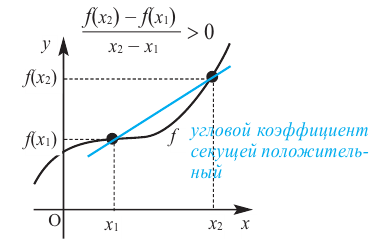
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция  возрастает.
возрастает.
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция  убывает.
убывает.
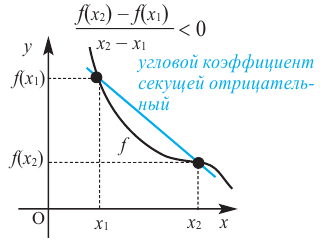
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 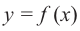 положительна, т. е.
положительна, т. е. 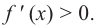 Так как
Так как 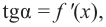 то угловой коэффициент касательной будет положительным. А это значит, что касательная с положительным направлением оси абсцисс образует острый угол и на заданном промежутке график “поднимается “, т. е. функция возрастает. Если
то угловой коэффициент касательной будет положительным. А это значит, что касательная с положительным направлением оси абсцисс образует острый угол и на заданном промежутке график “поднимается “, т. е. функция возрастает. Если 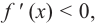 тогда касательная с положительным направлением оси абсцисс образует тупой угол, график “спускается”, т. е. функция убывает.
тогда касательная с положительным направлением оси абсцисс образует тупой угол, график “спускается”, т. е. функция убывает.
Теорема. Если функция 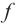 дифференцируема в каждой точке заданного промежутка, то:
дифференцируема в каждой точке заданного промежутка, то:
Примечание: если функция 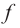 непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку.
непрерывна в каком-либо из концов промежутка возрастания (убывания), то эту точку присоединяют к этому промежутку.
По графику функции 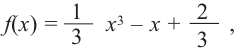 исследуйте промежутки возрастания и убывания функции.
исследуйте промежутки возрастания и убывания функции.
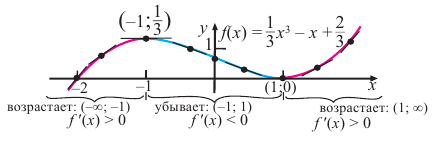
На интервалах 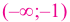 и
и 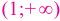 угловой коэффициент касательной положительный, поэтому на каждом из промежутков
угловой коэффициент касательной положительный, поэтому на каждом из промежутков 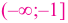 и
и 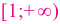 функция
функция 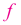 возрастает.
возрастает.
На интервале 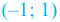 угловой коэффициент касательной отрицателен, поэтому на промежутке
угловой коэффициент касательной отрицателен, поэтому на промежутке 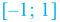 функция
функция 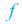 убывает.
убывает.
Пример №3
При помощи производной определите промежутки возрастания и убывания функции 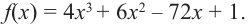
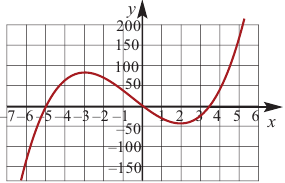
Решение: 1. Алгебраический метод.
Найдем производную функции
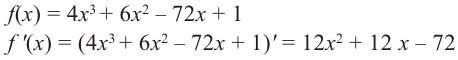
Функция 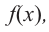 на промежутке удовлетворяющем неравенству
на промежутке удовлетворяющем неравенству 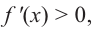 т. е.
т. е. 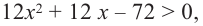 возрастает.
возрастает.
Для решения неравенства сначала надо решить соответствующее уравнение
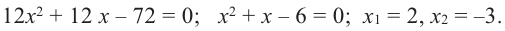
Значит, при 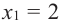 и
и 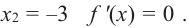 Точки
Точки 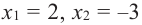 разбивают область определения функции на три интервала:
разбивают область определения функции на три интервала: 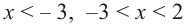 и
и 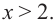 В каждом из интервалов выберем контрольную точку для проверки и установим знак производной.
В каждом из интервалов выберем контрольную точку для проверки и установим знак производной.

Из таблицы и непрерывности функции 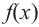 видно, что данная функция возрастает на промежутках
видно, что данная функция возрастает на промежутках 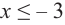 и
и 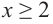 и убывает на промежутке
и убывает на промежутке 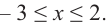 Из графика так же видно, что задания решение верно.
Из графика так же видно, что задания решение верно.
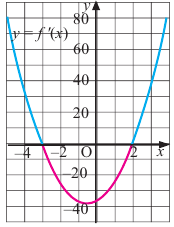
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
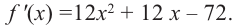
График производной 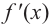 при
при 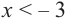 и
и 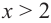 расположен выше оси
расположен выше оси 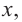 значит,
значит, 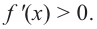 При
При 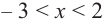 график производной расположен ниже оси
график производной расположен ниже оси 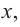 значит
значит 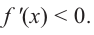 Так как функция
Так как функция 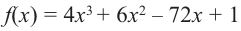 в точках
в точках 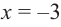 и
и 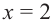 непрерывна, то на промежутках
непрерывна, то на промежутках 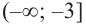 и
и 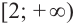 она возрастает, а на промежутке
она возрастает, а на промежутке 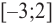 убывает.
убывает.
Пример №4
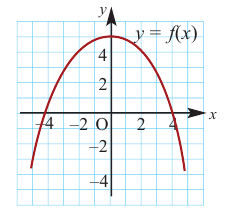
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 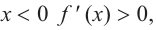 при
при 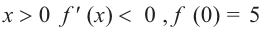
b) при 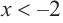 или
или 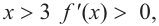 при
при 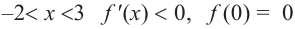
Решение:
а) при 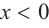 знак производной положительный:
знак производной положительный: 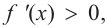 значит,
значит,
функция возрастает. При 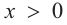 знак производной отрицательный:
знак производной отрицательный: 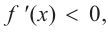 значит, функция убывает, при
значит, функция убывает, при 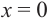 значение функции равно 5.
значение функции равно 5.
b) При 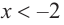 и
и 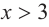 знак производной положительный:
знак производной положительный: 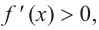 значит, функция возрастает. При
значит, функция возрастает. При 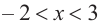 знак производной отрицательный:
знак производной отрицательный: 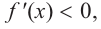 значит, функция убывает, при
значит, функция убывает, при 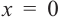 значение функции равно 0.
значение функции равно 0.
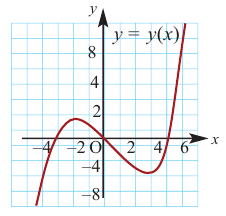
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
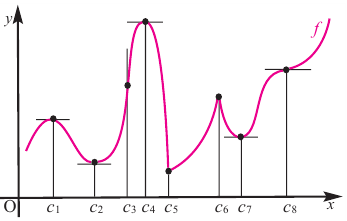
1. Для значений 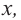 равных
равных 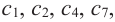
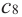 угловой коэффициент касательной к графику равен 0. Т. e.
угловой коэффициент касательной к графику равен 0. Т. e.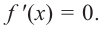 Эти точки являются критическими точками функции.
Эти точки являются критическими точками функции.
2. В точках 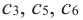 функция не имеет производной. Эти тоже критические точки функции.
функция не имеет производной. Эти тоже критические точки функции.
3. Для рассматриваемой нами функции критические точки 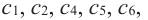
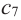 делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки
делят ее область определения на чередующиеся интервалы возрастания и убывания. Точки 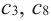 – критические точки, которые не изменяют возрастание и убывание (или наоборот).
– критические точки, которые не изменяют возрастание и убывание (или наоборот).
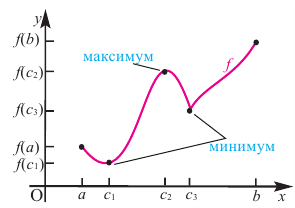
По графику видно, что в точках внутреннего экстремума(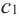 и
и 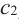 ) производная функции равна нулю, а в точке
) производная функции равна нулю, а в точке 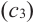 производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
производная не существует. Точки, в которых производная функции равна нулю, также называются стационарными точками.
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 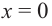 производная функции
производная функции 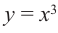 равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
равна нулю, но эта точка не является ни точкой максимума, ни точкой минимума.
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 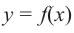 непрерывна на промежутке
непрерывна на промежутке 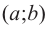 и
и 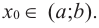 Если
Если 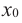 является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
является критической точкой, в окрестности которой функция дифференцируема, то, если в этой окрестности:
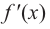 слева от точки
слева от точки 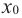 положительна, а справа – отрицательна, то точка
положительна, а справа – отрицательна, то точка 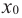 является точкой максимума.
является точкой максимума.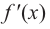 слева от
слева от 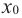 отрицательна, а справа – положительна, то точка
отрицательна, а справа – положительна, то точка 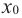 является точкой минимума
является точкой минимума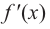 с каждой стороны от точки
с каждой стороны от точки 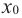 имеет одинаковые знаки, то точка
имеет одинаковые знаки, то точка 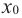 не является точкой экстремума.
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 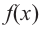 на отрезке
на отрезке 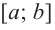 записываются как
записываются как 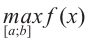 и
и 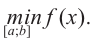
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
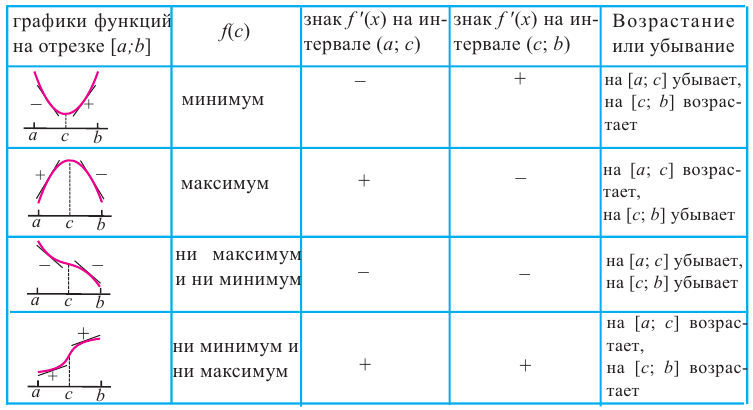
Пример №5
Для функции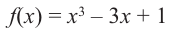 определите максимумы и минимумы и схематично изобразите график.
определите максимумы и минимумы и схематично изобразите график.
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции: 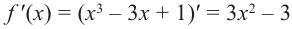
2. Критические точки функции: 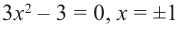
3. Точки 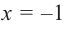 и
и 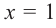 разбивают область определения функции на три промежутка.
разбивают область определения функции на три промежутка.
Проверим знак 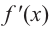 на интервалах, выбрав пробные точки:
на интервалах, выбрав пробные точки:
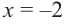 для интервала
для интервала 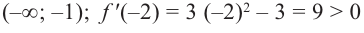
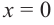 для интервала
для интервала 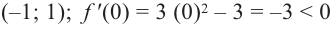
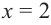 для интервала
для интервала 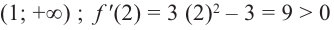
 При
При 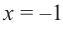 имеем
имеем 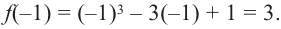
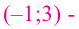 максимум
максимум
При 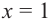 имеем
имеем 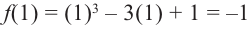
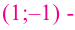 минимум
минимум
4. Используя полученные для функции 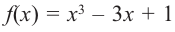 данные и найдя координаты нескольких дополнительных точек, построим график функции.
данные и найдя координаты нескольких дополнительных точек, построим график функции.

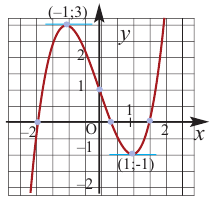
Пример №6
Найдите наибольшее и наименьшее значение функции 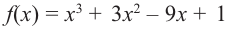 на отрезке
на отрезке 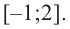
Решение: Сначала найдем критические точки.
Так как 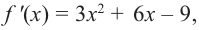 то критические точки можно найти из уравнения
то критические точки можно найти из уравнения 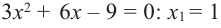 и
и 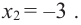 Критическая точка
Критическая точка 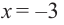 не принадлежит данному отрезку
не принадлежит данному отрезку 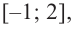 и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке
и поэтому мы ее не рассматриваем. Вычислим значение заданной функции в точке 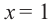 и на концах отрезка.
и на концах отрезка.
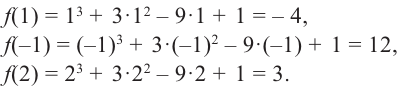
Из этих значений наименьшее – 4, наибольшее 12. Таким образом:
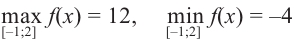
Пример №7
Найдите экстремумы функции 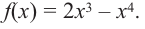
Решение: 1. Производная функции: 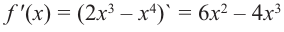
2. Критические точки: 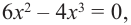
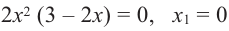 и
и 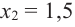
3. Интервалы, на которые критические точки делят область определения функции:
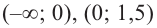 и
и 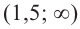
Проверим знак 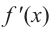 на интервалах, выбрав пробные точки.
на интервалах, выбрав пробные точки.
Для промежутка 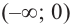 возьмем
возьмем 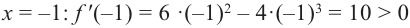
Для промежутка 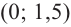 возьмем
возьмем 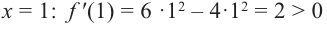
Для промежутка 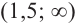 возьмем
возьмем 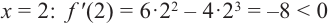

Используя полученную для функции 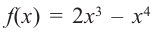 информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами
информацию и найдя значение функции еще в нескольких точках, можно построить график функции. При этом следует учитывать, что в точках с абсциссами 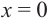 и
и 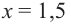 касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
касательная к графику горизонтальна. Построение графика можно проверить при помощи графкалькулятора.
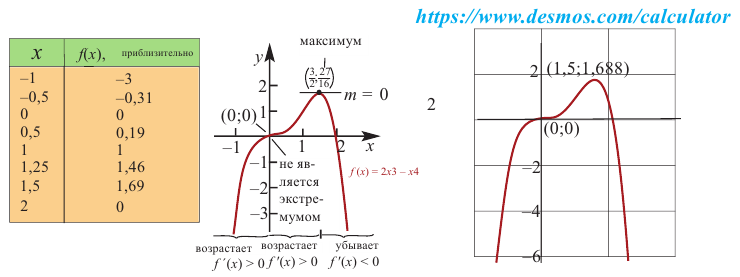
Пример №8
Найдите экстремумы функции 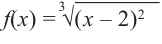
Решение: 1. Производная 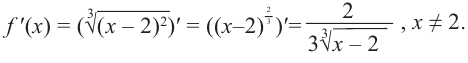
2. Критические точки: для этого надо решить уравнение 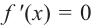 или найти точки, в которых производная не существует. В точке
или найти точки, в которых производная не существует. В точке 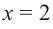 функция не имеет конечной производной. Однако точка
функция не имеет конечной производной. Однако точка 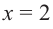 принадлежит области определения. Значит, точка
принадлежит области определения. Значит, точка 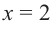 является критической точкой функции.
является критической точкой функции.
3. Промежутки, на которые критическая точка делит область определения функции: 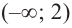 и
и 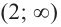
Определим знак 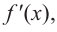 выбрав пробные точки для каждого промежутка:
выбрав пробные точки для каждого промежутка:
Для 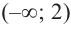 возьмем
возьмем 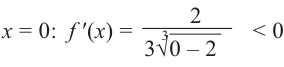
Для 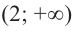 возьмем
возьмем 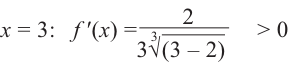

Пример №9
По графику функции производной 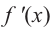 схематично изобразите график самой функции.
схематично изобразите график самой функции.
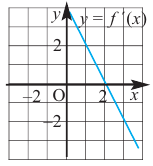
Решение:
Производная 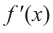 в точке
в точке 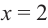 равна нулю, а при
равна нулю, а при 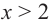 отрицательна, значит, на интервале
отрицательна, значит, на интервале 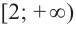 функция убывающая. При
функция убывающая. При 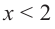 производная положительна, а это говорит о том, что функция/на промежутке
производная положительна, а это говорит о том, что функция/на промежутке 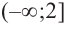 возрастает. Точкой перехода от возрастания к убыванию функции является точка
возрастает. Точкой перехода от возрастания к убыванию функции является точка 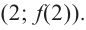 Соответствующий график представлен на рисунке.
Соответствующий график представлен на рисунке.
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция – многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
Пример:
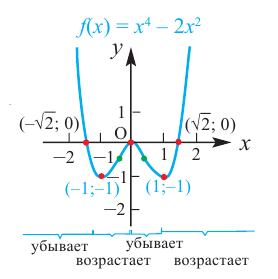
Постройте график функции 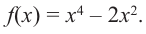
1) Точки пересечения с осями координат :
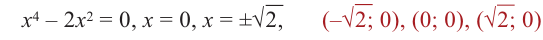
2) Критические точки ( точки, в которых производная равна нулю): 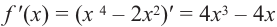
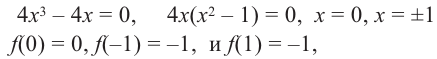
значит, точки 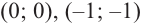 и
и 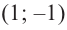 расположены на графике.
расположены на графике.
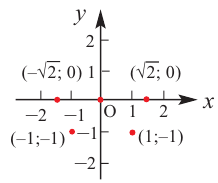
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 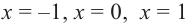 деляг область определения функции на четыре промежутка. Проверим знаки производной
деляг область определения функции на четыре промежутка. Проверим знаки производной 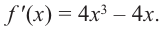

4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
Постройте график функции 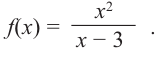
1) Область определения функции: 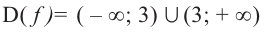
2) Асимптоты: 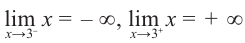
Прямая 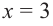 вертикальная асимптота функции.
вертикальная асимптота функции.
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее: 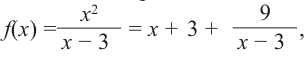
условии  имеем
имеем 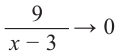 т. е. график функции
т. е. график функции 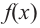 бесконечно приближается к прямой
бесконечно приближается к прямой 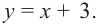 В этом случае прямая
В этом случае прямая 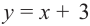 является наклонной асимптотой функции
является наклонной асимптотой функции 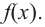 Вообще, если степень многочлена
Вообще, если степень многочлена 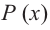 на 1 единицу больше степени многочлена
на 1 единицу больше степени многочлена 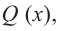 то рациональная функция
то рациональная функция 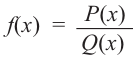 имеет наклонную асимптоту.
имеет наклонную асимптоту.
3) Точки пересечения с осями координат: 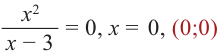
4) Критические точки:
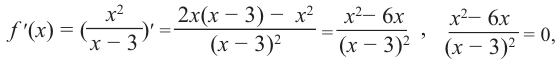
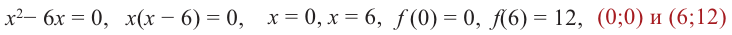
5) Промежутки возрастания и убывания: в точке 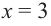 функция не определена, точки
функция не определена, точки 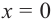 и
и 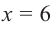 являются критическими точками функции. Определим знаки производной в каждом полученном интервале.
являются критическими точками функции. Определим знаки производной в каждом полученном интервале.

6) Построим график. Отметим на координатной плоскости точки 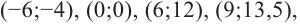 относящиеся к графику. Проведем вертикальную асимптоту
относящиеся к графику. Проведем вертикальную асимптоту 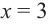 и наклонную асимптоту
и наклонную асимптоту 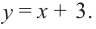 Используя полученные результаты, изобразим график функции.
Используя полученные результаты, изобразим график функции.
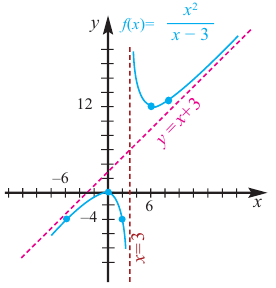
Обратите внимание! В области, близкой к точке 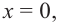 график функции ведет себя как парабола
график функции ведет себя как парабола 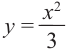
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 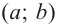 должны учитываться предельные значения функции на концах.
должны учитываться предельные значения функции на концах.
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума – наименьшее значение.
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 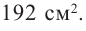 Найдите размеры коробки, при которых она будет иметь наибольший объем?
Найдите размеры коробки, при которых она будет иметь наибольший объем?
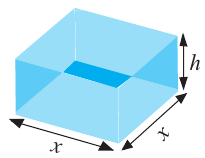
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 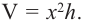 Используя другие данные задачи, выразим объем только через одну переменную
Используя другие данные задачи, выразим объем только через одну переменную 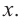 Вычислим площадь поверхности коробки. Она равна
Вычислим площадь поверхности коробки. Она равна 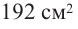 и состоит из 4 площадей боковых граней + площадь основания.
и состоит из 4 площадей боковых граней + площадь основания.
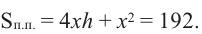
Тогда выразим 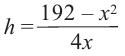 подставим в формулу
подставим в формулу 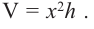 Зависимость объема коробки от переменной
Зависимость объема коробки от переменной 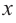 можно выразить следующим образом:
можно выразить следующим образом:
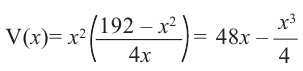
Теперь найдем область определения функции 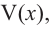 согласно условию задачи.
согласно условию задачи.
Понятно, что длина не может быть отрицательной, т. е. 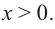 Площадь квадрата в основании коробки должна быть меньше 192, т. е.
Площадь квадрата в основании коробки должна быть меньше 192, т. е. 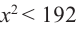
или 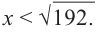 Значит,
Значит, 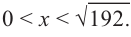
Найдем максимальное значение функции 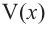 на интервале
на интервале 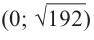
Для этого используем производную первого порядка:
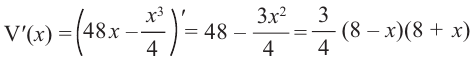
При 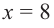 и
и 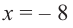 имеем, что
имеем, что 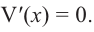
Однако. 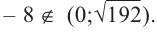 Значит, в рассматриваемом интервале критической точкой является
Значит, в рассматриваемом интервале критической точкой является 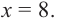
При 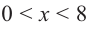 имеем
имеем 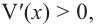 при
при 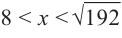 имеем
имеем 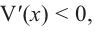 функция
функция
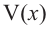 в точке
в точке 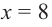 принимает максимальное значение.
принимает максимальное значение.
Если длина основания коробки будет 8 см, то высота будет равна
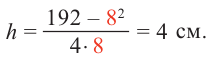
Значит, максимальный объем будет иметь коробка с размерами 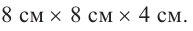
Построив при помощи графкалькулятора график функции 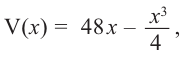 также можно увидеть, что при
также можно увидеть, что при 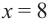 объем имеет максимальное значение. Постройте график функции при помощи производной и убедитесь в правильности решения.
объем имеет максимальное значение. Постройте график функции при помощи производной и убедитесь в правильности решения.
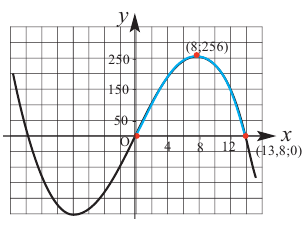
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
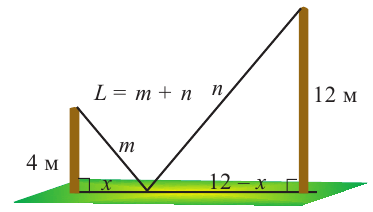
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
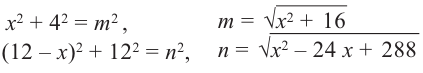
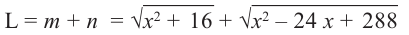
зависимость функции 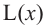 от переменной
от переменной 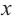 будет
будет
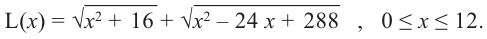
Производная функции 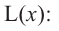
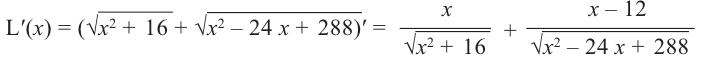
Найдем критические точки функции 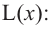
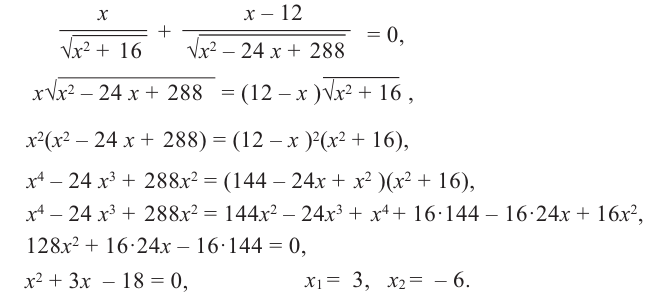
Сравнивая значения функции 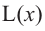 в точках
в точках 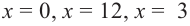 (это проверьте самостоятельно), получим, что наименьшее количество проволоки используется при
(это проверьте самостоятельно), получим, что наименьшее количество проволоки используется при 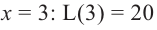 (метр)
(метр)
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 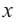 и выразите искомую величину функцией
и выразите искомую величину функцией 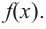 Найдите экстремумы данной функции.
Найдите экстремумы данной функции.
4. Полученные значения объясните экспериментально.
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250 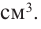
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 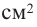 которого равна 0,05 гяпик, а для боковой поверхности используется материал цена 1
которого равна 0,05 гяпик, а для боковой поверхности используется материал цена 1 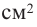 которого равна 0,12 гяпик. Какие размеры должна иметь банка, чтобы затраты на ее изготовление были минимальными?
которого равна 0,12 гяпик. Какие размеры должна иметь банка, чтобы затраты на ее изготовление были минимальными?
Решение: а) По условию задачи объем равен 250 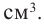 Эти данные дают нам возможность найти зависимость между
Эти данные дают нам возможность найти зависимость между 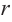 и
и 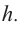
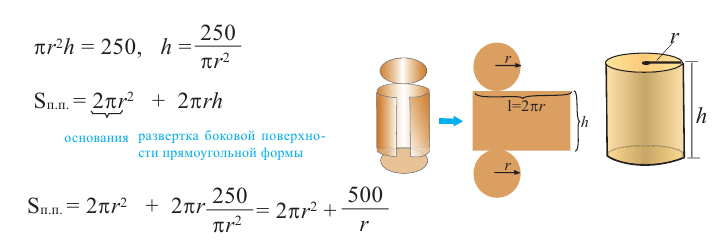
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 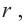 где
где 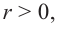 функция имеет наименьшее значение. Найдем производную функции
функция имеет наименьшее значение. Найдем производную функции 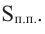
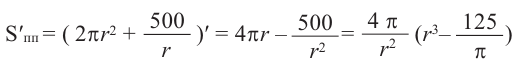 Критическая точка функции:
Критическая точка функции: 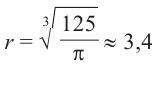 При
При 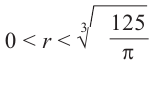 имеем
имеем 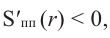 при
при 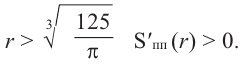
Значит, 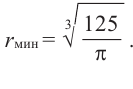
Подставим значение 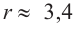 в формулу для высоты
в формулу для высоты 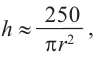 получим
получим 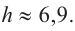
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 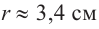 и
и 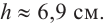
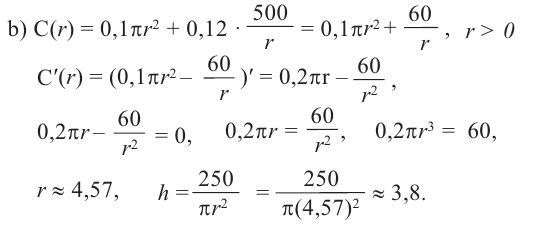
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
Рассмотрим задания из №6 ЕГЭ, в которых по графику функции требуется определить точки, в которых производная положительна либо отрицательна.
№1
На рисунке изображён график дифференцируемой функции y=f(x). На оси абсцисс отмечены восемь точек: x1, x2 ,x3, x4, … , x8. Среди этих точек найдите все точки, в которых производная функции f(x) положительна. В ответе укажите количество найденных точек.
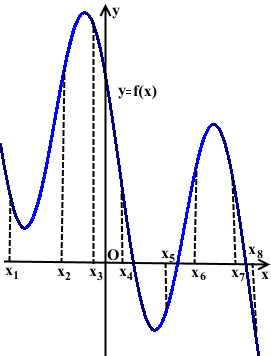
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает:
f'(x)>0, если f(x) возрастает.
Выделяем промежутки возрастания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам возрастания функции y=f(x) принадлежат три точки: x2, x5 и x6.
Значит, производная функции в этих трёх точках положительна:
f'(x2)>0,
f'(x5)>0,
f'(x6)>0.
Ответ: 3.
№2
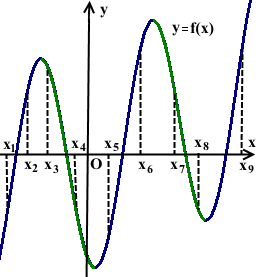 На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2 ,x3, x4 …x8, x9. В скольких из этих точек производная функции f(x) отрицательна?
На рисунке изображён график функции y=f(x) и отмечены девять точек на оси абсцисс: x1, x2 ,x3, x4 …x8, x9. В скольких из этих точек производная функции f(x) отрицательна?
Решение:
Производная функции f'(x) отрицательна там, где функция y=f(x) убывает:
f'(x)<0, если f(x) убывает.
Выделяем промежутки убывания функции y=f(x) и определяем количество точек, принадлежащих этим промежуткам.
Промежуткам убывания функции y=f(x) принадлежат четыре точки: x3, x4, x7 и x8. Значит, производная в этих четырёх точках отрицательна:
f'(x3)<0, f'(x4)<0, f'(x7)<0, f'(x8)<0.
Ответ: 4.
№3
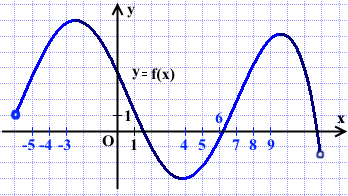 На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.
На рисунке изображен график функции y=f(x), определенной на интервале (−6; 12). Определите количество целых точек, в которых производная функции положительна.
Решение:
Производная функции f'(x) положительна там, где функция y=f(x) возрастает.
Выделяем промежутки возрастания.
Целые точки, входящие в промежутки возрастания: -5; -4; -3; 4; 5; 6; 7; 8; 9.
Всего девять точек.
Ответ: 9.
На этой странице вы узнаете
- Где проходит граница между теплом и холодом?
- Почему успех фильма не всегда зависит от наличия экшн-сцен?
- Чем кофе похож на функцию, ее первообразную и производную?
Многие из нас чем-то похожи на родителей. Не являясь их точной копией, мы перенимаем определенные черты. То же самое происходит и с графиками. О том, какие особенности “наследуют” друг у друга графики функции, производной и первообразной, поговорим в статье.
Связь графика функции и производной
Подготовим карандаши и линейки, мы начинаем погружение в мир графиков. Почему графики — это круто? Они дают нам наглядное представление о функции. Мы можем проанализировать ее, не прибегая к сложным формулам и трудоемким вычислениям.
Воспринимать визуальную информацию всегда легче. А графики — это как раз визуальное описание функции.
Возьмем график произвольной функции.
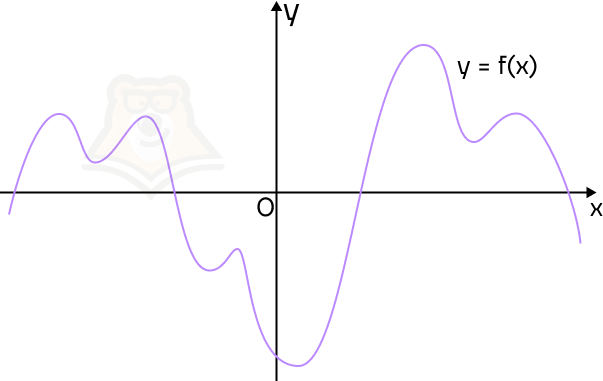
Прежде чем приступать к дальнейшему изучению материала, рекомендуем ознакомиться с «Определением и графиком функции», а также «Производной».
Мы точно видим, на каких промежутках график будет возрастать, а на каких убывать. Если представить, что мы пойдем по направлению оси х, то график будет возрастать на подъемах в горку и убывать на спусках с нее. Отметим промежутки возрастания зеленым фоном, а промежутки убывания красным.
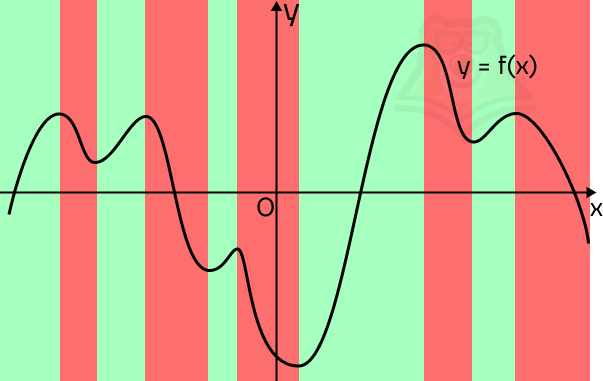
В зеленых промежутках производная будет положительна, а в красных отрицательна. Пока что просто запомним этот факт.
Обратим внимание на границы между зелеными и красными зонами. В этих точках функция будет менять свой знак с положительного на отрицательный или обратно. Такие точки называются точками экстремума.
Экстремум — это точка, в которой достигается максимальное или минимальное значение функции на заданном отрезке.
Точки экстремума — точки, в которых достигается экстремум.
В точках экстремума производная равна 0.
Теперь попробуем построить примерный график производной. Для начала опустим точки экстремума. Где они будут лежать на графике производной? На оси х.
Вспомним, что в точках экстремума производная функции будет равна 0. Пусть график будет задан
y = f'(x), тогда в точках экстремума получаем y = 0. Это и есть ось х.
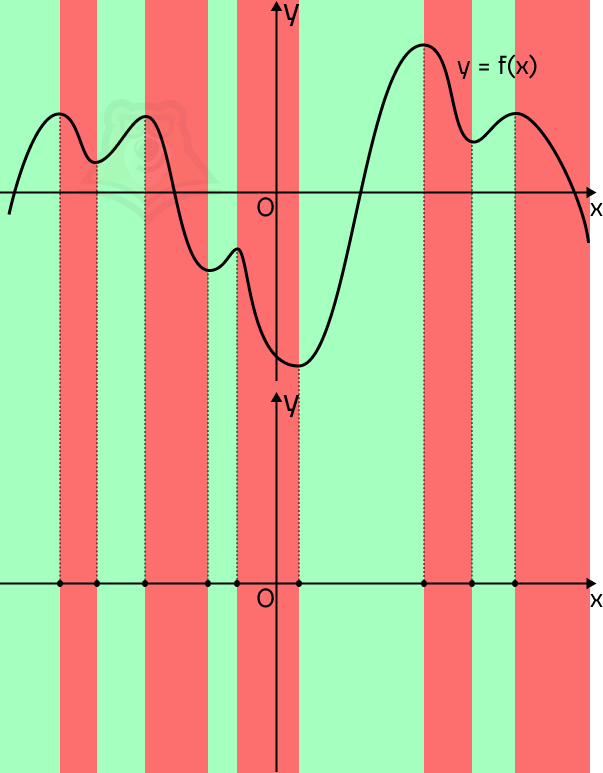
Так мы получили целых 9 точек, через которые пройдет производная. Осталось провести через них примерный график.
Вспомним, что:
- производная положительна на промежутках возрастания функции;
- производная отрицательна на промежутках убывания функции.
Как понять, что все точки на графике производной будут положительны или отрицательны? Достаточно посмотреть на то, с какой стороны от оси х они располагаются.
Положительные значения всегда будут лежать выше оси х. Это связано со значением y: значения функции будут положительны при положительных значениях у, и отрицательны при отрицательных значениях у.
Можно представить, что ось х — это полюс, который разделяет тропики и льды. Над осью х всегда будет светить солнце, а температура будет положительной. А вот под осью х всегда будут льды и снега, и температура — отрицательной.
Следовательно, знак производной на ее графике будет совпадать со знаком температуры в тропиках или льдах.
Итак, как нам нарисовать график производной? На зеленых участках ее график будет лежать над осью х, а на красных участках — под ней.
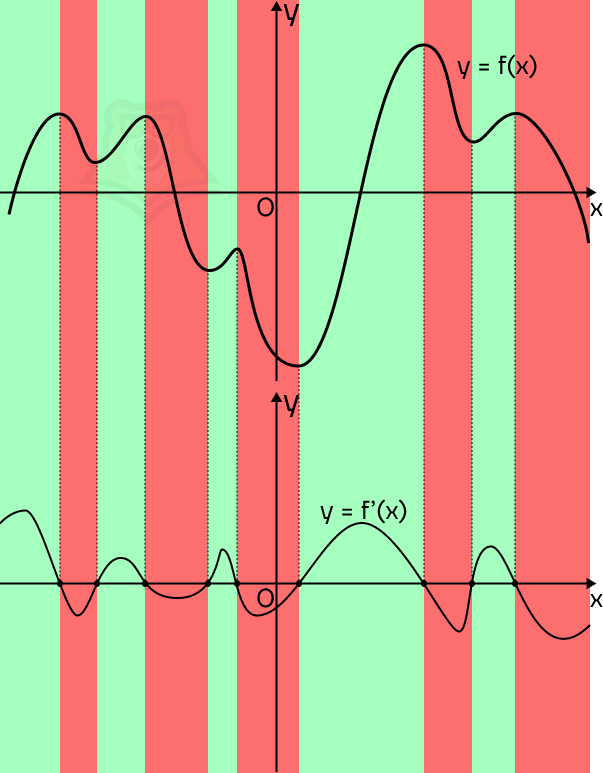
Подведем итоги:
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
Эти зависимости можно отследить на любых графиках функции и ее производной.
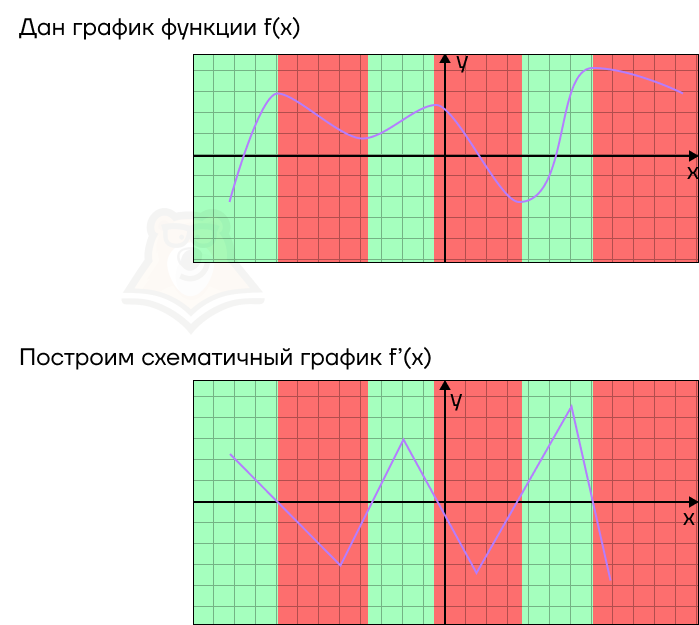
Если провести обратные рассуждения, то по графику производной можно восстановить примерный график функции. В этом случае:
- В точках, где график производной пересекает ось х, будут лежать точки экстремума. При этом если в точке производная меняет значение с положительного на отрицательное, то это точка максимума, а если с отрицательного на положительное, то это точка минимума.
- На промежутках, где график производной будет лежать выше оси х, функция будет возрастать.
- На промежутках, где график производной будет лежать ниже оси х, функция будет убывать.
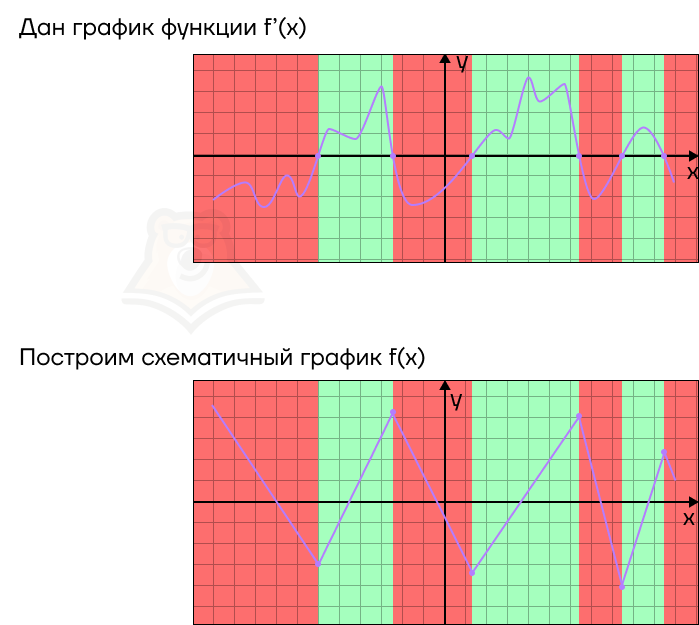
Разберем несколько примеров, где можно применить эти знания.
Пример 1. На рисунке изображен график функции f(x) и отмечены пять точек на оси абсцисс: x1, x2, x3, x4, x5. В скольких из этих точек производная функции отрицательна?
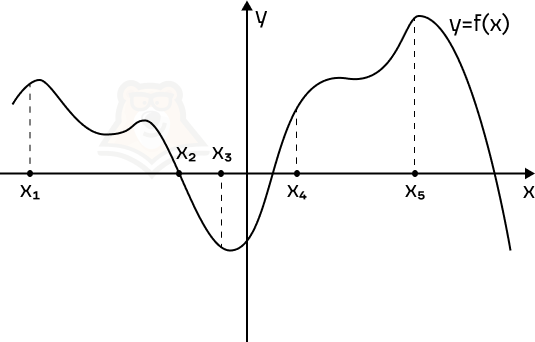
Решение. Производная отрицательна на промежутках убывания функции. Отметим такие промежутки.
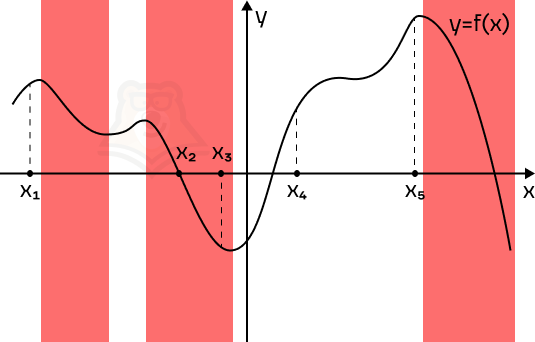
В точках, которые попали в эти промежутки, производная отрицательная. Всего таких точек 2.
Ответ: 2
Пример 2. На рисунке изображен график функции y = f'(x) — производной функции f(x), определенной на интервале (-5; 3). Найдите точку максимума функции f(x).
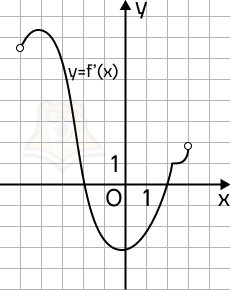
Решение. Точки экстремума на графике производной лежат на оси х. На данном графике таких точки две: x = -2, x = 2.
Точка максимума — это точка, в которой производная меняет знак с положительного на отрицательный. По графику определяем, что это точка x = -2.
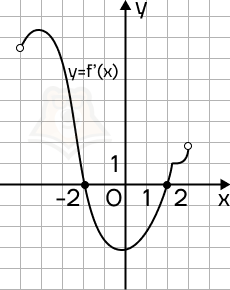
Ответ: -2
Представим, что мы составили графики “Заинтересованность зрителей фильмом” и “Наличие в фильме экшн-сцен”. Совпадут ли эти графики? Скорее всего, нет.
Экшн-сцены могут вызывать интерес у зрителей, равно как и романтические сцены или смешные повороты сюжета. Получается, что наличие экшн-сцен и заинтересованность фильмом — это разные величины в кинематографе, хотя и связаны между собой.
Также и графики производной и функции: они зависят друг от друга, но иллюстрируют совсем разные свойства функции, поэтому сильно отличаются.
Связь графика функции и первообразной
Мы разобрались, как связаны графики функции и ее производной. Есть ли связь между графиком функции и «Первообразной»?
Вспомним один важный факт: если взять производную от первообразной, то получим функцию.
F'(x) = f(x)
Похоже на функцию и ее производную, верно? На самом деле, ситуации ничем не отличаются.
В этом случае изначальной функцией будет первообразная, а ее производной — функция. Для наглядности составим таблицу.
| Было | Взяли производную | Стало | |
| Функция и производная | f(x) | f'(x) | f'(x) |
| Функция и первообразная | F(x) | F'(x) | f(x) |
Получается, для функции и первообразной будут действовать почти те же правила, что и для функции и ее производной.
При решении заданий с графиками первообразной достаточно проанализировать уравнение F'(x) = f(x). Рассмотрим несколько примеров.
Пример 3. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x) и отмечены шесть точек на оси абсцисс x1, x2, x3, x4, x5, x6. В скольких из этих точек функция f(x) отрицательна?
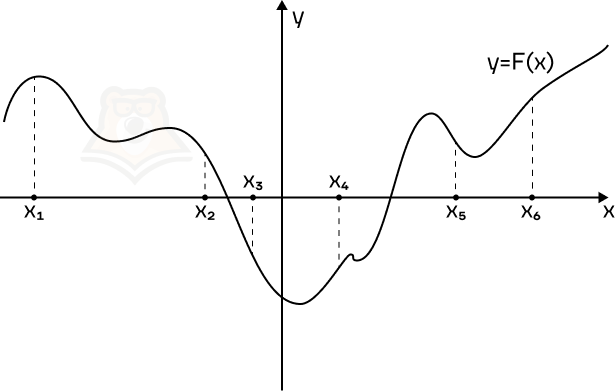
Решение. Поскольку F'(x) = f(x), то функция f(x) будет отрицательна в тех же точках, в которых будет отрицательна F'(x).
Поскольку на графике изображена функция y = F(x), то ее производная будет отрицательна на промежутках убывания функции. Отметим их красным.
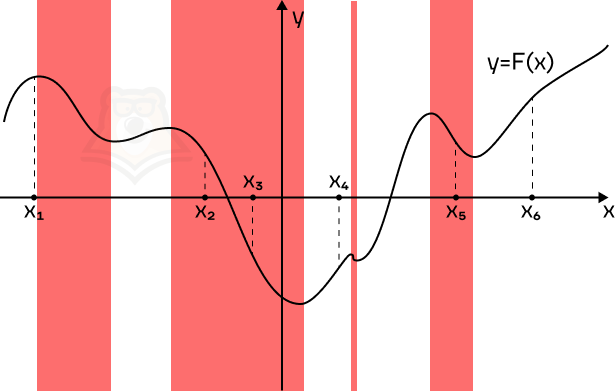
В эти промежутки попадают 3 из 6 точек.
Ответ: 3.
Пример 4. На рисунке изображен график функции y = F(x) — одной из первообразных функции f(x), определенной на интервале (-6; 7). Пользуясь рисунком, определите количество решений уравнения f(x) = 0 на отрезке [-5; 4].
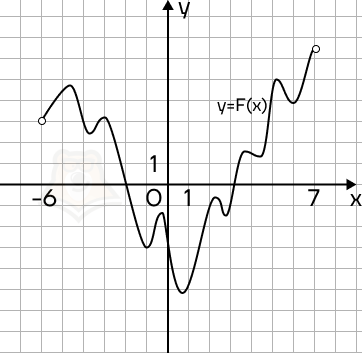
Решение. Вспомним, что F'(x) = f(x). Тогда если f(x) = 0, то и F'(x) = 0. Следовательно, на заданном промежутке нужно найти точки экстремума.
Отметим заданный промежуток красными линиями. На промежутке всего 9 точек экстремума, значит, в 9 точках f(x) будет равна 0.
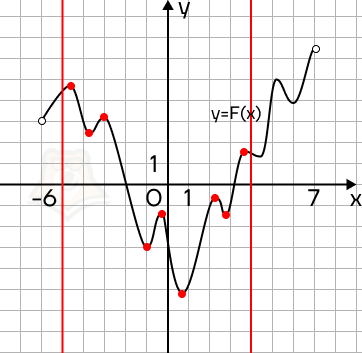
Ответ: 9
Представим, что в качестве функции у нас выступают кофейные зерна. Тогда производная — то, что мы получаем в результате их переработки — это вкусный напиток.
Из чего получаются сами кофейные зерна? Их собирают с кофейного дерева. То есть зерна будут производной от кофейного дерева, а кофейное дерево — это первообразная.
Так мы можем отследить следующую цепочку: кофейное дерево → кофейные зерна → кофе. И эта цепочка наглядно иллюстрирует связь первообразной, функции и ее производной.
Фактчек
- Графики функции, производной и первообразной связаны между собой.
- В точках экстремума функции график производной будет проходить через ось х.
- На промежутках возрастания функции график производной будет лежать выше оси х.
- На промежутках убывания функции график производной будет лежать ниже оси х.
- Для решения задач с первообразной необходимо вспомнить, что F'(x) = f(x). Любой график можно проанализировать с помощью этого уравнения также, как анализируются графики функции и ее производной.
Проверь себя
Задание 1.
На каких промежутках будет производная функции будет положительна?
- На промежутках убывания функции.
- На промежутках возрастания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 2.
На каких промежутках производная функции будет отрицательна?
- На промежутках возрастания функции.
- На промежутках убывания функции.
- В точках экстремума.
- Невозможно определить по графику.
Задание 3.
На рисунке изображен график производной функции f(x), на котором отмечена точка. Чем будет являться эта точка для функции f(x)?
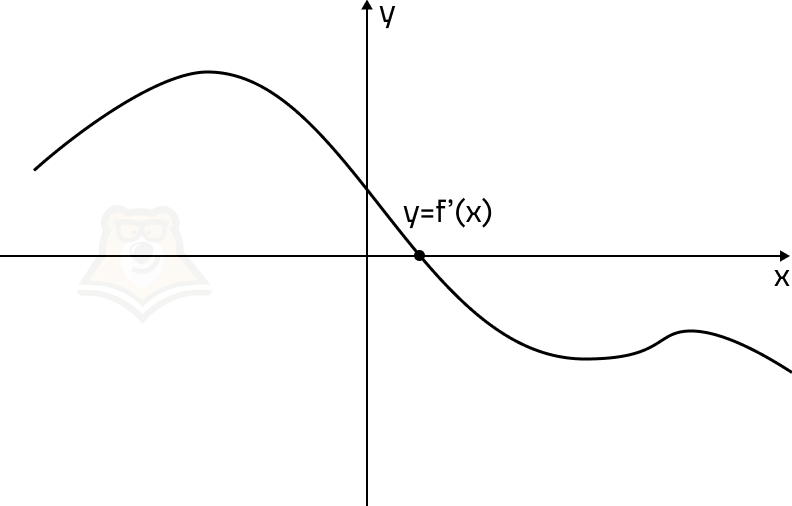
- Точка максимума функции.
- Точка минимума функции.
- Любая произвольная точка на функции.
- Невозможно определить по графику.
Задание 4.
Выберите верный вариант:
- F(x) = f'(x)
- F(x) = f(x)
- F'(x) = f'(x)
- F'(x) = f(x)
Ответы: 1. — 2 2. — 2 3. — 1 4. — 4
