Как найти в задачи среднее арифметическое

Определить среднюю скорость
можно и по-другому – сначала найти расстояния, пройденные с одной скоростью,
затем сложить эти расстояния и результат разделить на время.

На рисунке видно, что первые
три часа скорость автомобиля не менялась. Тогда можно найти расстояние,
пройденное за три часа:

66,2 × 3 = 198,6 км.

Аналогично можно определить
расстояние, которое было пройдено со скоростью 
78,4
км/час. В задаче сказано, что с такой скоростью автомобиль двигался  2 час.

78,4 × 2 = 156,8 км.

Сложим эти расстояния и результат разделим
на  5.

ЗАДАЧА:

План урока:

Понятие среднего арифметического

Алгоритм нахождения среднего арифметического

Интересные факты

Понятие среднего арифметического

К сестрам Марине, Наталье, Елене в гости приехала бабушка. Она привезла своим внучкам гостинцы: восемнадцать конфет, шесть шоколадок, шесть киндер-сюрпризов. Сказала угощение разделить поровну. Определите, сколько сладостей достанется каждой девочке?

Ответ на вопрос, можно получить двумя способами. Рассмотрим их.

1 

Чтобы выяснить, сколько сладостей достанется одной девочке, нужно каждый вид угощения разделить поровну – на 3.

Разделим конфеты между детьми:

18 : 3 = 6.

Теперь известно, что каждому ребенку досталось 6 конфет.

Разделим шоколадки:

6 :3 = 2.

Каждой внучке досталось две шоколадки.

Разделим шоколадные яйца:

6 : 3 = 2.

Выяснили, бабушка привезла по два киндер-сюрприза.

Стало известно, сколько гостинцев получил один ребенок. Теперь, вычислим, сколько сладостей досталось каждой девочке. Сложим количество конфет(6), шоколадок(2), киндер-сюрпризов(2), имеющихся у одной девочки:

6+2+2=10.

Получается, бабушка привезла по 10 сладостей.

Запишем решение задачи.

Как видите, способ, довольно простой, ноимеет длинную запись, занимает много времени. Рассмотрим второй способ решения задач такого вида.

2

Известно, сколько гостинцев привезла бабушка: конфет–восемнадцать, шоколадок – шесть, киндер-сюрпризов – шесть.  Чтобы узнать количество гостинцев, доставшееся каждой сестре, сложим гостинцы и разделим поровну. То есть, суммируем привезенные подарки, делим на 3. Такой способ решения, имеет название в математике – «Нахождение среднего арифметического». Сформулируем, определение, среднего арифметического:

Среднее арифметическое нескольких чисел – результат деления суммы этих чисел на их количество

Используя, рассмотренное определение, найдем общее количество угощения, для этого сложим количество сладостей каждого вида конфеты + шоколадки + киндеры:

18+6+6=30.

Получается, что всего было 30 угощений. Теперь, эту сумму(30) делим на количество слагаемых(3), использованных в сумме:

30 : 3 =10.

Каждой внучке досталось по 10 сладостей.

Запишем решение этой задачи с использованием второго способа.

Как видите, второй способ, более краткий и удобный. Главное – запомнить изученное определение. Ведь, решение задач такого вида часто встречается на протяжении всего учебного процесса!

Алгоритм нахождения среднего арифметического

Рассмотрим следующую задачу.

Два брата-садовода продавали собранные фрукты. Первый брат продал яблок на 25000 рублей, а второй брат продал груш на сумму 15000 рублей. Все заработанные деньги братья разделили поровну. Сколько денег заработал каждый садовод?

Чтобы ответить на вопрос, необходимо использовать изученное правило.

Чтобы найти среднее арифметическое нескольких чисел, нужно сумму этих чисел разделить на их количество. Для этого:
1. Определяем количество слагаемых;
2. Находим сумму всех слагаемых;
3. Делим полученную сумму на количество слагаемых

В начале давайте определим количество слагаемых. Так как фрукты продавали два садовода, то и делить выручку будем между ними. То есть количество слагаемых в сумме – два.

Теперь можем найти общую сумму, заработанную братьями. Для этого, складываем выручку первого и второго брата:

25000+15000=40000

Всего они заработали 40000 рублей.

Зная, что общая сумма равна 40000 рублей, мы можем найти сумму заработка каждого садовода. Для этого полученную сумму (40000) делим на количество слагаемых (2):

40000 : 2 = 20000.

Получается, заработок садовода составил 20000 рублей.

В ходе решения данной задачи мы составили алгоритм нахождения среднего арифметического.

Запомни!

Алгоритм вычисления среднего арифметического:
1. Находим слагаемые и считаем их количество;
2. Суммируем все слагаемые;
3. Полученную сумму делим на количество слагаемых

Держи табличку всегда под рукой, тогда сможешь найти среднее арифметическое любых чисел!

Выполним задание.

Найди среднее арифметическое чисел 10,20,30,40.

Чтобы выполнить необходимые вычисления, вспоминаем,

среднее арифметическое – частное суммы всех слагаемых и их количества

Мы уже знаем, что для вычисления заданий, такого вида, существует специальный алгоритм. Используя данный алгоритм,выполним все необходимые действия.

Следуя  определенному алгоритму, мы без труда выполнили задание.

Запомни формулу среднего арифметического!

В заключение нашего урока рассмотрим еще одну задачу.

Исходя из условия, в этой задаче нужно найти среднее количество учеников в одном классе. Чтобы ответить на главный вопрос, необходимо воспользоваться алгоритмом вычисления среднего арифметического.

Значит, если бы во всех пятых классах школы, училось равное количество учеников, в каждом классе было по 25 детей.

Запишем решение.

Сегодня вы узнали, как найти среднее арифметическое число. Внимательно рассмотрите урок, и запомните основные определения и алгоритмы! Тогда, любая контрольная будет по плечу!

Интересные факты

1. По статистике, дети улыбаются 400 раз в день, а взрослые всего 17. Улыбайтесь чаще!

1. В России продолжительность жизни мужчин составляет 70 лет, женщин – 78 лет!

1. Ежедневно в Росси рождается 5000 детей.

1. Ученые подсчитали, за всю жизнь, человек тратит 5 лет на процесс приема пищи,

1. Ученые подсчитали,  за 70 лет, человек поглощает более 50000 килограммов пищи, в том числе около 200-300 килограммов поваренной соли. Так же, каждый человек, достигший 70 летнего возраста,  выпил за всю жизнь 50000 литров воды, что больше в 1400 раз массы  человеческого тела.

1. Одной хорошей шариковой ручкой можно написать 50000 слов.

Когда трескается стекло, трещина распространяется со скоростью 5000 км/ч.

Пример:

Найти среднее арифметическое 2, 3 и 4.

Обозначим среднее арифметическое буквой «m». По определению выше найдем сумму всех чисел.

2 + 3 + 4 = 9

Разделим полученную сумму на количество взятых чисел. У нас по условию три числа.

В итоге мы получаем формулу среднего арифметического:

Для чего нужно среднее арифметическое?

Кроме того, что его постоянно предлагают найти на уроках, нахождение среднего арифметического весьма полезно и в жизни.

Например, вы решили продавать футбольные мячи. Но так как вы новичок в этом деле, совершенно непонятно по какой
цене вам продавать мячи.

Тогда вы решаете узнать, по какой цене в вашем районе уже продают футбольные мячи конкуренты. Узнаем цены
в магазинах и составим таблицу.

Магазин	Цена футбольного мяча
«Спорт-товары»	290 руб.
«Adidas»	360 руб.
«Все для футбола»	310 руб.

Цены на мячи в магазинах оказались совсем разные. Какую цену для продажи футбольного мяча нам лучше выбрать?

Если выбрать самую низкую (290 руб.), то мы будем продавать
товар себе в убыток. Если выбрать самую высокую (360 руб.), то покупатели не будут приобретать футбольные мячи у нас.

Нам нужна средняя цена. Здесь на помощь приходит среднее арифметическое.

Вычислим среднее арифметическое цен на футбольные мячи:

Средняя цена = =
= 320 руб.

Таким образом, мы получили среднюю цену (320 руб.), по которой мы можем продавать футбольный мяч не слишком дёшево и не
слишком дорого.

Средняя скорость движения

Со средним арифметическим тесно связано понятие средней скорости движения.

Наблюдая за движением транспорта в городе, можно заметить, что машины, то
разгоняются и едут с большой скоростью, то замедляются и едут с
маленькой скоростью.

Таких участков на пути следования автотранспорта бывает много. Поэтому
для удобства расчётов, используют понятие средней скорости движения.

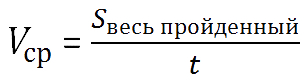
Рассмотрим задачу на среднюю скорость.

Разбор примера

Автомобиль двигался 3,2 ч по шоссе со скоростью 90 км/ч, затем
1,5 ч по
грунтовой дороге со скоростью 45 км/ч, наконец
0,3 ч по просёлочной дороге со скоростью 30 км/ч.
Найдите среднюю скорость движения автомобиля на всём пути.

Для расчёта средней скорости движения нужно знать весь путь, пройденный автомобилем,
и всё время, которое автомобиль двигался.

S₁ = V₁t₁

S₁ = 90 · 3,2 = 288 (км)

— шоссе.

S₂ = V₂t₂

S₂ = 45 · 1,5 = 67,5 (км)

— грунтовая дорога.

S₃ = V₃t₃

S₃ = 30 · 0,3 = 9 (км)

— просёлочная дорога.

S = S₁ + S₂ + S₃

S = 288 + 67,5 + 9 = 364,5 (км)

— весь путь, пройденный автомобилем.

t = t₁ + t₂ + t₃

t = 3,2 + 1,5 + 0,3 = 5 (ч)

— всё время.

V_ср = S : t

V_ср = 364,5 : 5 = 72,9

(км/ч) — средняя скорость движения автомобиля.

Ответ: V_ср = 72,9 (км/ч) — средняя скорость движения автомобиля.

---

Ваши комментарии

Оставить комментарий:

---

Среднее арифметическое

Среднее арифметическое – это частное от деления суммы чисел на их количество.

Из данных примеров можно сделать вывод, что для нахождения среднего арифметического, нужно сложить все числа и поделить их сумму на их количество.

Рассмотрим задачи, в которых требуется найти средне арифметическое нескольких чисел, относящихся к одной величине.

На этом уроке мы узнаем, что называют средним
арифметическим чисел. Узнаем, как находят среднее арифметическое. Узнаем, для
чего используют среднее арифметическое.

Очень часто в жизни вы встречаетесь со словом «средний».

Например

И сегодня на уроке мы познакомимся с одним из них.

Задача

Алина, Катя и Марина решили сходить в кинотеатр на
премьеру фильма. У Алины с собой было 30
рублей, у Кати 68 рублей, а у Марины – 22 рубля. Сколько стоит билет на фильм, если
девочки потратили все свои деньги на покупку 3–ёх
билетов?

Решение

Следовательно, билет в кинотеатр стоит 40 рублей.
Число 40 является средним арифметическим.

Определение

Средним арифметическим
нескольких
чисел называется частное от деления суммы этих чисел на их количество.

Задача

Юле по математике поставили в первой четверти оценку
3, во второй – 4,
в третьей – 5 и в последней четверти – 3. Как вы думаете, какую оценку поставит Юле
учитель за год?

Решение

Запомним правило нахождения среднего
арифметического.

Чтобы посчитать среднее арифметическое
нескольких чисел, надо:

1.     Найти
сумму всех чисел.

2.     Полученную
сумму разделить на количество слагаемых.

С помощью среднего арифметического
находят урожайность полей, среднюю массу мелких однородных предметов,
среднюю скорость движения автомобиля и т.д..

Задача на нахождения средней скорости

Автомобиль двигался 2 часа со скоростью 90
км/ч и ещё 3 часа со скоростью 70 км/ч. С какой скоростью проехал бы автомобиль
это же расстояние за это же время, если бы двигался с одной и той же постоянной
скоростью?

Решение

Тот же ответ мы получим, если будем считать за
каждый час пути по отдельности:

Запомните, чтобы узнать среднюю скорость,
нужно всё расстояние разделить на время движения.

Как вы думайте, где
может пригодиться умение находить среднее арифметическое? Давайте с вами
вспомним, про такую науку, как статистика и профессию статистик.

Статистика
– это один из разделов математики. Она помогает нам накапливать и анализировать
информацию, делать выводы, планировать результат.

Статистики, то есть
специалисты в этой области математики, разными способами получают информацию о
тех или иных явлениях, результатах деятельности. Затем они данную информацию
подвергают математической обработке различными методами. Получаемые
статистиками данные используются государственными учреждениями для разработки
долгосрочных планов, определения объёмов производства и др. показателей.

Сегодня, мы узнаем, как среднее арифметическое
помогает статистам в обработке данных.

Задача

В таблице приведены результаты наблюдений за
популяцией птенцов колибри. Найдём, сколько в среднем выводит птенцов колибри.

Решение

Значит, колибри в среднем выводит по 2 птенца.

Итоги

Итак, сегодня на уроке мы узнали, что такое среднее
арифметическое, как его находят и для чего используют.